Basic Pick and Place
(part 2)

MIT 6.4210/2: Robotic Manipulation
Fall 2022, Lecture 4

Follow live at https://slides.com/d/auj49nI/live
(or later at https://slides.com/russtedrake/fall22-lec04)
Basic Pick and Place
Step 1: Kinematic Frames / Spatial Algebra

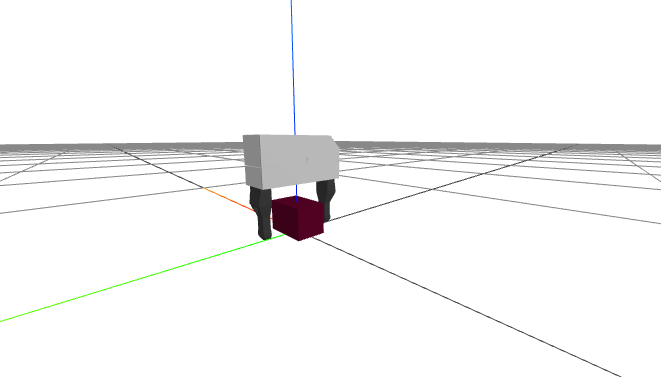
Step 2: Gripper Frame Plan "Sketch"
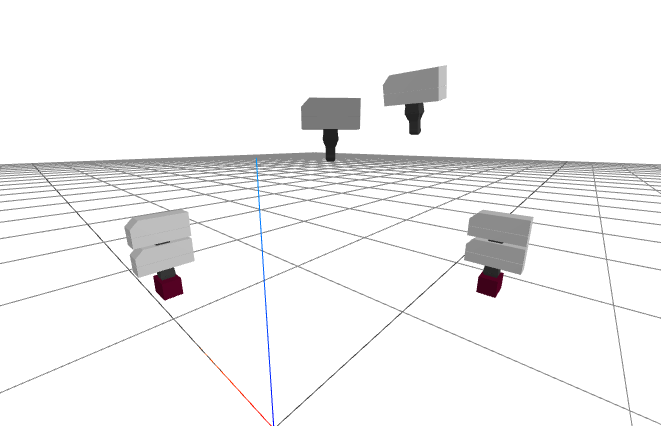
Step 3: Forward kinematics of the iiwa + WSG

X^B = f_{kin}^B(q)
generalized positions
pose of body (or frame) \(B\)
Representations for 3D Rotation
Check yourself: A single "free" body
plant = MultibodyPlant(time_step = 0.0)
Parser(plant).AddModelFromFile(FindResourceOrThrow(
"drake/examples/manipulation_station/models/061_foam_brick.sdf"))
plant.Finalize()
brick = plant.GetBodyByName("base_link")
context = plant.CreateDefaultContext()
X^B = f_{kin}^B(q)
What is \(X^B\) ?
X_B = plant.EvalBodyPoseInWorld(brick, context)What is \(q\) ?
q = plant.GetPositions(context)Step 4: Differential Kinematics

dX^B = \frac{\partial f_{kin}^B(q)}{\partial q} dq
= \underbrace{J^B(q)}dq
X^B = f_{kin}^B(q)
Kinematic "Jacobian"
Spatial Velocity
\frac{d}{dt} {}^AX^B_C \equiv \, ^AV^B_C = \begin{bmatrix}
{}^A\omega^B_C \\ {}^A\text{v}^B_C \end{bmatrix}
angular velocity
translational velocity
Q: How do we represent angular velocity, \(\omega^B\)??
(w_x, w_y, w_x)
A: Unlike 3D rotations, here 3 numbers are sufficient and efficient; so we use the same representation everywhere.
note the typesetting
Spatial Velocity Algebra
Check yourself: A single "free" body
plant = MultibodyPlant(time_step = 0.0)
Parser(plant).AddModelFromFile(FindResourceOrThrow(
"drake/examples/manipulation_station/models/061_foam_brick.sdf"))
plant.Finalize()
brick = plant.GetBodyByName("base_link")
context = plant.CreateDefaultContext()
\dot{q} = N(q) v
What is \(v\) ?
v = plant.GetVelocities(context)What is \(q\) ?
q = plant.GetPositions(context)v = plant.MapQDotToVelocity(context, qdot)qdot = plant.MapVelocityToQDot(context, v)For any MultibodyPlant (not just a single body):
Kinematics
- Forward kinematics: joint positions \(\Rightarrow\) pose
- Inverse kinematics*: pose \(\Rightarrow\) joint positions
-
Differential kinematics:
joint positions, velocities \(\Rightarrow\) spatial velocity
-
Differential inverse kinematics:
spatial velocity, joint positions \(\Rightarrow\) joint velocities
q \Rightarrow X^B
X^B \Rightarrow q
q, v \Rightarrow V^B
V^B, q \Rightarrow v
Our first Jacobian pseudo-inverse controller
plant.SetPositions(plant_context, iiwa, q)
J_G = plant.CalcJacobianSpatialVelocity(
plant_context, JacobianWrtVariable.kQDot,
G, [0,0,0], self._W, self._W)
J_G = J_G[:,0:7] # Ignore gripper terms
V_G_desired = np.array([0, # rotation about x
-.1, # rotation about y
0, # rotation about z
0, # x
-.05, # y
-.1]) # z
v_iiwa = np.linalg.pinv(J_G).dot(V_G_desired)
prog = MathematicalProgram()
x = prog.NewContinuousVariables(2)
prog.AddConstraint(x[0] + x[1] == 1)
prog.AddConstraint(x[0] <= x[1])
prog.AddCost(x[0] ** 2 + x[1] ** 2)
result = Solve(prog)