Motion Planning
Part II: Sampling-based
and global optimization

MIT 6.421
Robotic Manipulation
Fall 2023, Lecture 12
Follow live at https://slides.com/d/BghMcig/live
(or later at https://slides.com/russtedrake/fall23-lec12)
start
goal
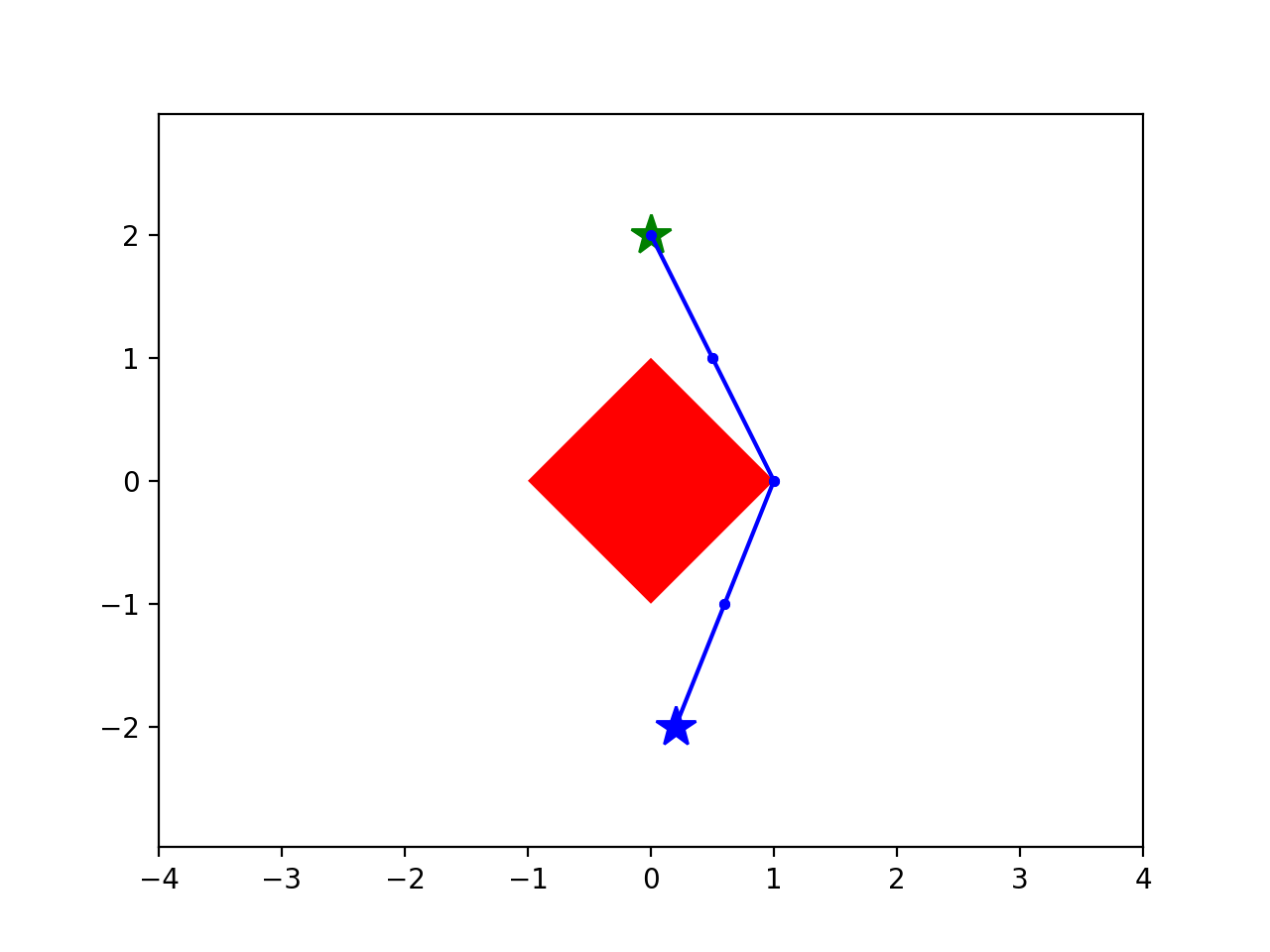
Motion planning as a (nonconvex) optimization

start
goal
fixed number of samples
collision-avoidance
(outside the \(L^1\) ball)
nonconvex

Rapidly-exploring random trees (RRTs)
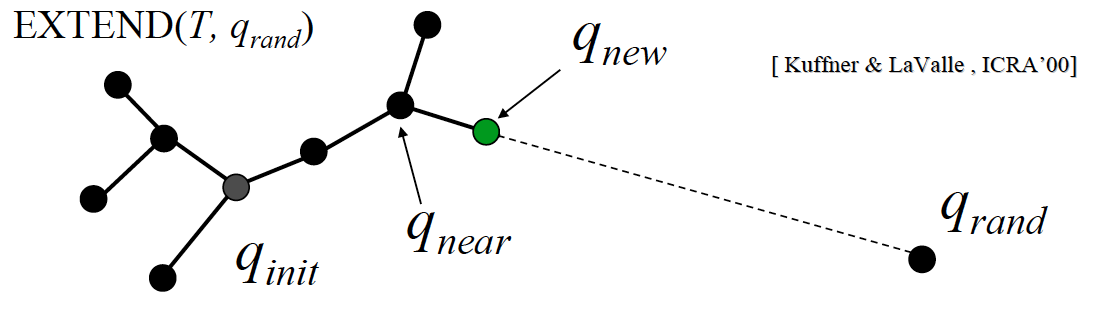
BUILD_RRT (qinit) {
T.init(qinit);
for k = 1 to K do
qrand = RANDOM_CONFIG();
EXTEND(T, qrand)
}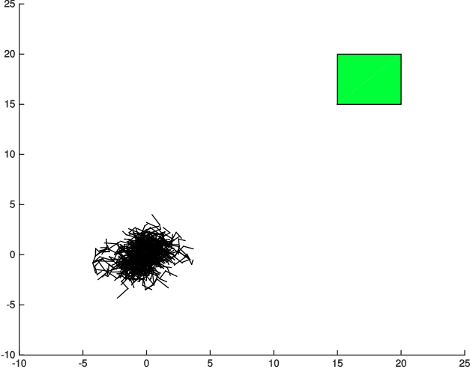
Naive Sampling
RRTs have a "Voronoi-bias"
goal
start
Amato, Nancy M., and Yan Wu. "A randomized roadmap method for path and manipulation planning." Proceedings of IEEE international conference on robotics and automation. Vol. 1. IEEE, 1996.
Probabilistic Roadmaps (PRMs)
"Multi-query" planner separates:
- Roadmap construction (offline)
- Graph search (online)
BUILD_ROADMAP () {
V = {}, E = {}
for k = 1 to K
repeat
q = RANDOM_CONFIG()
until q is collision free
V.insert(q)
for all q in V
for all qn in NearestNeighbors(q, V)
if {q,qn} is collision free
E.insert({q,qn})
}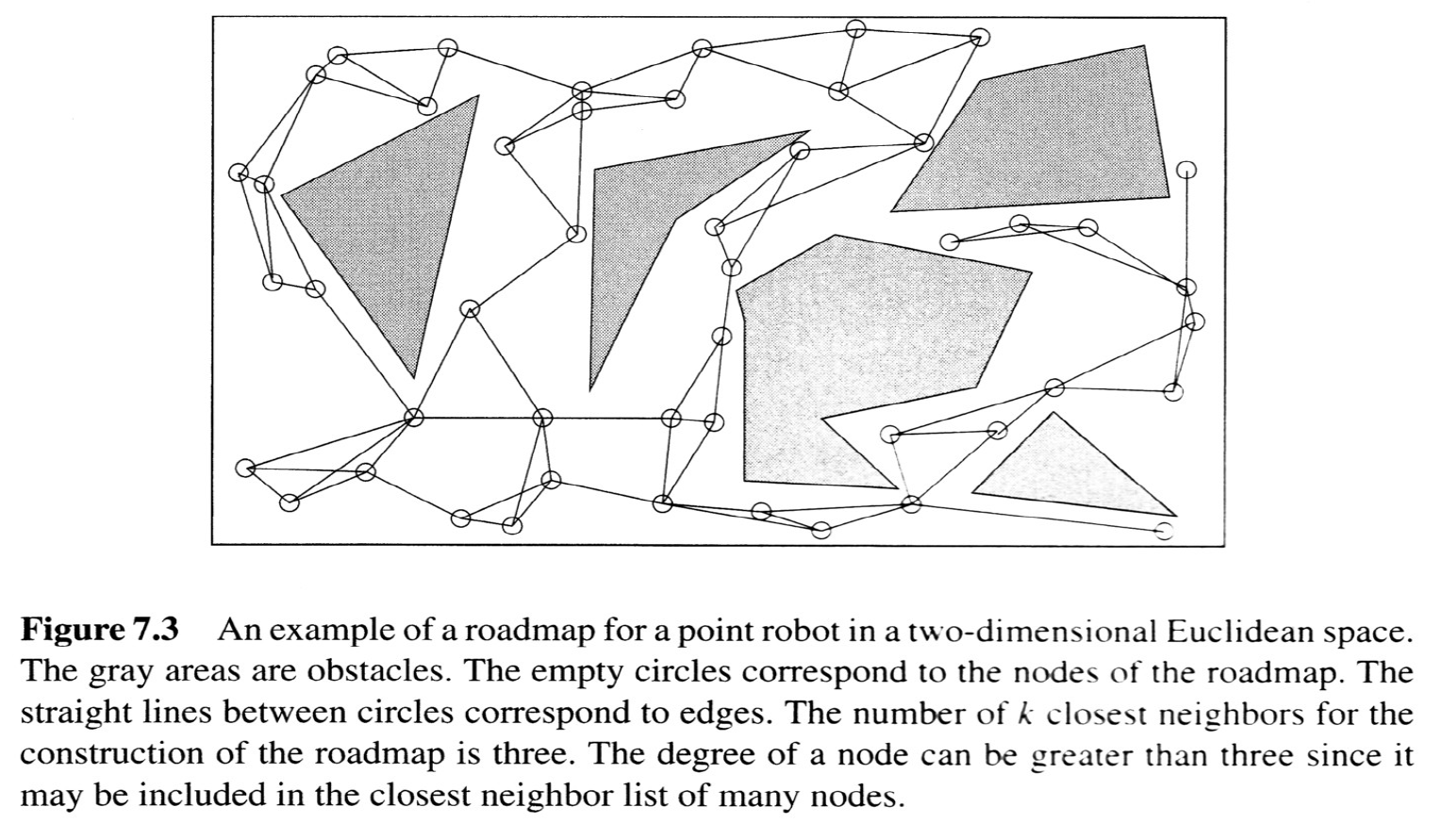
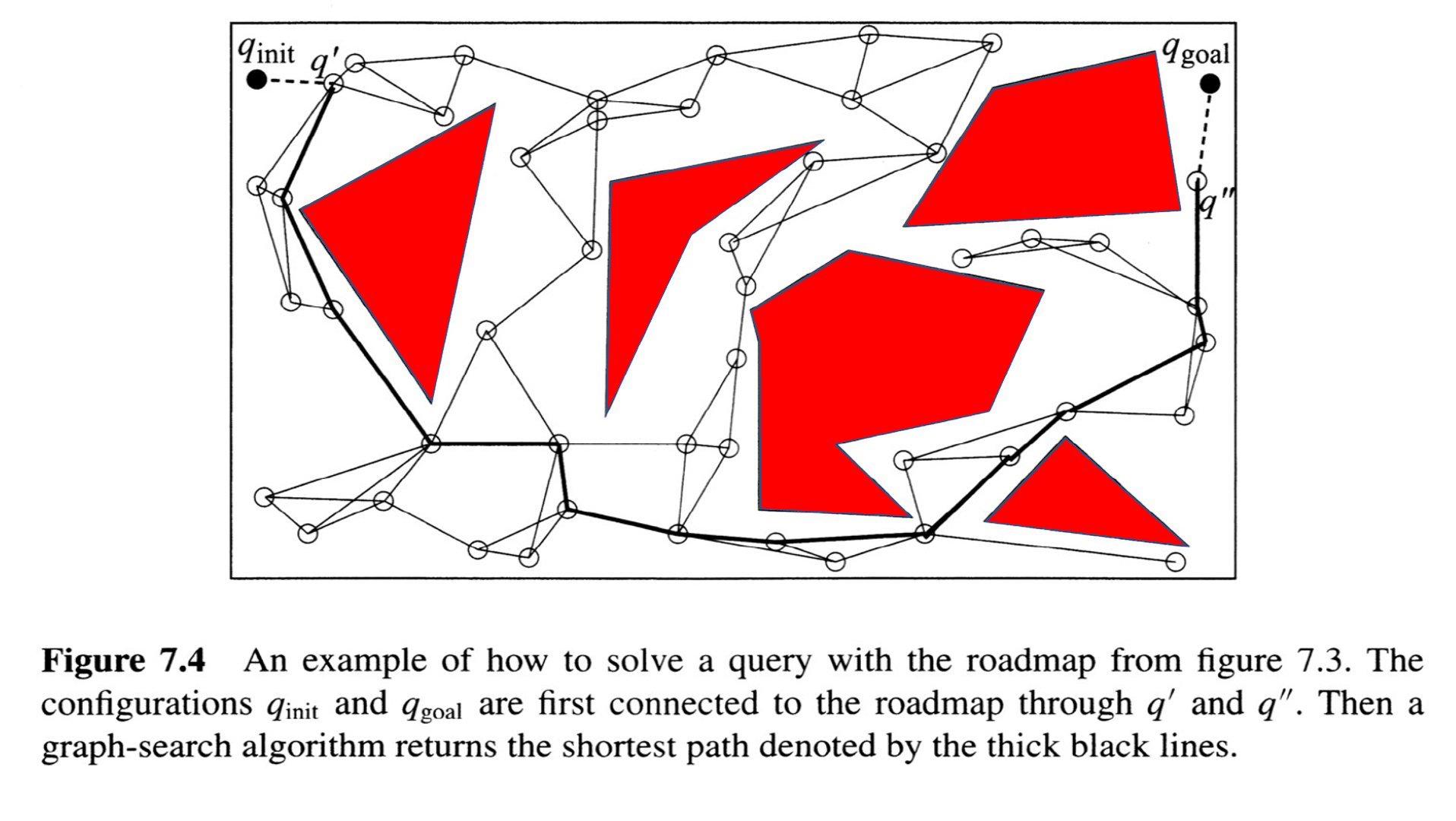
The Probabilistic Roadmap (PRM)
from Choset, Howie M., et al. Principles of robot motion: theory, algorithms, and implementation. MIT press, 2005.
The Probabilistic Roadmap (PRM)
from Choset, Howie M., et al. Principles of robot motion: theory, algorithms, and implementation. MIT press, 2005.


Open Motion Planning Library (OMPL)
Google "drake+ompl" to find some examples (on stackoverflow) of drake integration in C++. Using the python bindings should work, too.
Sampling-based planners coming to Drake
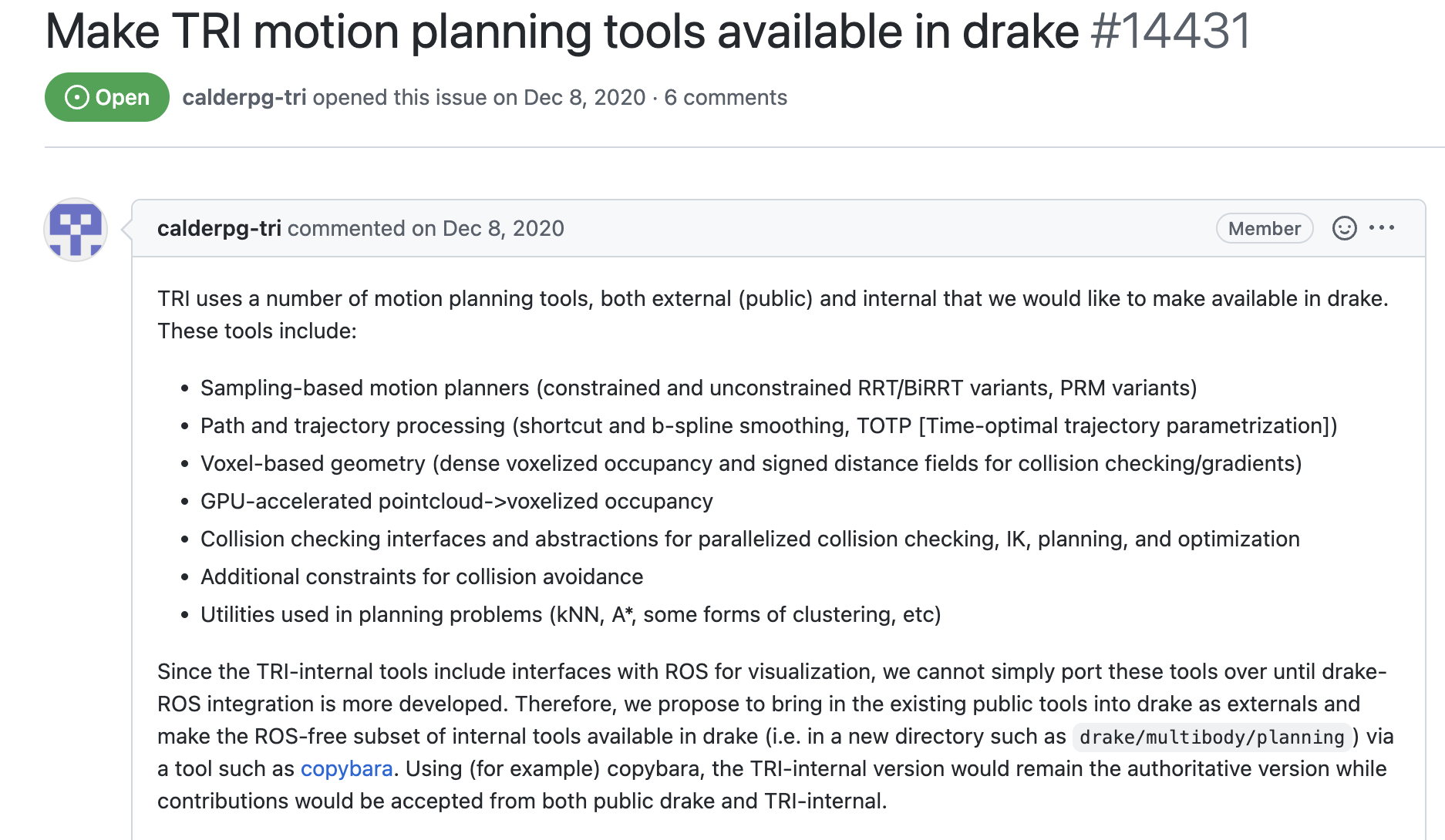
Sampling-based planners coming to Drake
/// Plans a path using a bidirectional RRT from start to goal.
PlanningResult PlanBiRRTPath(
const Eigen::VectorXd& start, const Eigen::VectorXd& goal,
const BiRRTPlannerParameters& parameters,
const CollisionCheckerBase& collision_checker,
const std::unordered_set<drake::multibody::BodyIndex>& ignored_bodies,
StateSamplingInterface<Eigen::VectorXd>* sampler);
/// Bidirectional T-RRT planner.
CostPlanningResult PlanTRRTPath(
const CostPlanningStateType& start, const Eigen::VectorXd& goal,
const TRRTPlannerParameters& parameters,
const CollisionCheckerBase& collision_checker,
const std::unordered_set<drake::multibody::BodyIndex>& ignored_bodies,
const MotionCostFunction& motion_cost_function,
StateSamplingInterface<Eigen::VectorXd>* sampler);
/// Roadmap creation and updating for kinematic PRM planning.
/// Generate a roadmap.
Graph<Eigen::VectorXd> BuildRoadmap(
int64_t roadmap_size, int64_t num_neighbors,
const CollisionCheckerBase& collision_checker,
const std::unordered_set<drake::multibody::BodyIndex>& ignored_bodies,
StateSamplingInterface<Eigen::VectorXd>* sampler);
/// Plans a path through the provided roadmap. In general, you should use the
/// *AddingNodes versions whenever possible to avoid copies of roadmap.
PlanningResult PlanPRMPath(
const Eigen::VectorXd& start, const Eigen::VectorXd& goal,
int64_t num_neighbors, const CollisionCheckerBase& collision_checker,
const std::unordered_set<drake::multibody::BodyIndex>& ignored_bodies,
const Graph<Eigen::VectorXd>& roadmap, bool parallelize = true);
Global optimization-based planning
Motion Planning around Obstacles with Convex Optimization.
Tobia Marcucci, Mark Petersen, David von Wrangel, Russ Tedrake.
Available at: https://arxiv.org/abs/2205.04422
Accepted for publication in Science Robotics
Motion planning with Graphs of Convex Sets (GCS)
Claims:
- Find better plans faster than sampling-based planners
- Avoid local minima from trajectory optimization
- Can guarantee paths are collision-free
- Naturally handles dynamic limits/constraints
- Scales to big problems (e.g. multiple arms)

start
goal
GCS Trajectory Optimization
Sampling-based motion planning
The Probabilistic Roadmap (PRM)
from Choset, Howie M., et al. Principles of robot motion: theory, algorithms, and implementation. MIT press, 2005.

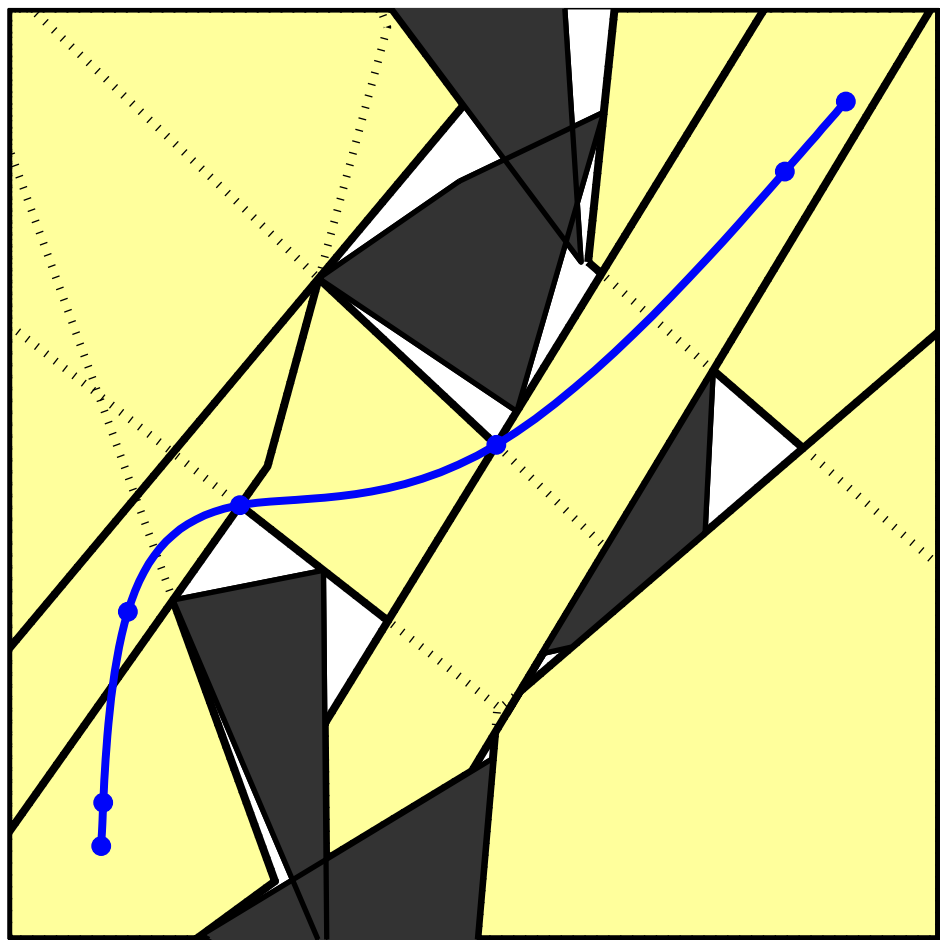
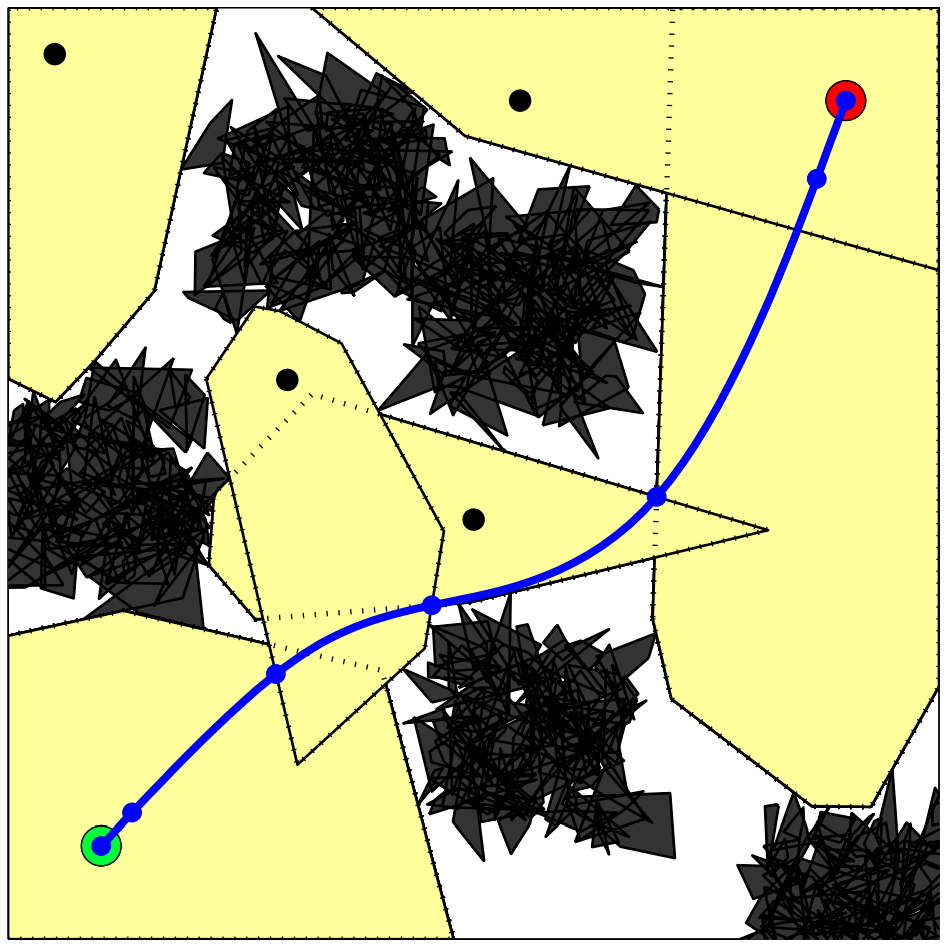
- PRM: A roadmap of points (vertices) connected by line segments
- GCS: A roadmap of convex sets (vertices) of continuous curves connected by continuity constraints
Key ingredients
- (Approximate) convex decomposition of collision-free configuration space. (aka "IRIS")
- Efficient algorithms for solving shortest paths on "Graphs of Convex Sets" (aka "GCS")
- Convex optimization over continuous curves w/ time scaling (\(\Rightarrow\) "GCS Trajectory Optimization")
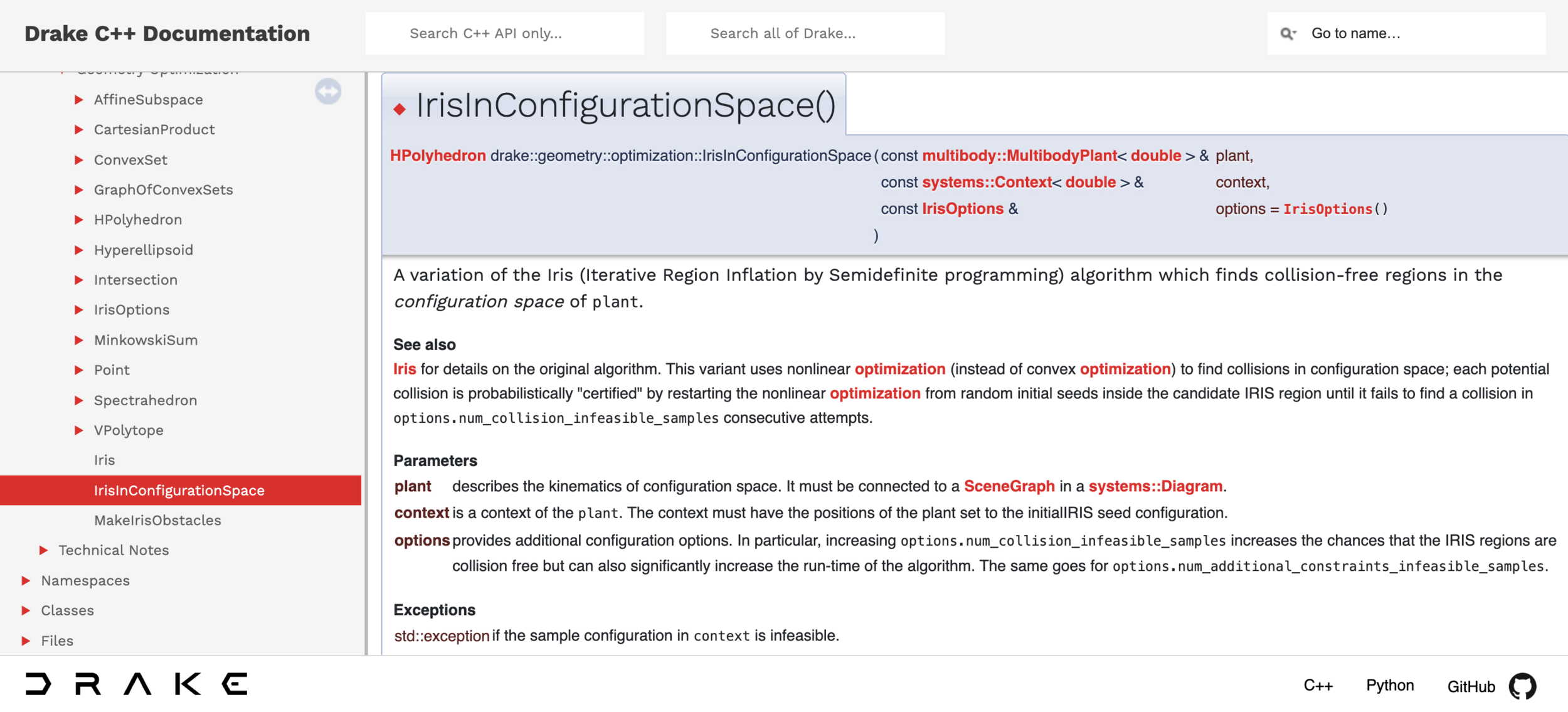
IRIS for Configuration-space regions
- IRIS (Fast approximate convex segmentation). Deits and Tedrake, 2014
- New versions work in configuration space:
- Nonlinear optimization for speed. IRIS-NP
- Sums-of-squares for rigorous certification. C-IRIS

Convex decomposition of configuration space
- Insight: Cliques in the visibility graph (almost) correspond to convex sets in configuration space
- Approach: (Approximate) minimum clique cover


(Approximate) Minimum clique cover

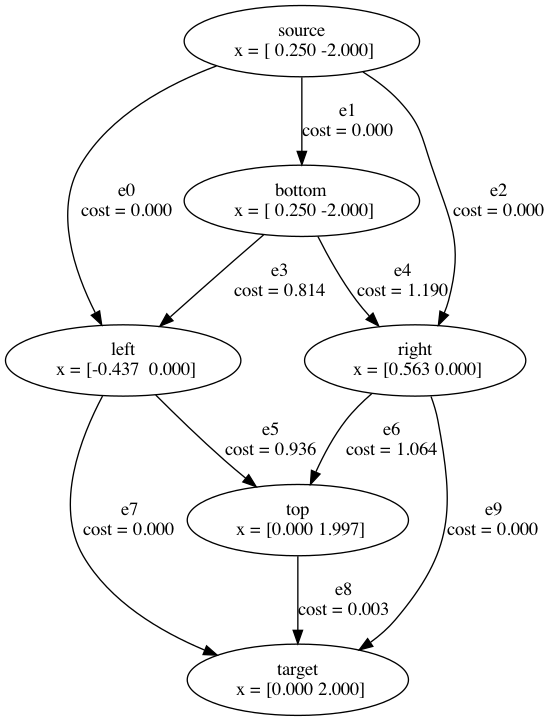
Graphs of Convex Sets


Note: The blue regions are not obstacles.
Graphs of Convex Sets


Mixed-integer formulation with a very tight convex relaxation
- Efficient branch and bound, or
- In practice we only solve the convex relaxation and round
Main idea: Multiply constraints + Perspective function machinery





+ time-rescaling
GCS Trajectory Optimization
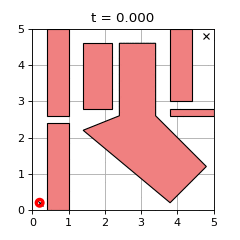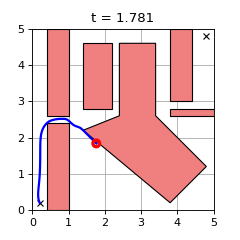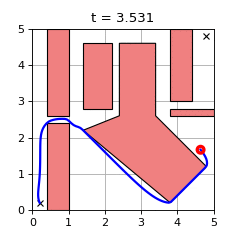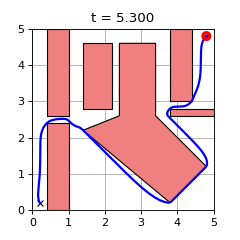
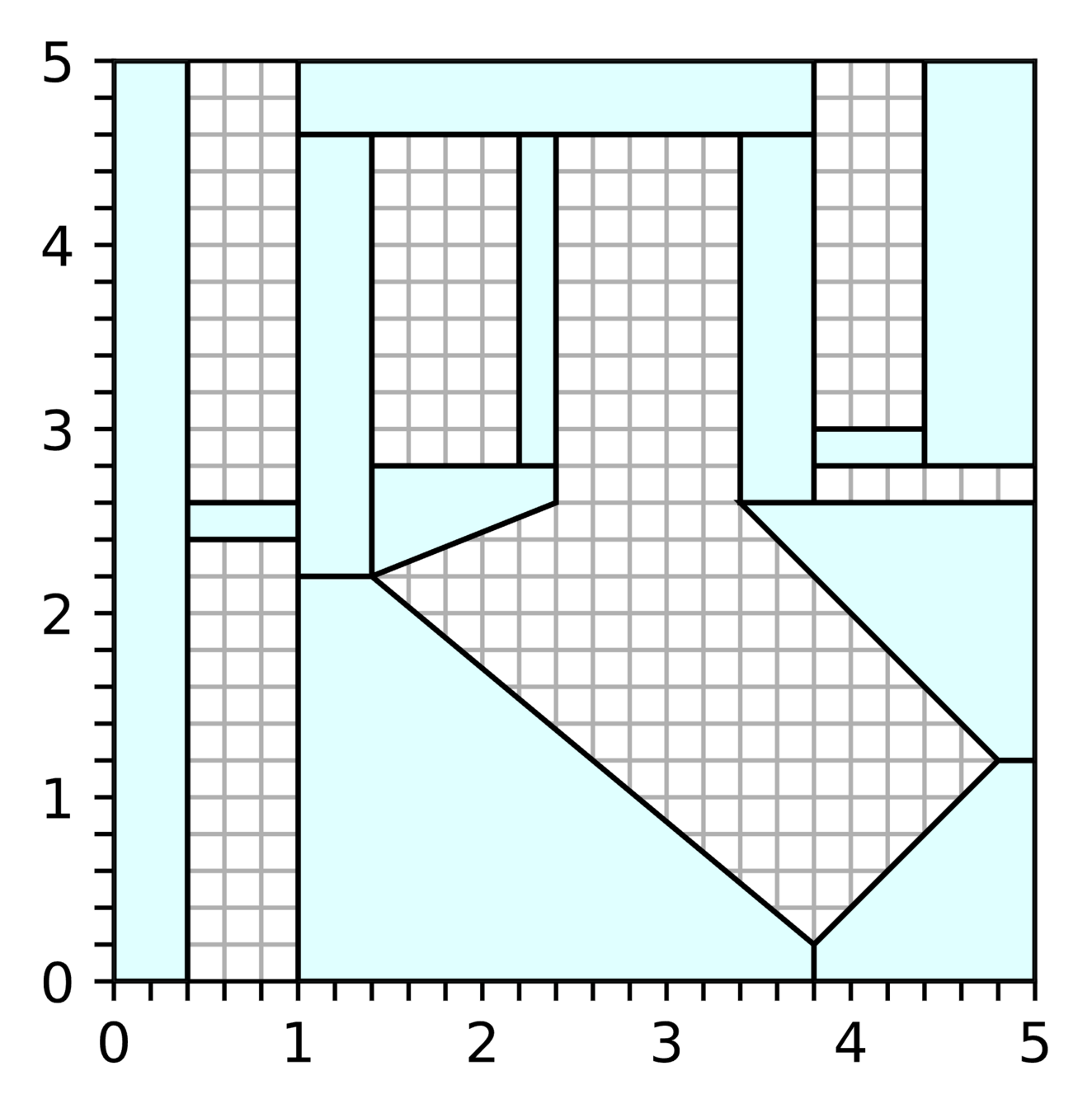
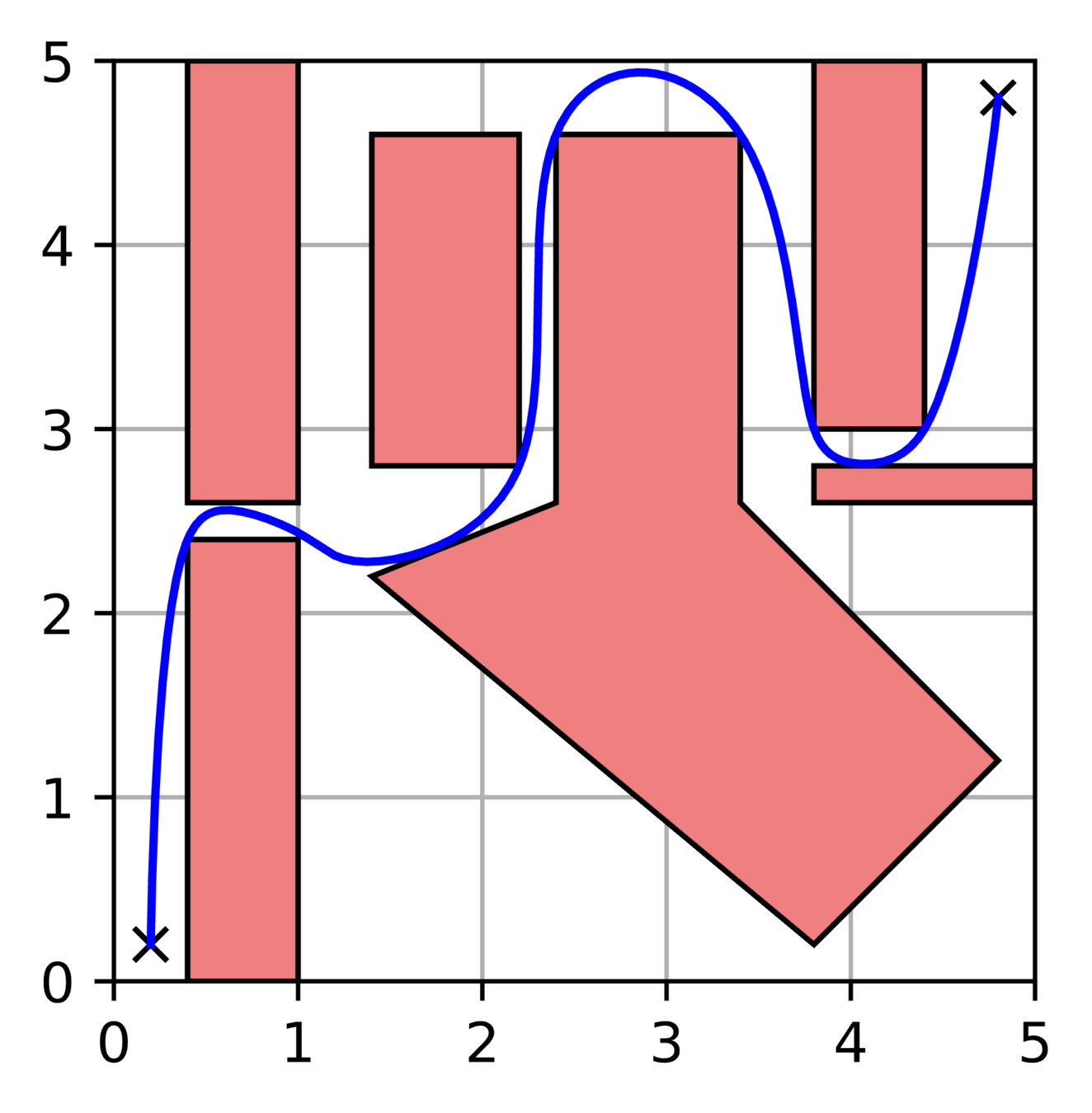
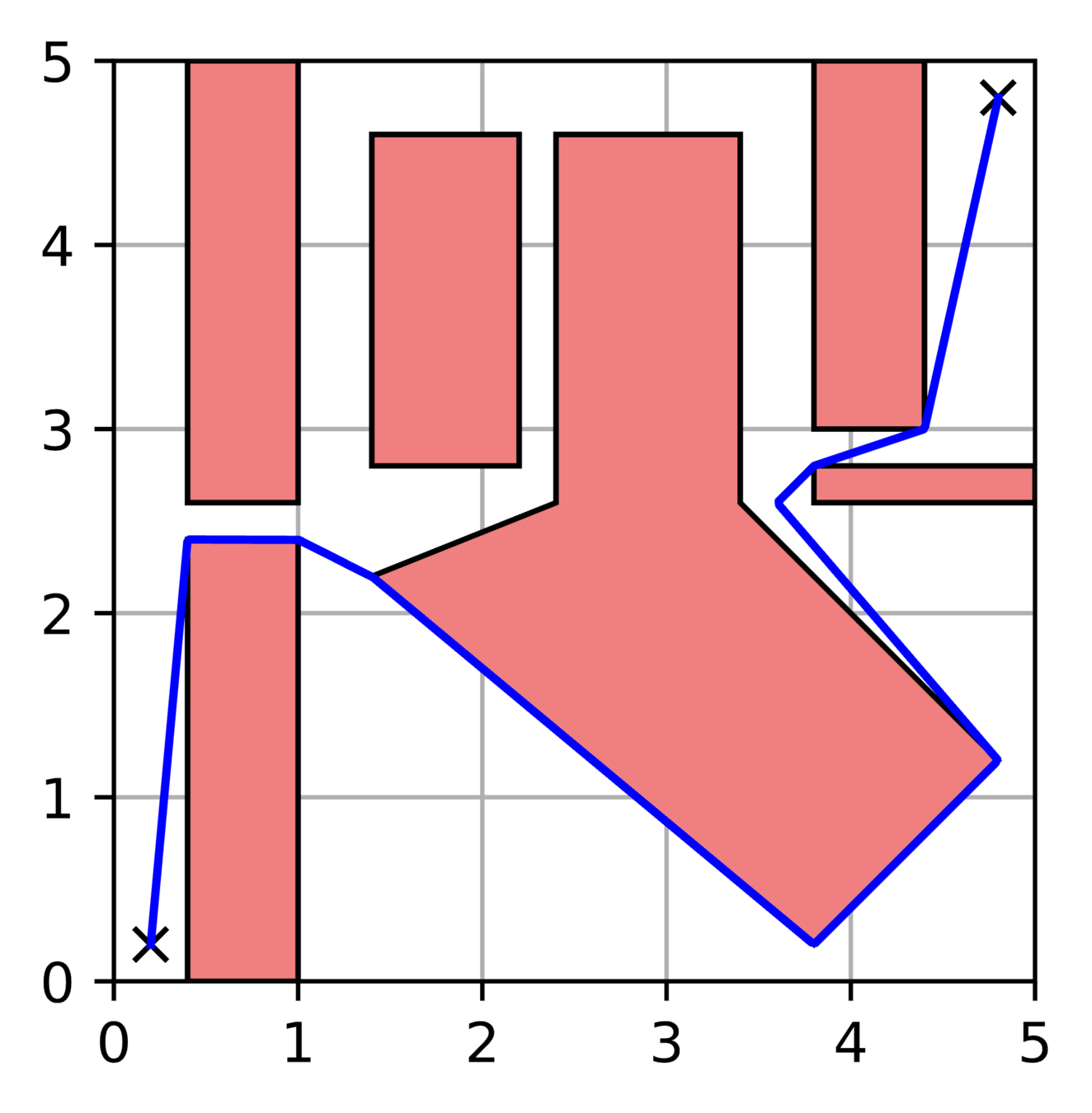
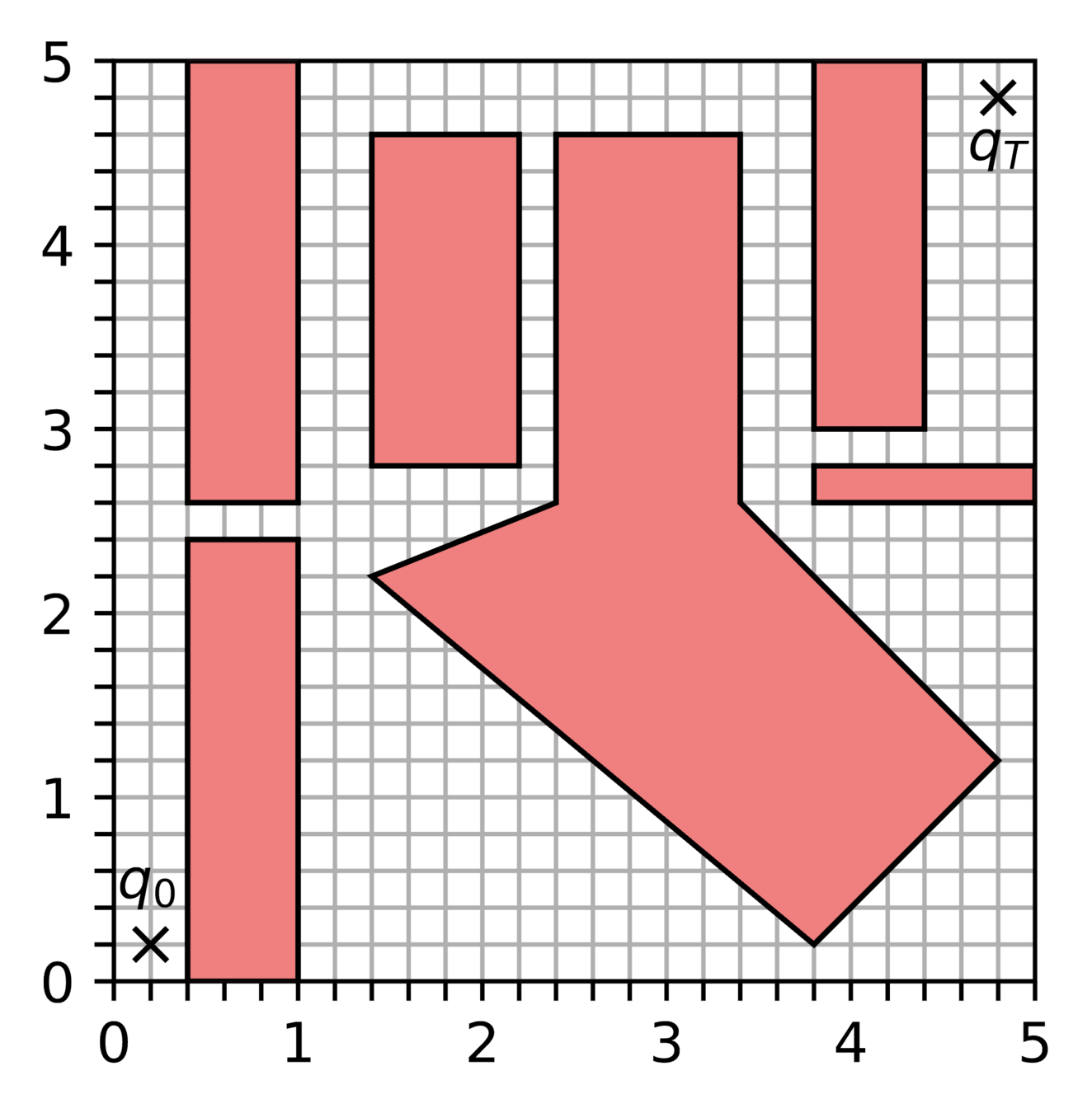
GCS Trajectory Optimization

Transitioning from basic research to real use cases
duration
path length
path "energy"
note: not just at samples
continuous derivatives
collision avoidance
velocity constraints
Graph of Convex Sets (GCS)
PRM
PRM w/ short-cutting


Preprocessor now makes easy optimizations fast!
Default playback at .25x
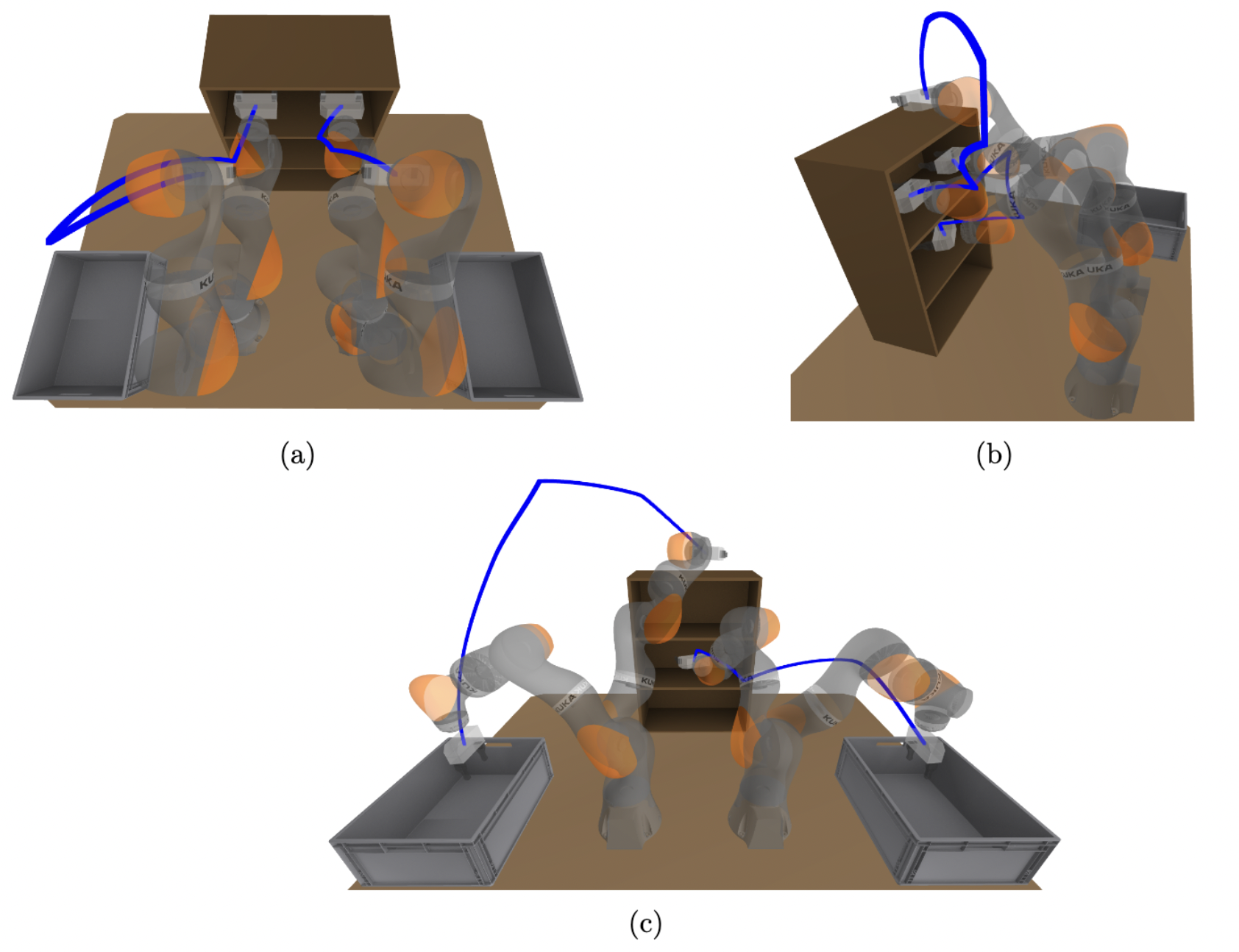
An early success story
An early success story

The Graph of Convex Sets (GCS) motion planning framework
Scaling
-
~10k regions in 3D
-
20k vertices and 400k edges.
- Online planning takes 0.3s
by Tobia Marcucci in collaboration w/ Stephen Boyd


PRM
GCS

Time-optimal rescaling

work w/ Mark Petersen

Having said all that...
I don't actually love "collision-free motion planning" as a formulation...

