Reinforcement Learning

(Part 2)

MIT 6.421:

Robotic Manipulation

Fall 2023, Lecture 20

Follow live at https://slides.com/d/HoT1aag/live

(or later at https://slides.com/russtedrake/fall23-lec20)

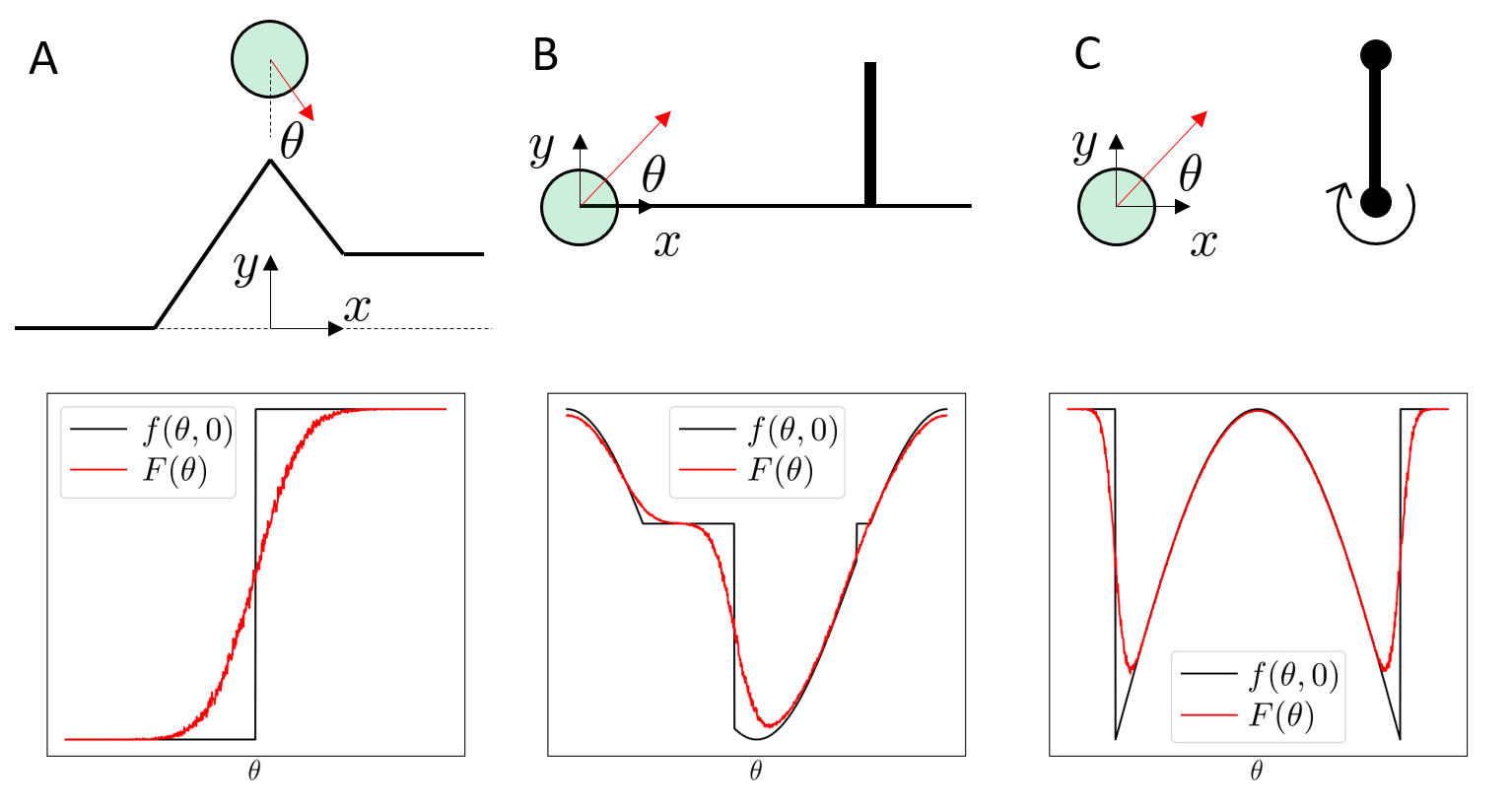
Beware "artificial" discontinuities

Do Differentiable Simulators Give Better Policy Gradients?

H. J. Terry Suh and Max Simchowitz and Kaiqing Zhang and Russ Tedrake

ICML 2022

Available at: https://arxiv.org/abs/2202.00817

Smoothing with stochasticity

\begin{gathered} \min_\theta f(\theta) \end{gathered}
\begin{gathered} \min_\theta E_w\left[ f(\theta, w) \right] \\ w \sim N(0, \Sigma) \end{gathered}

vs

Smoothing with stochasticity for Multibody Contact

Do Differentiable Simulators Give Better Policy Gradients?

The answer is subtle; the Heaviside example might shed some light.

\begin{gathered} \min_\theta f(\theta) \end{gathered}
\begin{gathered} \min_\theta E_w\left[ f(\theta, w) \right] \\ w \sim N(0, \Sigma) \end{gathered}

vs

Differentiable simulators give \(\frac{\partial f}{\partial \theta}\), but we want \(\frac{\partial}{\partial \theta} E_w[f(\theta, w)]\).

Randomized smoothing

J. Burke, F. E. Curtis, A. Lewis, M. Overton, and L. Simoes, Gradient Sampling Methods for Nonsmooth Optimization, 02 2020, pp. 201–225.

  • Approximate smoothed objective via Monte-carlo : \[ E_\mu \left[ f(x) \right] \approx \frac{1}{K} \sum_{i=1}^K f(x_i), \quad x_i \sim \mathcal{N}(\mu, \Sigma) \]
  • First-order gradient estimate \[ \frac{\partial}{\partial \mu} E_\mu \left[ f(x) \right] \approx \frac{1}{K} \sum_{i=1}^K \frac{\partial f(\mu + w_i)}{\partial \mu}, \quad w_i \sim \mathcal{N}(0, \Sigma) \]

 

  • Zero-order gradient estimate (aka REINFORCE) \[ \frac{\partial}{\partial \mu} E_\mu \left[ f(x) \right] \approx \frac{1}{K} \sum_{i=1}^K \left[f(\mu + w_i) - f(\mu)\right] w_i, \quad w_i \sim \mathcal{N}(0, \Sigma) \]

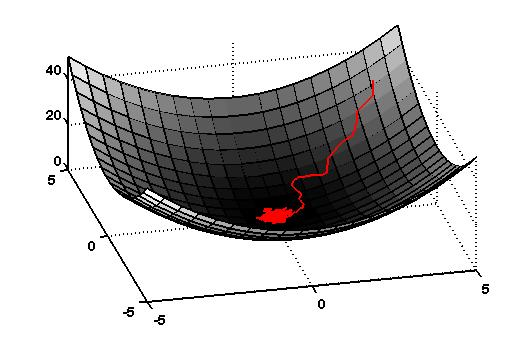
Lessons from stochastic optimization

  1. The two gradient estimates converge to the same quantity under sufficient regularity conditions.


     
  2. Convergence rate scales directly with variance of the estimators, zero-order often has higher variance.

But the regularity conditions aren't met in contact discontinuities, leading to a biased first-order estimator.

Often, but not always.

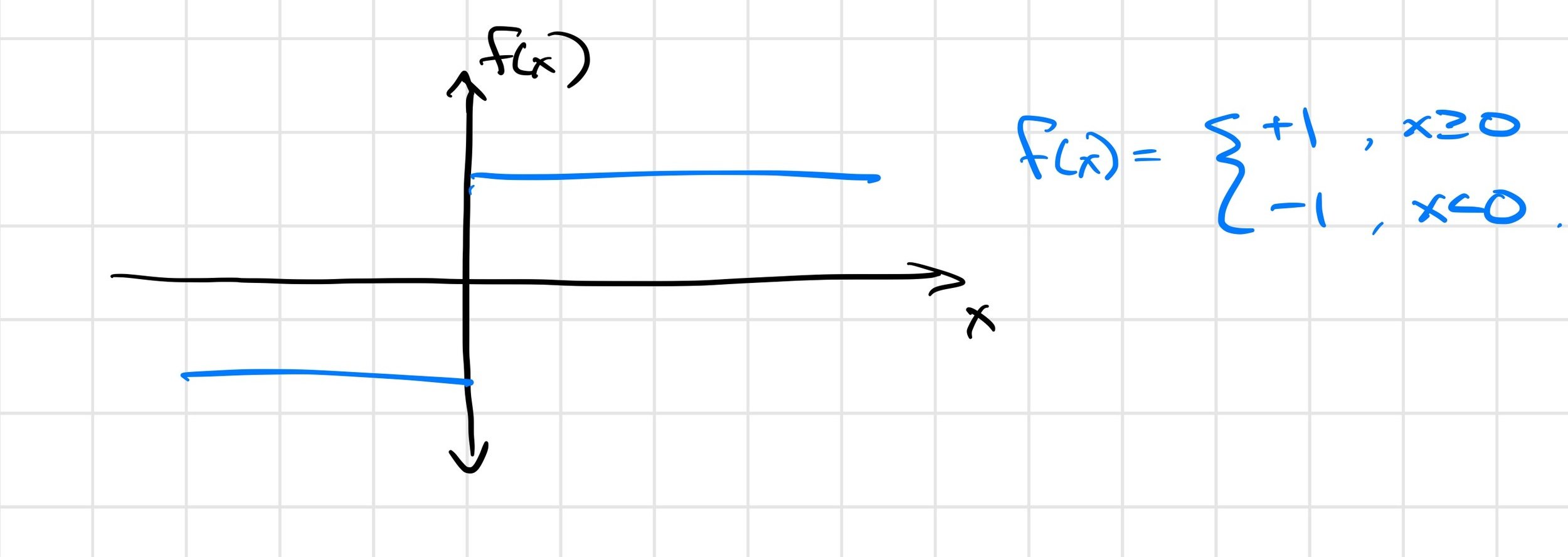
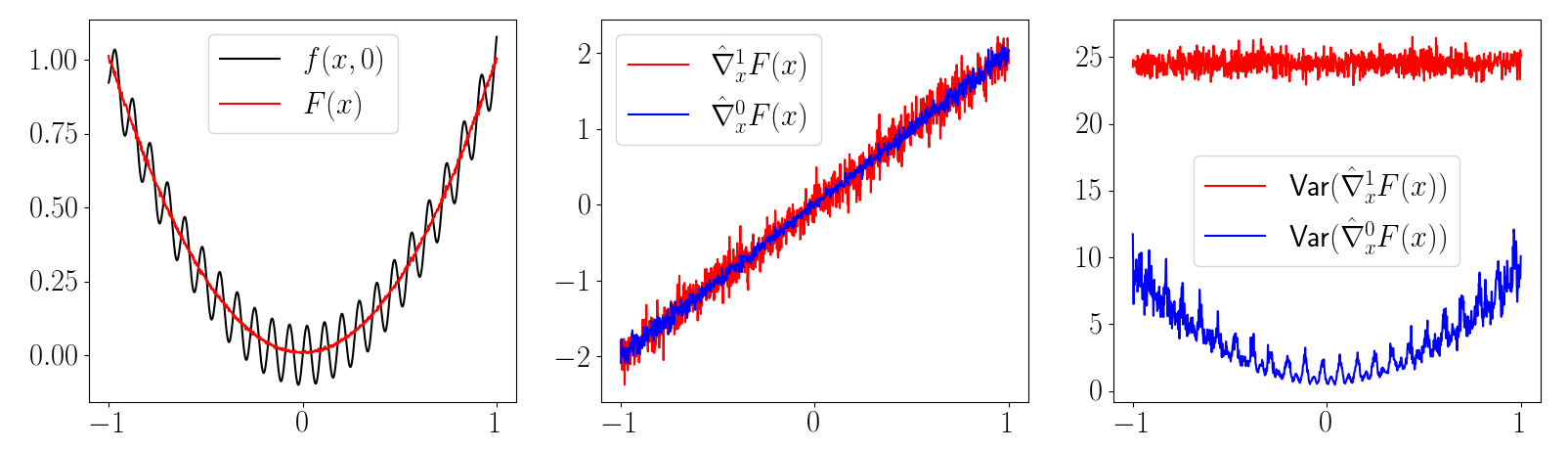
Example: The Heaviside function

\(\frac{\partial f(x)}{\partial x} = 0\) almost everywhere!

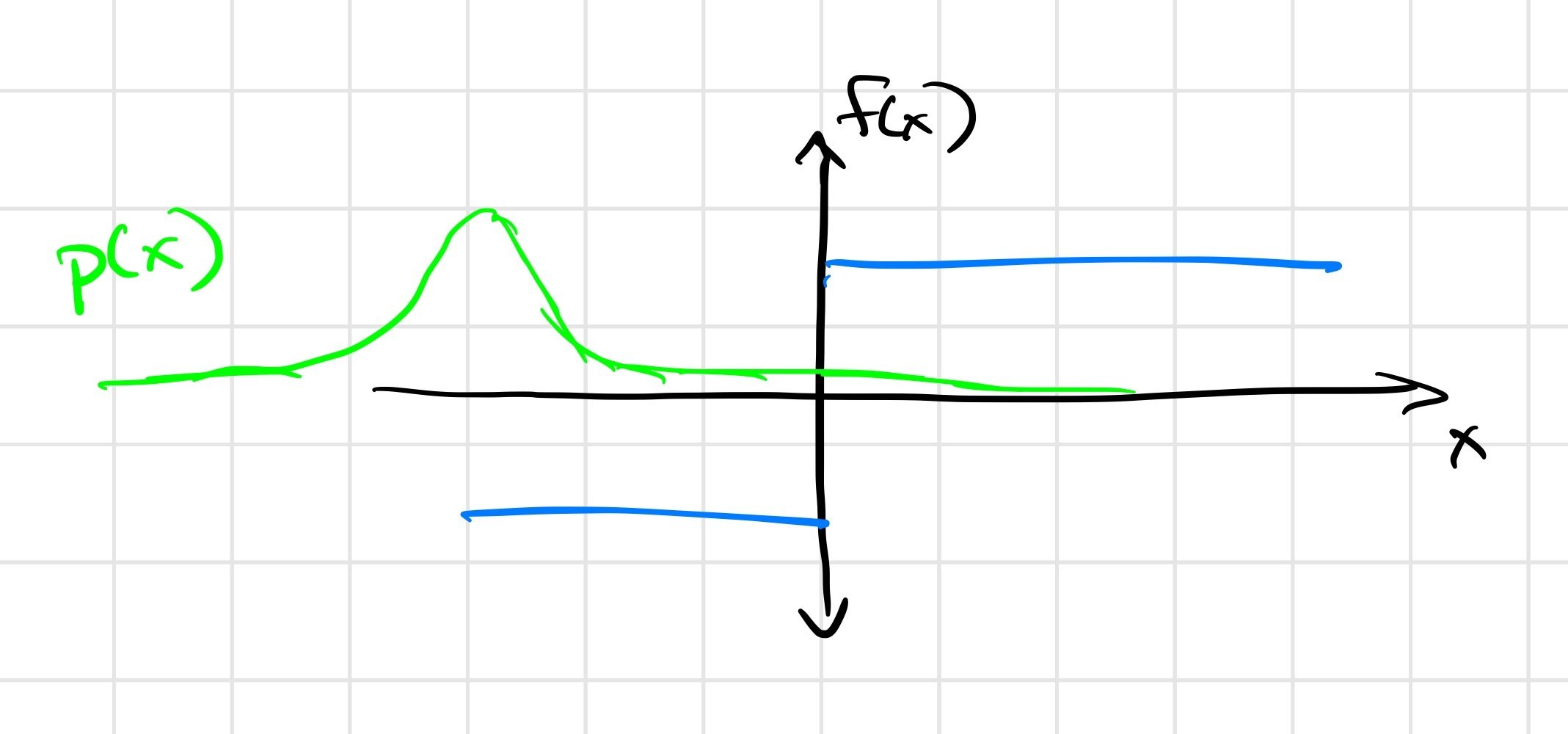
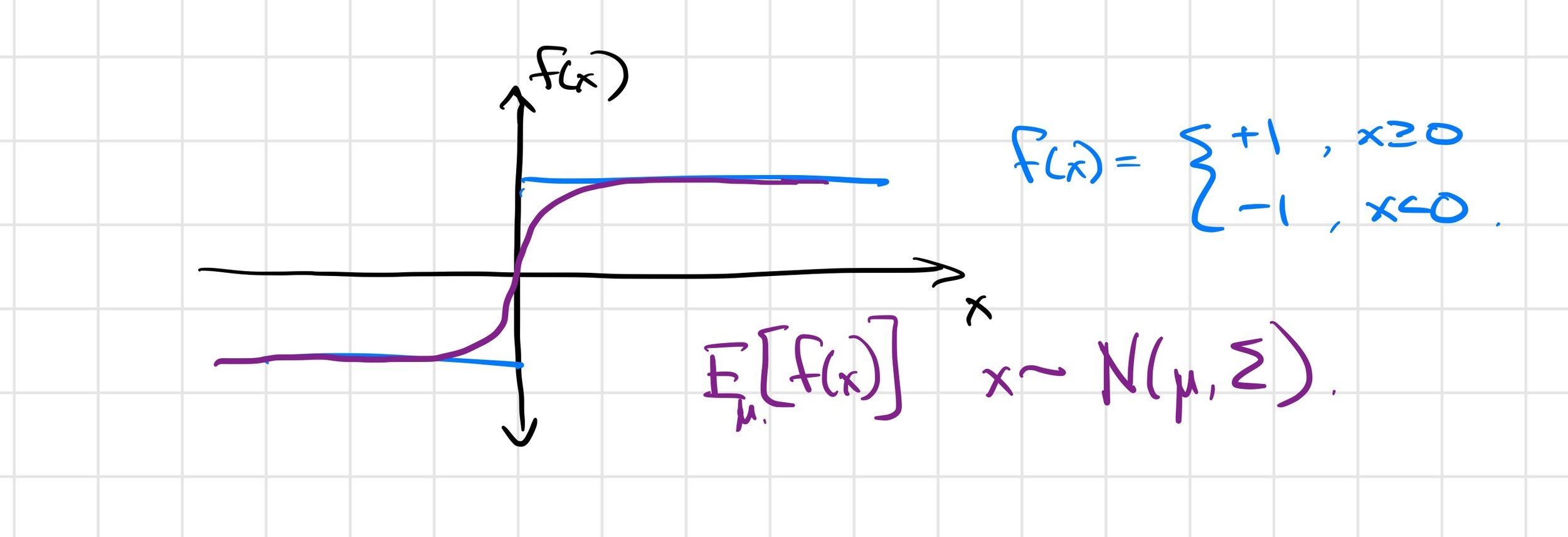
\( \Rightarrow \frac{1}{K} \sum_{i=1}^K \frac{\partial f(\mu + w_i)}{\partial \mu} = 0 \)

First-order estimator is biased

\( \not\approx  \frac{\partial}{\partial \mu} E_\mu [f(x)]  \)

Zero-order estimator is (still) unbiased

What about smooth (but stiff) approximations?

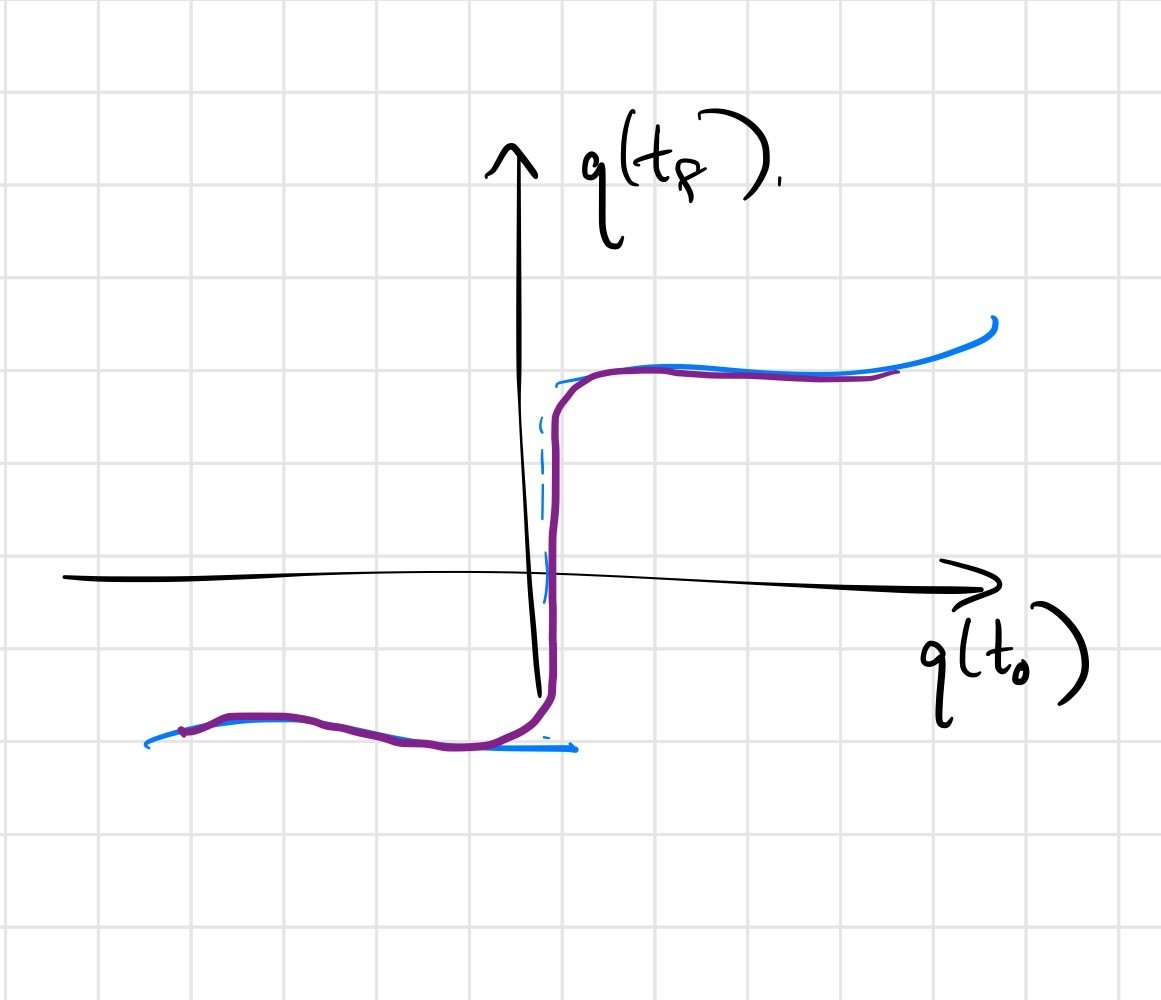
  • Continuous yet stiff approximations look like strict discontinuities in the finite-sample regime.
  • In the paper, we formalize "empirical bias" to capture this.

First-order estimates can also have high variance

e.g. with stiff contact models (large gradient \(\Rightarrow\) high variance)

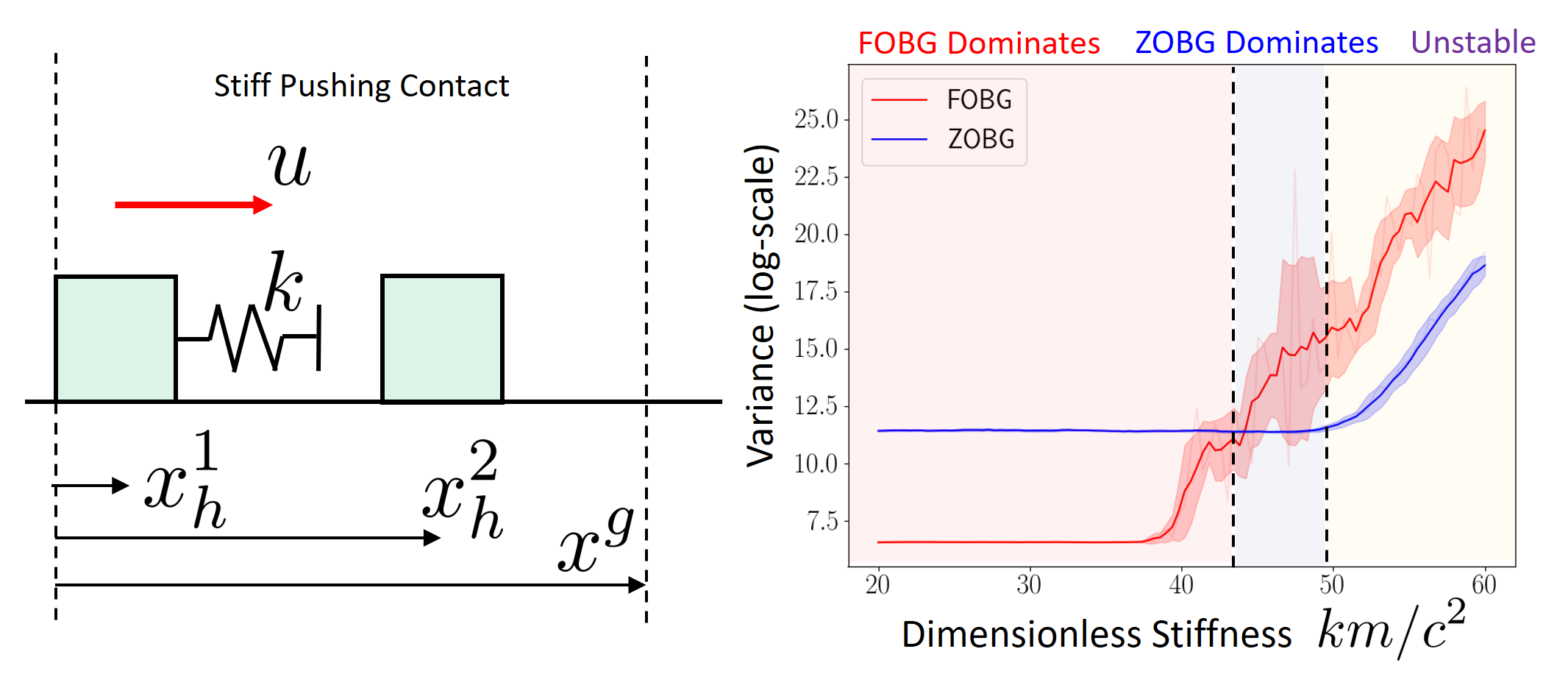
First-order estimates can also have high variance

Is stochasticity essential?

Deterministic smoothing - force at a distance

Global Planning for Contact-Rich Manipulation via
Local Smoothing of Quasi-dynamic Contact Models

Tao Pang, H. J. Terry Suh, Lujie Yang, and Russ Tedrake

Available at: https://arxiv.org/abs/2206.10787

Establish equivalence between randomized smoothing and a (deterministic/differentiable) force-at-a-distance contact model.