Planning with
Graphs of Convex Sets
(in the age of foundation models)
Russ Tedrake
MIT Robotics Seminar
Feb 16, 2024





Russ, How are we going to solve robotics?

The AlphaGo Playbook

- Step 1: Behavior Cloning
- from human expert games
- Step 2: Self-play
- Policy network
- Value network
- Monte Carlo tree search (MCTS)
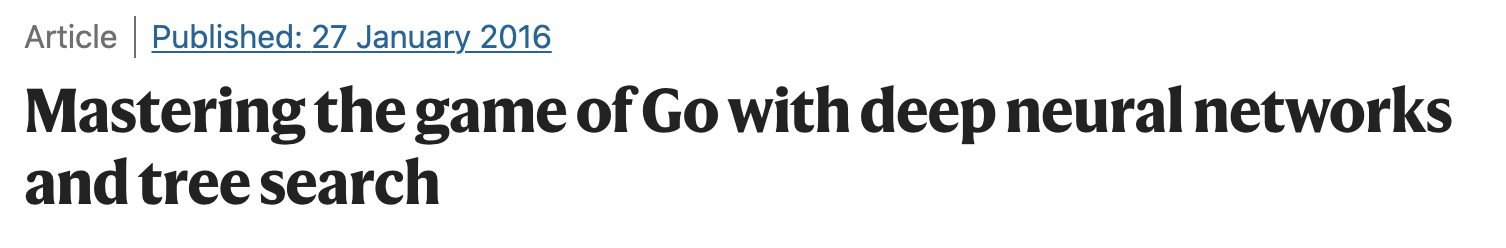
Learning and Planning
- Two aspects of "intelligence"; either alone seems insufficient
- Learning guides the planning (explore high-scoring actions)
- Planning speeds up the learning
- Planning immediately strengthens the policy -- potentially even when we move to "zero-shot" in "open world" domains.
Does this recipe work for robotics?

Step 1: Behavoir Cloning

Learns a distribution (score function) over actions
e.g. to deal with "multi-modal demonstrations"

Learning categorial distributions already worked well (e.g. AlphaGo)
Diffusion helped extend this to high-dimensional continuous trajectories
Towards Large Behavior Models (at TRI)



Foundation Models for Manipulation
Step 2: Self-Play (with MCTS)
- (Motion) planning in robotics
- Sampling-based
- Trajectory optimization
- ...
- The AlphaGo family
- Go, Shogi, Chess, .... Starcraft, ...
- For high-dimensional, continuous action spaces, MCTS replaced with more naive exploration (PPO)
- I worry we lost something important there
but our planners are weak (esp. planning through contact)
Planning with Newtonian mechanics
- I don't fear the sim2real gap
- Advanced contact simulation
- Domain randomization (train in sim, deploy in real)
- Co-train on simulation + real rollouts

The Robot Data Diet

Big data
Big transfer
Small data
No transfer

Ego-Exo
robot teleop

(the "transfer learning bet")

Open-X
simulation rollouts
Wanted: Strong planning with "intuitive physics"

Learning + Planning
- The first foundation models for manipulation will be generalists
- Online planning to strengthen/specialize the generalist policy

- Planning is potentially an essential component for "robot intelligence"; still lots of room for improvement.
- Planning w/ Newtonian mechanics can feed the pipeline
- And deepen our understanding,
- which leads to faster progress.
Shortest Paths in Graphs of Convex Sets.
Tobia Marcucci, Jack Umenberger, Pablo Parrilo, Russ Tedrake.
Available at: https://arxiv.org/abs/2101.11565


Motion Planning around Obstacles with Convex Optimization.
Tobia Marcucci, Mark Petersen, David von Wrangel, Russ Tedrake.
Available at: https://arxiv.org/abs/2205.04422





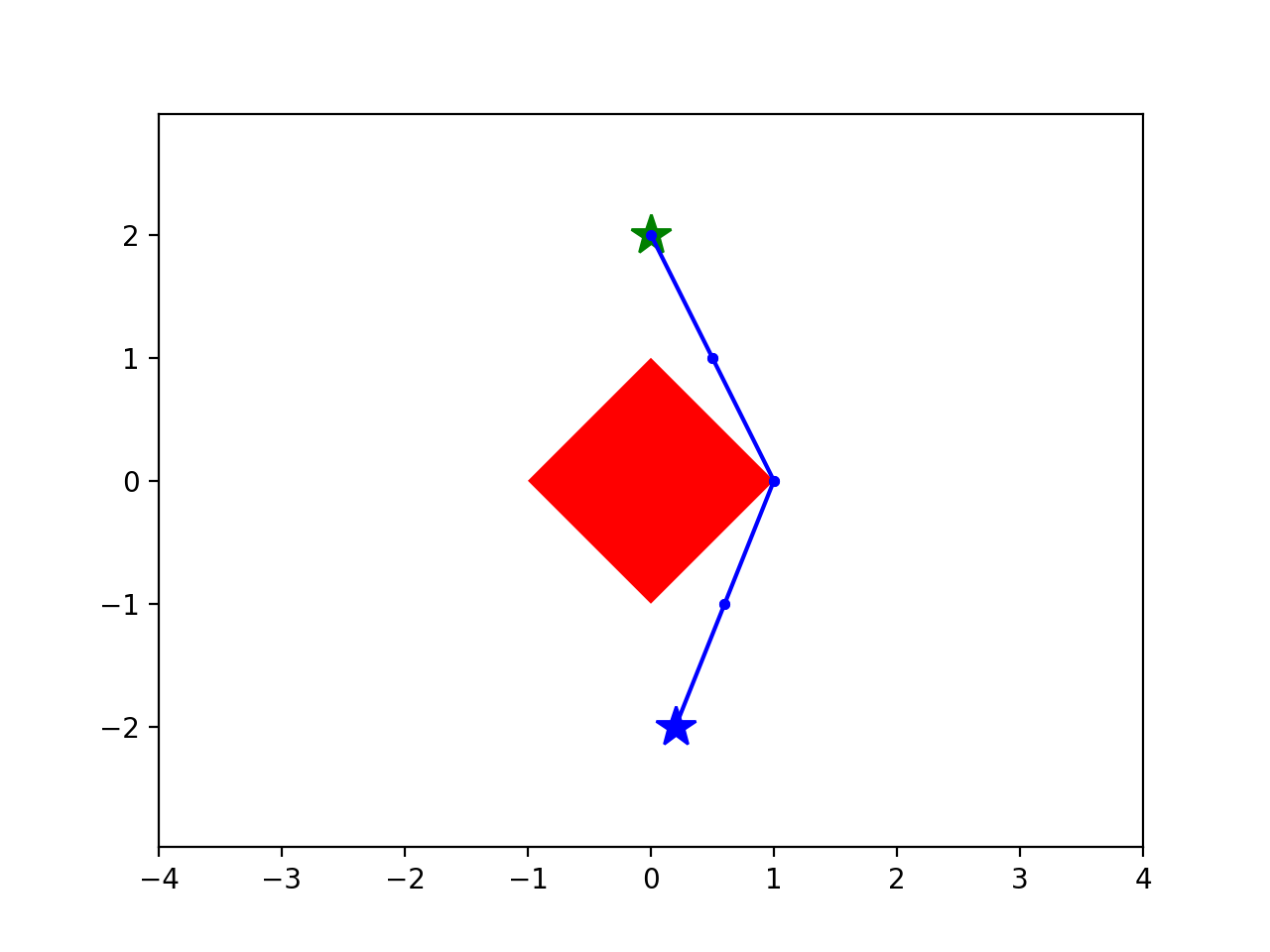
start
goal


- Combinatorial (e.g. over homotopy classes)
- Smooth optimization (over curves)
Two aspects of the motion planning problem:
Combinatorial: Sampling-based motion planning
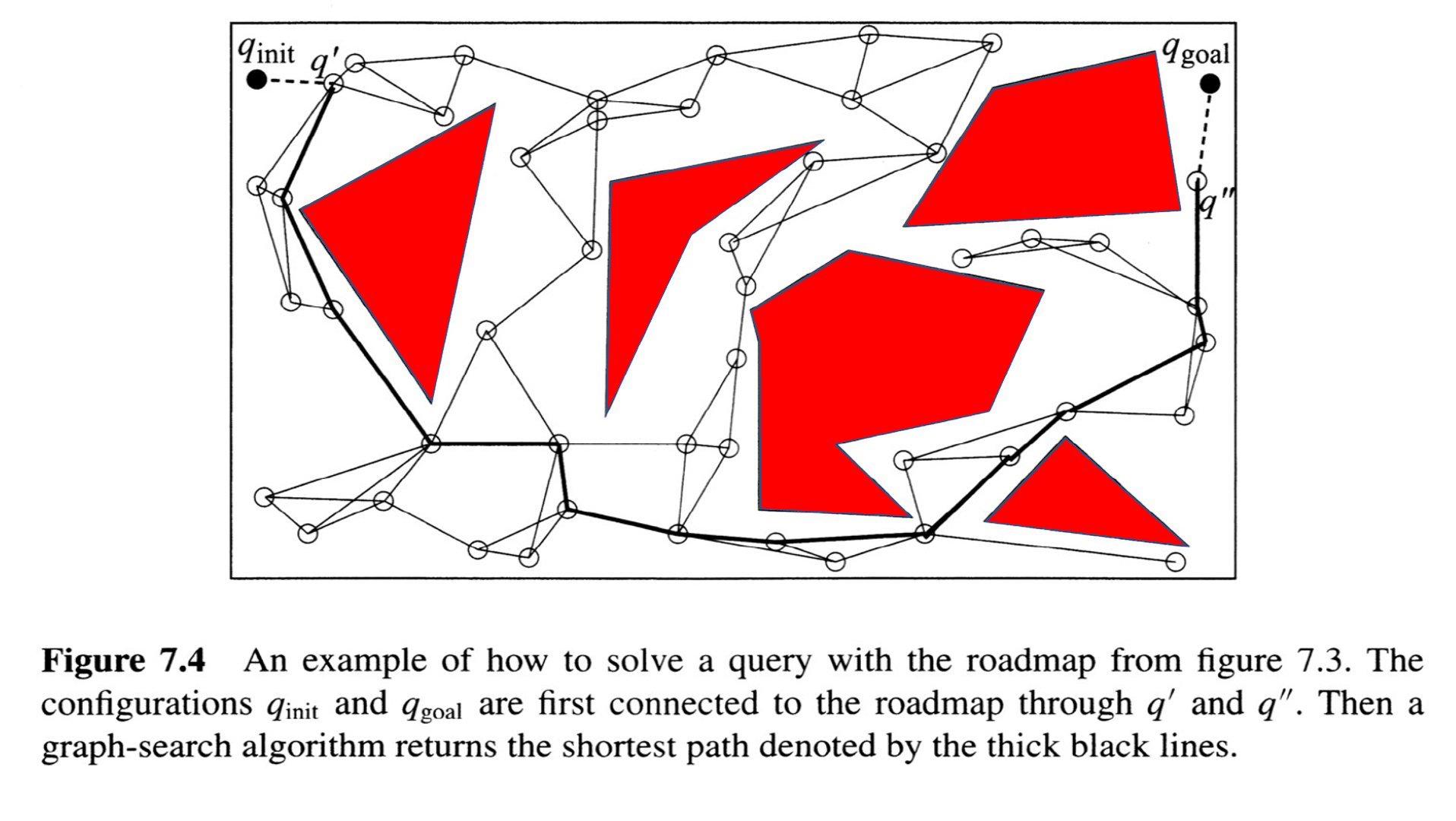
The Probabilistic Roadmap (PRM)
from Choset, Howie M., et al. Principles of robot motion: theory, algorithms, and implementation. MIT press, 2005.
Smooth: Trajectory Optimization
A preview of the results...
Default playback at .25x
GCS Trajectory Optimization
Sampling-based motion planning
The Probabilistic Roadmap (PRM)
from Choset, Howie M., et al. Principles of robot motion: theory, algorithms, and implementation. MIT press, 2005.

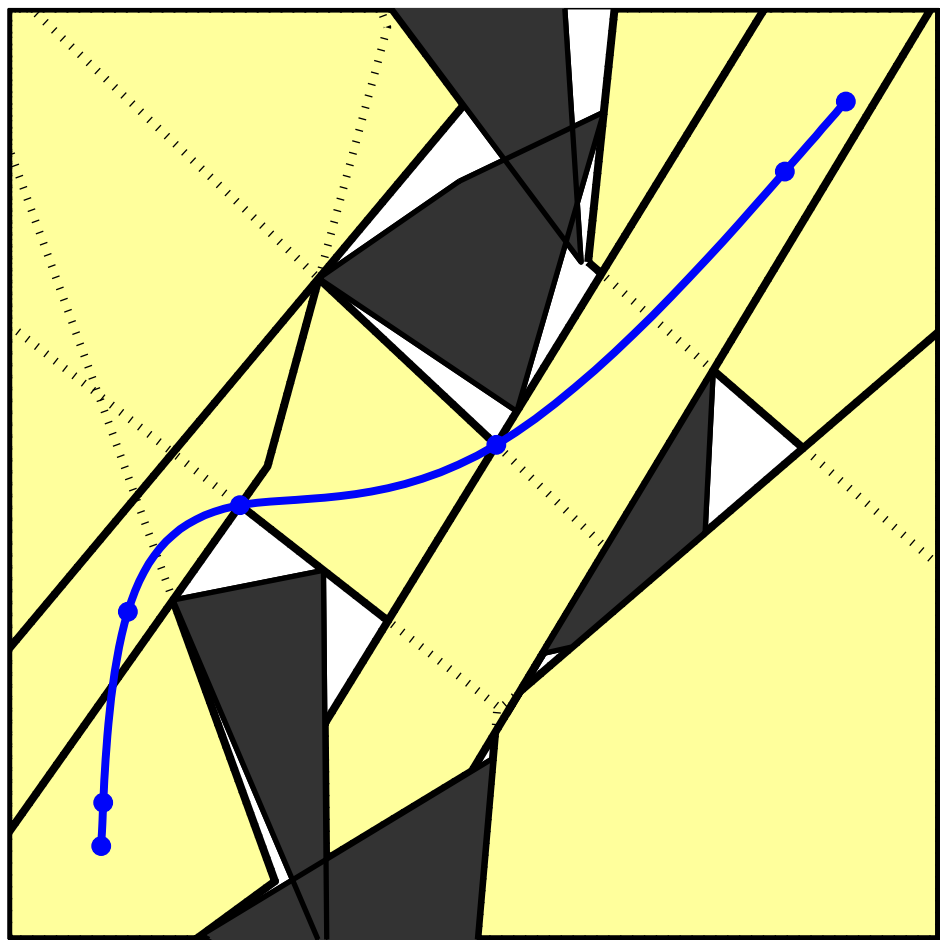
- PRM: A roadmap of points (vertices) connected by line segments
- GCSTrajOpt: A roadmap of convex sets (vertices) of continuous curves connected by continuity constraints
Key ingredients
- Efficient algorithms for solving shortest paths on "Graphs of Convex Sets" (aka "GCS")
- Transcription of the trajectory optimization problem into GCS
- (Approximate) convex decomposition of collision-free configuration space. (aka "IRIS")
- Convex optimization over continuous curves w/ time scaling (\(\Rightarrow\) "GCS Trajectory Optimization")
Graphs of Convex Sets


-
For each \(i \in V:\)
- Compact convex set \(X_i \subset \R^d\)
- A point \(x_i \in X_i \)
- Edge length given by a convex function \[ \ell(x_i, x_j) \]
- New machinery to tighten convex relaxation
Note: The blue regions are not obstacles.

start
goal
is the convex relaxation. (it's tight!)


Previous formulations were intractable; would have required \( 6.25 \times 10^6\) binaries.


minimum distance
minimum time
Transcription to a mixed-integer convex program, but with a very tight and efficient convex relaxation.
- Solve to global optimality w/ branch & bound orders of magnitude faster than previous work
- Solving only the convex optimization (+rounding) is almost always sufficient to obtain the globally optimal solution.
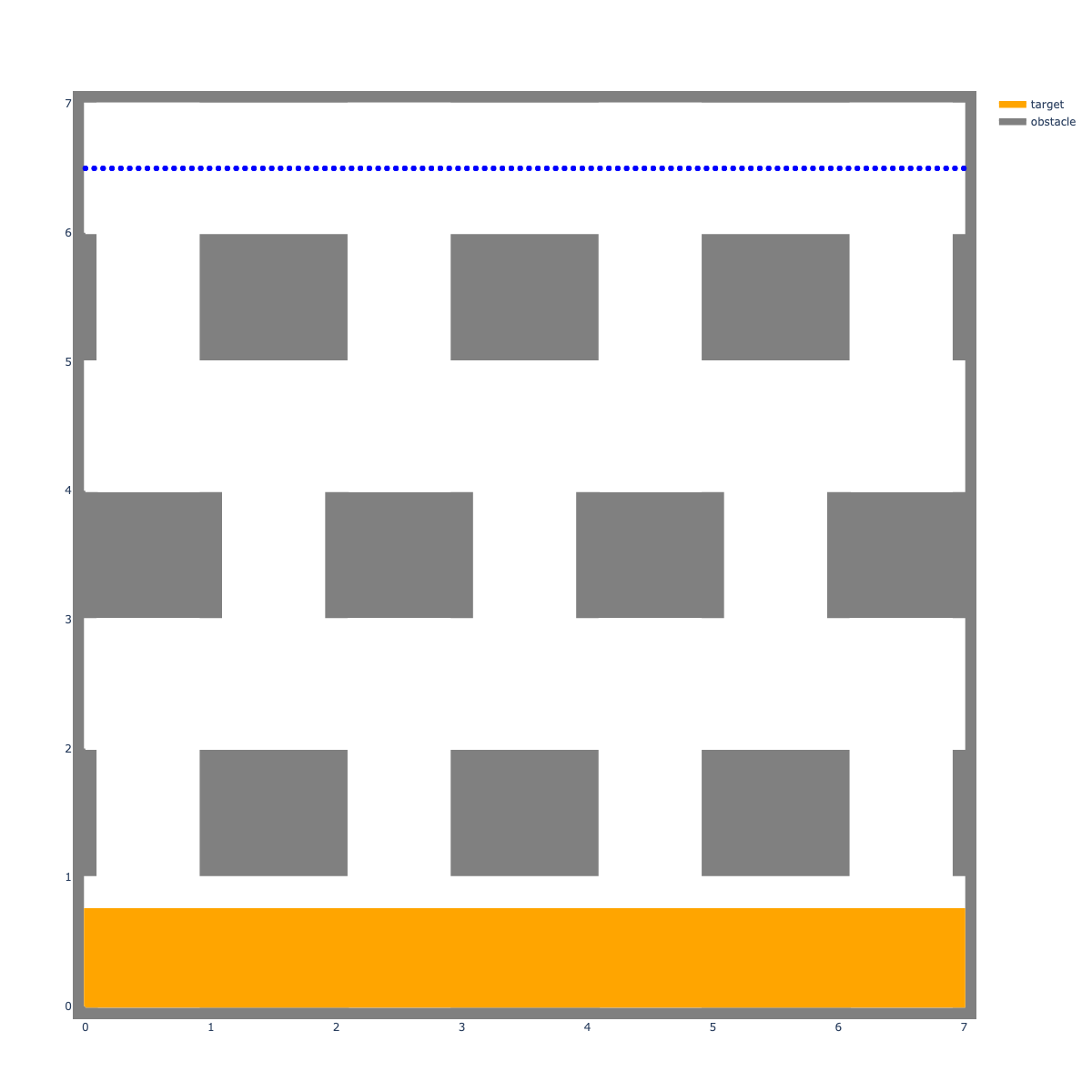
IRIS for Configuration-space regions
- IRIS (Fast approximate convex segmentation). Deits and Tedrake, 2014
- New versions work in configuration space:
- Nonlinear optimization for speed. IRIS-NP
- Sums-of-squares for rigorous certification. C-IRIS

Convex decomposition of configuration space
- Naive sampling can lead to inefficient coverage
- New algorithms optimize a convex cover
- Insight: Cliques in the visibility graph (almost) correspond to convex sets in configuration space
- Approach: (Approximate) minimum clique cover

(Approximate) Minimum clique cover









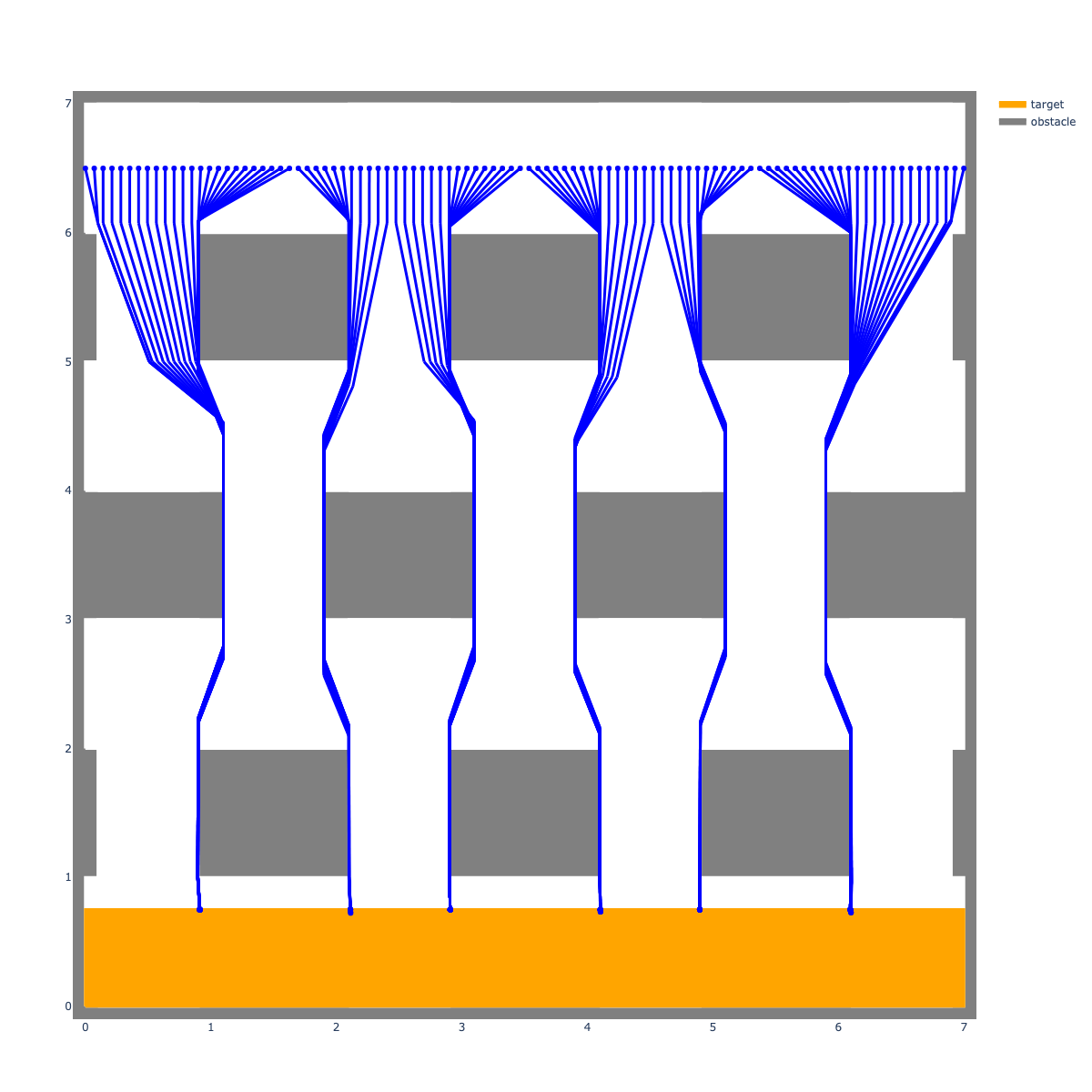
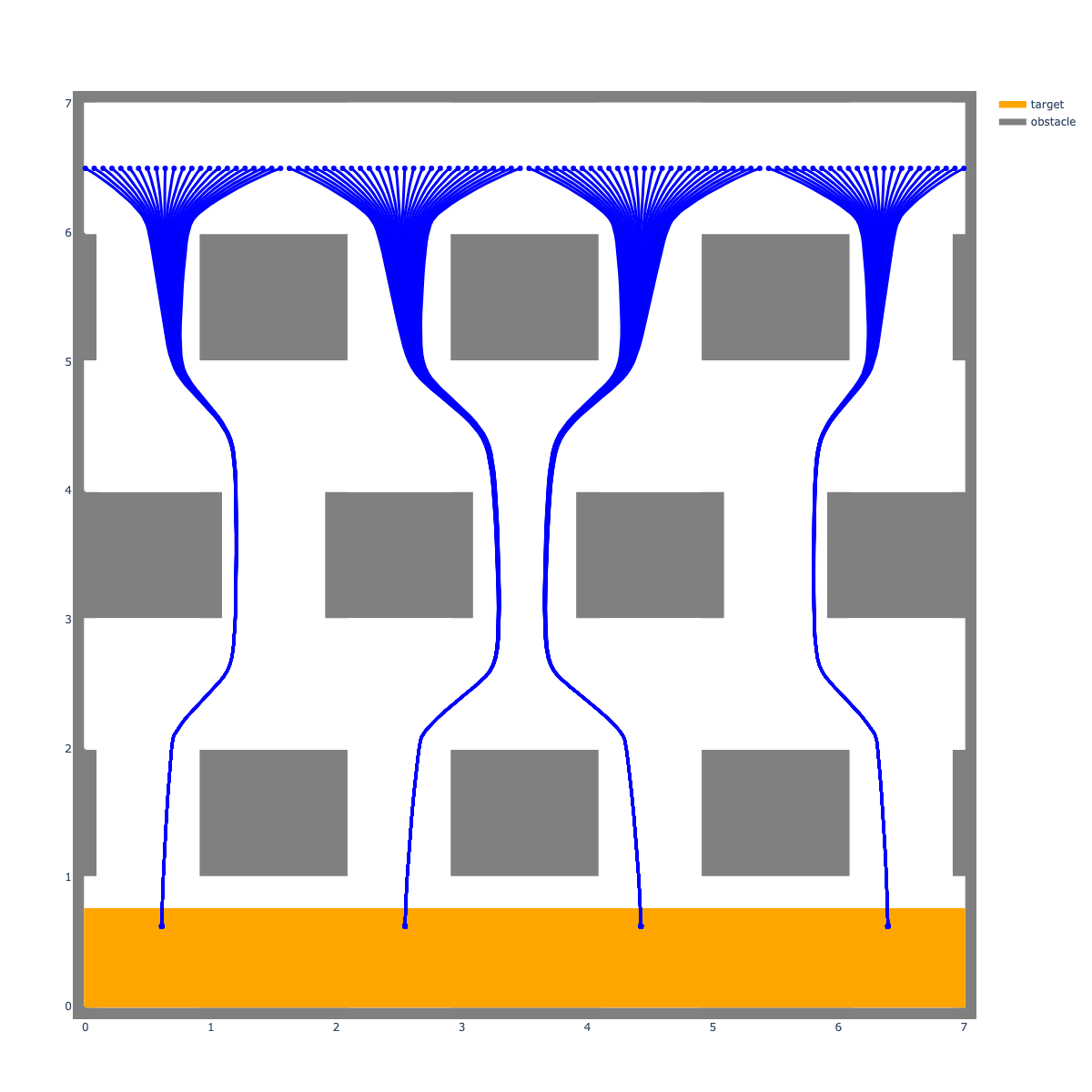
+ time-rescaling
GCS Trajectory Optimization
Preprocessor makes easy optimizations fast!


GCS Trajectory Optimization

Transitioning from basic research to real use cases
Adoption
Adoption

Dave Johnson (CEO): "wow -- gcs (left) is a LOT better! ... This is a pretty special upgrade which is going to become the gold standard for motion planning."


Tommy Cohn (w/ Seiji Shaw, Shruti Garg)
Planning on Manifolds


Robot Operating System (ROS), Picknik
Bernhard Paus Graesdal
Planning Through Contact with GCS
Going beyond collision-free motion planning...


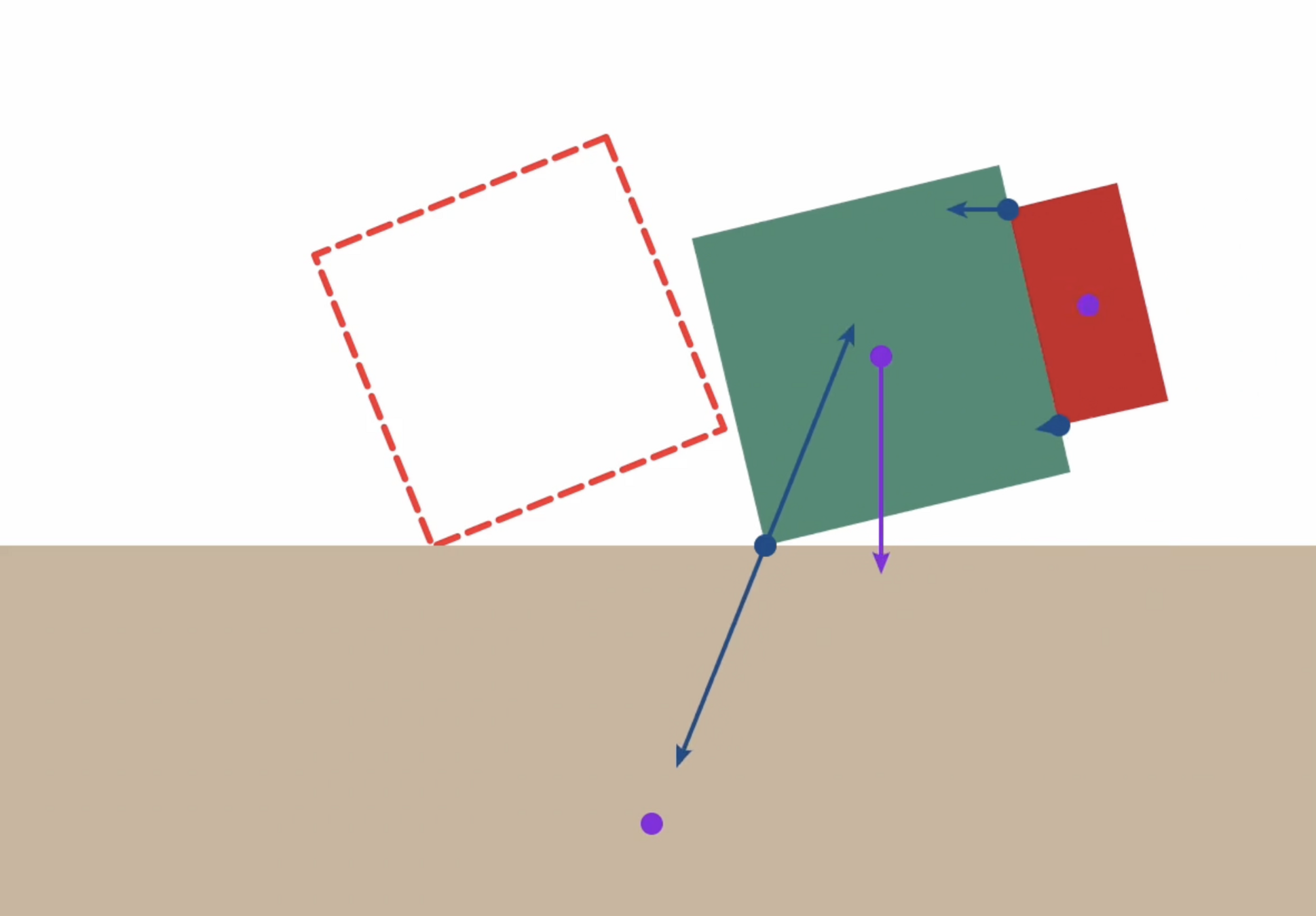
Planning Through Contact with GCS
C. Chi et al., “Diffusion Policy: Visuomotor Policy Learning via Action Diffusion.” Mar. 09, 2023
- How do we plan for such tasks?
N. Doshi et al., “Manipulation of unknown objects via contact configuration regulation.” Jun. 01, 2022
High-level approach
- Contact modes give a hybrid system
- Use GCS
- One vertex for each contact mode
- Simultaneously search for the mode sequence and the continuous motion
Using GCS for Planning Through Contact
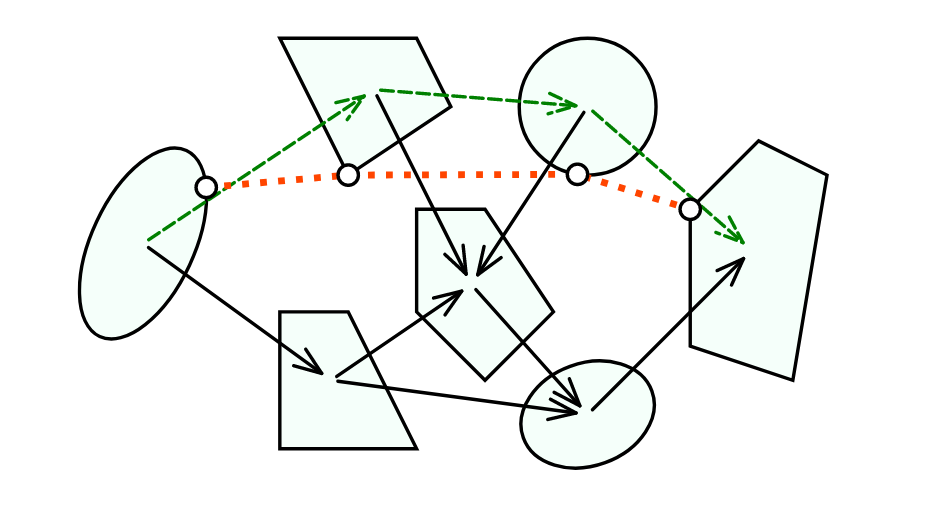
T. Marcucci, J. Umenberger, P. A. Parrilo, and R. Tedrake, “Shortest Paths in Graphs of Convex Sets.” 2022.
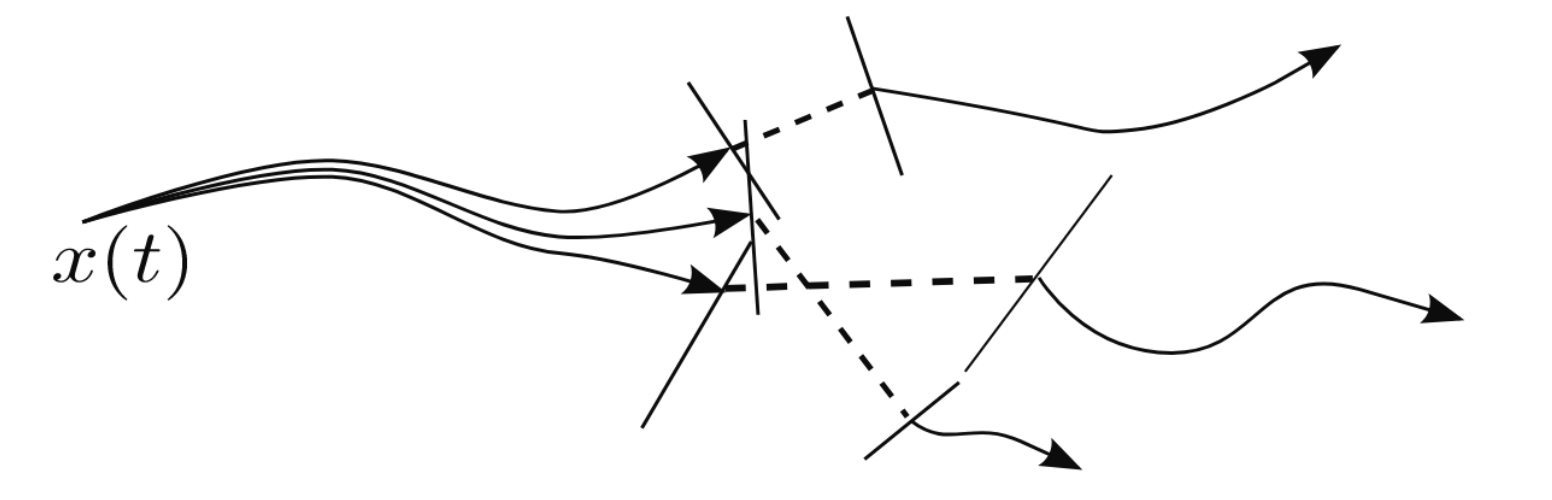
- Plan with quasi-static dynamics
- \( v \approx 0\) and \(M \dot v + C v \approx 0 \)
- No impacts
- Plan over object poses, contact forces and contact locations
Using GCS for Planning Through Contact
Formulation
- Our quasi-static dynamics and kinematic constraints form a nonconvex QCQP
- Semidefinite relaxation of QCQP (with some new additions)
- Feasible set is a Spectrahedron (a convex set)
How to encode dynamics and kinematics as a convex set?
- Build a graph of these spectrahedrons
- One for each contact mode
- Solve it using GCS!
Approach


- The convex relaxation doesn't have to be perfect
- \( \implies \) Only needs to contain enough information to take the correct high-level decisions
- Then we can refine the details as a final step!


or
\(\longrightarrow\)
\(\longrightarrow\)
\(\longrightarrow\)
\(\longrightarrow\)
\(\longrightarrow\)
\(\longrightarrow\)
\(\longrightarrow\)
Start
Goal
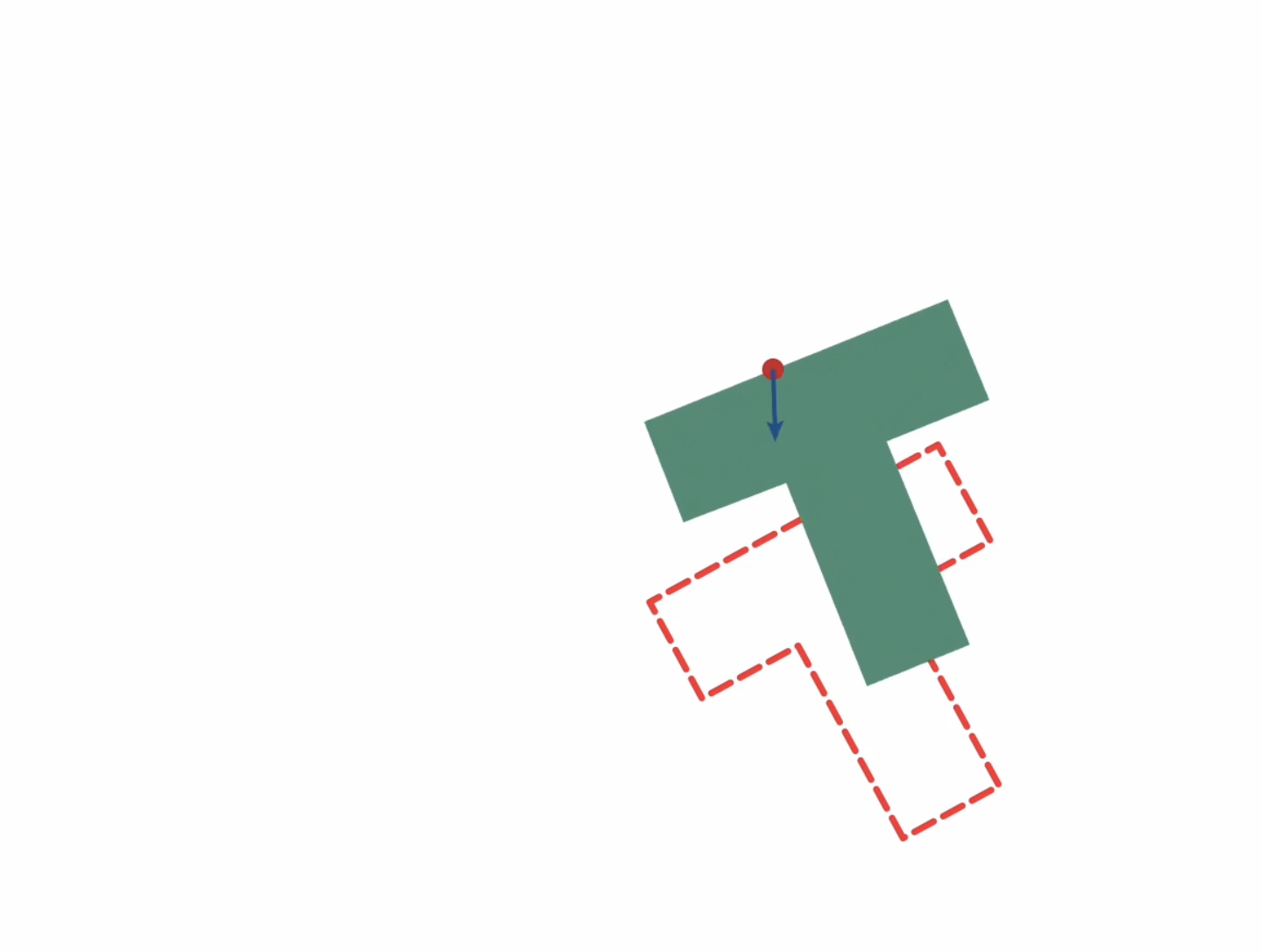
Planning through contact for Planar Pushing

GCS \(\Rightarrow\) Diffusion Policy

Planning through contact for general manipulation


start
goal


- Combinatorial (e.g. over homotopy classes)
- Smooth optimization (over curves)
Two aspects of the motion planning problem:

Lots of work on "contact graphs", but it's a little more subtle than that...
These algorithms are not arbitrary.
GCS helped us see the deeper connections between motion planning and structured optimization (SDP relaxations, moment hierarchies, etc).
An aside
Stronger optimization enables simpler cost functions.
(No cost-function tuning required)
From plans to feedback policies
(for planning under uncertainty and precomputing all paths)

What if:
- A single (slightly bigger) optimization offline, which solves for all initial conditions
So far:
- Solve an optimization for each initial condition
Lower bounds on the value function















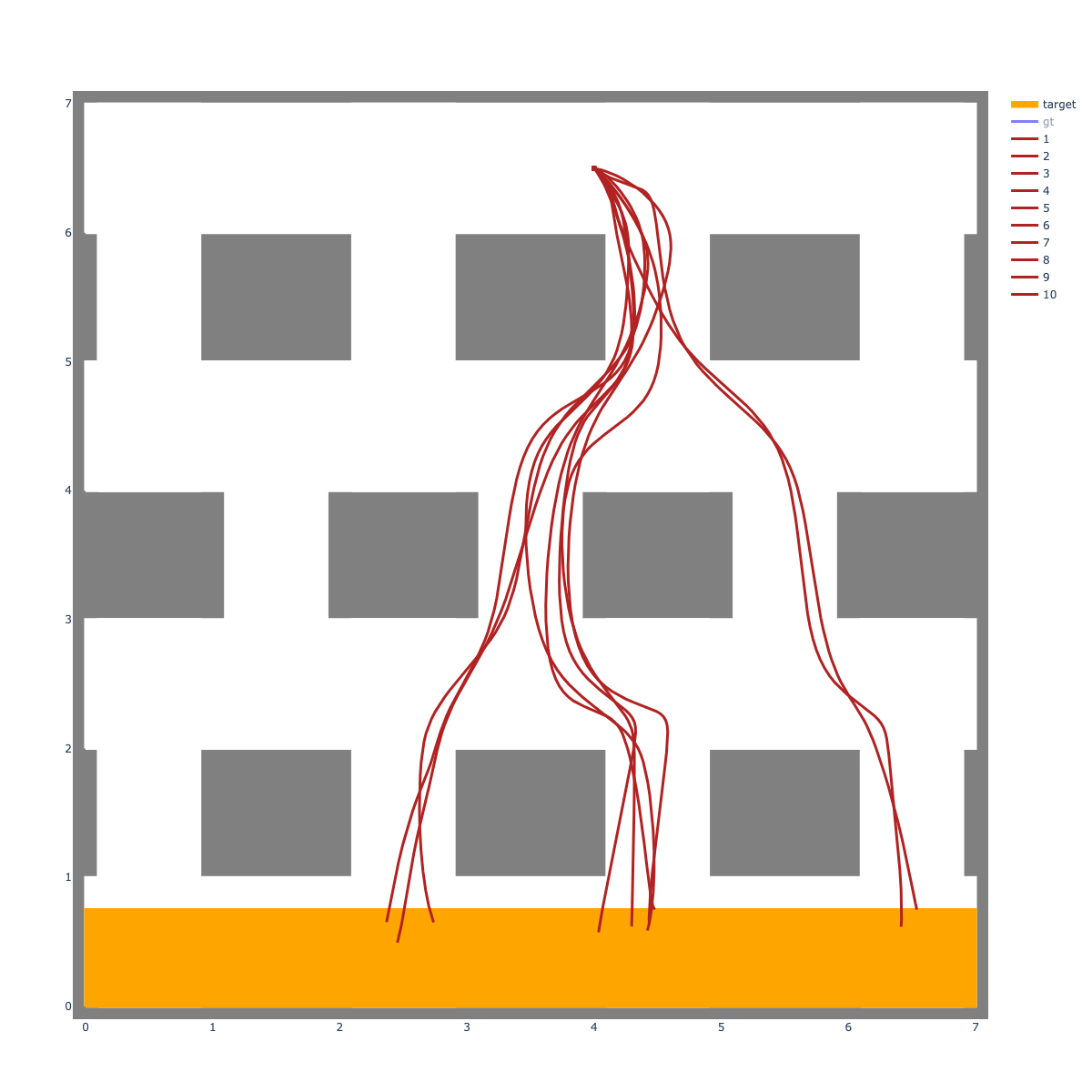
Task and Motion Planning

Task and motion planning
GCS version (top down)

Task and motion planning with GCS
Prelimary results by Savva Morozov
Task and motion planning
Philosophy:
- Take your favorite graph problem (max cut, traveling salesman, ...); then apply GCS.
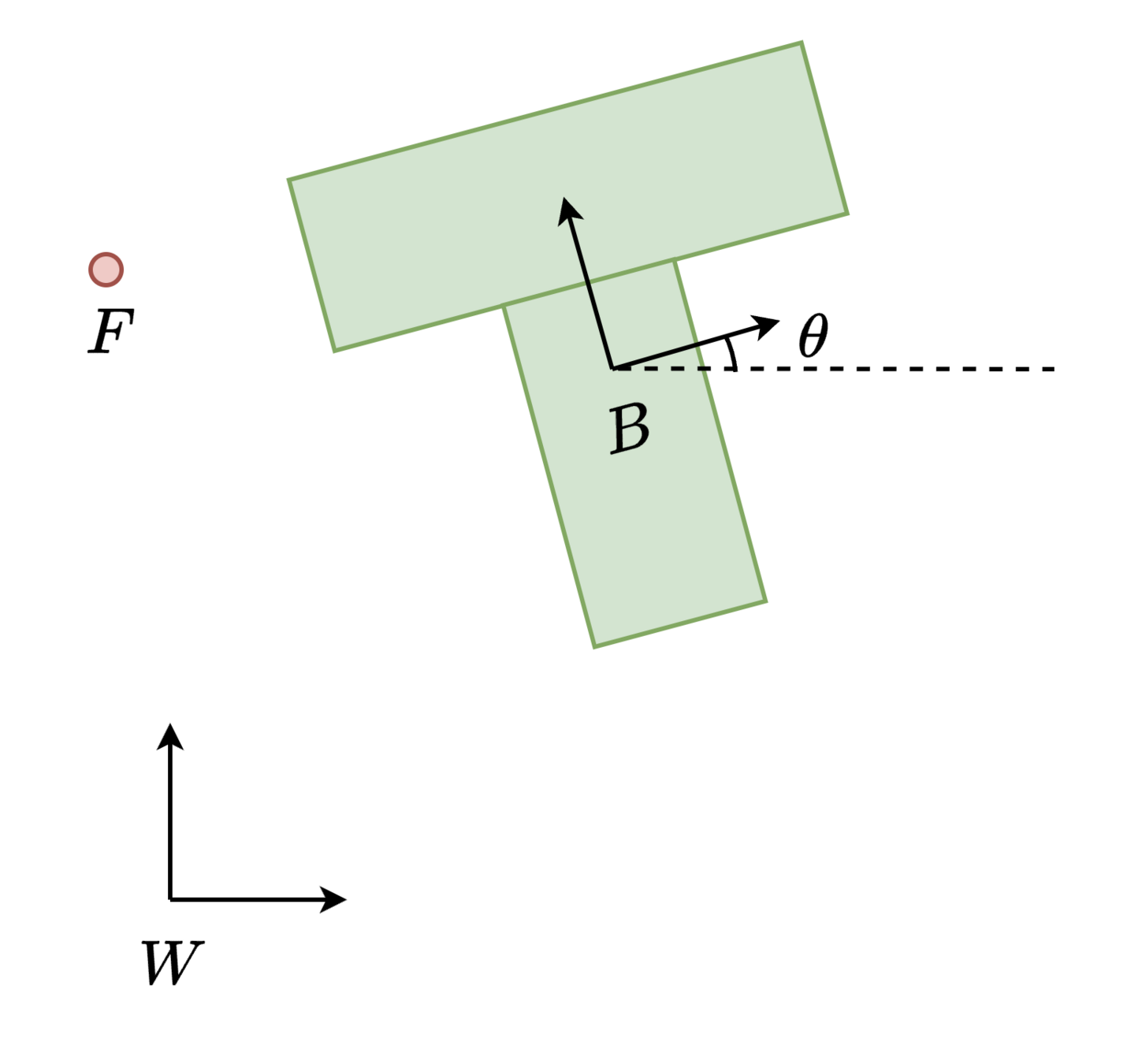
For moving boxes, the key combinatorial object is the permutahedron.
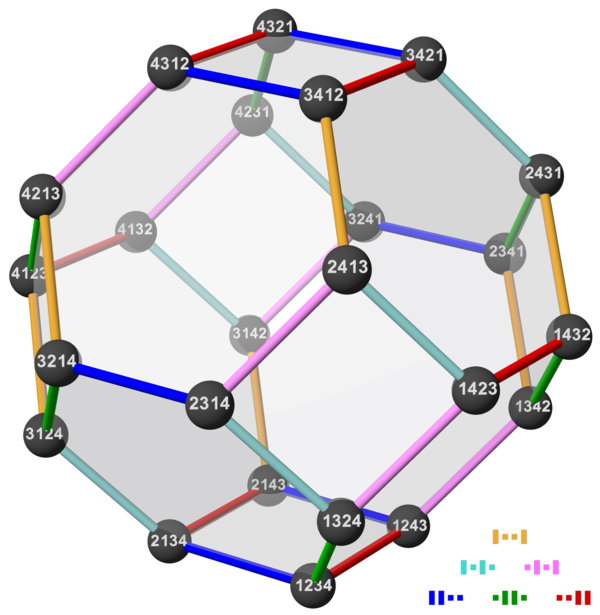
Task and motion planning

Linear Quadratic Regulator (LQR) as GCS
\[ \min_{x[\cdot],u[\cdot]} \sum_{n=0}^N x_n^T Q x_n + u_n^T Ru_n \\ \text{s.t. } x_{n+1} = Ax_n + Bu_n \]
Sets \( X_n: (x_n, u_n) \)
Edge cost
Edge constraint
n=0
n=1
n=2
n=N
\( \cdots \)
Piecewise-Affine Quadratic Regulator (PWAQR)
e.g. for hybrid trajectory optimization
n=0
n=1
n=N
...
\[ \min_{x[\cdot],u[\cdot]} \sum_{n=0}^N x_n^T Q_i x_n + u_n^T R_iu_n \\ \text{s.t. } x_{n+1} = A_ix_n + B_iu_n \\ \text{iff } (x_n,u_n) \in D_i \]
Scaling
-
~10k regions in 3D
-
20k vertices and 400k edges.
- Online planning takes 0.3s
by Tobia Marcucci in collaboration w/ Stephen Boyd

As a motion planning tool
This is version 0.1 of a new framework.
- Already competitive (better paths faster; higher DOF; supports differential constraints)
- We've provided a mature implementation
There is much more to do...
- Add support for additional costs / constraints
- torque limits, dynamics
- ...
- Dynamic collision geometry / moving obstacles
- Output feedback / information gathering
The AlphaGo Playbook

- Step 1: Behavior Cloning
- from human expert games
- Step 2: Self-play
- Policy network
- Value network
- Monte Carlo tree search (MCTS)
GCS generalization of Monte Carlo tree search
from A Survey of Monte Carlo Tree Search Methods by Browne et at, 2012


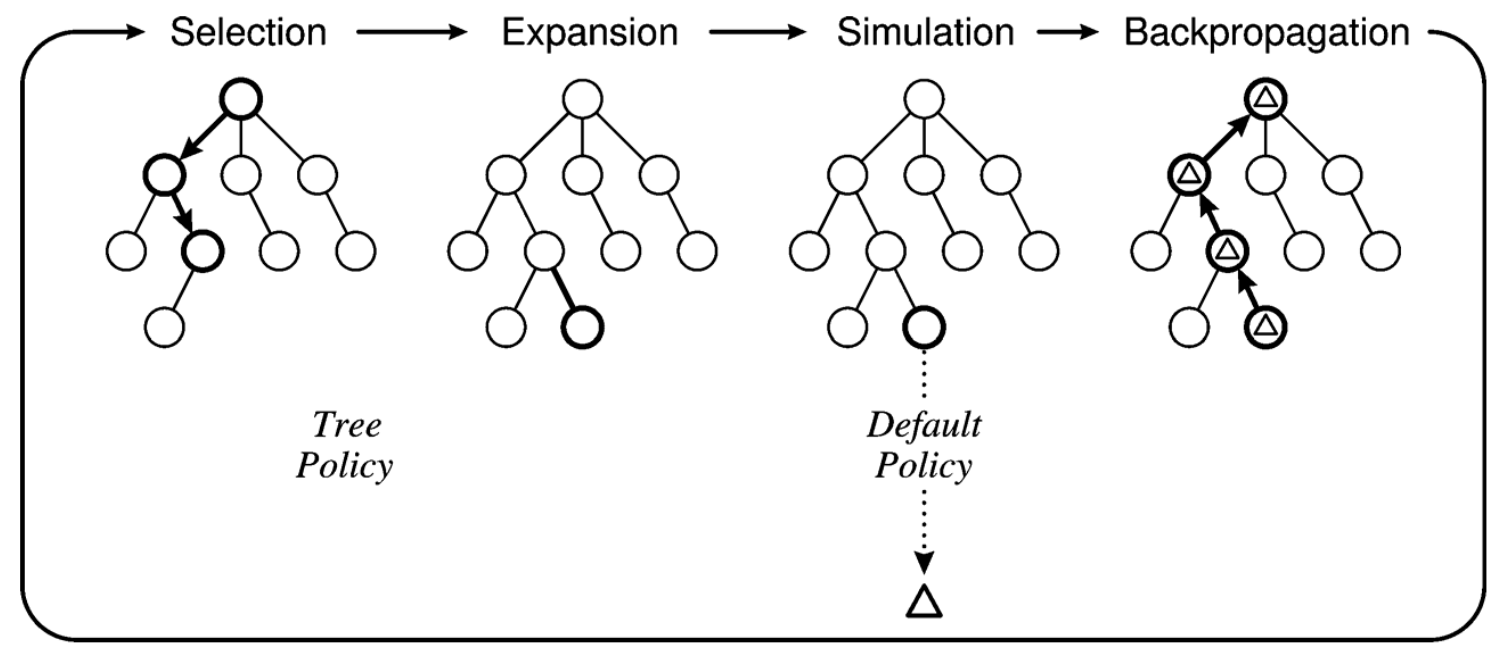
MCTS
Summary
- GCS modeling separates:
-
- combinatorial/discrete
- smooth/continuous
- Strongest planners I have had; often solves to global optimality
- and plenty more headroom
- Learning and Planning should work in harmony
Give it a try:
pip install drake
sudo apt install drake
Russ' bucket list
...
give a talk using all of the terms foundation models, generative AI, spectrahedron, and permutahedron, because it makes sense.
...

Shortest Paths in Graphs of Convex Sets.
Tobia Marcucci, Jack Umenberger, Pablo Parrilo, Russ Tedrake.
Available at: https://arxiv.org/abs/2101.11565


Motion Planning around Obstacles with Convex Optimization.
Tobia Marcucci, Mark Petersen, David von Wrangel, Russ Tedrake.
Available at: https://arxiv.org/abs/2205.04422



