Shortest Paths in Graphs of Convex Sets.
Tobia Marcucci, Jack Umenberger, Pablo Parrilo, Russ Tedrake.
Available at: https://arxiv.org/abs/2101.11565


Motion Planning around Obstacles with Convex Optimization.
Tobia Marcucci, Mark Petersen, David von Wrangel, Russ Tedrake.
Available at: https://arxiv.org/abs/2205.04422




Motion planning with obstacles as an optimization
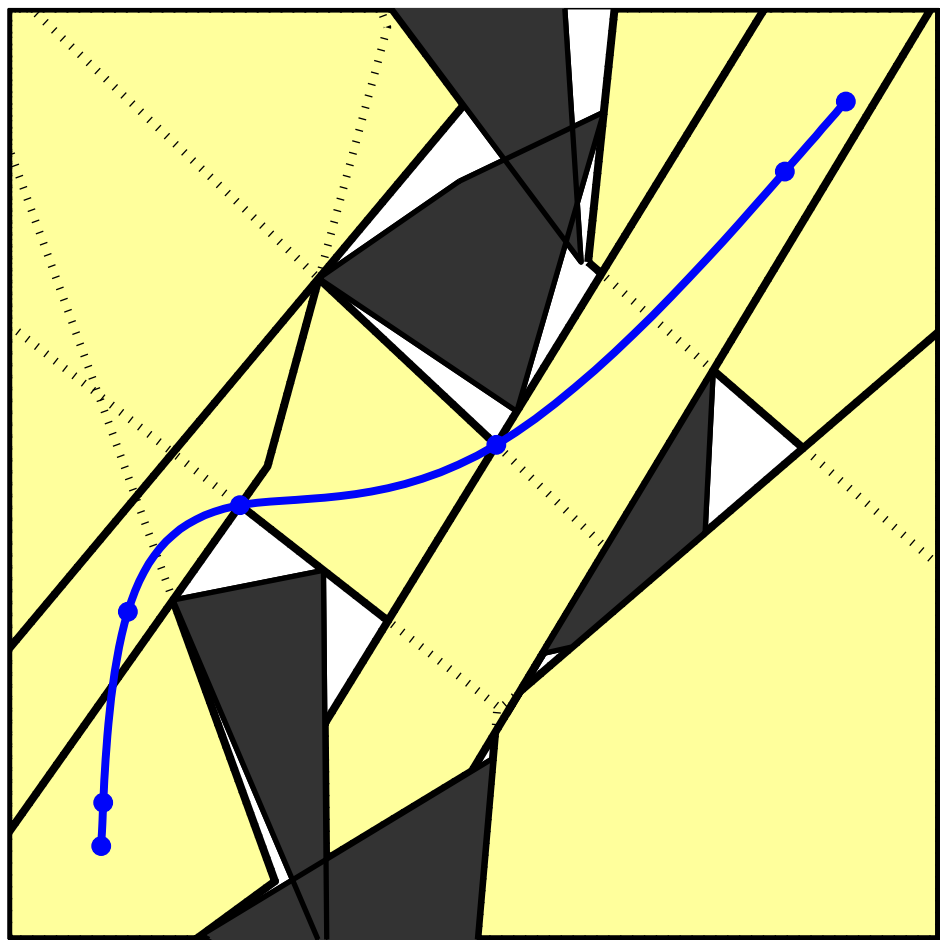
Running example: Shortest path around an obstacle
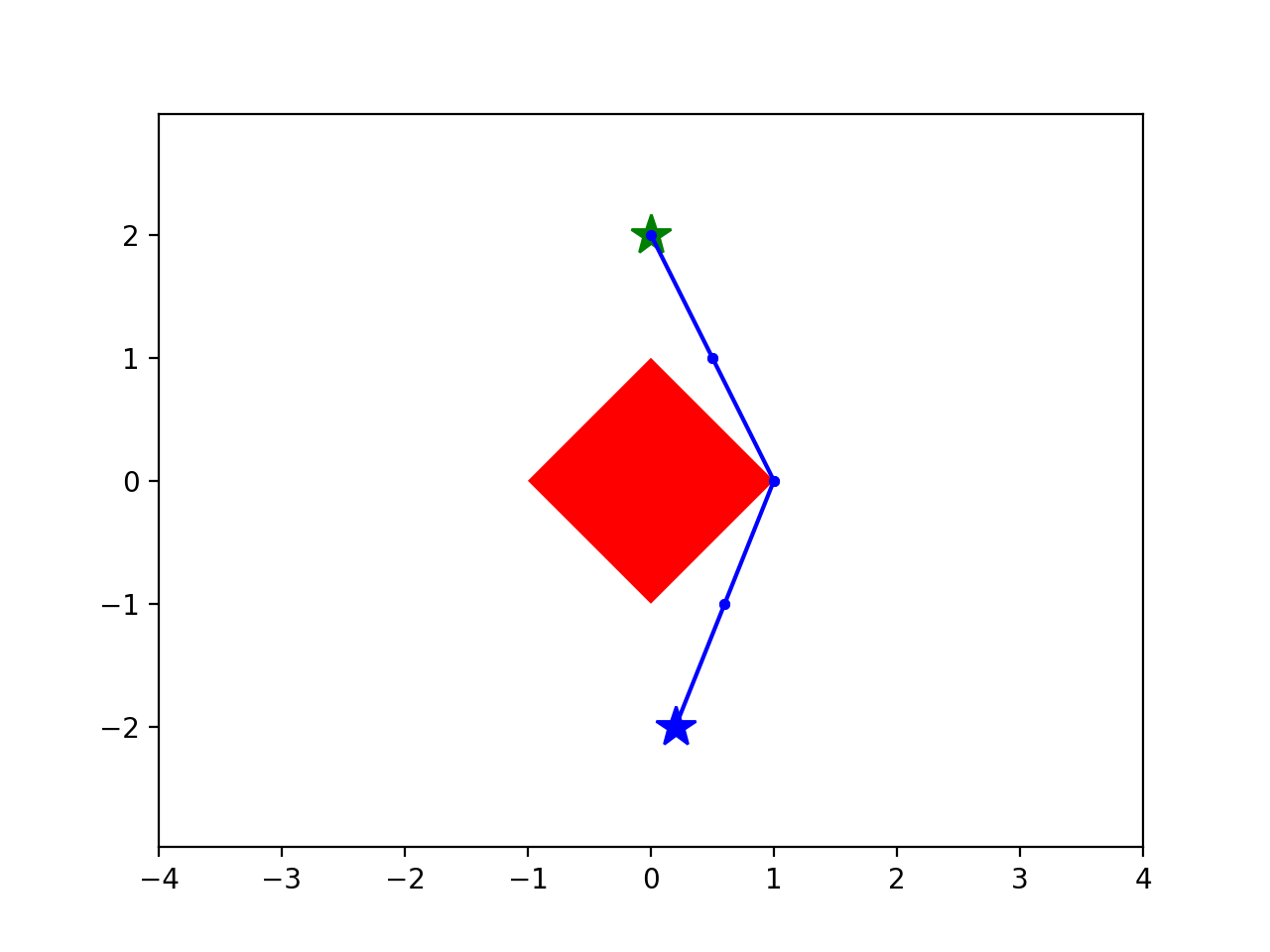
start
goal
Planning as a nonconvex optimization
Quick glimpse of the results...
Default playback at .25x


Preprocessor now makes easy optimizations fast!
Two key ingredients
- The linear programming formulation of the shortest path problem on a discrete graph.
- Convex formulations of continuous motion planning (without obstacle navigation), for example:

Kinematic Trajectory Optimization
(for robot arms)
Graphs of Convex Sets


-
For each \(i \in V:\)
- Compact convex set \(X_i \subset \R^d\)
- A point \(x_i \in X_i \)
- Edge length given by a convex function \[ \ell(x_i, x_j) \]
Note: The blue regions are not obstacles.
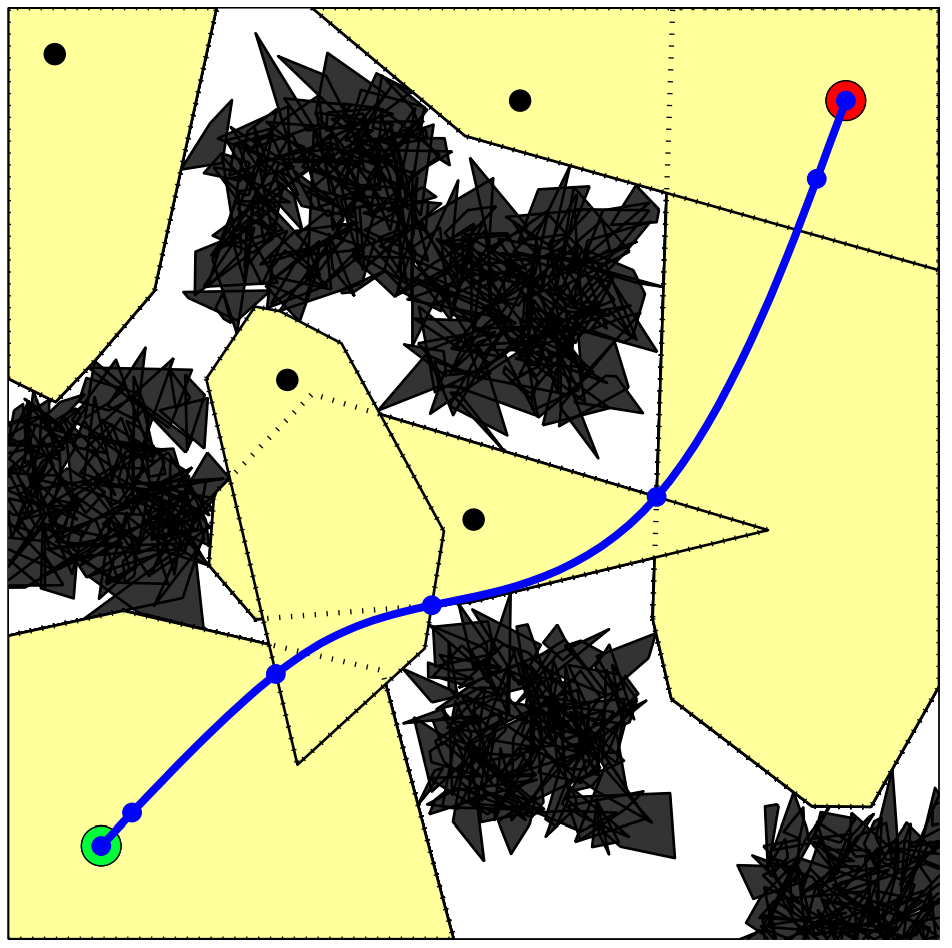
Motion planning with Graph of Convex Sets (GCS)

start
goal
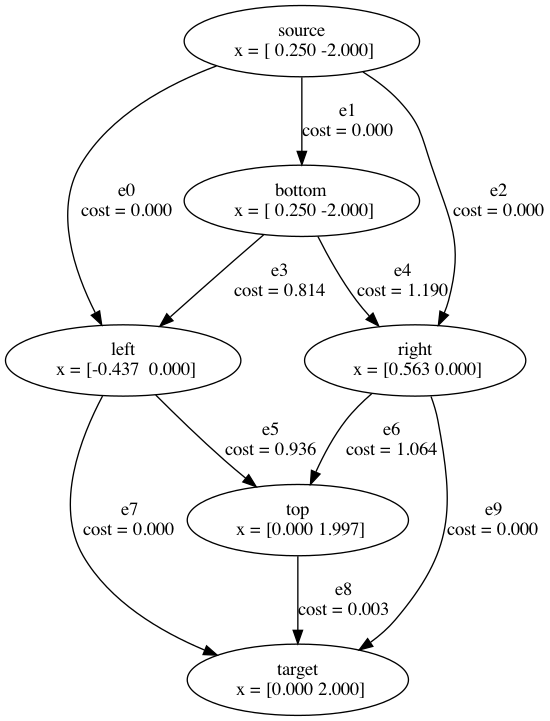
Motion planning with Graph of Convex Sets (GCS)
This is the convex relaxation
(it is tight!).
is the convex relaxation. (it's tight!)


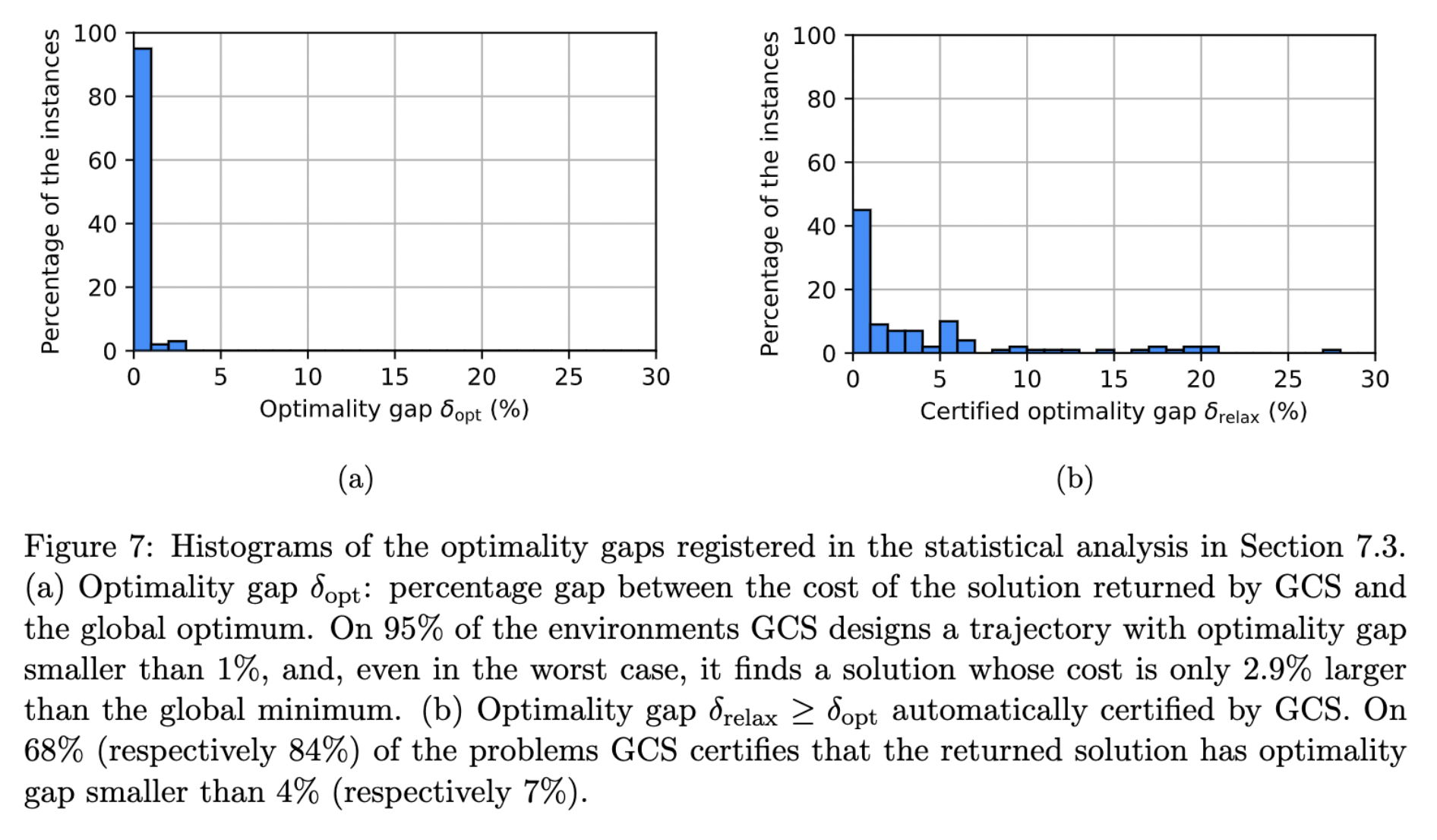
Previous formulations were intractable; would have required \( 6.25 \times 10^6\) binaries.
Transcription to a mixed-integer convex program, but with a very tight convex relaxation.
- Solve to global optimality w/ branch & bound orders of magnitude faster than previous work
- Solving only the convex optimization (+rounding) is almost always sufficient to obtain the globally optimal solution.

Sampling-based motion planning
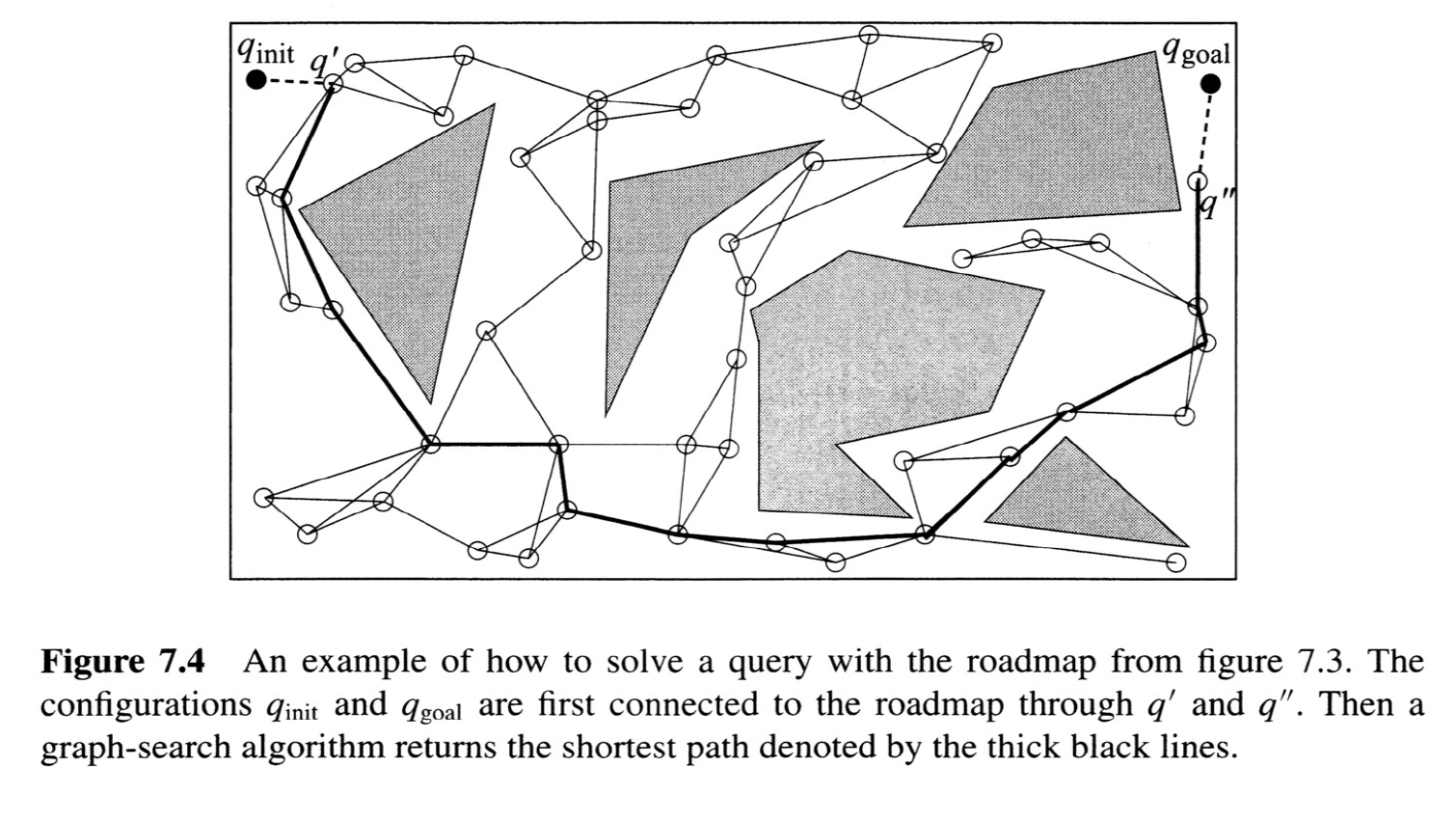
The Probabilistic Roadmap (PRM)
from Choset, Howie M., et al. Principles of robot motion: theory, algorithms, and implementation. MIT press, 2005.
- Guaranteed collision-free along piecewise polynomial trajectories
- Complete/globally optimal within convex decomposition
Not just for motion planning
- Tight formulations for many mixed discrete (on graphs) + continuous optimizations
- e.g. orders of magnitude faster for traveling salesman problems (TSP) with neighborhoods
- Task and motion planning
- Make Chris' "joint solution" approach tractable?
Graphs of Convex Sets


- The vertices in the graph are symbols.
- Adding continuous variables (convex sets) allows symbol grounding.
...and they are now deeply connected in the optimization.