Computing Lyapunov Functions II

Follow live at https://slides.com/d/ug2wzQI/live
(or later at https://slides.com/russtedrake/spring24-lec09)

MIT 6.8210: Underactuated Robotics
Spring 2024, Lecture 9

prog = MathematicalProgram()
x = prog.NewIndeterminates(2, "x")
f = [-x[0] - 2 * x[1]**2, -x[1] - x[0] * x[1] - 2 * x[1]**3]
V = x[0]**2 + 2 * x[1]**2
Vdot = V.Jacobian(x).dot(f)
prog.AddSosConstraint(-Vdot)
result = Solve(prog)
assert result.is_success()Verifying a Lyapunov candidate
prog = MathematicalProgram()
x = prog.NewIndeterminates(2, "x")
f = [-x[0] - 2 * x[1]**2, -x[1] - x[0] * x[1] - 2 * x[1]**3]
V = prog.NewSosPolynomial(Variables(x), 2)[0].ToExpression()
prog.AddLinearConstraint(V.Substitute({x[0]: 0, x[1]: 0}) == 0)
prog.AddLinearConstraint(V.Substitute({x[0]: 1, x[1]: 0}) == 1)
Vdot = V.Jacobian(x).dot(f)
prog.AddSosConstraint(-Vdot)
result = Solve(prog)
assert result.is_success()Searching for a Lyapunov candidate
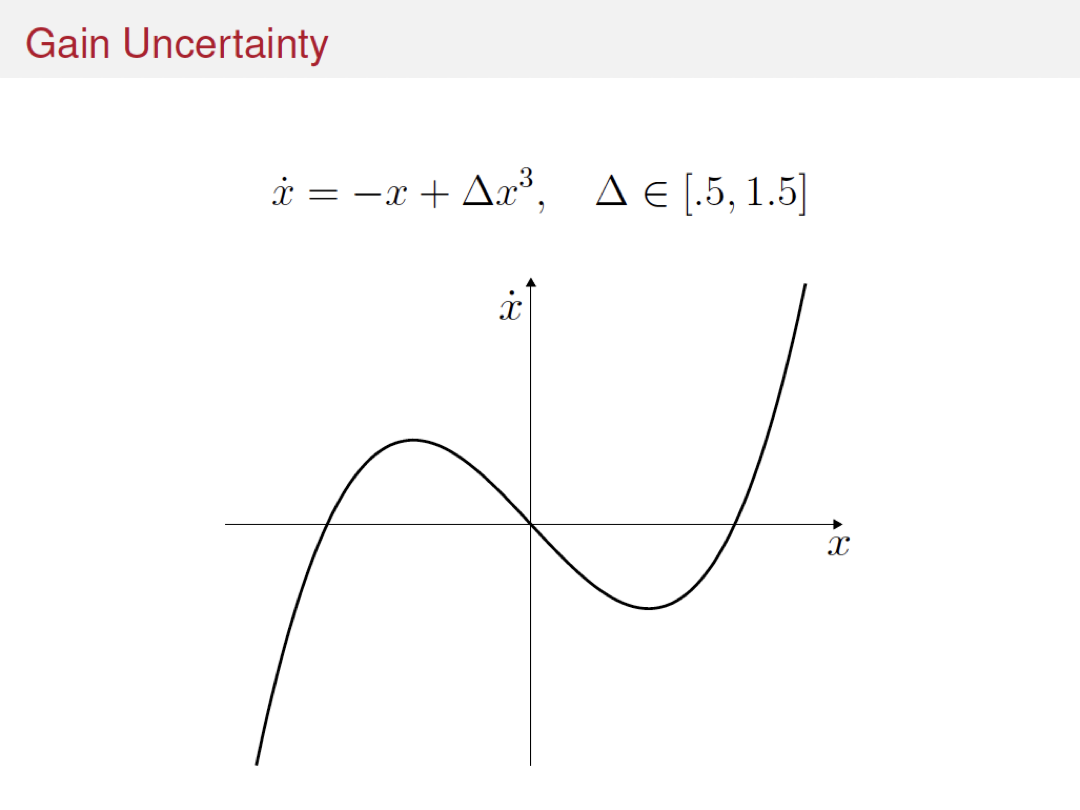
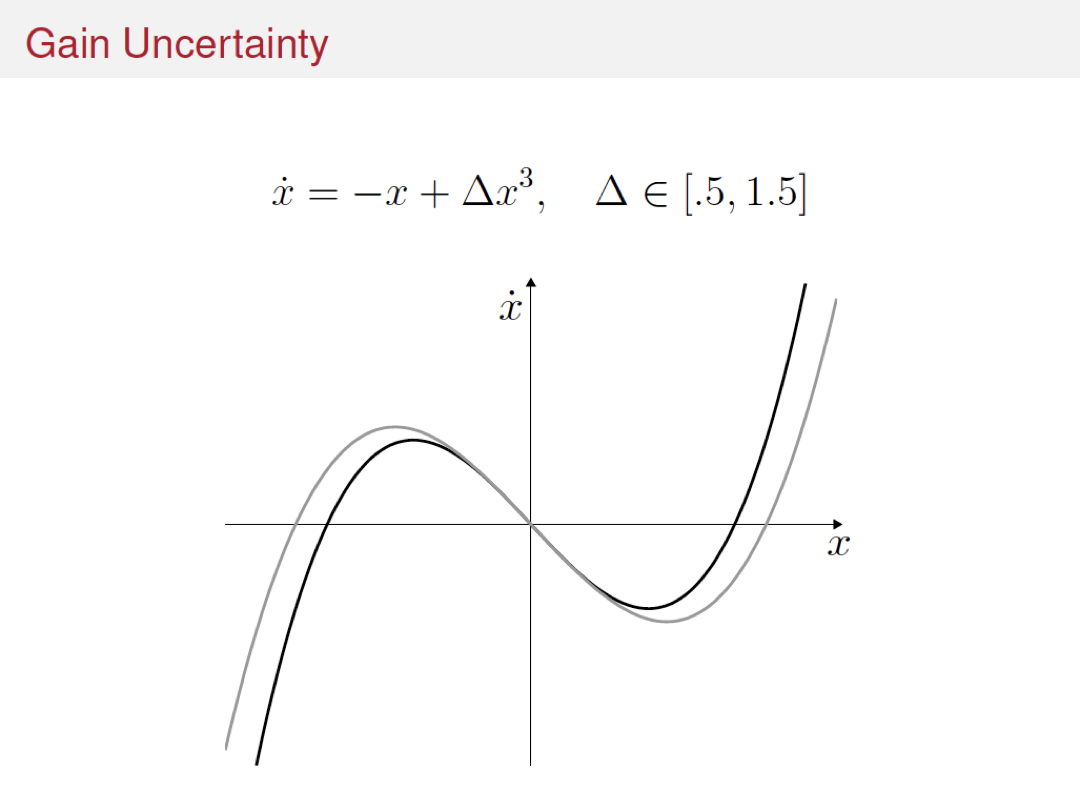
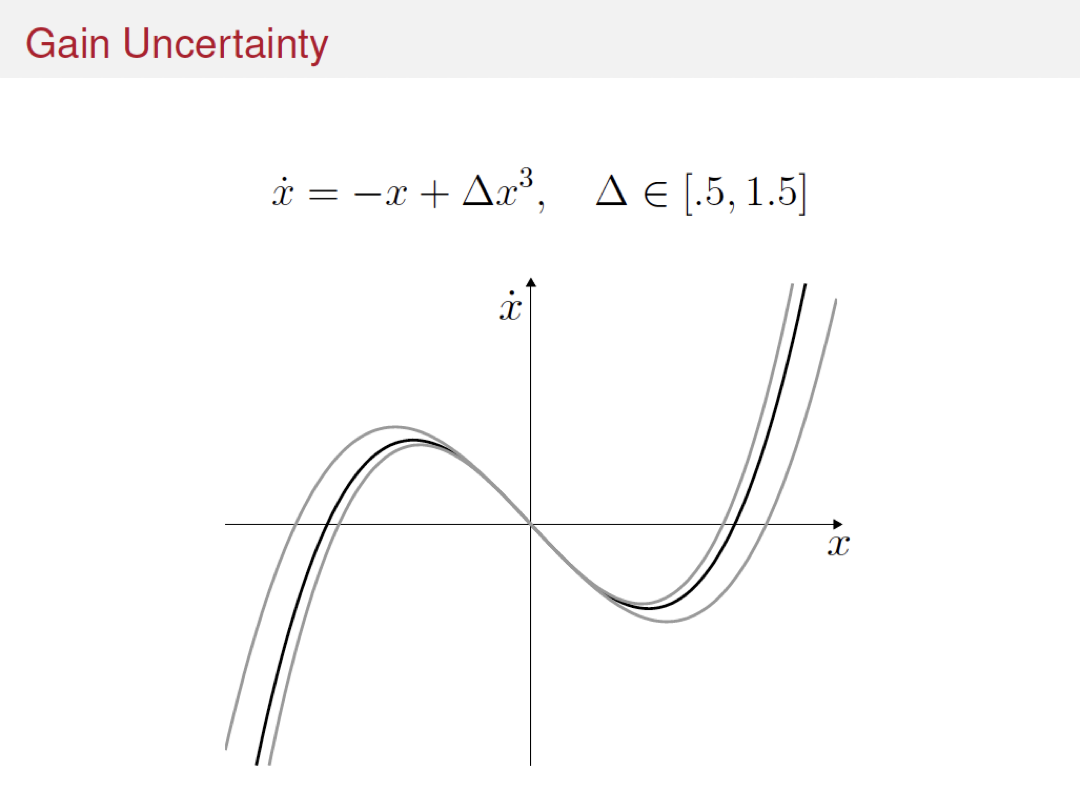
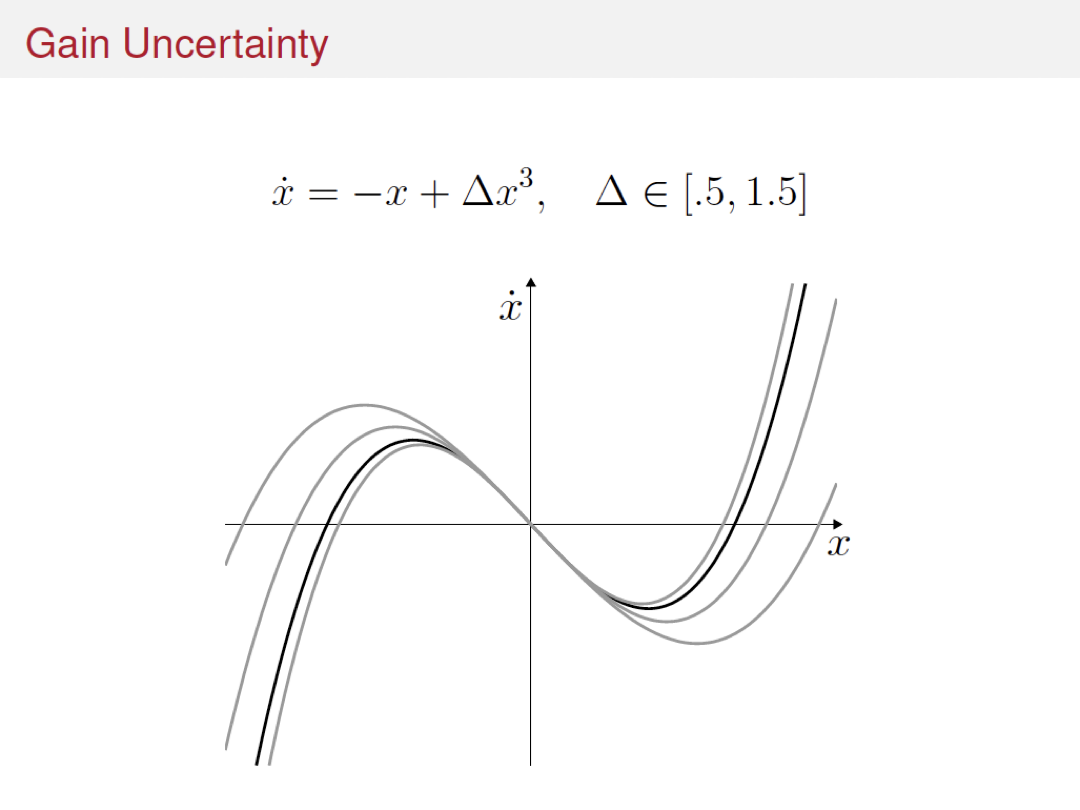
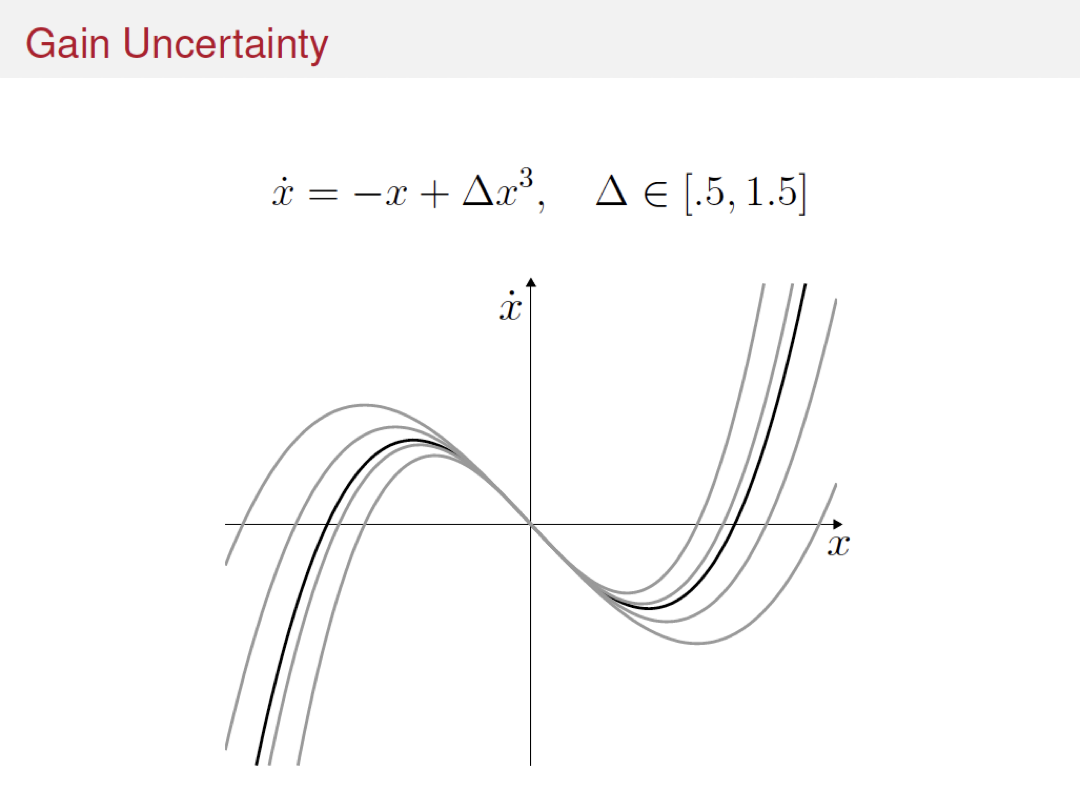
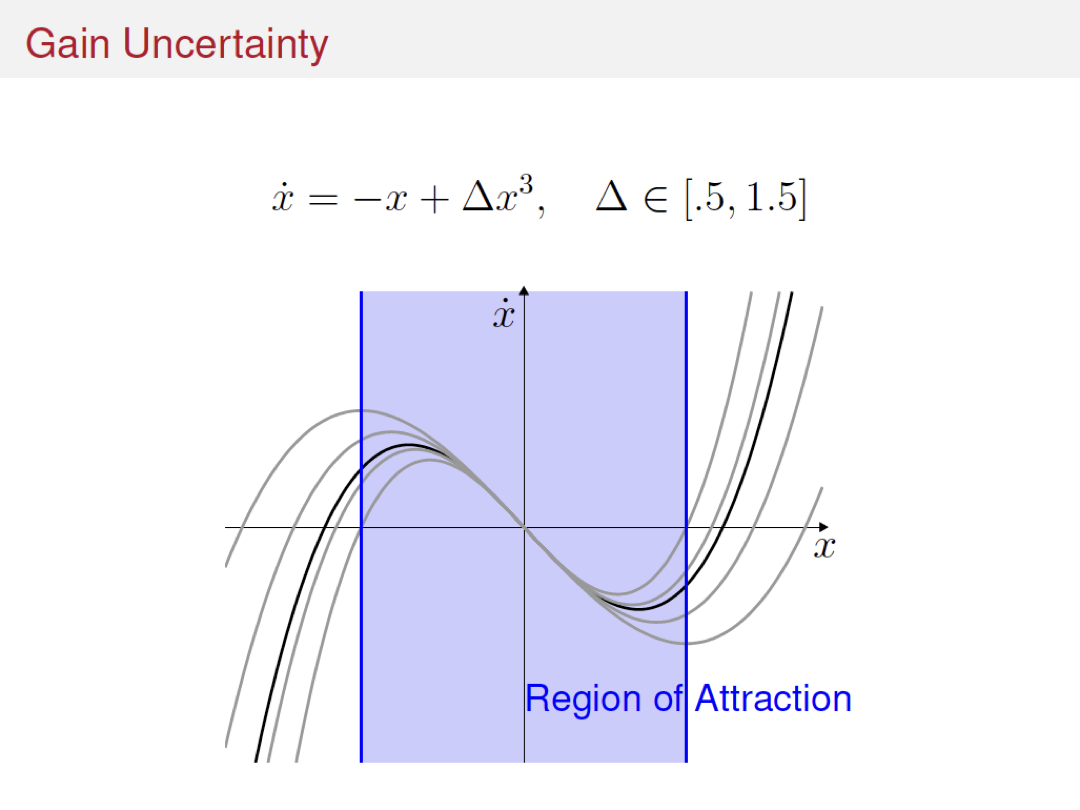
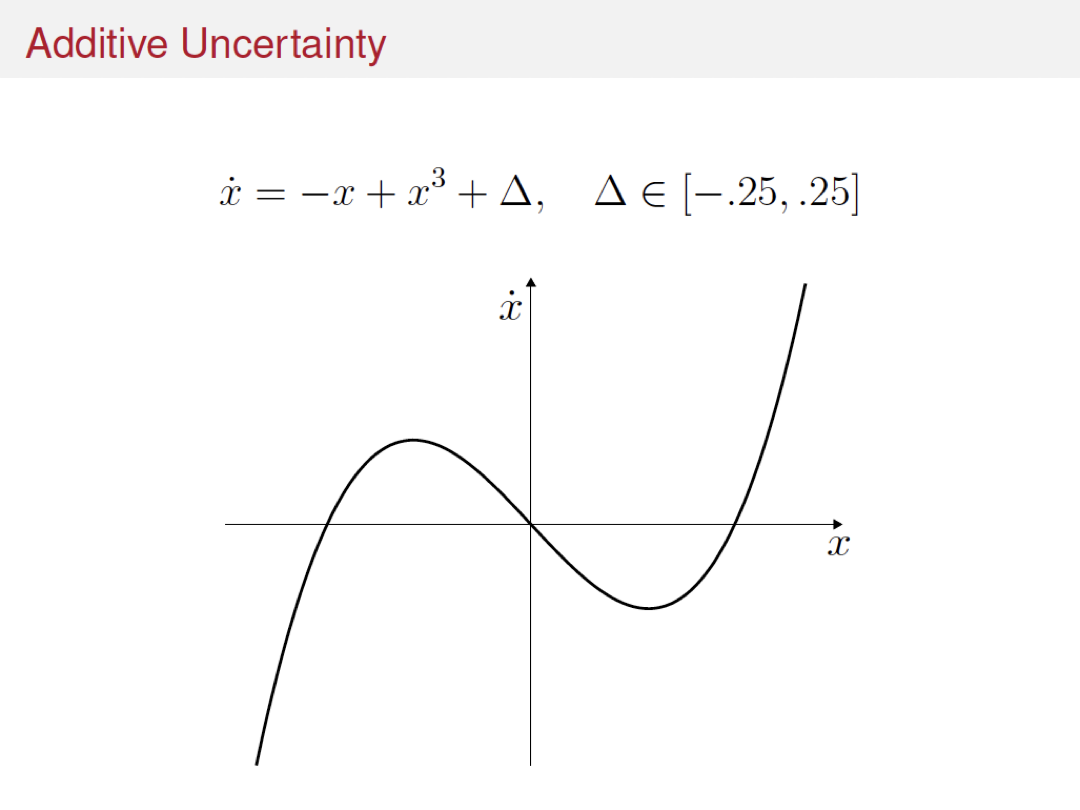
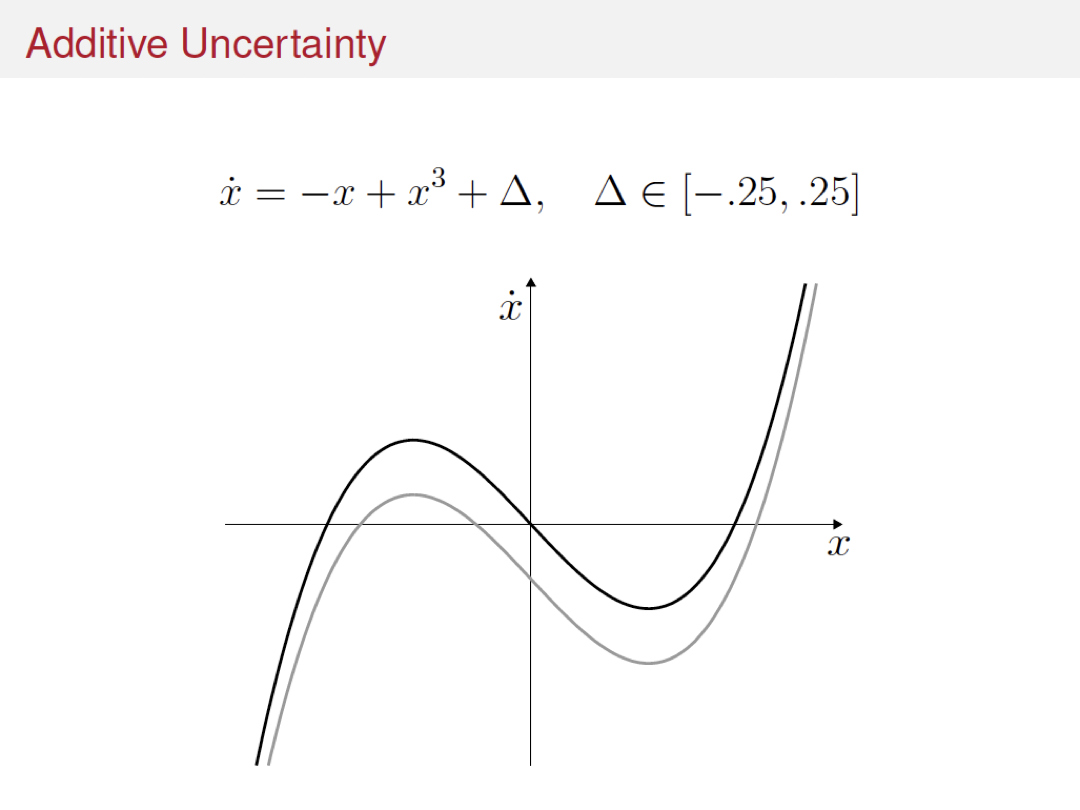
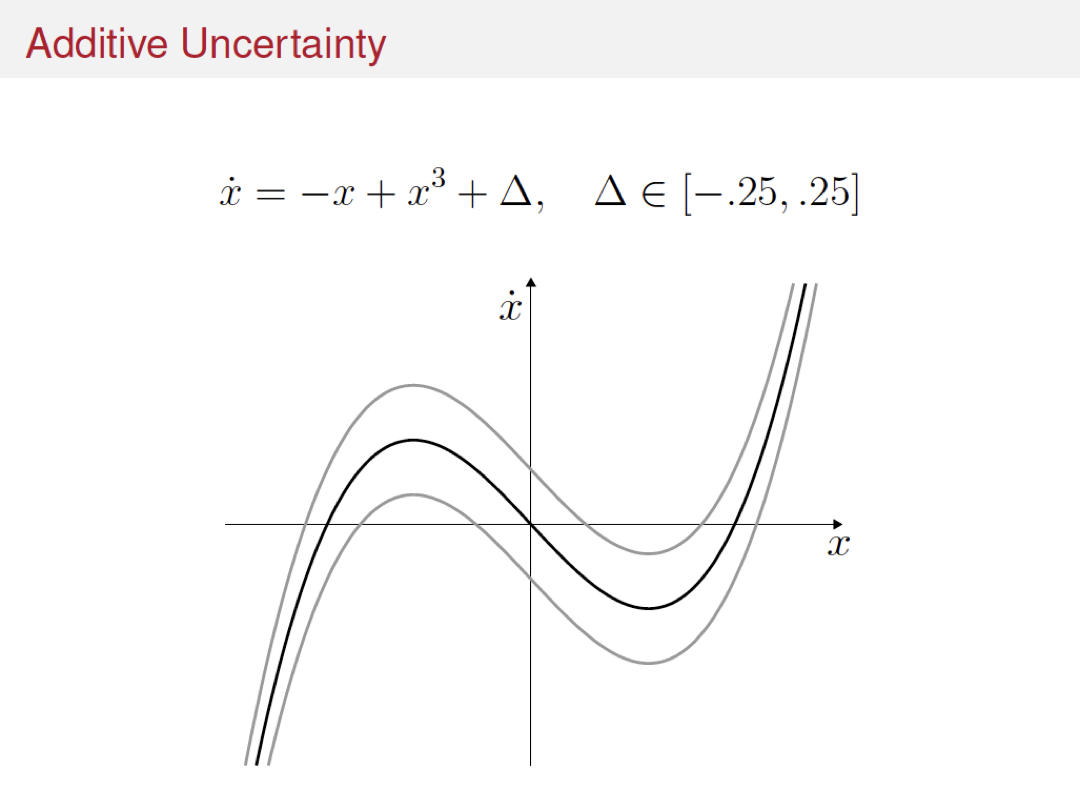
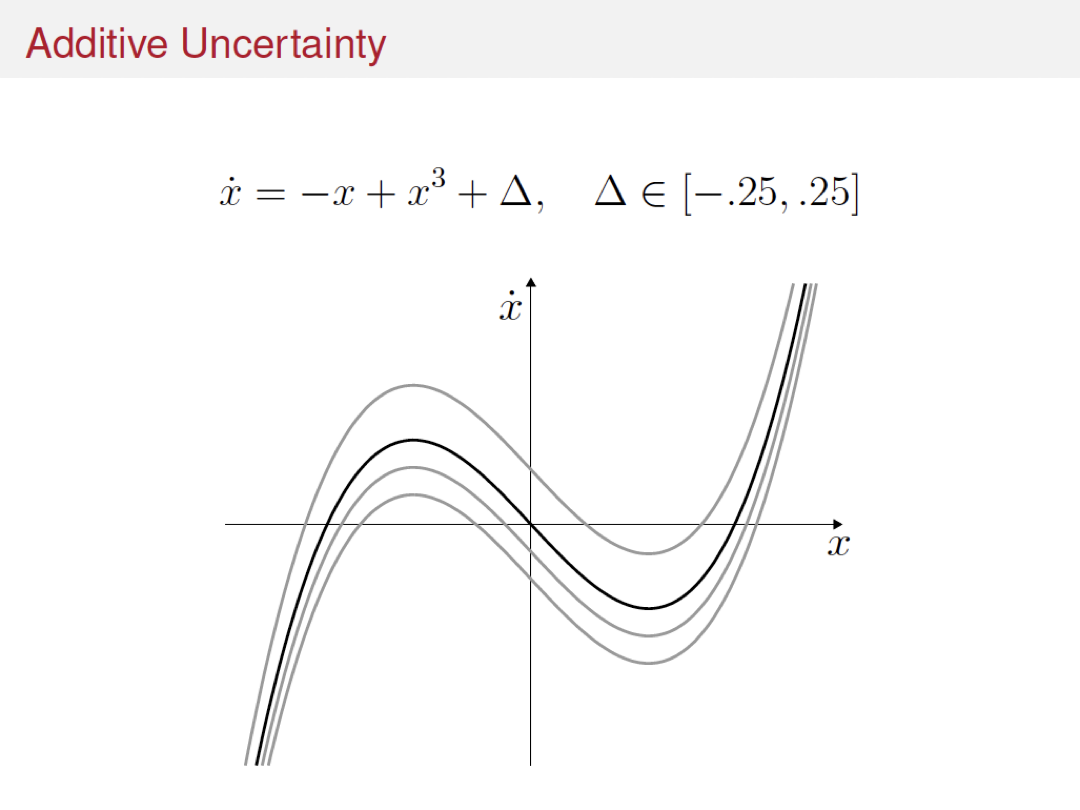
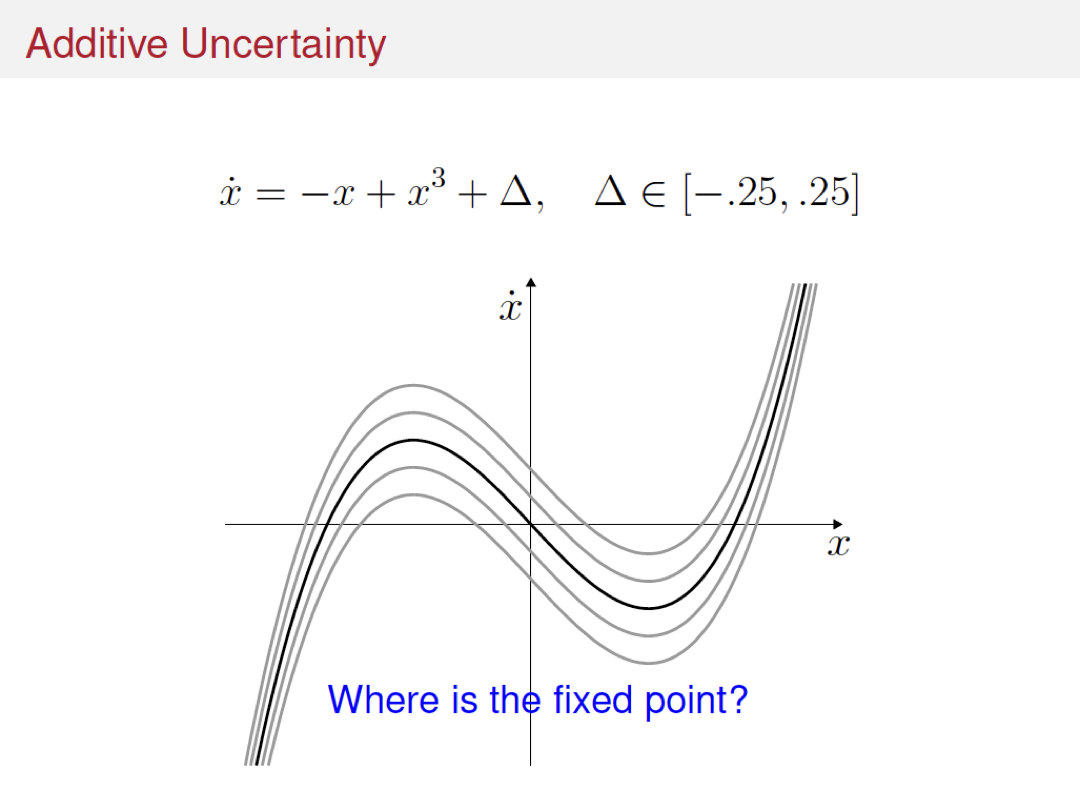
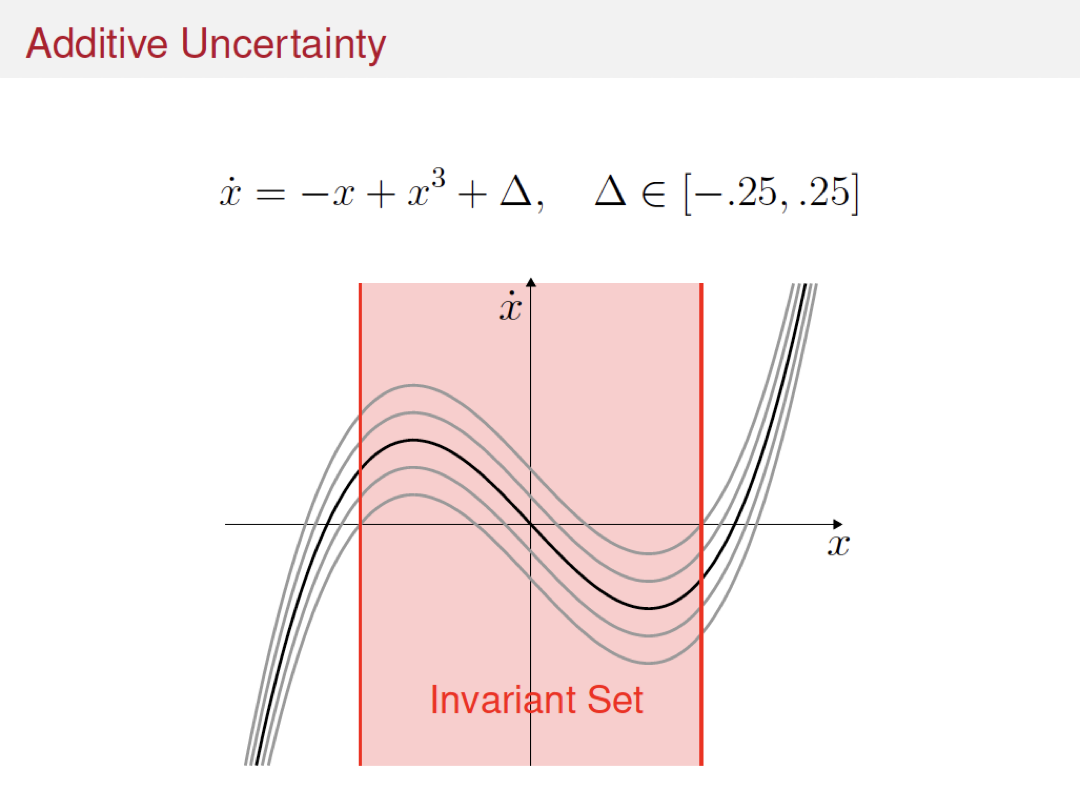
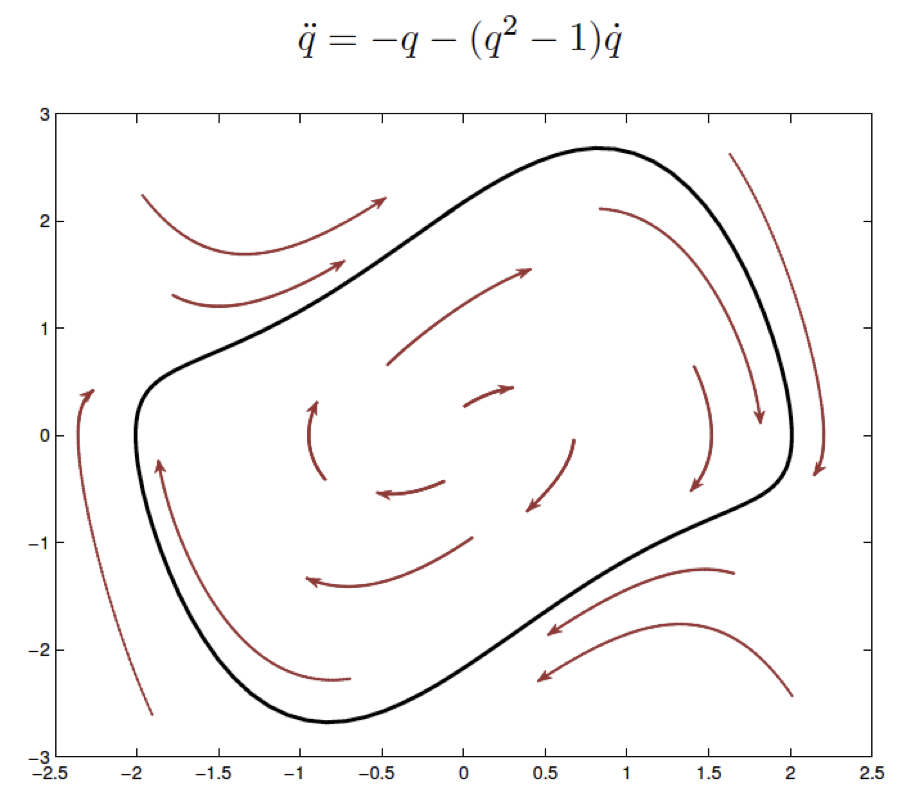
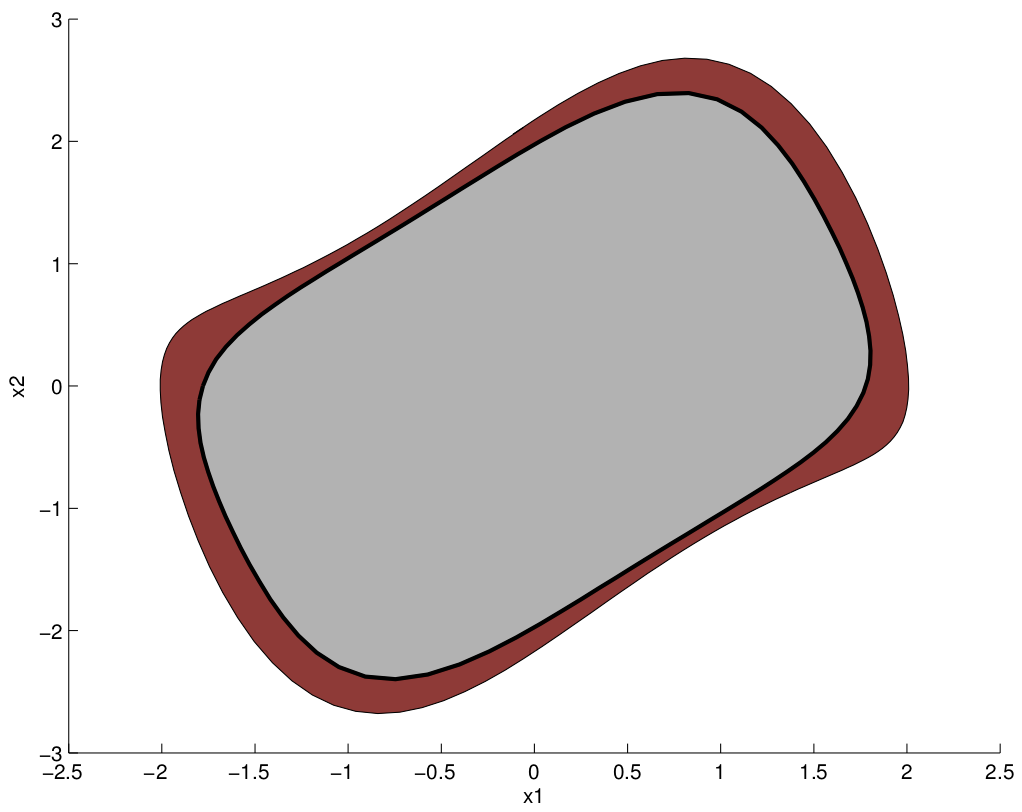
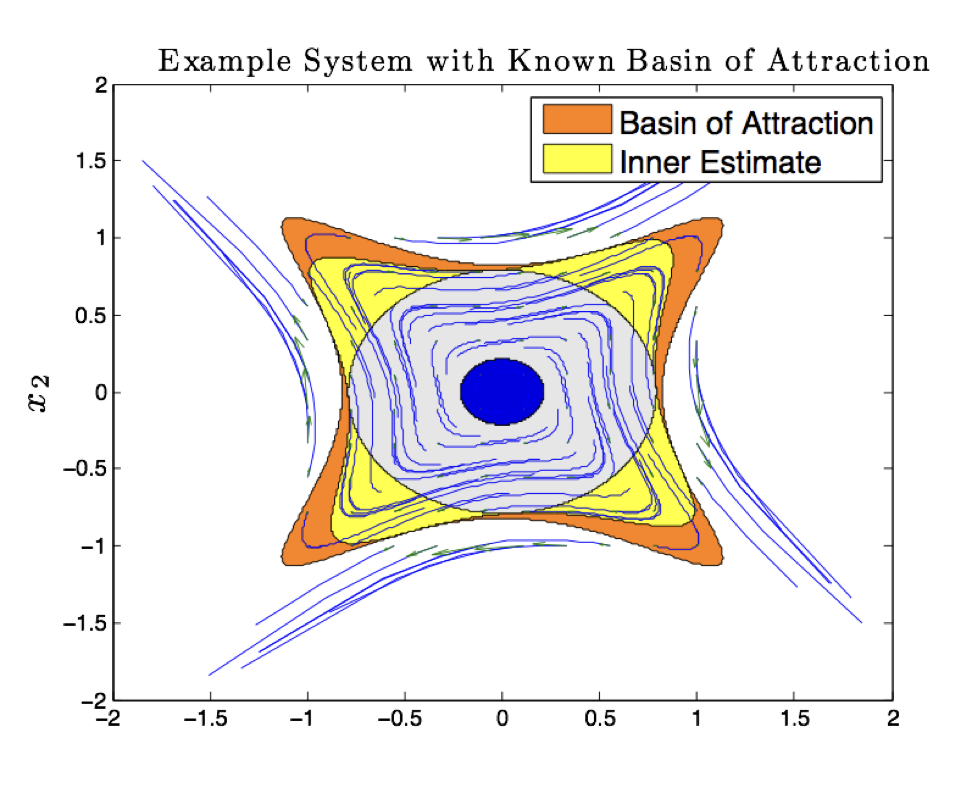

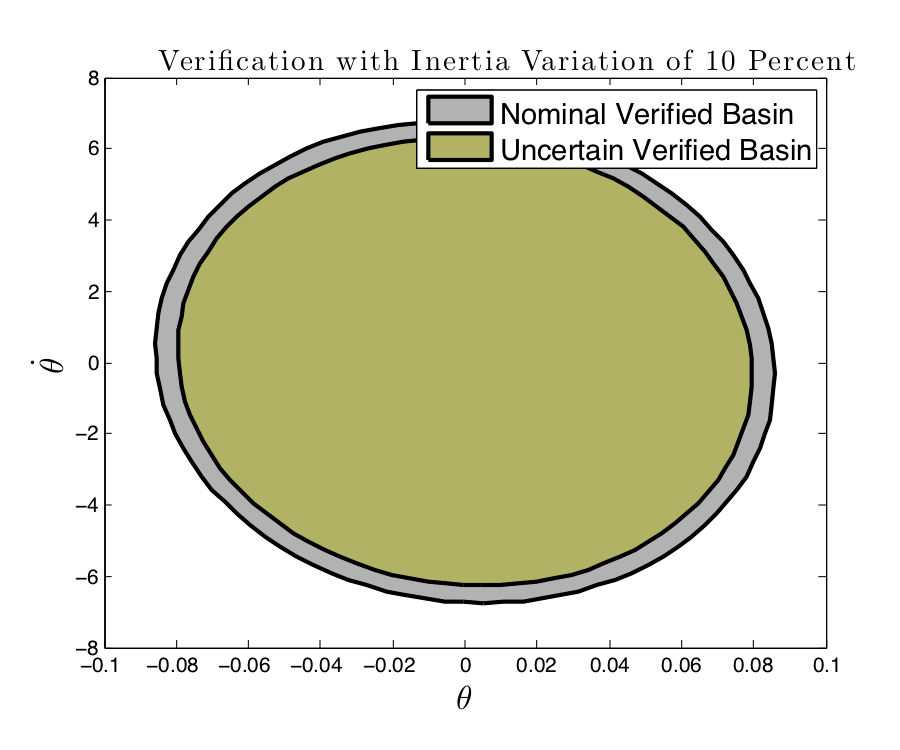
Variations and extensions
- Implicit dynamics
- Piecewise-continuous dynamics
- e.g. closed-loop w/ input limits
- contact mechanics
