Absorbing State Transitions in Monitored Systems
Sagnik Ghosh
For the Cond. Mat Journal Club

A meme
Background: Dynamical Phases
Consider Hamiltonians XXZ models on 1d chain. Shows Phase Transitions in Dynamics of Entanglement properties.
Bi-partite entanglement entropy grows as volume law in scrambling phase while in localised phase it grows as area law.
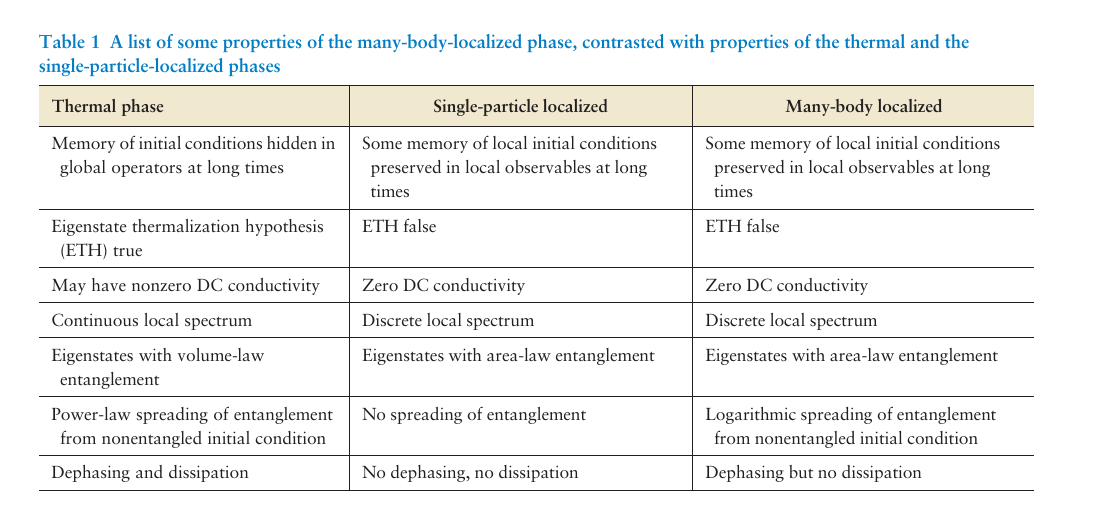
Background: Localisation
A. Disorder: Single particle, in presence of disorder

Background: Localisation
B. Many Body: Extensive number of local conserved quantities


Background: Localisation
B. Many Body: Extensive number of local conserved quantities
Background: Dynamical Phases
What are the other ways to stop a interacting Hamiltonian from scrambling?
B. measurement
A. background gauge charges
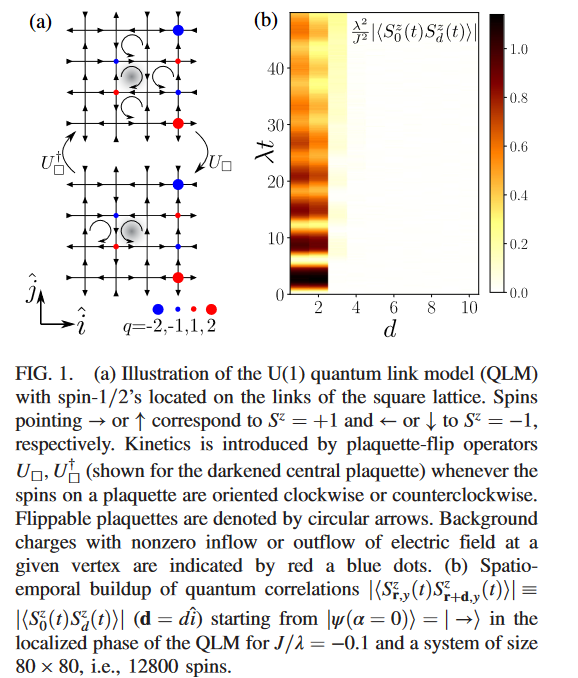
M Heyl et al. PRL 126, 130401 (2021)

Skinner et al. PRX 9, 031009 (2019)

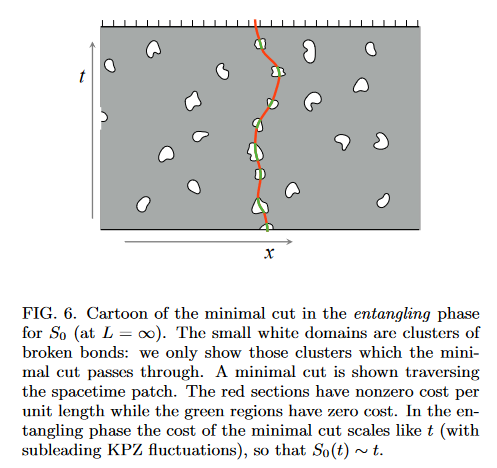
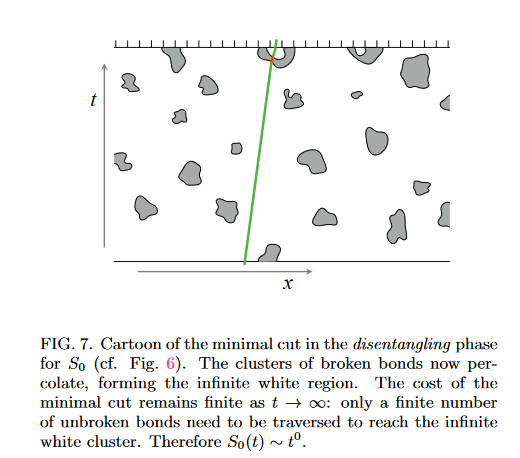
Measurement Induced Phase Transition
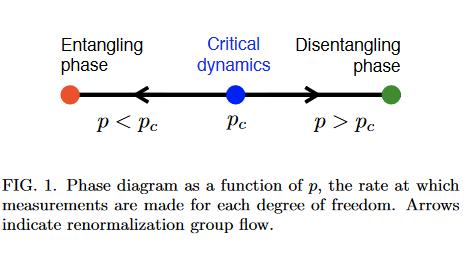

Skinner et al. PRX 9, 031009 (2019)

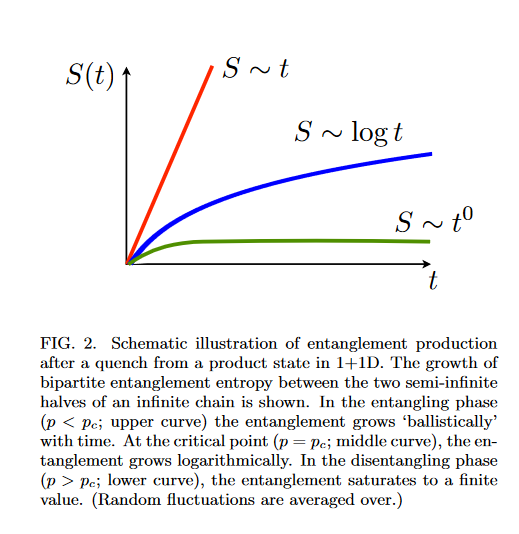
Measurement Induced Phase Transition
Skinner et al. PRX 9, 031009 (2019)
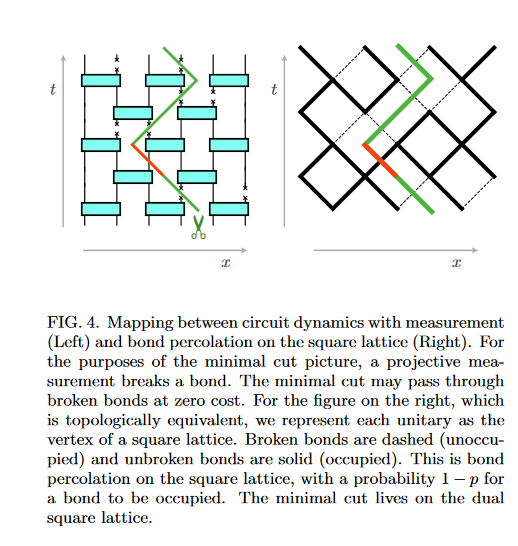
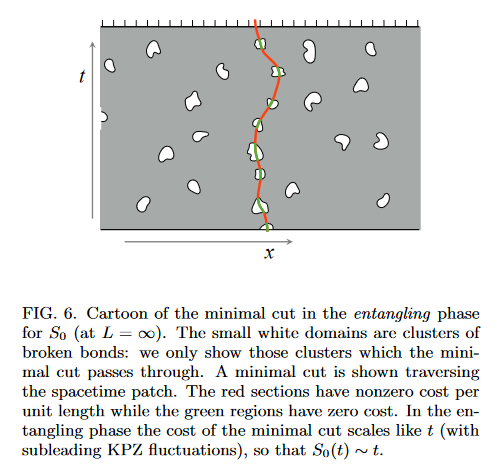
Measurement Induced Phase Transition
Skinner et al. PRX 9, 031009 (2019)

Experiental Realisation
The problem with Post Selection:
While taking the ensemble avg one has to only consider the trajectories which are labeled by the same measurement outcomes.
This requirement needs preparation of the exact same measurement outcomes after the random unitaries have applied experimentally, the volume of which scales exponentially with the system size.
Alternatives?
Vedika et al.
Model 1:
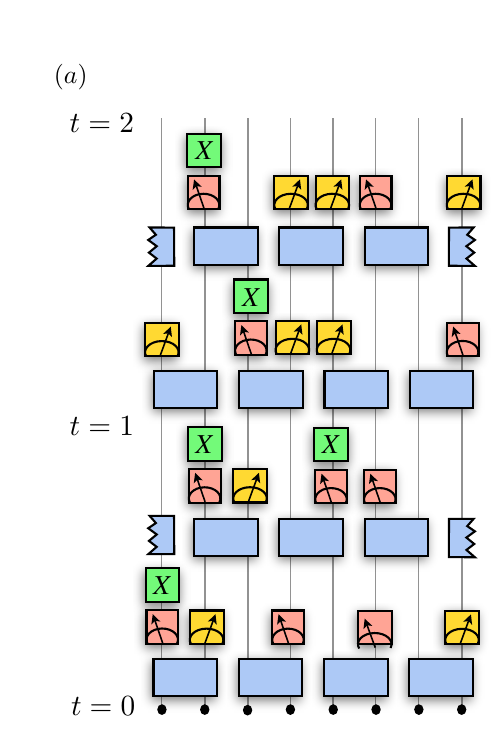
- periodic boundary conditions
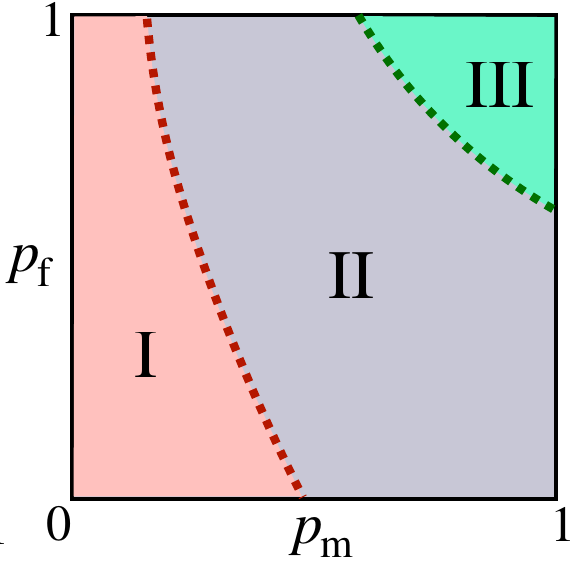
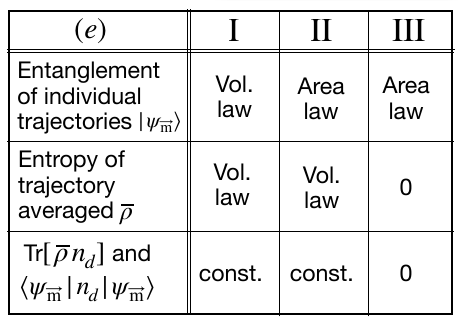
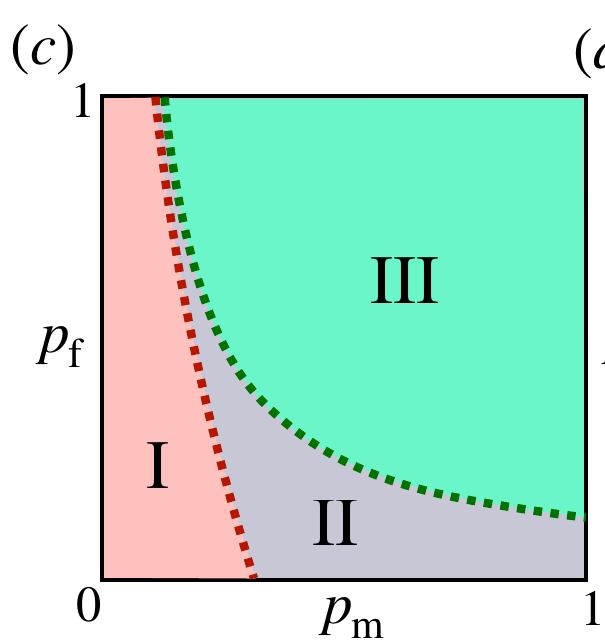
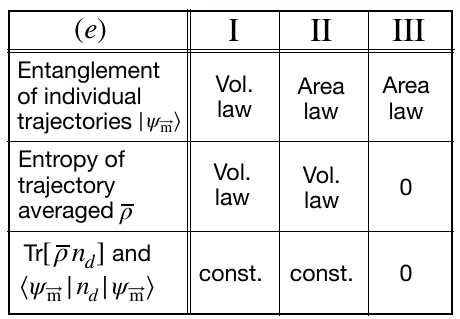
Model 1: Phase Diagram
1. for pf=0 it shows the usual MIPT. At small enough pm the rate pm*pf is till small enough, s.t the state remains non abosorbing even at pf=1
Trajectory averaged density matrix has a volume law in this phase.
2. increasing pm changes transitions us to the area law phase.
Avergaing over trajectories with random sequences of +-1 still produces a density matrix with extensive entropy.
3. (Note our target state has a pure density matrix). With increase of pf we enter a phase where all trajectories rapidly enter target state.
Model 1: Phase Diagram

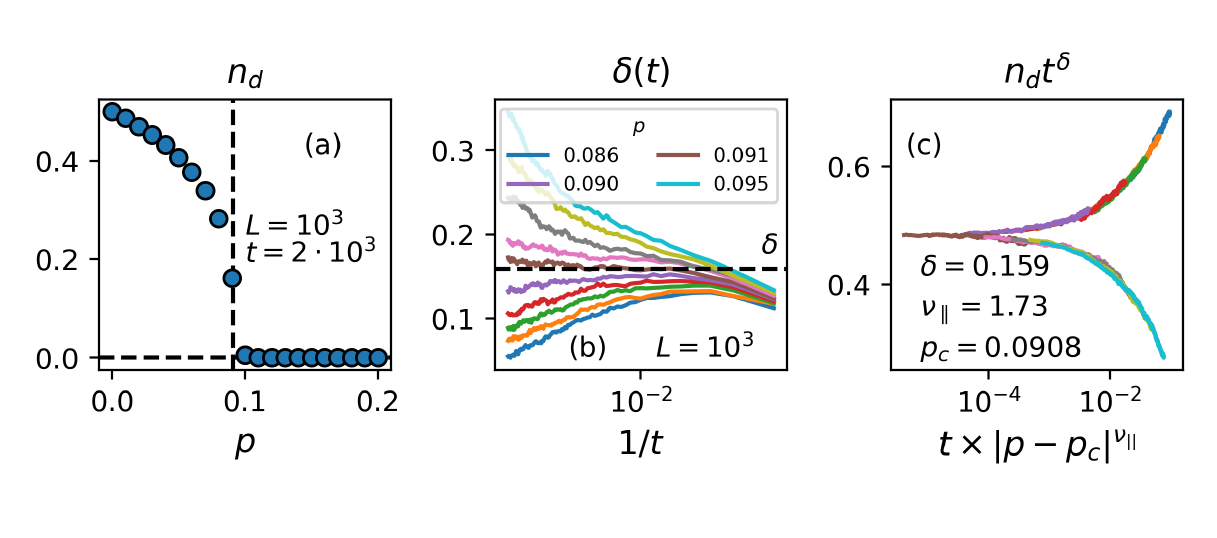
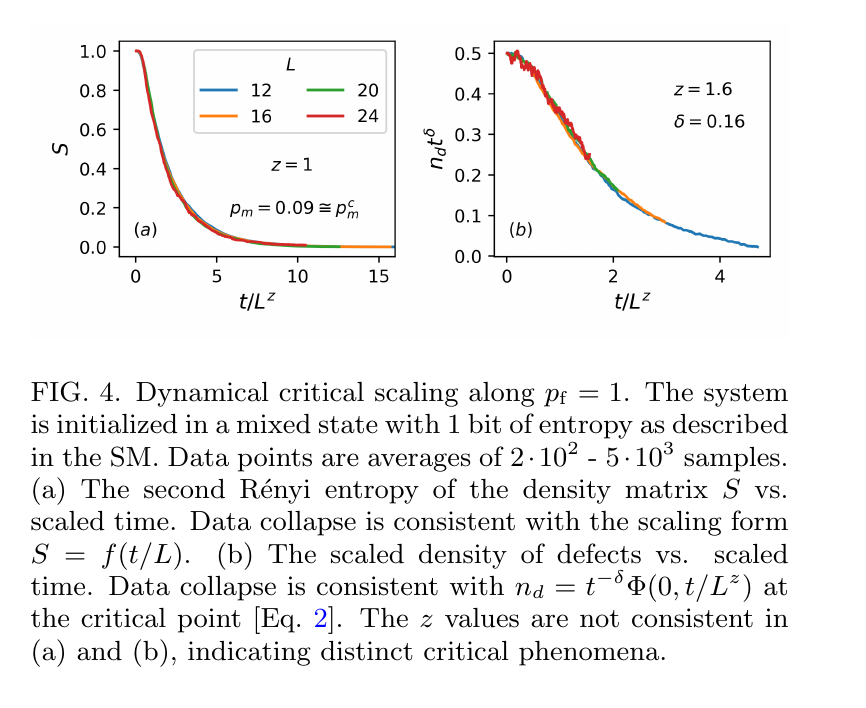
Critical Exponents:

Model 1: Phase Transition
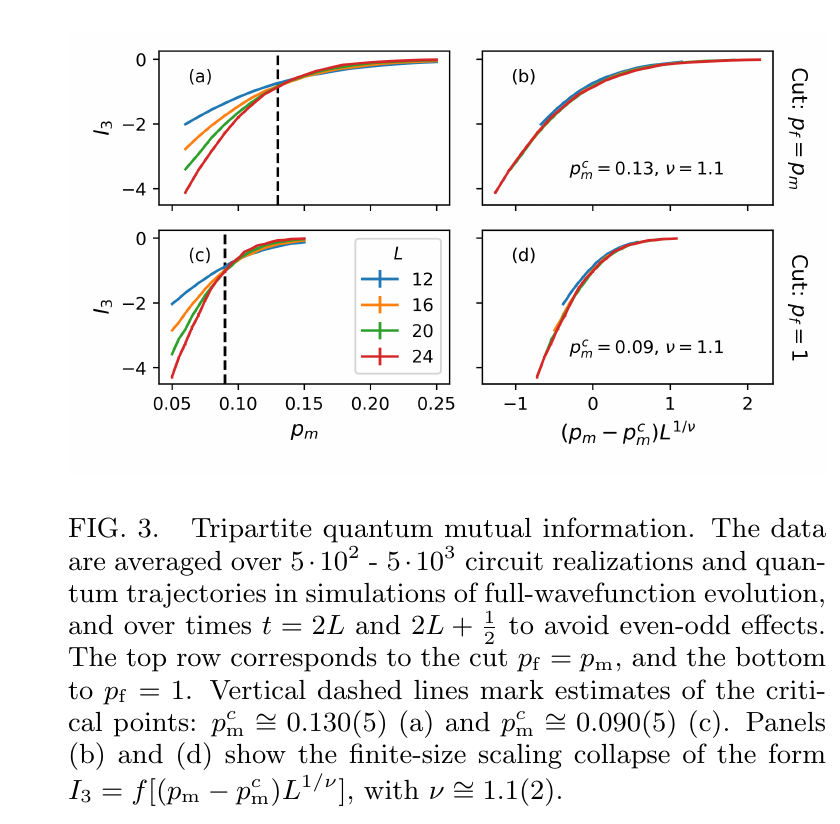
Model 1: at full feedback are the two transitions same?


Model 1: at full feedback are the two transitions same?
Model 2:

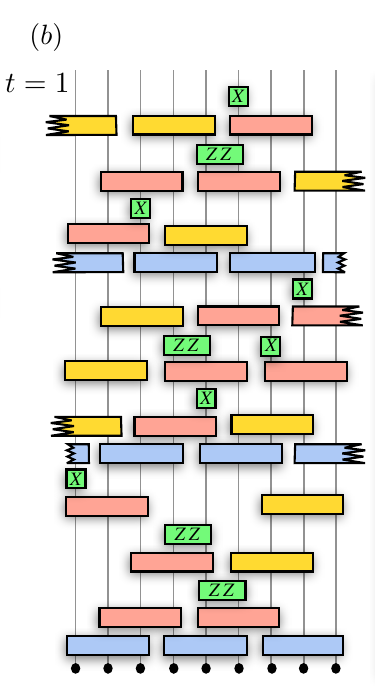
Text
Model 2:
| Corrective Gate |
Symmetry | Phase Diagram |
|---|---|---|
| C_i=-1 flipped with Z_i | brocken | same as model 1 |
| C_i=-1 flipped with X_i-1 or X_i+1 | preserved | too seperated |
| C_i=-1 flipped with X_i-1 ,X_i+1, Z_i-1Zi ,Z_iZ_i+1 | breaks Z2xZ2 but preserves overall parity |
shows phase separaation |
(for 2 the correction either hops errors or corrects them in pairs)
Model 2: Phase Diagram for case 3