En búsqueda de la Energía Oscura con Euclid y experimentos cosmológicos de cuarta generación

 

 

 

Santiago Casas

 

 

Postdoctoral Researcher

TTK, RWTH Aachen University

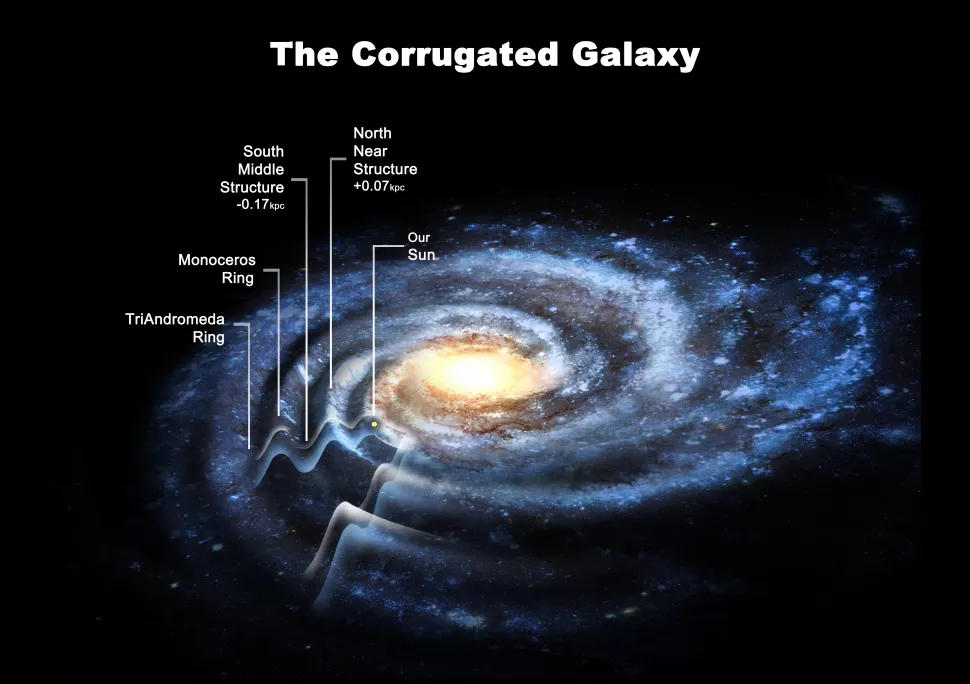
La Vía Láctea

http://www.esa.int/Science_Exploration/Space_Science

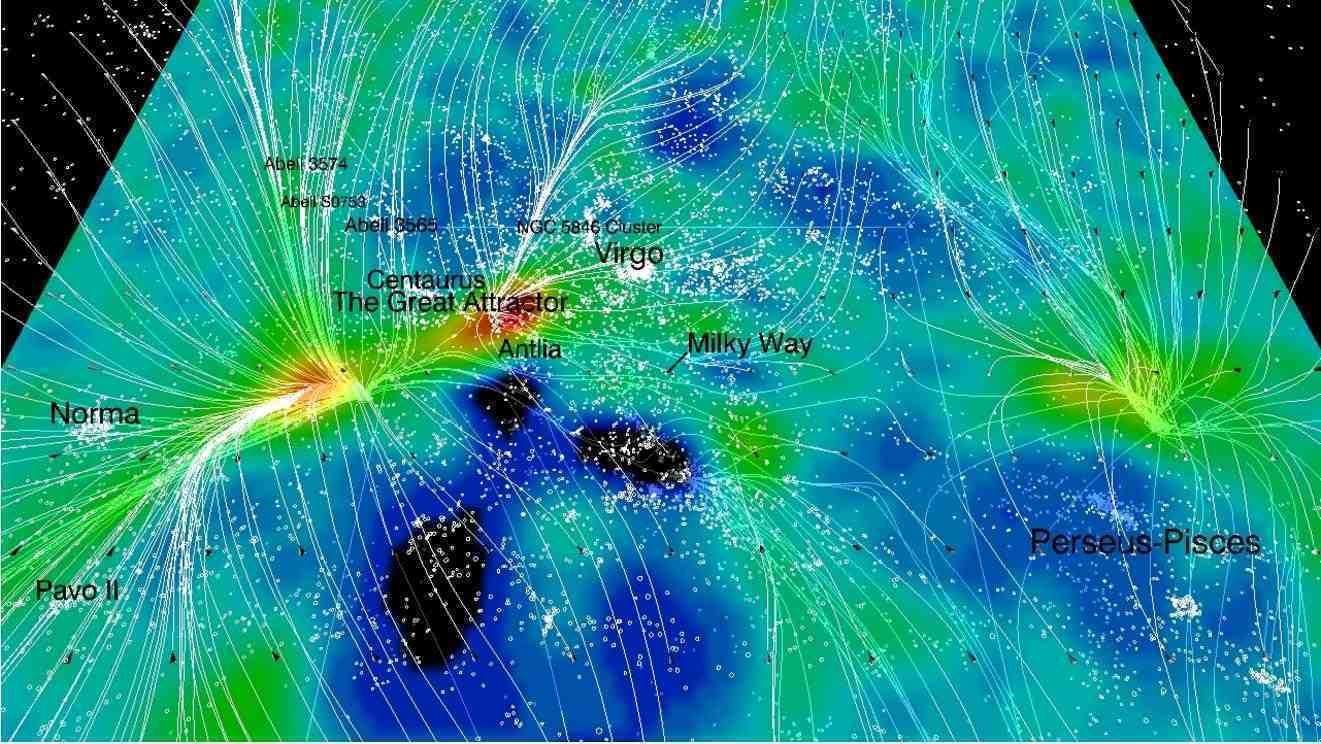
El Universo Local

Laniakea: https://projets.ip2i.in2p3.fr//cosmicflows/

La red cósmica

Millenium Simulation: https://wwwmpa.mpa-garching.mpg.de/

Grandes estructuras del Universo

Illustris Simulation: www.nature.com/articles/nature13316

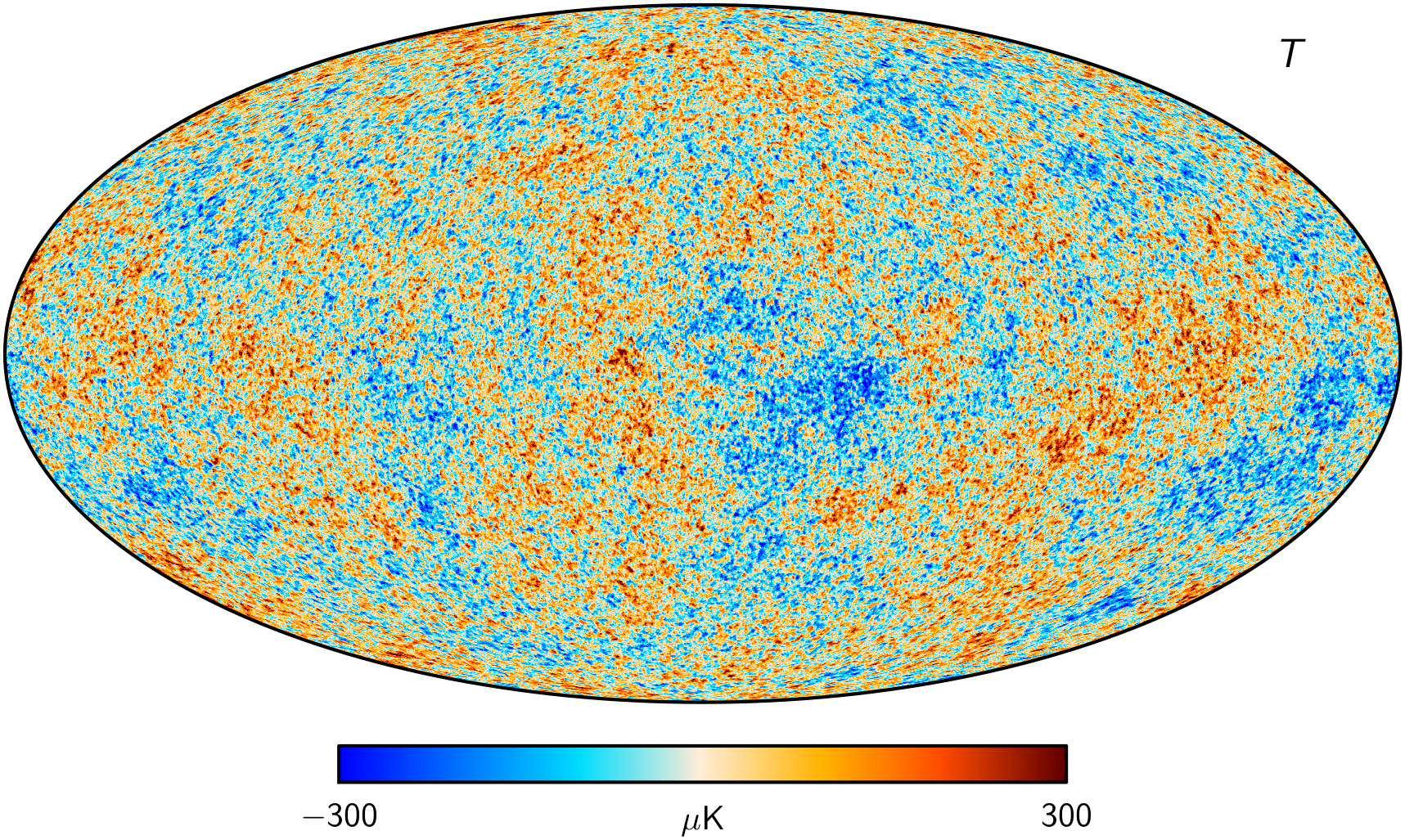
Radiación Cósmica de Fondo de Microondas (CMB)

Planck 2018 CMB Temperature map (Commander) .  wiki.cosmos.esa.int/planck-legacy-archive/index.php/CMB_maps

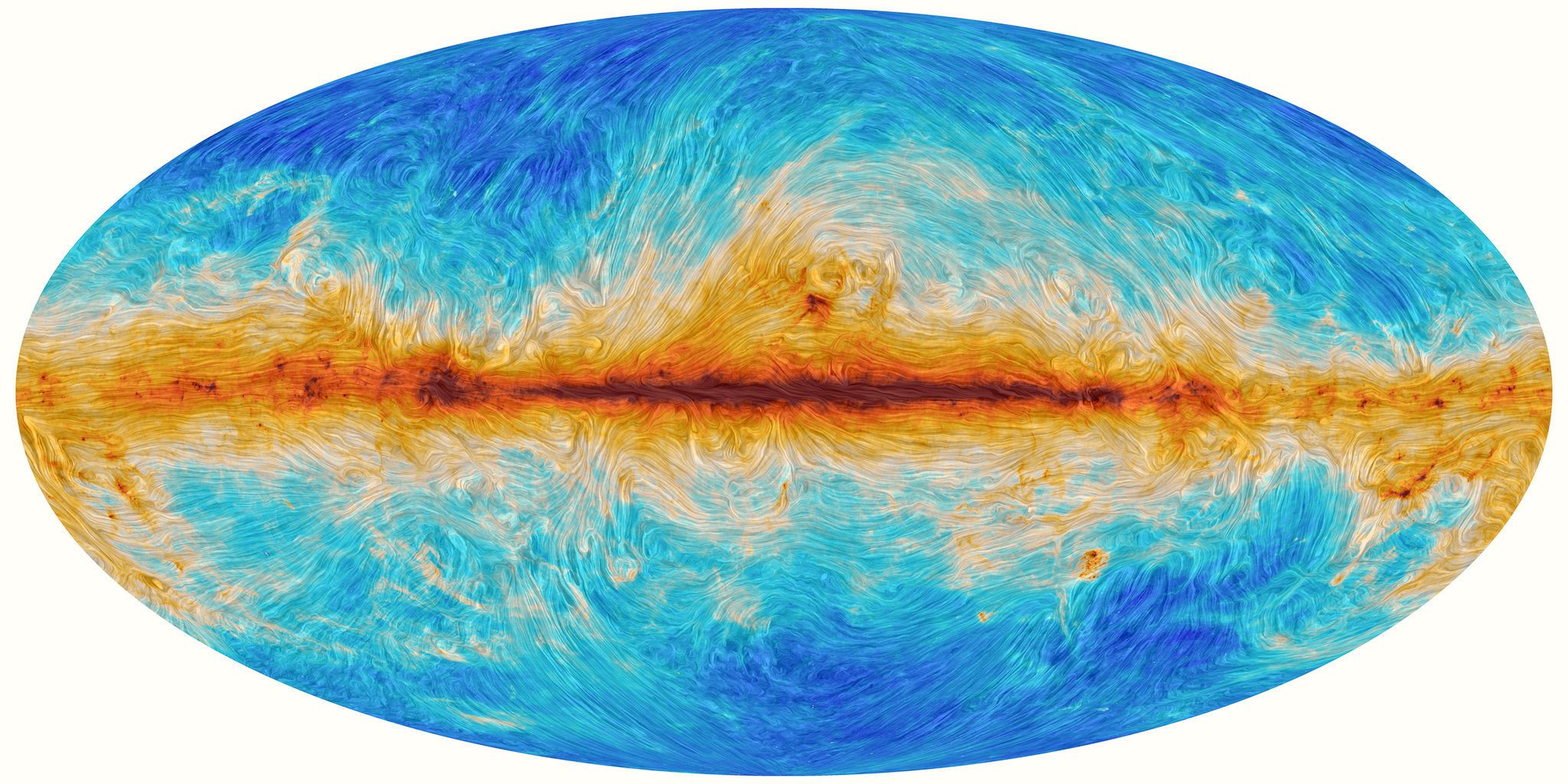
Radiación Cósmica de Fondo de Microondas (CMB)

Planck 2018 CMB Dust polarization map .  wiki.cosmos.esa.int/planck-legacy-archive/index.php/CMB_maps

La Historia de Expansión del Universo

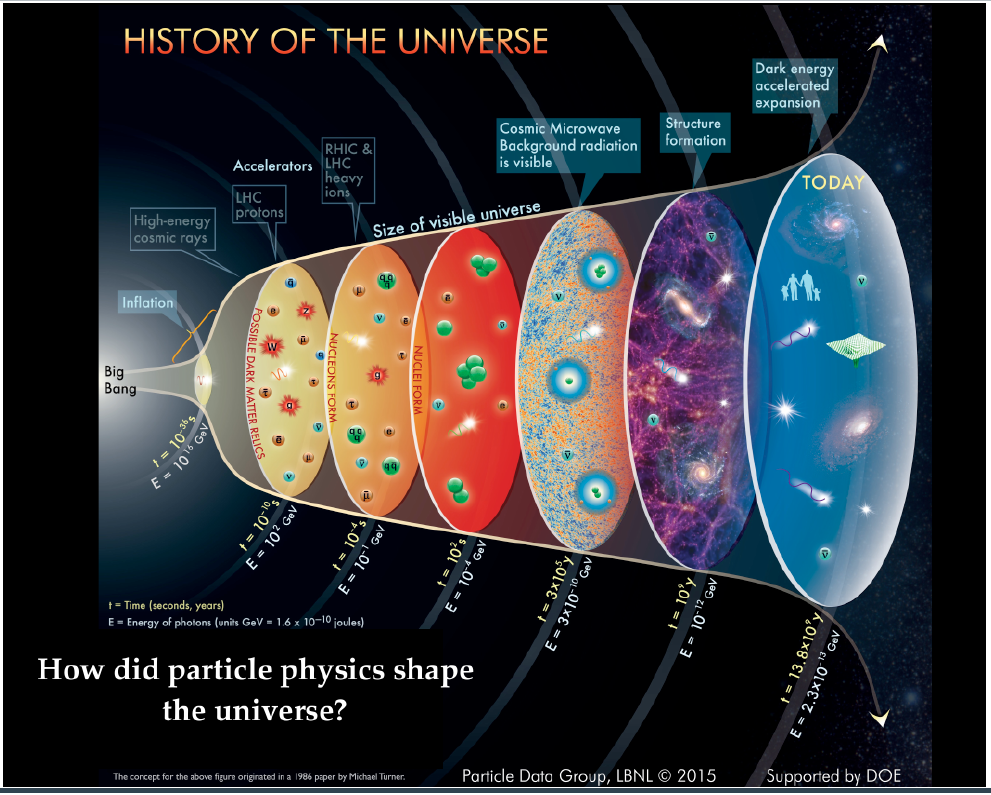
  • Inflation
  • Baryo/Leptogenesis
  • Recombination
  • Neutral Hydrogen
  • Dark Matter structures
  • Galaxies
  • Accelerated expansion

 

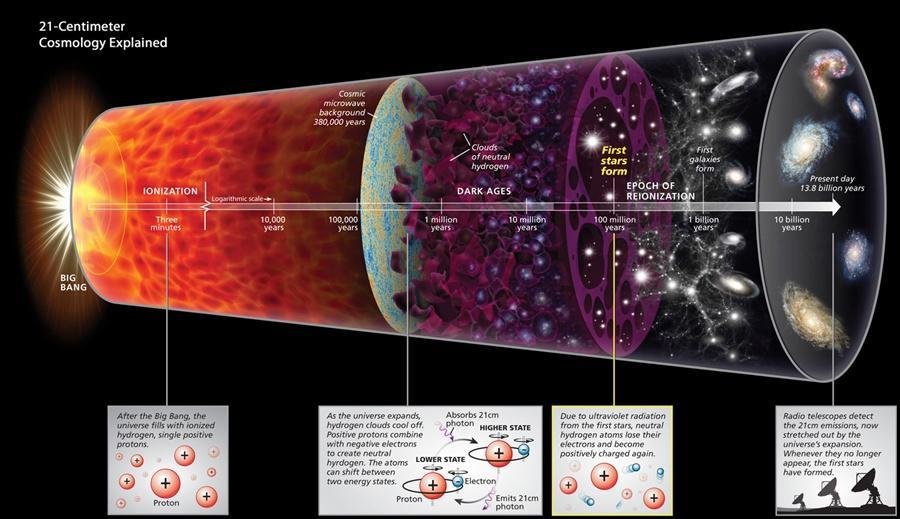
La Historia de Expansión del Universo

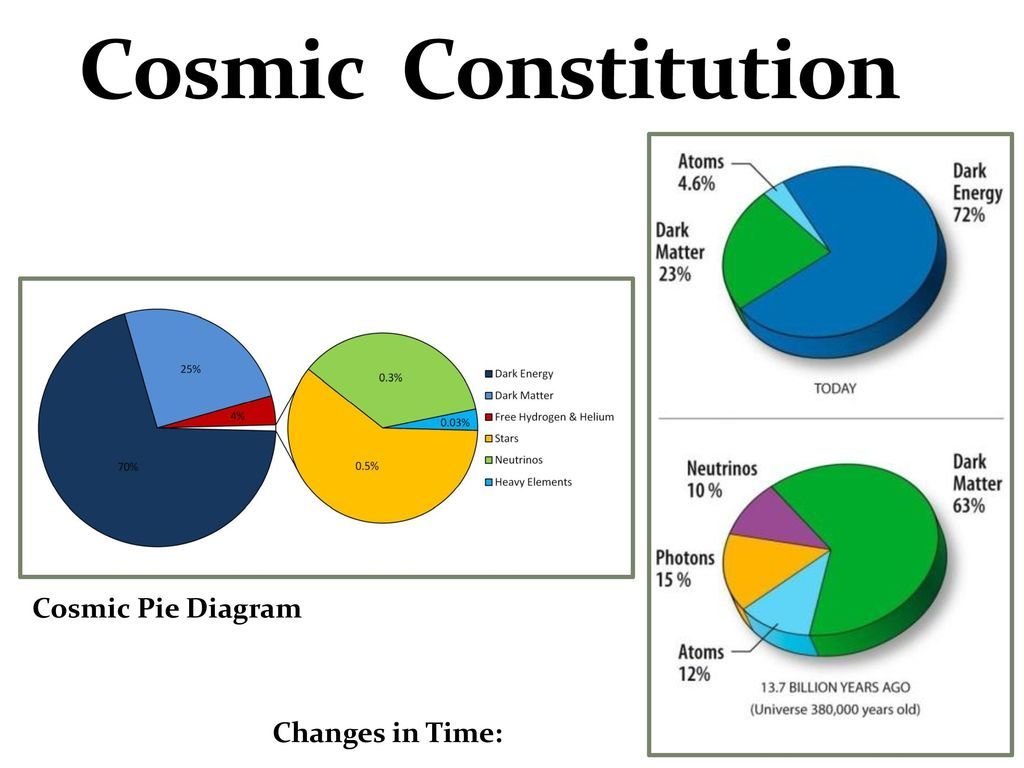
La composición del Universo

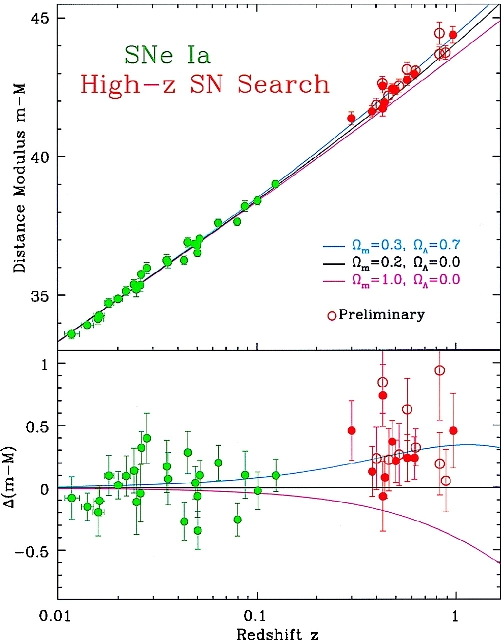
El Modelo Estándar: \(\Lambda\)CDM

G_{\mu \nu} + \Lambda g_{\mu \nu} = 8\pi G T_{\mu \nu}

Ecuación de campo de Einstein

Supernovas 1998, Premio Nobel 2011

Relatividad General y
condiciones iniciales cuánticas

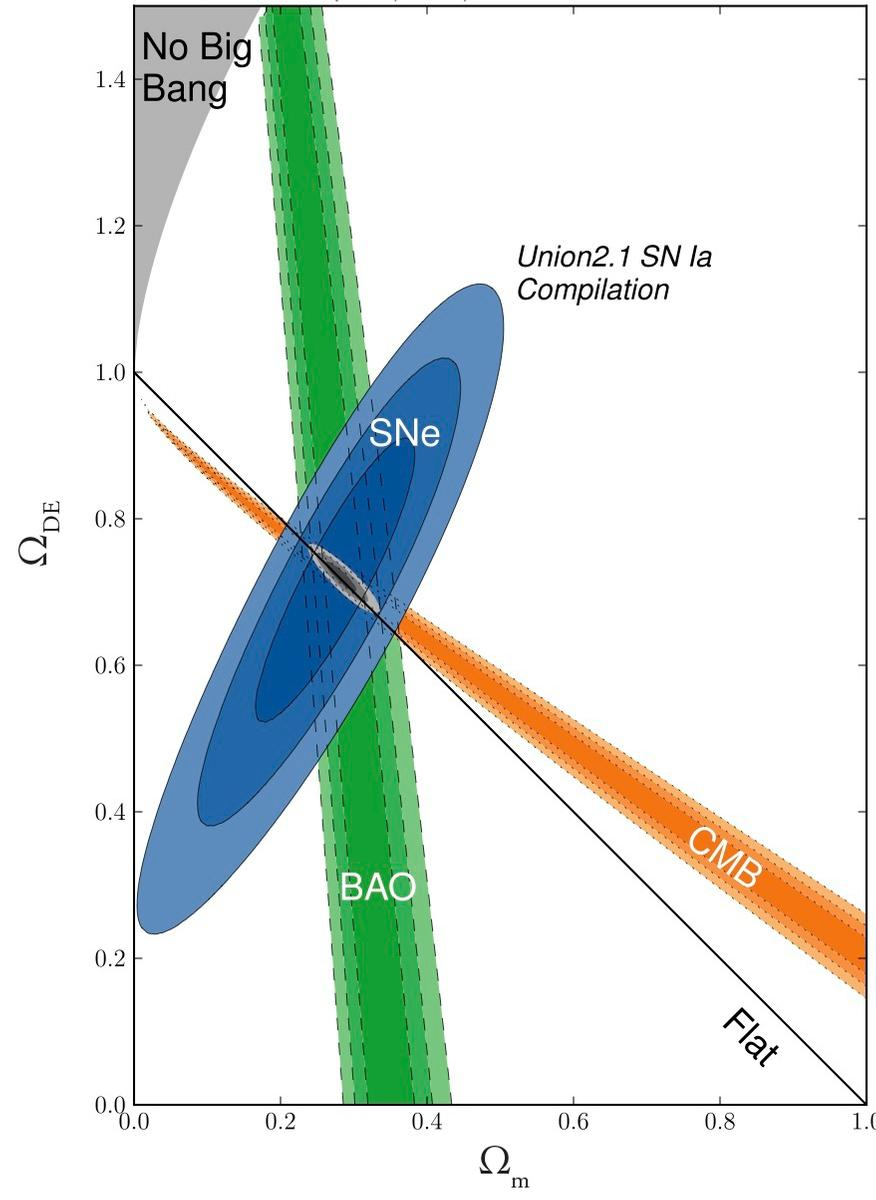
Concordancia de observaciones, CMB (Premio Nobel 2006, COBE)

The Standard \(\Lambda\)CDM model

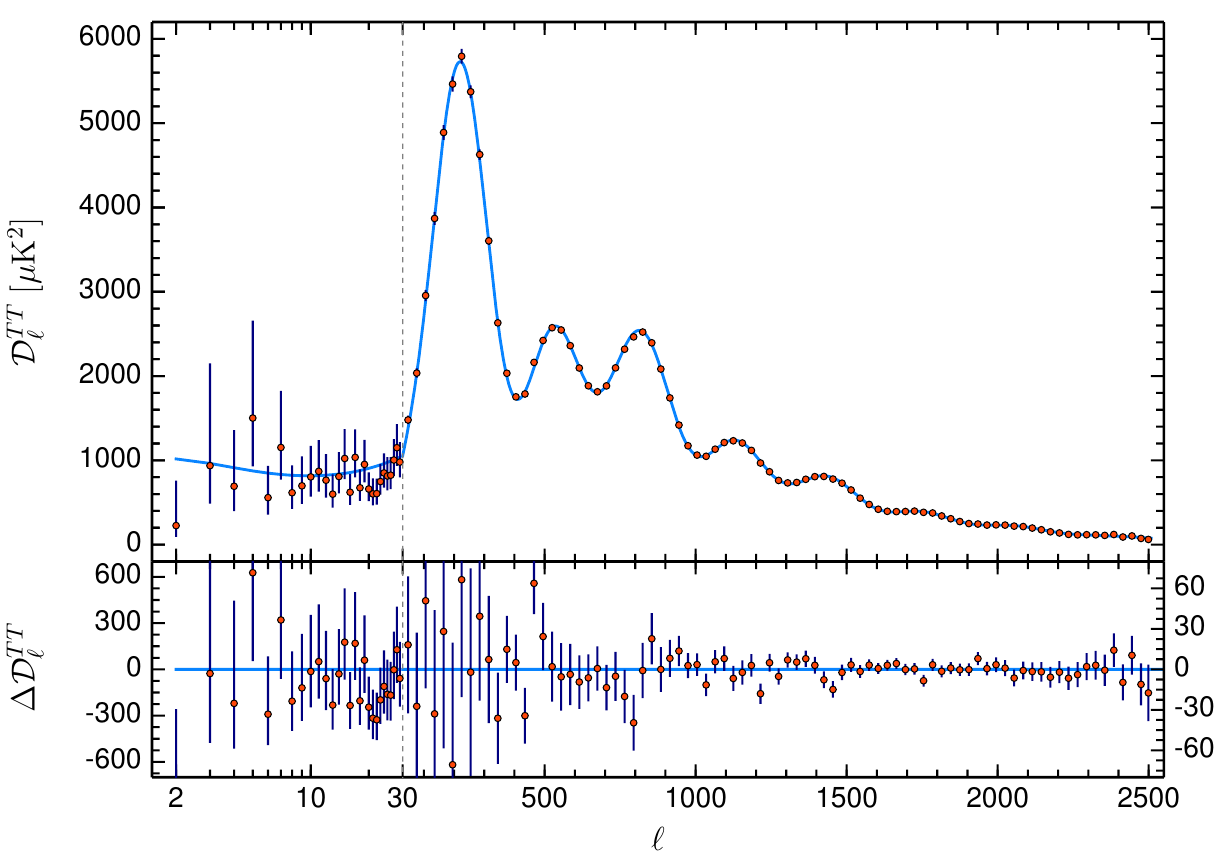
  • \(\Lambda\)CDM is still best fit to observations.
  • Predictive model with few free parameters.
G_{\mu \nu} + \Lambda g_{\mu \nu} = 8\pi G T_{\mu \nu}

Concordance Cosmology:

  • Lensing
  • CMB
  • Clustering
  • Supernovae
  • Clusters

The Standard \(\Lambda\)CDM model

G_{\mu \nu} + \Lambda g_{\mu \nu} = 8\pi G T_{\mu \nu}
  • \(\Lambda\)CDM is still best fit to observations.
  • Some questions remain:
  • \(\Lambda\) and CDM.
  • Cosmological Constant Problem:

Quantum Gravity?

O(100) orders of magnitude wrong
(Zeldovich 1967, Weinberg 1989, Martin 2012).
 Composed of naturalness and coincidence
sub-problems, among others.

String Theory Landscape?

Cómo Sabemos Todo Esto?

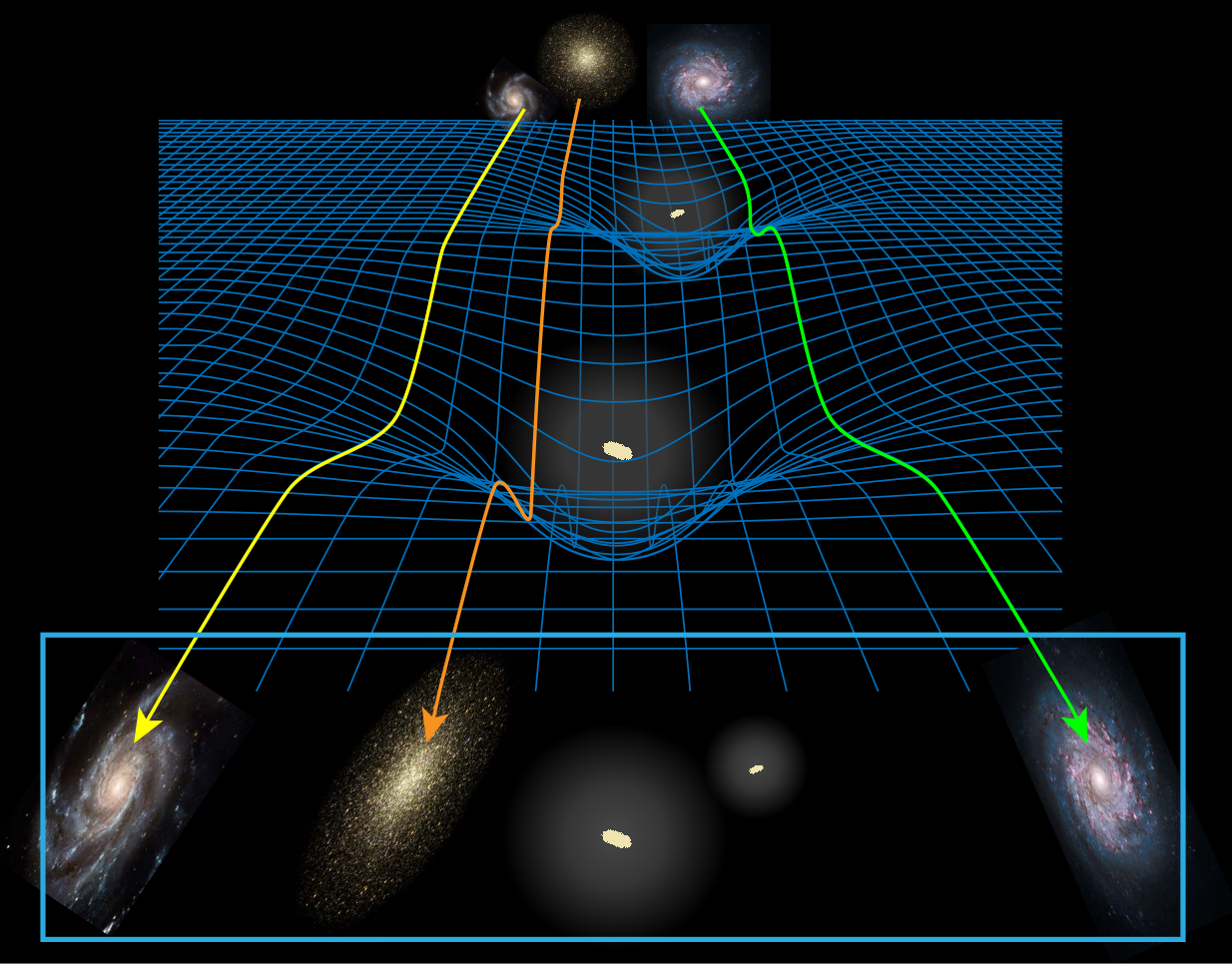
1. Lentes Gravitacionales

Cómo Sabemos Todo Esto?

2. Radiación Cósmica de Fondo

Satélite Planck de la ESA

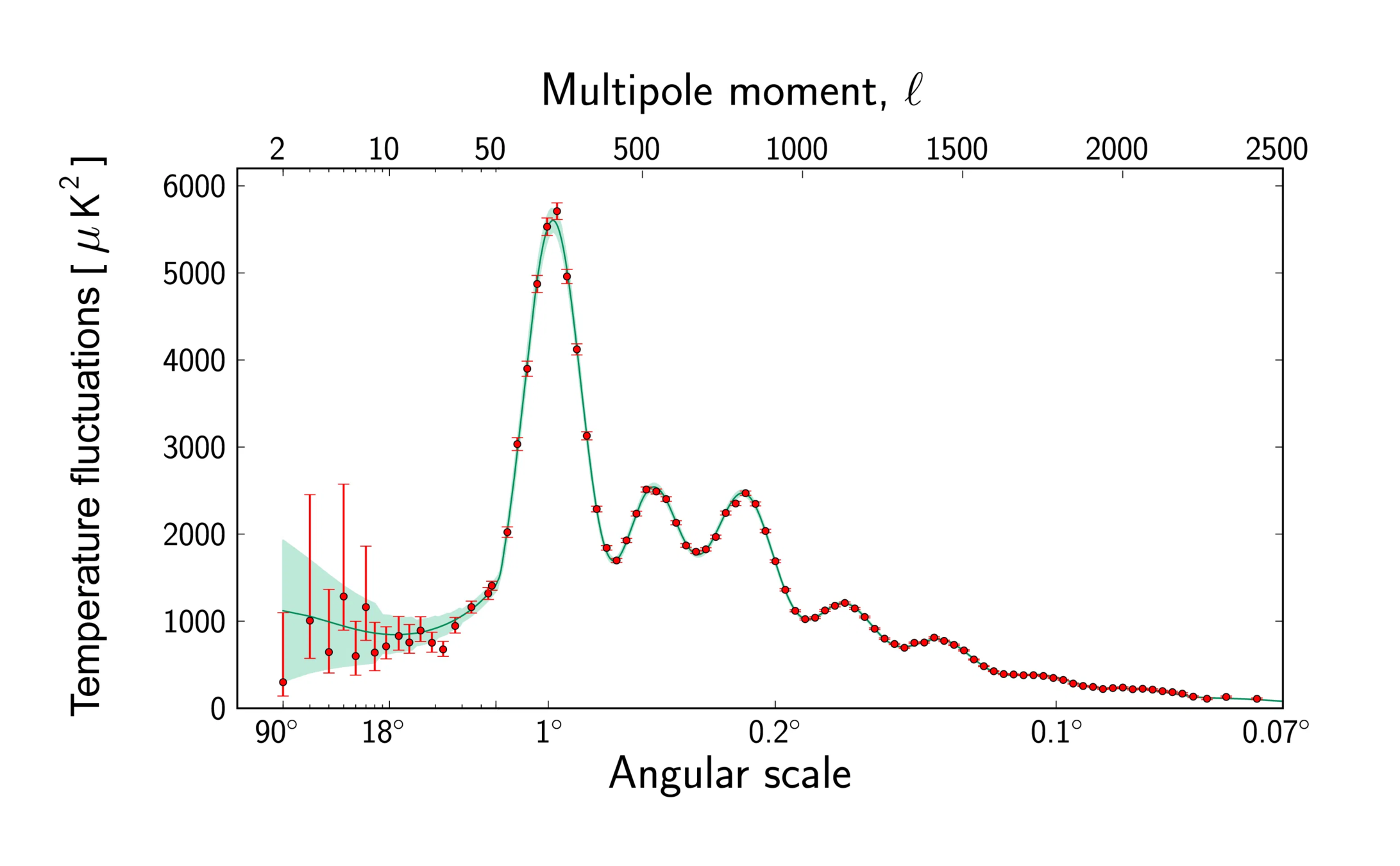
Datos y teoría calzan

Cómo Sabemos Todo Esto?

3. Galaxy Clustering

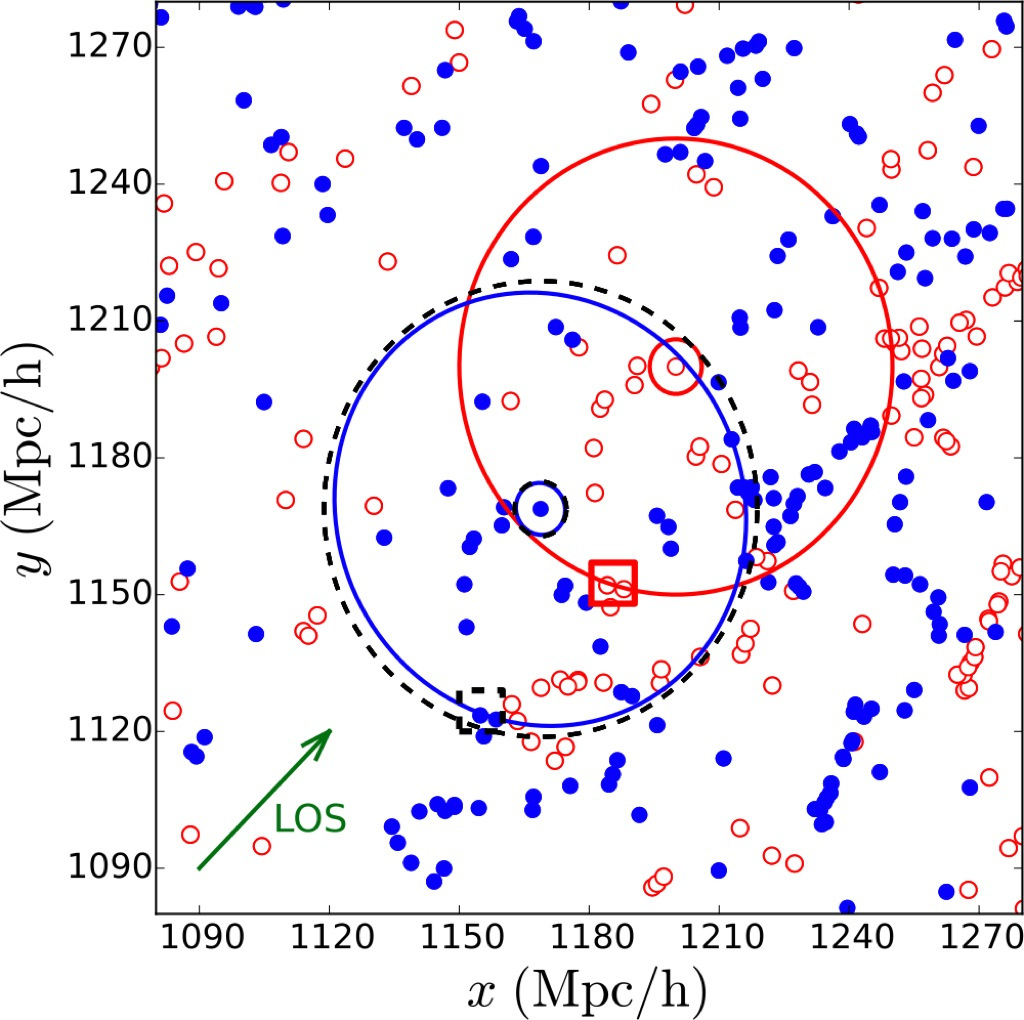
Efectos de la gravedad sobre el espacio tiempo

Funciones de correlación

Tensiones en \(\Lambda\)CDM

H0 tension at 5\(\sigma\)

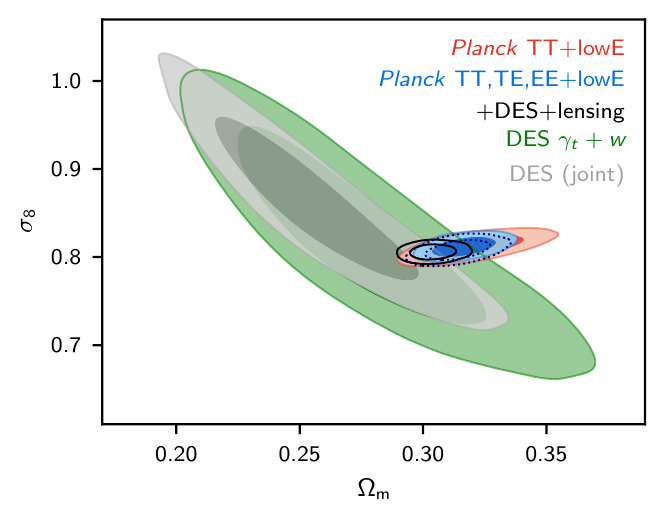
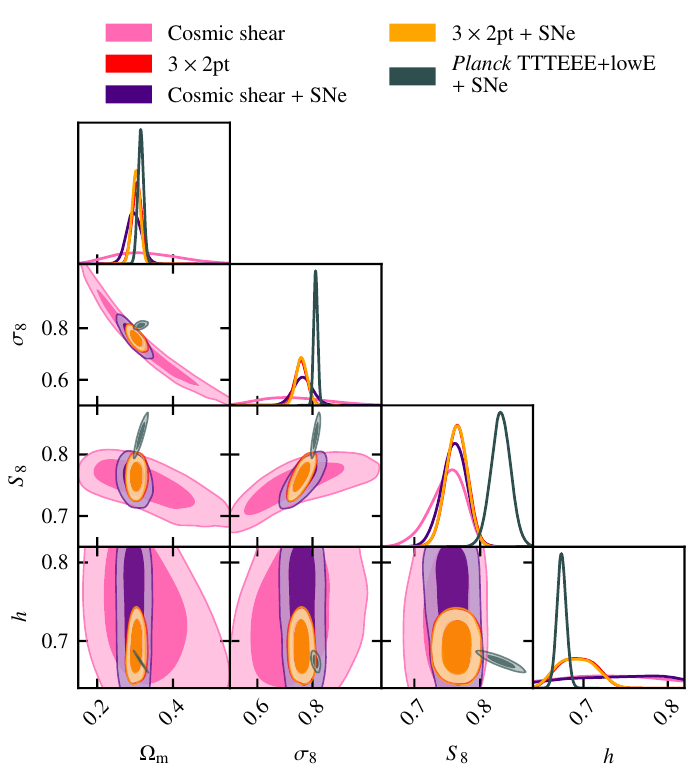
Clustering amplitude \(\sigma8\)

  • \(\sigma_8\) - \(\Omega_m\)  discrepancy at ~\(2\sigma\)
  • Tension between late and early-time Universe
  • Tension in clustering amplitude and matter content

Neutrinos Masivos en Cosmologia

Neutrinos Masivos en Cosmologia

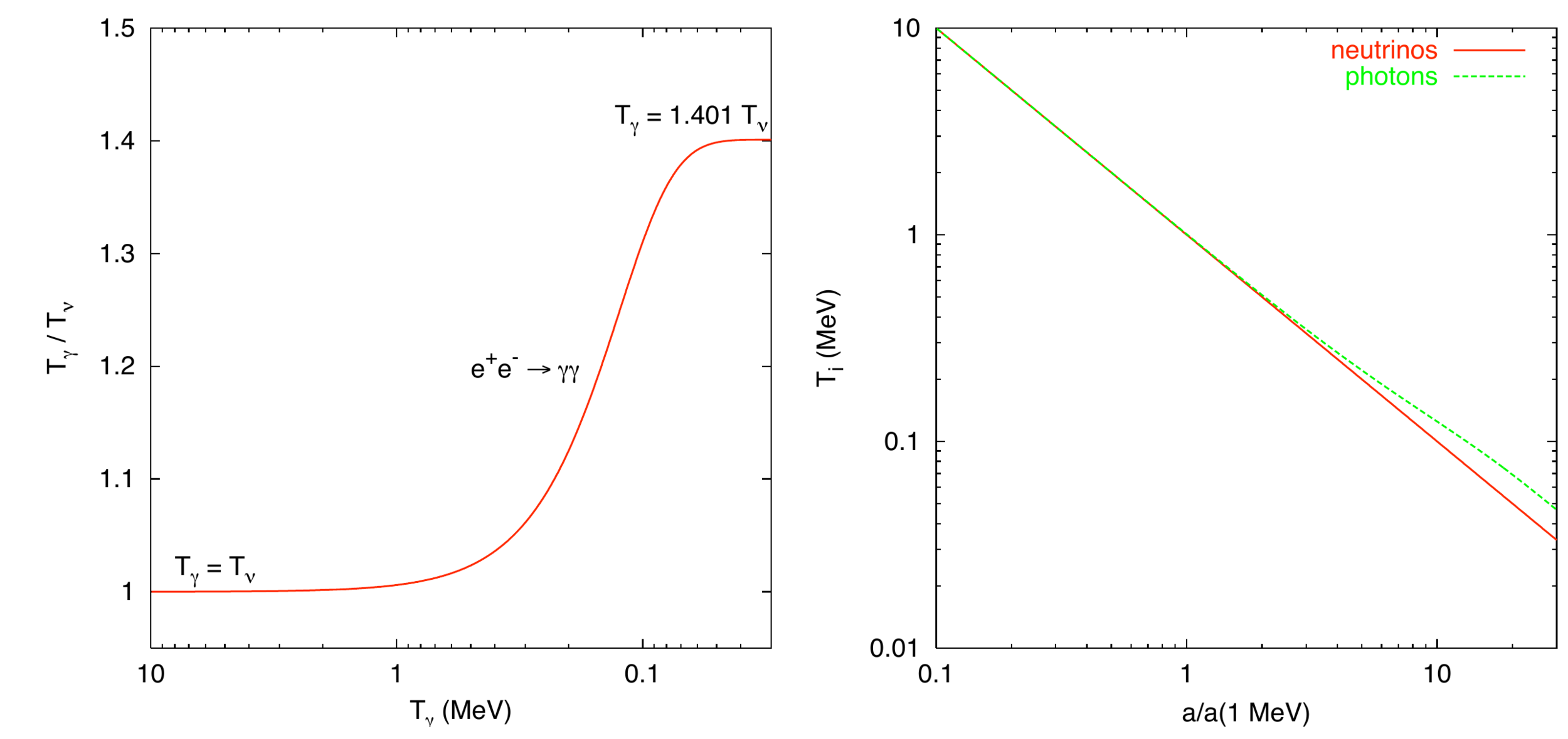
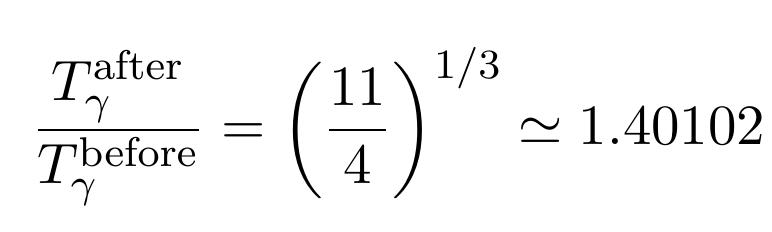
  • Neutrinos and Photons initially at thermal equilibrium
  • Neutrinos decouple at \(\approx\) 1MeV
  • Energy injection into photons from \(e^+ e^- \) annihilation

Neutrinos Masivos en Cosmologia

N_{\rm eff} = 3.0440

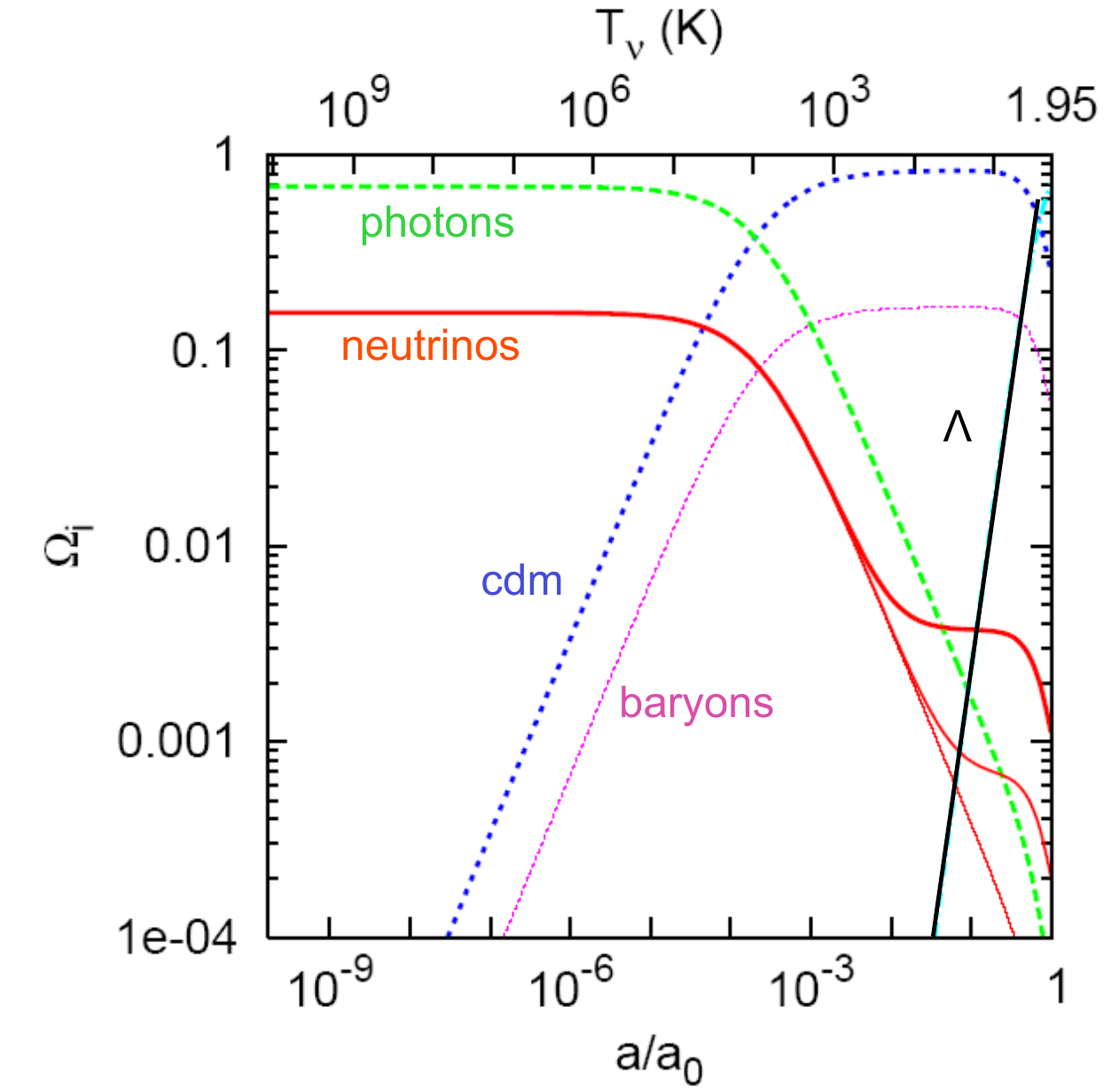
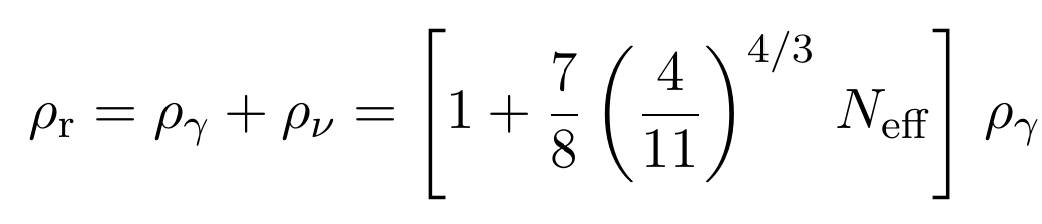
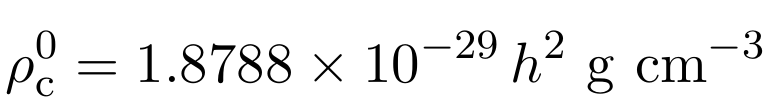
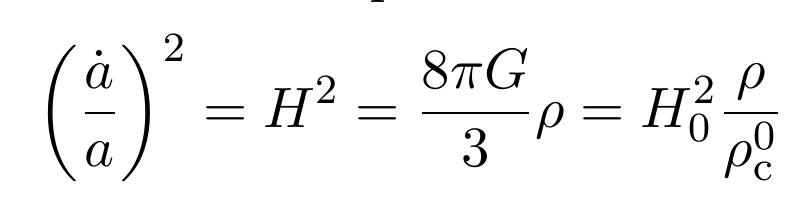
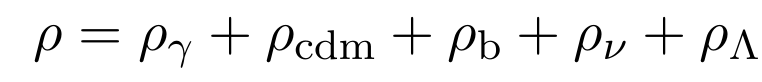
Froustey et al, arXiv:2008.01074, arXiv: 2110.11296

  • If neutrinos are massless: relativistic, dilute as \(a^{-4}\)
  • If massive: non-relativistic, one has to follow the Friedmann function evolution

Perturbaciones Lineales

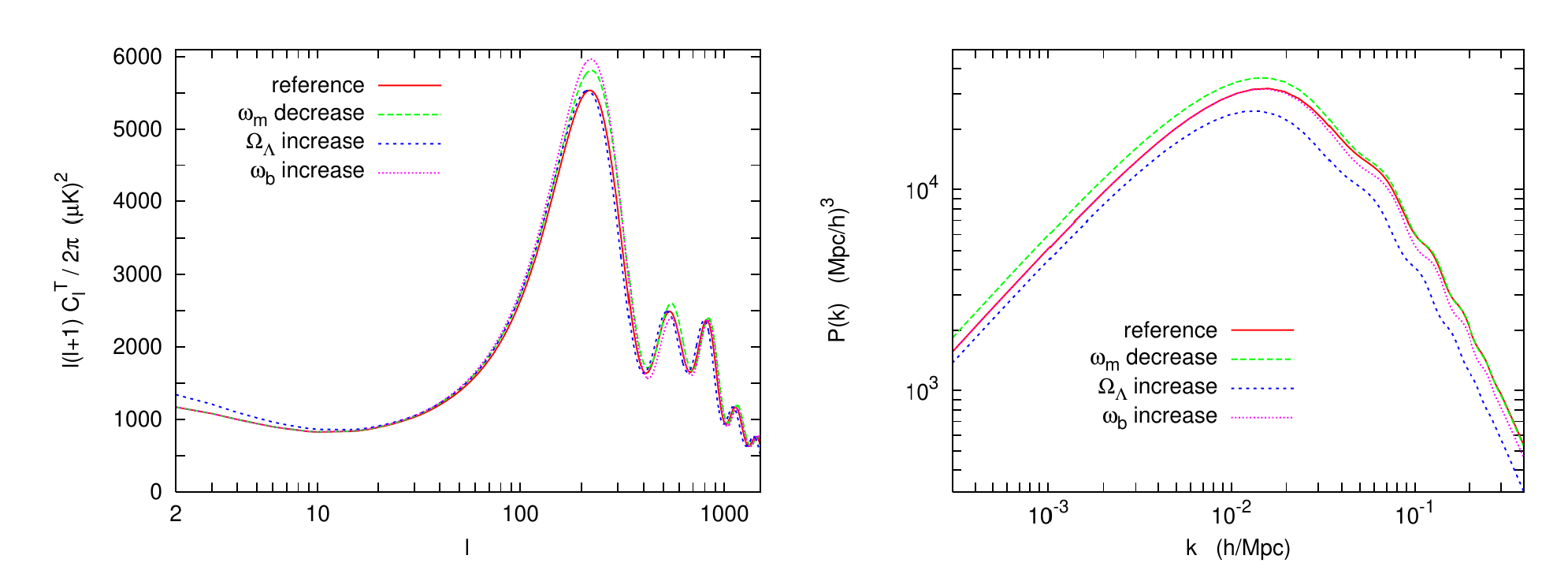
The power spectrum is calculated from the linear density perturbations solving the Vlasov-Poisson system

Perturbaciones Lineales

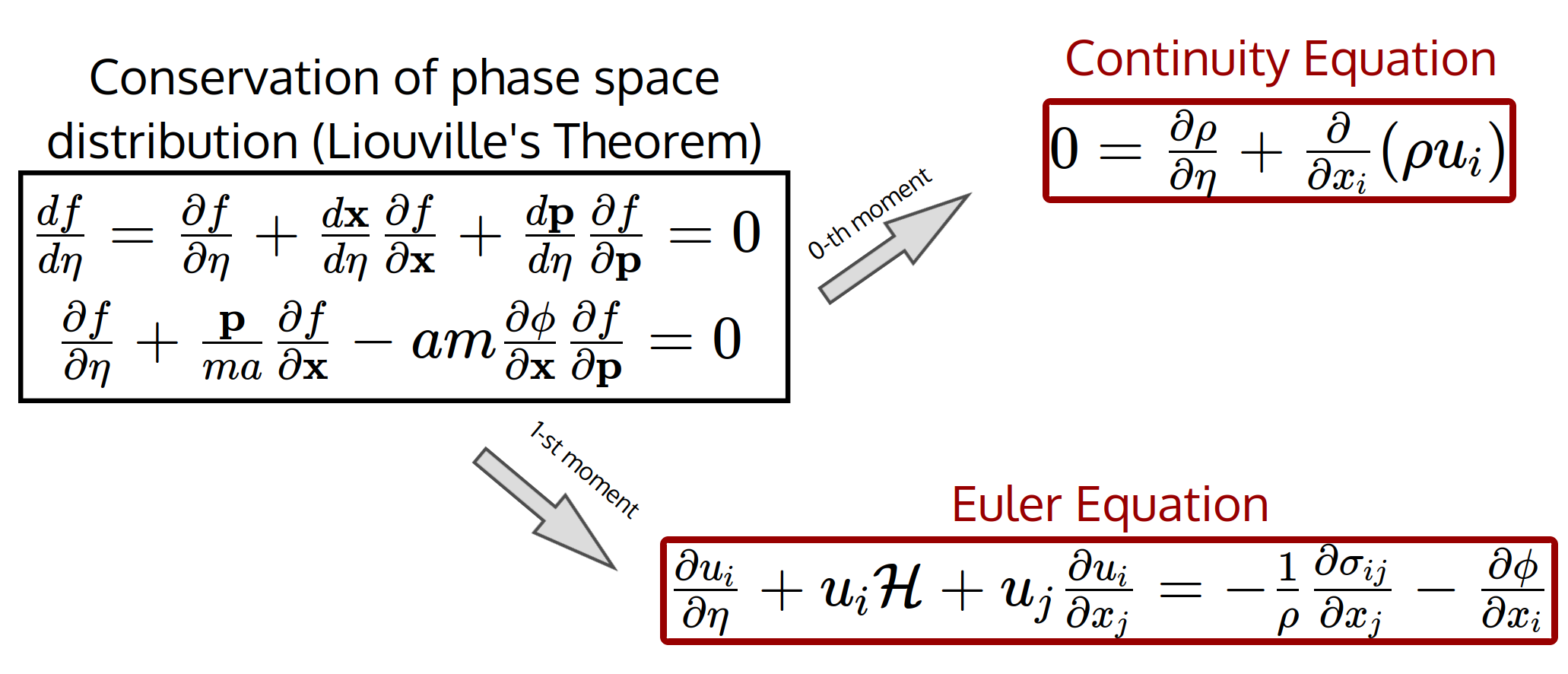
Vlasov-Poisson system is a set of diff.eqn. in which all matter-radiation species are coupled

Slides by: Dennis Linde

Neutrinos masivos: Free streaming

  • Neutrinos free stream below a scale of k_FS.
  • They do not cluster below that scale.
  • Suppression of the power spectrum.
  • The non-relativistic transition imposes a minimum in k_FS
  • Cosmology-dependent

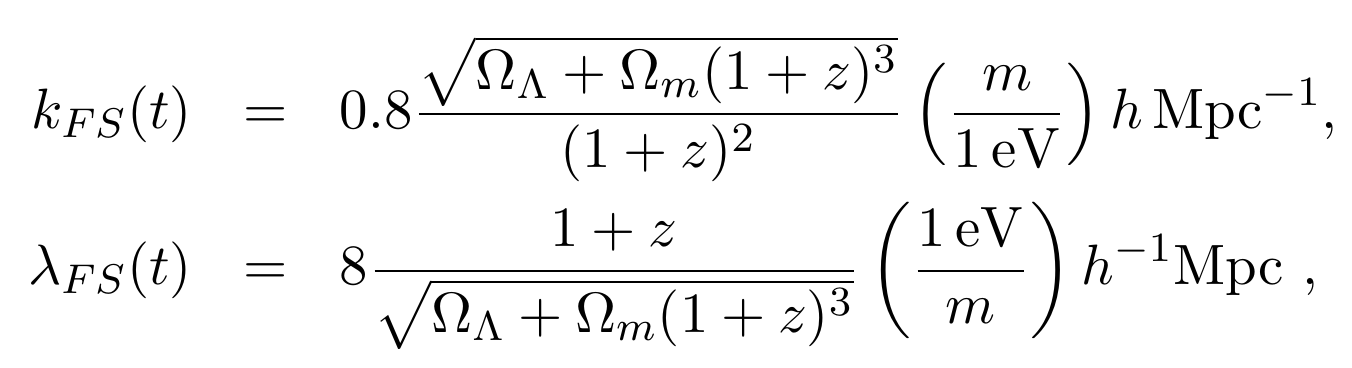
Neutrinos masivos: Free streaming

P^{f_\nu}(k) = (1-f_\nu)^2 P(k)

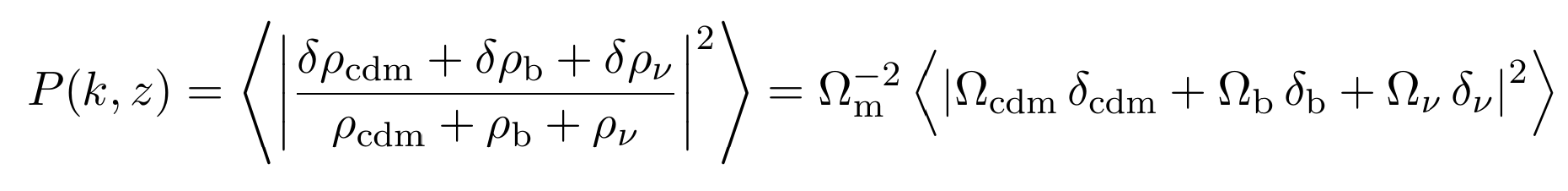
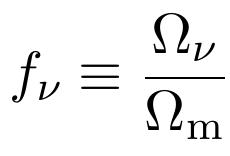
Suppression of the power spectrum, at first order depends on energy density ratios

Neutrinos masivos: Free streaming

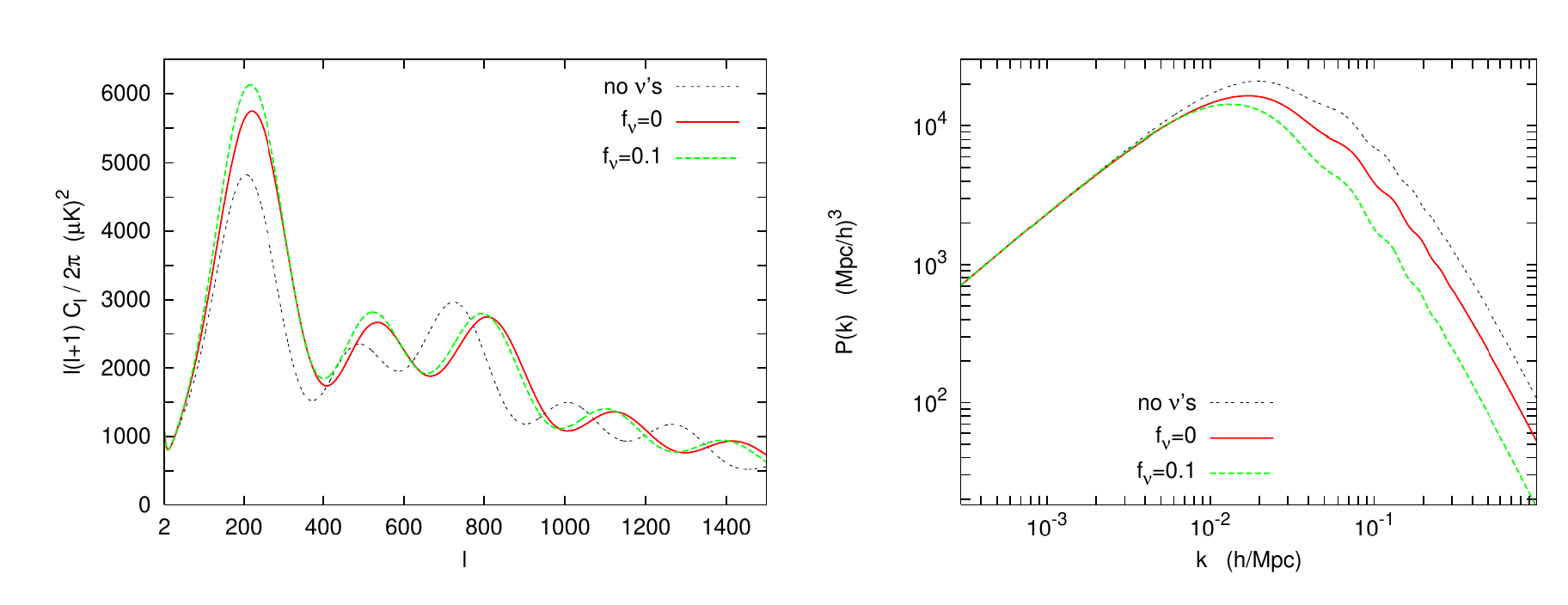
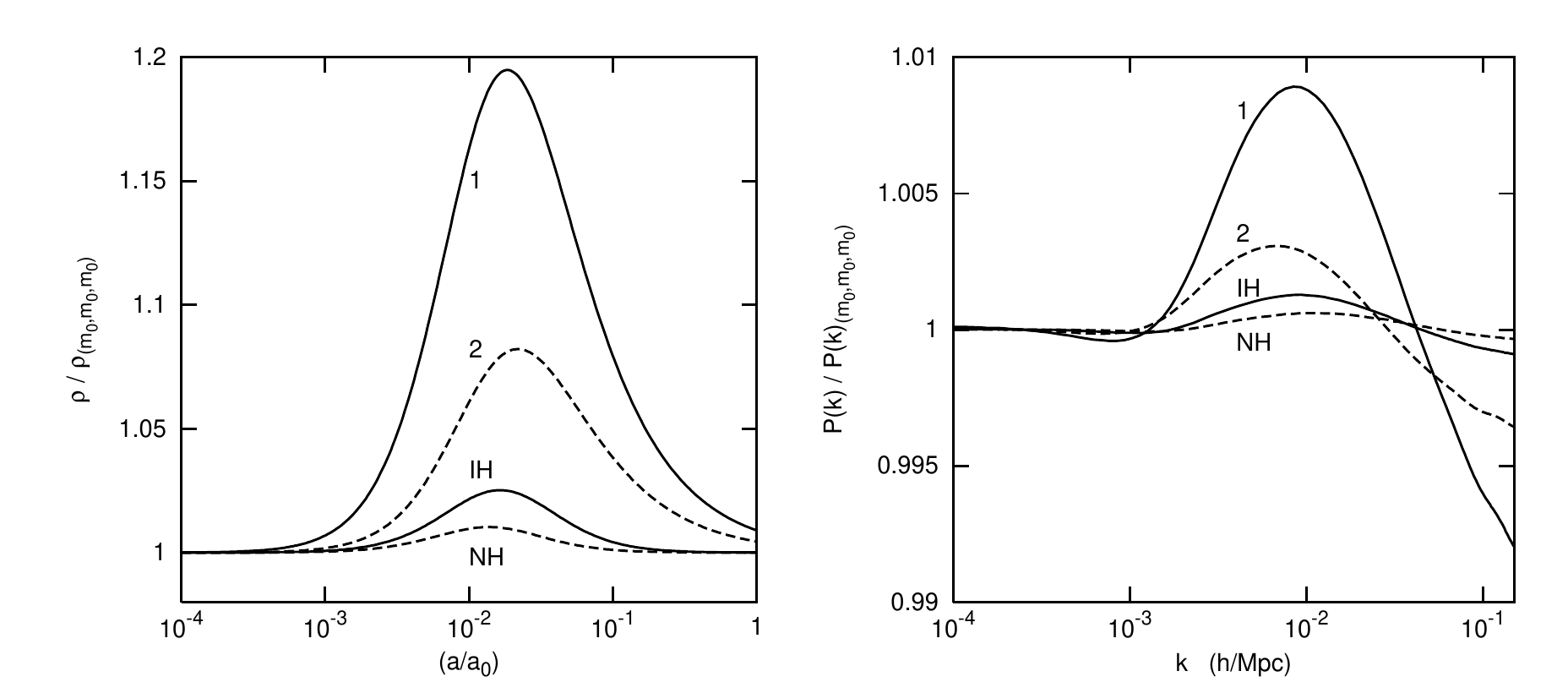
CMB angular spectrum and matter power spectrum are both dependent on neutrino mass, N_eff and ordering

Euclid Space Satellite

Euclid Space Satellite

  • Two instruments:
  •  VIS (visible photometer): shape and orientation of 1.5 billion galaxies!
  •  NISP (near infrared spectrograph): 30 million galaxy spectra!
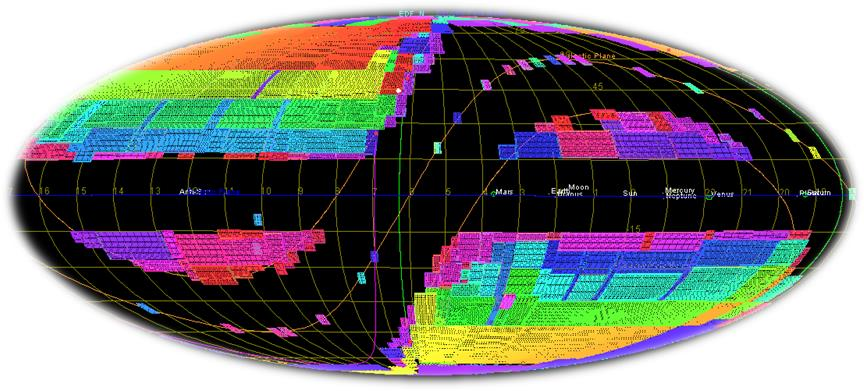
  • 15 000 square degrees in the sky
  •  16 countries, ~1500 members
  •  ~170 Petabyte of data!

Credits: Rodlophe Cledassou, CNES

Euclid Space Satellite

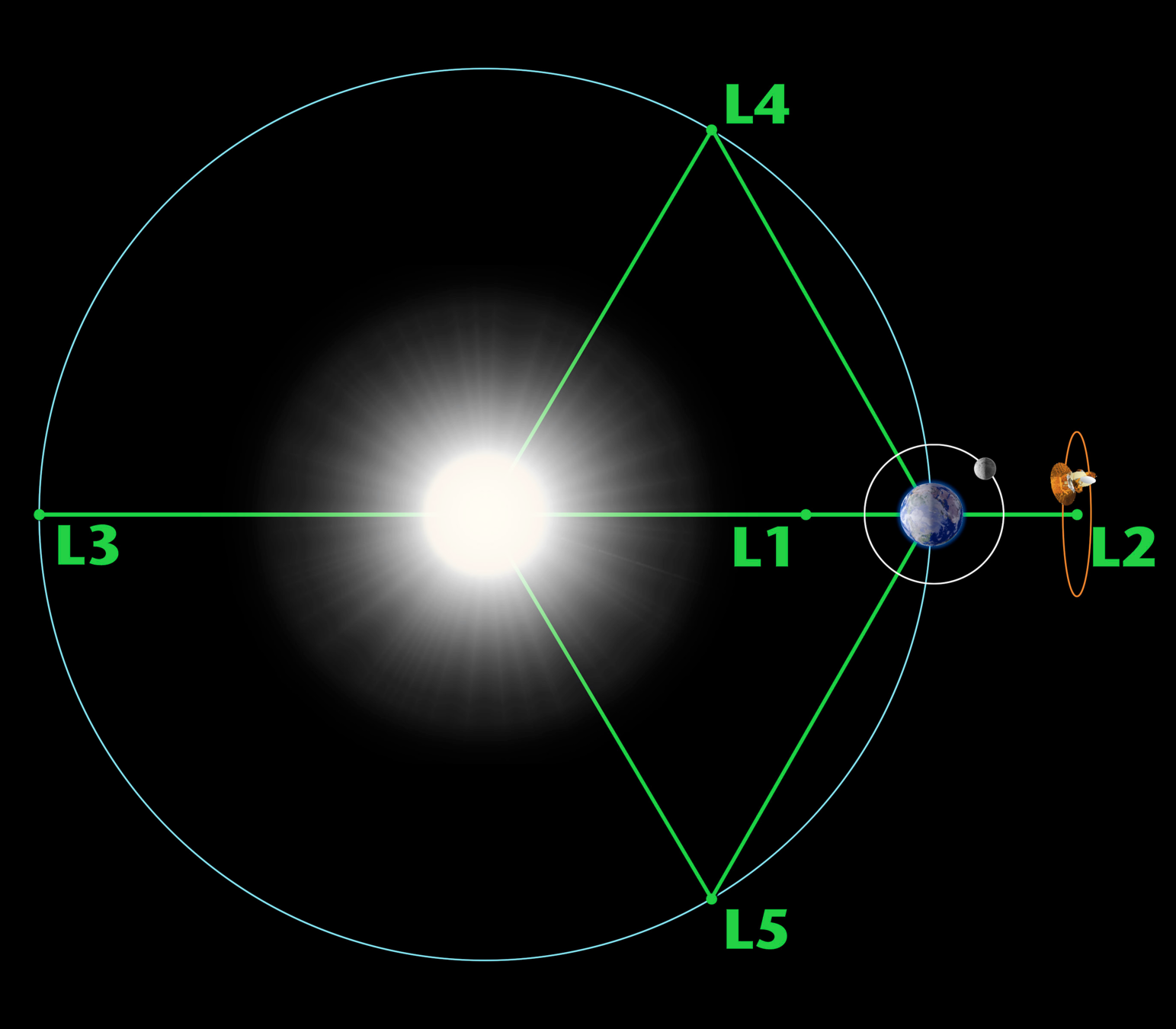
Localizado en el punto de Lagrange L2

Credits: Rodlophe Cledassou, CNES

VIS

Instrumento VIS:

  • Medirá 1000 millones de galaxias en el espectro visible e infrarrojo.
  • Con esto podemos medir los débiles lentes gravitacionales.

Credits: Rodlophe Cledassou, CNES

NISP: Near-Infrarred Spectrograph

Instrumento NISP:

  • Medirá 100 millones de espectros de galaxias en el espectro infrarrojo.
  • Con esto podemos medir las distancias y velocidades de las galaxias.
  • Crear mapa 3D del Universo.

Credits: Rodolphe Cledassou, CNES

Euclid Mask

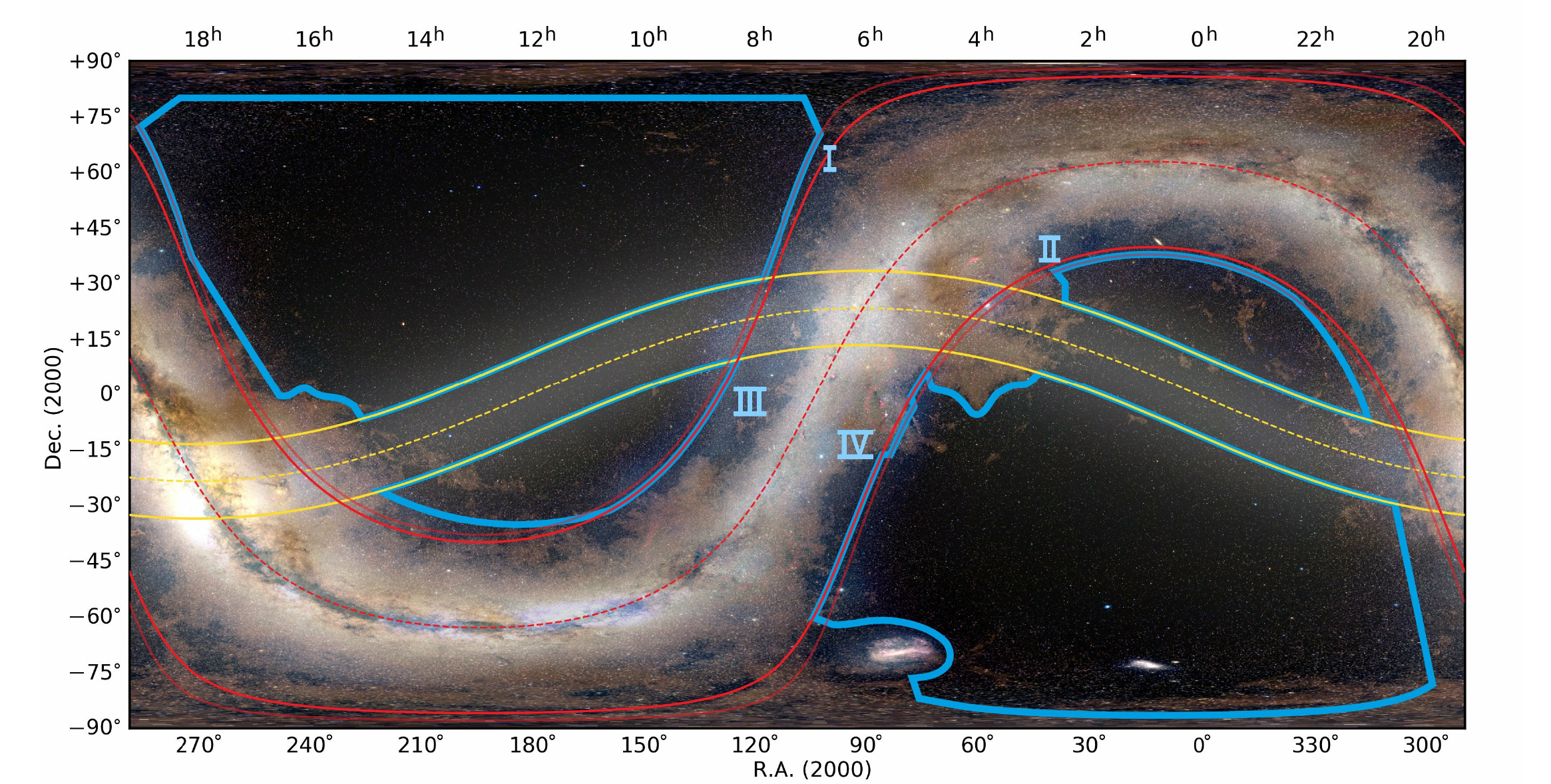
15,000 square degrees

Credits: Tobias Liaudat, CosmoStat

Euclid Shape Pipeline

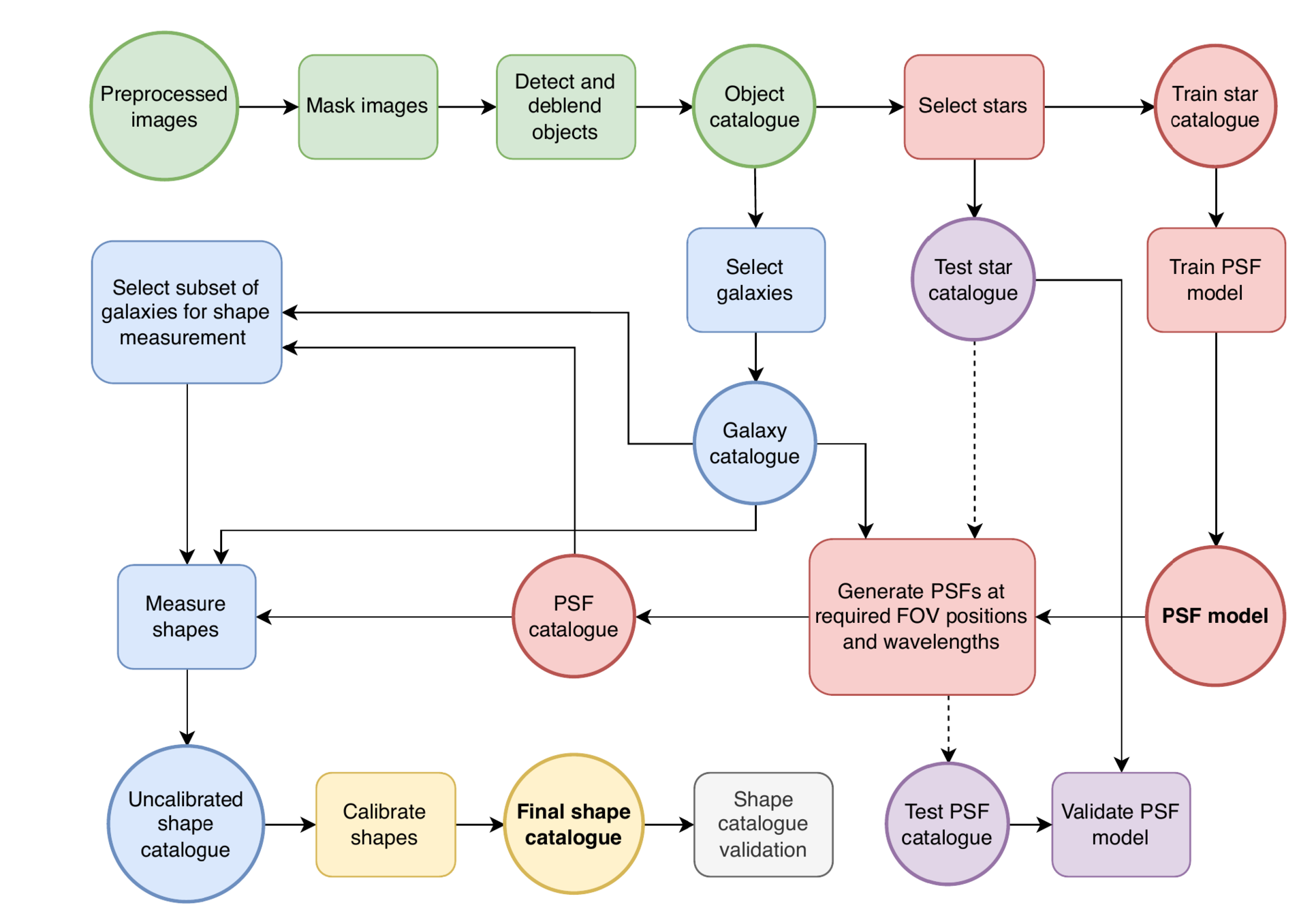
Credits: Rodlophe Cledassou, CNES

Euclid

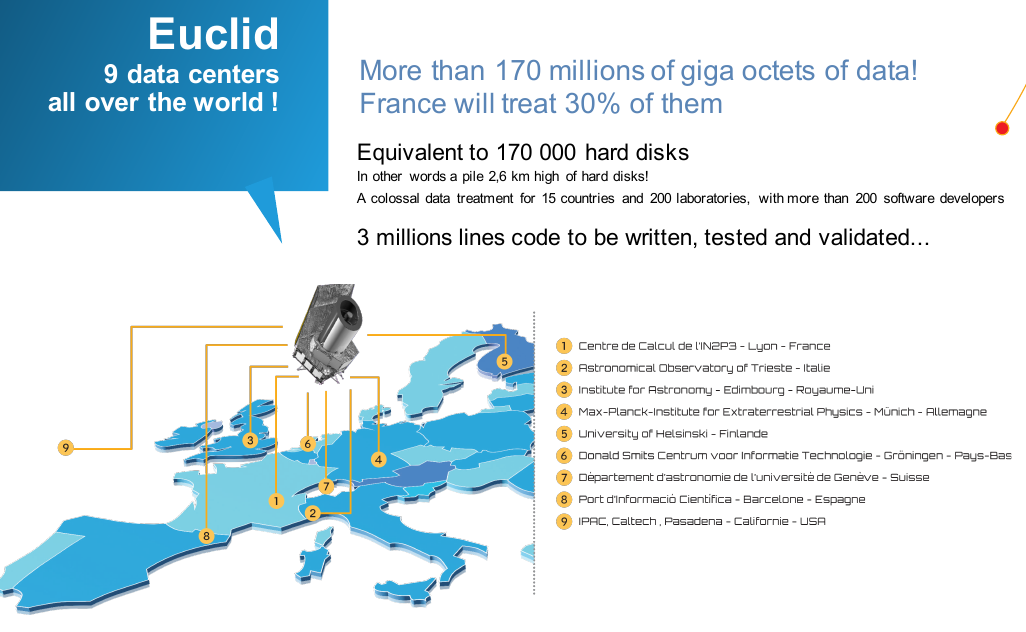
https://www.esa.int/ESA/Our_Missions

Otros satélites de la ESA

Lentes Gravitacionales

Galaxy Clustering

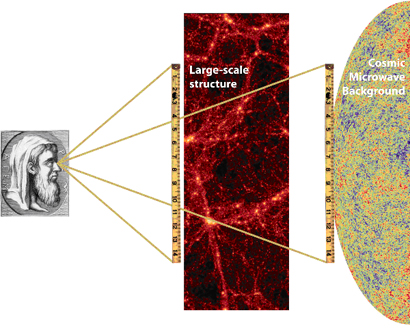
BAO

Clustering

RSD

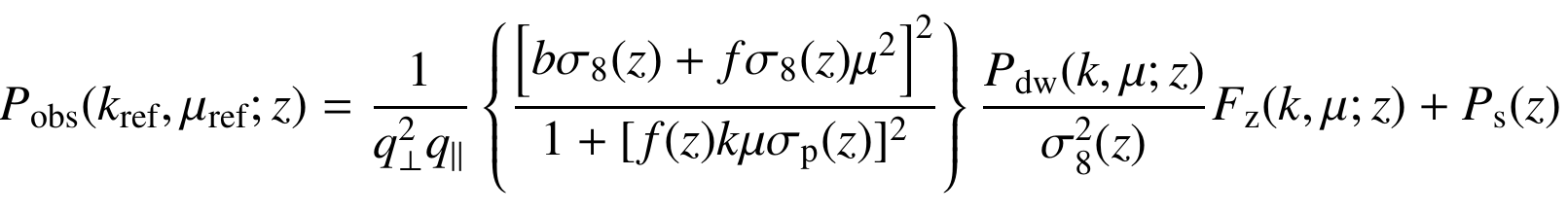
Spec-z

Euclid Collaboration, IST:Forecasts, arXiv: 1910.09273

Galaxy Clustering

Slides by: Dennis Linde

Galaxy Clustering

Angulo et al, 1406.4143

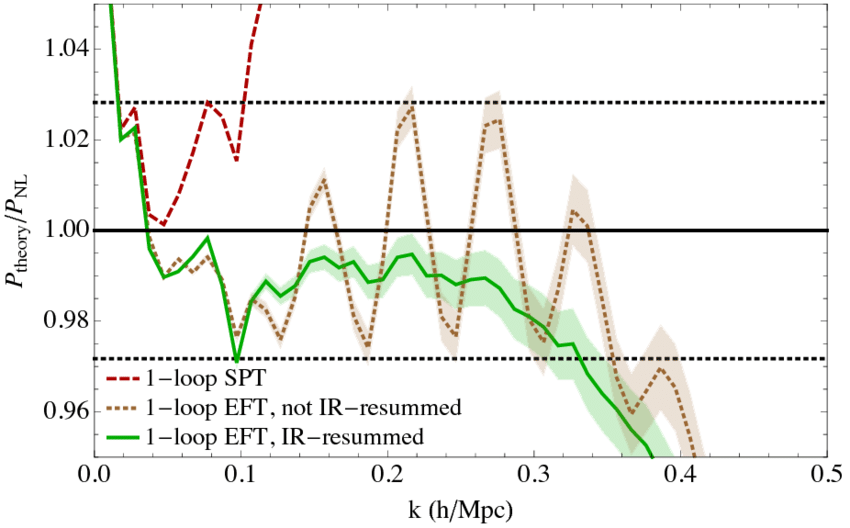
The Matter Power Spectrum

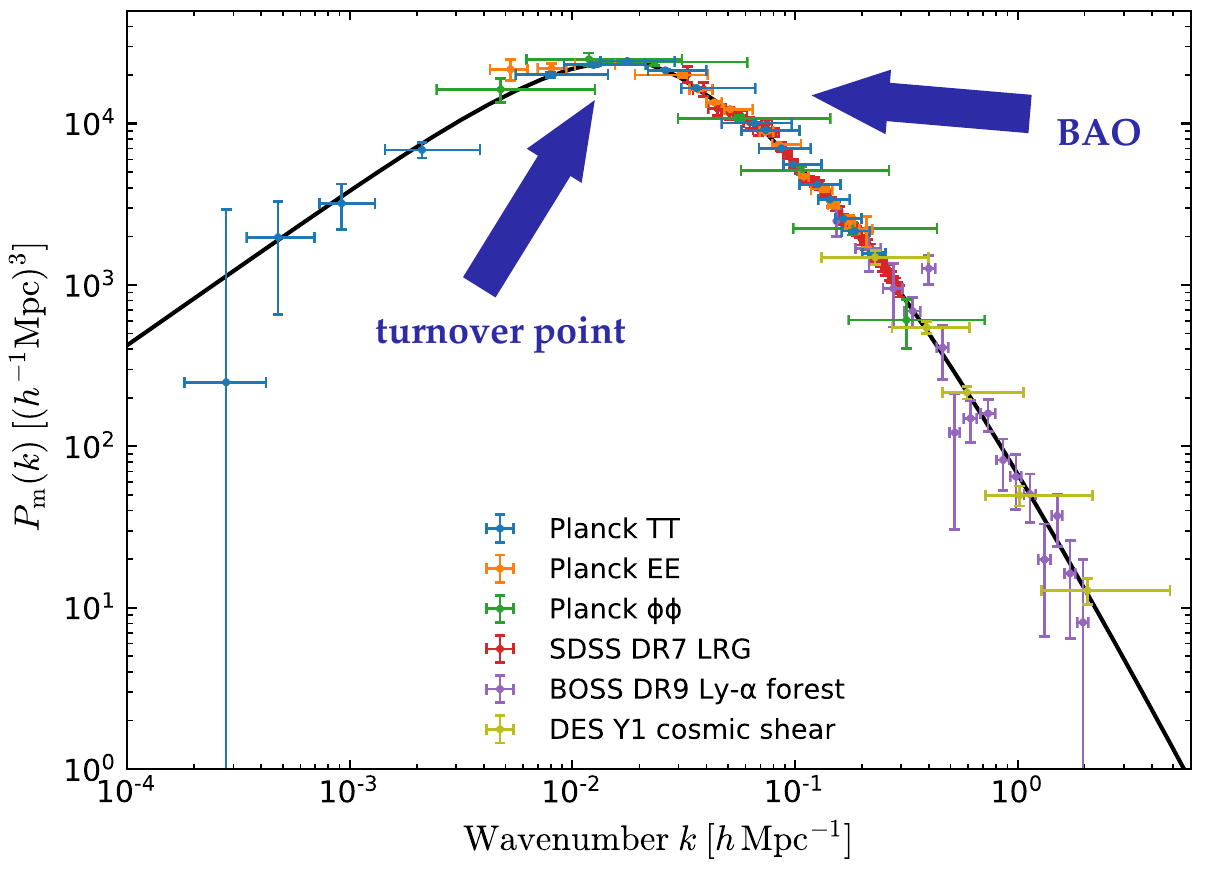
Current data:

Image: https://www.cosmos.esa.int/web/planck/picture-gallery

The Matter Power Spectrum

Euclid:

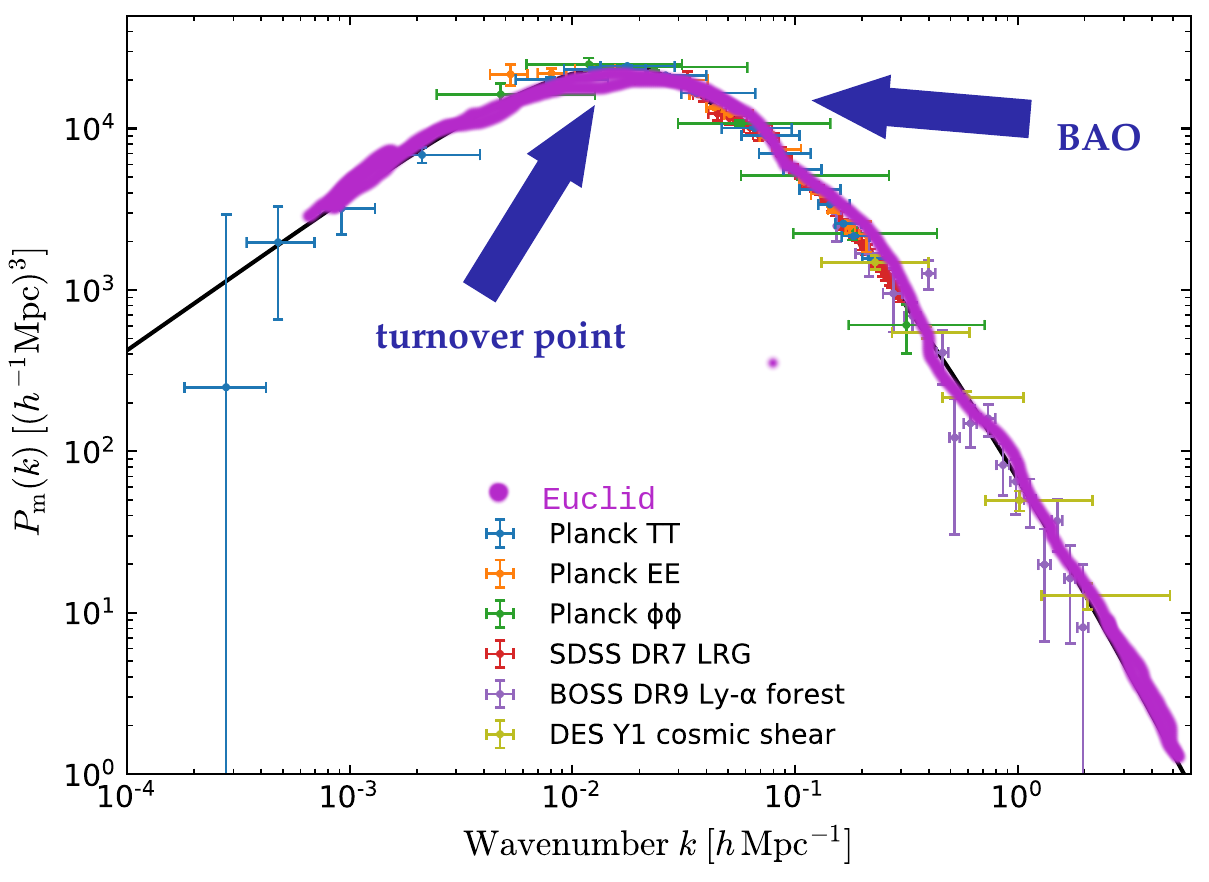
Scales from: ~ \(10^{-3}\) to \(10\) hMpc\(^{-1}\)

Euclid: IST:Forecasts

Awardees of the Euclid STAR Prize Team 2019

Euclid preparation: VII. Forecast validation for Euclid cosmological probes.  arXiv:1910.09273

Euclid: IST:Forecasts

Euclid preparation: VII. Forecast validation for Euclid cosmological probes.  arXiv:1910.09273

Fisher Matrix Forecasts

Euclid preparation: VII. Forecast validation for Euclid cosmological probes.  arXiv:1910.09273

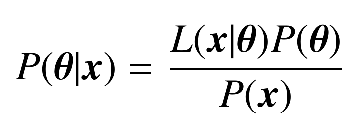
Bayes Theorem:

Probability of the model parameters given the data

Fisher Information Matrix:

Curvature (Hessian) of the Likelihood

Gaussian Likelihood in data space:

-2\ln {L}({\bm x}|{\bm\theta})=\left({\bm x}-{\bm \mu}({\bm\theta})\right)^t{ C}^{-1}\left({\bm x}-{\bm \mu}({\bm\theta})\right)

Fisher Matrix Forecasts

Euclid preparation: VII. Forecast validation for Euclid cosmological probes.  arXiv:1910.09273

Fisher Matrix for a Gaussian likelihood:

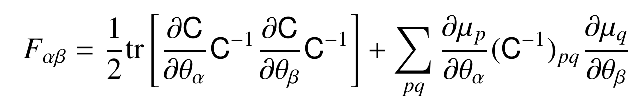
Parameter covariance:

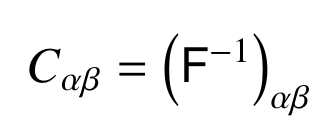
Defines an ellipse:

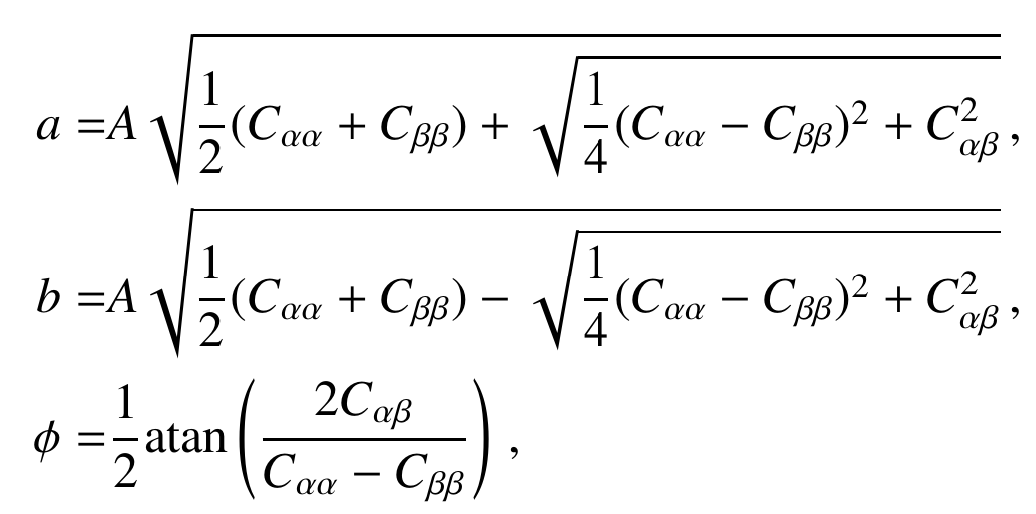
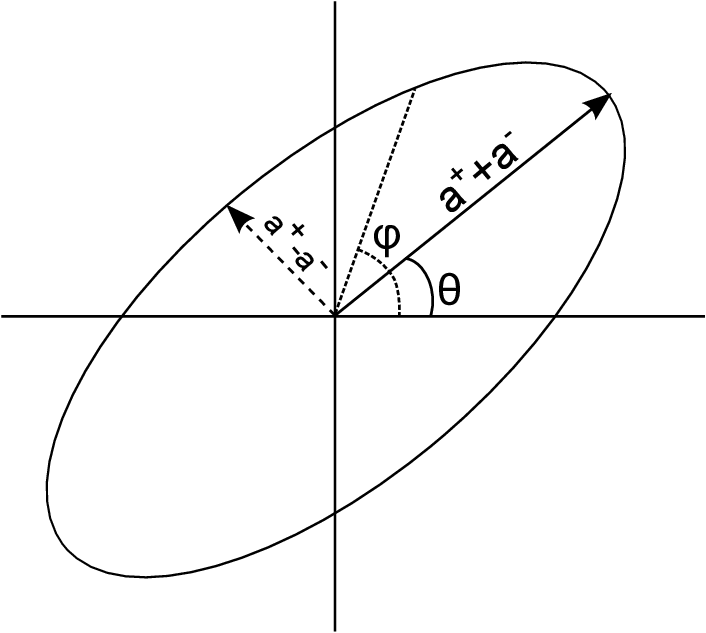
MCMC Forecasts

Euclid IST:L and IST:NL in preparation

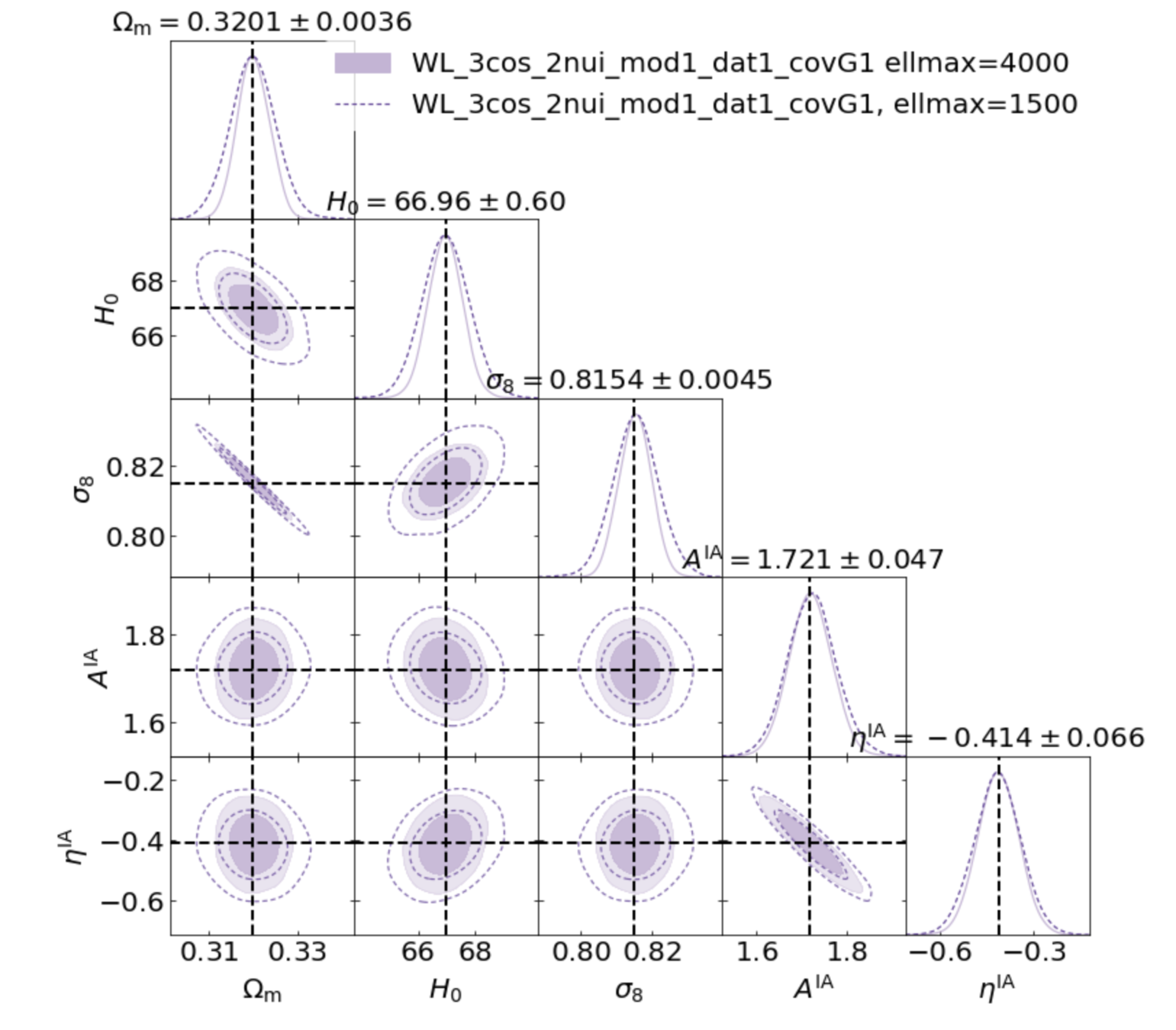
  • Define Likelihood pipeline in real and redshift space
  • Run Markov-Chain-Monte-Carlo sampling parameter space and probability
  • Plot probability density contours
  • Deviations from Gaussian due to non-linear dependencies in the posterior

Neutrino constraints from Planck

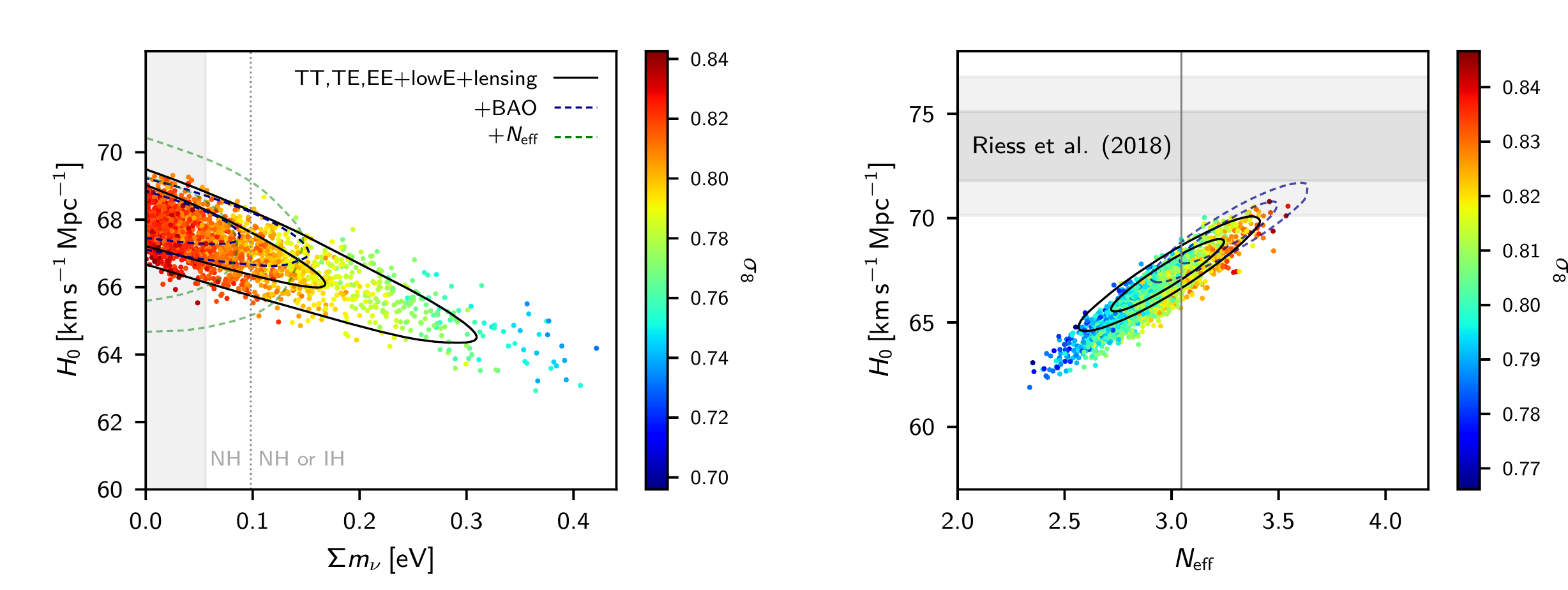
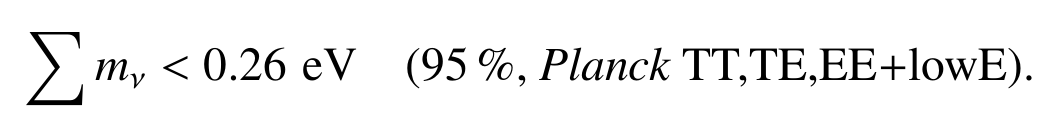
Neutrino forecasts for Euclid

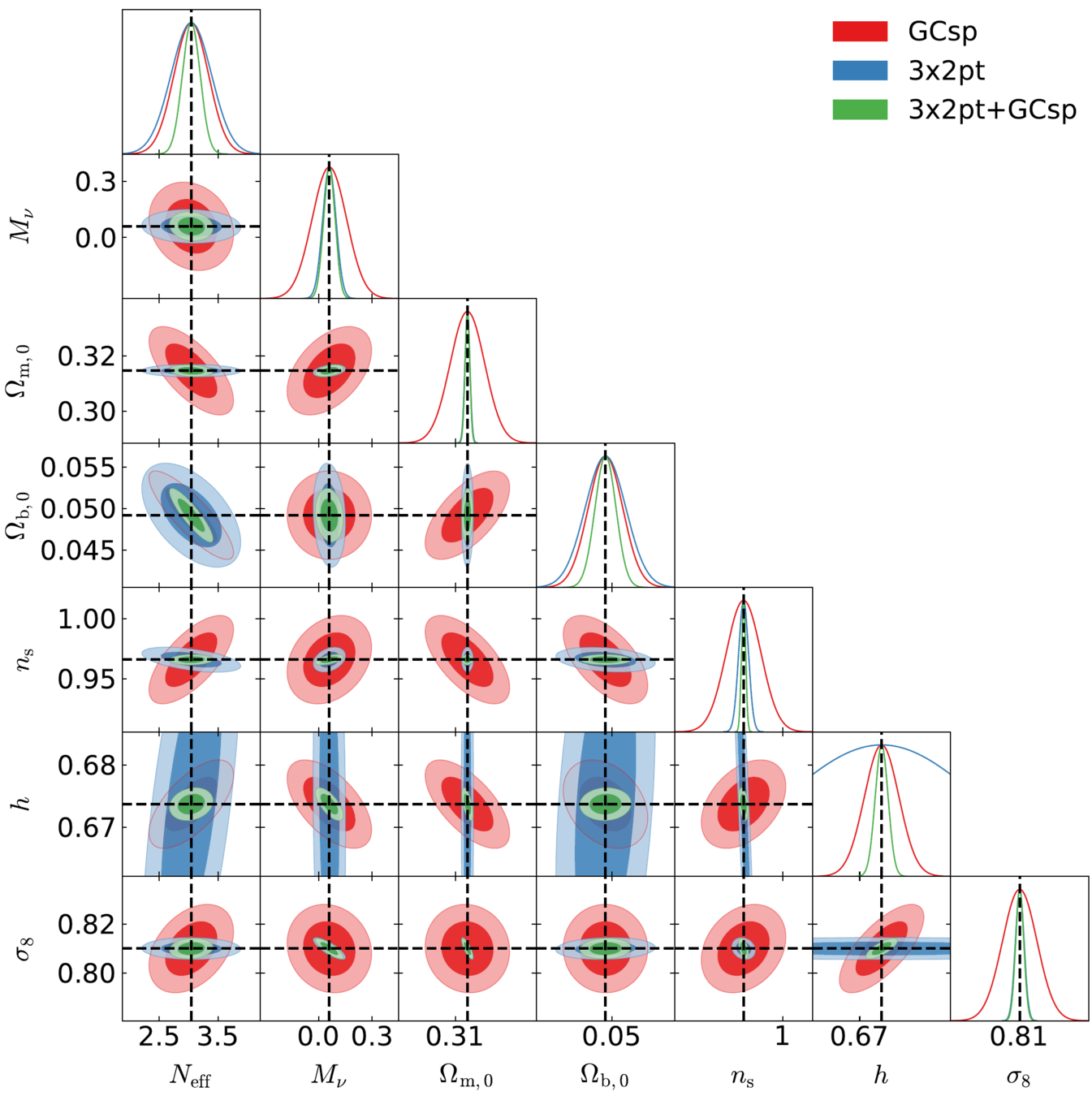
Plots by: Sabarish Sabarish Venkataramani

\Omega_m = 0.314 \pm 0.00086\\ \Omega_b = 0.049 \pm 0.0013 \\ h = 0.67 \pm 0.00108 \\ n_s = 0.966 \pm 0.00179\\ \sigma_8 = 0.81 \pm 0.00172\\ M_\nu = 0.06 \, \mathrm{eV} \pm 0.0320\\ N_{\rm eff} = 3.044 \pm 0.151\\

Euclid Full:

GC spectro + 3x2pt photo

Code: CosmicFish

S.Casas and M.Martinelli

CosmicFish Code

Code: CosmicFish

S.Casas, M.Martinelli and M.Raveri

Soon to be released: New full pythonic version

Gravedad Modificada y Energia Oscura

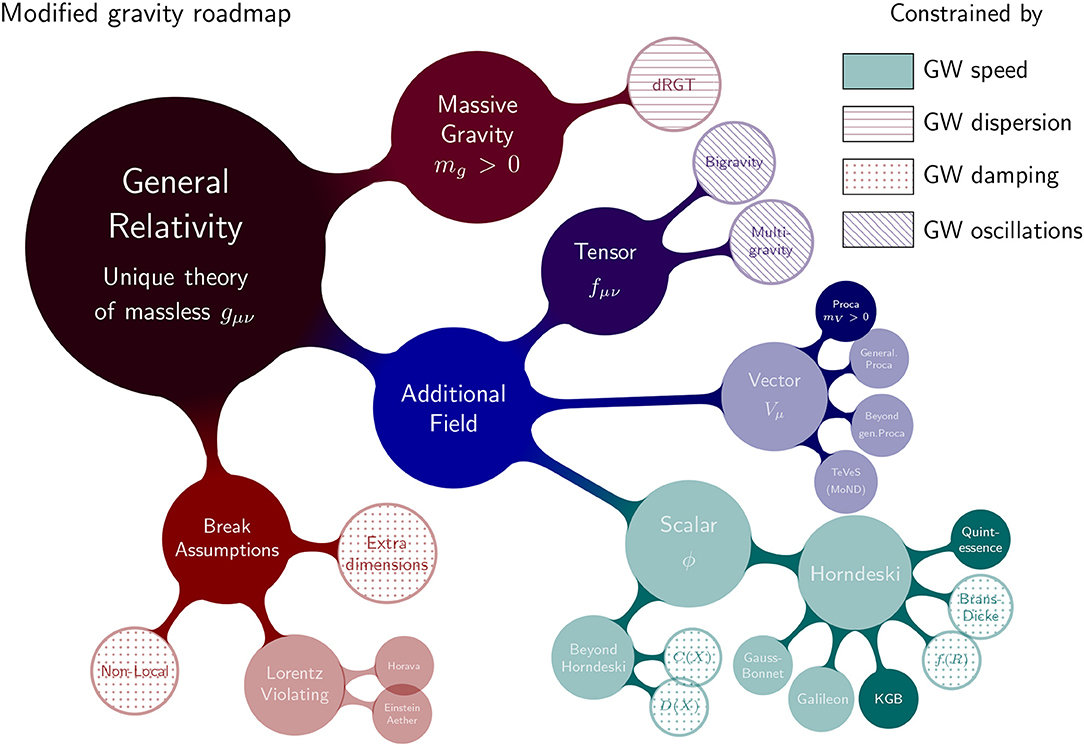
Ezquiaga, Zumalacárregui, Front. Astron. Space Sci., 2018

Gravedad Modificada y Energia Oscura

Parametrized modified gravity

\rm{d}s^2 = -(1+2\Psi) \rm{d}t^2 + a^2(1-2\Phi) \rm{d}x^2

In \(\Lambda\)CDM the two linear gravitational potentials \(\Psi\) and \(\Phi\) are equal to each other

We can describe general modifications of gravity (of the metric) at the linear level with 2 functions of scale (\(k\)) and time (\(a\))

\Sigma(a,k) = \frac{1}{2}\mu(a,k)(1+\eta(a,k))

Only two independent functions!

Vera Rubin LSST

  • Located in Chile, 8.4m telescope
  • 20 billion galaxies
  • Redshifts: 0 < z ~< 3
  • 18,000 square degrees
  • 11 years of observation

Vera Rubin LSST

DESI telescope

  • 14 000 square degrees in the sky
  • 30 million accurate galaxy spectra
  • Redshifts: 0 < z < 2
  • Quasars up to z~3.5
  • 5 years of observation
  • Starting 2021

Vera Rubin LSST

Euclid vs. DESI+Rubin

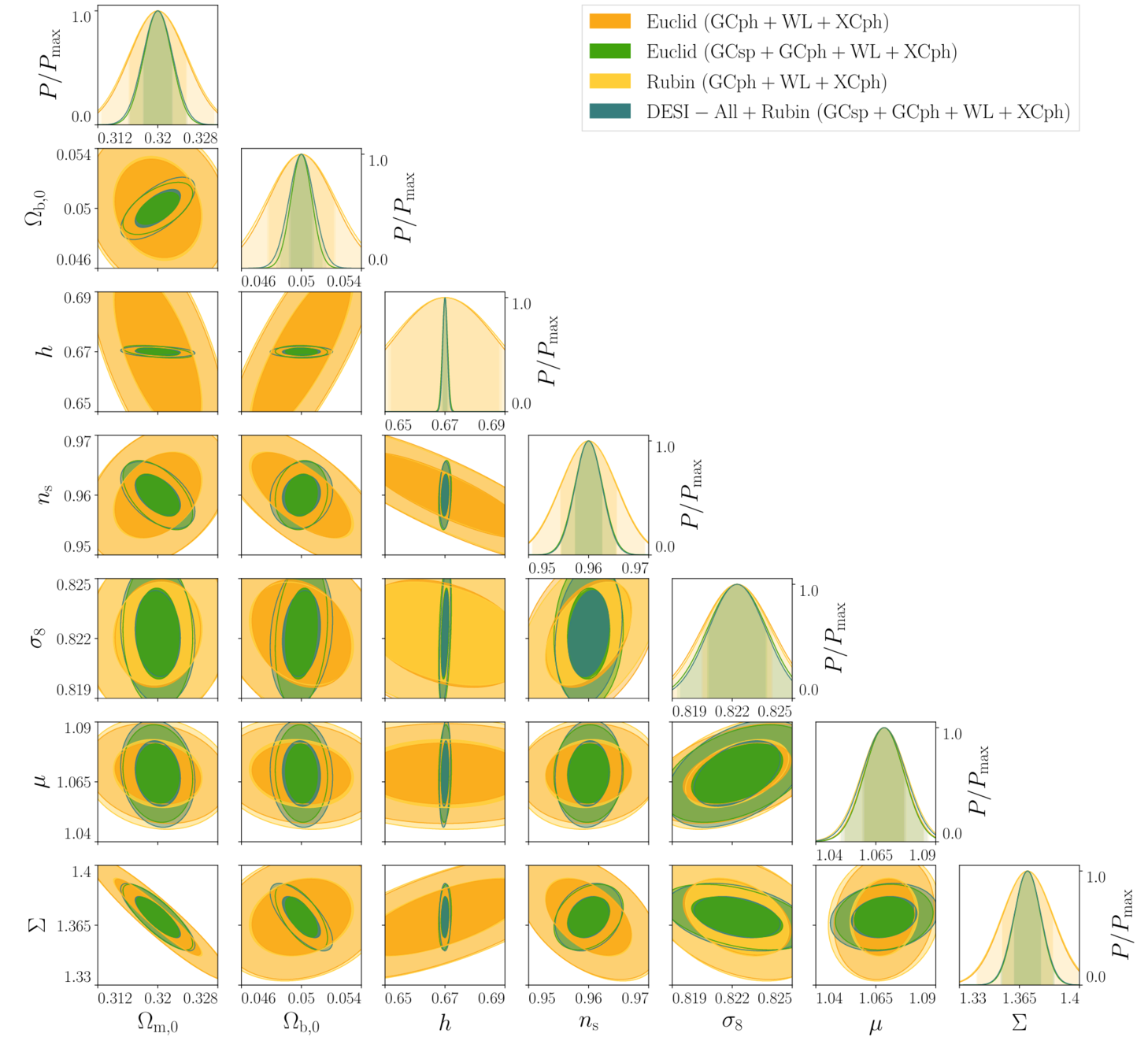
  • Forecasts for Modfied Gravity parametrizations
  • Euclid using spectroscopic and photometric probes, is roughly as powerful as Rubin+DESI

Vera Rubin LSST

Text

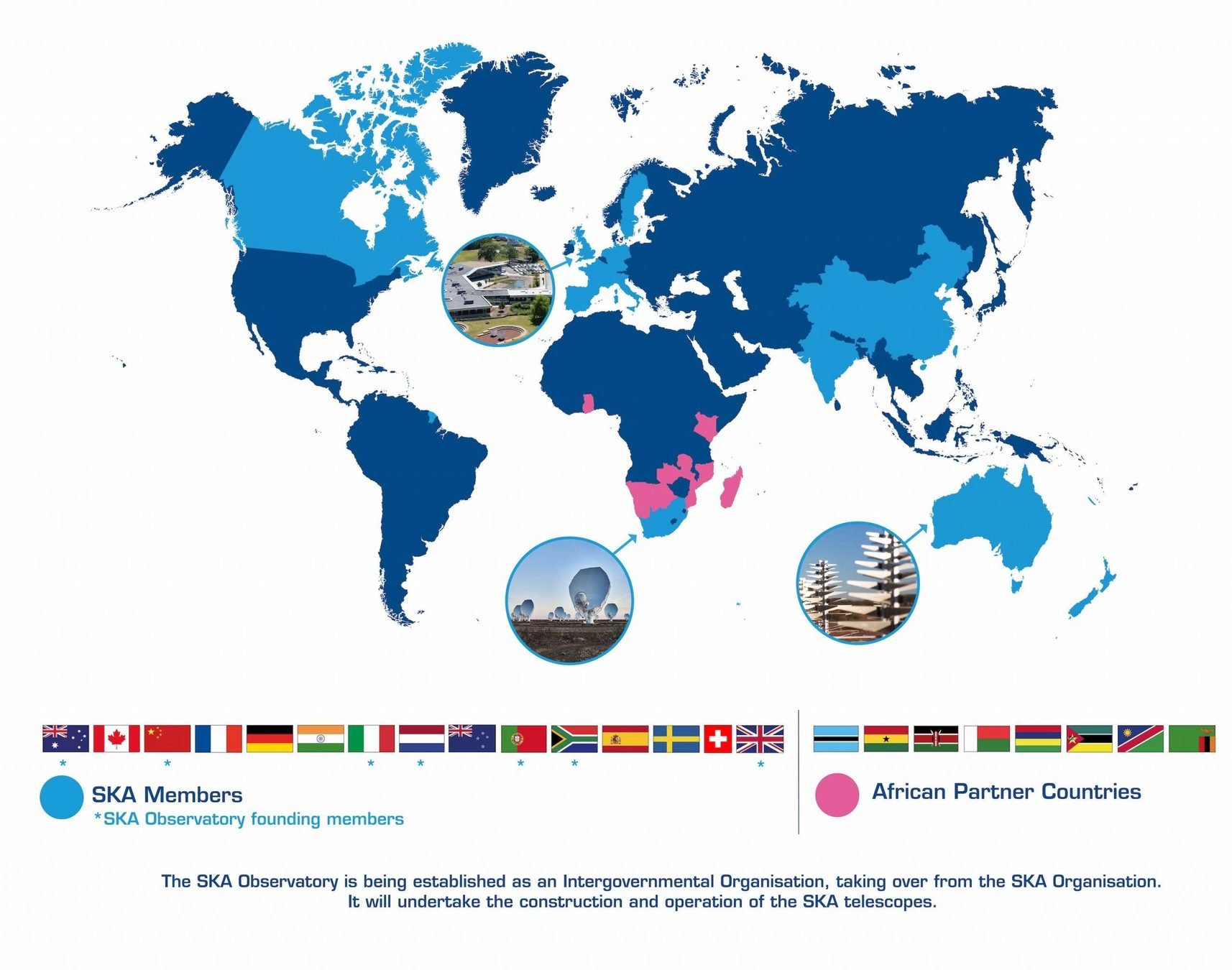
The Square Kilometer Array Obs. (SKAO)

  • Next-generation Radioastronomy observatory
  • Largest radiotelescope in the world: eventually 1km^2 area.
  • 15 countries + partners
  • Australia + South Africa installations
  • ~2 billion Euros up to 2030.
  • 5Tbps data rate and 250 Pflops needed for computation

Vera Rubin LSST

Text

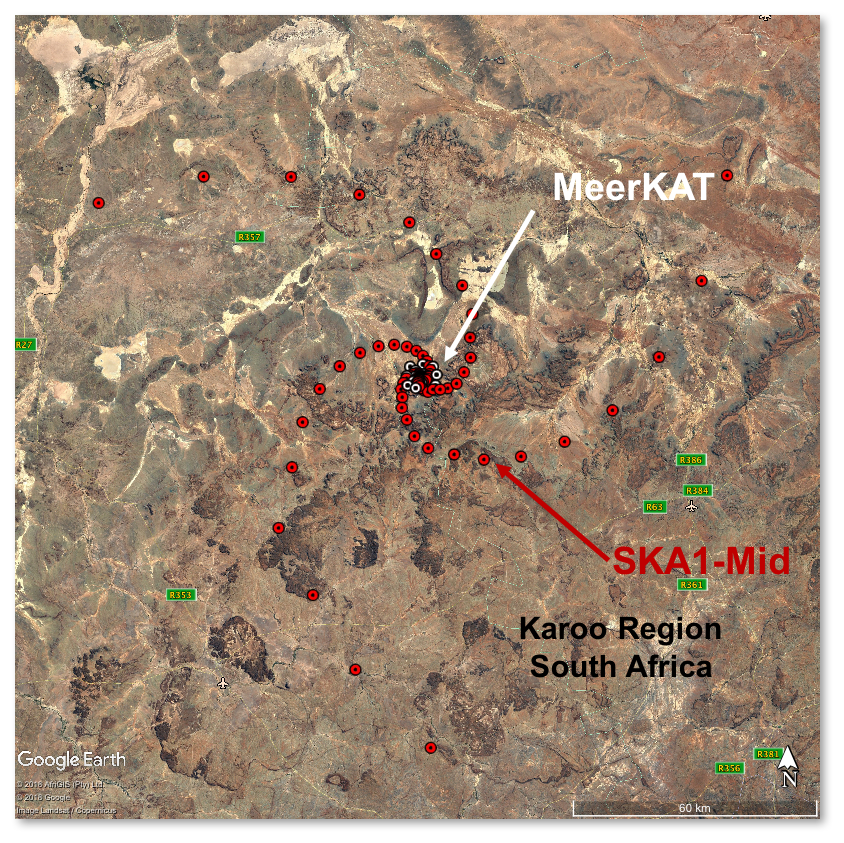
The Square Kilometer Array (SKA)

  • SKA Phase 1: SKA1-Low and SKA1-Mid
  • SKA1-Low: 130,000 dipole antennas, 65km max. baseline
  • SKA1-Mid: ~200 dishes of ~15m diameter, max. baseline  150km
  • Precursors: ASKAP, MEERKAT, HERA...

Vera Rubin LSST

Text

The Square Kilometer Array (SKA)

  • 15,000-20,000 square degrees in the sky
  • Precursors: 10^7, SKA-phase1: 10^8, SKA-phase2: 10^9 galaxies
  • SKA1-MID: 0 < z  < 3
  • SKA1-Low: 3 < z < ~ 20
  • Cosmology is just one small area, Exoplanets, Craddle of Life, Reionization, Cosmic Magnetism....

Vera Rubin LSST

Text

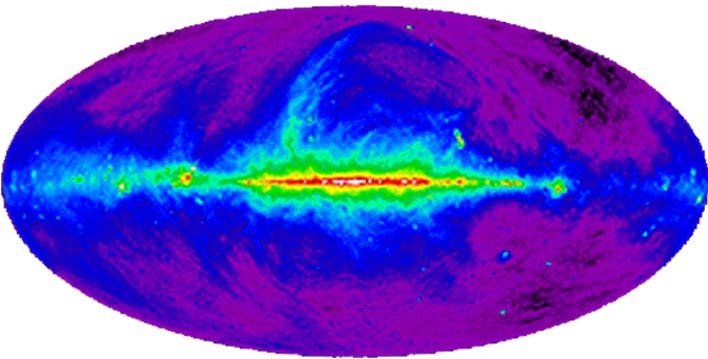
The Square Kilometer Array (SKA)

SKA Probes

Image credit: Isabella Carucci

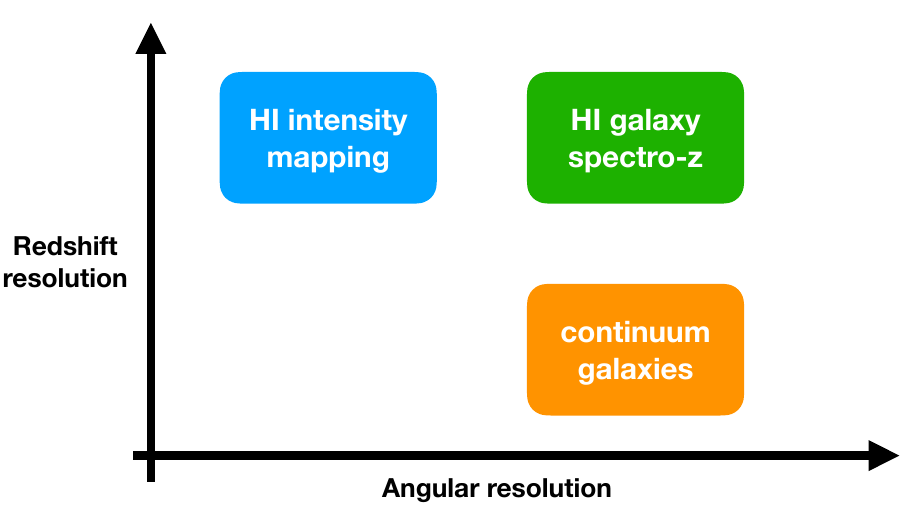
  • Continuum emission:  Allows detection of position and shapes of galaxies.

  • Line emission of neutral Hydrogen (HI, 21cm):

  1. Using redshifted HI line -> spectroscopic galaxy survey

2. Intensity Mapping: Large scale correlations in HI brightness temperature -> very good redshift resolution,
good probe of structres

Vera Rubin LSST

Text

The Square Kilometer Array (SKA)

SKA Probes

SKA Surveys

  • IM: Intensity mapping survey
    \(0.4 < z < 2.5\)
  • Very good redshift resolution:  \(\Delta z \approx \mathcal{O}(10^{-3}) \)
  • We use: 11 redshift bins
  • Single dish mode:
    \(N_d = 197\)
    \(t_{obs} = 10000 \, \rm{hr} \)
    We limit to the scales
    \(0.001 < k < 0.25 \, [h/\rm{Mpc}] \)
     

 

SKA1 Medium Deep Band 1:  \(20000 \,\rm{deg}^2\)

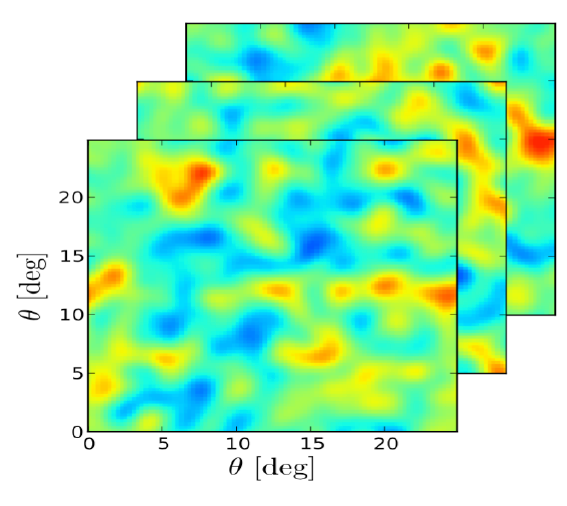
Vera Rubin LSST

Text

The Square Kilometer Array (SKA)

SKA Probes

SKA Surveys

Galaxy Clustering - IM Synergies

  • SKA1 and Euclid probe complementary redshifts in spectroscopic GC.
  • IM and GC cross-correlation offers gain in information and reduction of systematics
  • 4 overlapping z-bins

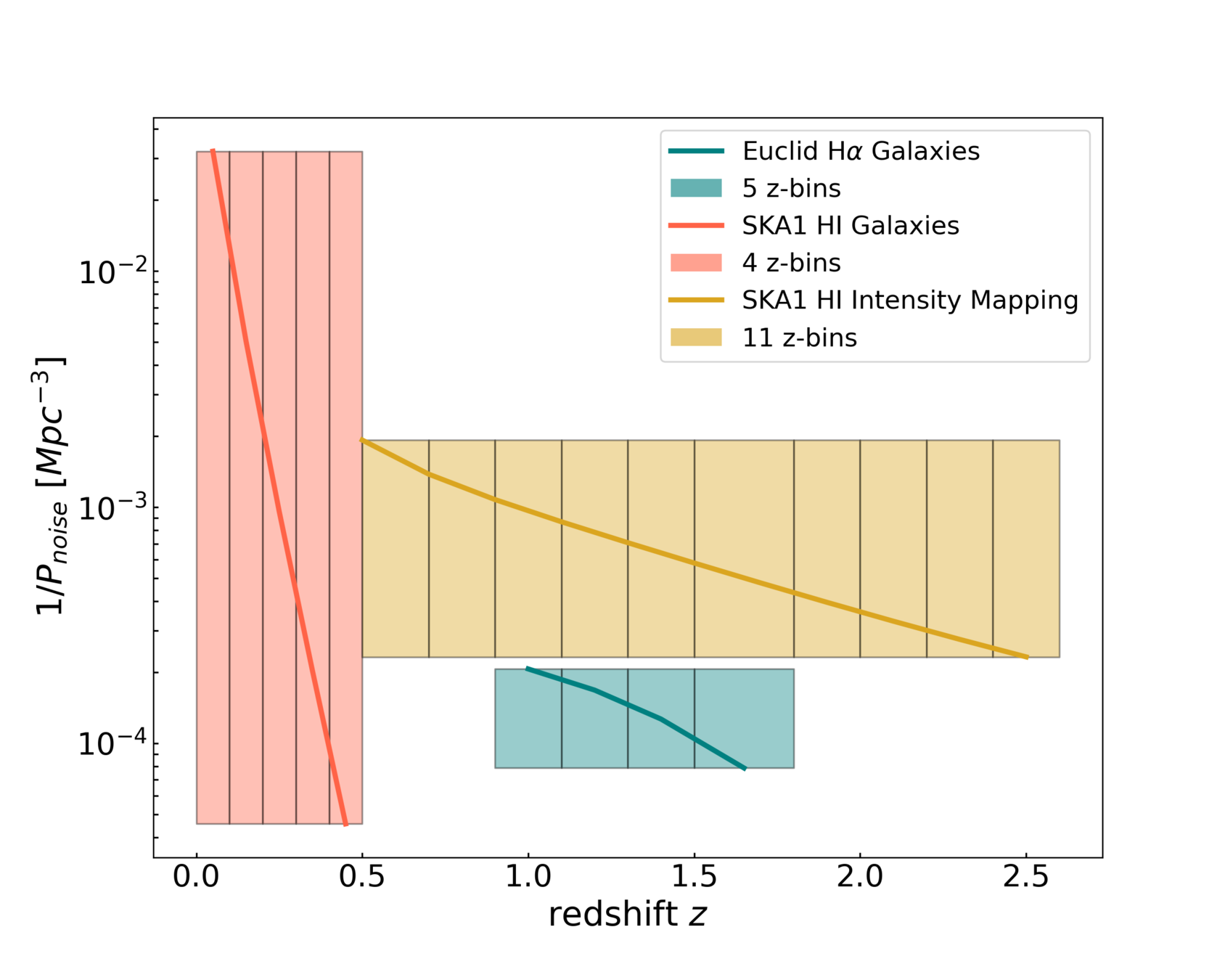
Vera Rubin LSST

Text

The Square Kilometer Array (SKA)

SKA Probes

SKA Surveys

Galaxy Clustering - IM Synergies

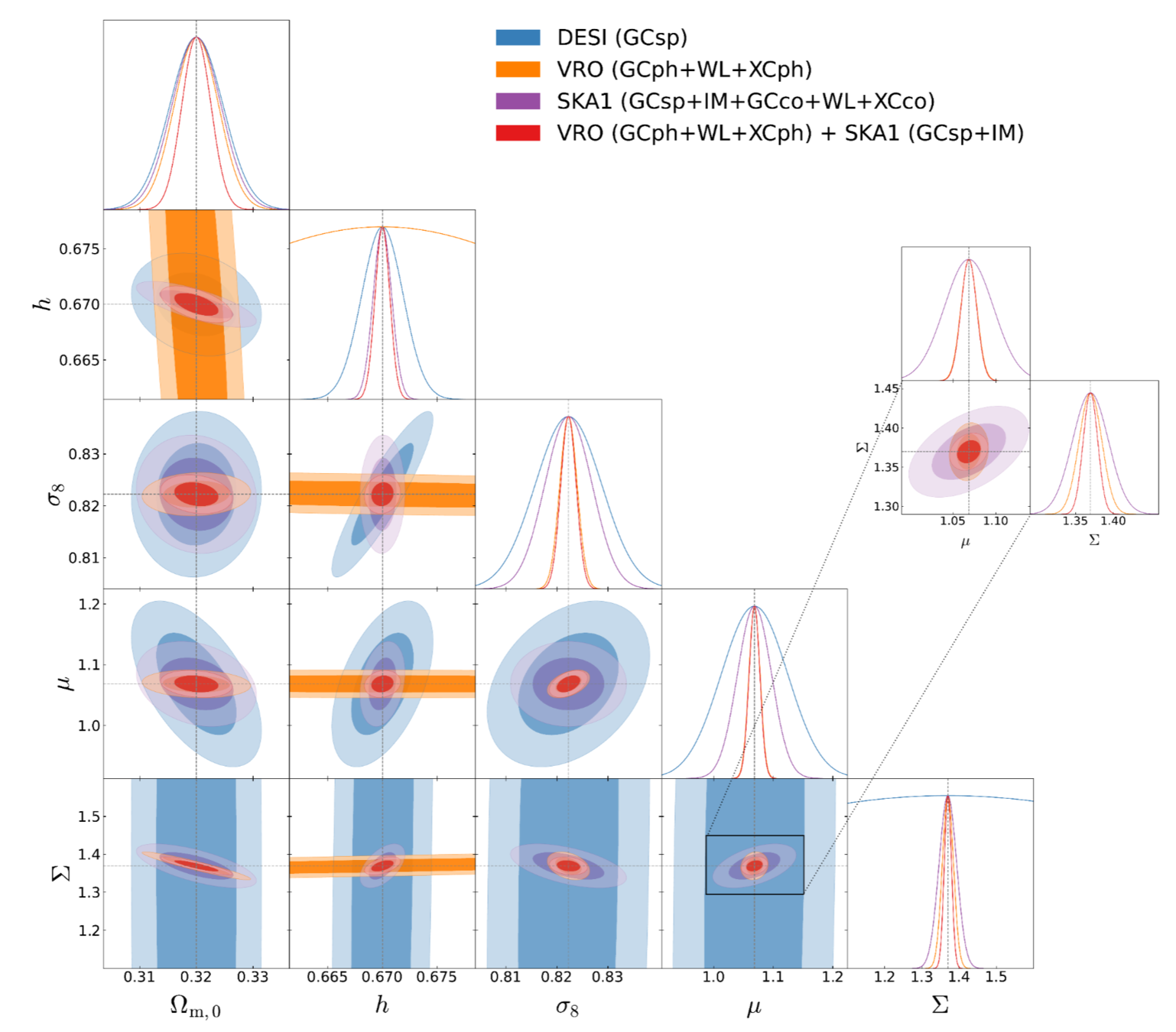
Casas, Martinelli, Pettorino, Carucci, Camera (in preparation)

f(R) Hu-Sawicki model

Text

Modification of the Einstein-Hilbert action

\newcommand{\sg}{\ensuremath{\sigma_{8}}} \newcommand{\de}{\mathrm{d}} S = \frac{c^4}{16\pi G} \int{\de^4 x \sqrt{-g} \left[R+f(R)\right]}

Induces changes in the gravitational potentials *

*for negligible matter anisotropic stress

-k^2\Psi =\frac{4\pi\,G}{c^4} \,a^2\mu\bar\rho\Delta\,
-k^2\left(\Phi+\Psi\right) = \frac{8\pi\,G}{c^4}\,a^2 \Sigma \bar\rho\Delta

Scale-dependent growth of matter perturbations

Small changes in lensing potential

\mu(a,k) = \frac{1}{1+f_R(a)}\frac {1+4k^2a^{-2}m_{f_R}^{-2}(a) }{1+3k^2a^{-2}m_{f_R}^{-2}(a)}
\Sigma(a)=\frac{1}{1+f_{R}(a)}\,

Free parameter: \(f_{R0}\)

f(R) = - 6 \Omega_{\rm DE} H_0^2 + |f_{R0}| \frac{\bar R_0^2}{R}\,

Hu, Sawicki (2007)

"Fifth-force" scale for cosmological densities

\(\lambda_C =32 \rm{Mpc}\sqrt{|f_{R0}|/10^{-4}}\)

Euclid: Casas et al (2022) in preparation

f(R) Hu-Sawicki model

Text

Euclid: Casas et al (2022) in preparation

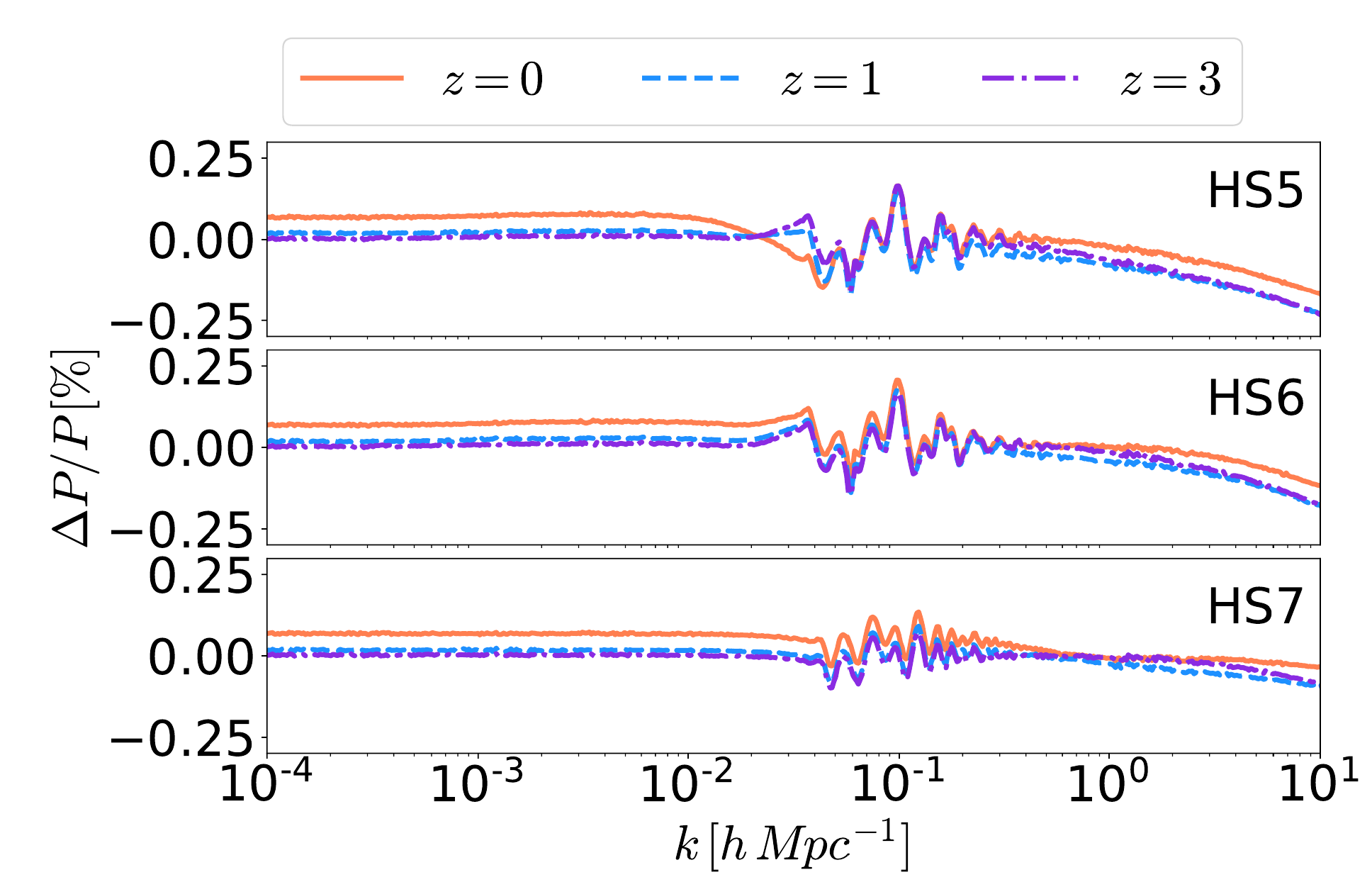
Codes used: for background and scale-dependent linear perturbations: MGCAMB and EFTCAMB

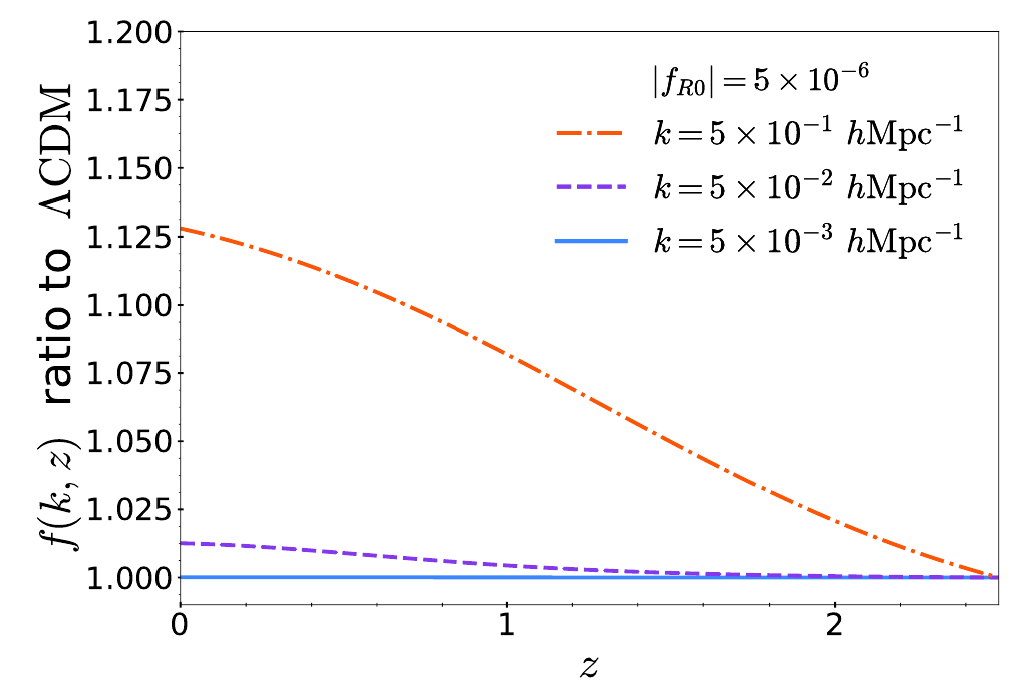
For non-linear power spectrum:

Winther et al (2019) fitting formula

f(R) Hu-Sawicki model

Text

Euclid: Casas et al (2022) in preparation

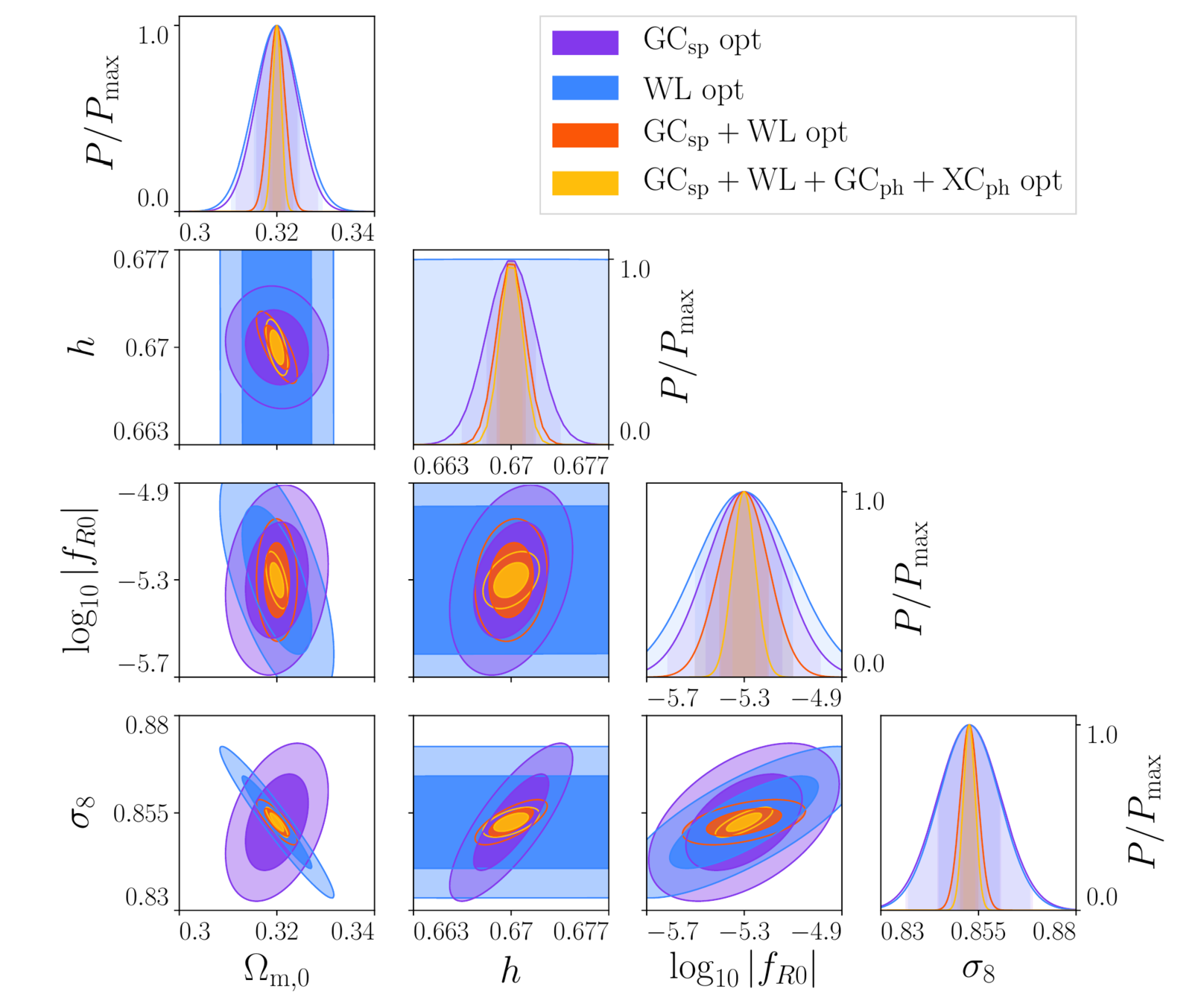
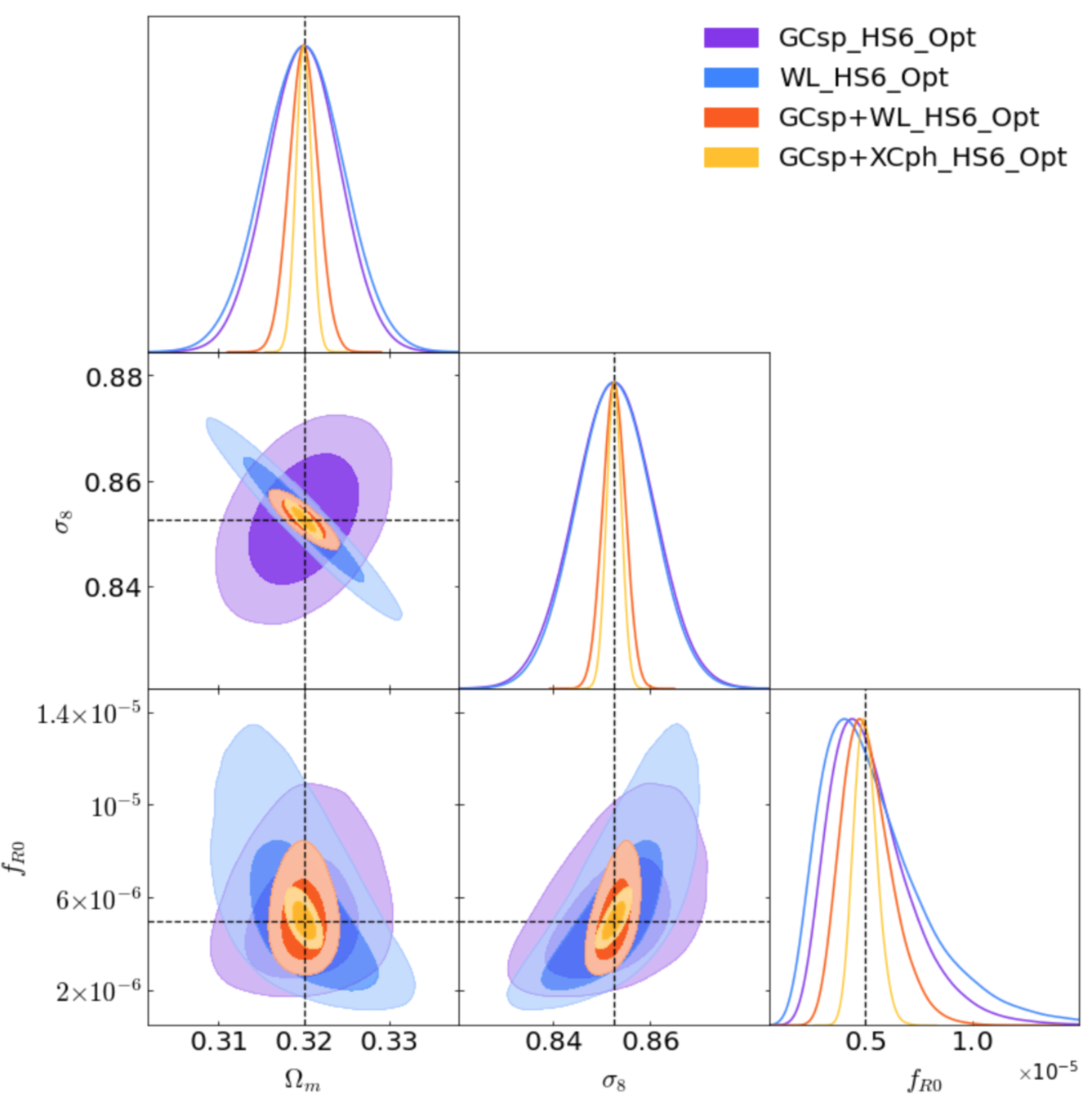
 \(\sigma_{\log f_{R0}}=0.05\) (0.9%)

Full probe combination, optimistic Euclid constraints:

\(f_{R0}=(5.0^{+ 0.58}_{-0.52} \times 10^{-6})\)

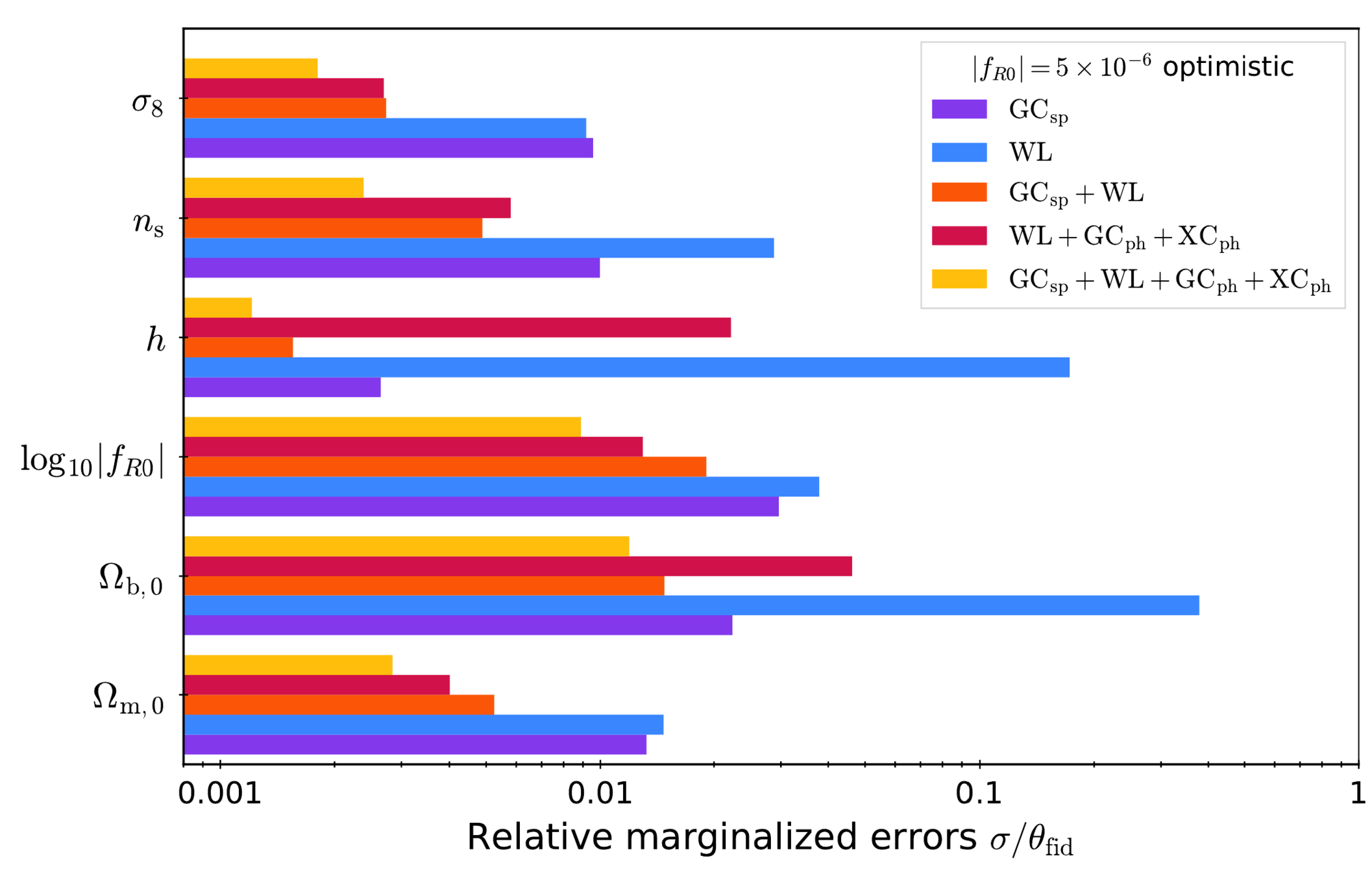
Paper also contains impact of:

  • Non-linear scales
  • Cross-correlations
  • Pessimistic settings
  • LCDM-limit

f(R) Hu-Sawicki model

Text

Euclid: Casas et al (2022) in preparation

N-body simulations for Dark Energy

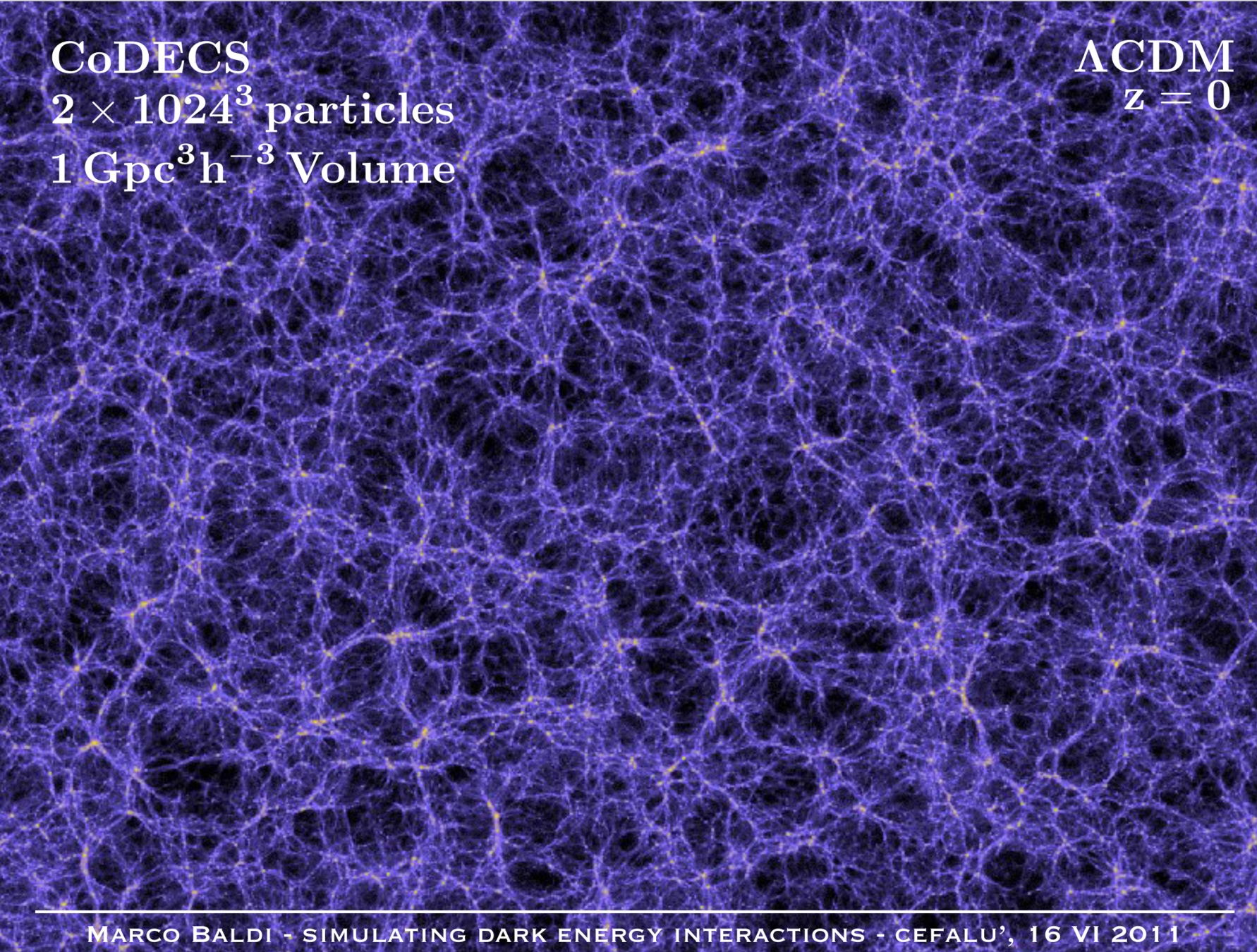
f(R) Hu-Sawicki model and degeneracies

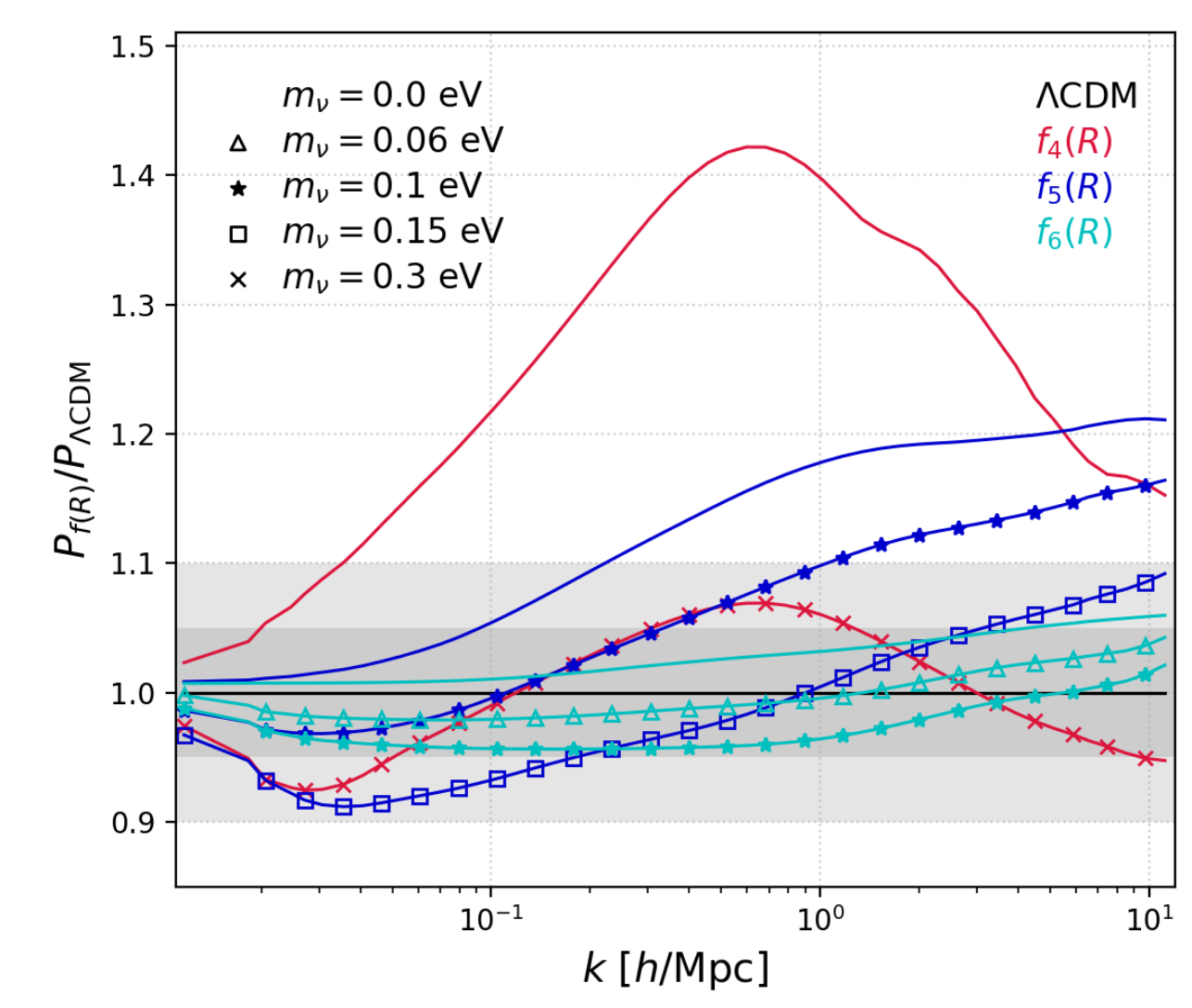
\newcommand{\sg}{\ensuremath{\sigma_{8}}} \newcommand{\de}{\mathrm{d}} S = \frac{c^4}{16\pi G} \int{\de^4 x \sqrt{-g} \left[R+f(R)\right]}
  • Degeneracy:
  • Suppression from neutrinos
  • Enhancement from fifth-force (modified G)
  • Degeneracies can be broke by looking at non-gaussian terms beyond the Pk

More exotic models

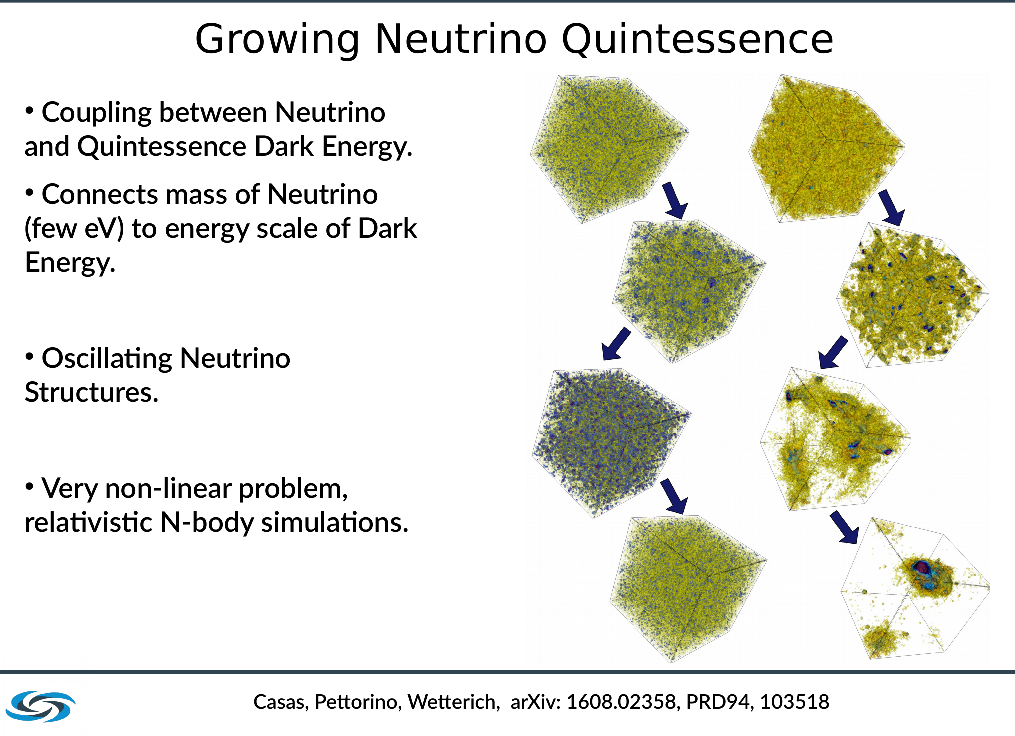
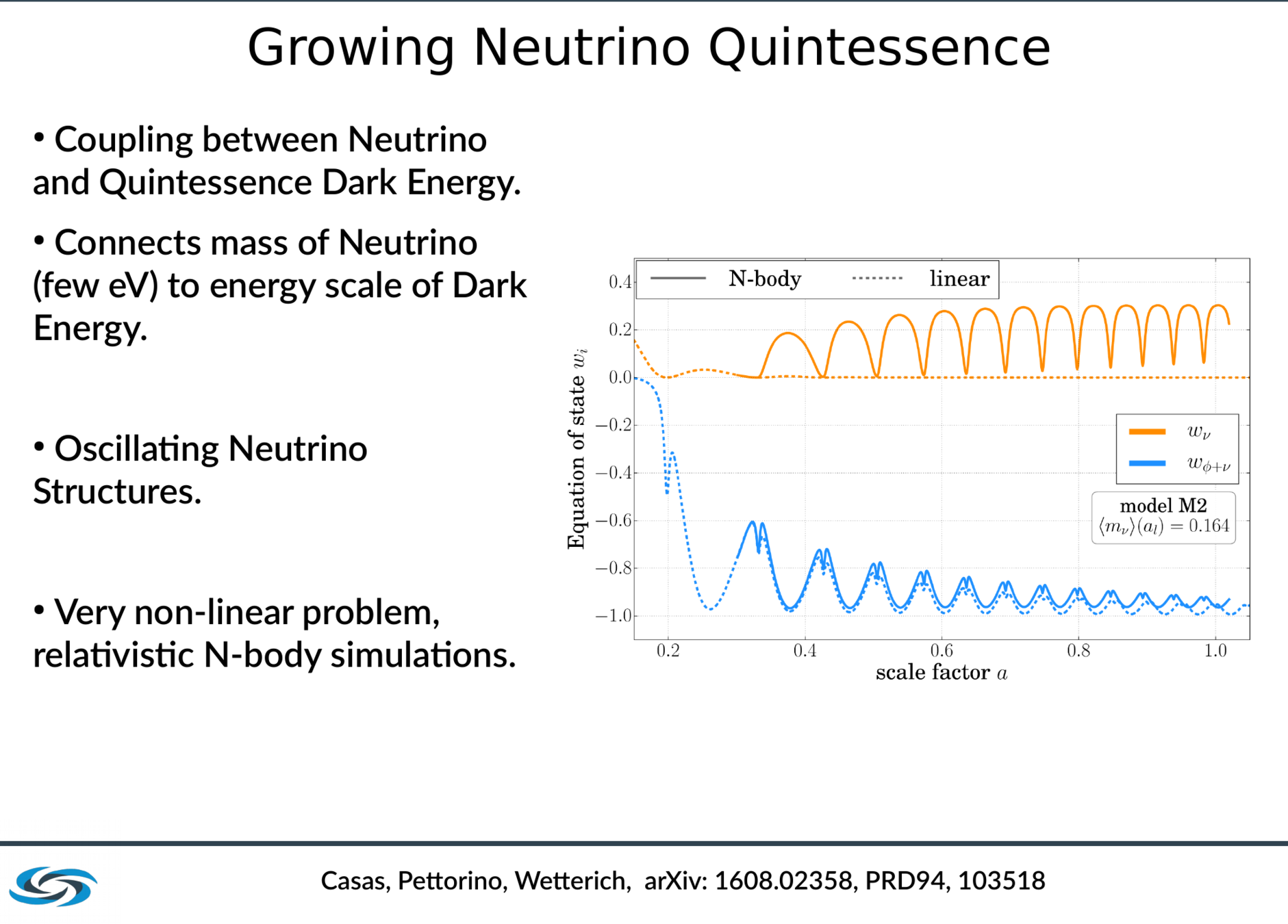
More exotic models

The problem of non-linearities

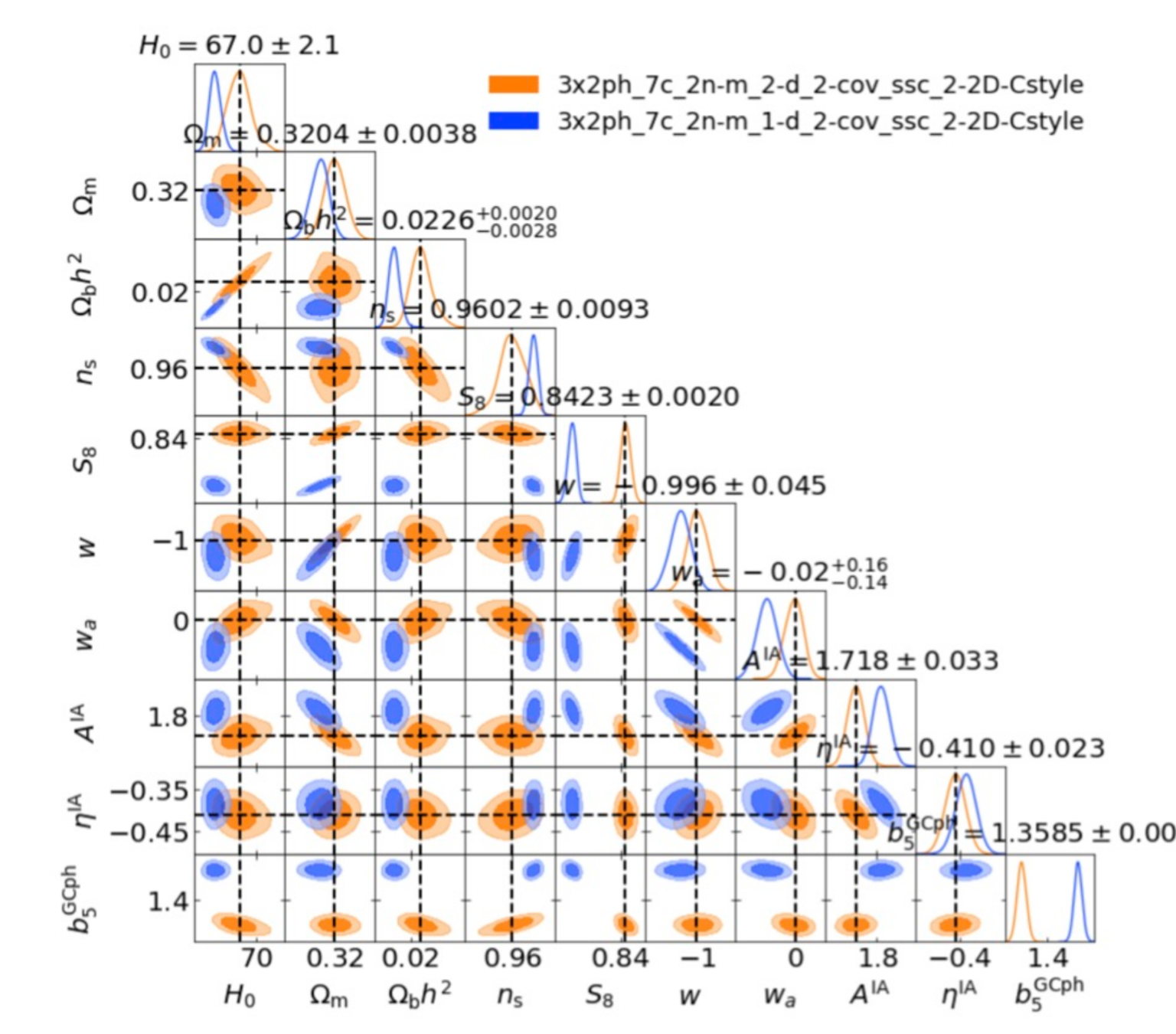
  • Euclid Likelihood Code: CLOE
  • Baryonic physics
  • N-body simulations
  • Non-linear power spectrum
  • Strong parameter biases

The problem of non-linearities

  • Euclid Likelihood Code: CLOE
  • Baryonic physics
  • N-body simulations
  • Non-linear power spectrum
  • Strong parameter biases

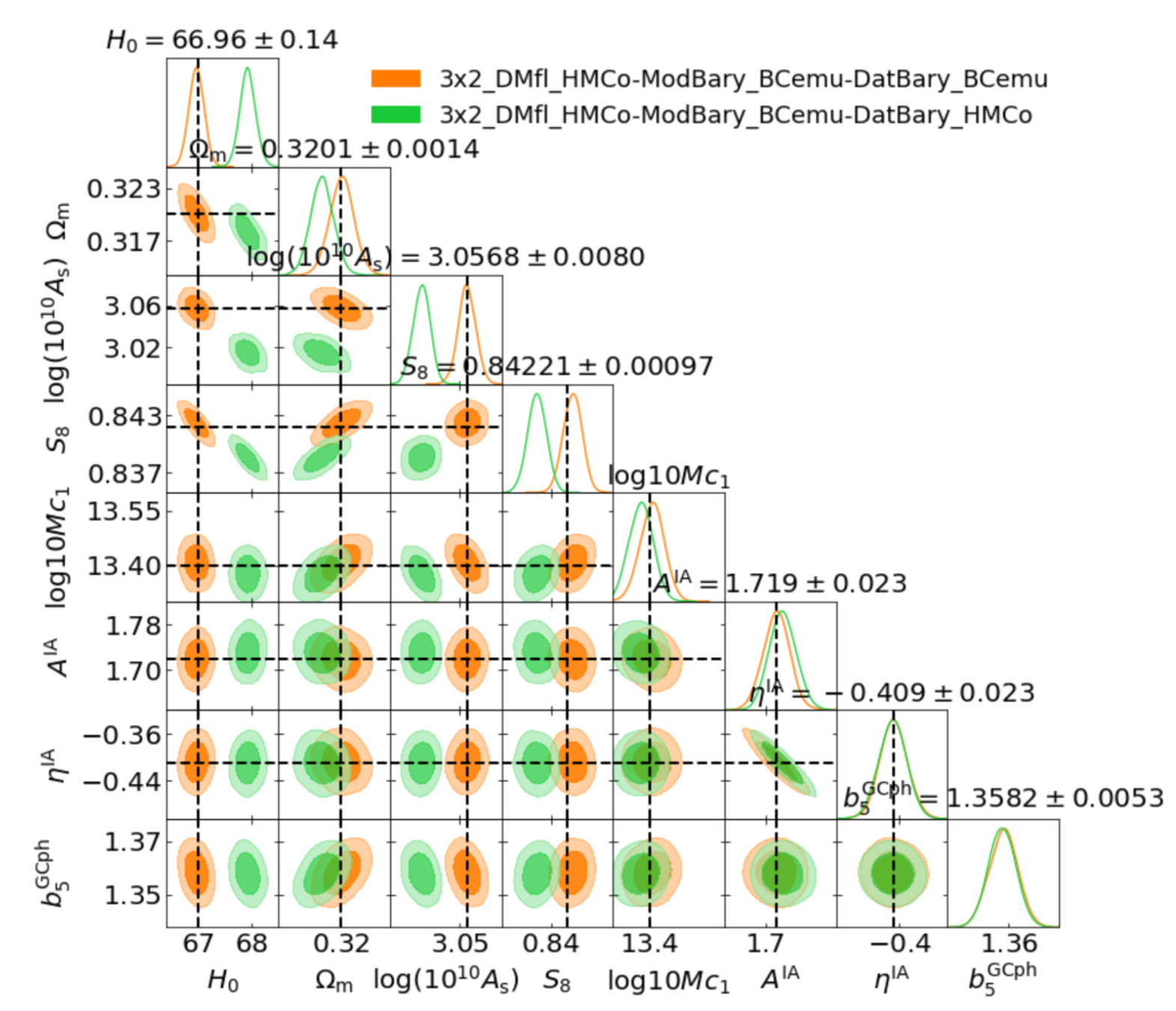
Text

Text

Conclusiones

  • Euclid va a proveer una cantidad de datos sin precedentes en la cosmología.
  • Gracias a sus imágenes detalladas y la determinación de distancias y posiciones, podemos hacer un mapa 4D del Universo (espacio y tiempo).
  • Los neutrinos tienen importantes efectos en los observables cosmológicos
  • Aún muchas teorías de gravedad modificada son compatibles con los datos
  • Muchos challenges en el modelaje no-linear

Muchas Gracias!!