Dynamical Systems

ML in Feedback Sys #5

Prof Sarah Dean

Reminders

Sign up to scribe and rank preferences for paper presentations by TODAY!
- SR19 "Near optimal finite time identification of arbitrary linear dynamical systems" (9/26)
Required: meet with Atul at least 2 days before you are scheduled to present
Working in pairs/groups, self-assessment

$F$

Dynamical System

$s$

$F(s)$

$s_{t+1} = F(s_t)$

An equilibrium point $s_{eq}$ is

stable if "for any desired accuracy, you can find a tolerance that guarantees it in perpetuity"
unstable if it is not stable
asymptotically stable if it is stable and "you can find a tolerance that guarantees converges to $s_{eq}$"

Stability

$s_{eq}$ is stable if for all $\epsilon>0$, there exists a $\delta=\delta(\epsilon)$ such that for all $t>0$, $$ \|s_0-s_{eq}\|<\delta \implies \|s_t-s_{eq}\|<\epsilon $$

Stability

$s = (x,y)$ and for some function with $f(0)=0$:
- $x_{t+1} = f(y_t)$,
- $y_{t+1} = y_t$
stable with $\epsilon^2 = f(\delta)^2 + \delta^2$

$s_{t+1} = \begin{bmatrix} 0 & 5\\ 0 & 1\end{bmatrix} s_t$ is stable with $\delta=\frac{1}{5}\epsilon$

Linear stability

Determined by eigenvalues of dynamics matrix $A$

$\mathbb C$

asymptotically stable

unstable

marginally (un)stable

Stability via linearization

Stability via linear approximation of nonlinear $F$

Stability via linearization

Stability via linear approximation of nonlinear $F$

example: discrete-time damped pendulum

$\theta_{t+1} = \theta_t + h \omega_t$

$\omega_{t+1} =\omega_t + h\left(\frac{g}{\ell}\sin\theta_t-d\omega_t\right)$

angle $\theta$

angular velocity $\omega$

gravity

length $\ell$

$\approx (1-dh)\omega_t + h\frac{g}{\ell}(\sin \theta_{eq}+\cos\theta_{eq}(\theta-\theta_{eq})$

$\sin x\approx \sin x_0 + \cos x_0(x - x_0)$

equilibria at $\theta=k\pi$ for $k\in\mathbb N$

Stability via linearization

Stability via linear approximation of nonlinear $F$

example: discrete-time damped pendulum

angle $\theta$

angular velocity $\omega$

gravity

length $\ell$

$$\begin{bmatrix}\theta_{t+1}-\theta_{eq}\\ \omega_{t+1}-\omega_{eq}\end{bmatrix} \approx \begin{bmatrix} 1 & h\\ h \frac{g}{\ell}\cos(\theta_{eq})& 1-dh\end{bmatrix}\begin{bmatrix}\theta_{t}-\theta_{eq}\\ \omega_{t}-\omega_{eq}\end{bmatrix} $$

at $\theta_{eq}=0$, real eigenvalues $0<\lambda_2<1<\lambda_1$

at $\theta_{eq}=\pi$, complex eigenvalues with $|\lambda|<1$ for small $d$

Exercise: work out the details of this analysis (simulation notebook)

$\lambda = 1-h\frac{d}{2} \pm h\sqrt{(\frac{d}{2})^2+\frac{g}{\ell}\cos(\theta_{eq})}$

Stability via linearization

Stability via linear approximation of nonlinear $F$

example: discrete-time damped pendulum

angle $\theta$

angular velocity $\omega$

gravity

length $\ell$

at $\theta_{eq}=0$, real eigenvalues $0<\lambda_2<1<\lambda_1$

at $\theta_{eq}=\pi$, complex eigenvalues with $|\lambda|<1$ for small $d$

Linearization via Taylor Series:

$s_{t+1} = F(s_t) $

Stability via linearization

Stability via linear approximation of nonlinear $F$

The Jacobian $J$ of $G:\mathbb R^{n}\to\mathbb R^{m}$ is defined as $$ J(x) = \begin{bmatrix}\frac{\partial G_1}{\partial x_1} & \dots & \frac{\partial G_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial G_m}{\partial x_1} &\dots & \frac{\partial G_m}{\partial x_n}\end{bmatrix}$$

$F(s_{eq}) + J(s_{eq}) (s_t - s_{eq}) $ + higher order terms

$s_{eq} + J(s_{eq}) (s_t - s_{eq}) $ + higher order terms

$s_{t+1}-s_{eq} \approx J(s_{eq})(s_t-s_{eq})$

Consider the dynamics of gradient descent on a twice differentiable function $g:\mathbb R^d\to\mathbb R^d$

$\theta_{t+1} = \theta_t - \alpha\nabla g(\theta_t)$

Jacobian $J(\theta) = I - \alpha \nabla^2 g(\theta)$

Example: gradient descent

Let $\{\gamma_i\}_{i=1}^d$ be the eigenvalues of the Hessian $\nabla^2 g(\theta_{eq})$
Then the eigenvalues of the Jacobian are $1-\alpha\gamma_i$
- if any $\gamma_i\leq 0$, $\theta_{eq}$ is not stable
  - i.e. saddle, local maximum, or degenerate critical point of $g$
- as long as $\alpha<\frac{1}{\gamma_i}$ for all $i$, $\theta_{eq}$ is stable

Definition: A Lyapunov function $V:\mathcal S\to \mathbb R$ for $F$ is continuous and

(positive definite) $V(0)=0$ and $V(0)>0$ for all $s\in\mathcal S - \{0\}$
(decreasing) $V(F(s)) - V(s) \leq 0$ for all $s\in\mathcal S$
Optionally,
- (strict) $V(F(s)) - V(s) < 0$ for all $s\in\mathcal S-\{0\}$
- (global) $\|s\|_2\to \infty \implies V(s)\to\infty$

Stability via Lyapunov

Reference: Bof, Carli, Schenato, "Lyapunov Theory for Discrete Time Systems "

Stability via Lyapunov

Theorem (1.2, 1.4): Suppose that $F$ is locally Lipschitz, $s_{eq}=0$ is a fixed point, and $V$ is a Lyapunov function for $F,s_{eq}$. Then, $s_{eq}=0$ is

stable
asymptotically stable if $V$ satisfies the strict property
globally asymptotically stable if $V$ satisfies the strict and global properties

Reference: Bof, Carli, Schenato, "Lyapunov Theory for Discrete Time Systems "

Quadratic Lyapunov functions

Stable matrices have quadratic Lyapunov functions of the form $V(s) = s^\top P s$ (Theorem 3.2)
- For example, $P = \sum_{t=0}^\infty (A^\top)^t A^t$
Exercise: show that the above is a strict and global Lyapunov function for $s_{t+1}=As_t$.

When Jacobian $J(0)$ is stable, can show that $V(s)=s^\top P s$ is a strict Lyapunov function for $s_{t+1} = F(s_t)$.

Quadratic Lyapunov functions

Theorem (3.3): Suppose $F$ is locally Lipschitz, $0$ is a fixed point, and let $\{\lambda_i\}_{i=1}^n\subset \mathbb C$ be the eigenvalues of the Jacobian $J(0)$. Then $0$ is

asymptotically stable if $\max_{i\in[n]}|\lambda_i|<1$
unstable if $\max_{i\in[n]}|\lambda_i|> 1$

$F$

Dynamical System

$s$

$F(s)$

$s_{t+1} = F(s_t)$

$F$

Dynamical System

$s$

$s_{t+1} = F(s_t, w_t)$

$y_t = G(s_t)$

$w_t$

$y_t$

Inputs and outputs

input signal $w_t$ represents external phenomena
- action/control input
- disturbance/process noise
output signal $y_t$ represents what is measured

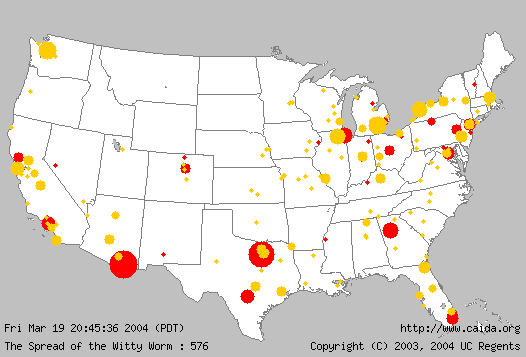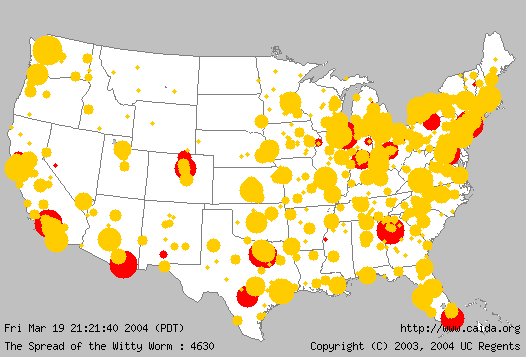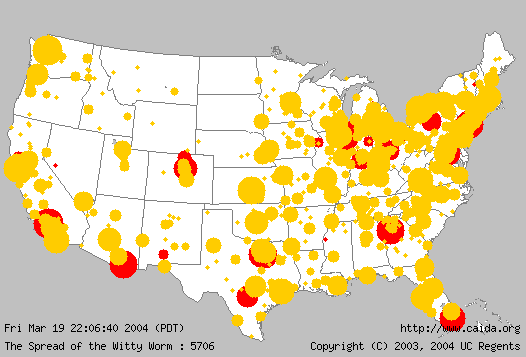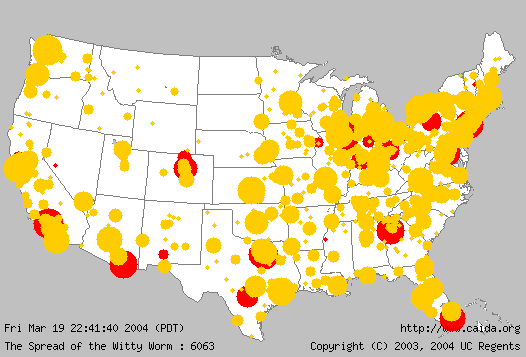
System response

$F$

$s$

$(w_0, w_1, ... )$

$\Phi$

$(y_0, y_1, ...)$

Linear system response

$s_{t+1} = As_t+ w_t$

$y_t = Cs_t$

$$y_{t} = CA^t s_0+ \sum_{k=1}^{t}CA^{k-1}w_{t-k}$$

Linear-Gaussian system

If $s_0\sim\mathcal N(\mu, \Sigma)$ and $w_t\sim \mathcal N(\mu,\Sigma)$, then

$y_t\sim \mathcal N(\sum_{k=0}^{t}CA^{k}\mu, \sum_{k=0}^{t}CA^{k}\Sigma(A^{k})^\top C^\top)$

The limit as $t\to\infty$ is the steady state distribution

Linear stochastic system

If $\mathbb E[s_0] = \mathbb E[w_t] =\mu$ and $\mathrm{Cov}[s_0] = \mathrm{Cov}[w_t] = \Sigma$, then

$\mathbb E[y_t] = \sum_{k=0}^{t}CA^{k}\mu$

$\mathrm{Cov}[y_t] = \sum_{k=0}^{t}CA^{k}\Sigma(A^{k})^\top C^\top$

Can characterize moments without knowing whole distribution

Bounded inputs & bounded outputs

What if inputs are not stochastic?

The sequence $(w_0, w_1, ...)$ can be adversarially chosen, but is bounded

at every $t$: $\|w_t\|\leq B$ for all $t$
on average: $\sqrt{\lim_{T\to\infty}\frac{1}{T}\sum_{t=0}^{T-1} \|w_t\|_2^2}\leq B$

often possible to show that output are also bounded (upcoming lectures)

Input-to-state stability

For a system $s_{t+1} = F(s_t) + w_t$ where $F(0)=0$

Suppose that there is a $V:\mathcal S\to\mathbb R_+$ that

defines a metric: $\alpha_1 \|s\|_2^2 \leq V(s) \leq \alpha_2 \|s\|_2^2 $ and $$\sqrt{V(s+s')}\leq \sqrt{V(s)}+\sqrt{V(s')}$$
is contracting: $V(F(s)) \leq \gamma V(s)$ for some $\gamma<1$ and all $s\in\mathcal S$

Then if $\|w_t\|_2\leq B$ for all $t$, $\displaystyle \lim_{t\to\infty} \|s_t\|_2 \leq \sqrt{\frac{\alpha_2}{\alpha_1}}\frac{B}{1-\sqrt{\gamma}} $

$\sqrt{V(s_{t+1})} = \sqrt{V(F(s_t) + w_t)} \leq \sqrt{V(F(s_t))} + \sqrt{V(w_t)} \leq \sqrt{\gamma V(s_t)} + \sqrt{\alpha_2}\|w_t\|_2 $

$\implies \sqrt{V(s_{t})} \leq \gamma^{t/2}\sqrt{ V(s_0)} + \sum_{k=1}^t \gamma^{(k-1)/2}\sqrt{\alpha_2}\|w_{t-k}\|_2$

$\implies \|s_t\|_2 \leq \gamma^{t/2}\sqrt{ \frac{\alpha_2}{\alpha_1}}\|s_0\|_2 + \sum_{k=1}^t \gamma^{(k-1)/2}\sqrt{\frac{\alpha_2}{\alpha_1}}\|w_{t-k}\|_2$

Proof

Consider the dynamics of stochastic gradient descent on a twice differentiable function $g:\mathbb R^d\to\mathbb R^d$

$\theta_{t+1} = \theta_t - \alpha g_t$

Example: stochastic gradient descent

$= \theta_t - \alpha \nabla g(\theta_t) + \underbrace{\alpha (\nabla g(\theta_t) - g_t) }_{w_t} $

may converge to ball around minima
in general, could jump between minima
in practice, decreasing step size $\alpha_t\propto 1/t$

Next time: see these ideas in action!

Recap

References: Bof, Carli, Schenato, "Lyapunov Theory for Discrete Time Systems "

Nonlinear stability
- Linearization
- Lyapunov functions
Inputs and outputs
- System response
- Stability

Dynamical Systems

ML in Feedback Sys #5

Reminders

\(F\)

Dynamical System

Stability

Stability

Linear stability

Stability via linearization

Stability via linearization

Stability via linearization

Stability via linearization

Stability via linearization

Example: gradient descent

Stability via Lyapunov

Stability via Lyapunov

Quadratic Lyapunov functions

Quadratic Lyapunov functions

\(F\)

Dynamical System

\(F\)

Dynamical System

Inputs and outputs

System response

\(F\)

\(\Phi\)

Linear system response

Linear-Gaussian system

Linear stochastic system

Bounded inputs & bounded outputs

Input-to-state stability

Proof

Example: stochastic gradient descent

Recap