Lifting Nonlinear Dynamics
ML in Feedback Sys #6
Fall 2025, Prof Sarah Dean
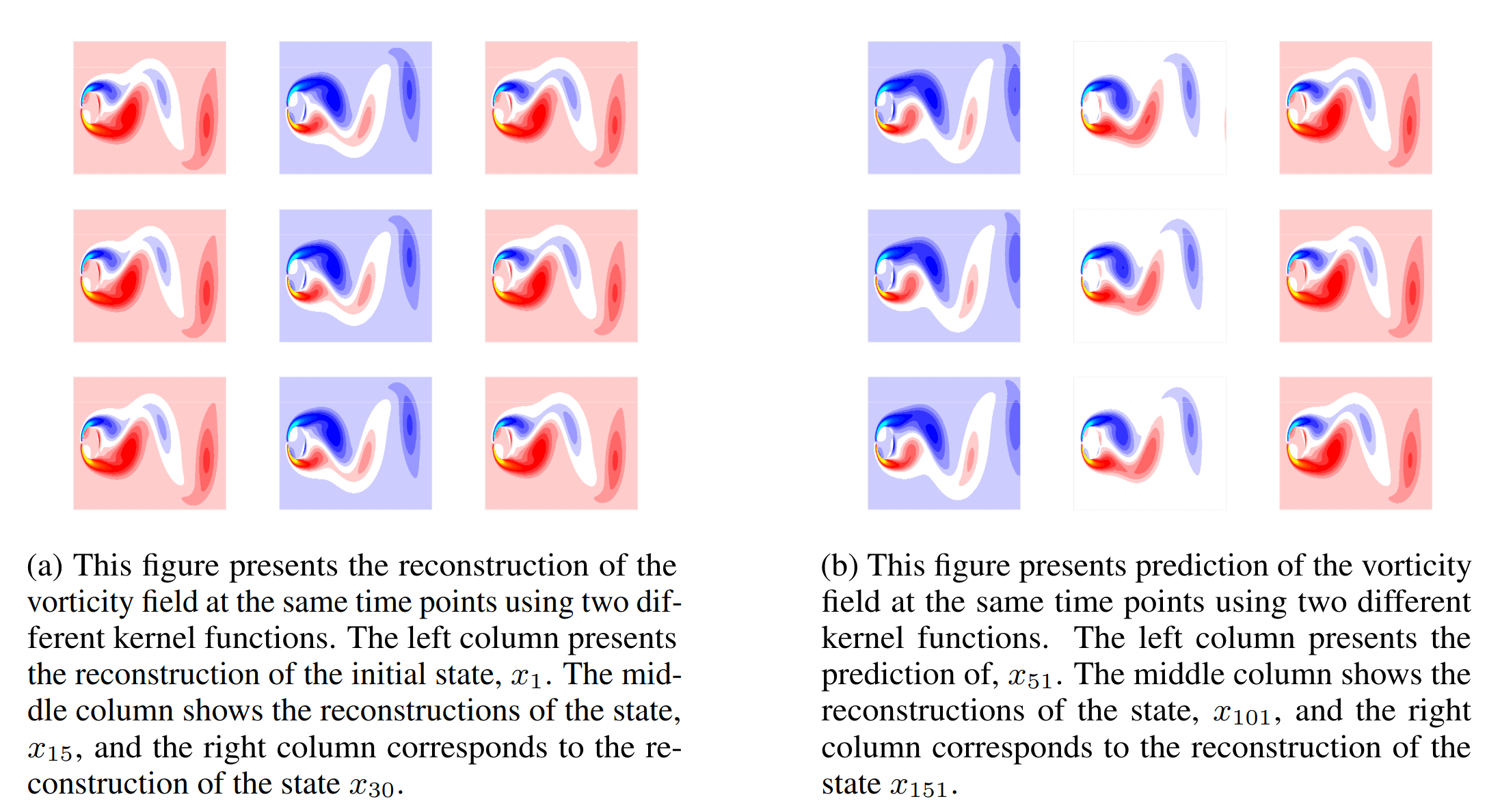
Kernel dynamic mode decomposition
"What we do"
- Given: data \(\{x_k\}_{k=1}^{n+1}\) and kernel function \(k:\mathcal X\times\mathcal X\to\mathbb R\)
- Train a temporal model:
- Construct kernel matrices \(K\in\mathbb R^{n\times n}\) and \(K_{+}\in\mathbb R^{n\times n}\) with $$K_{ij} = k(x_i,x_j) ~~\text{and}~~[K_+]_{ij} = k(x_i,x_{j+1})$$
- Construct \(X = \begin{bmatrix}x_1 & \dots & x_{n} \end{bmatrix}^\top\) and \(k_n(x_0)=\begin{bmatrix} k(x_0, x_1) & \dots & k(x_0, x_n) \end{bmatrix}^\top\)
- Define \(K_\lambda = K+\lambda I\) and compute eigendecomposition of \(K_\lambda^{-1}K_+ = V\Lambda V^{-1}\)
- Make predictions from \(x_0\) with $$\hat x_t = X V\Lambda^{t} V^{-1} K_\lambda^{-1}k_n(x_0) = \sum_{i=1}^n w_i \lambda_i^t b_i(x_0)$$
columns \(w_i\)
"modes"
diag(\(\lambda_i\))
"spectrum"
entries \(b_i(x_0)\)
"initial amplitudes"
Lifted linear dynamics
"Why we do it"
- Fact 1: For many nonlinear \(F\), there exists a linear operator \(\mathcal F\) and nonlinear transformation \(\varphi\) such that \(\varphi(F(x)) = \mathcal F \varphi(x)\) and hence the lifted dynamics are linear \(\varphi(x_{k+1}) = \mathcal F \varphi(x_k)\)
- Consider the ERM least squares problem: $$\hat\Theta = \arg\min_{\Theta\in \mathbb R^{ d_\varphi \times d_\varphi}} \sum_{k=1}^n (\Theta^\top \varphi(x_k) - \varphi(x_{k+1}))^2 + \lambda \|\Theta\|_F^2$$
- and the corresponding LDS predictions: \(\widehat{\varphi( x_t)} = (\hat\Theta^\top)^t\varphi( x_0)\)
- Fact 2: Suppose \(R\varphi(x) = x\). Then the predictions by ERM+LDS are almost* identical to KDMD with \(k(x,x') = \varphi(x)^\top \varphi(x')\) $$\hat x_t = R(\hat \Theta^\top)^t \varphi(x_0)=\sum_{i=1}^n w_i \lambda_i^t b_i(x_0)$$
- Fact 3: KDMD depends only on the size of the data \(n\) and not on the dimension of the transformation \(d_\varphi\)
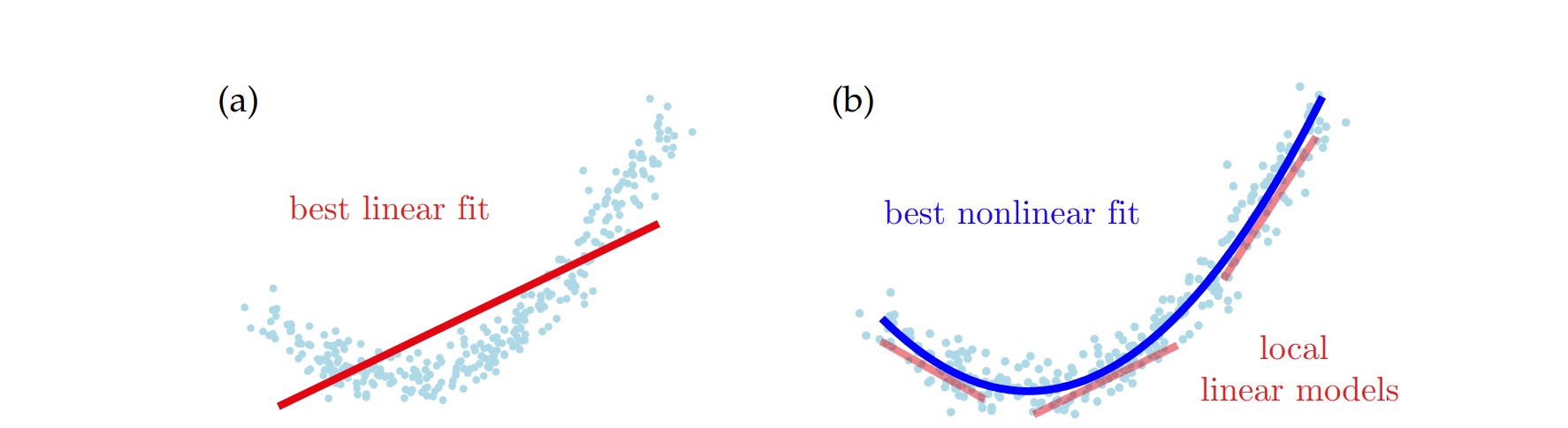
Lifting dynamics: example
- Fact 1: For many nonlinear \(F\), there exists a linear operator \(\mathcal F\) and nonlinear transformation \(\varphi\) such that \(\varphi(F(x)) = \mathcal F \varphi(x)\) and hence the lifted dynamics are linear \(\varphi(x_{k+1}) = \mathcal F \varphi(x_k)\)
- Example: 2d second order polynomial $$x_{t+1} = \begin{bmatrix} p_{t+1} \\ q_{t+1}\end{bmatrix} = \begin{bmatrix} a & \\ & b \end{bmatrix} \begin{bmatrix} p_{t} \\ q_{t}\end{bmatrix} + \begin{bmatrix} 0 \\ c\end{bmatrix}p_{t}^2 $$
- define the lift as \(\varphi(p,q) =\begin{bmatrix} p & q & p^2 \end{bmatrix}^\top\)
- \(\varphi(F(x)) = \begin{bmatrix} ap \\ bq+cp^2 \\ a^2p^2 \end{bmatrix} = \underbrace{\begin{bmatrix} a && \\ & b & c \\ && a^2 \end{bmatrix}}_{\mathcal F} \varphi(s)\)
- simulation notebook
Koopman operator
- Fact 1: For many nonlinear \(F\), there exists a linear operator \(\mathcal F\) and nonlinear transformation \(\varphi\) such that \(F(\varphi(x)) = \mathcal F \varphi(x)\) and hence the lifted dynamics are linear \(\varphi(x_{k+1}) = \mathcal F \varphi(x_k)\)
- Example: \(F\) is some polynomial of degree \(p\)
- Consider \(\psi(x)\) to be monomials up to degree \(p\)
- Then \(F(x) = \Theta^\top \psi(x)\) by definition
- \(\psi(F(x))\) will also be a polynomial in \(x\)
- but in general will be of higher degree...
- We don't always get "closure" in finite dimensions
- \(\mathcal F\) is called the Koopman operator and may be infinite dimensional
- The nonlinear transform \(\varphi\) will also be infinite dimensional and satisfies an inclusion property, meaning that \(x\) is linearly reconstructable from \(\varphi(x)\), i.e. \(R\varphi(x)=x\)

Lifted predictions
Deriving the form of the predictions:
$$\hat\Theta = \arg\min_{\Theta\in \mathbb R^{ d_\varphi \times d_\varphi}} \sum_{k=1}^n (\Theta^\top \varphi(x_k) - \varphi(x_{k+1}))^2 + \lambda \|\Theta\|_F^2$$
- \(\hat\Theta^\top = \sum_{k=1}^n \varphi(x_{k+1})\varphi(x_k)^\top \Big( \sum_{k=1}^n \varphi(x_k)\varphi( x_k)^\top + \lambda I\Big)^{-1}\)
- \( =\Phi_+^\top \Phi (\Phi^\top\Phi + \lambda I)^{-1} \) (in matrix form)
- \(= \Phi_+^\top (\Phi\Phi^\top + \lambda I)^{-1} \Phi \) (matrix inversion lemma)
- \(\hat\Theta^\top\varphi(x_0) = \Phi_+^\top K_\lambda^{-1} \Phi \varphi(x_0) = \Phi_+^\top K_\lambda^{-1} k_n(x_0) \)
- \((\hat\Theta^\top)^2 \varphi(x_0) = \Big(\Phi_+^\top (\Phi\Phi^\top + \lambda I)^{-1} \Phi \Big) \Phi_+^\top K_\lambda^{-1} k_n(x_0) \)
- \(= \Phi_+^\top K_\lambda^{-1} K_+ K_\lambda^{-1} k_n(x_0)\)
- Continuing: \((\hat\Theta^\top)^t \varphi(x_0)= \Phi_+^\top (K_\lambda^{-1} K_+)^{t-1} K_\lambda^{-1} k_n(x_0) \)
Lifted predictions
Deriving the form of the predictions:
- \(\widehat{\varphi( x_t)}=(\hat\Theta^\top)^t \varphi(x_0)= \Phi_+^\top (K_\lambda^{-1} K_+)^{t-1} K_\lambda^{-1} k_n(x_0) \)
- Data smoothing step: regularized projection of \(\varphi(x_2),...,\varphi(x_{n+1})\) onto the span of \(\varphi(x_1),...,\varphi(x_{n})\)$$\underbrace{\Phi^\top (\Phi \Phi^\top+\lambda I)^{-1} \Phi}_{\text{projection}} \Phi_+^\top = \Phi^\top K_\lambda^{-1} K_+ $$
- In the prediction equation, replace \(\Phi_+^\top\leftarrow \Phi^\top K_\lambda^{-1} K_+\)
- For \(\lambda\to 0\) (i.e. pseudoinverse), if \(\varphi(x_{n+1})\) is in the span of \(\varphi(x_1),...,\varphi(x_n)\) then nothing changes after the smoothing step
- Final form: \(\widehat{\varphi( x_t)}= \Phi^\top (K_\lambda^{-1} K_+)^{t} K_\lambda^{-1} k_n(x_0) \)
Equivalence
- So far, ERM+LDS+smoothing predictions are $$\widehat{\varphi( x_t)}= \Phi^\top (K_\lambda^{-1} K_+)^{t} K_\lambda^{-1} k_n(x_0) =\Phi^\top V\Lambda^t V^{-1} K_\lambda^{-1} k_n(x_0) $$
- To predict the future state, use inclusion property of \(\varphi\) $$\hat x_t = R\widehat{\varphi(x_t)} =R\Phi^\top V\Lambda^t V^{-1} K_\lambda^{-1} k_n(x_0) $$ $$\qquad= X^\top V\Lambda^t V^{-1} K_\lambda^{-1} k_n(x_0) $$ $$\qquad =\sum_{i=1}^n w_i \lambda_i^t b_i(x_0)$$
- Fact 2: Suppose \(\varphi\) satisfies the inclusion property with map \(R\). Then the predictions by ERM+LDS with a data smoothing step are identical to KDMD with kernel \(k(x,x') = \varphi(x)^\top \varphi(x')\) $$\hat x_t = R(\hat \Theta^\top)^t \varphi(x_0)=\sum_{i=1}^n w_i \lambda_i^t b_i(x_0)$$
Dimension and modes
- Fact 3: KDMD depends only on the size of the data \(n\) and not on the dimension of the transformation \(d_\varphi\)
- Key intermediate quantities: \( K, K_+ \in \mathbb R^{n\times n}, X\in\mathbb R^{d\times n} \)
- Main training step: computing eigendecomposition of \(K_\lambda^{-1} K_+\)
- Via generalized eigenproblem \( K_+ v = \lambda K_\lambda v\) takes \(O(n^2)\) memory and \(O(n^3)\) computation
- Key model parameters \(W\in\mathbb R^{d\times n}\), \(\mathbf{\lambda}\in\mathbb R^n\), \(b:\mathbb R^d\to\mathbb R^n\)
- Even faster computation (training and prediction) if we discard small magnitude eigenvalues, keeping only \(r\) modes: $$\hat x_t = \sum_{i=1}^r w_i \lambda_i^t b_i(x_0)$$
KDMD vs. KRR
- Predict \(\hat x_{t} = X_+^\top \tilde K_\lambda^{-1}\tilde k_n(\hat x_{t-1})\)
- where \(\tilde K\in\mathbb R^{n\times n}\) with \(\tilde K_{ij} = \tilde k(x_i,x_j)\)
and \(X_+ = \begin{bmatrix}x_2 & \dots & x_{n+1}\end{bmatrix}^\top\)
- Predict \(\hat x_{t} = X^\top (K_\lambda^{-1} K_+)^{t} K_\lambda^{-1} k_n(x_0)\)
- where \(K\in\mathbb R^{n\times n}\) and \(K_{+}\in\mathbb R^{n\times n}\) with $$K_{ij} = k(x_i,x_j) ~~\text{and}~~[K_+]_{ij} = k(x_i,x_{j+1})$$ \(X = \begin{bmatrix}x_1 & \dots & x_{n} \end{bmatrix}^\top\) and \(k_n(x_0)=\begin{bmatrix} k(x_0, x_1) & \dots & k(x_0, x_n) \end{bmatrix}^\top\)
Given: data \(\{x_k\}_{k=1}^{n+1}\), find nonlinear dynamics model
- "What we do"
- "Why we do it"
- (almost) equivalent to LS+LDS predictions $$\hat x_t = R(\hat \Theta^\top)^t \varphi(x_0)$$ where \(k(x,x') = \varphi(x)^\top \varphi(x')\) and \(x = R\varphi(x)\)
- Selecting a kernel \(k\) \(\iff\) choosing nonlinear lift \(\varphi\) $$\varphi(F(x)) \approx \mathcal F \varphi(x)$$
- equivalent to predictions by LS $$\hat x_{t+1} = \hat \Theta^\top \tilde\varphi(x_t)$$ where \(\tilde k(x,x') = \tilde \varphi(x)^\top \tilde \varphi(x')\)
- Selecting a kernel \(\tilde k\) \(\iff\) choosing nonlinear features \(\tilde \varphi\) $$ F(x) \approx \Theta^\top \tilde\varphi(x)$$
Recap
- Kernel dynamic mode decomposition
- Koopman operators and lifting
Next time: autoregressive models and partial state observation
Announcements
- Second assignment due tonight
- Third assignment released, due next Thurs