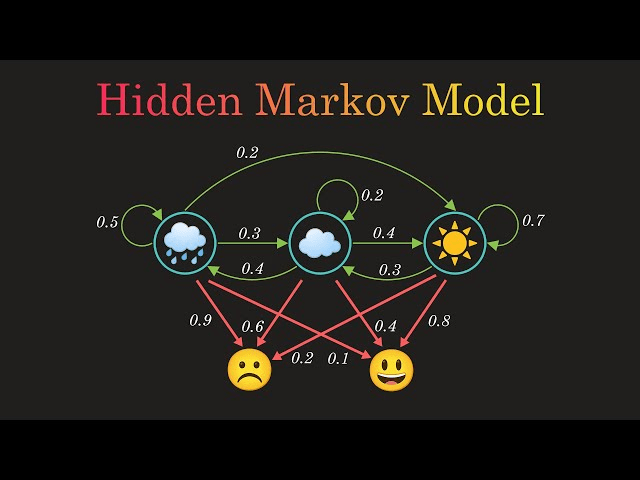
09 - Hidden Markov Models - ML in Feedback Sys F25

Hidden Markov Models

Fall 2025, Prof Sarah Dean

"What we do"

Given transition probabilities, observation probabilities, and initial state distribution $\mu_0$, $$P_{ij} = \mathbb P\{S_{t+1}=j|S_t=i\} ,\qquad B_{ij}=\mathbb P\{Y_{t}=j|S_t=i\}$$
For streaming observations $y_t$, $t\geq 0$:
- Predict state distribution: $ \mu_{t+1|t} = P^\top \mu_{t|t}$
- Update state distribution: $$ \mu_{t+1|t+1}= Be_{y_{t+1}} \odot \mu_{t+1|t} / (e_{y_{t+1}}^\top B^\top \mu_{t+1|t})$$
Predict distribution of future observations $$ y_{t+k|t}\sim B^\top (P^\top)^k\mu_{t|t}$$

"Why we do it"

Consider a hidden Markov model with transitions $P$ and observation probabilities $B$ $$ S_{t+1} \sim P^\top e_{s_t},\quad Y_t \sim B^\top e_{s_t} $$

Fact: the filtering algorithm computes the posterior $$ \mathbb P\{S_{t}=i|y_0,...,y_t\}=\mu_{t|t}[i] $$
Fact: the relationship between the observations and the estimated state is bilinear, so predictions depend polynomially on past observations

Model in which a Markovian state is latent
Discrete setting with $|\mathcal S|$ states and $|\mathcal Y|$ observations
Specified by $|\mathcal S|^2+|\mathcal S||\mathcal Y|$ transition and observation probabilities $$P_{ij} = \mathbb P\{S_{t+1}=j|S_t=i\} ,\qquad B_{ij}=\mathbb P\{Y_{t}=j|S_t=i\}$$
For discrete states and observations, given that $S_t=s_t$, $$ S_{t+1} \sim P^\top e_{s_t},\quad Y_t \sim B^\top e_{s_t} $$

Model in which a Markovian state is latent
Discrete setting with $|\mathcal S|$ states and $|\mathcal Y|$ observations
Specified by $|\mathcal S|^3|\mathcal Y|$ transition and observation probabilities $$P_{ij} = \mathbb P\{S_{t+1}=j|S_t=i\} ,\qquad B_{ij}=\mathbb P\{Y_{t}=j|S_t=i\}$$
For discrete states and observations, given that $S_t\sim \mu_t$, $$ S_{t+1} \sim P^\top \mu_t,\quad Y_t \sim B^\top \mu_t$$
Recall the stationary distribution and convergence are determined by eigenvectors/values of $P$

Fact: the filtering algorithm computes the posterior $$ \mathbb P\{S_{t}=i|y_0,...,y_t\}=\mu_{t|t}[i] $$
For streaming observations $y_t$, $t\geq 0$:
- Prediction step: $ \mu_{t+1|t} = P^\top \mu_{t|t}$
  - $\mathbb P\{S_{t+1}=i|y_{0:t}\} = \sum_{j=1}^{|\mathcal S|} \mathbb P\{S_{t+1}=i|S_{t}=j\} \mathbb P\{S_{t}=j|y_{0:t}\}$
- Update step: $ \mu_{t+1|t+1}= Be_{y_{t+1}} \odot \mu_{t+1|t} / (e_{y_{t+1}}^\top B^\top \mu_{t+1|t})$
  - $\mathbb P\{S_{t+1}=i|y_{0:t+1}\} \propto \mathbb P\{Y_{t+1}=y_{t+1}|S_{t+1}=i\} \mathbb P\{S_{t+1}=i|y_{0:t}\} $

Computations are linear function of the state distribution
- Predict is $O(|\mathcal S|^2)$: $ \mu_{t+1|t} = P^\top \mu_{t|t}$
- Update is $O(|\mathcal S|^2)$ $$ \mu_{t+1|t+1}= Be_{y_{t+1}} \odot \mu_{t+1|t} / (e_{y_{t+1}}^\top B^\top \mu_{t+1|t})$$
Comparing with Kalman filter:
- Predict is $O(d_s^3)$
  $\hat s_{t\mid t-1} =F\hat s_{t-1\mid t-1},~~P_{t\mid t-1} = FP_{t-1\mid t-1} F^\top + \Sigma_w$
- Update is $O(d_s^2 d_y + d_y^3)$
  $L_{t} = P_{t\mid t-1}H^\top ( HP_{t\mid t-1} H^\top+\Sigma_v)^{-1}$
  $\hat s_{t\mid t} = \hat s_{t\mid t-1}+ L_{t}(y_{t}-H\hat s_{t\mid t-1}),~~ P_{t\mid t} = (I - L_{t}H)P_{t\mid t-1}$

Computations are linear function of the state distribution
- Predict: $ \mu_{t+1|t} = P^\top \mu_{t|t}$ is $O(|\mathcal S|^2)$
- Update is $O(|\mathcal S|^2)$ $$ \mu_{t+1|t+1}= Be_{y_{t+1}} \odot \mu_{t+1|t} / (e_{y_{t+1}}^\top B^\top \mu_{t+1|t})$$
Let $D_{y_t} = \mathrm{diag}(Be_{y_{t}})P^\top$, then $$\mu_{t+1|t+1}= D_{y_{t+1}} \mu_{t|t} / (\mathbb 1^\top D_{y_{t+1}} \mu_{t|t})$$
Unrolled recursion: $$\mu_{t|t}= D_{y_t}D_{y_{t-1}}...D_{y_0} \mu_{0} / (\mathbb 1^\top D_{y_t}D_{y_{t-1}}...D_{y_0} \mu_{0}) $$
Predictions $ y_{t+k|t}\sim B^\top (P^\top)^k\mu_{t|t}$

Update is bilinear in state and observation $$\mu_{t+1|t+1}= D_{y_{t+1}} \mu_{t|t} / (\mathbb 1^\top D_{y_{t+1}} \mu_{t|t})$$
Predictions are given by $$ y_{t+k|t}\sim B^\top (P^\top)^kD_{y_t}D_{y_{t-1}}...D_{y_0} \mu_{0} / (\mathbb 1^\top D_{y_t}D_{y_{t-1}}...D_{y_0} \mu_{0}) $$
- where we have $D_{y_t} = \mathrm{diag}(Be_{y_{t}})P^\top$
- Dependence on product of observations
Compare with KF recursion, where update was linear $$\hat y_{t|t-1} = H\Big(\prod_{k=0}^{t-1} F_{L,k}\Big) \hat s_{0}+ \sum_{k=1}^{t}H \Big(\prod_{\ell=0}^{k-1} F_{L,\ell}\Big) L_{t-1}y_{t-k+1}$$
- where $F-L_tHF$ is independent of observations (since observation noise is independent)
- Linear dependence on observations

Update is bilinear in state and observation $$\mu_{t+1|t+1}= D_{y_{t+1}} \mu_{t|t} / (\mathbb 1^\top D_{y_{t+1}} \mu_{t|t})$$
Predictions are given by $$ y_{t+k|t}\sim B^\top (P^\top)^kD_{y_t}D_{y_{t-1}}...D_{y_0} \mu_{0} / (\mathbb 1^\top D_{y_t}D_{y_{t-1}}...D_{y_0} \mu_{0}) $$
- where we have $D_{y_t} = \mathrm{diag}(Be_{y_{t}})P^\top$
- Dependence on product of observations
Still have that $\epsilon$ approximation is possible with a finite $L$ window (Sharan et al., 2016)
However would need to use polynomial features to represent as some linear $y_{t+k|t}\sim\Theta^\top\varphi(y_0,...,y_{L-1})$
- scaling exponentially in $L$ and $|\mathcal Y|$

We focus on filtering and output prediction
This is known as "forward" algorithm for HMM inference
Other important tasks include:
- Smoothing ("backwards" algorithm) computes for $k\leq t$ $$\mathbb P\{S_k|y_0,...,y_t\}$$
- Maximum a posteriori state sequence with "Viterbi algorithm" is an example of dynamic programming $$\max_{s_0,...,s_t} \mathbb P\{S_k=s_k|y_{0:t}\}$$
- For PO-LDS, these tasks amount to solving the full least-squares problem to compute $\hat s_{k|t}$

Linear least squares for predicting (vector valued) labels $y$ from features $x$
- Categorical/discrete data with one-hot embeddings
- Works for nonlinear phenomena, just need a nonlinear feature transformation/kernel
When data comes in the form of a sequence, how do we determine labels and features?
- Use elements of sequence as labels $y_t$
- Use previous $L$ as features $y_{t-1:t-L}$
We justify validity so far with theory on
- Optimization: convexity and regularization
- Representation: for dynamical systems, Markov chains, and partial observations

Linear least squares for predicting (vector valued) labels $y$ from features $x$
For sequence data: use autoregressive models
We justify validity so far with theory on
- Optimization: convexity and regularization
- Representation: for dynamical systems, Markov chains, and partial observations
To further judge validity, we need to think about generalization
- There is no substitute for real world evaluation!
- We will consider generalization theory next lecture

Next time: generalization and online learning