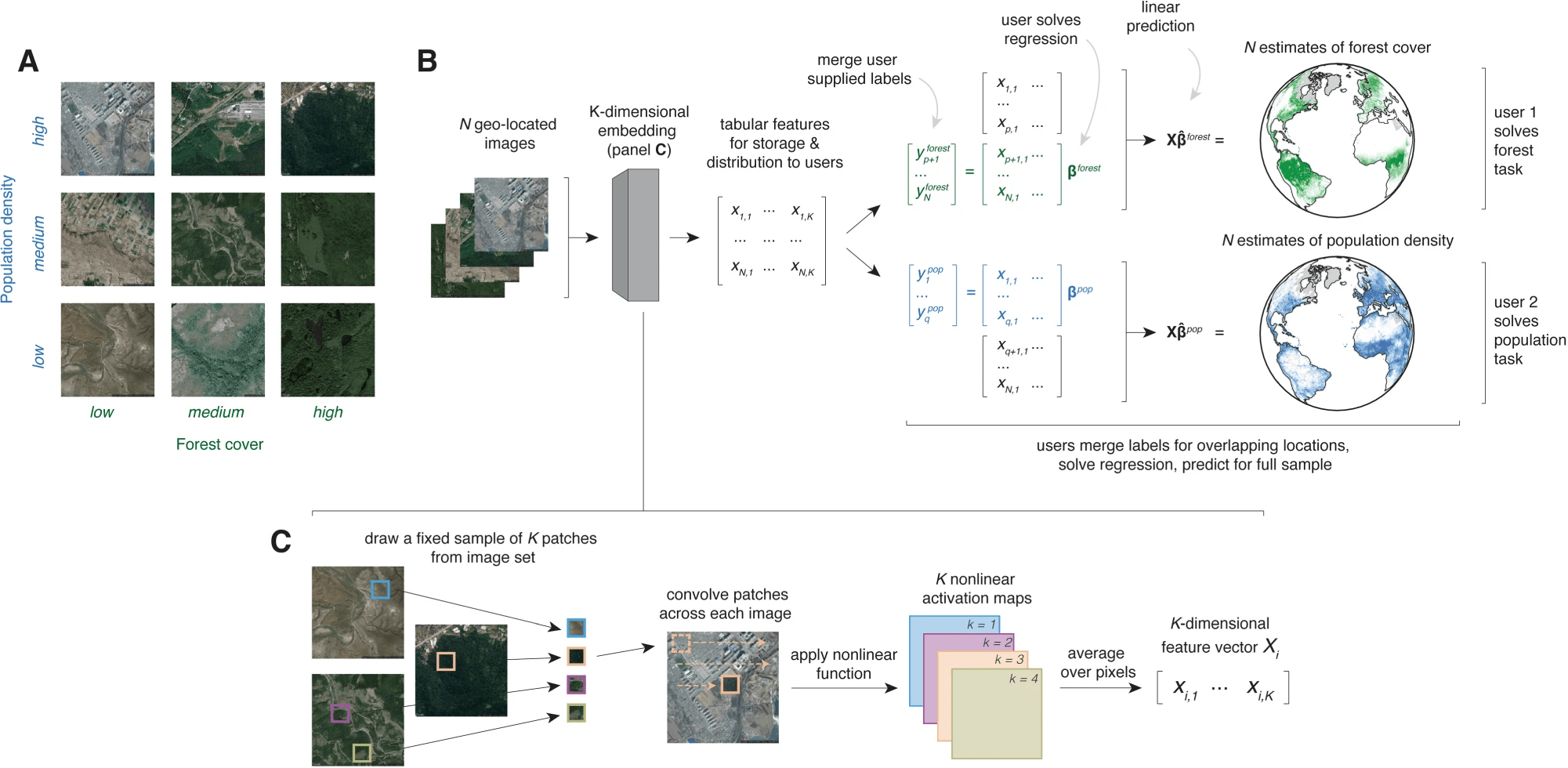
Generalization in least squares

ML in Feedback Sys #10

Fall 2025, Prof Sarah Dean

A generalizable and accessible approach to machine learning with global satellite imagery (Rolf et al., 2021)

Text

How good are my prediction on data outside of the training set?

Least squares generalization

"What we do"

$$\theta_t = \arg\min_\theta \sum_{k=1}^t (\theta^\top x_k - y_k)^2 + \lambda\|\theta\|_2^2 $$

  • Option 1: online adaptation
    • At every time \(t\):
      • Observe next \(x_t\), predict \(\hat y_t=\theta_t^\top x_t\)
      • Observe true \(y_t\), adapt model \(\theta_{t+1}\) via GD or ERM
  • Option 2: confidence intervals
    • Define \(V_t=\sum_{k=1}^tx_kx_k^\top + \lambda I \)
    • Make a prediction with confidence intervals $$\mathcal{C I}_t(x) = \Big[\theta_t^\top x\pm  \sqrt{\beta_t x^\top V_t^{-1}x}\Big]$$

Least squares generalization

"Why we do it"

$$\theta_t = \arg\min_\theta \sum_{k=1}^t (\theta^\top x_k - y_k)^2 + \lambda\|\theta\|_2^2 $$

  • Online adaptation to \(x_t,y_t\)
    • Fact 1: Average error converges for a constant \(C\) $$  \frac{1}{T}\sum_{t=1}^T \mathrm{err}_t(\theta_t) \leq \frac{1}{T}\sum_{t=1}^T\mathrm{err}_t(\theta_\star) + \frac{C}{\sqrt{T}}$$ where \(\theta_\star\) is the best model in hindsight
  • Confidence intervals
    • Fact 2: If \(\mathbb E[y_t|x_t] = \theta_\star^\top x_t\) and \(y_t\) has bounded variance, then with high probability, $$\mathbb E[y|x]\in \mathcal{C I}_t(x) $$

model

\(p_t:\mathcal X\to\mathcal Y\)

observation

prediction

Online learning

\(x_t\)

Goal: cumulatively over time, predictions \(\hat y_t = p_t(x_t)\) are close to true \(y_t\)

accumulate

\(\{(x_t, y_t)\}\)

Online Learning

  • for \(t=1,2,...\)
    • receive \(x_t\)
    • predict \(\hat y_t\)
    • receive true \(y_t\)
    • suffer loss \(\ell(y_t,\hat y_t)\)

ex - rainfall prediction, online advertising, election forecasting, ...

Reference: Ch 1&2 of Shalev-Shwartz "Online Learning and Online Convex Optimization"

Online learning

The regret of an algorithm which plays \((\hat y_t)_{t=1}^T\) in an environment playing \((x_t, y_t)_{t=1}^T\) is $$ R(T) = \sum_{t=1}^T \ell(y_t, \hat y_t) - \min_{p\in\mathcal P} \sum_{t=1}^T \ell(y_t, p(x_t)) $$

Cumulative loss and regret

"best in hindsight"

often consider worst-case regret, i.e. \(\sup_{(x_t, y_t)_{t=1}^T} R(T)\)

"adversarial"

Online linear regression

  • \(R(T) = \sum_{t=1}^T \ell_t(\theta_t) - \sum_{t=1}^T \ell_t(\theta_\star)\)
    • \(\implies \frac{1}{T}\sum_{t=1}^T \ell_t(\theta_t) = \frac{1}{T} \sum_{t=1}^T \ell_t(\theta_\star) + \frac{1}{T} R(T) \)
  • Theorem (2.12 & 2.7): Suppose each \(\ell_t\) is convex and \(L_t\) Lipschitz and let \(\frac{1}{T}\sum_{t=1}^T L_t^2\leq L^2\). Let \(\|\theta_\star\|_2\leq B\) and run either FTRL with \(\lambda = \frac{L\sqrt{T}}{\sqrt{2}B}\) or OGD with \(\alpha = \frac{B}{L\sqrt{2T}}\). Then $$  R(T) \leq BL\sqrt{2T}.$$
  • Fact 1 follows from this Theorem with \(C=BL\sqrt{2}\)
  • Proof of Theorem in extra slides below

Online ERM aka "Follow the (Regularized) Leader"

$$\theta_t = \arg\min \sum_{k=1}^{t-1} \ell_k(\theta) +  \lambda\|\theta\|_2^2$$

Online Gradient Descent

$$\theta_t = \theta_{t-1} - \alpha \nabla \ell_{t-1}(\theta_{t-1})$$

For simplicity, define \(\ell_t(\theta) = (x_t^\top \theta-y_t)^2\)

Convexity & continuity

Parabola

For differentiable and convex \(\ell:\mathcal \Theta\to\mathbb R\), $$\ell(\theta') \geq \ell(\theta) + \nabla \ell(\theta)^\top (\theta'-\theta)$$

Definition: \(\ell\) is \(L\)-Lipschitz continuous if there exists \(L\) so that for all \(\theta\in\Theta\) we have $$ \|\ell(\theta)-\ell(\theta')\|_2 \leq L\|\theta-\theta'\|_2 $$

A differentiable function \(\ell\) is \(L\)-Lipschitz if \(\|\nabla \ell(\theta)\|_2 \leq L\) for all \(\theta\in\Theta\).

Fact: The GD update is equivalent to $$\theta_t= \arg\min \nabla \ell_{t-1}(\theta_{t-1})^\top (\theta-\theta_{t-1}) +\frac{1}{2\alpha}\|\theta-\theta_{t-1}\|_2^2$$

  • i.e., locally minimizing first order approximation of \(\ell_{t-1}\) $$\ell(\theta) \approx \nabla \ell(\theta_{t-1})^\top (\theta - \theta_{t-1}) + \ell(\theta_{t-1})$$

Online Gradient Descent

$$\theta_t = \theta_{t-1} - \alpha \nabla \ell_{t-1}(\theta_{t-1})$$

OGD: incremental optimization

Parabola

because \( \theta_{t+1} = \arg\min\sum_{k=1}^{t} \nabla \ell_k(\theta_k)^\top\theta + \frac{1}{2\alpha}\|\theta\|_2^2\)

because by convexity, \(\ell_t(\theta) \geq \ell_t(\theta_t) + \nabla \ell_t(\theta_t)^\top (\theta-\theta_t)\)

For any fixed \(\theta\in\Theta\),

$$\textstyle \sum_{t=1}^T \ell_t(\theta_t)-\ell_t(\theta) \leq \sum_{t=1}^T \nabla \ell_t(\theta_t)^\top (\theta_t-\theta)$$

Can show by induction that for \(\theta_1=0\),

$$ \textstyle \sum_{t=1}^T \nabla \ell_t(\theta_t)^\top (\theta_t-\theta) \leq \frac{1}{2\alpha}\|\theta\|_2^2+ \sum_{t=1}^T \nabla \ell_t(\theta_t)^\top (\theta_t-\theta_{t+1})$$

\(=\frac{1}{2\alpha}\|\theta\|_2^2+ \sum_{t=1}^T \alpha\|\nabla \ell_t(\theta_t)\|_2^2\)

Putting it all together, $$ R(T) =  \sum_{t=1}^T \ell_t(\theta_t)-\ell_t(\theta_\star) \leq \frac{1}{2\alpha}\|\theta_\star\|_2^2+ \alpha\sum_{t=1}^T L_t^2$$

OGD: proof sketch

because \(\ell_t\) is \(L_t\) Lipschitz

Finally, plug in \(\frac{1}{T}\sum_{t=1}^T L_t^2\leq L^2\),\(\|\theta_\star\|_2\leq B\), and set \(\alpha=\frac{L\sqrt{T}}{\sqrt{2}B}\).

Lemma (2.1, 2.3): For any fixed \(\theta\in\Theta\), under FTRL

$$ \sum_{t=1}^T \ell_t(\theta_t)-\ell_t(\theta) \leq \lambda\|\theta\|_2^2-\lambda\|\theta_1\|_2^2+  \sum_{t=1}^T \ell_t(\theta_t)-\ell_t(\theta_{t+1})$$

Lemma (2.10): For \(\ell_t\) convex and \(L_t\) Lipschitz,

$$  \ell_t(\theta_t)-\ell_t(\theta_{t+1}) \leq \frac{2L_t^2}{\lambda}$$

$$ R(T) =  \sum_{t=1}^T \ell_t(\theta_t)-\ell_t(\theta_\star) \leq \lambda\|\theta_\star\|  +2TL^2/\lambda$$

FTRL: proof sketch

For linear functions, FTRL is exactly equivalent to OGD! In general, similar arguments.

Prediction error

  • Fact 2: If \(\mathbb E[y_t|x_t] = \theta_\star^\top x_t\) and \(y_t\) has bounded variance, then with high probability, $$\mathbb E[y|x]\in \Big[\theta_t^\top x\pm  \sqrt{\beta_t x^\top V_t^{-1}x}\Big]$$where we define \(V_t=\sum_{k=1}^tx_kx_k^\top + \lambda I \)
  • Define \(\varepsilon_t = y_t-\mathbb E[y_t|x_t] \)

  • Then we can write \(\hat\theta_t-\theta_\star\)

    • \(=V_t^{-1}\sum_{k=1}^t x_k y_k - \theta_\star\)
    • \(=V_t^{-1}\sum_{k=1}^t x_k(\theta_\star^\top x_k +\varepsilon_k) - \theta_\star\)
    • \(=V_t^{-1}\sum_{k=1}^t x_k\varepsilon_k\)

  • Therefore, \((\hat\theta_t-\theta_\star)^\top x =\sum_{k=1}^t \varepsilon_k (V_t^{-1}x_k)^\top x\)

Prediction error

  • Fact 2: If \(\mathbb E[y_t|x_t] = \theta_\star^\top x_t\) and \(y_t\) has bounded variance, then with high probability, $$\mathbb E[y|x]\in \Big[\theta_t^\top x\pm  \sqrt{\beta_t x^\top V_t^{-1}x}\Big]$$where we define \(V_t=\sum_{k=1}^tx_kx_k^\top + \lambda I \)

  • We have that \((\hat\theta_t-\theta_\star)^\top x =\sum_{k=1}^t \varepsilon_k (V_t^{-1}x_k)^\top x\)

  • If \((\varepsilon_k)_{k\leq t}\) are Gaussian and independent from \((x_k)_{k\leq t}\), then this error is distributed as \(\mathcal N(0, \sigma^2\sum_{k=1}^t ((V_t^{-1}x_k)^\top x)^2)\)

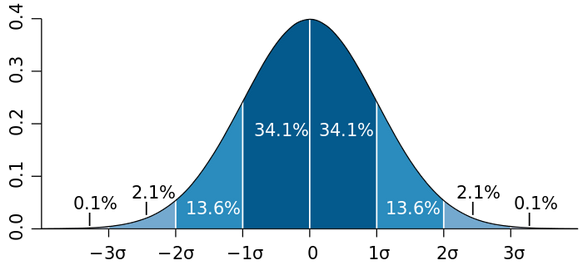
  • z-scores \(\approx\) tail bounds
  • w.p. \(1-\delta\), \(|u| \leq  \sigma_u\sqrt{2\log(2/\delta)}\)

With probability \(1-\delta\), we have \(|(\hat\theta_t-\theta_\star)^\top x| \leq  \sigma\sqrt{2\log(2/\delta) }{\sqrt{x^\top V_t^{-1}x}}\)

Interlude: Tail bounds

  • Gaussian tail bound: Suppose \(r_i\sim \mathcal N (\mu,\sigma^2)\). Then for \(r_1,\dots, r_N\) i.i.d., with probability \(1-\delta\), $$\left|\frac{1}{N} \sum_{i=1}^N r_i - \mu \right| \leq \sigma \sqrt{\frac{2\log 2/\delta}{N}} $$
    • Because \(\frac{1}{N} \sum_{i=1}^N r_i\sim  \mathcal N (\mu,\frac{\sigma^2}{N})\)
  • Same bound holds for broader class
    of random variables called
    sub-Gaussian
  • For example, bounded random variables are sub-Guassian. Hoeffding's Inequality: Suppose \(r_i\in[a, b]\) and \(\mathbb E[r_i] = \mu\). Then for \(r_1,\dots, r_N\) i.i.d., with probability \(1-\delta\), $$\left|\frac{1}{N} \sum_{i=1}^N r_i - \mu \right| \leq |b-a|\sqrt{\frac{2\log 2/\delta}{N}} $$

z-score: w.p. \(1-\delta\), \(|u| \leq  \sigma\sqrt{2\log(2/\delta)}\)

Prediction error

  • Fact 2: If \(\mathbb E[y_t|x_t] = \theta_\star^\top x_t\) and \(y_t\) has bounded variance, then with high probability, $$\mathbb E[y|x]\in \Big[\theta_t^\top x\pm  \sqrt{\beta_t x^\top V_t^{-1}x}\Big]$$where we define \(V_t=\sum_{k=1}^tx_kx_k^\top + \lambda I \)

  • We have that \((\hat\theta_t-\theta_\star)^\top x =\sum_{k=1}^t \varepsilon_k (V_t^{-1}x_k)^\top x\)

  • Gaussian case: \(1-\delta\) confidence interval is \(\theta_t^\top x\pm \sigma\sqrt{2\log(2/\delta) }{\sqrt{x^\top V_t^{-1}x}}\)

  • More generally, tail bounds of this form exist when:

    • \(\varepsilon_k\) is bounded (\(\beta\) has similar form) (Hoeffding's inequality)

    • \(\varepsilon_k\) is sub-Gaussian (\(\beta\) has similar form) (Markov's inequality)

    • \(\varepsilon_k\) has bounded variance (\(\beta\) scales with \(1/\delta\)) (Chebychev's inequality)

Reference: Ch 1&2 of Shalev-Shwartz "Online Learning and Online Convex Optimization", Ch 19-20 in Bandit Algorithms by Lattimore & Szepesvari

Recap

  • Online learning: adaptation leads to diminishing error on average (compared to best-in-hindsight), with no assumption on data generation!
  • Confidence intervals arise from tail bounds on random variables, requiring assumptions of stochastic noise

Next week: from prediction to action!

Announcements

  • Fourth assignment due today
  • Fifth assignment posted, due next Thursday
  • Next week: discuss projects & paper presentations (see Syllabus)