12 - Bandits - ML in Feedback Sys

Contextual Bandits

ML in Feedback Sys #12

Prof Sarah Dean

Reminders

Final project proposal due October 7
Upcoming paper presentations
- Meet with Atul in advance

Learning to Forecast Dynamical Systems from Streaming Data, Giannakis, Henriksen, Tropp, Ward

"Kernel Analog Forecasting"
Recall: kernel ridge regression
- similar to LS, but nonlinear/nonparametric
Similarly, study nonlinear dynamical systems using Koopman operator theory

Reporting back on SIAM MDS

Prediction in

a static world (train/test)
a streaming world
a dynamic world
- filtering, system ID

Unit 2: Action

first in a streaming world

Recap: learning to predict (Unit 1)

filter
$\mathcal Y^t \to \mathcal Y$
or $\to \mathcal S$

observation

prediction

Prediction in dynamic world

$y_t$

accumulate

$\{y_t\}$

$F$

$s$

$\hat y_{t+1}$ or $\hat s_t$

identify

$\hat F$

model

$f_t:\mathcal X\to\mathcal Y$

observation

prediction

Prediction in a streaming world

$x_t$

accumulate

$\{(x_t, y_t)\}$

$\hat y_{t}$

policy

$\pi_t:\mathcal X\to\mathcal A$

observation

action

$x_t$

accumulate

$\{(x_t, a_t, r_t)\}$

$a_{t}$

Action in a streaming world

Contextual Bandits

for $t=1,2,...$
- receive context $x_t$
- take action $a_t\in\mathcal A$
- receive reward $r_t$

ex - traffic routing, online advertising, campaign planning, experiment design, ...

Contextual Bandits

History of the name

Whittle, Peter (1979), "Discussion of Dr Gittins' paper", Journal of the Royal Statistical Society, Series B, 41 (2): 148–177

A Stochastic Model with Applications to Learning, 1953.

cites the problem as arising due to "Professor Merrill Flood, then at the RAND Corporation" encountered in experimental work on learning models

rats and coin flips, publication list

An Elementary Survey of Statistical Decision Theory, 1954

Contextual Bandits

for $t=1,2,...$
- receive context $x_t$
- take action $a_t\in\mathcal A$
- receive reward $$r_t = r(x_t, a_t) + \varepsilon_t$$

ex - traffic routing, online advertising, campaign planning, experiment design, ...

Contextual Bandits

Related Goals:

choose best action given context
- $\max_a r(x_t, a)$
predict reward of action in context
- $\hat r_a \approx r(x_t, a)$
estimate reward function
- $\hat r:\mathcal X\times \mathcal A\to \mathbb R$

Taking action $a_t\in\mathcal A$ in context $x_t$ yields reward $$r_t = r(x_t, a_t) + \varepsilon_t,\qquad \mathbb E[\varepsilon_t]=0,~~\mathbb E[\varepsilon_t^2] = \sigma^2$$

Contextual Bandits

Example: $K$-armed bandits

single unchanging context
discrete action set $\mathcal A = \{1,\dots,K\}$
each action has average reward $r(a) = \mu_a$

Ex: $K$-armed linear contextual bandits

e.g. machine model affects rewards, so context
$x=($•$, $•$, $•$, $•$, $•$, $•$, $•$, $•$)$

contexts $x_t\in\mathbb R^d$
discrete action set $\mathcal A = \{1,\dots,K\}$
average reward $r(x, a) = \mu_a(x) = \theta_a^\top x$

Example: linear bandits

e.g. betting on horseracing

single unchanging context
continuous action set $\mathcal A = \{a\mid\|a\|\leq 1\}$
average reward $r(a) = \theta_\star^\top a$

Related Goals:

choose best action given context: $\max_a r(x_t, a)$
predict reward of action in context: $\hat r_a \approx r(x_t, a)$
estimate reward function: $\hat r:\mathcal X\times \mathcal A\to \mathbb R$

Taking action $a_t\in\mathcal A$ in context $x_t$ yields reward $$r_t = r(x_t, a_t) + \varepsilon_t,\qquad \mathbb E[\varepsilon_t]=0,~~\mathbb E[\varepsilon_t^2] = \sigma^2$$

Contextual Bandits

Taking action $a_t\in\mathcal A$ in context $x_t$ yields reward $$r_t = \langle\theta_\star, \varphi(x_t, a_t)\rangle + \varepsilon_t$$

Linear Contextual Bandits

$K$ armed bandits
- $\mathbb E[r(a)] = \begin{bmatrix} \mu_1\\\vdots\\ \mu_K\end{bmatrix}^\top \begin{bmatrix} \mathbf 1\{a=1\}\\\vdots\\ \mathbf 1\{a=K\}\end{bmatrix} $

Taking action $a_t\in\mathcal A$ in context $x_t$ yields reward $$r_t = \langle\theta_\star, \varphi(x_t, a_t)\rangle + \varepsilon_t$$

Linear Contextual Bandits

$K$ armed bandits
- $\varphi(a) = e_a$
$K$ armed contextual linear bandits
- $\mathbb E[r(x, a)] = \begin{bmatrix} \theta_1 \\\vdots\\ \theta_K \end{bmatrix}^\top \begin{bmatrix} x\mathbf 1\{a=1\}\\\vdots\\ x\mathbf 1\{a=K\}\end{bmatrix} $

Taking action $a_t\in\mathcal A$ in context $x_t$ yields reward $$r_t = \langle\theta_\star, \varphi(x_t, a_t)\rangle + \varepsilon_t$$

Linear Contextual Bandits

$K$ armed bandits
- $\varphi(a) = e_a$
$K$ armed contextual linear bandits
- $\varphi(a) = e_a \otimes x$
Linear bandits
- $\mathbb E[r(a)] = \theta_\star^\top a$

Taking action $a_t\in\mathcal A$ in context $x_t$ yields reward $$r_t = \langle\theta_\star, \varphi(x_t, a_t)\rangle + \varepsilon_t$$

Linear Contextual Bandits

$\iff$

Equivalent perspective:

Receive action set $\mathcal A_t$
Choose $\varphi_t\in\mathcal A_t$
Receive reward $\mathbb E[r_t] = \langle\theta_\star,\varphi_t\rangle $

Define $\mathcal A_t = \{\varphi(x_t, a) \mid a\in\mathcal A\}$

Contextual Bandits Examples

$K$ armed contextual bandits where $\mathbb E[r(x, a)] = \tilde \theta_a^\top x$

observe rewards determined by $\theta_* = \begin{bmatrix} \tilde \theta_1\\ \vdots \\ \tilde\theta_K\end{bmatrix}$

choose $\varphi_t\in \mathcal A_t = \{e_1\otimes x_t,\dots, e_K \otimes x_t\}$

$\iff$

Contextual Bandits Examples

Linear contextual bandits where $\mathbb E[r(x, a)] = ( \Theta_\star x)^\top a$

Contextual Bandits Examples

Linear contextual bandits where $\mathbb E[r(x, a)] = ( \Theta_\star x)^\top a$

observe rewards determined by $\theta_* = \mathrm{vec}(\Theta_\star)$

choose $\varphi_t\in \mathcal A_t = \{\mathrm{vec}(ax^\top)\mid \|a\|\leq 1\}$

$\iff$

Contextual Bandits Examples

Exercise: Formulate the following in the contextual bandit framework.

At each timestep, observe the state of a dynamical system which is reset according to a distribution $s_{0,t} \sim \mathcal D_0\in\Delta(\mathbb R^n)$.
Choose an action $a_t\in\mathbb R^m$ and pay a cost $s_1^\top Qs_1+a_t^\top R a_t$ where $s_1=As_{0,t}+Ba_t$, $Q,R\succeq 0$ are cost matrices, and $A,B$ are dynamics matrices.

Taking action $\varphi_t\in\mathcal A_t$ yields reward $$\mathbb E[r_t] = \langle\theta_\star, \varphi_t\rangle $$

Linear Contextual Bandits

Strategy:

estimate $\hat\theta$ from data $\{\varphi_t, r_t\}$
select good actions from $\mathcal A_t$ based on estimated $\hat\theta$

Least squares

Estimate $\hat\theta$ from data $\{(\varphi_k, r_k)\}_{k=1}^t$

$$\hat\theta_t = \arg\min_\theta \sum_{k=1}^t (\theta^\top \varphi_k - r_k)^2$$

$$\hat\theta_t ={\underbrace{ \left(\sum_{k=1}^t \varphi_k\varphi_k^\top\right)}_{V_t}}^{-1}\sum_{k=1}^t \varphi_k r_k $$

Recall that $\hat\theta_t-\theta_\star$

$=V_t^{-1}\sum_{k=1}^t \varphi_k r_k - \theta_\star$
$=V_t^{-1}\sum_{k=1}^t \varphi_k(\theta_\star^\top \varphi_k +\varepsilon_k) - \theta_\star$
$=V_t^{-1}\sum_{k=1}^t \varphi_k\varepsilon_k$

Therefore, $(\hat\theta_t-\theta_\star)^\top \varphi =\sum_{k=1}^t \varepsilon_k (V_t^{-1}\varphi_k)^\top \varphi$

Prediction errors

How much should I trust my predicted reward $\hat\theta^\top \varphi$?

$(\hat\theta_t-\theta_\star)^\top \varphi =\sum_{k=1}^t \varepsilon_k (V_t^{-1}\varphi_k)^\top \varphi$

With probability $1-\delta$, we have $|(\hat\theta_t-\theta_\star)^\top \varphi| \leq \sigma\sqrt{2\log(2/\delta) }\underbrace{\sqrt{\varphi^\top V_t^{-1}\varphi}}_{\|\varphi\|_{V_t^{-1}}}$

If $(\varepsilon_k)_{k\leq t}$ are Gaussian and independent from $(\varphi_k)_{k\leq t}$, then this error is distributed as $\mathcal N(0, \sigma^2\sum_{k=1}^t ((V_t^{-1}\varphi_k)^\top \varphi)^2)$

Prediction errors

How much should I trust my predicted reward $\hat\theta^\top \varphi$?

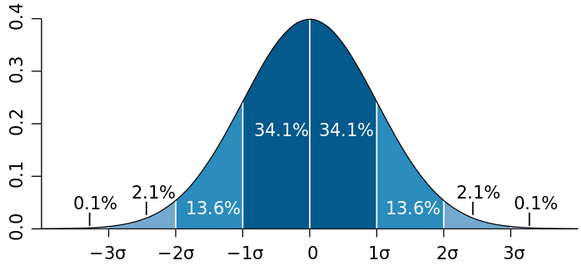
Tail bounds $\approx$ z-scores
w.p. $1-\delta$, $|u| \leq \sigma\sqrt{2\log(2/\delta)}$

Confidence Ellipsoids

How much should I trust the estimate $\hat \theta$?

Define the confidence ellipsoid $$\mathcal C_t = \{\theta\in\mathbb R^d \mid \|\theta-\hat\theta_t\|_{V_t}^2\leq \beta_t\} $$

For the right choice of $\beta_t$, we can show that with high probability, $\theta_\star\in\mathcal C_t$

Reference: Ch 19-20 in Bandit Algorithms by Lattimore & Szepesvari

What is the form of $\mathcal C_t$ for the $K$ armed bandit setting?
For a fixed action $\varphi$, what is $$\max_{\theta\in\mathcal C_t} (\theta-\theta_\star)^\top \varphi$$ and how does this relate to the prediction errors?
Suppose $\theta_\star\in\mathcal C_t$ and we choose $$\varphi_t = \arg\max_{\varphi\in\mathcal A_t} \max_{\theta\in\mathcal C_t} \theta^\top \varphi$$ then what is the optimality gap $$ \max_{\varphi\in\mathcal A_t} \theta_\star^\top \varphi - \theta_\star^\top \varphi_t ? $$

Exercises

Next time: low regret algorithms

Recap

Prediction recap
Contextual bandit setting
Linear contextual bandit
Confidence bounds

Reference: Ch 19-20 in Bandit Algorithms by Lattimore & Szepesvari

Contextual Bandits

ML in Feedback Sys #12

Reminders

Reporting back on SIAM MDS

Recap: learning to predict (Unit 1)

Prediction in dynamic world

\(F\)

Prediction in a streaming world

Action in a streaming world

Contextual Bandits

History of the name

Contextual Bandits

Contextual Bandits

Example: \(K\)-armed bandits

Ex: \(K\)-armed linear contextual bandits

Example: linear bandits

Contextual Bandits

Linear Contextual Bandits

Linear Contextual Bandits

Linear Contextual Bandits

Linear Contextual Bandits

Contextual Bandits Examples

Contextual Bandits Examples

Contextual Bandits Examples

Contextual Bandits Examples

Linear Contextual Bandits

Least squares

Prediction errors

Prediction errors

Confidence Ellipsoids

Exercises

Recap