Set-based and Machine Learning Perspectives on Control-affine Dynamics

Sarah Dean, Cornell

Data-driven nonlinear control

Nonlinear control affine dynamics with state \(\mathbf x\in\mathbb R^n\) and input \(\mathbf u\in\mathbb R^m\)

\(\dot{\mathbf x} = \mathbf f(\mathbf x)+\mathbf g(\mathbf x)\mathbf u\)

\({\mathbf x}_{t+1} = \mathbf f(\mathbf x_t)+\mathbf g(\mathbf x_t)\mathbf u_t\)

functions \(\mathbf f\) and \(\mathbf g\) unknown (or partially unknown)

  • Goal: sketch roadmap to sample complexity theory for data-driven nonlinear control
  • Three related perspectives:
  1. Robust control + set-based learning
  2. Kernel-based learning with approximations
  3. Sample complexity theory for bilinear systems

This talk:

1. Towards Robust Data-Driven Control Synthesis for Nonlinear Systems with Actuation Uncertainty with Andrew Taylor, Victor Dorobantu, Benjamin Recht, Yisong Yue, Aaron Ames

 

2. Random Features Approximation for Control-Affine Systems with Kimia Kazemian, Yahya Sattar

3. Finite Sample Identification of Partially Observed Bilinear Dynamical Systems with Yahya Sattar, Yassir Jedra, Maryam Fazel

1. Robust control + set-based learning

Aaron Ames

Ben Recht

Andrew Taylor

Yisong Yue

Victor Dorobantu

Ryan Cosner

Towards Robust Data-Driven Control Synthesis for Nonlinear Systems with Actuation Uncertainty

Setting: nonlinear control

Nonlinear control affine dynamics

\(\mathbf x\in\mathbb R^n, \mathbf u\in\mathbb R^m\)

Goal: design \(\mathbf k\) to certify desired behavior

\(\mathbf u = \mathbf k(\mathbf x)\)

\(\dot{\mathbf x} = \mathbf f(\mathbf x)+\mathbf g(\mathbf x)\mathbf u\)

Approach: Control Certificate Functions

Certficate function \(C:\mathbb{R}^n\to \mathbb R\)

Comparison function \(\alpha:\mathbb{R}\to \mathbb R\)

Control Certificate Condition:

\( \dot C(\mathbf x, \mathbf u)  \leq -\alpha(C(\mathbf x)) \)

\(\mathbf k(\mathbf x) \in \{\mathbf u \mid \dot C(\mathbf x, \mathbf u)  \leq -\alpha(C(\mathbf x)) \}\)

\(\implies\)  desired behavior

Ex: Control Lyapunov Function (stability)

Ex: Control Barrier Function (safety)

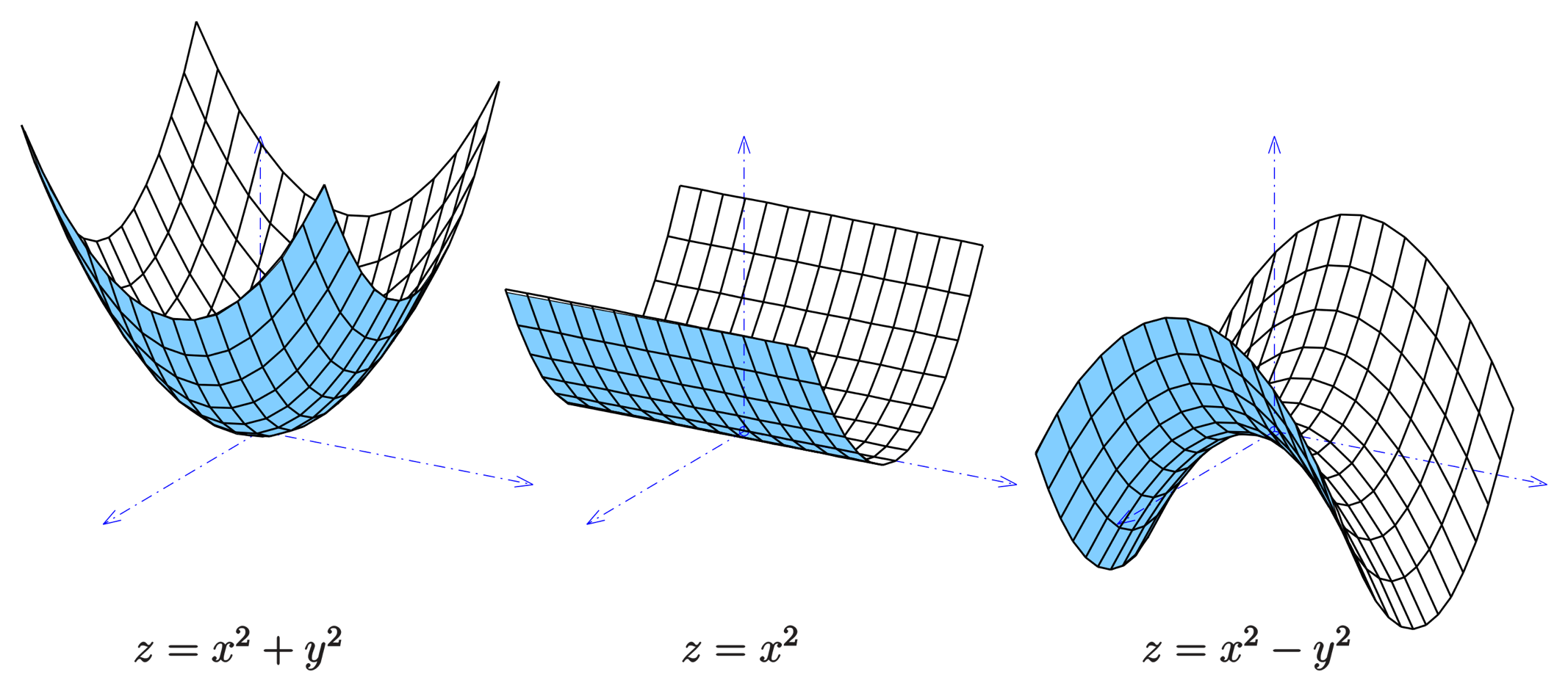
\(C(\mathbf x)\)

\(\mathbf x=0\)

\(\mathbf x\)

\(C(\mathbf x)\leq 0\)

\(\mathbf x\)

Encode control objectives on the basis of instantaneous behavior

Ex: Control Lyapunov Functions (CLF)

Lyapunov function satisfying

\(\alpha_1(\|\mathbf x\|) \leq C(\mathbf x) \leq \alpha_2(\|\mathbf x\|)\)

for \(\alpha_1,\alpha_2\in\mathcal K\)

and comparison function satisfying

\(\alpha \in \mathcal K\)

then if CCF condition can be enforced, stability to the origin guaranteed

CLF-QP:

\(\mathbf k(\mathbf x) = \arg\min_{\mathbf u} \|\mathbf u - \mathbf k_d(\mathbf x)\|_2^2\)

\(\text{s.t.}~~ \dot C(\mathbf x, \mathbf u)\leq -\alpha(C(\mathbf x))\)

(Artstein, 1983; Sontag, 1989; Freeman & Kokotovic, 1996)

(Ames & Powell, 2013)

Given:

\(C(\mathbf x)\)

\(\mathbf x=0\)

\(\mathbf x\)

Ex: Control Barrier Functions (CBF)

then if CCF condition can be enforced, safe set \(\mathcal S\) is guaranteed forward invariant.

 (Ames et al., 2017)

barrier function satisfying

\(C(\mathbf x) \leq 0\iff \mathbf x\in\mathcal S\)

and comparison function

\(\alpha \in \mathcal K_e\)

CBF-QP:

\(\mathbf k(\mathbf x) = \arg\min_{\mathbf u} \|\mathbf u - \mathbf k_d(\mathbf x)\|_2^2\)

\(\text{s.t.}~~ \dot C(\mathbf x, \mathbf u)\leq -\alpha(C(\mathbf x))\)

 (Ames et al. 2014, 2017)

Given

\(C(\mathbf x)\leq 0\)

\(\mathbf x\)

Example: Feedback Linearizable Systems

  • knowing the degree of actuation is sufficient for designing CCF

Control Certificate Condition:

\(K(\mathbf x) =  \{\mathbf u \mid \dot C(\mathbf x, \mathbf u) = \nabla C(\mathbf x)^\top (\mathbf f(\mathbf x)+\mathbf g(\mathbf x)\mathbf u) \leq -\alpha(C(\mathbf x)) \}\)

We call \(C\) a Control Certificate Function if \(K(\mathbf x)\) is nonempty for all \(\mathbf x\)

Control Certificate Function

\( L_{\mathbf f} C(\mathbf x)+ L_{\mathbf g}C(\mathbf x)\mathbf u\)

(Dimitrova & Majumdar, 2014)

(Boffi et al., 2020)

Designing CCFs is nontrivial---but not the focus today

Problem setting: uncertain dynamics

Nonlinear control affine dynamics:  \(\dot{\mathbf x} = \mathbf f(\mathbf x)+\mathbf g(\mathbf x)\mathbf u\)

State observation

Unknown dynamics \(\mathbf f\) and \(\mathbf g\)

Assumptions:

  1. \(\mathbf f\) and \(\mathbf g\) are Lipshitz and we know upper bounds on the constants: \(\mathcal L_{\mathbf f}\) and \(\mathcal L_{\mathbf g}\)

  2. Access to data \(\{(\dot{\mathbf x}_i, \mathbf x_i, \mathbf u_i)\}_{i=1}^N\)

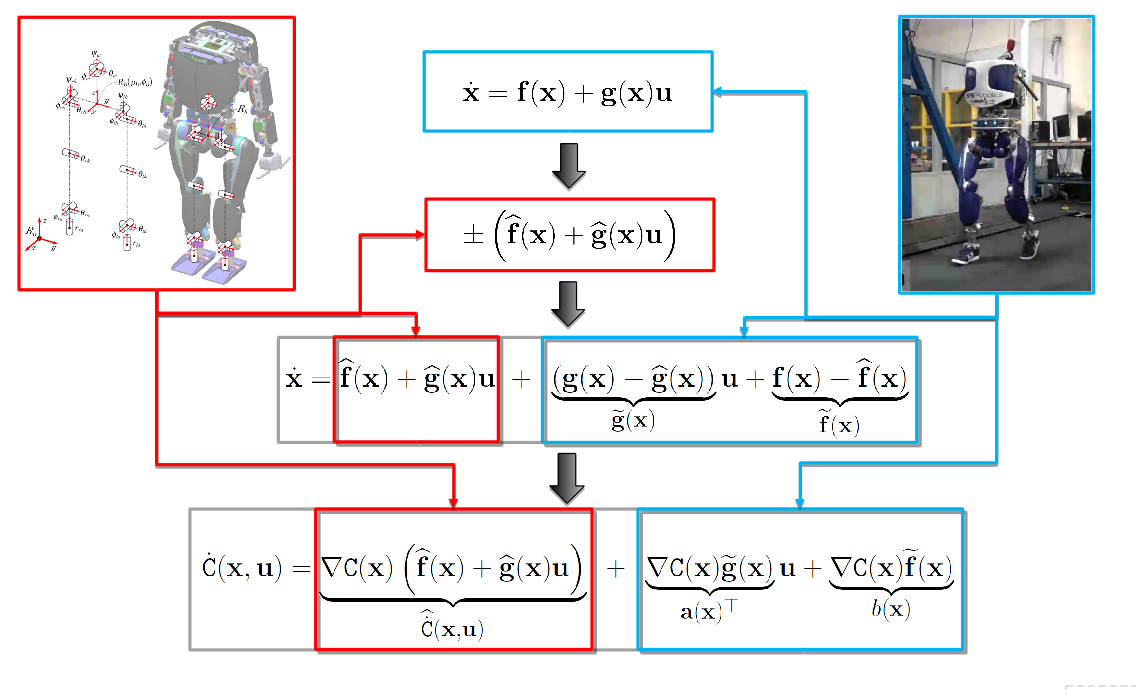
To robustify CCF, characterize all possible \(\mathbf f\) and \(\mathbf g\) consistent with data \(\{(\dot{\mathbf x}_i, \mathbf x_i, \mathbf u_i)\}_{i=1}^N\)

Data-driven uncertainty set

Pointwise uncertainty set:

\(\mathcal U_i(\mathbf x) = \{(\mathbf a, \mathbf B) \mid \|\mathbf a + \mathbf B \mathbf u_i-\dot{\mathbf x}_i\| \leq (\mathcal L_{\mathbf f} + \mathcal L_{\mathbf g}\|\mathbf u_i\|)\|\mathbf x - \mathbf x_i\|\}\)

We can guarantee that \(\mathbf f(\mathbf x), \mathbf g(\mathbf x) \in \mathcal U_i(\mathbf x)\)

\( \|\mathbf f(\mathbf x)+\mathbf g(\mathbf x) \mathbf u_i -\dot{\mathbf x}_i \|\leq \|\mathbf f(\mathbf x)-\mathbf f(\mathbf x_i)\|+\|\mathbf g(\mathbf x) \mathbf -\mathbf g(\mathbf x_i) \|\|\mathbf u_i\|\)

\(\mathbf f(\mathbf x)+\mathbf g(\mathbf x) \mathbf u_i = \dot{\mathbf x}_i + (\mathbf f(\mathbf x)-\mathbf f(\mathbf x_i))+(\mathbf g(\mathbf x) \mathbf -\mathbf g(\mathbf x_i) )\mathbf u_i\)

\(\mathbf f(\mathbf x), \mathbf g(\mathbf x) \in \cap_{i=1}^N \mathcal U_i(\mathbf x)= \mathcal U(\mathbf x)\)

Uncertainty Set Visualization

\(\begin{bmatrix} u_1\\ 1 \end{bmatrix}\)

\(\left |\begin{bmatrix}  u_i\\1 \end{bmatrix}^\top\begin{bmatrix} b \\ a \end{bmatrix} - \dot{ x}_i \right|\leq \mathcal L_i |x-x_i| \)

\(\begin{bmatrix} g(x) \\f(x)\end{bmatrix}\)

\(\begin{bmatrix} u_2\\ 1 \end{bmatrix}\)

'Slice' between two planes

Width determined by \(|x-x_i|\)

Direction determined by \(u_i\)

\(\begin{bmatrix} g(x_1) \\f(x_1)\end{bmatrix}\)

Robust CCF Optimization Problem

R-OP:

\(\mathbf k_\mathrm{rob}(\mathbf x)=\argmin\limits_{\mathbf u \in \mathbb{R}^m} \| \mathbf u - \mathbf k_d(\widehat{\mathbf x}) \|\)

\(~~~~~~~~~\text{s.t.}~~\nabla C(\mathbf x)^\top (\mathbf a + \mathbf B\mathbf u)\leq -\alpha(C(\mathbf x))\)

\(~~~~~~~~~~~~~~~~\text{for all}~(\mathbf a, \mathbf B)\in\mathcal U(\mathbf x)\)

Main Result: R-OP is convex, equivalent to a SOCP with \(n\times N\) additional optimization variables, and guarantees that

\(\dot{C}(\mathbf x,\mathbf k_\mathrm{rob}(\mathbf x)) \leq -\alpha C(\mathbf x)\)

Robust Feasibility

Feasibility Result: R-OP is feasible at \(\mathbf x\)
if and only if

\(( -\gamma\alpha(C(\mathbf x)), \mathbf 0)\notin  \nabla C(x)^\top \mathcal U(\mathbf x)\) for all \(\gamma>1\)

open loop unsafe/unstable

\(\mathbb R^m\)

\(\mathbb R\)

\(\begin{bmatrix} \nabla C(\mathbf x)^\top \mathbf g(\mathbf x) \\\nabla C(\mathbf x)^\top \mathbf f(\mathbf x)\end{bmatrix}\)

\(\mathcal U_C(\mathbf x) \)

\(-\alpha(C(\mathbf x))\)

R-OP:

\(\mathbf k_\mathrm{rob}(\mathbf x)=\argmin\limits_{\mathbf u \in \mathbb{R}^m} \| \mathbf u - \mathbf k_d(\widehat{\mathbf x}) \|\)

\(~~~~~~~~~\text{s.t.}~~\nabla C(\mathbf x)^\top (\mathbf a + \mathbf B\mathbf u)\leq -\alpha(C(\mathbf x))\)

\(~~~~~~~~~~~~~~~~\text{for all}~(\mathbf a, \mathbf B)\in\mathcal U(\mathbf x)\)

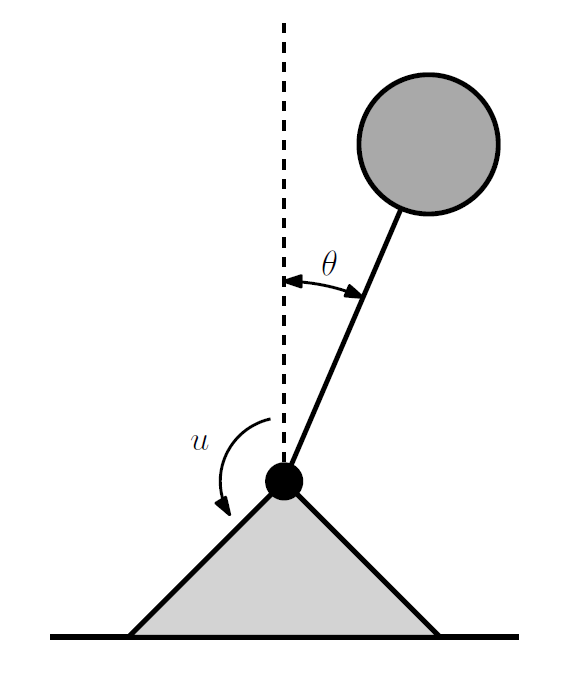
Simulation

  • Inverted pendulum with input gain attenuation \(\propto e^{-\theta^2}\)

  • Stability (CLF) and safety (CBF)

  • Data: densely sampled states, both dense and sparsely sampled inputs

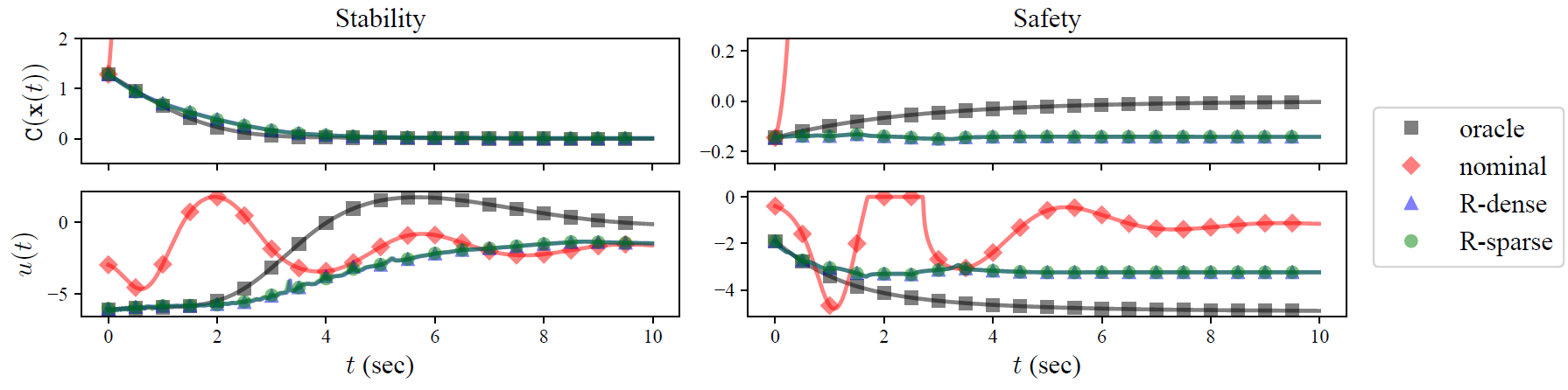
nominal controller unsafe/unstable

data-driven controllers safe/stable

sparse and dense controllers nearly identical

Episodic Learning

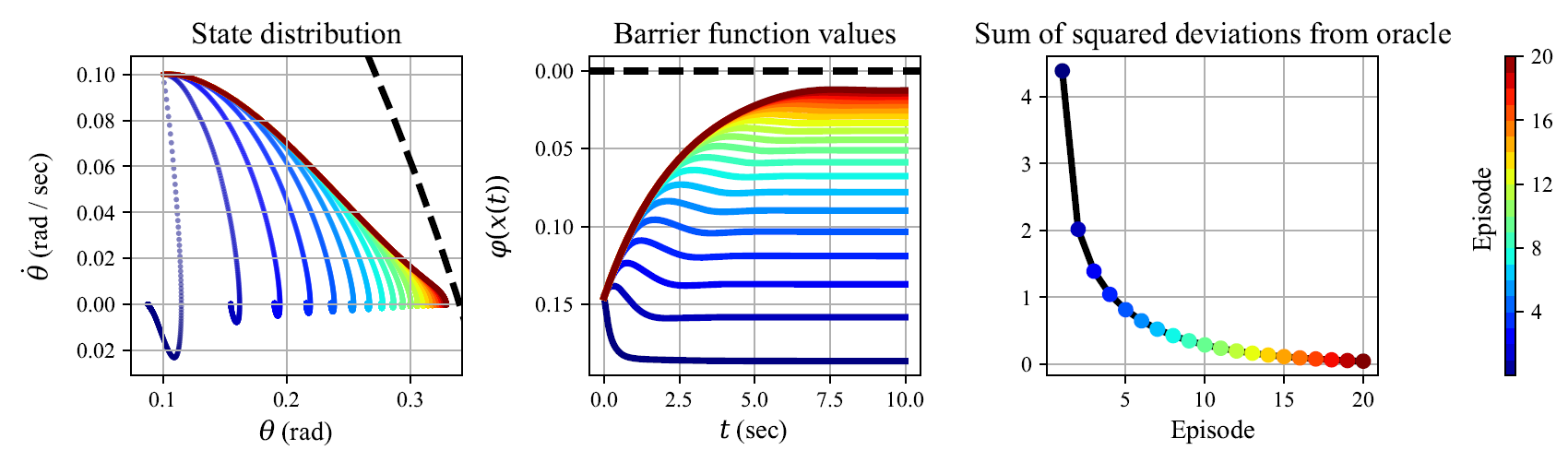
Append data from each episode and restart trajectory

Open Questions

  1. Control: Design of feasible robust CCFs
    • (or other nonlinear control strategy)
  2. Modelling: Efficiency
    • pointwise SOCP complexity is polynomial (cubic/quartic) in \(nN\)
  3. Data: Sample Complexity
    • intuition: dense state coverage (exponential in dimension), linear control coverage (linear in dimension)
    • instead: episodic perspective?

2. Kernel-based learning with approx.

Random Features Approximation for Control-Affine Systems

Yahya Sattar

Kimia Kazemian

Setting: control-affine models

Data \(\{(z_i, \mathbf x_i, \mathbf u_i)\}_{i=1}^N\) where \(z_i\) is posited to have a control-affine dependence on \(\mathbf x_i, \mathbf u_i\)

Ex - modelling \(j^{th}\) state coordinate
of control affine dynamics $$z_i = [\dot{\mathbf x}_i]_j = f_j(\mathbf x_i) + \mathbf g_j(\mathbf x_i)^\top \mathbf u_i$$

Ex - modelling CCF $$z_i = \dot C(\mathbf x_i,\mathbf u_i) = \nabla C(\mathbf x_i)^\top \mathbf f(\mathbf x_i) +\nabla C(\mathbf x_i)^\top \mathbf g(\mathbf x_i)^\top\mathbf u_i$$

Approach: kernel regression and random feature approximation

Background: Kernel Regression

Given a kernel function, for generic data \(\{(z_i, \mathbf s_i)\}_{i=1}^N\), kernel ridge regression gives the predictor

Rigorous pointwise uncertainty quantification  \(\sigma(\mathbf s)\) (Gaussian process)

Many kernel function are expressive enough to approximate continuous functions arbitrarily well

\(h(\mathbf s) = \mathbf k(\mathbf s)^\top (\mathbf K+\lambda \mathbf I_N)^{-1}\mathbf z \)

where \(\mathbf k(\mathbf s)_i = k(\mathbf s, \mathbf s_i),\quad \mathbf K_{ij} = k(\mathbf s_i,\mathbf s_j),\quad i,j=1,...,N\)

Background: Random Features

\(h_k(\mathbf s) = \mathbf k(\mathbf s)^\top (\mathbf K+\lambda \mathbf I_N)^{-1}\mathbf z \)

training requires \(N\times N\) matrix inversion (cubic)

prediction requires \(N\) inner products (linear)

Strategy: replace kernel function with inner products of random basis \(\mathbf \phi:\mathbb R^n\to R^D\) so \(k(\mathbf s, \mathbf s') \leftarrow \boldsymbol \psi(\mathbf s) ^\top \boldsymbol \psi(\mathbf s') \)

\(h_\psi(\mathbf s) = \boldsymbol \psi (\mathbf s)^\top (\Psi^\top \Psi+\lambda \mathbf I_D)^{-1} \Psi^\top \mathbf z \)

where \(\Psi = \begin{bmatrix} \boldsymbol \psi(\mathbf s_1) ^\top  \\ \vdots \\ \boldsymbol \psi(\mathbf s_N) ^\top \end{bmatrix} \) has dimension \(N\times D\)

For large enough \(D\) and appropriately defined \(\boldsymbol \psi\), \(h_\psi\approx h_k\)

Background: Random Features

\(h_k(\mathbf s) = \mathbf k(\mathbf s)^\top (\mathbf K+\lambda \mathbf I_N)^{-1}\mathbf z \)

training requires \(N\times N\) matrix inversion (cubic)

prediction requires \(N\) inner products (linear)

Strategy: replace kernel function with inner products of random basis \(\boldsymbol \psi:\mathbb R^n\to \mathbb R^D\) so \(k(\mathbf s, \mathbf s') \leftarrow \boldsymbol \psi(\mathbf s) ^\top \boldsymbol \psi(\mathbf s') \)

\(h_\psi(\mathbf s) = \boldsymbol \psi (\mathbf s)^\top (\Psi^\top \Psi+\lambda \mathbf I_D)^{-1} \Psi^\top \mathbf z \)

training is now \(O(ND^2+D^3)\)

prediction is \(O(D)\)

For large enough \(D\) and appropriately defined \(\boldsymbol \psi\), \(h_\psi\approx h_k\)

\(\boldsymbol\theta\)

\mathbb E_{\vartheta}[\psi(s)^\top \psi(s')]=k(s, s')
\text{i.i.d. from } p(\vartheta)

*Ali Rahimi and Benjamin Recht. Random features for large-scale kernel machines. In Proceedings of the 20th International Conference on Neural Information Processing Systems, NIPS’07

\newcommand{\bv}[1]{{\boldsymbol{#1}}} \newcommand{\bvgrk}[1]{{\boldsymbol{#1}}} \newcommand{\vs}{\bv{s}} \newcommand{\vvartheta}{\bvgrk{\vartheta}} \renewcommand{\R}{\mathbb{R}} k(\vs,\vs') = \int_{ \vvartheta \in \R^d} e^{-i 2 \pi \vvartheta^\top (\vs - \vs')} p(\vvartheta) d \vvartheta =: \mathbb E_\vvartheta [\zeta_\vvartheta(s)\zeta_\vvartheta(s')^*]

Define \( \zeta_\vartheta(s)=e^{-i2\pi\vartheta^\top s}\), then observe:

Euler's formula: \(e^{ix}= \cos x+ i \sin x\)

\psi_i(x):= \sqrt{2/D}\begin{bmatrix}\sin(\vartheta_{i,1}^\top x) & \cos(\vartheta_{i,1}^\top x) & \dots &\sin(\vartheta_{i,D/2}^\top x) & \cos(\vartheta_{i,D/2}^\top x)\end{bmatrix}^\top

Background: Random Features

Strategy: replace kernel function with inner products of random basis \(k(\mathbf s, \mathbf s') \leftarrow \boldsymbol \psi(\mathbf s) ^\top \boldsymbol \psi(\mathbf s') \)

Example: Gaussian (RBF) Kernel

\psi_i(x):= \sqrt{2/D}\begin{bmatrix}\sin(\vartheta_{i,1}^\top x) & \cos(\vartheta_{i,1}^\top x) & \dots &\sin(\vartheta_{i,D/2}^\top x) & \cos(\vartheta_{i,D/2}^\top x)\end{bmatrix}^\top
k(s,s')\!= e^{-\frac{1}{\gamma}\|s-s'\|_2^2}, \quad p(\vartheta) \!\sim \!\mathcal{N}(0,2\gamma I_d)
\varphi = e^{-\gamma s^2}\begin{bmatrix}1 &\sqrt{\frac{2\gamma}{1!}}x &\sqrt{\frac{(2\gamma)^2}{2!}}x^2& \dots\end{bmatrix}
\psi(s)^\top \psi(s') \approx k(s, s')=\varphi(s)^\top\varphi(s')

Compound kernels and features

Individual kernels/feature functions (each input dimension) $$k_j(\mathbf x,\mathbf x),\quad \boldsymbol \psi_j(\mathbf {x}),\quad j=1,...,m+1$$

Affine Dot Product (ADP) Basis $$\boldsymbol \phi_c(\mathbf x,\mathbf u)=\begin{bmatrix} u_1\boldsymbol \psi_1(\mathbf x) \\ \dots \\  u_{m}\boldsymbol \psi_{m} (\mathbf x) \\ \boldsymbol \psi_{m+1}(\mathbf x) \end{bmatrix} \in \mathbb R^{D(m+1)}$$

Affine Dense (AD) Basis $$\boldsymbol \phi_d(\mathbf x,\mathbf u)=\begin{bmatrix} \boldsymbol \psi_1(\mathbf x)^\top  \\ \dots \\  \boldsymbol \psi_{m} (\mathbf x)^\top  \\ \boldsymbol \psi_{m+1}(\mathbf x)^\top  \end{bmatrix}^\top  \begin{bmatrix} \mathbf u \\ 1 \end{bmatrix} \in \mathbb R^D$$

corresponds to ADP compound kernel defined by \(k_1,...,k_{m+1}\) (Castaneda et al., 2020)

corresponds to AD compound kernel defined by \(k_1,...,k_{m+1}\) (novel)

Compound kernels and features

Individual kernels/feature functions (each input dimension) $$k_j(\mathbf x,\mathbf x),\quad \boldsymbol \psi_j(\mathbf {x}),\quad j=1,...,m+1$$

Affine Dot Product (ADP) Kernel $$k_c(\mathbf {x,u,x', u'})=\sum_{j=1}^m u_j u'_j k_j(\mathbf x,\mathbf x') +k_{m+1}(\mathbf x,\mathbf x')$$

Affine Dense (AD) Kernel $$k_d(\mathbf {x,u,x', u'})=\sum_{j=1}^m u_j u'_j k_j(\mathbf x,\mathbf x') + \sum_{\ell=1}^m \sum_{j\neq \ell }^m u_j u'_\ell k_j(\mathbf x,0)k_\ell(0,\mathbf x') +k_{m+1}(\mathbf x,\mathbf x')$$

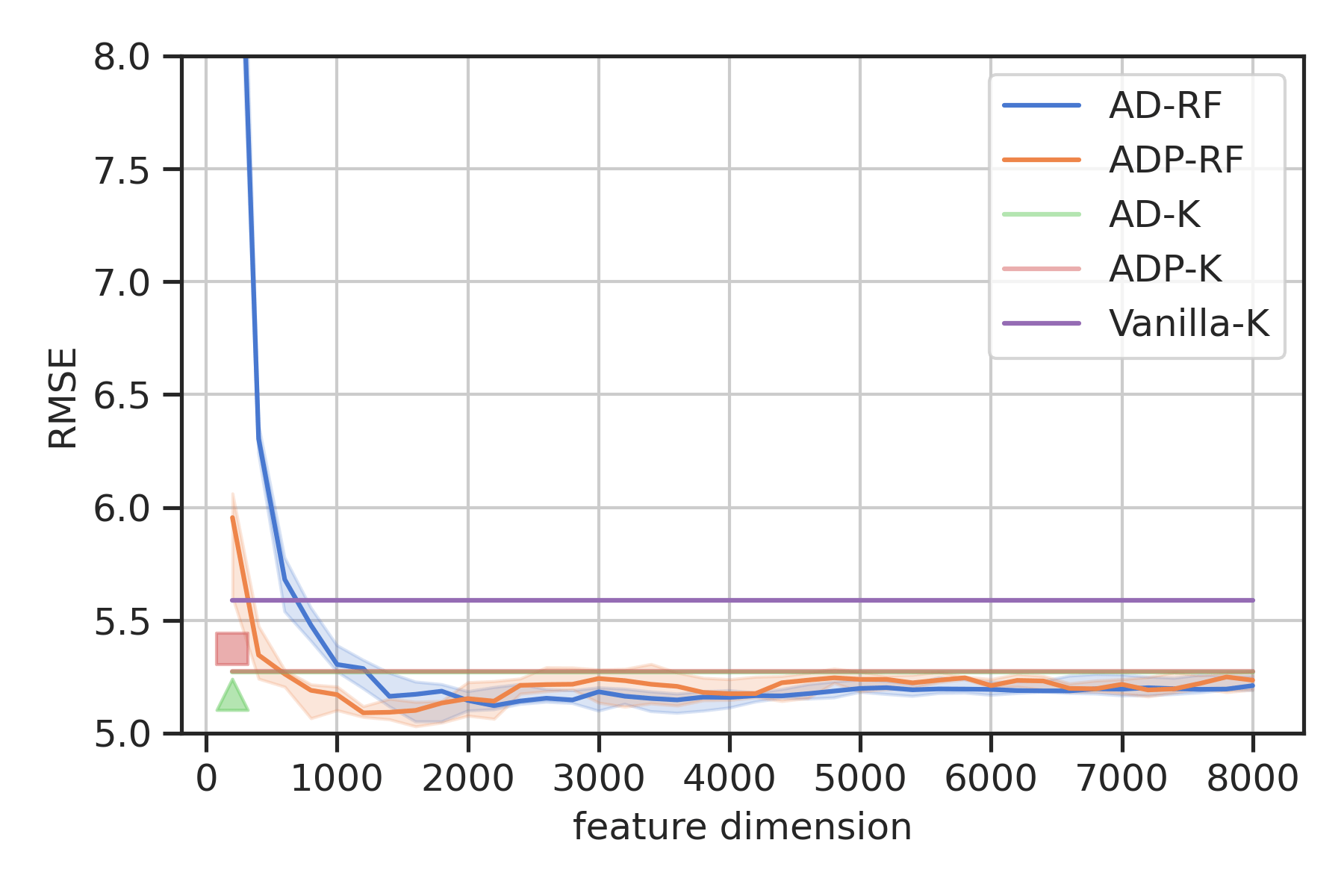
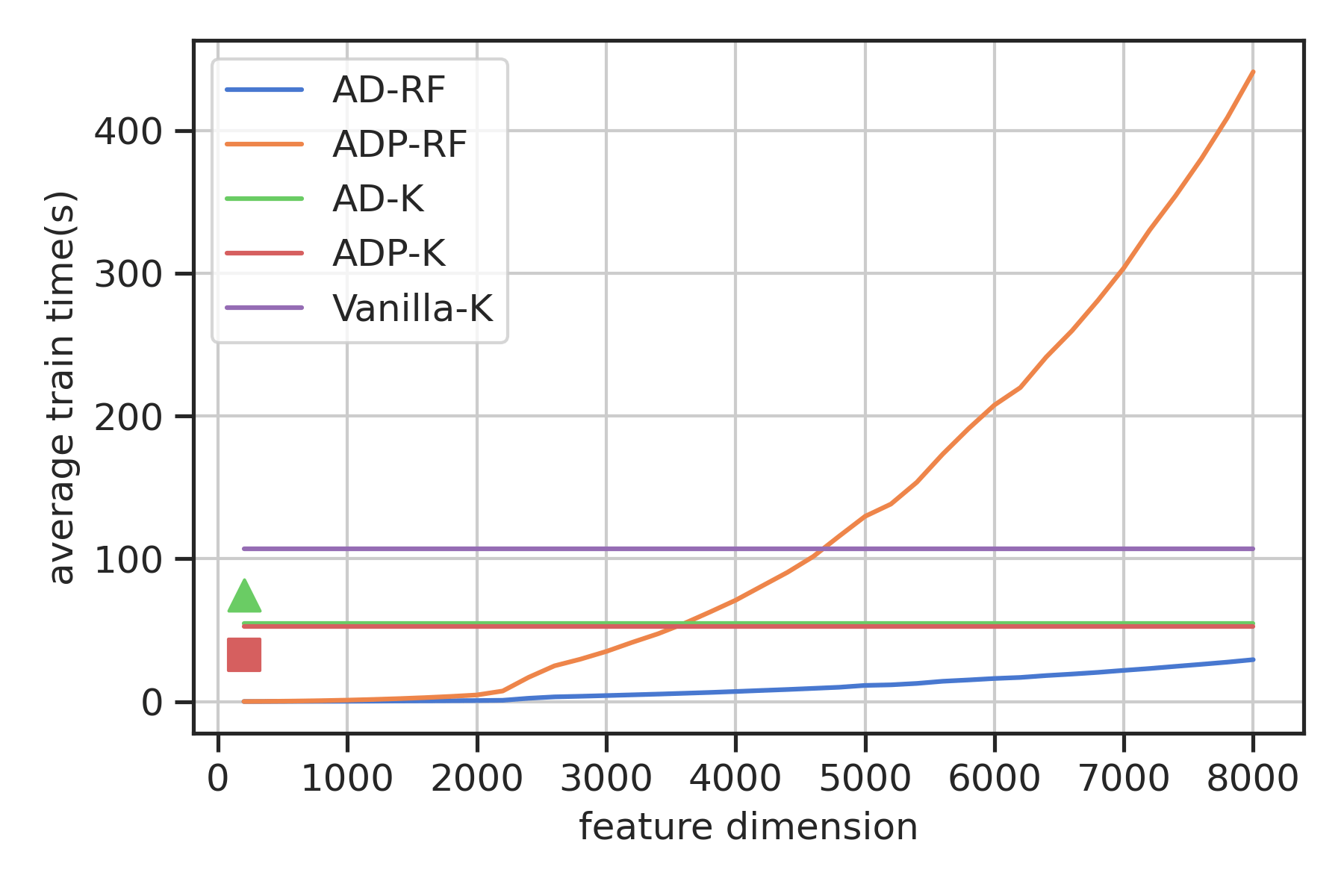
AD-K

time: \(\quad O(N^3)\)
space: \(\quad O(N^2) \)

ADP-RF

time: \(\quad O(N(D(m+1))^2)\)
space: \(\quad O(ND(m+1)) \)

AD-RF

time: \(\quad O(ND^2)\)
space: \(\quad O(ND) \)

Vanilla K

time: \(\quad O((N+m)^3)\)
space: \( \quad O((n+m)^2) \)

ADP-K

time: \( \quad O(N^3)\)
space: \(\quad O(N^2) \)

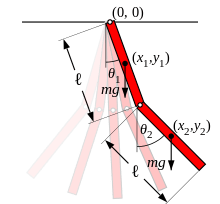
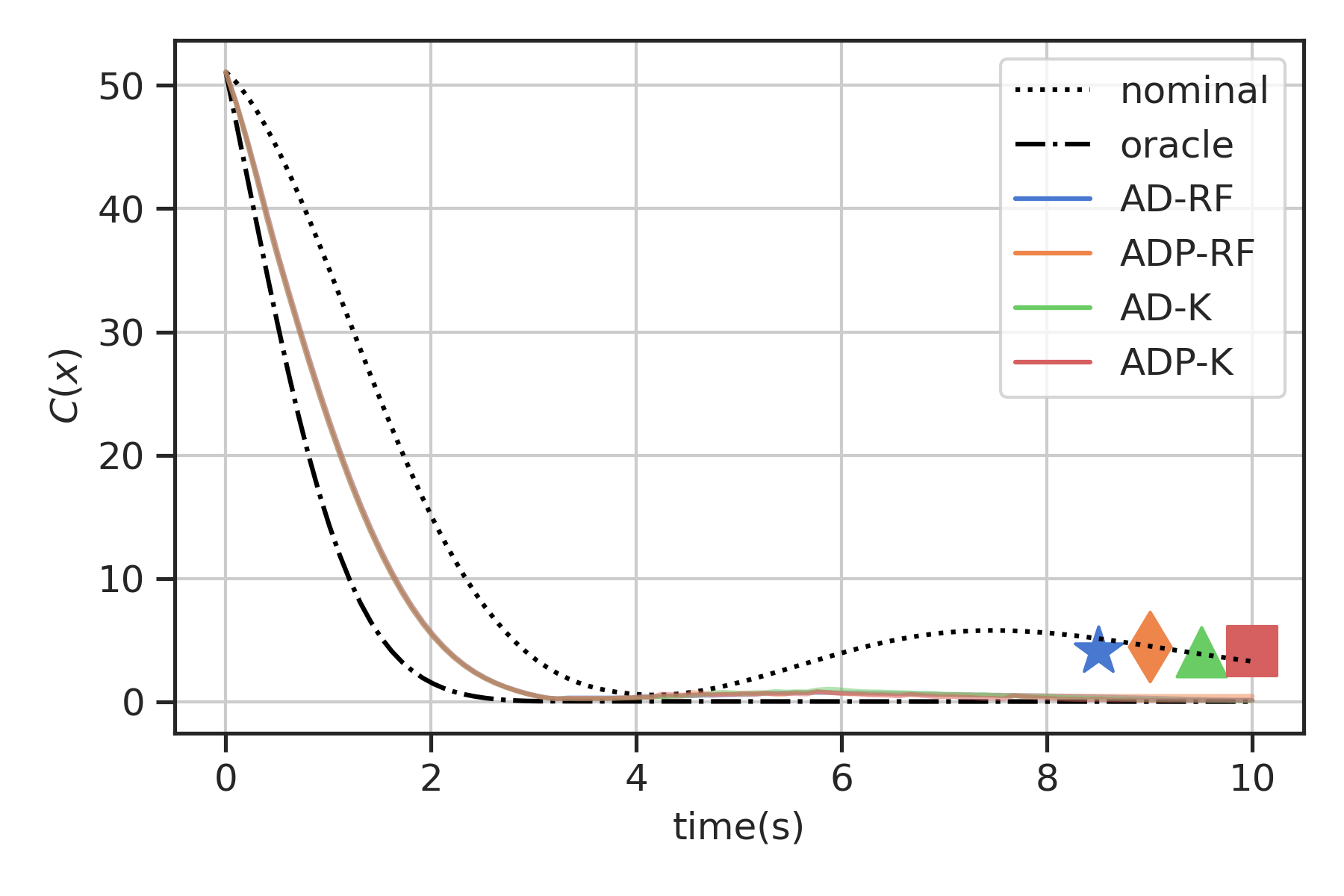
Simulation

  • Double inverted pendulum (\(n=4,m=2)\)

  • Goal: Swing up (CLF)

  • Data: \(N=8.8\)k collected with nominal

  • RBF kernels and random Fourier features

Simulation

  • Double inverted pendulum (\(n=4,m=2)\)

  • Goal: Swing up (CLF)

  • Data: \(N=1.8\)k nominal (subsampled) \(+\) \(1\)k episodic data collection

  • Basis \(D=N/5\)

Open Questions

  1. Modelling: Efficiency
    • Prune data (adaptively?)
    • Fast linear algebra
  2. Data: Sample Complexity
    • Kernel intuition: exponential in (state) dimension
    • Alternatively, notice that the (partial) model outputs are  bilinear in transformed state:

\(h_\psi(\mathbf x,\mathbf u) =\boldsymbol \theta^\top \boldsymbol \psi_{1:m+1}(\mathbf x)^\top   \begin{bmatrix} \mathbf u \\ 1 \end{bmatrix}\)

3. Sample complexity theory for bilinear systems

Finite Sample Identification of Partially Observed Bilinear Dynamical Systems

Yahya Sattar

Yassir Jedra

Maryam Fazel

Setting: Bilinear Dynamical Systems (BLDS)

Can approximate control-affine dynamics via Carleman linearization (Kowalski & Steeb, 1991) or Koopman transform (Goswami & Paley, 2017)

Where:

  • \( \mathbf x_t \in \mathbb{R}^n \): State  
  • \( \mathbf u_t \in \mathbb{R}^m \): Input  
  • \( \mathbf y_t \in \mathbb{R}^p \): Output  
  • \( \mathbf w_t \in \mathbb{R}^n \): Process noise  
  • \( \mathbf z_t \in \mathbb{R}^p \): Measurement noise  
  • \( A_0, A_1, ..., A_m \in \mathbb{R}^{n \times n} \), \( B \in \mathbb{R}^{n \times m} \), \( C \in \mathbb{R}^{p \times n} \), \( D \in \mathbb{R}^{p \times m} \)

$$\mathbf x_{t+1} = (\mathbf u_t \circ \mathbf A)\mathbf x_t + B \mathbf u_t + \mathbf w_t \\ \mathbf y_t = C \mathbf x_t + D \mathbf u_t + \mathbf z_t\qquad\quad $$

where we define

$$\mathbf u_t \circ \mathbf A  = A_0 + \sum_{k=1}^m (\mathbf u_t)_k A_k$$

Setting: Bilinear Dynamical Systems (BLDS)

Can approximate control-affine dynamics via Carleman linearization (Kowalski & Steeb, 1991) or Koopman transform (Goswami & Paley, 2017)

$$\mathbf x_{t+1} = (\mathbf u_t \circ \mathbf A)\mathbf x_t + B \mathbf u_t + \mathbf w_t \\ \mathbf y_t = C \mathbf x_t + D \mathbf u_t + \mathbf z_t\qquad\quad $$

where we define

$$\mathbf u_t \circ \mathbf A  = A_0 + \sum_{k=1}^m (\mathbf u_t)_k A_k$$

  • Suppose \( A_0, A_1, ..., A_m , B,C ,D \) unknown
  • Approach: learn input/output map with least squares

Output in terms of past \(L\) inputs:

$$\mathbf y_t = \sum_{\ell=1}^L C \left( \prod_{i=1}^{\ell-1} (\mathbf u_{t-i} \circ \mathbf A) \right) B \mathbf u_{t-\ell} + D \mathbf u_t + \text{noise and error} $$

Truncation error:

$$C \left( \prod_{\ell=1}^L (\mathbf u_{t-\ell} \circ \mathbf A) \right) \mathbf x_{t-L} $$

Process and measurement noise: $$\sum_{\ell=1}^L C \left( \prod_{i=1}^{\ell-1} (\mathbf u_{t-i} \circ \mathbf A) \right) \mathbf w_{t-\ell} + \mathbf v_t  $$

Input/output map

\(t\)

\(L\)

\(\underbrace{\qquad\qquad}\)

inputs

outputs

time

Learning the Markov-like Parameters

Define:

  • \( \bar{u}_t = [1, u_t] \)
  • \( \tilde{u}t = u_t, u{t-1}, \bar{u}{t-1} \otimes u{t-2}, \ldots \)
  • \( \tilde{w}t = z_t, w{t-1}, \ldots \)

Then:

$$y_t = \tilde{G} \tilde{u}_t + F \tilde{w}_t + \epsilon_t $$

Output in terms of past \(L\) inputs:

$$\mathbf y_t = \sum_{\ell=1}^L C \left( \prod_{i=1}^{\ell-1} (\mathbf u_{t-i} \circ \mathbf A) \right) B \mathbf u_{t-\ell} + D \mathbf u_t + \text{noise and error} $$

Input/output map

\(t\)

\(L\)

\(\underbrace{\qquad\qquad}\)

inputs

outputs

time

$$\mathbf y_t = {G} \tilde{\mathbf u}_t + \text{noise and error} $$

  • Define $$\bar{\mathbf u} = \begin{bmatrix}1 & \mathbf u^\top \end{bmatrix}^\top $$
  • $$\tilde{\mathbf u}_t = \begin{bmatrix} \mathbf u_t \\ \mathbf u_{t-1} \\ \bar{\mathbf u}_{t-1} \otimes \mathbf u_{t-2} \\ \bar{\mathbf u}_{t-1} \otimes \bar{\mathbf u}_{t-2} \otimes \mathbf u_{t-3}\\ \vdots \\ \bar{\mathbf u}_{t-1} \otimes \bar{\mathbf u}_{t-2} \otimes \dots \otimes \mathbf u_{t-L} \end{bmatrix} \in \mathbb R^{\tilde m}$$ where \( \tilde m={(m+1)^L+m-1}\)
  • Define \(\mathcal A\) as the set of matrix monomials in \(A_0,...,A_m\) up to degree \(L\) $$G = \mathsf{concat}(D, CMD | M\in\mathcal A) \in\mathbb R^{p\times \tilde m}$$ where \( \tilde m={(m+1)^L+m-1}\)
  • $$\bar{\mathbf u} = \begin{bmatrix}1 & \mathbf u^\top \end{bmatrix}^\top $$
  • $$\tilde{\mathbf u}_t = \begin{bmatrix} \mathbf u_t \\ \mathbf u_{t-1} \\ \bar{\mathbf u}_{t-1} \otimes \mathbf u_{t-2} \\ \bar{\mathbf u}_{t-1} \otimes \bar{\mathbf u}_{t-2} \otimes \mathbf u_{t-3}\\ \vdots \\ \bar{\mathbf u}_{t-1} \otimes \bar{\mathbf u}_{t-2} \otimes \dots \otimes \mathbf u_{t-L} \end{bmatrix} \in \mathbb R^{\tilde m}$$

Least squares estimation

$$\mathbf y_t = {G} \tilde{\mathbf u}_t + \text{noise and error} $$

$$\hat{G} := \left( \sum_{t=L}^T \mathbf y_t \tilde{\mathbf u}_t^\top \right) \left( \sum_{t=L}^T \tilde{\mathbf u}_t \tilde{\mathbf u}_t^\top \right)^\dagger $$

Theorem (Informal):
Under i.i.d. uniform inputs, stability, and sub-Gaussian noise assumptions, with high probability:

$$\|\hat{G} - G\| \lesssim \sqrt{\frac{m^2 L(m+1)^{L+1} (\log(L/\delta)+p+nL)}{(T-L)(1-\rho)}} $$

  • Stability is input-dependent
  • Determined by matrix products \(\mathbf u_t \circ \mathbf A\)
  • Define: Joint spectral radius for a set of matrices \(\mathcal M\) $$\rho(\mathcal{M}) = \lim_{k\to\infty}\sup_{M_1,...,M_k\in\mathcal M} \|M_1M_2...M_k\|^{1/k}$$ and \(\varphi(\mathcal M, \rho) = \sup_{k\geq1,M_1,...,M_k\in\mathcal M} \frac{1}{\rho^k}\|M_1M_2...M_k\|\)
  • Define: BLDS is \((\mathcal U,\kappa,\rho)\)-stable if \(\rho(\mathcal M)\leq \rho<1\) and \(\varphi(\mathcal M, \rho) \leq \kappa\) for \(\mathcal M = \{\mathbf u\circ \mathbf A | u\in\mathcal U\}\)

Stability of BLDS

Assumptions

  • Inputs are chosen uniformly at random from sphere \( \sqrt{m} \mathcal S^{m-1}\)
  • BLDS is \(( \sqrt{m} \mathcal S^{m-1},\rho,\kappa)\) stable
  • Process and measurement noise are sub-Gaussian

Proof Ingredients

1. Persistence of Excitation

$$\lambda_{\min} \left( \sum_{t=L}^T \tilde{u}_t \tilde{u}_t^\top \right) \geq \frac{T-L}{4} $$

  • Necessary for consistent estimation
  • Requires isotropic inputs

2. Bounded Effect of Noise

  • Multiplier process
  • Requires independent noise

3. Truncation Bias

  • Requires stability
  • Unlike in LTI systems, also requires independent noise

Theorem (Informal):
Under i.i.d. uniform inputs, stability, and sub-Gaussian noise assumptions, with high probability:

$$\|\hat{G} - G\| \lesssim \sqrt{\frac{m^2 L(m+1)^{L+1} (\log(L/\delta)+p+nL)}{(T-L)(1-\rho)}} $$

Open Questions

  1. Can we relax stability assumption?
  2. Can we estimate reduced number of parameters?
  3. Can we reduce or remove dependence on state dimension?
  4. Can we formalize control-affine model connections?
  5. Can we combine with control for end-to-end performance guarantee?
  1. Towards Robust Data-Driven Control Synthesis for Nonlinear Systems with Actuation Uncertainty (https://arxiv.org/abs/2011.10730) with Andrew Taylor, Victor Dorobantu, Benjamin Recht, Yisong Yue, Aaron Ames
  2. Random Features Approximation for Control-Affine Systems (https://arxiv.org/abs/2406.06514) with Kimia Kazemian, Yahya Sattar
  3. Finite Sample Identification of Partially Observed Bilinear Dynamical Systems (https://arxiv.org/abs/2501.07652) with Yahya Sattar, Yassir Jedra, Maryam Fazel

Thanks! Questions?