Bias in Algorithms
Sarah Dean
CS 194/294 Guest Lecture, 3/1/21
About Me
- PhD student in EECS
- "Reliable Machine Learning in Feedback Systems"
- formally reasoning about safety, stability, equity, wellbeing
- Co-founded GEESE (geesegraduates.org)


Algorithms are consequential and ubiquitous






Bias in Algorithms
Bias: prejudice, usually in a way considered to be unfair
(mathematical) systematic distortion of a statistical result
Prejudice: preconceived opinion
(legal) harm or injury resulting from some action or judgment
Algorithm: a set of rules to be followed, especially by a computer
Promises of algorithmic screening
- explicit criteria
- equally applied
- auditable
Ex: Algorithmic Resume Screening


"I usually look for candidates who will be a good fit"
Ex: Algorithmic Resume Screening


Promises of algorithmic data-driven screening
-
explicit criteria"superhuman" accuracy - equally applied
- auditable
Ex: Data-Driven Resume Screening

Hand-coded algorithms are hard!
Machine learning extracts statistical patterns from employment records to automatically generate accurate and optimal classifications
Does Data-Driven Screening Discriminate?
Federal laws make it illegal to discriminate on the basis of race, color, religion, sex, national origin, pregnancy, disability, age, and genetic information.


Important quantities:
Formalizing Algorithmic Decisions


features \(X\) and label \(Y\)
(e.g. resume and employment outcome)
classifier \(c(X) = \hat Y\)
(e.g. interview invitation)

- Accuracy: \(\mathbb P( \hat Y = Y)\)
- Positive rate: \(\mathbb P( \hat Y = 1)\)
- Among truly (un)qualified (conditioned on \(Y\))
- Among positive (negative) decisions (conditioned on \(\hat Y\))
Statistical Classification Criteria

Accuracy
\(\mathbb P( \hat Y = Y)\) = ________
Positive rate
\(\mathbb P( \hat Y = 1)\) = ________
False positive rate
\(\mathbb P( \hat Y = 1\mid Y = 0)\) = ________
False negative rate
\(\mathbb P( \hat Y = 0\mid Y = 1)\) = ________
Positive predictive value
\(\mathbb P( Y = 1\mid\hat Y = 1)\) = ________
Negative predictive value
\(\mathbb P( Y = 0\mid\hat Y = 0)\) = ________
\(X\)
\(Y=1\)
\(Y=0\)
\(c(X)\)
\(3/4\)
\(9/20\)
\(1/5\)
\(3/10\)
\(7/9\)
\(8/11\)
Formal Nondiscrimination Criteria


features \(X\) and label \(Y\)
(e.g. resume and employment outcome)
classifier \(c(X) = \hat Y\)
(e.g. interview invitation)


individual with protected attribute \(A\)
(e.g. race or gender)
Independence: decision does not depend on \(A\)
\(\hat Y \perp A\)
e.g. applicants are accepted at equal rates across gender
Separation: given outcome, decision does not depend on \(A\)
\(\hat Y \perp A~\mid~Y\)
e.g. qualified applicants are accepted at equal rates across gender
Sufficiency: given decision, outcome does not depend on \(A\)
\( Y \perp A~\mid~\hat Y\)
e.g. accepted applicants are qualified at equal rates across gender
Ex: Pre-trial Detention

- COMPAS: a criminal risk assessment tool used in pretrial release decisions
- \(X\) survey about defendant
- \(\hat Y\) designation as high- or low-risk
- Audit of data from Broward county, FL
- \(A\) race of defendant
- \(Y\) recidivism within two years
“Black defendants who did not recidivate over a two-year period were nearly twice as likely to be misclassified. [...] White defendants who re-offended within the next two years were mistakenly labeled low risk almost twice as often.”
Ex: Pre-trial Detention

“In comparison with whites, a slightly lower percentage of blacks were ‘Labeled Higher Risk, But Didn’t Re-Offend.’ [...] A slightly higher percentage of blacks were ‘Labeled Lower Risk, Yet Did Re-Offend.”’

\(\mathbb P(\hat Y = 1\mid Y=0, A=\text{Black})> \mathbb P(\hat Y = 1\mid Y=0, A=\text{White}) \)
\(\mathbb P(\hat Y = 0\mid Y=1, A=\text{Black})< \mathbb P(\hat Y = 0\mid Y=1, A=\text{White}) \)
\(\mathbb P(Y = 0\mid \hat Y=1, A=\text{Black})\approx \mathbb P( Y = 0\mid \hat Y=1, A=\text{White}) \)
\(\mathbb P(Y = 1\mid \hat Y=0, A=\text{Black})\approx \mathbb P( Y = 1\mid \hat Y=0, A=\text{White}) \)
COMPAS risk predictions do not satisfy separation
Ex: Pre-trial Detention

COMPAS risk predictions do satisfy sufficiency

If we use machine learning to design a classification algorithm, how do we ensure nondiscrimination?
Achieving Nondiscrimination Criteria
Attempt #1: Remove protected attribute \(A\) from features


Attempt #2: Careful algorithmic calibration
Achieving Nondiscrimination Criteria
- Pre-processing: remove correlations between \(A\) and features \(X\) in dataset. Requires knowledge of \(A\) during data cleaning
-
In-processing: modify learning algorithm to respect criteria.
Requires knowledge of \(A\) at training time -
Post-processing: adjust thresholds in group-dependent manner.
Requires knowledge of \(A\) at decision time
Limitations of Nondiscrimination Criteria
- Tradeoffs: It is impossible to simultaneously satisfy separation and sufficiency if populations have different base rates
- Observational: since they are statistical criteria, they can measure only correlation; intuitive notions of discrimination involve causation, but these can only be measured with careful modelling
- Unclear legal grounding: anti-discrimination law looks for disparate treatment or disparate impact; while algorithmic decisions may have disparate impact, achieving criteria involves disparate treatment
- Limited view: focusing on risk prediction might miss the bigger picture of how these tools are used by larger systems to make decisisons
Pre-existing Bias: exists independently, usually prior to the creation of the system, with roots in social institutions, practices, attitudes
Bias in Computer Systems
Technical Bias: arises from technical constraints and considerations; limitations of formalisms and quantification of the qualitative
Emergent Bias: arises in context of use as a result of changing societal knowledge, population, or cultural values
Classic taxonomy by Friedman & Nissenbaum (1996)
individual \(X\)
Machine Learning Pipeline

training data
\((X_i, Y_i)\)
model
\(c:\mathcal X\to \mathcal Y\)
prediction \(\hat Y\)
measurement
learning
action
Bias in Training Data

training data
\((X_i, Y_i)\)
Existing inequalities can manifest as pre-existing bias

measurement
Bias in Training Data

training data
\((X_i, Y_i)\)
Technical bias may result from the process of constructing a dataset:
- Sample bias: who and where we sample
- Feature/label bias: which attributes we include
- Measurement bias: how we quantify attributes
measurement
Bias in Training Procedure
training data
\((X_i, Y_i)\)
model
\(c:\mathcal X\to \mathcal Y\)
Further technical bias results from formulating learning task and training the model: optimization bias
learning

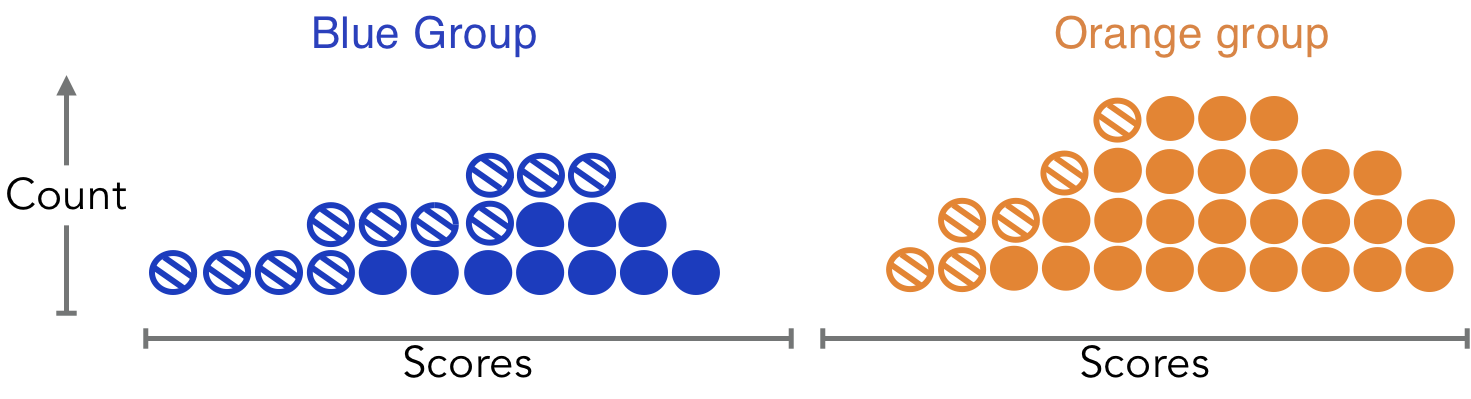

e.g. optimizing for average accuracy will prioritize majority groups
Ex: Miscalibration in Recommendation
Designing recommendations which optimize engagement leads to over-recommending the most prevalent types (Steck, 2018)
rom-com 80% of the time
horror 20% of the time
optimize for probable click
recommend rom-com 100% of the time










Validity of Prediction Tasks
Small Is Beautiful: Economics as if People Mattered, E.F. Schumacher:
- Full predictability exists only in the absence of human freedom
- Relative predictability exists with regard to the behavior pattern of very large numbers of people doing 'normal' things
- Relatively full predictability exists with regard to human actions controlled by a plan which eliminates freedom
- Individual decisions by individuals are in principle unpredictable


Bias in Deployment
Emergent bias results from real-world dynamics, including those induced by the decisions themselves
individual \(X\)

model
\(c:\mathcal X\to \mathcal Y\)
prediction \(\hat Y\)
e.g. Goodhart's law: "When a measure becomes a target, it ceases to be a good measure."
action


Predictive policing models predict crime rate across locations based on previously recorded crimes
Ex: Emergent Bias in Policing



PredPol analyzed by Lum & Isaac (2016)
recorded drug arrests
police deployment
estimated actual drug use
Bias Beyond Classification







image cropping
facial recognition
information retrieval
generative models
Main References
- Barocas, Hardt, Narayanan. Fairness and machine learning: Limitations and Opportunities, Intro and Ch 1.
- Friedman & Nissenbaum. Bias in computer systems. TOIS, 1996.
- Dobbe, Dean, Gilbert, Kohli. A broader view on bias in automated decision-making: Reflecting on epistemology and dynamics. FAT/ML, 2018.