Delayed Impact of Fair Machine Learning
Lydia T. Liu, Sarah Dean, Esther Rolf, Max Simchowitz, and Moritz Hardt
University of California, Berkeley





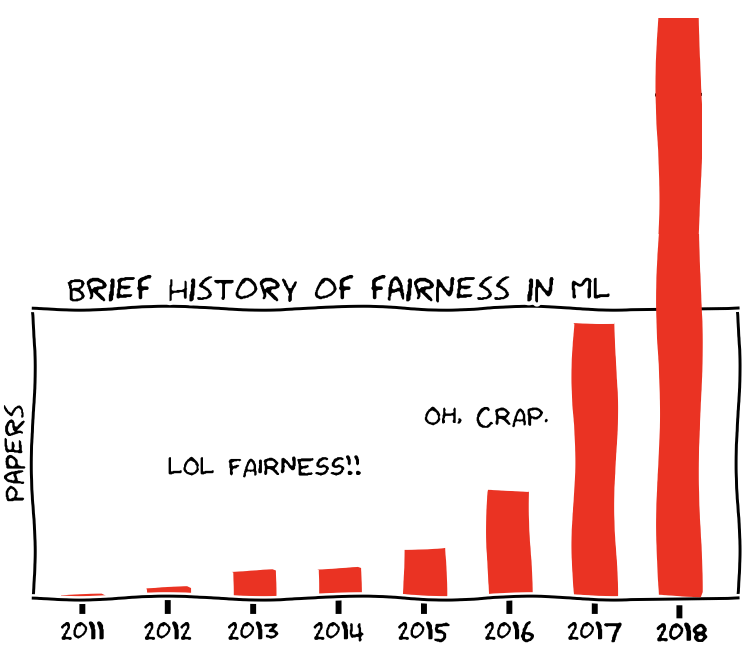
“21 definitions of fairness” [Narayanan 2018]
- Demographic Parity
- Equality of Opportunity
- Predictive value parity
- Group Calibration
. . .
- Many fairness criteria can be achieved individually using efficient algorithms post-processing [e.g. Hardt et al. 2016]; reduction to black-box machine learning [e.g. Dwork et al. 2018; Agarwal et al. 2018]; agnostic learning [e.g. Kearns et al. 2018; Herbert-Johnson et al. 2018]; unconstrained machine learning [Liu et al. 2018b]
- But typically impossible to satisfy simultaneously [e.g. Kleinberg et al. 2016; Chouldechova, 2017]

?
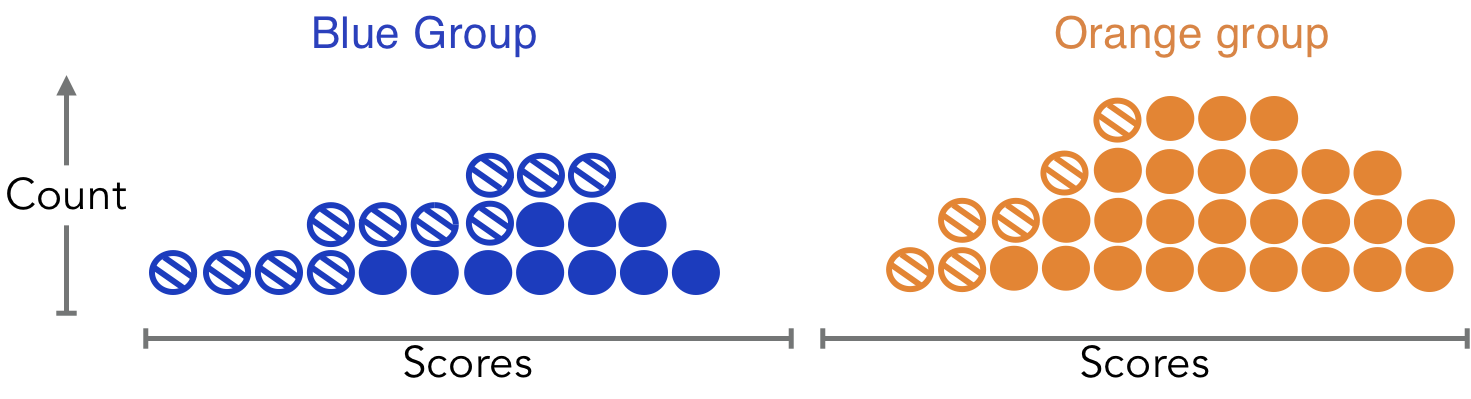
Two groups with different score distributions (e.g. credit scores)


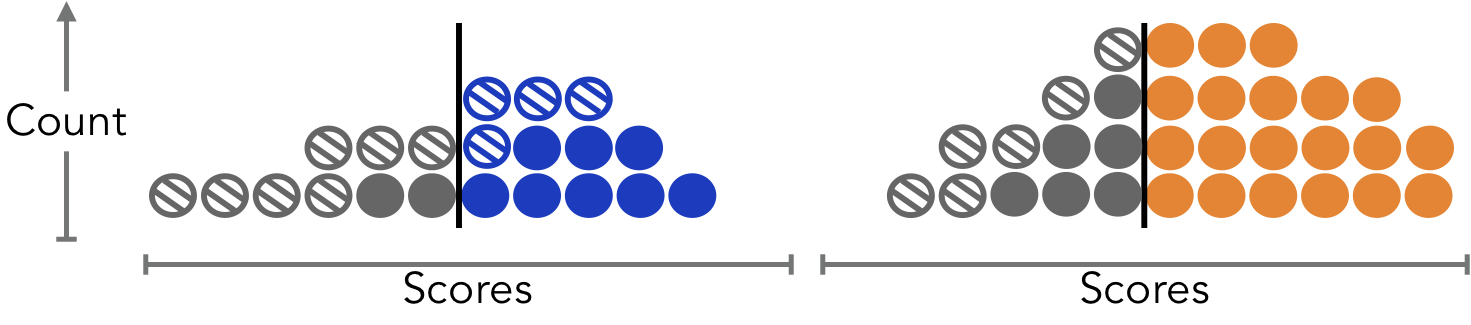
Approve loans according to Demographic Parity.

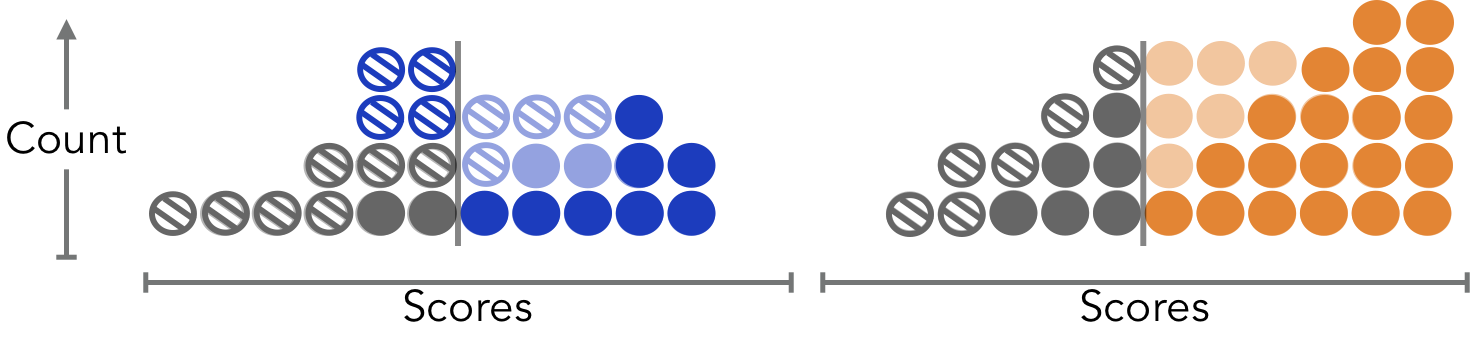


Credit scores change with repayment (+) or default (-).
Harm!

What Happened?
Fairness criteria didn’t seem to help the protected group,
once we considered the impact of loans on scores.
Our Work
- Introduce the “outcome curve”, a tool for comparing the delayed impact of fairness criteria
- Provide a complete characterization of the delayed impact of different fairness criteria
- Show that fairness constraints may cause harm to groups they intended to protect
Scores and Decisions
Model Delayed Impact


- A score \(R\) is a scalar random variable corresponding to success probability if accepted
- Scores of accepted individuals change depending on their success.
- The average change in score of each group is the delayed impact \(\Delta \mu\)
- Institution accepts individuals based on threshold \(T\), chosen to maximize expected utility

Lemma: \(\Delta\mu\) is a concave function of acceptance rate \(\beta\) under mild assumptions.
Outcome Curve
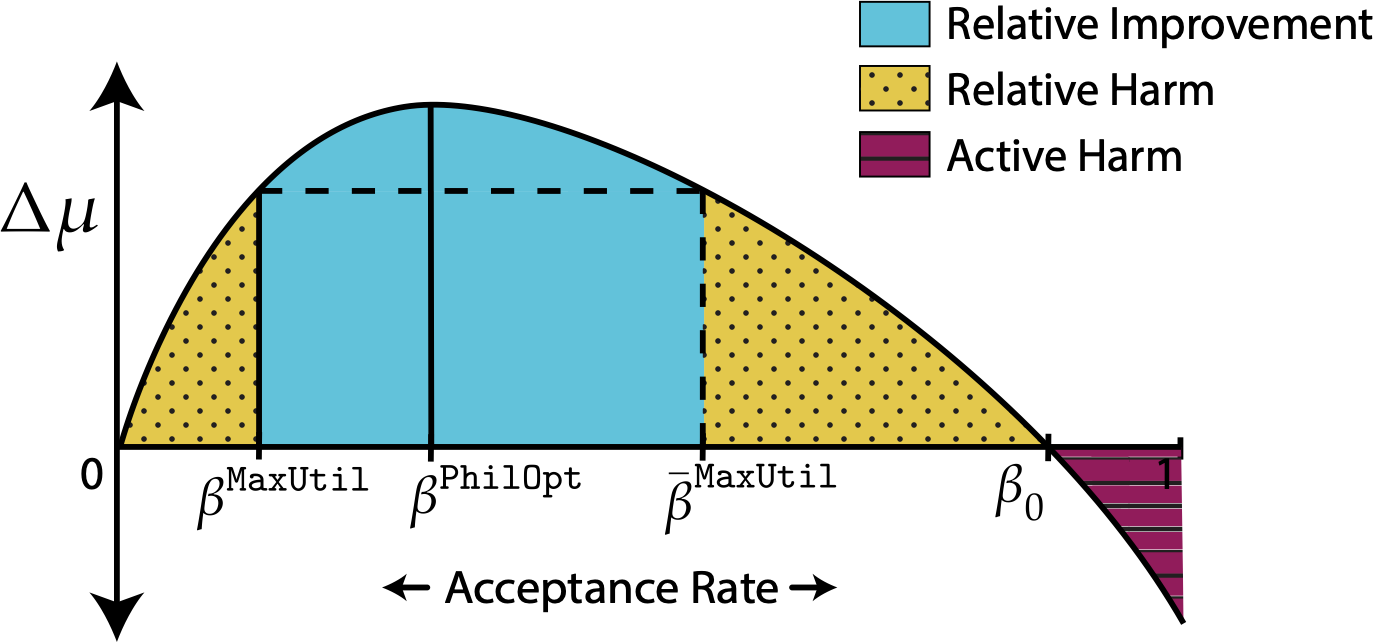
average score change
Fairness Constraints
Alternative to unconstrained utility maximization
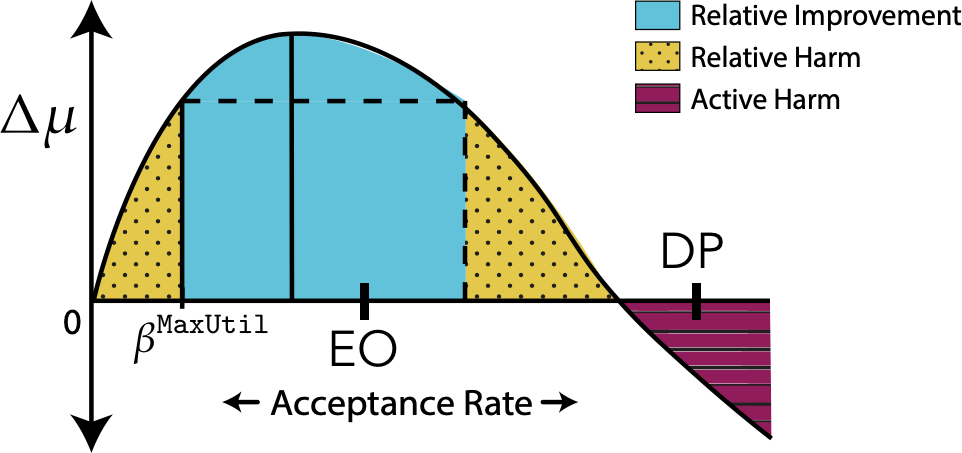
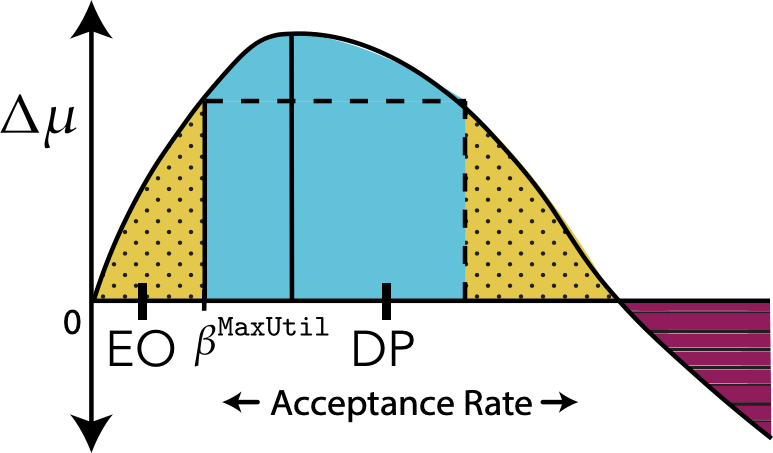
Demographic Parity: Equal Acceptance Rate
Equal Opportunity: Equal True Positive Rates



All outcome regimes are possible
Result 1
Equal opportunity and demographic parity may cause relative improvement, relative harm, or active harm.
Unconstrained utility maximization never causes active harm.
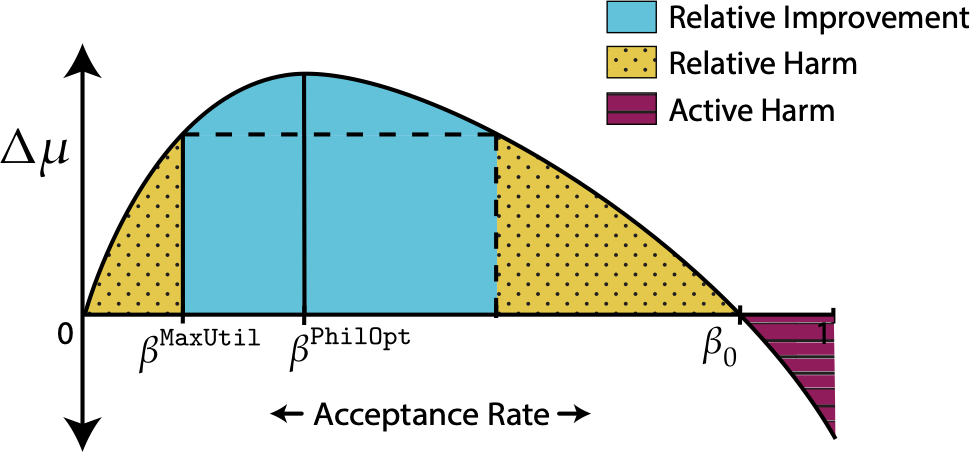
Main Results
Result 2
Demographic parity (DP) may cause active or relative harm by over-acceptance; equal opportunity (EO) doesn't.
Result 3
Equal opportunity may cause relative harm by under-acceptance; demographic parity never under-accepts.
Choice of Fairness Criteria Matters

Experiments on FICO Credit Scores
- 300,000+ TransUnion TransRisk scores from 2003
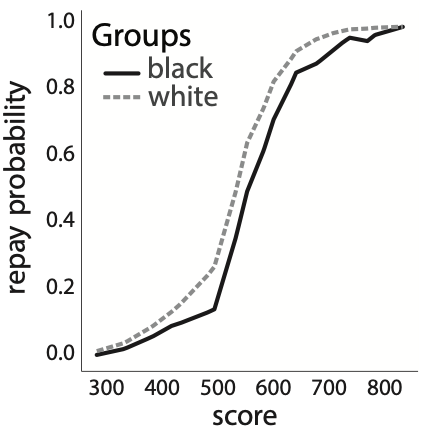
- Estimate score distributions and repayment probabilities
- Model bank’s profit/loss ratio as +1:-4
- Model impact of repayment and default on credit score as +75 and -150
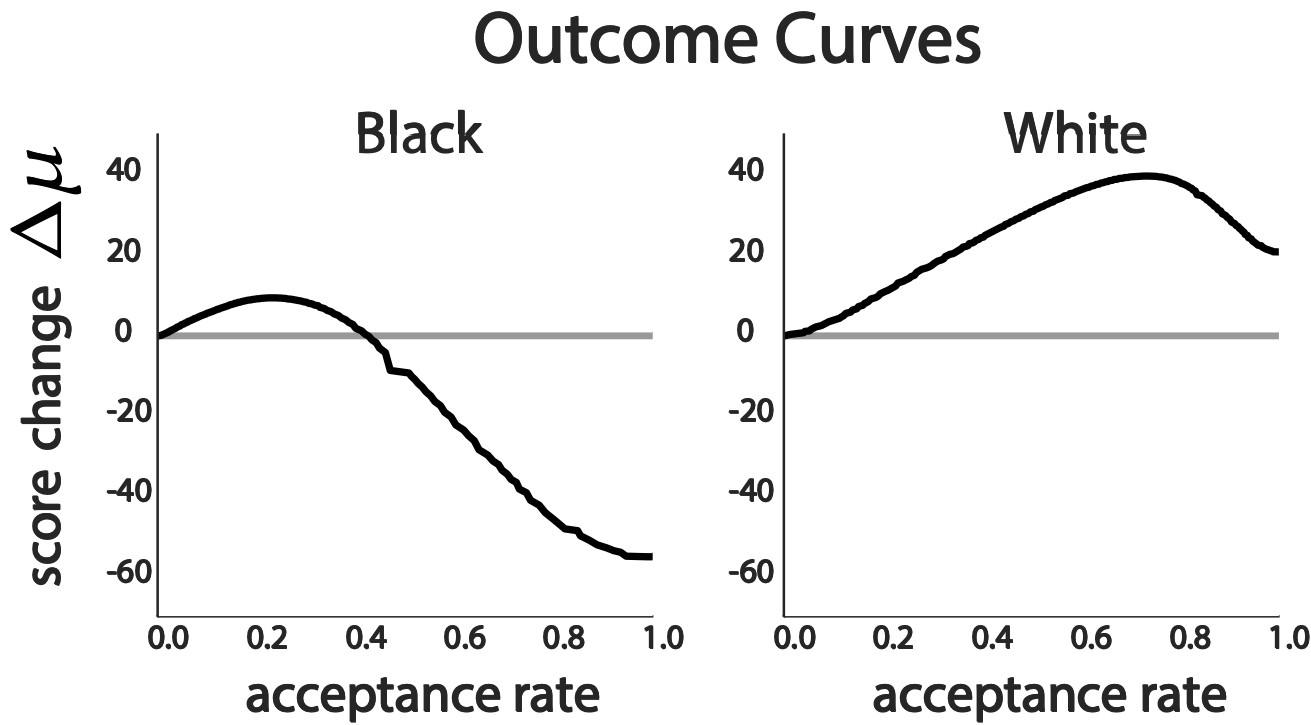





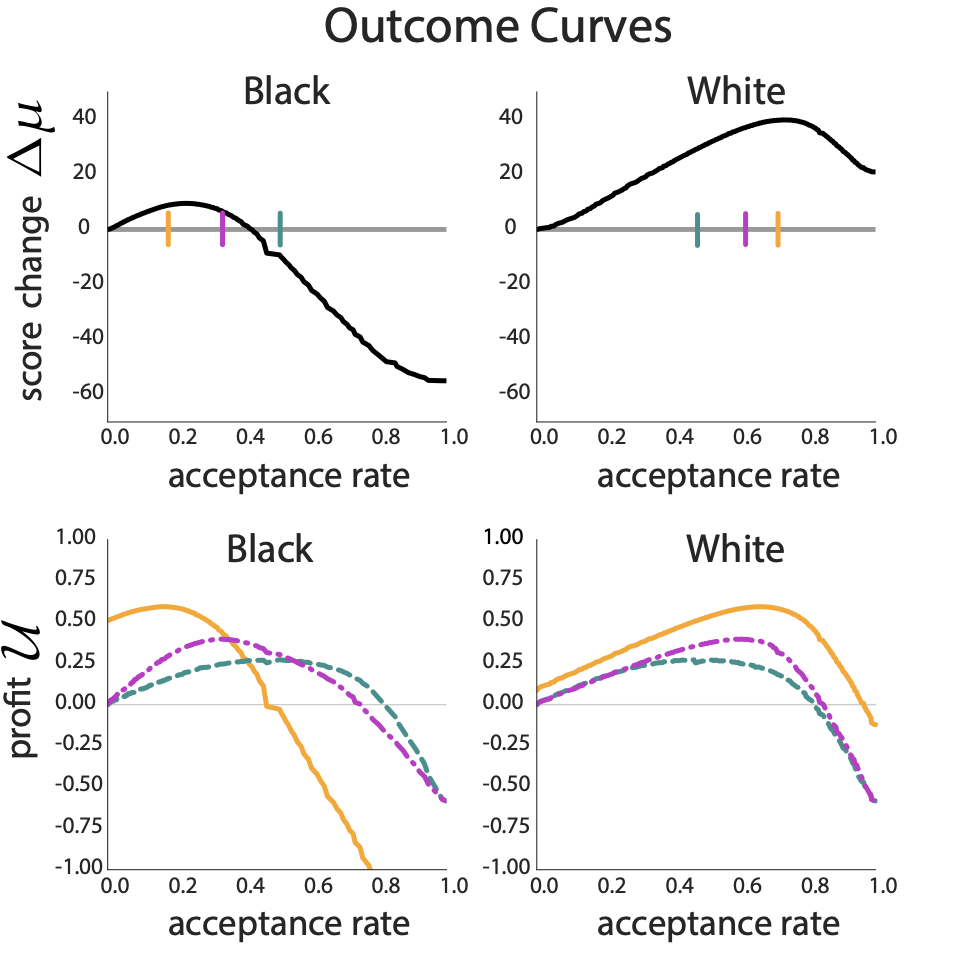
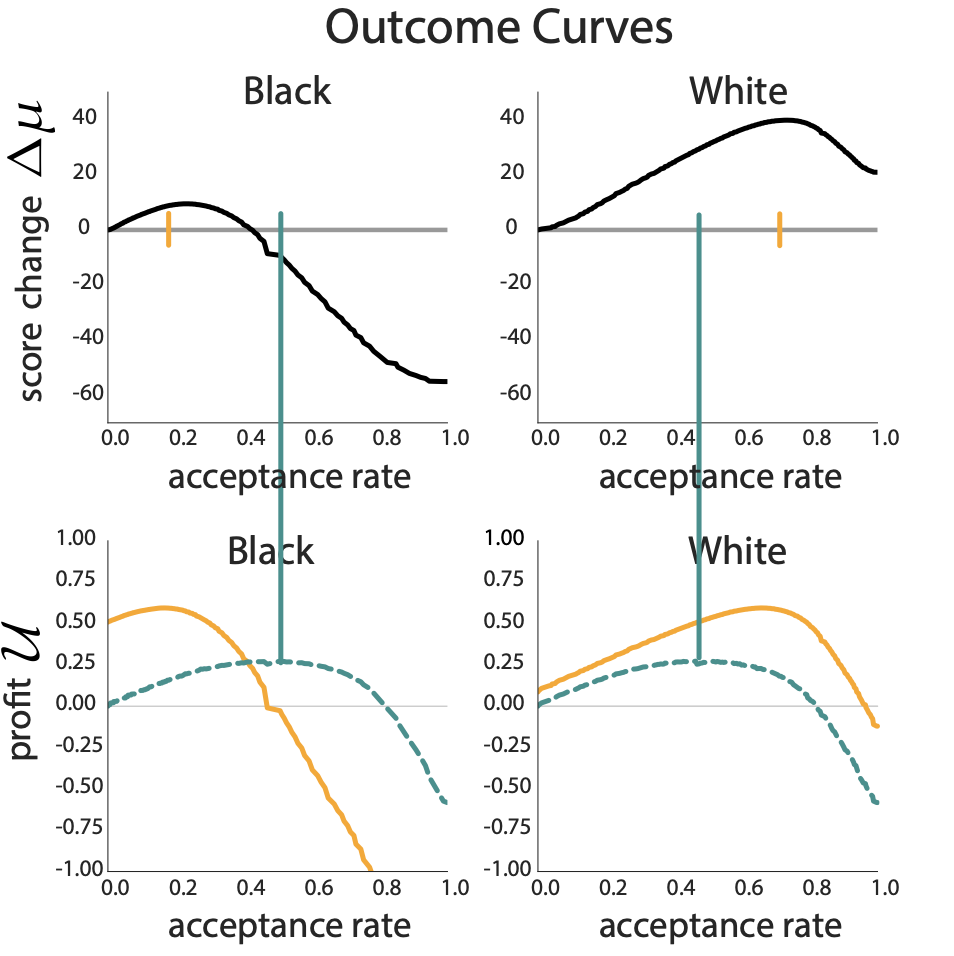
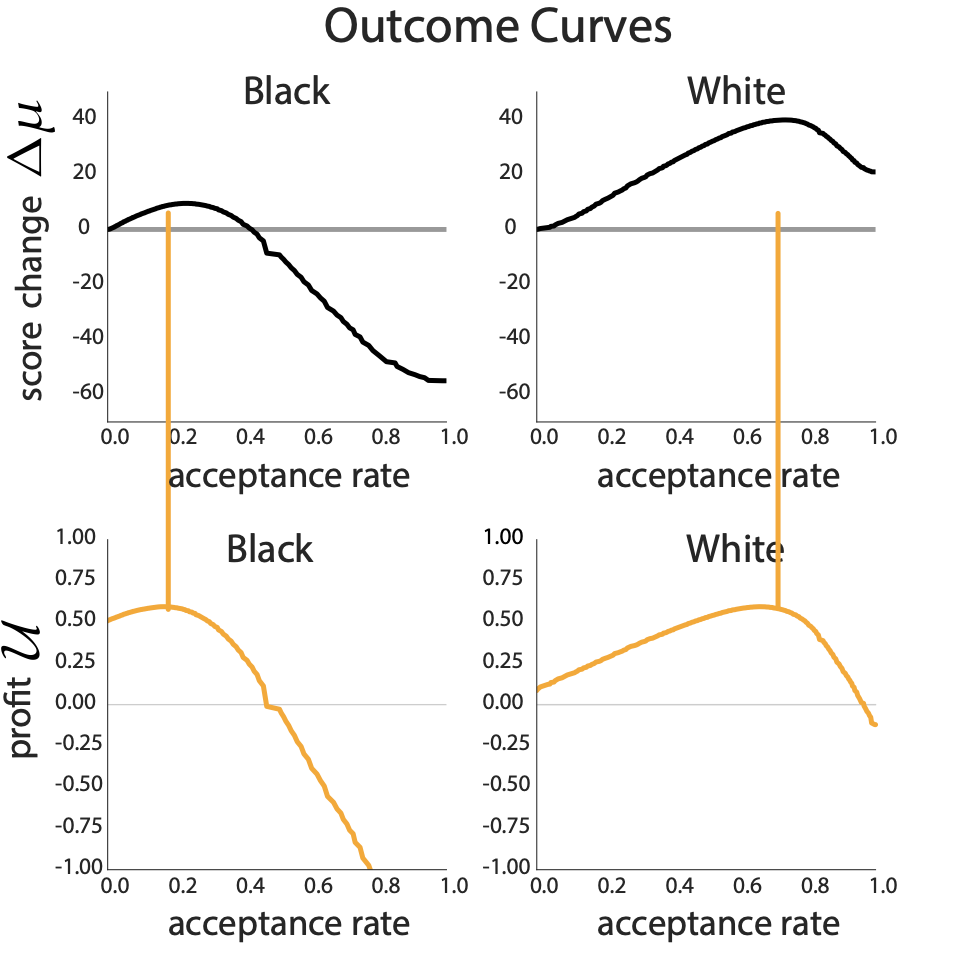


Why the large difference in delayed impact?
Maxima of outcome and utility curves under fairness criteria are more misaligned in the minority black group
Discussion
Future Work
- Outcome curves provide a way to deviate from maximum utility while improving outcomes
- Need for domain-specific models of delayed impact
- Context-sensitive nature of fairness in machine learning
- Measuring and modeling outcomes directly
- Practical tradeoffs of using machine learning for human-centered policies
- Long term dynamics of the distributional outcomes of algorithmic decisions [Hu and Chen 2018; Hashimoto et al. 2018; Mouzannar et al. 2019]
Thank you!
Details in full paper:
https://arxiv.org/abs/1803.04383
Algorithmic decisions are everywhere

- A score \(R\) is a scalar random variable, e.g. credit scores 300-850
- A group has a distribution over scores:
- Scores correspond to success probabilities (e.g. likelihood of repaying a loan) if accepted
- Higher score implies higher probability of success

Score Distribution Within Protected Group
- Institution accepts individuals based on threshold \(T\), chosen to maximize expected utility:
- When there are multiple groups, thresholds can be group-dependent.
Classifiers are Thresholds


\(\mathbb{E}[\mathrm{utility}|T] = \mathbb{E}[\mathrm{reward~from~repayments}|T] - \mathbb{E}[\mathrm{loss~from~defaults}|T]\)
- Scores of accepted individuals change depending on their success.
- The average change in score of each group is the delayed impact:
Model Delayed Impact on Groups
\(R_\mathrm{new} = \begin{cases} R_\mathrm{old}+c_+ &\text{if repaid} \\ R_\mathrm{old}-c_- &\text{if defaulted} \end{cases}\)

\(\Delta \mu = \mathbb{E}[R_\mathrm{new}-R_\mathrm{old}]\)
Measurement Error Increases Potential for Improvement
Result 4
If scores are systematically underestimated in the protected group, then regime of relative improvement is widened


- 300,000+ TransUnion TransRisk scores from 2003
- Scores range from 300 to 850 and are meant to predict default risk
What we did
- Use empirical data labeled by race (“white” and “black”) to estimate group score distributions, repayment probabilities, and relative sizes
- Model the bank’s profit/loss ratio, e.g. +1:-4
- Model the delayed impact of repayment/default on credit score, e.g. +75/-150
- Compute “outcome curves” and delayed impact under different fairness criteria
Experiments on FICO Credit Scores