Preference and Participation Dynamics in Learning Systems
Sarah Dean, Cornell University
4th Annual Learning for Dynamics & Control Conference, June 2022
Large-scale automated systems
enabled by machine learning







\(\to\)
historical movie ratings
new movie rating




from actions impacting the world
Dynamics arise
from data impacting the policy
Outline

1. Preference dynamics
2. Participation dynamics







Preference Dynamics
\(u_t\)
\(y_t = g_t(x_t, u_t) \)
Interests may be impacted by recommended content
\(x_{t+1} = f_t(x_t, u_t)\)
expressed preferences
recommended content
recommender policy





Preference Dynamics
\(u_t\)
\(y_t = \langle x_t, u_t\rangle + w_t \)
Interests may be impacted by recommended content
\(x_{t+1} = f_t(x_t, u_t)\)
expressed preferences
recommended content
recommender policy





underlies factorization-based methods
Preference Dynamics
\(u_t\)
\(y_t = \langle x_t, u_t\rangle + w_t \)
expressed preferences
recommended content
recommender policy





underlies factorization-based methods
A model inspired by biased assimilation updates proportional to affinity
\(x_{t+1} \propto x_t + \eta_t\langle x_t, u_t\rangle u_t\)
Preference Dynamics
items \(u_t\in\mathcal U\subseteq \mathcal S^{d-1}\)
\(y_t = \langle x_t, u_t\rangle + w_t \)
A model inspired by biased assimilation updates proportional to affinity
\(x_{t+1} \propto x_t + \eta_t\langle x_t, u_t\rangle u_t\)
preferences \(x\in\mathcal S^{d-1}\)




Proposed by Hązła et al. (2019) as model of opinion dynamics
Preference Dynamics
\(y_t = \langle x_t, u_t\rangle + w_t \)
A model inspired by biased assimilation updates proportional to affinity
\(x_{t+1} \propto x_t + \eta_t\langle x_t, u_t\rangle u_t\)
Non-personalized exposure leads to polarization (Hązła et al. 2019; Gaitonde et al. 2021)
Preference Dynamics
\(y_t = \langle x_t, u_t\rangle + w_t \)
A model inspired by biased assimilation updates proportional to affinity
\(x_{t+1} \propto x_t + \eta_t\langle x_t, u_t\rangle u_t\)
Personalized fixed recommendation \(u_t=u\)
$$ x_t = \alpha_t x_0 + \beta_t u$$
positive and decreasing
increasing magnitude, same sign as \(\langle x_0, u\rangle\)
Affinity Maximization
regret of fixed strategy
Result: As long as \(|\langle x_0, u\rangle| > c\) and noise is \(\sigma^2\) sub-Gaussian, $$R(T)= \sum_{t=0}^{T-1} 1 - \langle x_t, u_t \rangle \leq C_\eta(1/c^2 - 1) + \sigma^2\log T/c^2$$
Alg: Explore-then-Commit
- For \(t=0,\dots,\sigma^2 \log T/c^2\):
- recommend \(u_t=u\) and observe \(y_t\)
- For \(t=\sigma^2 \log T/c^2,\dots,T\):
- if \(\sum_t y_t < 0\): choose \(u_t=-u\)
- else: recommend \(u_t=u\)
maximum possible affinity
regret of explore-then-commit
Achieving high affinity is straightforward when \(\mathcal U\) contains "opposites"
Non-manipulation (Krueger et al., 2020) is an alternative goal
$$R(T) = \sum_{t=0}^{T-1} 1 - \langle x_0, x_t \rangle $$
Preference Stationarity
When \(x_0\notin \mathcal U\), use randomized strategy to select \(u_t\) i.i.d.
$$\mathbb E[x_{t+1}] \propto (I+\eta_t\mathbb E[uu^\top])x_t$$
Informal Result: Suppose \(x_0\) is the dominant eigenvector of \(\mathbb E[uu^\top]\) and step size \(\eta_t \) decays like \(\frac{1}{1+t}\). Then
$$R(T) \lesssim \log T $$
Proof sketch:
$$\langle x_0 ,x_t\rangle = \frac{x_0^\top (I+u_{t-1}u_{t-1}^\top)\dots(I+u_{0}u_{0}^\top)x_0}{\|(I+u_{t-1}u_{t-1}^\top)\dots(I+u_{0}u_{0}^\top) x_0\|_2}$$
Using concentration for matrix products (Huang et al., 2021),
$$1-\langle x_0 ,x_t\rangle^2 \lesssim \frac{1}{t}$$
Mode Collapse
Rather than polarization....
...preferences may "collapse"
but this can be avoided using randomization
Necessary to have \(x_0\in\text{span}(\mathcal U)\) for
- estimating initial preference from observations
- designing stationary randomization
Observation function \(F(x_0; u_{0:T}) = y_{0:T}\) where \(y_t = \langle x_t, u_t\rangle\).
Result: \(F:\mathcal S^{d-1}\to \R^T\) is locally invertible if and only if \(u_{0:T}\) span \(\mathbb R^d\).
Randomization Design
Preference Estimation
find \(q\) such that \(q\geq 0\), \(U\mathrm{diag}(U^\top x_0) q = x_0\),
\(I-U\mathrm{diag}(q)U^\top\succeq 0\)
Result: \(x_0\) is dominant eigenvector if randomization is proportional to \(q\).
Result: Problem is feasible if and only if \(x_0\) is in the span of \(\tilde \mathcal U = \{\mathrm{sign}(u^\top x_0)\cdot u\mid u\in \mathcal U\}\)
Open questions:
- SysID for biased assimilation dynamics
- Incorporate other phenomena (e.g. satiation, inconsistencies)
Preference Dynamics Summary



Key points:
- Preferences with biased assimilation
- High ratings vs. stationary preferences
- Mode collapse rather than polarization



Outline
1. Preference dynamics
2. Participation dynamics






Does social media have the ability to manipulate us, or merely to segment and target?
For single learner, leads to representation disparity (Hashimoto et al., 2018; Zhang et al., 2019)

Choose to participate depending on accuracy (e.g. music recommendation)
Participation Dynamics
Self-reinforcing feedback loop when learners retrain
Sub-populations \(i\in[1,n]\)
Participation Dynamics
Learners \(j\in[1,m]\)
- parameters \(\Theta = (\theta_1,\dots,\theta_m)\)
- each learner \(j\) reduces observed (average) risk
- participation \(\alpha\in\mathbb R^{n\times m}\)
- each sub-pop \(i\) favors learners with lower risk
\(\alpha^{t+1} = \nu(\alpha^t, \Theta^t)\)
\(\Theta^{t+1} = \mu(\alpha^{t+1}, \Theta^t)\)
evolve according to risks \(\mathcal R_i (\theta_j)\)
"risk minimizing in the limit"
strongly convex




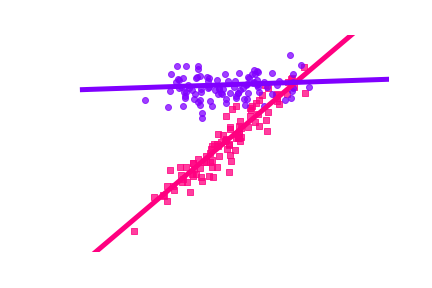
Example: linear regression with
- sub-populations and
- learners 1 and 2
2
1
Result: An equilibrium \((\alpha^{eq}, \Theta^{eq})\) must have \(\Theta^{eq}=\arg\min \mathcal R(\alpha^{eq},\Theta)\) and is asymptotically stable if and only if
- \(\alpha^{eq}\) corresponds to split market
- and \(\mathcal R_i(\theta_{\gamma(i)})< \mathcal R_i(\theta_j)~~\forall~~i,j\)
Definition: The total risk is \(\mathcal R(\alpha,\Theta) = \sum_{i=1}^n \sum_{j=1}^m \alpha_{ij} \mathcal R_i(\theta_j)\)
Proof sketch: asympototically stable equilibria correspond to the isolated local minima of \(\mathcal R(\alpha,\Theta)\)
Definition: In a split market, each sub-pop \(i\) allocates all participation to a single learner \(\gamma(i)\)
Participation Equilibria
- ✅ Stable equilibria (locally) maximize social welfare
- ❌ Generally NP hard to find global max by analogy to clustering (Aloise et al., 2009)
- ❌ Utilitarian welfare does not guarantee low worst-case risk
- ✅ Increasing the number of learners decreases risk and increases social welfare
Utilitarian social welfare is inversely related to total risk
A notion of fairness is the worst-case risk over sub-pops
Welfare and Fairness Implications






Participation Dynamics Summary
Open questions:
- Finite sample effects
- Alternative participation dynamics
- Alternative learning dynamics (e.g. DRO or competitive)
Key points:
- Myopic risk reduction (participation and learning)
- Segregated equilibria with locally maximized social welfare
- Importance of multiple learners



Conclusion






Study dynamics to what end?
- diagnostics
- algorithm design
- safety verification
How to bridge the social and the technical? (Gilbert et al., 2022)
- Preference Dynamics Under Personalized Recommendations (https://arxiv.org/abs/2205.13026) with Jamie Morgenstern
- Multi-learner risk reduction under endogenous participation dynamics (https://arxiv.org/abs/2206.02667) with Mihaela Curmei, Lillian J. Ratliff, Jamie Morgenstern, Maryam Fazel
References
- Aloise, Deshpande, Hansen, Popat, 2009. NP-hardness of Euclidean sum-of-squares clustering. Machine learning.
- Gaitonde, Kleinberg, Tardos, 2021. Polarization in geometric opinion dynamics. EC.
- Gilbert, Dean, Lambert, Zick, Snoswell, 2022. Reward Reports for Reinforcement Learning. arXiv:2204.10817.
- Hashimoto, Srivastava, Namkoong, Liang, 2018. Fairness without demographics in repeated loss minimization. ICML.
- Hązła, Jin, Mossel, Ramnarayan, 2019. A geometric model of opinion polarization. arXiv:1910.05274.
- Huang, Niles-Weed, Ward, 2021. Streaming k-PCA: Efficient guarantees for Oja’s algorithm, beyond rank-one updates. COLT.
-
Krueger, Maharaj, Leike, 2020. Hidden incentives for auto-induced distributional shift. arXiv:2009.09153.
- Zhang, Khaliligarekani, Tekin, Liu, 2019. Group retention when using machine learning in sequential decision making: the interplay between user dynamics and fairness. NeurIPS.
Thanks! Questions?



