Guaranteeing Safety of Learned Perception Modules via Measurement-Robust Control Barrier Functions
Sarah Dean\(^1\) Andrew J. Taylor\(^2\) Ryan K. Cosner\(^2\)
Benjamin Recht\(^1\) Aaron D. Ames\(^2\)
\(^1\)UC Berkeley \(^2\)Caltech





Motivation: Sensing
Robotic systems use increasingly complex sensors



Motivation: Safety
Complex calibration problems—opportunities for measurement model error
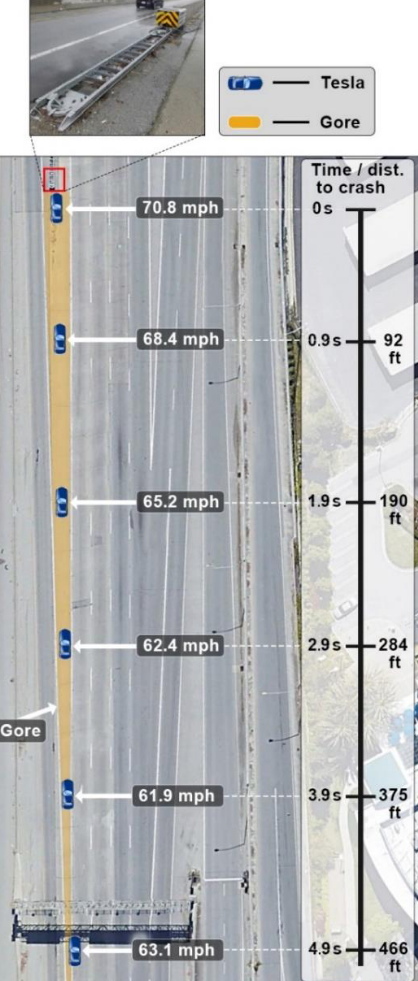
Motivation: Safety
Complex calibration procedures—opportunities for measurement model error

How do we ensure that complex and data-driven sensing can be safe and effective for controlling robotic systems?
Problem setting
Nonlinear control affine dynamics: \(\dot{\mathbf x} = \mathbf f(\mathbf x)+\mathbf g(\mathbf x)\mathbf u\)
System observed by \(\mathbf p(\mathbf x) = \mathbf y\), state estimated by \(\widehat{ \mathbf q}(\mathbf y) = \widehat{\mathbf x}\)
Subset of state space:
\(\mathcal C = \{\mathbf x \mid h(\mathbf x) \geq 0\}\)
Safety defined as invariance of \(\mathcal C\)



System observed by \(\mathbf p(\mathbf x) = \mathbf y\), state estimated by \(\widehat{ \mathbf q}(\mathbf y) = \widehat{\mathbf x}\)
\(\widehat{\mathbf q}\)

Preliminaries: Safety via CBF
The function \(h\) is a control barrier function if for some \(\alpha\in\mathcal K_\infty^e\)
This condition ensures the existence of \(\mathbf u\) such that
\(\frac{\partial h}{\partial \mathbf x}( \mathbf x) \dot{ \mathbf x} \geq -\alpha(h(\mathbf x))\)
\(\sup\limits_{\mathbf u\in\mathbb{R}^m} \frac{\partial h}{\partial \mathbf x}( \mathbf x) (\mathbf f( \mathbf x) + \mathbf g(\mathbf x)\mathbf u) \geq -\alpha(h(\mathbf x))\)

If \(\mathbf u\) chosen such that \(\dot{h}(\mathbf x, \mathbf u) \geq -\alpha( h(\mathbf x))\) then \(h(\mathbf x)\) remains nonnegative, so the safe set \(\mathcal C\) is invariant
\(\dot h( \mathbf x, \mathbf u) \geq -\alpha(h(\mathbf x))\)
(Ames et al. 2014, 2017)
Preliminaries: Safety via CBF
If \(\mathbf u\) chosen such that \(\dot{h}(\mathbf x, \mathbf u) \geq -\alpha( h(\mathbf x))\) then \(h(\mathbf x)\) remains nonnegative, so the safe set \(\mathcal C\) is invariant
The set of inputs which ensure safety:
\(K_\mathrm{cbf}(\mathbf x) = \{\mathbf u\mid \frac{\partial h}{\partial \mathbf x}( \mathbf x) \mathbf f( \mathbf x) + \frac{\partial h}{\partial \mathbf x}( \mathbf x)\mathbf g(\mathbf x)\mathbf u \geq -\alpha(h(\mathbf x))\}\)
To filter a given controller \(\mathbf k_d({\mathbf x})\) via convex optimization:
\(\argmin\limits_{\mathbf u \in \mathbb{R}^m} \| \mathbf u - \mathbf k_d({\mathbf x}) \|\)
\(~~~~~~\text{s.t.} ~~L_{\mathbf f}h( \mathbf x) + L_{\mathbf g}h(\mathbf x)\mathbf u \geq -\alpha(h(\mathbf x))\)
Measurement Model Error
Estimated state reconstructed by approximate inverse
\(\widehat{\mathbf x} = \widehat{\mathbf q}(\mathbf y)=\mathbf x + (\widehat{\mathbf q}(\mathbf y) - {\mathbf q}(\mathbf y))=\mathbf x + {\mathbf e}(\mathbf y) \)
Our setting has imperfect state observation
Considering all \(\mathbf x\) in uncertainty set:
\(\min\limits_{\mathbf x\in \mathcal X(\mathbf y)} L_{\mathbf f} h(\mathbf x) + L_{\mathbf g}h(\mathbf x) \mathbf u + \alpha(h(\mathbf x)) \geq 0\)
\(\min\limits_{\|\mathbf e\|\leq \epsilon(\mathbf y)} L_{\mathbf f} h(\widehat{\mathbf x}-\mathbf e) + L_{\mathbf g}h(\widehat{\mathbf x}-\mathbf e) \mathbf u + \alpha(h(\widehat{\mathbf x}-\mathbf e)) \geq 0\)

(Clark 2020, Nilsson 2020)
Measurement-Robust CBF
We define the set of inputs which ensure robust safety:
\(K_\mathrm{mr}(\mathbf y) = \{\mathbf u\mid L_{\mathbf f}h( \widehat{\mathbf x}) + L_{\mathbf g}h(\widehat{\mathbf x})\mathbf u - (a(\mathbf y) + b(\mathbf y)\|\mathbf u\|) \geq -\alpha(h(\widehat{\mathbf x}))\}\)
for given \(a, b~:~\mathbb{R}^k\to\mathbb{R}_+\).
Main Result: As long as
- perception errors are bounded by \(\epsilon(\mathbf y)\)
- and \(L_{\mathbf f}h\), \(L_{\mathbf g}h\), and \(\alpha\circ h\) are Lipschitz,
then by setting \(a(\mathbf y) = (\mathcal L_{L_{\mathbf f}h}+\mathcal L_{\alpha \circ h})\epsilon(\mathbf y)\) and \(b(\mathbf y) =\mathcal L_{L_{\mathbf g}h} \epsilon(\mathbf y)\),
any controller contained in \(K_\mathrm{mr}(\mathbf y)\) renders the system safe.
Feasibility of MR-CBF
The MR-CBF optimization problem (SOCP)
is feasible as long as
\(\epsilon(\mathbf y) \leq \max \Big( \frac{\|L_{\mathbf g}h(\widehat{\mathbf x})\|}{\mathcal L_{L_{\mathbf g}h} },\frac{L_{\mathbf f}h( \widehat{\mathbf x}) +\alpha(h(\widehat{\mathbf x}))}{\mathcal L_{L_{\mathbf f}h}+\mathcal L_{\alpha \circ h}}\Big)\)

which can be achieved from data
\(\argmin\limits_{\mathbf u \in \mathbb{R}^m} \| \mathbf u - \mathbf k_d(\widehat{\mathbf x}) \|\)
\(~~~~~~~~\text{s.t.}~~L_{\mathbf f}h( \widehat{\mathbf x}) + L_{\mathbf g}h(\widehat{\mathbf x})\mathbf u\)
\(- ((\mathcal L_{L_{\mathbf f}h}+\mathcal L_{\alpha \circ h})\epsilon(\mathbf y) + \mathcal L_{L_{\mathbf g}h} \epsilon(\mathbf y)\|\mathbf u\|) \geq -\alpha(h(\widehat{\mathbf x}))\)
Simulation Setting

Segway robot constrained to planar motion
Safety defined by pitch angle and rate
\(|\dot{\theta}_y +10(\theta_y-\theta_y^\mathrm{eq}) |\leq 4\)

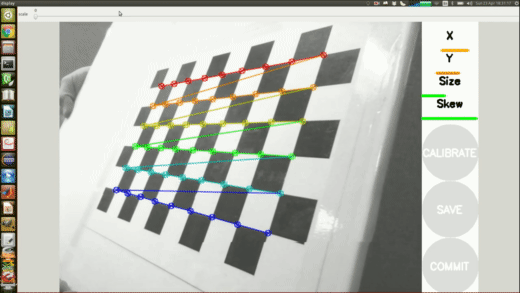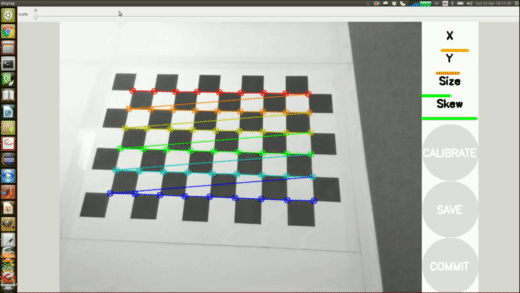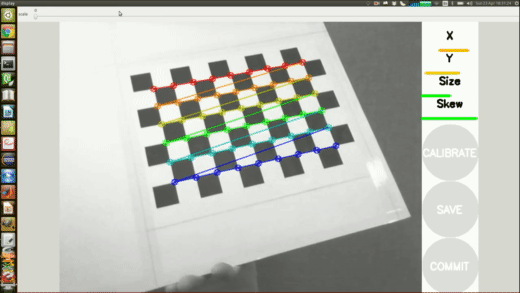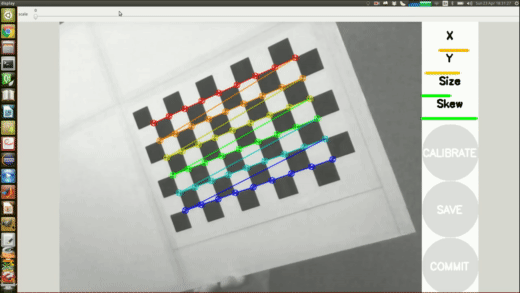
Pitch angle \(\theta_y\) and position \(r\) measured only by camera
Learned Perception Module
Training data collected from grid of \(\theta_y\) and \(r\) (\(N=800\))

Model mapping image to \(\theta_y,r\) trained using sklearn kernel ridge regression with radial basis functions

Simulated Trajectories
Filtered PD control from 15 kHz camera feed
CBF filter does not ensure safety, MR-OP filter does
Conclusion
- MR-CBF ensures robust safety
- MR-CBF can be used as a safety filter via SOCP
- Depends on system continuity and bounded perception errors
For details, see our paper at https://arxiv.org/abs/2010.16001





Guaranteeing Safety of Learned Perception Modules via Measurement-Robust Control Barrier Functions
Sarah Dean Andrew J. Taylor Ryan K. Cosner Benjamin Recht Aaron D. Ames
References
-
Ames, Aaron D., Jessy W. Grizzle, and Paulo Tabuada. "Control barrier function based quadratic programs with application to adaptive cruise control." IEEE CDC, 2014.
-
Ames, Aaron D., et al. "Control barrier function based quadratic programs for safety critical systems." IEEE TAC, 2016.
-
Nilsson, Petter, and Aaron D. Ames. "Lyapunov-like conditions for tight exit probability bounds through comparison theorems for sdes." IEEE ACC, 2020.
-
Clark, Andrew. "Control barrier functions for complete and incomplete information stochastic systems." IEEE ACC, 2019.