Certainty Equivalent Perception-Based Control

Sarah Dean and Benjamin Recht

UC Berkeley

L4DC, 8 June 2021

Motivation

Machine learning is a promising avenue for incorporating rich sensing modalities

Can we make strong guarantees in these settings?

backup slide about EKF/modelling vs. end-to-end

Perception-based optimal control

\(\displaystyle \min_{\pi\in\Pi} ~~\mathrm{cost}(x_0,u_0,x_1,\dots)\)

\(~~~\mathrm{s.t.}~~ u_t = \pi_t(z_{0:t})\)

\(~~~~~~~~~~x_{t+1} = \mathrm{dynamics}_t(x_t,u_t)\)

\(~~~~~~~~~~z_t = \mathrm{observation}_t(Cx_t)~\)

observation

\(\mathrm{dynamics~\&}\)\(\mathrm{observation}\)

\(\pi\)

\(z_t\)

\(u_t\)

\(x_t\)

output

\(y_t=Cx_t\)

Observation-feedback optimal control problem

Perception-based optimal control

\(\displaystyle \min_{\pi\in\Pi} ~~\mathrm{cost}(\widehat x_0,u_0,\widehat x_1,\dots)\)

\(~~~\mathrm{s.t.}~~ u_t = \pi_t(\widehat x_{0:t})\)

\(~~~~~~~~~~\widehat x_{t+1} = \mathrm{dynamics}_t(\widehat x_t,u_t)\)

\(~~~~~~~~~~\widehat x_t =\mathrm{EKF}(z_{0:t})~\)

\(\mathrm{dynamics,}\)\(\mathrm{obs, EKF}\)

\(\pi\)

\(\widehat x_t\)

\(u_t\)

\(x_t\)

Classic approach: physical models and filtering

Perception-based optimal control

\(\displaystyle \min_{\pi\in\Pi} ~~\mathrm{cost}(x_0,u_0,x_1,\dots)\)

\(~~~\mathrm{s.t.}~~ u_t = \widehat \pi_t(z_{0:t})\)

\(\mathrm{dynamics~\&}\)\(\mathrm{observation}\)

\(\widehat \pi\)

\(z_t\)

\(u_t\)

\(x_t\)

End-to-end approach: learn everything from data

Perception-based optimal control

\(\displaystyle \min_{\pi\in\Pi} ~~\mathrm{cost}(x_0,u_0,x_1,\dots)\)

\(~~~\mathrm{s.t.}~~ u_t = \pi_t(y_{0:t})\)

\(~~~~~~~~~~x_{t+1} = \mathrm{dynamics}_t(x_t,u_t)\)

\(~~~~~~~~~~y_t = \mathrm{perception}(\mathrm{observation}_t(Cx_t))~\)

\(\mathrm{dynamics~\&}\)\(\mathrm{obs,~percept.}\)

\(\pi\)

\(y_t\)

\(u_t\)

\(x_t\)

Our focus: learned perception map

Problem setting

\(\text{s.t.}~~x_{t+1} = {A }x_t+ {B} u_t\)

Robust reference tracking with linear dynamics and nonlinear partial observation

\(z_{t} =g(Cx_t)\)

\(\displaystyle\mathrm{cost} = \sup_{\substack{t\geq 0\\\mathbf x^\mathrm{ref} \in \mathcal R\\ \|x_0\|\leq \sigma_0}}\left\|\begin{bmatrix} Q (x_t - x_t^\mathrm{ref})\\ Ru_t \end{bmatrix}\right\|_\infty\)

Assumption 1:

\(A,B,C\) and \(Q,R\) are known and well posed

Assumption 2:

\(\mathcal R\) encodes a bounded radius of operation

Assumption 3:

Invertible \(h(g(y)) = y\) and \(g,h\) continuous

\(\displaystyle \min_{\pi}\)

\(\displaystyle \min_{\mathbf K}\)

\(u_{t} =\pi(z_{0:t}, x^\mathrm{ref}_{0:t})\)

Assumption 4:

Noisy training signal \(y^\mathrm{train}_{t} =Cx_t+\eta_t\)

\(y_t = h(z_t) = Cx_t\)

\(u_t = \mathbf K(y_{0:t}, x^\mathrm{ref}_{0:t})\)

Certainty equivalent controller \(\widehat \pi(z_{0:t}, x^\mathrm{ref}_{0:t}) = \mathbf K_\star (\widehat h(z_{0:t}), x^\mathrm{ref}_{0:t}) \)
where \(\widehat h\) is learned from data

Transform to linear output feedback problem with \(h\)

\(\pi_\star(z_{0:t}, x^\mathrm{ref}_{0:t}) = \mathbf K_\star (h(z_{0:t}), x^\mathrm{ref}_{0:t}) \)

Assumption 3 applies when:

each position results in a unique image
small changes to position result in small changes to image

\(\mathrm{dynamics~\&}\)\(\mathrm{observation}\)

\(\mathbf K\)

\(z_t\)

\(u_t\)

\(x_t\)

\(y_t\)

\(\mathrm{linear}\)
\(\mathrm{dynamics}\)

\(\mathbf K\)

\(y_t\)

\(u_t\)

\(x_t\)

\(h\)

Main Result (Informal)

\(\mathrm{cost}(\widehat\pi) - \mathrm{cost}(\pi_\star) \lesssim\) \( L \) \(r_\star\) \(s_\star\) \( \left(\frac{\sigma}{T}\right)\)\({}^{\frac{1}{p+4}}\)

depending on the continuity of \(g\) and \(h\), the radius of operation, the sensitivity of the optimal controller, the sensor noise, amount of data, and the dimension of the output

Ingredients

The certainty-equivalent controller has bounded suboptimality w.h.p.

1. Uniform convergence of \(\widehat h\)

sampling scheme

2. Closed-loop performance

Related Work

Classic controls: Weiner system identification

SISO (Greblicki et al. 97) or restrictive assumptions (Westwick & Verhaegen 96; Janczak et al. 07)
Focus on ID rather than control performance

Recent work:

Block MDP (Misra et al. 2020) and Rich LQR (Mhamedi et al. 2020) settings

Sample complexity has polynomial dependence
Finite state space or horizon sidestep stability concerns

Necessity of pointwise bounds

Example: 1D unstable linear system with arbitrary linear controller

\(x_{t+1} = a x_t + u_t\qquad u_t = \mathbf{K}(x^\mathrm{ref}_{0:t},\widehat h(z_{0:t}))\)

near perfect perception map: \(\widehat h(g(x)) = \begin{cases} 0 & x = \bar x,~ |x|>r\\ x &\text{otherwise} \end{cases}\)

There exists a reference signal contained in \([-r,r]\) that causes the system to pass through \(\bar x\) and subsequently go unstable

\(\bar x\)

\(r\)

\(-r\)

\(t\)

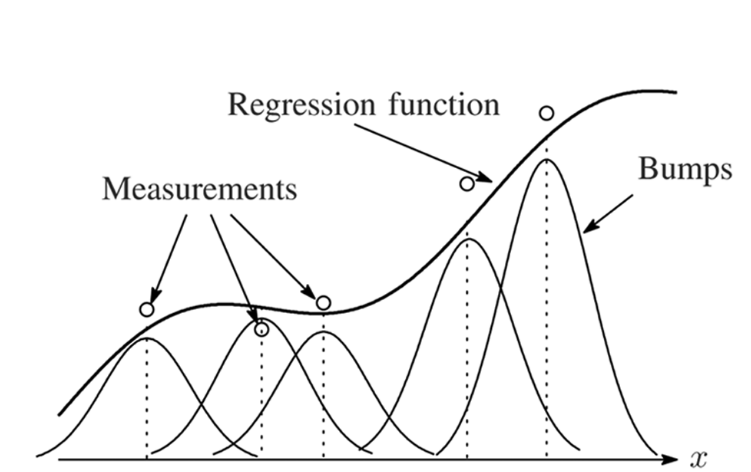
Nonparametric regression

Nadarya Watson Regression: from training data \(\{(z_t, y_t^\mathrm{train})\}_{t=0}^T\)

predictions are weighted averages,

\(\displaystyle \widehat h(z) = \sum_{t=0}^T \frac{k_\gamma(z_t, z)}{\sum_{\ell=0}^T k_\gamma(z_\ell, z)} y_t^\mathrm{train} \)

Theorem (uniform convergence): Suppose training data uniformly sampled from \( \{y\mid \|y\|_\infty\leq r\}\) and bandwidth \(\gamma \propto T^{\frac{1}{p+4}}\). Whenever the system state contained in \(\{x\mid\|Cx\|_\infty \leq r\}\), then w.h.p.

\(\|h(z) - \widehat h(z)\|_\infty \lesssim rL_g L_h \left(\frac{p^2\sigma_\eta^4}{T}\right)^{\frac{1}{p+4}}\)

bandwidth

Nonparametric regression

Nadarya Watson Regression: from training data \(\{(z_t, y_t^\mathrm{train})\}_{t=0}^T\)

\(\displaystyle \widehat h(z) = \sum_{t=0}^T \frac{k_\gamma(z_t, z)}{s_T(z)} y_t^\mathrm{train} \)

\(=\sum_{t=0}^T k_\gamma(z_t, z)\)

The kernel function has the form \(\kappa\left(\frac{\rho(z_t, z)}{\gamma}\right)\) for

\(\gamma\in\mathbb{R}_+\) bandwidth
metric \(\rho:\mathbb{R}^q\to \mathbb{R}_+\)
\(\kappa:\mathbb{R}_+\to[0,1]\) Lipschitz and bounded support

Sampling with linear control

Drive system to uniform samples \(y_\ell^\mathrm{ref}\) using training output \(y_t^\mathrm{train}\)

\(\mathbf K\)

\(y^\mathrm{ref}_\ell \sim \mathrm{Unif}\{|y|\leq r\}\)

\(\mathrm{dynamics~\&}\)\(\mathrm{observation}\)

\(z_t\)

\(u_t\)

\(x_t\)

\(y_t^\mathrm{train}\)

How to achieve uniform sampling?

Closed-loop guarantees

How does imperfect perception affect system evolution?

Define errors \(e_t = \widehat h(z_t) - h(z_t) = \widehat h(z_t) - Cx_t\)

\(\displaystyle u_t = \sum_{k=0}^t K_k^y \widehat h(z_{t-k}) + K_k^\mathrm{ref} x^\mathrm{ref}_{t-k}\)

\(\displaystyle x_{t+1}=Ax_t+Bu_t\)

\(\displaystyle u_t = \sum_{k=0}^t K_k^y Cx_{t-k} + K_k^y Ce_{t-k} + K_k^\mathrm{ref} x^\mathrm{ref}_{t-k}\)

\(x_t = \sum_{k=0}^t \Phi_{xe}(k) e_{t-k} + \Phi_{xr}(k) x^\mathrm{ref}_{t-k}\)

Linearly.

\(u_t = \sum_{k=0}^t \Phi_{ue}(k) e_{t-k} + \Phi_{ur}(k) x^\mathrm{ref}_{t-k}\)

Proposition: Suppose that perception errors are uniformly bounded by \(\varepsilon_h\) and let \(\mathbf \Phi\) be system response associated with \(\mathbf K_\star\). Then,

\(\mathrm{cost}(\widehat\pi) \leq \mathrm{cost}(\pi_\star) + \varepsilon_h ~\left\|\begin{bmatrix} Q\mathbf \Phi_{xe}\\ R\mathbf \Phi_{ue} \end{bmatrix}\right\|_{\mathcal L_1} \)

Main Result

\(\mathrm{cost}(\widehat\pi) - \mathrm{cost}(\pi_\star) \lesssim\) \(rL_g L_h \left(\frac{p^2\sigma_\eta^4}{T}\right)^{\frac{1}{p+4}}\) \(\left\|\begin{bmatrix} Q\mathbf \Phi_{xn}\\ R\mathbf \Phi_{un} \end{bmatrix}\right\|_{\mathcal L_1} \)

The certainty-equivalent controller has bounded suboptimality w.h.p.

Ingredients

1. Uniform convergence of \(\widehat h\)

bounded errors

2. Closed-loop performance

propagation of errors

Simulation Experiments

Simplified UAV model: 2D double integrator

\(x_{t+1} = \begin{bmatrix}1 & 0.1 & & \\ 0 & 1 & & \\ & & 1 & 0.1 \\ & & 0 & 1\end{bmatrix} x_t +\begin{bmatrix}0 & \\ 1 & \\ & 0 \\ & 1 \end{bmatrix} u_t \)

\(y_t = \begin{bmatrix} 1 & 0 & & \\ & & 1 & 0\end{bmatrix} x_t\)

\(z_t\) from CARLA simulator

Data-driven perception

Data collected with linear control and periodic reference signal:

Nadarya Watson (NW) with kernel \(k_\gamma(z, z_t) = \mathbf{1}\{\|z-z_t\|_2 \leq \gamma\}\)

Kernel Ridge Regression (KRR) with radial basis functions

Visual Odometry (VO) matches \(z\) to some \(z_t\) in database of labelled training images, uses homography between images to estimate pose

Simultaneous Localization and Mapping (SLAM) like VO with memory: adds new observations to database online, and initializes estimates based on previous timestep

Perception errors

classic nonparametric methods look similar

memoryless classic computer vision is similar, if noisier/wider

very different!

building obstructs view

Thanks for your attention!

Certainty-Equivalent Perception-Based Control
Sarah Dean and Benjamin Recht