User Dynamics in Machine Learning Systems
Sarah Dean, Cornell CS
Networks & Cognition Workshop, June 2023
Our digital world is increasingly algorithmically mediated









Motivation
and these algorithms are powered by machine learning

\(\to\)
historical movie ratings
new movie rating

Machine Learning Systems



from actions impacting the world
Dynamics arise
from data impacting the policy
Machine Learning Systems
- Preference Dynamics
- Implications: Personalization & Harm
- Retention Dynamics
Outline


How do we design reliable algorithms that account for user dynamics?
Setting: Preference Dynamics
\(a_t\)
\(y_t\)
Interests may be impacted by recommended content
preference state \(s_t\)
expressed preferences
recommended content
recommender policy





Setting: Preference Dynamics
\(a_t\)
\(y_t = \langle s_t, a_t\rangle + w_t \)
Interests may be impacted by recommended content
expressed preferences
recommended content
recommender policy





\(\approx\)
\(y_{ui} \approx s_u^\top a_i\)
underlies factorization-based methods
preference state \(s_t\)
Setting: Preference Dynamics
\(a_t\)
\(y_t = \langle s_t, a_t\rangle + w_t \)
Interests may be impacted by recommended content
expressed preferences
recommended content
recommender policy





underlies factorization-based methods
state \(s_t\) updates to \(s_{t+1}\)
Preference Dynamics
items \(a_t\in\mathcal A\subseteq \mathcal S^{d-1}\)
\(y_t = \langle s_t, a_t\rangle + w_t \)
\(s_{t+1} = f_t(s_t, a_t)\)
preferences \(s\in\mathcal S^{d-1}\)
Preference Dynamics
items \(a_t\in\mathcal A\subseteq \mathcal S^{d-1}\)
\(y_t = \langle s_t, a_t\rangle + w_t \)
\(s_{t+1} \propto s_t + \eta_t a_t\)
preferences \(s\in\mathcal S^{d-1}\)

Assimilation: interests may become more similar to recommended content
initial preference
resulting preference
Preference Dynamics
items \(a_t\in\mathcal A\subseteq \mathcal S^{d-1}\)
\(y_t = \langle s_t, a_t\rangle + w_t \)
Biased Assimilation: interest update is proportional to affinity
\(s_{t+1} \propto s_t + \eta_t\langle s_t, a_t\rangle a_t\)
preferences \(s\in\mathcal S^{d-1}\)


Proposed by Hązła et al. (2019) as model of opinion dynamics


initial preference
resulting preference
Prior Work
2. Biased assimilation
\(s_{t+1} \propto s_t + \eta_t\langle s_t, a_t\rangle a_t\)
When recommendations are made globally, the outcomes differ:
initial preference
resulting preference
1. Assimilation
\(s_{t+1} \propto s_t + \eta_t a_t\)
polarization (Hązła et al. 2019; Gaitonde et al. 2021)
homogenized preferences
Personalized Recommendations
Regardless of whether assimilation is biased,
Personalized fixed recommendation \(a_t=a\)
$$ s_t = \alpha_t s_0 + \beta_t a$$
positive and decreasing
increasing magnitude (same sign as \(\langle s_0, a\rangle\) if biased assimilation)
\(s_{t+1} \propto s_t + \eta_t\langle s_t, a_t\rangle a_t\)
\(s_{t+1} \propto s_t + \eta_t a_t\)
Personalized Recommendations
Regardless of whether assimilation is biased,
\(s_{t+1} \propto s_t + \eta_t\langle s_t, a_t\rangle a_t\)
\(s_{t+1} \propto s_t + \eta_t a_t\)
Implications [DM22]
-
It is not necessary to identify preferences to make high affinity recommendations
Personalized Recommendations
Regardless of whether assimilation is biased,
\(s_{t+1} \propto s_t + \eta_t\langle s_t, a_t\rangle a_t\)
\(s_{t+1} \propto s_t + \eta_t a_t\)
initial preference
resulting preference
Implications [DM22]
-
It is not necessary to identify preferences to make high affinity recommendations
-
Preferences "collapse" towards whatever users are often recommended
Personalized Recommendations
Regardless of whether assimilation is biased,
\(s_{t+1} \propto s_t + \eta_t\langle s_t, a_t\rangle a_t\)
\(s_{t+1} \propto s_t + \eta_t a_t\)
initial preference
resulting preference
Implications [DM22]
-
It is not necessary to identify preferences to make high affinity recommendations
-
Preferences "collapse" towards whatever users are often recommended
-
Non-manipulation (and other goals) can be achieved through randomization
Harmful Recommendations
Simple choice model: given a recommendation, a user
- Selects the recommendation with probability determined by affinity
- Otherwise, selects from among all content based on affinities
Preference dynamics lead to a new perspective on harm
Simple definition: harm caused by consumption of harmful content
♪
♫
𝅘𝅥
𝅗𝅥
𝅘𝅥𝅯
♫
𝅗𝅥
♫
𝅘𝅥𝅯
♪
♫
𝅘𝅥
𝅗𝅥
\(\mathbb P\{\mathrm{click}\}\)
Harmful Recommendations
Due to preference dynamics, there may be downstream harm, even when no harmful content is recommended
♪
♫
𝅘𝅥
𝅗𝅥
𝅘𝅥𝅯
♫
𝅗𝅥
Recommendation: ♫
♫
𝅘𝅥𝅯
♪
♫
𝅘𝅥
𝅗𝅥
Recommendation: 𝅘𝅥𝅯
♫
𝅘𝅥𝅯
♪
♫
𝅘𝅥
𝅗𝅥
\(\mathbb P\{\mathrm{click}\}\)
\(\mathbb P \{\mathrm{click}\}\)
Harmful Recommendations
Due to preference dynamics, there may be downstream harm, even when no harmful content is recommended
♪
♫
𝅘𝅥
𝅗𝅥
𝅘𝅥𝅯
♫
𝅗𝅥
Recommendation: ♫
♫
𝅘𝅥𝅯
♪
♫
𝅘𝅥
𝅗𝅥
Recommendation: 𝅘𝅥𝅯
♫
𝅘𝅥𝅯
♪
♫
𝅘𝅥
𝅗𝅥
\(\mathbb P\{\mathrm{click}\}\)
\(\mathbb P \{\mathrm{click}\}\)
Harmful Recommendations
Due to preference dynamics, there may be downstream harm, even when no harmful content is recommended
Recommendation: ♫
♫
𝅘𝅥𝅯
♪
♫
𝅘𝅥
𝅗𝅥
Recommendation: 𝅘𝅥𝅯
This motivates a new recommendation objective which takes into account the probability of future harm [CDEIKW23]
♫
𝅘𝅥𝅯
♪
♫
𝅘𝅥
𝅗𝅥
\(\mathbb P\{\mathrm{click}\}\)
\(\mathbb P \{\mathrm{click}\}\)
User Choice & Retention





Even if individual preferences are immutable, population level effects may be observed due to retention dynamics
♫
𝅘𝅥
𝅗𝅥
♫
𝅗𝅥
The dynamic of retention & specialization can lead to representation disparity (Hashimoto et al.) and segmentation [DCRMF23]


User Choice & Retention
Even if individual preferences are immutable, population level effects may be observed due to retention dynamics
𝅘𝅥
The dynamic of retention & specialization can lead to representation disparity (Hashimoto et al.) and segmentation [DCRMF23]



Example: linear regression with users and
2
1
User Choice & Retention
Even if individual preferences are immutable, population level effects may be observed due to retention dynamics
𝅘𝅥
The dynamic of retention & specialization can lead to representation disparity (Hashimoto et al.) and segmentation [DCRMF23]
Example: linear regression with users and
2
1
User Choice & Retention
Even if individual preferences are immutable, population level effects may be observed due to retention dynamics
The dynamic of retention & specialization can lead to representation disparity (Hashimoto et al.) and segmentation [DCRMF23]




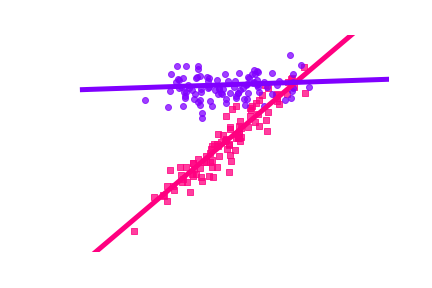
Example: linear regression with users and
- services 1 and 2
2
1
- Preference Dynamics
- Implications: Personalization & Harm
- Retention Dynamics
- Behavioral dynamics vs. user agency
- Network and social dynamics
- Beyond users: producer and market dynamics
Conclusion & Discussion









- Preference Dynamics Under Personalized Recommendations at EC22 (arxiv:2205.13026) with Jamie Morgenstern
- Harm Mitigation in Recommender Systems (in submission) with Jerry Chee, Sindhu Ernala, Stratis Ioannidis, Shankar Kalyanaraman, Udi Weinsberg
- Emergent segmentation from participation dynamics and multi-learner retraining (in submission, arxiv:2206.02667) with Mihaela Curmei, Lillian J. Ratliff, Jamie Morgenstern, Maryam Fazel
Other References
- Gaitonde, Kleinberg, Tardos, 2021. Polarization in geometric opinion dynamics. EC.
- Hązła, Jin, Mossel, Ramnarayan, 2019. A geometric model of opinion polarization. arXiv:1910.05274.
-
Hashimoto, Srivastava, Namkoong, Liang, 2018. Fairness Without Demographics in Repeated Loss Minimization. ICML.
Thanks! Questions?

References







