Towards
Markov Decision Processes and Best Responses in Epidemic Models
A framework based on stochastic optimal control and dynamic programming.
Gabriel Salcedo-Varela, David González-Sánchez,
Saúl Díaz-Infante Velasco,
saul.diazinfante@unison.mx,
November, 2023
Red Mexicana de Biología y Matemática
Data
- Modelling
Control
To fix ideas:
- TYLCV Disease
- is spread by the insect whitefly (Bemisia tabaci)
-
How to Manage TYLCV?
-
Replanting infected plants suffers random fluctuations due to is leading identification because a yellow plant is not necessarily infected.
- The protocol to manage infected plants suggests replanting neighbors. Then naturally, a farmer could randomly replant a healthy plant instead of a latent one.
- Thus strategies like fumigation with insecticide suffer random fluctuationsin their efficiency.
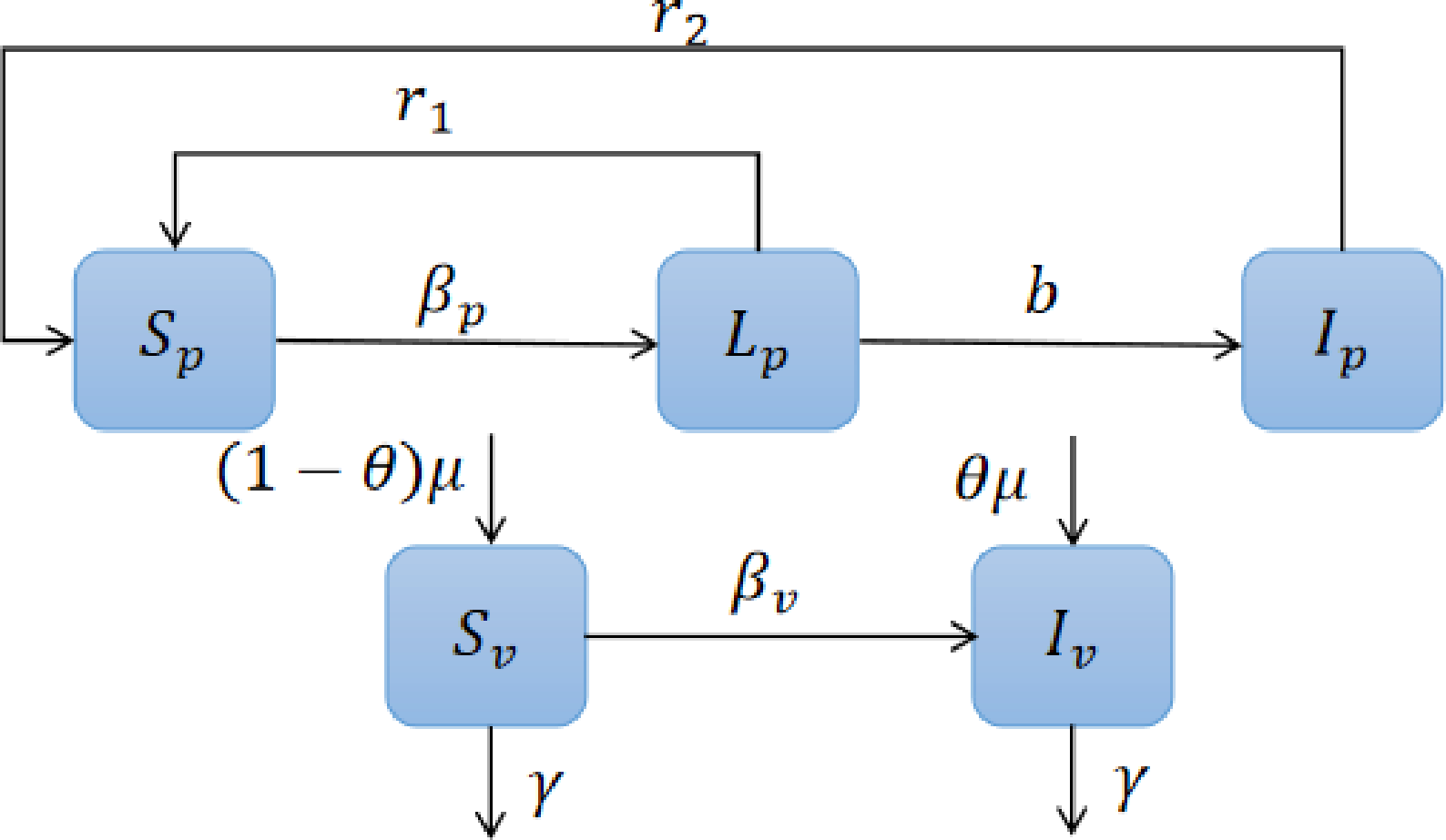
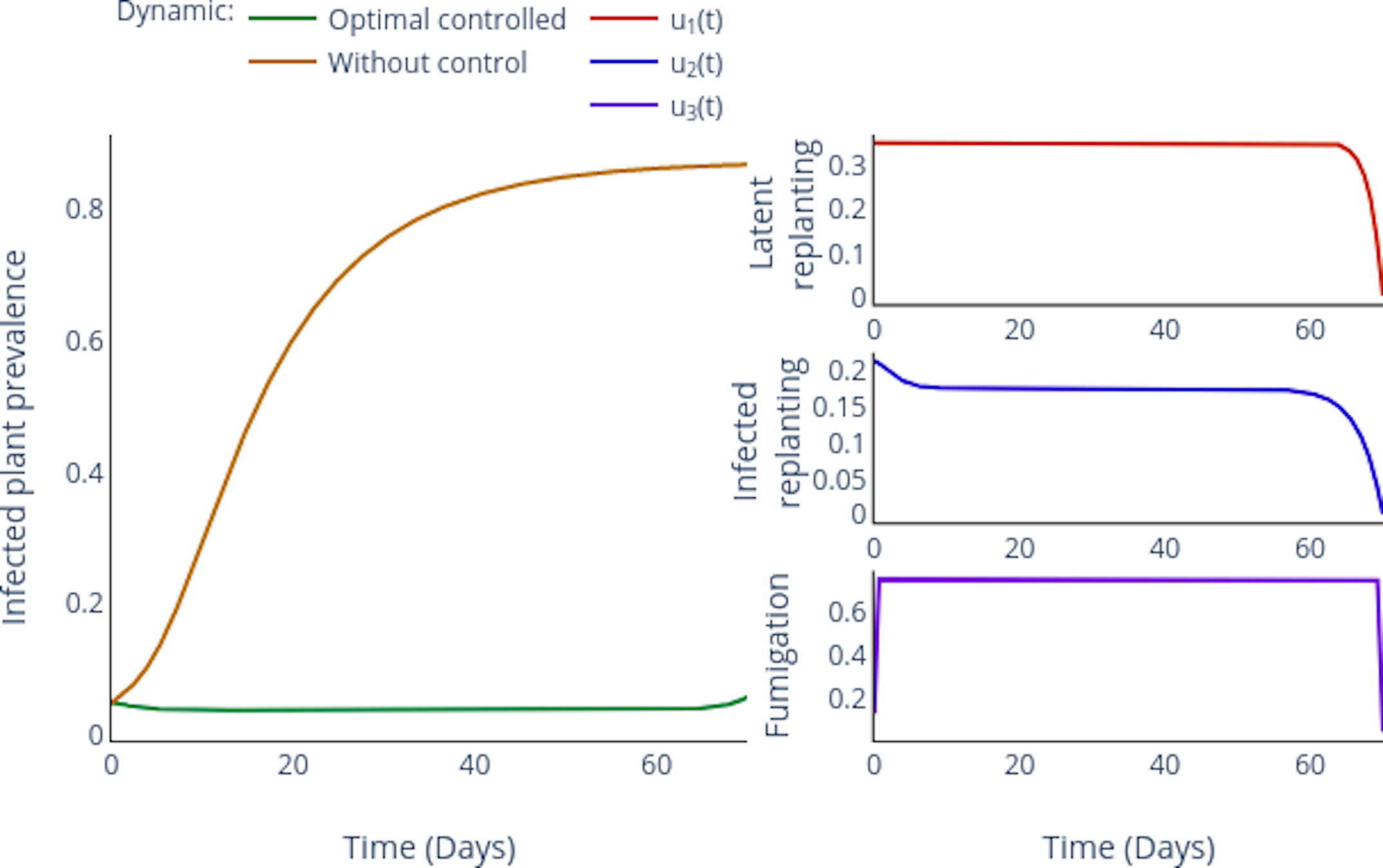
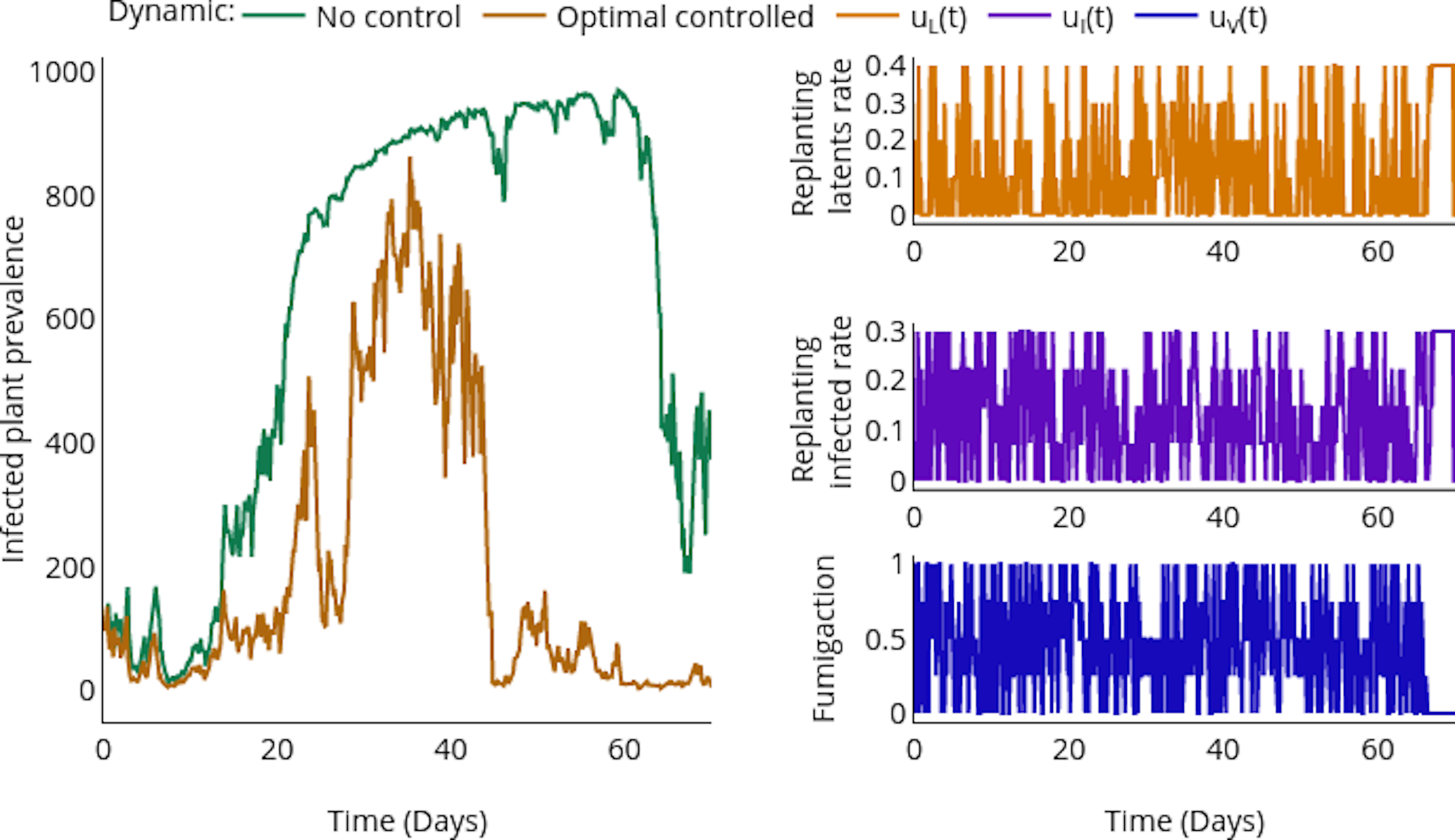
Controls
- Replanting
- Fumigation
\begin{aligned}
\dot{S_p} &=
-\beta_p S_p I_v +\textcolor{blue}{r_1}L_p + \textcolor{blue}{r_2} I_p,\\
\dot{L_p} &=
\beta_p S_p I_v -(b +\textcolor{blue}{r_1}) L_p,\\
\dot{I_p} &=
b L_p - \textcolor{blue}{r_2} I_p,\\
\dot{S_v} &=
-\beta_v S_v I_p - (\gamma +\textcolor{orange}{ \gamma_f}) S_v +(1-\theta)\mu,\\
\dot{I_v} &=
\beta_v S_v I_p -(\gamma+\textcolor{orange}{\gamma_f}) I_v +\theta\mu.
\end{aligned}
\begin{aligned}
& \min_{\bar{u}(\cdot)\in \mathcal{U}_{x_0}[t_0,T]}J(u)
\\
\text{Subject to} &
\\
\dot{S_p} &=
- \beta_p S_p I_v
+ \textcolor{blue}{(r_1 +u_1)} L_p
+ \textcolor{blue}{(r_2 + u_2)} I_p,
\\
\dot{L_p} &=
\beta_p S_p I_v -(b +
\textcolor{blue}{(r_1 + u_1))} L_p,
\\
\dot{I_p} &=
b L_p -
\textcolor{blue}{(r_2 + u_2)} I_p,
\\
\dot{S_v} &=
- \beta_v S_v I_p
- (\gamma+ \textcolor{orange}{(\gamma_f + u_3)} ) S_v
+ (1-\theta)\mu,
\\
\dot{I_v} &=
\beta_v S_v I_p
- (\gamma + \textcolor{orange}{(\gamma_f + u_3)}) I_v
+ \theta\mu,
\\
&S_p(0) = S_{p_0}, L_p(0) = L_{p_0}, I_p(0) = I_{p_0},
\\
&S_v(0) = S_{v_0}, I_v(0) = I_{v_0},
u_i(t) \in [0, u_i ^ {max}].
\end{aligned}
\begin{aligned}
J(u) &= \int_{0}^T \Big[A_1 I_p(t) + A_2 L_p(t) + A_3 I_v(t)
+ \sum^3_{i=1}c_i u_i(t)^2 \Big] dt,
\end{aligned}
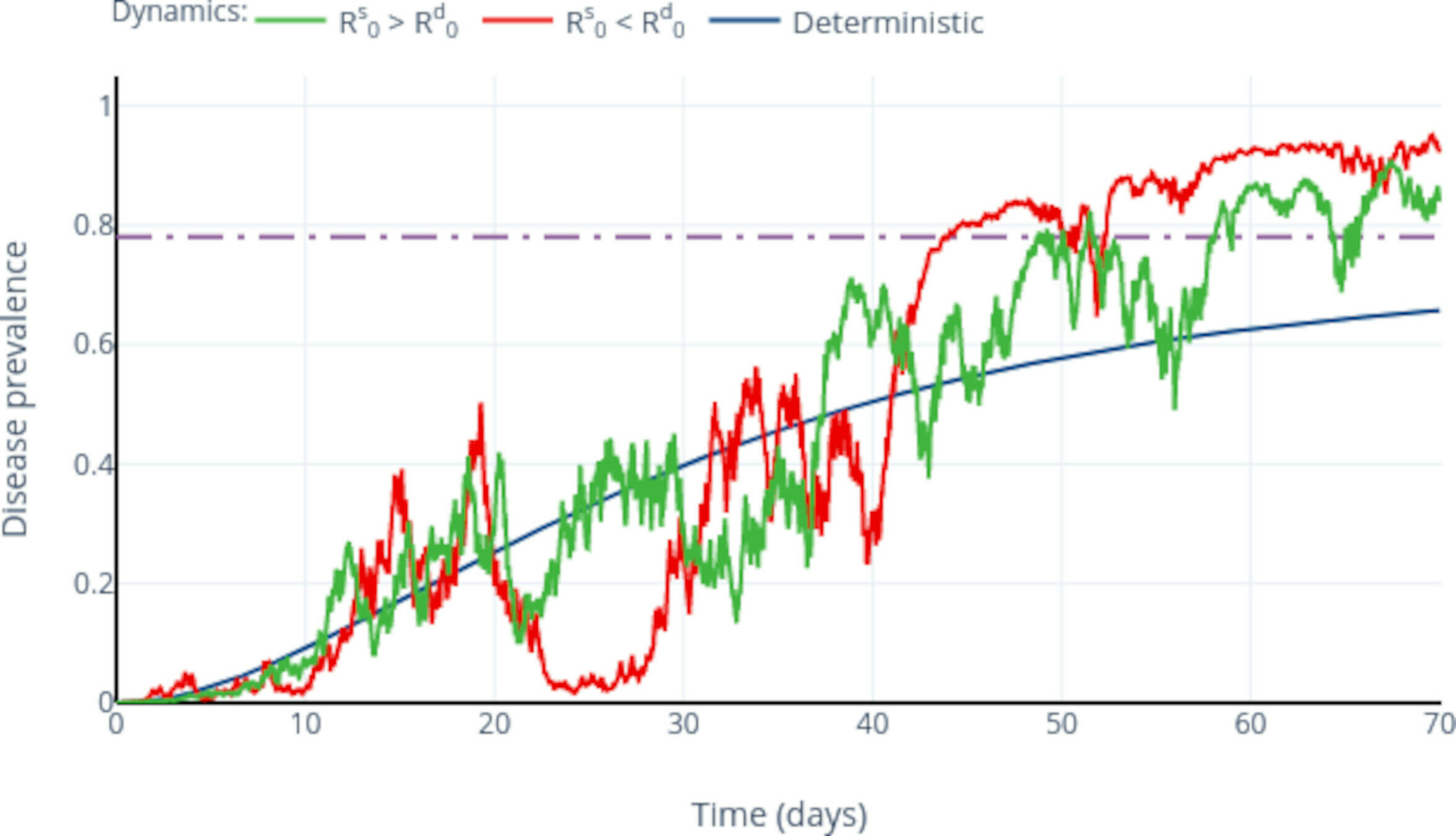
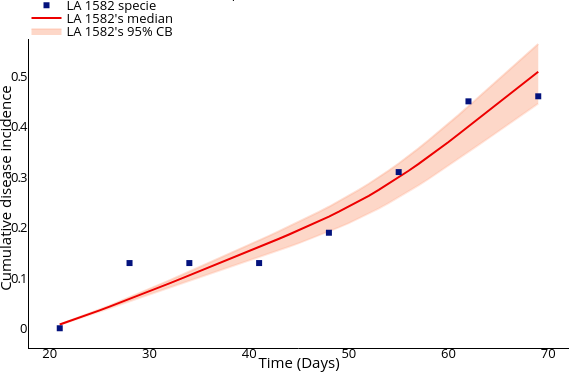
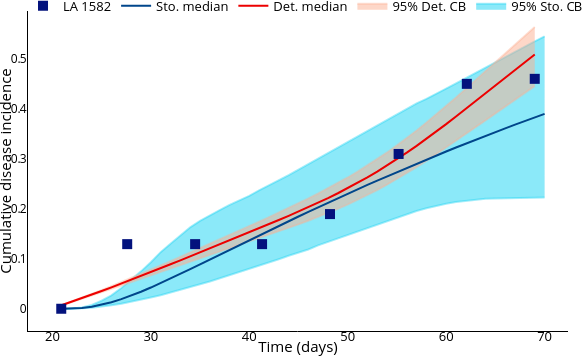
Enhancing parameter calibration through noise
\begin{aligned}
\frac{d}{dt}x(t) = f(t,x(t)) &
\rightsquigarrow dx(t) = f(t,x(t))dt + g(t,x(t))dB(t)
\\
\alpha &
\rightsquigarrow \alpha + P(x(t))\frac{dB(t)}{dt}
\end{aligned}
\begin{aligned}
\frac{dS_p}{dt} &=
-\beta_p S_p \frac{I_v}{N_v} + \textcolor{blue}{r_1} L_p
+ \textcolor{blue}{r_2} I_p,\\
\frac{dL_p}{dt} &=
\beta_p S_p \frac{I_v}{N_v}
- (b + \textcolor{blue}{r_1}) L_p,\\
\frac{dI_p}{dt} &=
b L_p - \textcolor{blue}{r_2} I_p,\\
\frac{dS_v}{dt} &=
-\beta_v S_v \frac{I_p}{N_p}
- (\gamma + \textcolor{orange}{\gamma_f}) S_v + (1-\theta)\mu,\\
\frac{dI_v}{dt} &=
\beta_v S_v \frac{I_p}{N_p}
- (\gamma + \textcolor{orange}{\gamma_f}) I_v +\theta\mu,\\
\end{aligned}
\begin{aligned}
r_1 dt \rightsquigarrow r_1 dt + \sigma_L\frac{S_p}{N_p}dB_p(t),
\\
r_2 dt \rightsquigarrow r_2 dt + \sigma_I\frac{S_p}{N_p} dB_p(t),
\\
\gamma_f dt \rightsquigarrow \gamma_f dt + \sigma_v dB_v(t).
\end{aligned}
\begin{aligned}
d S_p &=
\left(
-\beta_p S_p \frac{I_v}{N_v} + \textcolor{blue}{r_1} L_p
+ \textcolor{blue}{r_2} I_p
\right)dt
+ \textcolor{blue}{\frac{S_p(\sigma_L L_p
+
\sigma_I I_p)}{N_p}} dB_p(t),
\\
dL_p &=
\left(
\beta_p S_p \frac{I_v}{N_v}
- (b + \textcolor{blue}{r_1}) L_p \right) dt
- \textcolor{blue}{\sigma_L \frac{S_p L_p}{N_p}} dB_p(t),
\\
d I_p &=
\left(
b L_p - \textcolor{blue}{r_2} I_p
\right) dt
- \textcolor{blue}{\sigma_I \frac{S_pI_p}{N_p}} dB_p(t),
\\
dS_v &=
\left(
-\beta_v S_v \frac{I_p}{N_p} - (\gamma + \textcolor{orange}{\gamma_f}) S_v
+ (1-\theta) \mu \right)dt
- \textcolor{orange}{\sigma_v S_v} dB_v(t),
\\
d I_v &=
\left(
\beta_v S_v \frac{I_p}{N_p} - (\gamma + \textcolor{orange}{\gamma_f}) I_v
+ \theta \mu
\right) dt
- \textcolor{orange}{\sigma_v I_v} dB_v(t).
\end{aligned}
const { data: unknownAssetsBalances } = useQueriesData(
unknownAssetsIds.map((id) => ({
...queries.assets.balances.addressToken(addressHash, id),
enabled: unknownAssetsIds.length > 0
}))
)
let tokensWithBalanceAndMetadata = flatMap(tokenBalances, (t) => {
const metadata = find(fungibleTokens, { id: t.id })
return metadata ? [{ ...t, ...metadata, balance: BigInt(t.balance), lockedBalance: BigInt(t.lockedBalance) }] : []
})
tokensWithBalanceAndMetadata = sortBy(tokensWithBalanceAndMetadata, [
(t) => !t.verified,
(t) => !t.name,
(t) => t.name.toLowerCase(),
'id'
])
\begin{aligned}
dx(t) &= f(t, x(t), \textcolor{orange}{u(t)})dt + g(t, x(t), u(t)) dW(t),\\
x(0) &= x_0 \in \mathbb{R}^n,
\\
\\
J(u(\cdot)) &= \mathbb{E} \left\{ \int^T_0 c(t,x(t),u(t)) dt + h(x(T))\right\}.
\end{aligned}
\begin{aligned}
&J(\bar{\pi}) = \inf_{\pi \in\, \mathcal{U}[0,T]} J(\pi)\\
\text{Suject to}&\\
dx(t) &= f(t, x(t), u(t))dt + g(t, x(t), u(t)) dW(t),\\
x(0) &= x_0 \in \mathbb{R}^n,
\end{aligned}
\begin{aligned}
\forall t & \in[0,T],
\ x, \ \hat{x} \in \mathbb{R}^n,
\ u \in U,
\\
&|\varphi(t,x,u) - \varphi(t, \hat{x},u)|\leq L|x-\hat{x}|,
\end{aligned}
\begin{aligned}
f:[0,T] \times \mathbb{R} ^ n \times U
&\to \mathbb{R}^n,
\\
g:[0,T] \times\mathbb{R} ^ n \times U
&\to \mathbb{R}^{n\times m},
\\
c:[0,T] \times\mathbb{R} ^ n \times U
&\to \mathbb{R},
\\
h:\mathbb{R}^n
\to \mathbb{R}&
\end{aligned}
\begin{aligned}
(s,y) \in [0,T) &\times \mathbb{R}^n,
\\
V(s,y)
&= \inf_{ u(\cdot) \in \mathcal{U} [s,T]}
J(s, y; u(\cdot) ),
\\
V(T,y) &= h(y), \qquad \forall y\in \mathbb{R}^n,
\end{aligned}
\begin{aligned}
& -V_t +
\sup_{u \in U} H_G (t ,x, u, -V_x, -V_{xx})=0,
(t,x) \in [0,T)\times\mathbb{R}^n,
\\
& V \Big|_{t=T} = h(x), \qquad x\in \mathbb{R} ^ n,
\\
& H_G(t,x,u,p,P) = \langle p, f(t,x,u) \rangle - c(t,x,u)
\\
&+\dfrac{1}{2} \mathtt{trace}\Big( g^\top(t,x,u)Pg(t,x,u)\Big)
\\
& = H_{det}(t,u,x,p) +\dfrac{1}{2} \mathtt{trace}\Big( g^\top(t,x,u)Pg(t,x,u)\Big)
\end{aligned}
\begin{aligned}
\forall (t,u) & \in [0,T]\times U
\\
&|\varphi(t,0,u)|\leq L
\end{aligned}
OPC:
Value Function
HJB
\begin{aligned}
dx(t) &= f(t, x(t), \textcolor{orange}{u(t)})dt + g(t, x(t), u(t)) dW(t),\\
x(0) &= x_0 \in \mathbb{R}^n,
\\
J(u(\cdot)) &= \mathbb{E} \left\{ \int^T_0 c(t,x(t),u(t)) dt + h(x(T))\right\}.
\end{aligned}
\begin{aligned}
J(u) = \mathbb{E}\int_{0}^{T}
& \Bigg[
A_1 I_p(t) + A_2 L_p(t) + A_3 I_v (t)
\\
& + c_1 u ^ 2_1(t) + c_2 u ^ 2_2(t) + c_3 u ^ 2_3(t)
\Bigg] dt,
\end{aligned}
\begin{aligned}
&\qquad\qquad\qquad\qquad\min_{u\in \mathcal{U}[0,T]} J(u) \\
&\qquad \text{subject to } \\
&dS_p
=
\left(
-\beta_pS_p\frac{I_v}{N_v}+(r_1 +u_1) L_p + (r_2 + u_2)L_p
\right)dt
\\
&+
\frac{S_p}{N_p}\left(
\sigma_L L_p+\sigma_I I_p \right)dB_p,\\
&dL_p
=
\left(
\beta_pS_p\frac{I_v}{N_v}-(b+r_1 +u_1)L_p
\right)dt
-\sigma_L\frac{S_p}{N_p}L_pdB_p,
\\
&dI_p
= \left(
b L_p - (r_2 + u_2) I_p
\right)dt - \sigma_I\frac{S_p}{N_p}I_p dB_p,
\\
&dS_v
=
\left( -\frac{\beta_v}{N_p}S_vI_p
-(\gamma +\gamma_f+ u_3) S_v + (1-\theta)\mu\right)dt
-\sigma_v S_vdB_v,
\\
&dI_v
=
\left( \frac{\beta_v}{N_p}S_vI_p - (\gamma +\gamma_f+u_3) I_v +\theta \mu \right) dt
- \sigma_v S_v dB_v.
\end{aligned}
\begin{aligned}
V(s,x) =
\inf_{u(\cdot) \in \mathcal {U}[s,T]}
&\mathbb{E}
\Bigg\{
\int_{s}^{T}
\Big[
A_1 I_p(t) + A_2 L_p(t) + A_3 I_v (t)
\\
& + c_1 u ^ 2_1(t) + c_2 u ^ 2_2(t) + c_3 u ^ 2_3(t)
\Big]
dt
\Bigg\}
\end{aligned}
\begin{aligned}
V(s,x) =
\inf_{u(\cdot) \in \mathcal {U}[s,T]}
&\mathbb{E}
\Bigg\{
\int_{s}^{T}
\Big[
A_1 I_p(t) + A_2 L_p(t) + A_3 I_v (t)
\\
& + c_1 u ^ 2_1(t) + c_2 u ^ 2_2(t) + c_3 u ^ 2_3(t)
\Big]
dt
\Bigg\}
\end{aligned}
\begin{aligned}
&-V_t + \sup_{u \in U} H_G(t, x, u, -V_x, -V_{xx})=0
\end{aligned}
\begin{aligned}
H_G(t,x,u,p,P) &= \langle p, f(t,x,u) \rangle - c(t,x,u)
\\
&+\dfrac{1}{2} \mathtt{trace}\Big( g^\top(t,x,u)Pg(t,x,u)\Big)
\end{aligned}
\begin{aligned}
H_{det} &(t,u,x,-V_x) = A_1I_v+A_2L_p+A_3I_v
+\sum_{i=1}^{3}c_iu_i^2\\
&-V_{x_1}(-\beta_p S_p I_v +(r_1 +u_1)L_p
+ (r_2 + u_2) I_p)\\
& -V_{x_2}(\beta_p S_p I_v-(b +r_1 + u_1)L_p)\\
&-{V_{x_3}}(b L_p - (r_2 + u_2) I_p)\\
&-V_{x_4}(-\beta_v S_v I_p - (\gamma+\gamma_f+u_3) S_v
+(1-\theta)\mu)\\
&-V_{x_5}(\beta_v S_v I_p
-(\gamma+\gamma_f+u_3) I_v+\theta\mu).
\end{aligned}
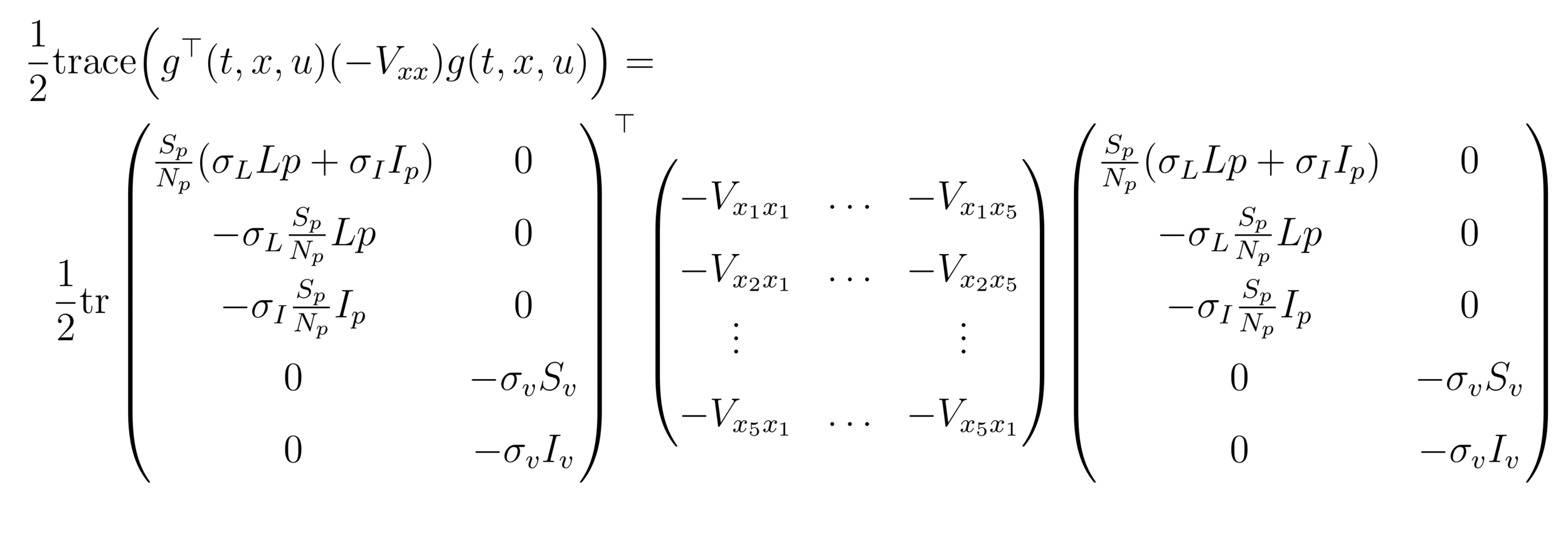
HJB (Dynamic Programming)- Course of dimensionality
\approx \
\mathtt{HJB}
HJB(Neuro-Dynamic Programming)
Abstract dynamic programming.
Athena Scientific, Belmont, MA, 2013. viii+248 pp.
ISBN:978-1-886529-42-7
ISBN:1-886529-42-6
Rollout, policy iteration, and distributed reinforcement learning.
Revised and updated second printing
Athena Sci. Optim. Comput. Ser.
Athena Scientific, Belmont, MA, [2020], ©2020. xiii+483 pp.
ISBN:978-1-886529-07-6
Reinforcement learning and optimal control
Athena Sci. Optim. Comput. Ser.
Athena Scientific, Belmont, MA, 2019, xiv+373 pp.
ISBN: 978-1-886529-39-7
Gracias
1.Salcedo-Varela, G. & Diaz-Infante, S. Threshold behaviour of a stochastic vector plant model for Tomato Yellow Curl Leaves disease: a study based on mathematical analysis and simulation. Int J Comput Math 1–0 (2022) doi:10.1080/00207160.2022.2152680.
2. Salcedo‐Varela, G. A., Peñuñuri, F., González‐Sánchez, D. & Díaz‐Infante, S. Synchronizing lockdown and vaccination policies for COVID‐19: An optimal control approach based on piecewise constant strategies. Optim. Control Appl. Methods (2023) doi:10.1002/oca.3032.
3.Diaz-Infante, S., Gonzalez-Sanchez, D. & Salcedo-Varela, G. Handbook of Visual, Experimental and Computational Mathematics, Bridges through Data. 1–19 (2023) doi:10.1007/978-3-030-93954-0_37-1.
https://slides.com/sauldiazinfantevelasco/slides_red_mex_bio_mat
