\(K\)-matrix formalism in light-meson spectroscopy

Sebastián Ordóñez

Email: jsordonezs@unal.edu.co

 

 

Supervisor: Diego A. Milanés

Email: damilanesc@unal.edu.co

Phenomenology of High Energy Physics Group

Departamento de Física

Universidad Nacional de Colombia

The decay  \(D^{0}\longrightarrow K^{0}_{s}\pi^{+}\pi^{-}\)

Outline

  • Introduction

- Review of Multibody Charm Analysis

  • Analysis

- Dalitz Plot Analysis and \(K\)-matrix formalism (The issue)

- Isobar Model vs \(K\)-matrix approach

  • Results and Conclusions

- Implementation of \(K\)-matrix formalism in \(D\)-decays

- Conclusions

Multibody Charm Analysis

  • Why are \(D\) meson decays interesting?  Let us see:
    • \(D\) meson is a unique laboratory to study light quark spectroscopy. Three-body decay of these mesons exhibit rich interference between intermediate states, i.e. resonances.
    • They allow us to research low-mass scalar mesons given their large coupling to such states.
    • They offer rich phenomenology, including unique sensitive to \(CP\) violation and charm mixing (New Physics).
    • An important example, with rich resonant structure, is              \(D^{0}\longrightarrow K_{s}\pi^{+}\pi^{-}\). (Belle Collab. and BaBar Collab.)

Dalitz Plot Analysis

  • What are Dalitz Plots?  In few words,  DP is a two-dimensional representation of a three-body decay, \(X\longrightarrow ABC\).
    • The two axis of the plot are
  • Why are DP useful in hadron spectroscopy?  Phase space density is a constant across the kinematically allowed region.
s_{AB}= (p_{A}+p_{B})^{2},\\ s_{AC}= (p_{A}+p_{C})^{2}.
\boxed{d\Gamma = \frac{1}{(2\pi)^{3}32\sqrt{s^{3}}} |\mathcal{M}|^{2}ds_{AB}ds_{AC}}

Any structure seen in the Dalitz Plot is a direct consequence encoded in \(|\mathcal{M}|^{2}\), the underlying dynamics!

Dalitz Plot Analysis

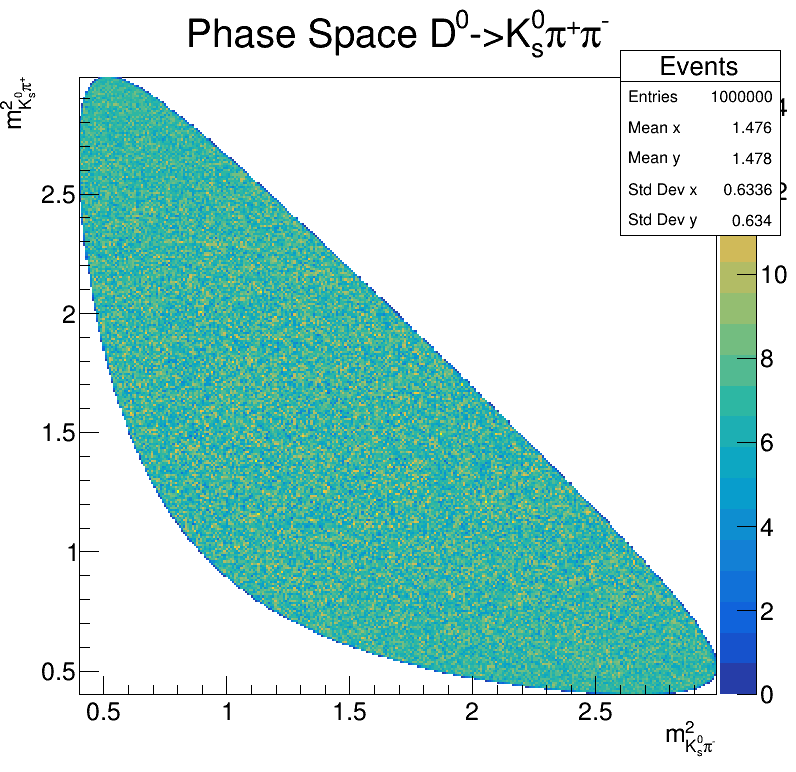
Let us suppose for a moment that we have an homogeneous event distribution. 

Phase Space \(D^{0}\longrightarrow K^{0}_{s}\pi^{+}\pi^{-}\)

Dalitz Plot Analysis

Phase Space \(D^{0}\longrightarrow K^{0}_{s}\pi^{+}\pi^{-}\)

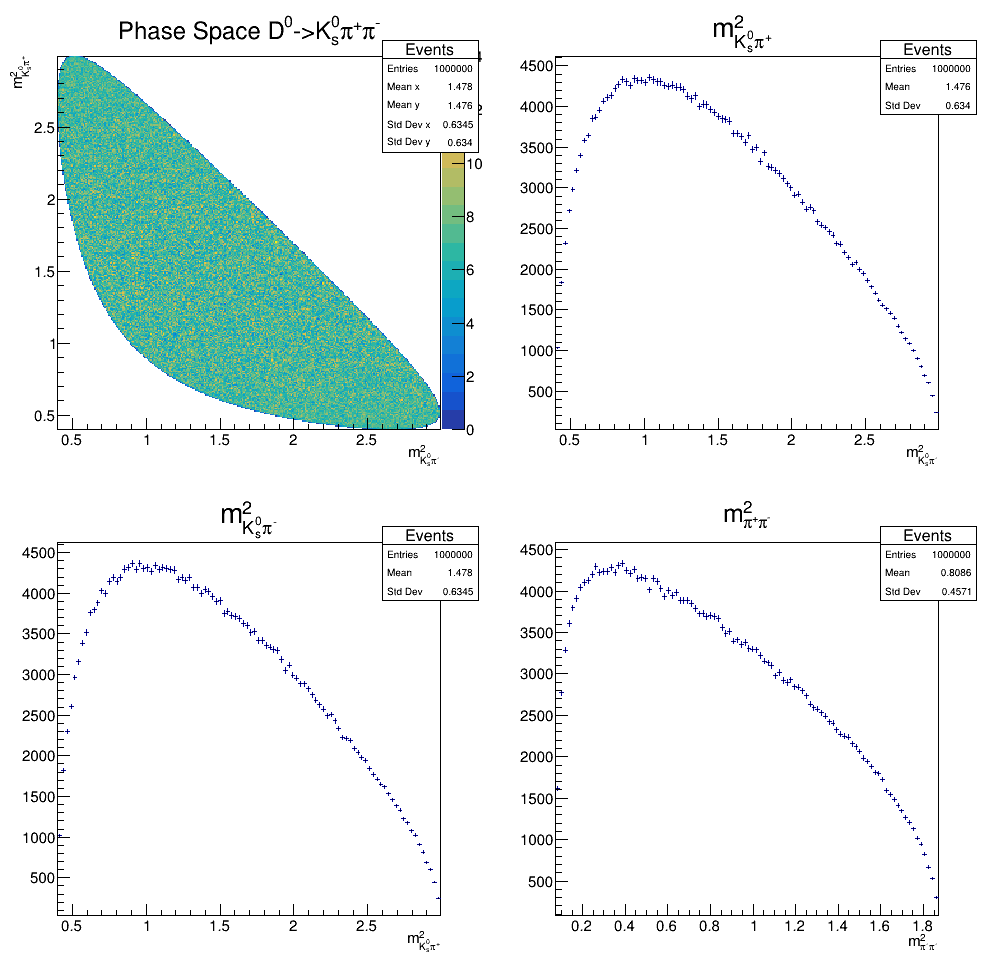
Dalitz Plot Analysis

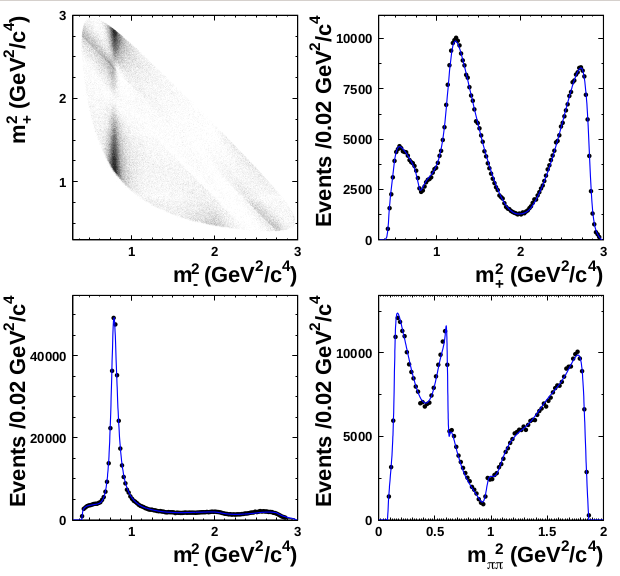
The Belle Collaboration, Measurement of \(D^{0}−\bar{D}^{0}\) mixing in \(D^{0}\longrightarrow K_{s}^{0}\pi^{+}\pi^{-}\). Physical Review Letters, 99(13):211,2007.

\boxed{D^{0}\longrightarrow K_{S}^{0}\pi^{+}\pi^{-}}

Dalitz Plot Analysis

The Belle Collaboration, Measurement of \(D^{0}−\bar{D}^{0}\) mixing in \(D^{0}\longrightarrow K_{s}^{0}\pi^{+}\pi^{-}\). Physical Review Letters, 99(13):211,2007.

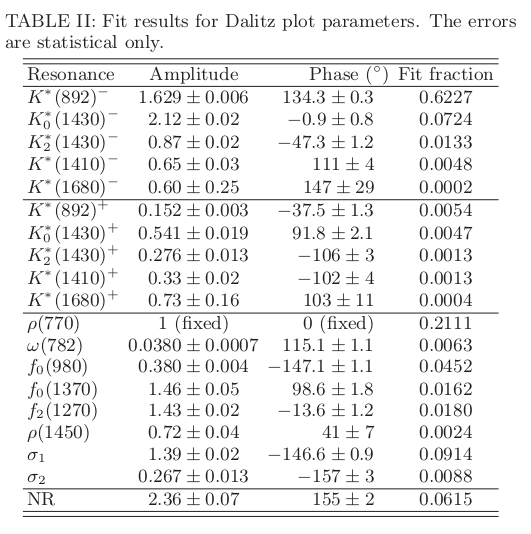
Isobar Model

  • In this context, a model for \(\mathcal{M}\) is needed. In particular a model for \(D^{0}\) is needed, i.e. ( \(K\pi\)) \(\pi\), \(K\)(\(\pi\pi\)). The isobar approach proposes

 

 

  • In this model, the matrix element \(\mathcal{M}\) is modeled as a sum of interfering decay amplitudes
\boxed{\mathcal{M}_{R}^{l}(ABC|R)= T^{l}(s_{R})\times B_{X}^{l}(s_{R}) B_{R}^{l}(s_{R})\times Z^{l}(s_{R}, s_{AB}, s_{BC})}
\boxed{X \longrightarrow ABC \iff X\longrightarrow RC + R\longrightarrow AB }

In most analyses, each resonant is described by a Breit-Wigner (BW) lineshape

Isobar Model

  • When more than one resonance contributes to the decay, we sum over the amplitude of all the intermediate resonances, i.e

 

 

\boxed{\mathcal{M}_{DP} = c_{0}+\sum_{R}c_{R}\mathcal{M}_{R}^{l}(s_{AB}, s_{BC}),}
  • A question arises... In the era of precision measurements, how to deal with the underlying strong dynamics effects?
    • ​The \(\pi\pi\), \(K\pi\)  S-wave are characterized by broad, overlapping states.
    • Unitarity is not explicitly guaranteed by a simple sum              of BW functions.           

Isobar Model

  • Let us see the case of two resonances in the same partial wave that couples to the same channel. First, non-overlapping resonances

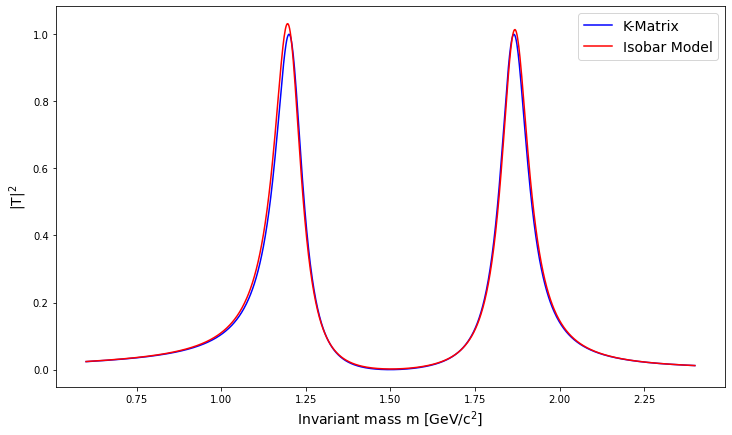
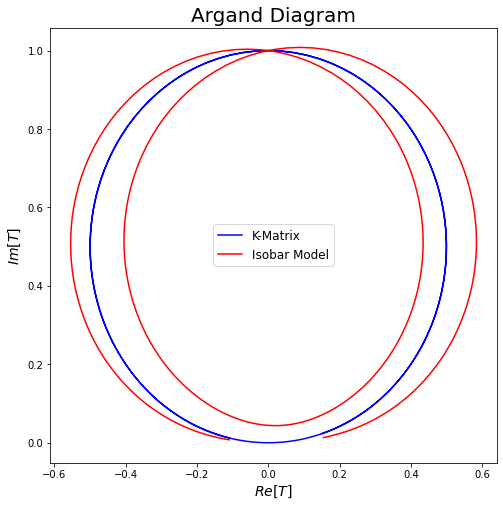
The issue

Now, the case of overlapping resonances

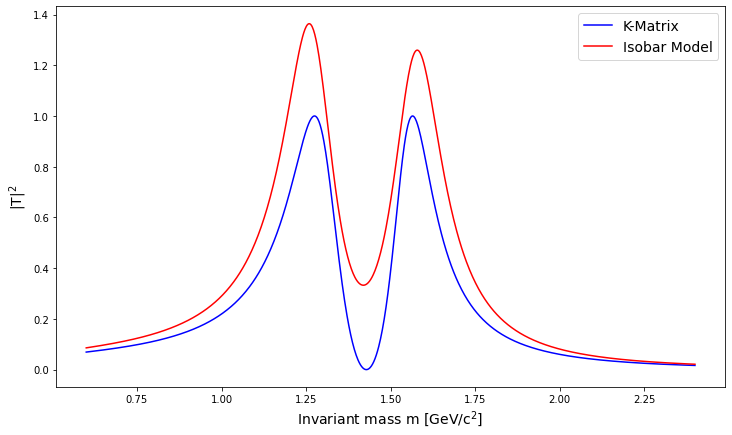
Spoiler: \(K\)-matrix approach works well in this case too and BW leads to violation of unitarity.

The \(K\)-matrix

  • What is \(K\)-matrix?  It follows from the unitary \(S\)-matrix 

\boxed{S = I + 2i\rho^{1/2}T\rho^{1/2}}

We can express any unitary operator in terms of an hermitian operator

\boxed{S=(I-i\rho^{1/2}K\rho^{1/2})^{-1}(I+i\rho^{1/2} K\rho^{1/2})}

In terms of the \(T\)-matrix

\boxed{T=(I-iK\rho)^{-1}K}

E.P. Wigner, Phys. Rev 70(15), 1946

S.U. Chung et al. Ann. Physik 4(404), 1995

The advantages of \(K\)-matrix approach

  • It heavily simplifies the formalization of any scattering problem since the unitarity of \(S\) is automatically respected.
  • For a single-pole problem a \(K\)-matrix reduces to the standard BW formula.
  • The \(K\)-matrix approach can be extended to production processes.
\boxed{T=(I-iK\rho)^{-1}K}
\boxed{F=(I-iK\rho)^{-1}P}

Thanks to I.J.R. Aitchison (Nucl. Phys. A189 514,1972)

The advantages of \(K\)-matrix approach

  • \(K\)-matrix allows for the inclusion of all the knowledge coming from scattering experiments.
\boxed{F=(I-iK\rho)^{-1}P}

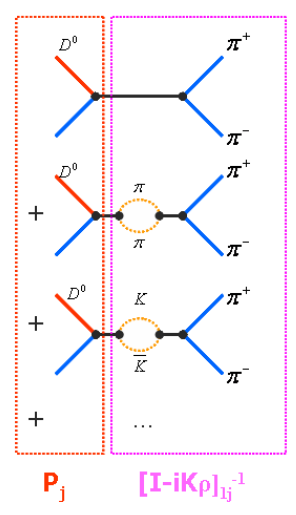
Describes coupling of resonances to \(D\)

Comes from scattering data

The advantages of \(K\)-matrix approach

  • This \(P\)-vector must have the same poles as those of the \(K\)-matrix,  its parameterization is given by
\boxed{P_{j}(s)=f_{1j}^{prod}\frac{1-s_{0}^{prod}}{s-s_{0}^{prod}}+\sum_{\alpha}\frac{\beta_{\alpha}g_{j}^{\alpha}}{m_{\alpha}^{2}-s}}
\boxed{K_{ij}^{00}(s)=\left(\sum_{R}\frac{g_{i}^{R}g_{j}^{R}}{m_{R}^{2}-s}+f_{ij}^{scatt}\frac{1-s_{0}^{scatt}}{s-s_{0}^{scatt}}\right) \left\{\frac{1-s_{A0}}{s-s_{A0}}\left(s-s_{A}\frac{m_{\pi}^{2}}{2}\right)\right\}}

We take the channels j as \(\pi\pi,KK,\eta\eta, \eta'\eta', 4\pi\)

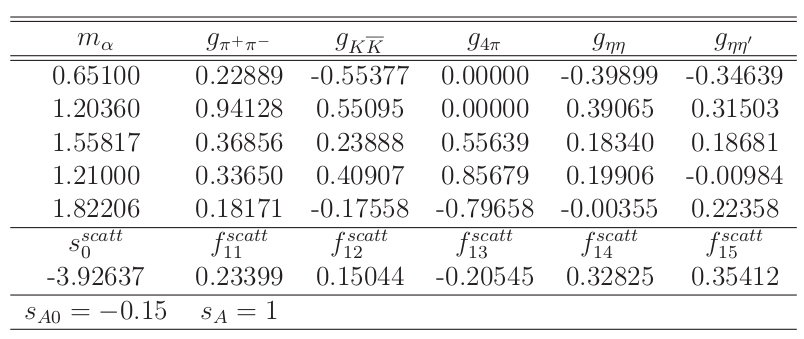
V.V Anisovich and A.V.Sarantsev Eur.Phys.J.A16 (2003) 229

"\(K\)-matrix analysis of the \(00^{++}\)-wave in the mass region below \(1900\) MeV"

\(\pi\pi\) S-wave scattering parameterization

\(\pi\pi\) S-wave scattering parameterization

f_{0}(980)
f_{0}(1500)

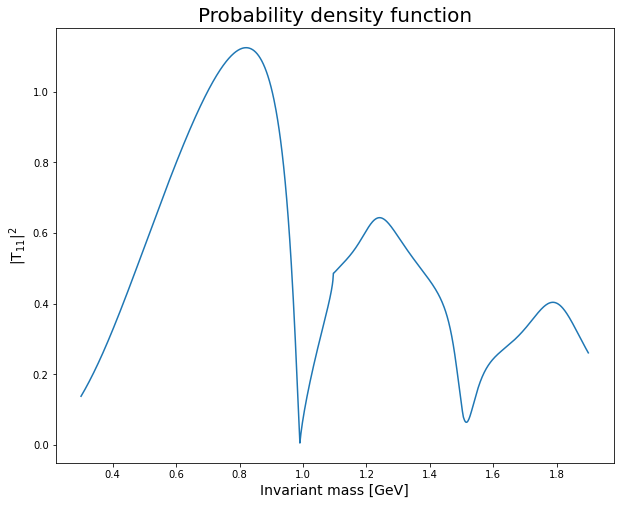
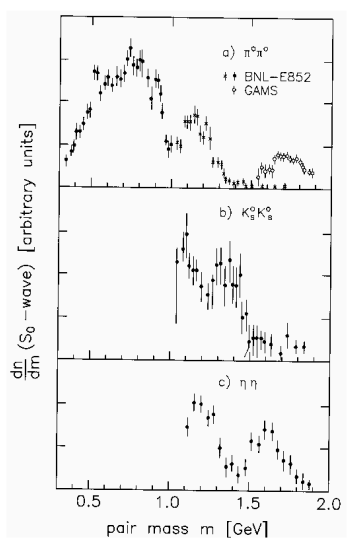
\(\pi\pi\) S-wave scattering parameterization

What about unitarity in this case?

  • It provided the \(K\)-matrix input to our \(D\)-meson analysis

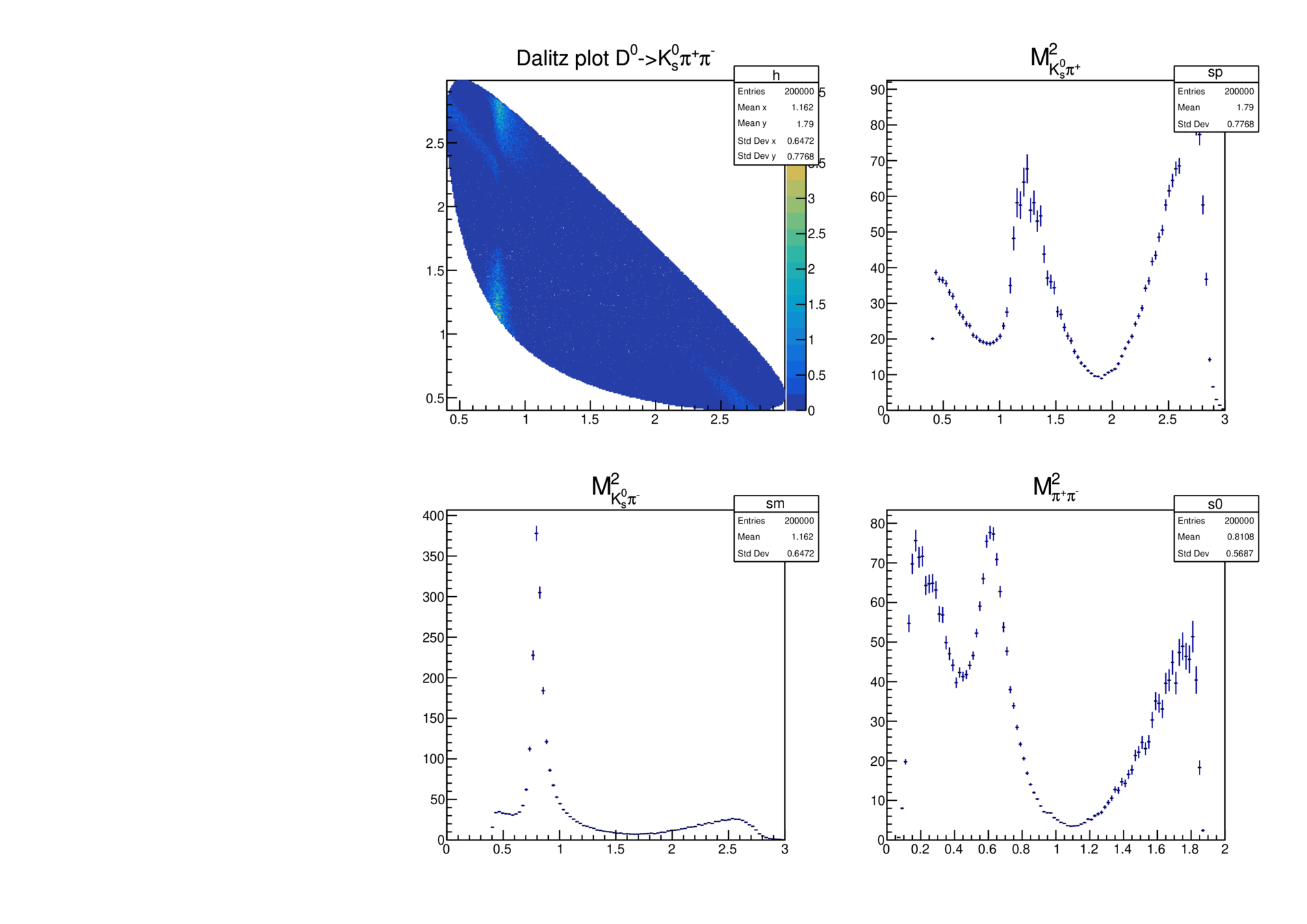
\(D^{0}\longrightarrow K^{0}_{s}\pi^{+}\pi^{-}\) using \(K\)-matrix description

  • By using \(K\)-matrix approach  for the total decay amplitude, we guarantee unitarity and also we perform a more accurate description of dynamics. The \(D^{0}\) decay amplitude is given by
\boxed{\mathcal{M}_{DP} = F_{\pi\pi}(m_{0}^{2}) + A_{K\pi}(m_{+-}^{2}) +\sum_{R}c_{R}\mathcal{M}_{R}^{l}(s_{AB}, s_{BC})}
  • In summary:
    • For \(\pi\pi\) \(S\)-wave we use \(K\)-matrix and the production vector.
    • For \(K\pi\) \(S\)-wave we employ the LASS-like parameterization.
    • For \(P\)-wave are given by BW resonances.

 

 

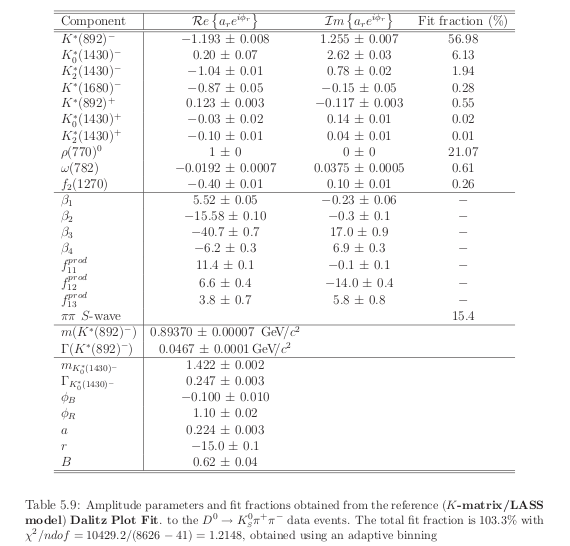
D. Milanés, Measurement of \(D^{0}-\bar{D}^{0}\) mixing in the BABAR experiment. PhD thesis,
Universidad de Valencia, Departmento de Física Teórica, 2010.

\(D^{0}\longrightarrow K^{0}_{s}\pi^{+}\pi^{-}\) using \(K\)-matrix description

Conclusions

  • Dalitz plot analysis is teaching us much about hadronic
    decays. It will definitely keep us company over the next
    few years.
  • \(K\)-matrix formalism guarantee unitarity and also we perform a more accurate description of dynamics. This is not ensured by other approaches as Isobar
    Model.
  • These datasets constitute a huge opportunity, but also a challenge to improve the theoretical descriptions of soft hadronic effects in multibody decays.

Thank you!

Questions?