Joint graph-feature embeddings using GCAEs
Sébastien Lerique, Jacobo Levy-Abitbol, Márton Karsai, Éric Fleury
IXXI, École Normale Supérieure de Lyon
Twitter users can...


... be tightly connected
... relate through similar interests
... write in similar styles
graph node2vec: \(d_n(u_i, u_j)\)
average user word2vec: \(d_w(u_i, u_j)\)
Questions
-
Create a task-independent representation of network + features
-
What is the dependency between network structure and feature structure
-
Plot the cost of compressing network + features down to a given dimension \(n\)



network—feature dependencies
network—feature independence
Use deep learning to create embeddings



A framework
Graph convolutional neural networks + Auto-encoders
How is this framework useful
Speculative questions we want to ask
Application and scaling
With great datasets come great computing headaches
Graph-convolutional neural networks



\(H^{(l+1)} = \sigma(H^{(l)}W^{(l)})\)
\(H^{(0)} = X\)
\(H^{(L)} = Z\)
\(H^{(l+1)} = \sigma(\color{DarkRed}{\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}}H^{(l)}W^{(l)})\)
\(H^{(0)} = X\)
\(H^{(L)} = Z\)
\(\color{DarkGreen}{\tilde{A} = A + I}\)
\(\color{DarkGreen}{\tilde{D}_{ii} = \sum_j \tilde{A}_{ij}}\)

Kipf & Welling (2016)

Neural networks

x
y
green
red

\(H^{(l+1)} = \sigma(H^{(l)}W^{(l)})\)
\(H^{(0)} = X\)
\(H^{(L)} = Z\)
Inspired by colah's blog
Semi-supervised graph-convolution learning
Four well-marked communities of size 10, small noise

More semi-supervised GCN netflix
Overlapping communities of size 12, small noise
Two feature communities in a near-clique, small noise
Five well-marked communities of size 20, moderate noise

(Variational) Auto-encoders

From blog.keras.io
- Bottleneck compression → creates embeddings
- Flexible training objectives
- Free encoder/decoder architectures
high dimension
high dimension
low dimension
Example — auto-encoding MNIST digits

MNIST Examples by Josef Steppan (CC-BY-SA 4.0)
60,000 training images
28x28 pixels
784 dims
784 dims
2D

From blog.keras.io
GCN + Variational auto-encoders = 🎉💖🎉
node features
embedding
GCN
node features
adjacency matrix

Socio-economic status
Language style
Topics
Socio-economic status
Language style
Topics


Compressed & combined representation of nodes + network
Kipf & Welling (2016)
GCN+VAE learning
Five well-marked communities of size 10, moderate label noise


Applications
a.k.a., questions we can (will be able to) ask
Explore the dependency between network structure and feature structure
Cost of compressing network + features down to a given dimension \(n\)
Task-independent representation of network + features with uncertainty
Continuous change from feature communities to network communities

Speculation
Link prediction
Community detection
Graph reconstruction
Node classification
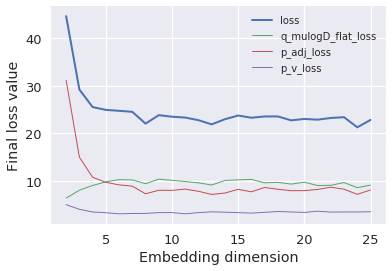
BlogCatalog compression cost
10,312 nodes
333,983 edges
39 groups

Full dataset
200 nodes
162 edges
36 groups
Toy model
Scaling GCN

node2vec, Grover & Leskovec (2016)
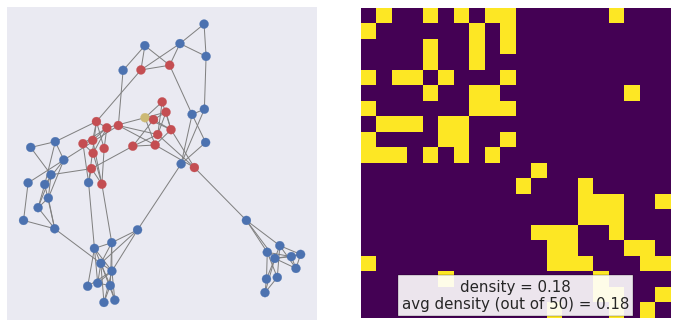
Walk on triangles

Walk outwards
| Dataset | # nodes | # edges |
|---|---|---|
| BlogCatalog | 10K | 333K |
| Flickr | 80K |
5.9M |
| YouTube | 1.1M | 3M |
| 178K | 44K |
✔
👷
👷
👷
Mutual mention network on 25% of the GMT+1/GMT+2 twittosphere in French
Mini-batch sampling


node2vec, Grover & Leskovec (2016)
walk back \(\propto \frac{1}{p}\)
walk out \(\propto \frac{1}{q}\)
walk in triangle \(\propto 1\)

Walk on triangles — p=100, q=100

Walk out — p=1, q=.01
Thank you!
Sébastien Lerique, Jacobo Levy-Abitbol, Márton Karsai, Éric Fleury
IXXI, École Normale Supérieure de Lyon


