Visualizing the loss landscape of neural nets
Hao Li, Zheng Xu, Gavin Taylor, Christoph Studer, Tom Goldstein
(NIPS 2018)
What is the relationship between trainability, generalisation, and architecture choices?
- architecture choices \(\rightarrow\) loss landscape
- global loss landscape (convex or not) \(\leftrightarrow\) trainability
- landscape surrounding minima \(\rightarrow\) generalisation

Questions
Tricks of the trade
- Mini-batching
- Batch normalisation
- Self-normalisation
- Dropout
- Residual connections

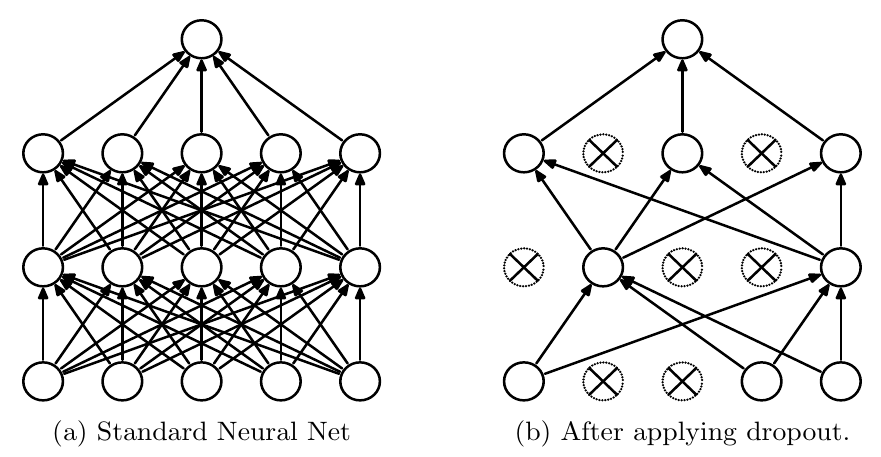

Techniques for visualising
between two minima
Minimise \(L(\theta) = \frac{1}{m} \sum_{i=1}^m l(x_i, y_i; \theta)\)
\(x_i\) feature vectors
\(y_i\) labels
\(\theta\) model parameters
For two parameter sets \(\theta_1\) and \(\theta_2\),
plot \(f(\alpha) = L((1 - \alpha) \theta_1 + \alpha \theta_2)\)

Techniques for visualising
around one minimum
Around a parameter set \(\theta\):
- For 1D, choose a direction vector \(\delta\), and plot \( f(\alpha) = L(\theta + \alpha \delta) \)
- For 2D, choose two direction vectors \(\delta\) and \(\eta\), and plot \( f(\alpha, \beta) = L(\theta + \alpha \delta + \beta \eta) \)

Scaling problem
Filter-wise normalisation
Direction vectors have same dimensionality as \(\theta\)
Normalise each direction vector filter-wise: \(d_{i,j} \leftarrow \frac{d_{i,j}}{||d_{i,j}||} ||\theta_{i,j}||\)


Test models

VGG (2014)

AlexNet (2012)

ResNet (2015)
Wide-ResNet (2016)
ResNet-noshort

DenseNet (2016)
Residual connections \(\leftrightarrow\) network depth




Residual connections \(\leftrightarrow\) network width

Does this capture convexity?
Ok, now what about \(\Longleftarrow\)?
Plot \(\left|\frac{\lambda_{min}}{\lambda_{max}}\right|\) for the original Hessian at each point

The principle curvatures of a randomly projected (Gaussian) surface are weighted averages of the principle curvatures of the original surface (with Chi-square coefficients)
So: non-convexity in the projected surface
\(\Longleftrightarrow\) non-positive projected Hessian eigenvalues
\(\Longrightarrow\) non-positive original Hessian eigenvalues
\(\Longleftrightarrow\) non-convexity in original surface



Visualising optimisation paths

In high dimension, random vectors are mostly orthogonal to anything independent (\(E[S_C(v_1, v_2)] \sim \sqrt{\frac{2}{\pi n}}\))
So random projections don't capture much
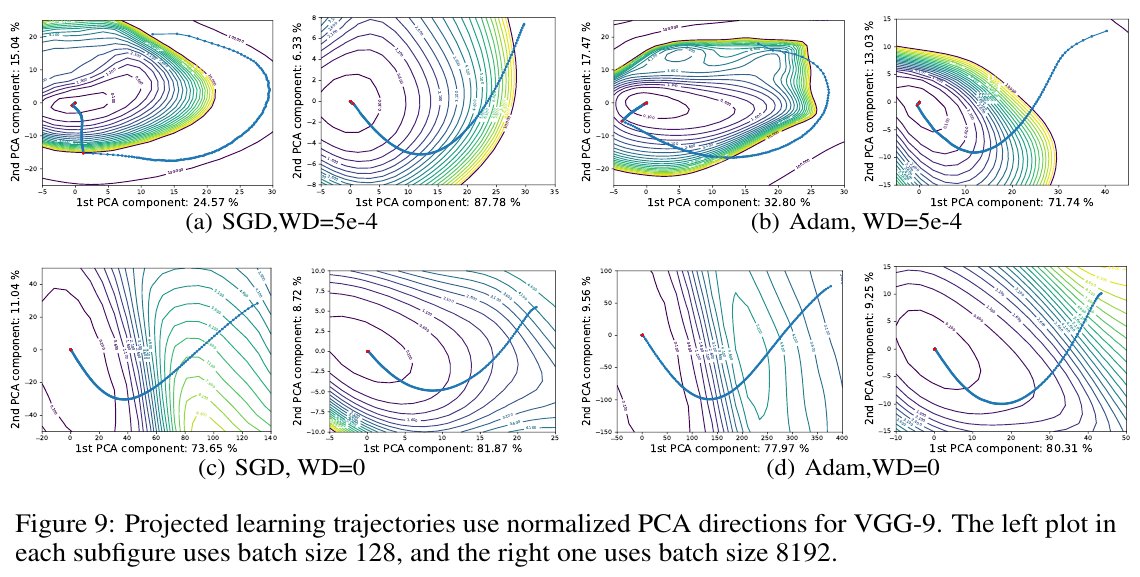
Visualising optimisation paths
use PCAs instead