Mastery Learning Algorithms
From the Surprisingly Simple to the Insidiously Inequitable

Shayan Doroudi
Assistant Professor
University of California Irvine
School of Education
KidsLoop
November 30, 2021
One Size Fits All
Mastery Learning
The Promise of Mastery Learning
The Promise of Mastery Learning
Idea dates back to early 20th century.
(e.g., Winnetka Plan, Morrison Plan)
Big Data + State-of-the-Art Algorithms = Better Mastery Learning?
But today, adaptive learning platforms could enable assessing mastery on a fine-grained level.













All of these platforms use simple heuristics to assess mastery!
The Reality of Mastery Learning
Common approaches to assess mastery rely on simple algorithms that are often not data-driven.
The Reality of Mastery Learning
“The [BKT] model overestimates the true learning and performance parameters for below-average students who make many errors. While these students receive more remedial exercises than the above average students, they nevertheless receive less remedial practice than they need and perform worse on the test than expected.”
Corbett and Anderson, 1995
“17% of students would be expected to have a probability of mastery of only 60% or less when the population model would expect the student is at a probability of mastery of 95% or higher”
Lee and Brunskill, 2012
The Reality of Mastery Learning
Mastery learning algorithms may not always give the right amount of practice for each student.
The Reality of Mastery Learning
Key Questions
1. Is it justifiable to use simple heuristics for mastery learning in an age of big data?
2. Are mastery learning algorithms equitable for all students?
Outline
Surprisingly Simple Algorithms
Insidiously Inequitable Algorithms
Surprisingly Simple Algorithms
Keep giving problems until student gives N correct answers in a row.
N-Consecutive Correct in a Row
(N-CCR)
N-Consecutive Correct in a Row
(N-CCR)
✘
✘
✘
✘
✔
✔
✔
✔
✔
✔
✔
✔
N-CCR in Practice
Used in ASSISTments’ Skill Builders.
A gamified version of it is used in Khan Academy:

+1 pt for each correct answer;
-1 pt for each wrong answer;
Keep giving problems until student gets N pts.
Tug-of-War Heuristic
Tug-of-War Heuristic
✘
✘
✔
+1
Tug-of-War Heuristic
✘
✘
✔
-1
Tug-of-War Heuristic
✘
✘
✔
✔
+1
Tug-of-War Heuristic
✘
✘
✔
✔
✔
+1
Tug-of-War Heuristic
✘
✘
✘
✔
✔
✔
-1
Tug-of-War Heuristic
✘
✘
✘
✔
✔
✔
✔
+1
Tug-of-War Heuristic
✘
✘
✘
✔
✔
✔
✔
✔
+1
Tug-of-War Heuristic
✘
✘
✘
✘
✔
✔
✔
✔
✔
-1
Tug-of-War Heuristic
✘
✘
✘
✘
✔
✔
✔
✔
✔
✔
+1
Tug-of-War Heuristic
✘
✘
✘
✘
✔
✔
✔
✔
✔
✔
✔
+1
Tug-of-War Heuristic
✘
✘
✘
✘
✔
✔
✔
✔
✔
✔
✔
✔
+1
Tug-of-War Heuristic
A variant of Tug-of-War heuristic is used in ALEKS.
Tug-of-War Heuristic in Practice
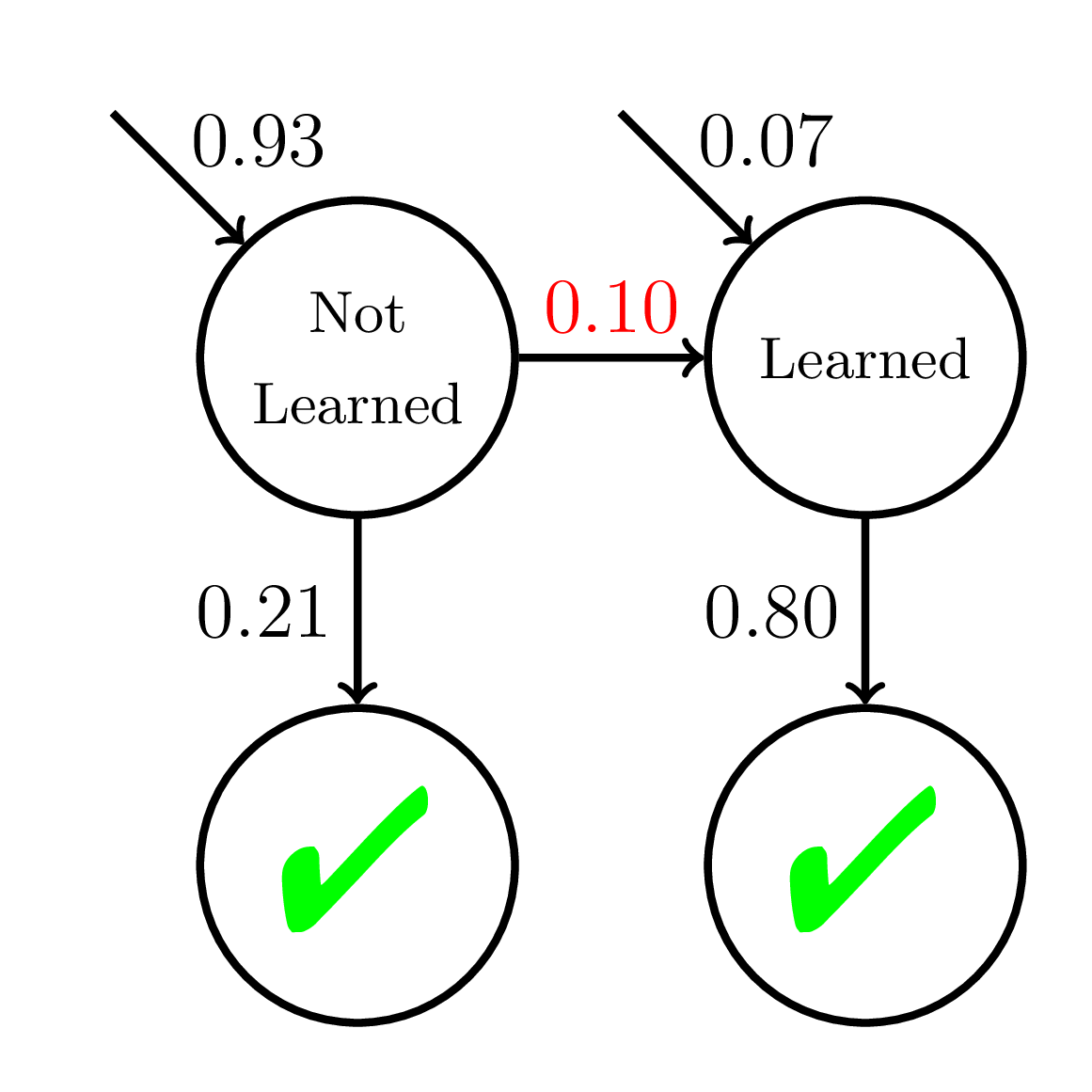
Bayesian Knowledge Tracing (BKT)

Corbett and Anderson, 1995
Cognitive Mastery Learning
Keep giving practice opportunities on a skill/concept until student reaches mastery:
Then move onto the next skill/concept
Corbett and Anderson, 1995
Cognitive Mastery Learning in Practice
Used in Carnegie Learning’s MATHia
Often used with hand set parameters (i.e., not data-driven).
Key Question
Is it justifiable to use simple heuristics for mastery learning in an age of big data?
Mastery learning heuristics implicitly make certain assumptions about learning.
We should identify what those assumptions are.
N-CCR Reinterpreted
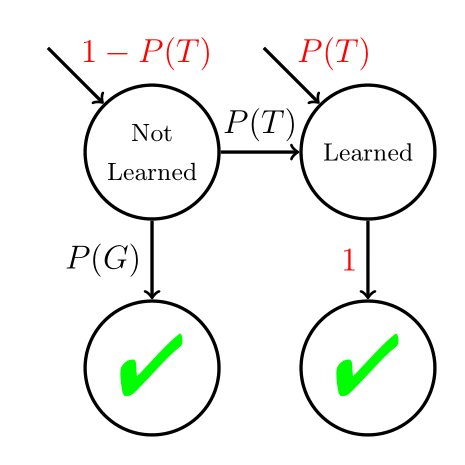
N-CCR is the optimal mastery learning policy for a BKT model where P(S) = 0.
Tug-of-War Reinterpreted
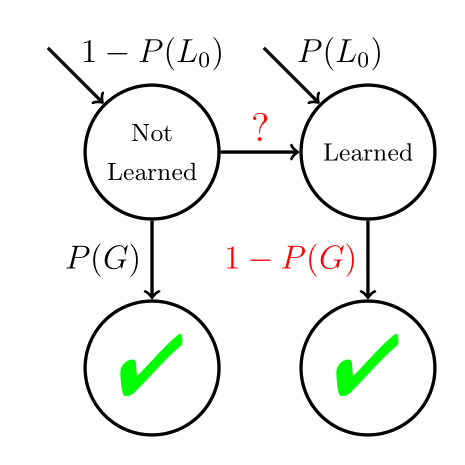
If P(G) = P(S)
and we make no assumptions about the probability of learning, the
Tug-of-War heuristic is the “optimal policy,” where N controls how conservative the policy is.
Bernoulli CUSUM Algorithm
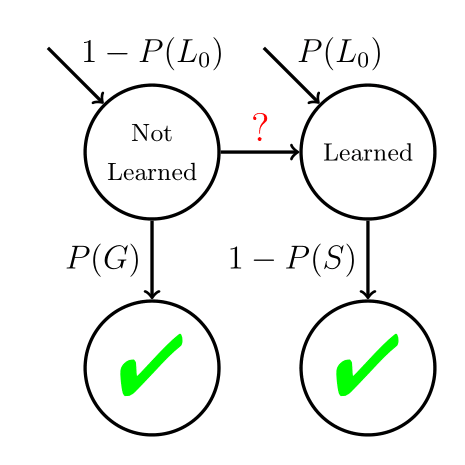
Mastery learning can be interpreted as a “change point detection problem,” which is well-studied in statistics.
The optimal solution is the Bernoulli CUSUM Algorithm.
The Tug-of-War heuristic is a special case.
Takeaway
The Tug-of-War heuristic may actually be reasonable if we assume learning is all-or-nothing and P(G) is close to P(S).
Insidiously Inequitable Algorithms
Key Question
Are mastery learning algorithms equitable for all students?
200 students
20 practice opportunities
Fast Learners
Slow Learners
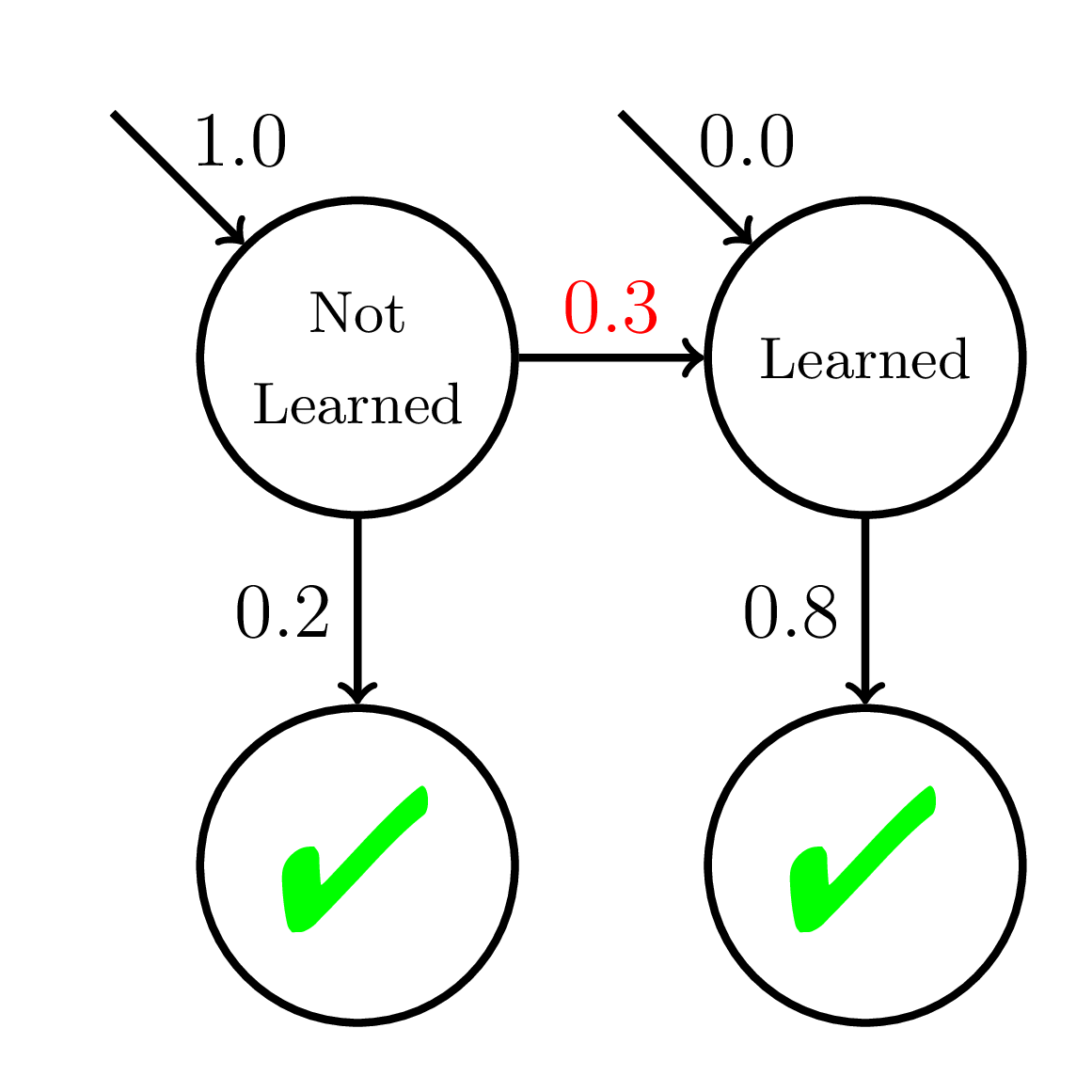
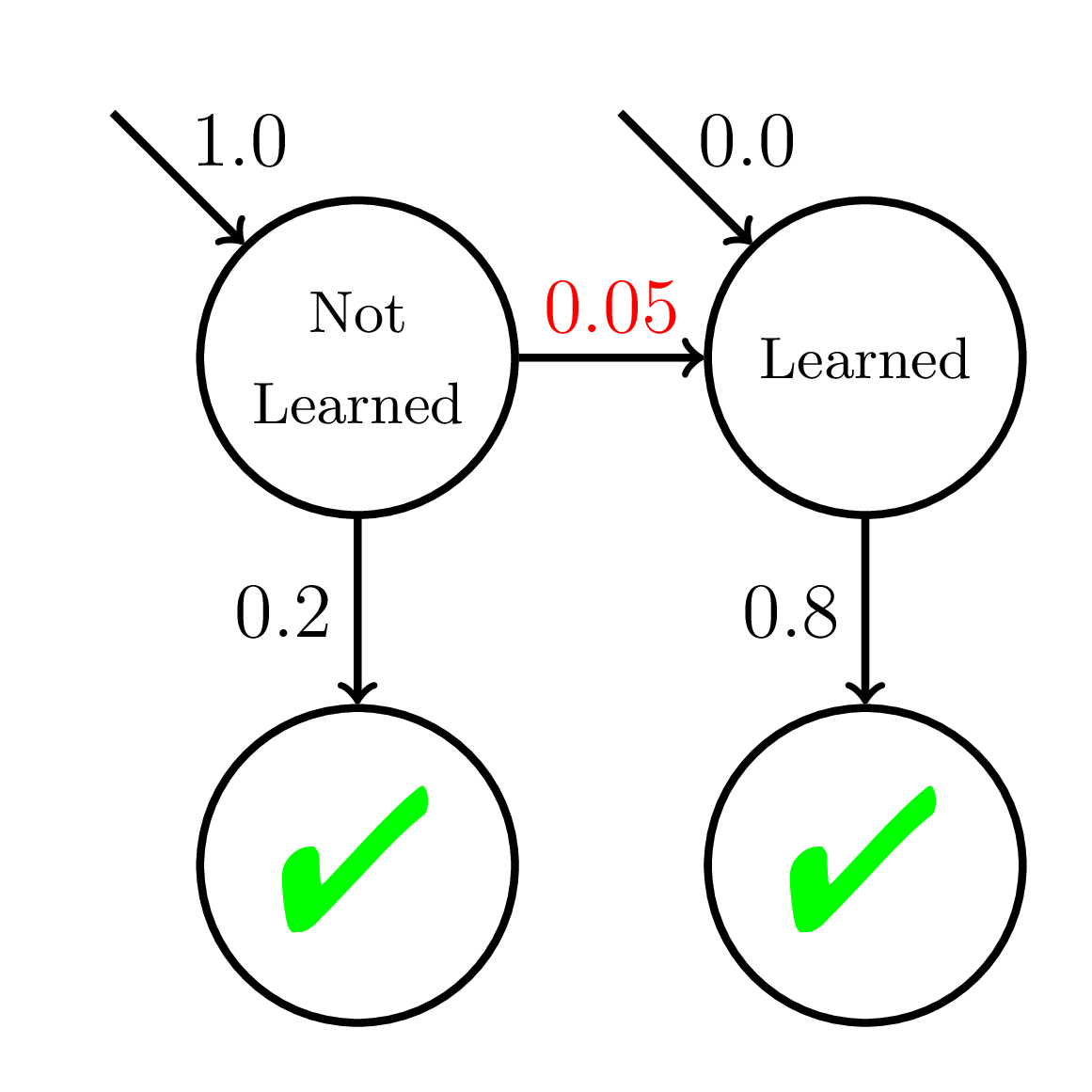
BKT-Mixed
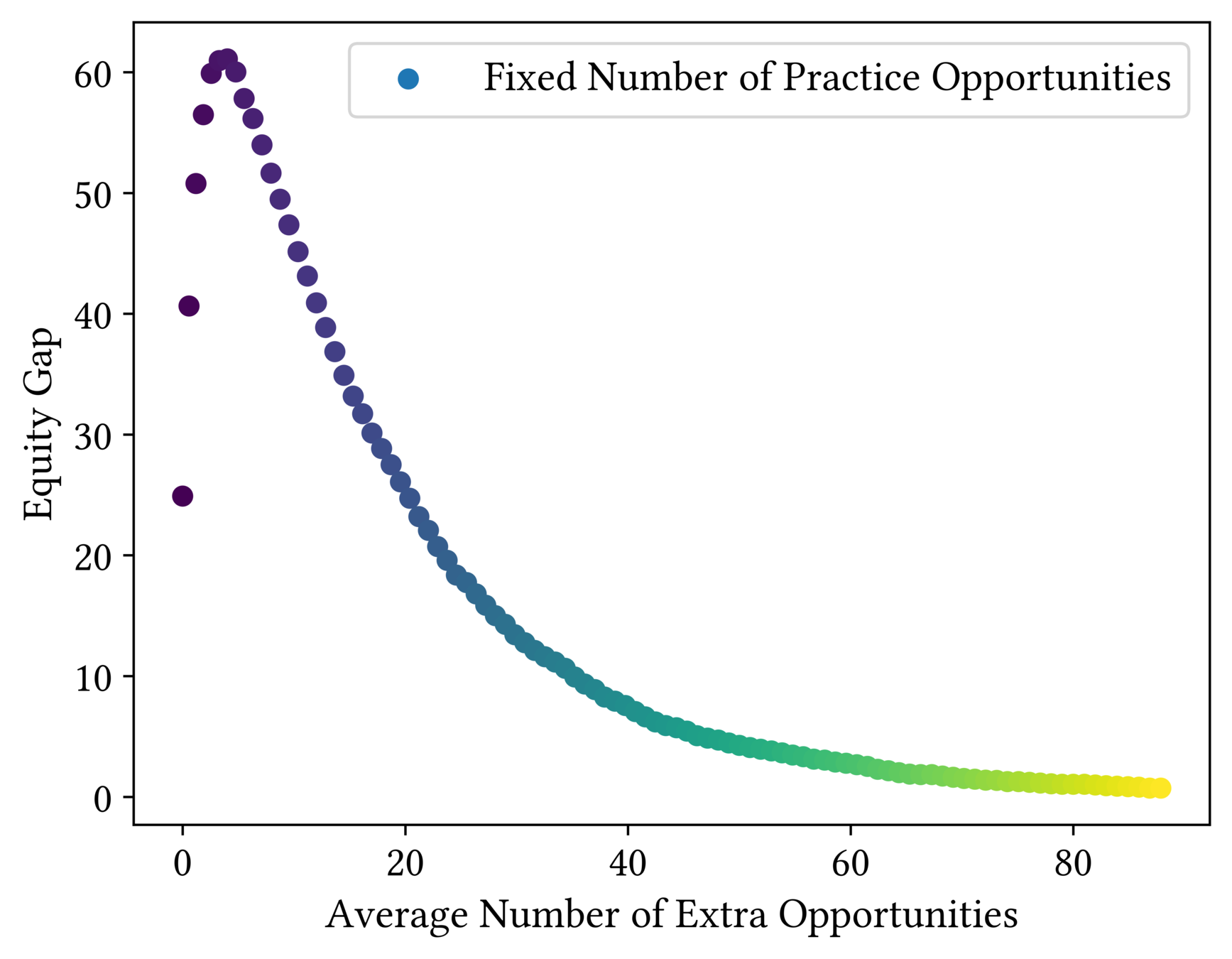
How Fair Is One-Size-Fits-All?
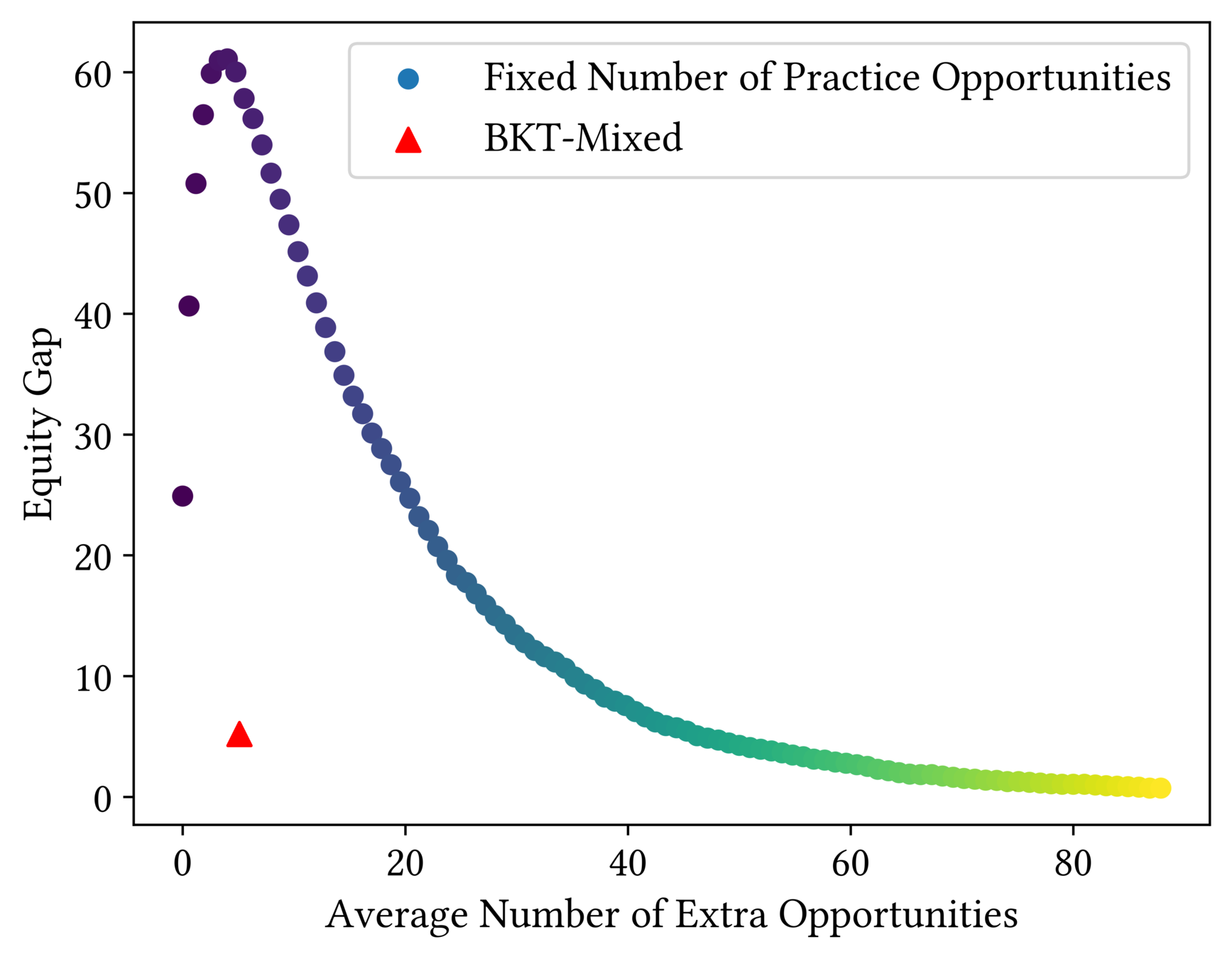
How Fair is BKT?

Inequitable!
How Fair is BKT?
Equitability of Knowledge Tracing
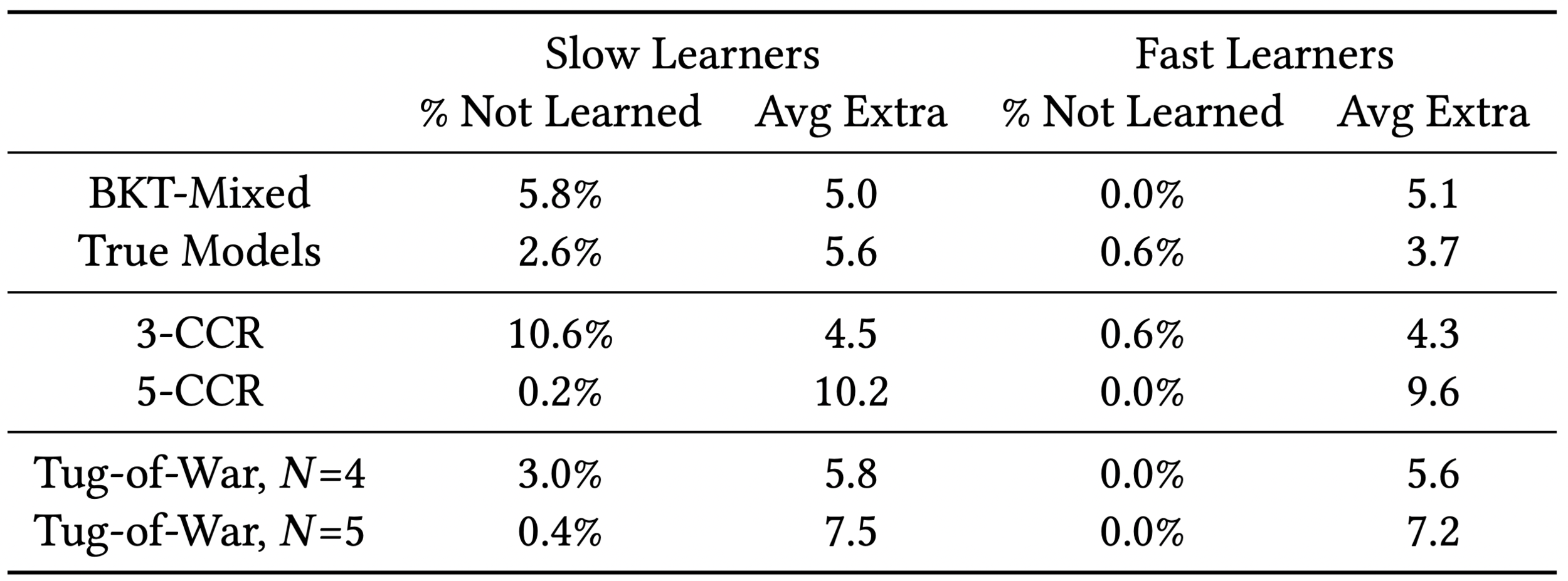
Solution: Tug-of-War Heuristic

Tug-of-War heuristic not make assumptions about the learning rate!
Equitability of Mastery Learning Heuristics

Equitability of Mastery Learning Heuristics

Takeaway
The Tug-of-War heuristic can be more equitable since it does not make assumptions about the rate of learning.
but...
it still assumes learning is all-or-nothing!
What if learning is not all-or-nothing?
200 students
20 practice opportunities
200 students
20 practice opportunities
Fast Learners
Slow Learners
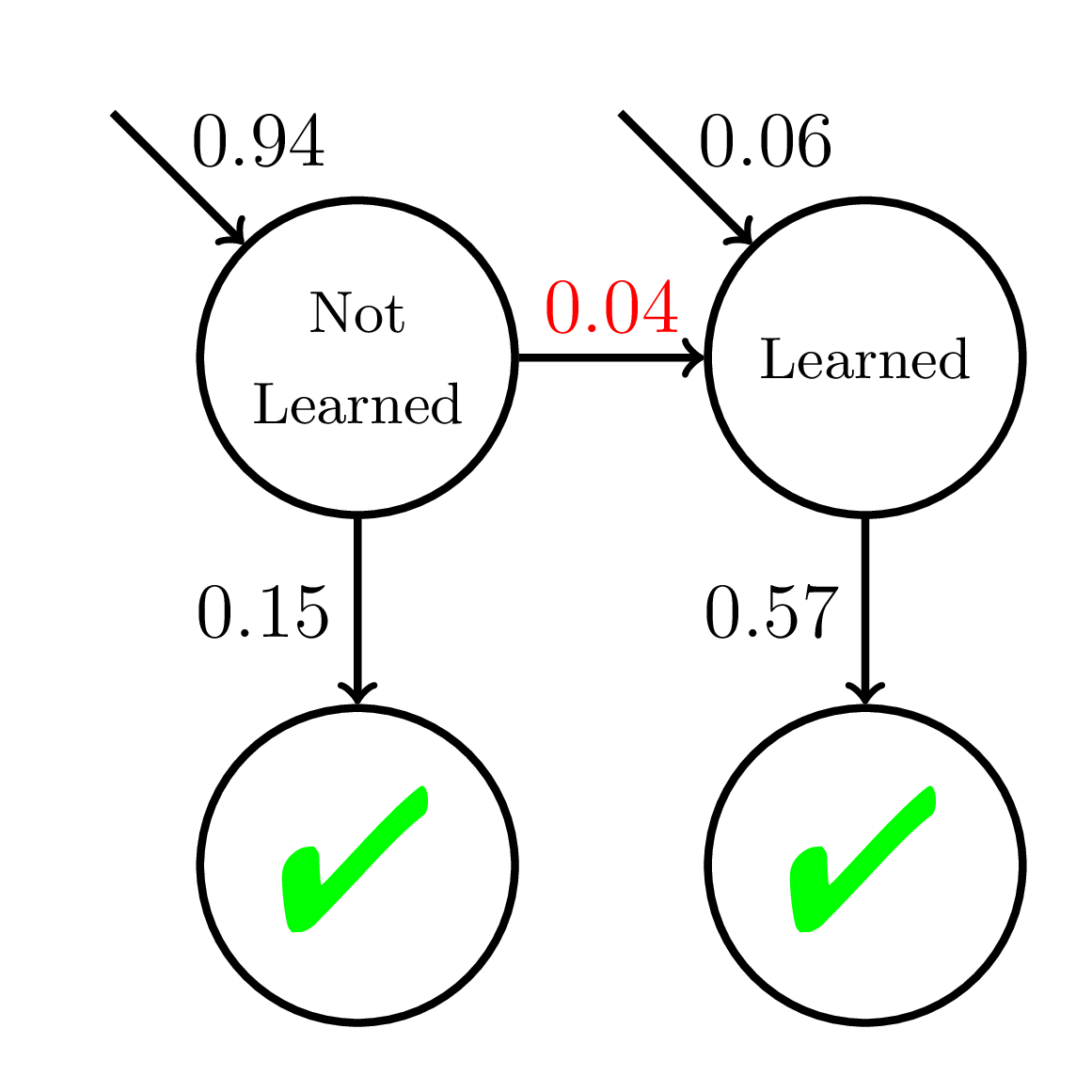
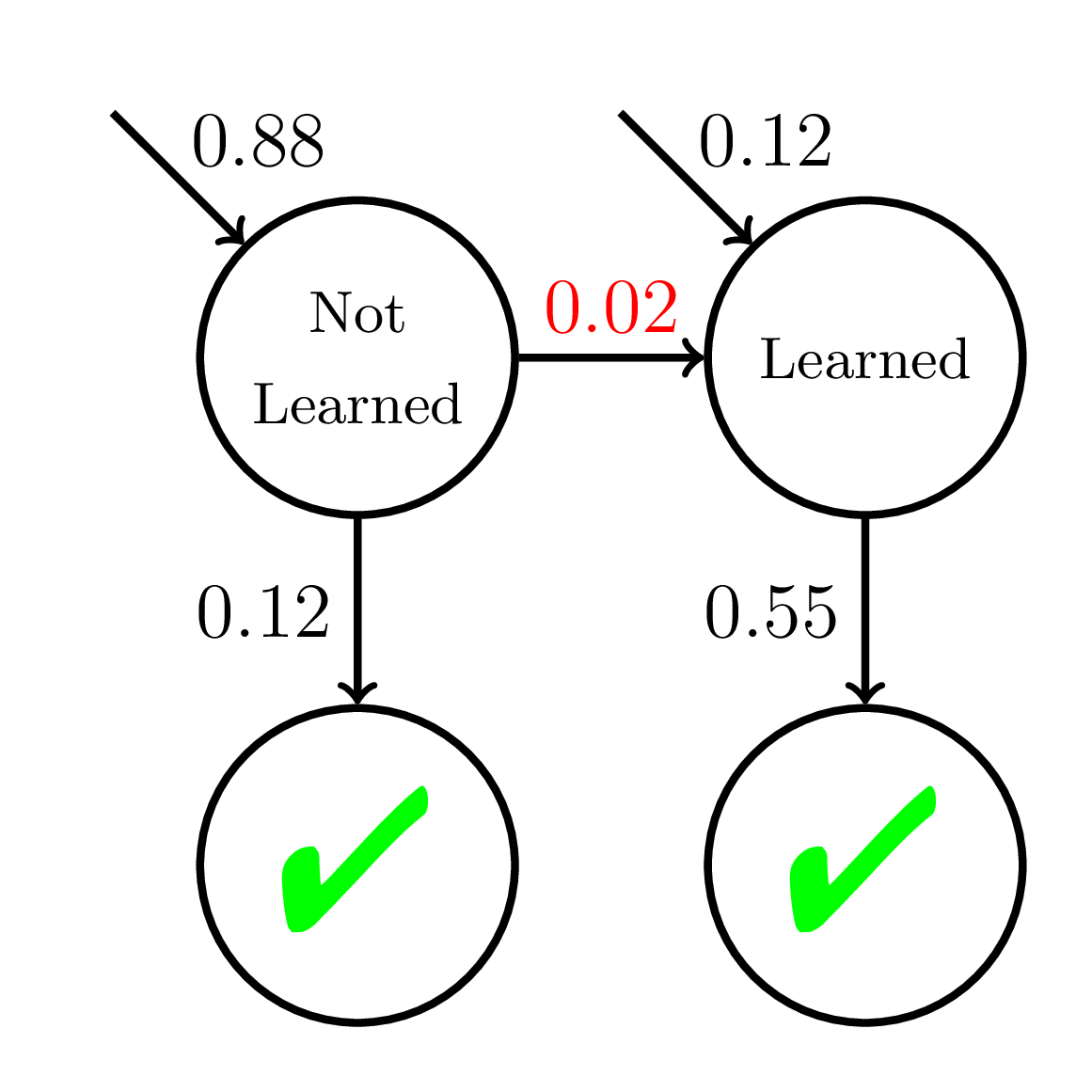
Equity of Wrong Model
Average P(Correct)
at Mastery:
0.56
Average P(Correct) at Mastery:
0.45


Mastery
Learning


Mastery
Learning
Fast Learners
Slow Learners


Equity of Wrong Model
In Search of Equitable Algorithms
We do not really know how students learn, so we need to look for mastery learning algorithms that are robust to different assumptions about learning.
The Tug-of-War heuristic is robust to different assumptions about when or how fast a student will learn, but not whether learning is a gradual process.
But What is Equity?
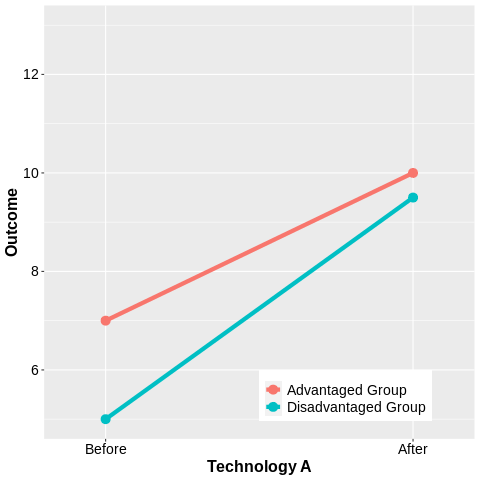
But What is Equity?
All students should get the same treatment?
All students should reach the same level of mastery.
Personalized learning algorithms are built on disparate treatment...
Every student should be allowed to achieve their full potential.
This could result in widening achievement gaps.
This could result in holding some students back.
The solution is not purely technical.
We must determine what we value.
In Search of Equitable Algorithms
We must design socio-technical solutions that align with those values.
Takeaways
Simple solutions can go a long way, but they still have shortcomings.
But simple solutions can also help us surface our own assumptions and make their shortcomings explicit.
We can only achieve equity if we put our assumptions and values on the table.
Acknowledgements
Doroudi, S. (2020, July). Mastery learning heuristics and their hidden models. In Proceedings of the 21st International Conference on Artificial Intelligence in Education (pp. 86-91). Springer.
Doroudi, S., & Brunskill, E. (2019, March). Fairer but not fair enough: On the equitability of knowledge tracing. In Proceedings of the 9th International Conference on Learning Analytics & Knowledge (pp. 335-339). ACM.
Some of this work was done with Emma Brunskill at Stanford University and was supported in part by a Google grant and a Microsoft Research Faculty Fellowship.
References:
Backup Slides
Fairness of Various Algorithms
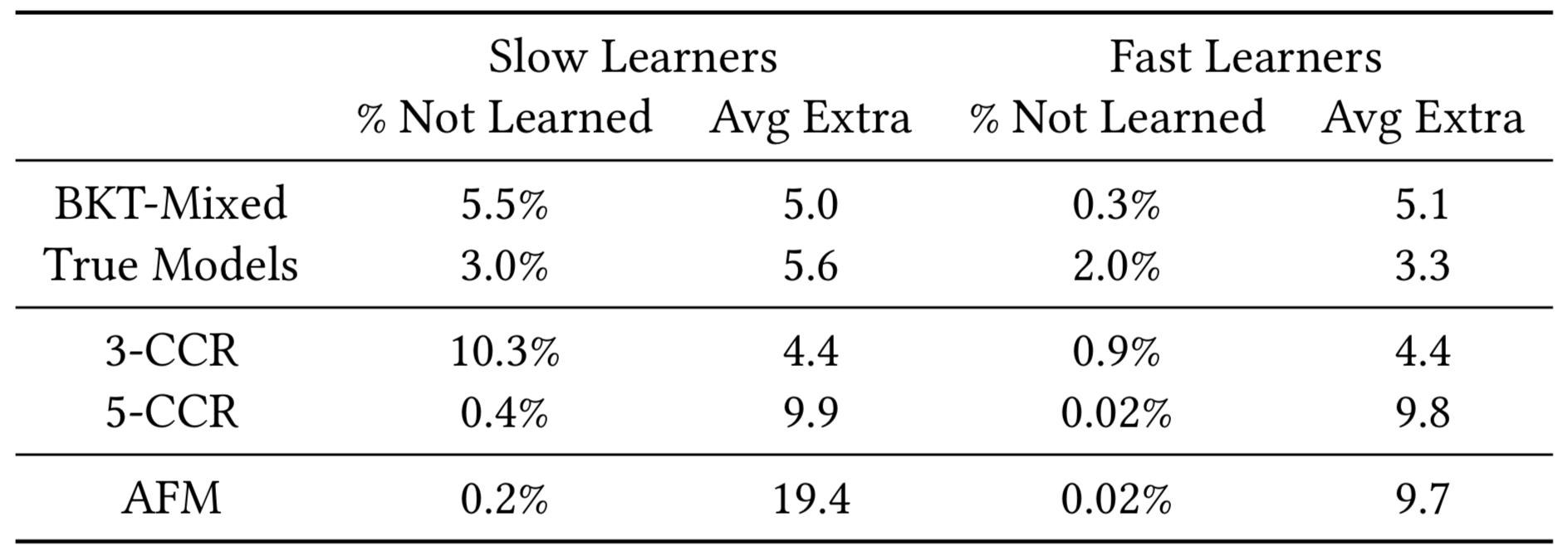
|
Student Models |
Mastery Learning BKT |
|---|---|
| AFM - Fast Learners | 56% |
| AFM - Slow Learners | 45% |
Equity Under Model Mismatch
|
Student Models |
Mastery Learning BKT |
|---|---|
| AFM - Fast Learners | 56% |
| AFM - Slow Learners | 45% |
| BKT - Fast Learners | 98%* |
| BKT - Slow Learners | 97.3%* |
*Percent of students who are in learned state.
Equity Under Model Mismatch
|
Student Models |
Mastery Learning
BKT |
Mastery Learning AFM |
|---|---|---|
| AFM - Fast Learners | 56% | 96% |
| AFM - Slow Learners | 45% | 95% |
| BKT - Fast Learners | 98%* | |
| BKT - Slow Learners | 97.3%* |
*Percent of students who are in learned state.
Equity Under Model Mismatch
Equity Under Model Mismatch
|
Student Models |
Mastery Learning
BKT |
Mastery Learning AFM |
|---|---|---|
| AFM - Fast Learners | 56% | 96% |
| AFM - Slow Learners | 45% | 95% |
| BKT - Fast Learners | 98%* | 99.8%* |
| BKT - Slow Learners | 97.3%* | 99.5%* |
*Percent of students who are in learned state.