Simulating Adaptive Policies
Shayan Doroudi
University of California, Irvine
LearnLab 2021 Summer School CML Track



InstructionalPolicy
Activity
Response


Outer Loop
Adaptive Policy
Activity
Response


Non-Adaptive Policy
Activity
Response

InstructionalPolicy
Activity
Response


Student
Model
We can evaluate how well an instructional policy will perform by simulating it with a student model.
InstructionalPolicy
Activity
Response


Student
Model
We can also evaluate the quality of a model by seeing how well it predicts the results of an instructional policy.
Data

Real
Data
compare with
InstructionalPolicy
Activity
Response


Student
Model

InstructionalPolicy
Activity
Response


Student
Model

Data


InstructionalPolicy
Activity
Response


Student
Model

Data


Student
Model
Student
Model
InstructionalPolicy
Activity
Response


Student
Model

Student
Model
Eval
Model
InstructionalPolicy
Activity
Response


Policy
Model

Eval
Model
InstructionalPolicy
Activity
Response


Policy
Model

Two Kinds of Models
Computational Models
Statistical Models
Theory-Driven
(Cognitive Science)
Data-Driven
(Machine Learning)
Predictive Models
Mechanistic Models
(e.g., AL, ACT-R)
(e.g., BKT, AFM, DKT)
Can be treated as mechanistic models, but they are often loosely theoretically motivated.
Comp
Model
InstructionalPolicy
Activity
Response


Stat
Model

Two Kinds of Models
Stat
Model
InstructionalPolicy
Activity
Response


Stat
Model

Two Kinds of Models
Comp
Model
InstructionalPolicy
Activity
Response


Comp
Model

Two Kinds of Models
Stat
Model
InstructionalPolicy
Activity
Response


Comp
Model

Two Kinds of Models
Bayesian Knowledge Tracing (BKT)

Corbett and Anderson, 1995
Mastery Learning
Keep giving practice opportunities on a skill/concept until student reaches mastery:
Then move onto the next skill/concept
Corbett and Anderson, 1995
Bayesian Knowledge Tracing (BKT)
Doroudi and Brunskill, 2017
Be careful of interpreting BKT as a mechanistic model!
When there is model misspecification, the parameters might not mean what you think they do!
Additive Factor Model (AFM)
Cen, 2009
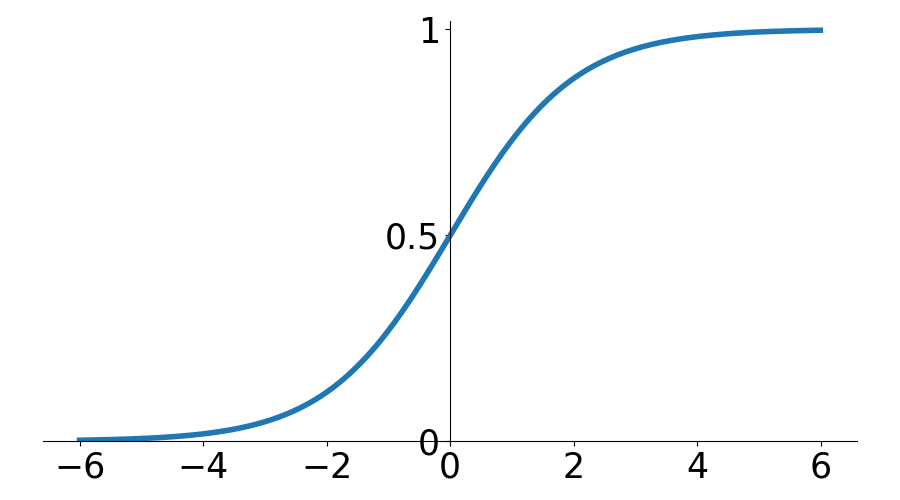
\(\theta\) - Student Ability \(\sim \mathcal{N}(0, 1)\)
\(\beta\) - Item Difficulty
\(\gamma\) - Learning Rate
P(Correct)
Eval
Model
InstructionalPolicy
Activity
Response


Policy
Model

Different Kinds of Instructional Decisions
Determine how to sequence different types of activities (e.g., videos vs. worked examples vs. problems)
Determine “when to stop” (i.e., how many problems to give for each KC).
Determine when to revisit certain skills (e.g., spaced practice)
Determine how to sequence different pieces of interrelated content
Eval
Model
InstructionalPolicy
Activity
Response


Policy
Model

Different Kinds of Policies
BKT Mastery Learning Policy
Streak Heuristic (N-CCR)
Tug-of-War Heuristic
Reinforcement Learning Based Adaptive Policies
(Markov Decision Processes)
Spaced Repetition Policies
Tug-of-War Heuristic
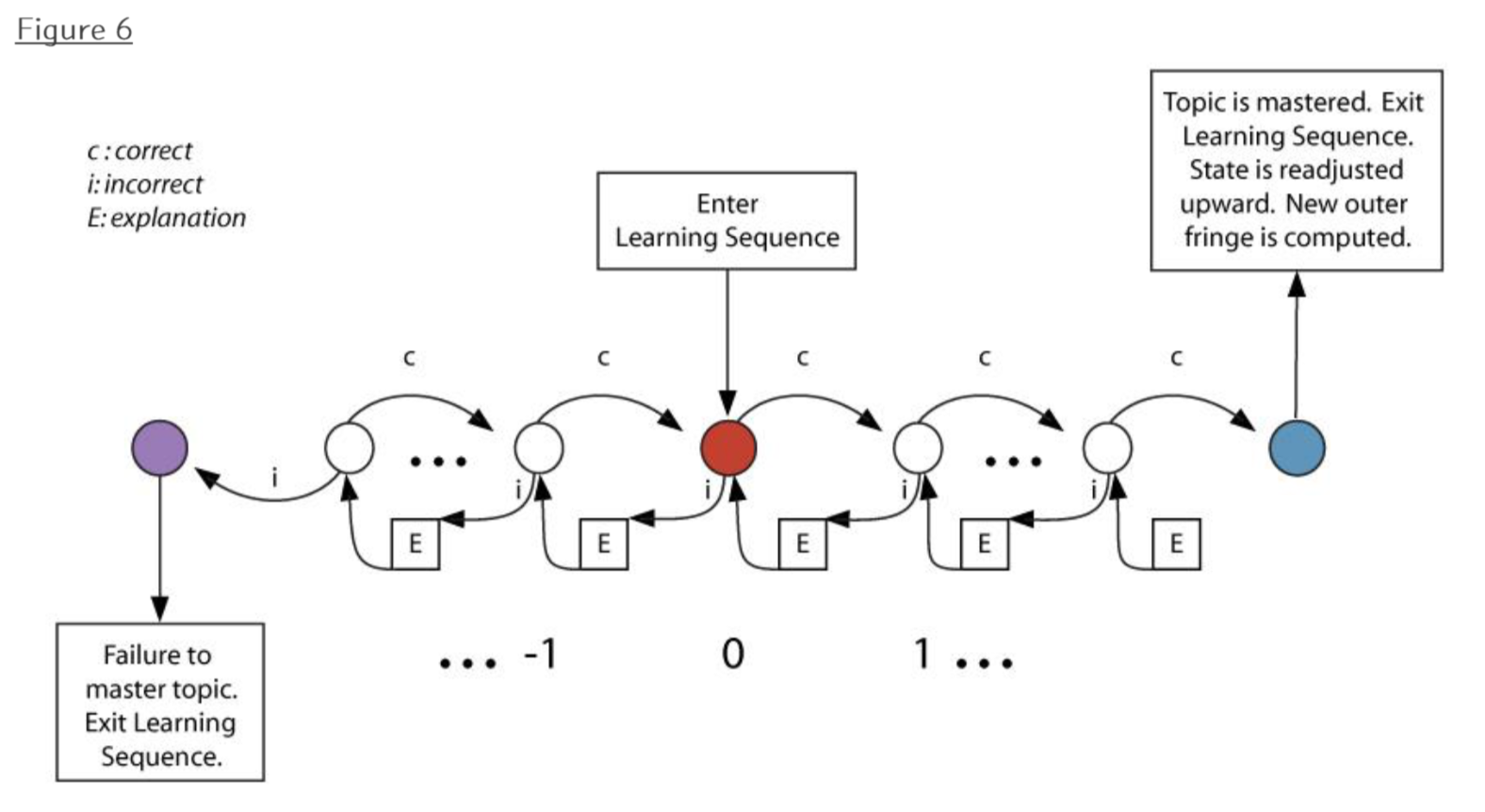
From ALEKS / McGraw Hill Education
Policies in Practice
Many policies used in commercial adaptive learning platforms are not data-driven:
- Carnegie Learning's BKT model parameters are determined by experts
- ALEKS uses a heuristic policy.
- Khan Academy and ASSISTments use variants of the streak heuristic.
- Commercial spaced repetition software use heuristics like SuperMemo or Leitner System.
Eval
Model
InstructionalPolicy
Activity
Response


Policy
Model

How Do We Get a Policy?
Optimization
Can use techniques from reinforcement learning (e.g., MDP planning) to directly obtain the optimal policy for any model.
Give the KC least likely to be known
Karush and Dear, 1967
For BKT, assuming we want to maximize the number of KCs learned and each KC is independent, the optimal policy is:
Optimization
Can use techniques from reinforcement learning (e.g., MDP planning) to directly obtain the optimal policy for any model.
BKT Mastery Learning Policy
For BKT, if we want to teach each KC to mastery before moving on, the “optimal” policy is:
How Do We Get a Policy?
Optimization
Can use techniques from reinforcement learning (e.g., MDP planning) to directly obtain the optimal policy for any model.
For BKT with \(P(S) = 0\), if we want to teach each KC to mastery before moving on, the “optimal” policy is:
Streak Heuristic (N-CCR)
Doroudi, 2020
How Do We Get a Policy?
Optimization
Can use techniques from reinforcement learning (e.g., MDP planning) to directly obtain the optimal policy for any model.
If we make the all-or-nothing assumption of BKT, but do not know anything about the probability of learning, the “optimal” policy is:
Tug-of-War Heuristic
Doroudi, 2020
How Do We Get a Policy?
Simulation
Policy
Model
Response
Activity


Different Kinds of Simulations:
- Try every activity, and pick the best.
- Run several sequences of activities, and pick the best first activity.
- Run several sequences of activities many times, and pick the best first activity.
How Do We Get a Policy?
How Do we Get a Policy?
Simulation
Policy
Model
Activity
Response


How Do we Get a Policy?
Simulation
Policy
Model
Response
Activity


Eval
Model
InstructionalPolicy
Activity
Response


Policy
Model

Policy
Model
InstructionalPolicy
Activity
Response


Policy
Model

Direct Model-Based Evaluation
Likely to be overly optimistic about policy’s performance!
Eval
Model
InstructionalPolicy
Activity
Response


Policy
Model

Robust Evaluation
Eval
Model
Policy
Model
Robust Evaluation Matrix
Doroudi, Aleven, and Brunskill, Learning @ Scale 2017
| Student Models | Policy 1 |
Policy 2 |
Policy 3 |
|---|---|---|---|
| Student Model 1 | |||
| Student Model 2 | |||
| Student Model 3 |
\(V_{SM_1,P_1}\) \(V_{SM_1,P_2}\) \(V_{SM_1,P_3}\)
\(V_{SM_2,P_1}\) \(V_{SM_2,P_2}\) \(V_{SM_2,P_3}\)
\(V_{SM_3,P_1}\) \(V_{SM_3,P_2}\) \(V_{SM_3,P_3}\)
Data
New Instructional Policy





Experiment
New
Model
Fractions
Tutor
Fractions
Tutor


Fractions
Tutor
vs.
Baseline Policy
Doroudi, Aleven, and Brunskill, Learning @ Scale 2017
Simulated Experiment
New
Model
New
Model
Doroudi, Aleven, and Brunskill, Learning @ Scale 2017
Data
New Instructional Policy





New
Model
Fractions
Tutor


vs.
Baseline Policy
| Baseline Policy |
Adaptive Policy | |
|---|---|---|
| Simulated Results | 5.9 ± 0.9 | 9.1 ± 0.8 |
Doroudi, Aleven, and Brunskill, Learning @ Scale 2017
Posttest Scores (out of 16 points)
Simulation Results
| Baseline Policy |
Adaptive Policy | |
|---|---|---|
| Simulated Results | 5.9 ± 0.9 | 9.1 ± 0.8 |
| Experimental Results | 5.5 ± 2.6 | 4.9 ± 1.8 |
Posttest Scores (out of 16 points)
Doroudi, Aleven, and Brunskill, Learning @ Scale 2017
Experiment Results
Robust Evaluation
| Baseline Policy |
Adaptive Policy | |
|---|---|---|
| New Model | 5.9 ± 0.9 | 9.1 ± 0.8 |
Doroudi, Aleven, and Brunskill, Learning @ Scale 2017
Posttest Scores (out of 16 points)
Robust Evaluation
| Baseline Policy |
Adaptive Policy | |
|---|---|---|
| New Model | 5.9 ± 0.9 | 9.1 ± 0.8 |
| Bayesian Knowledge Tracing | 6.5 ± 0.8 | 7.0 ± 1.0 |
Doroudi, Aleven, and Brunskill, Learning @ Scale 2017
Posttest Scores (out of 16 points)
Robust Evaluation
| Baseline Policy |
Adaptive Policy | |
|---|---|---|
| New Model | 5.9 ± 0.9 | 9.1 ± 0.8 |
| Bayesian Knowledge Tracing | 6.5 ± 0.8 | 7.0 ± 1.0 |
| Deep Knowledge Tracing | 9.9 ± 1.5 | 8.6 ± 2.1 |
Doroudi, Aleven, and Brunskill, Learning @ Scale 2017
Posttest Scores (out of 16 points)
Robust Evaluation Matrix
| Student Models |
Baseline Policy |
Adaptive Policy |
|---|---|---|
| New Model | 5.9 ± 0.9 | 9.1 ± 0.8 |
| Bayesian Knowledge Tracing | 6.5 ± 0.8 | 7.0 ± 1.0 |
| Deep Knowledge Tracing | 9.9 ± 1.5 | 8.6 ± 2.1 |
Doroudi, Aleven, and Brunskill, Learning @ Scale 2017
Posttest Scores (out of 16 points)
Robust Evaluation Matrix
| Student Models |
Baseline Policy |
Adaptive Policy | Awesome Policy |
|---|---|---|---|
| New Model | 5.9 ± 0.9 | 9.1 ± 0.8 | 16 |
| Bayesian Knowledge Tracing | 6.5 ± 0.8 | 7.0 ± 1.0 | 16 |
| Deep Knowledge Tracing | 9.9 ± 1.5 | 8.6 ± 2.1 | 16 |
Doroudi, Aleven, and Brunskill, Learning @ Scale 2017
Posttest Scores (out of 16 points)
(not real!)
Robust Evaluation Matrix
Doroudi, Aleven, and Brunskill, Learning @ Scale 2017
| Student Models | Policy 1 |
Policy 2 |
Policy 3 |
|---|---|---|---|
| Demographic 1 | |||
| Demographic 2 | |||
| Demographic 3 |
\(V_{SM_1,P_1}\) \(V_{SM_1,P_2}\) \(V_{SM_1,P_3}\)
\(V_{SM_2,P_1}\) \(V_{SM_2,P_2}\) \(V_{SM_2,P_3}\)
\(V_{SM_3,P_1}\) \(V_{SM_3,P_2}\) \(V_{SM_3,P_3}\)
Can tell us which policies are equitable
Robust Evaluation Matrix
|
Student Models |
Mastery Learning BKT |
|---|---|
| AFM - Fast Learners | 56% |
| AFM - Slow Learners | 45% |
Doroudi and Brunskill, 2019
Robust Evaluation Matrix
|
Student Models |
Mastery Learning BKT |
|---|---|
| AFM - Fast Learners | 56% |
| AFM - Slow Learners | 45% |
| BKT - Fast Learners | 98%* |
| BKT - Slow Learners | 97.3%* |
*Percent of students who are in learned state.
Doroudi and Brunskill, 2019
|
Student Models |
Mastery Learning
BKT |
Mastery Learning AFM |
|---|---|---|
| AFM - Fast Learners | 56% | 96% |
| AFM - Slow Learners | 45% | 95% |
| BKT - Fast Learners | 98%* | |
| BKT - Slow Learners | 97.3%* |
*Percent of students who are in learned state.
Robust Evaluation Matrix
Doroudi and Brunskill, 2019
|
Student Models |
Mastery Learning
BKT |
Mastery Learning AFM |
|---|---|---|
| AFM - Fast Learners | 56% | 96% |
| AFM - Slow Learners | 45% | 95% |
| BKT - Fast Learners | 98%* | 99.8%* |
| BKT - Slow Learners | 97.3%* | 99.5%* |
*Percent of students who are in learned state.
Robust Evaluation Matrix
Doroudi and Brunskill, 2019
We attempt to treat the same problem with several alternative models each with different simplifications but with a common...assumption. Then, if these models, despite their different assumptions, lead to similar results, we have what we can call a robust theorem that is relatively free of the details of the model.
Hence, our truth is the intersection of independent lies.
- Richard Levins, 1966
“All Models are Wrong
But Some are Useful”
George Box, 1979
Acknowledgements
The research reported here was supported, in whole or in part, by the Institute of Education Sciences, U.S. Department of Education, through Grants R305A130215 and R305B150008 to Carnegie Mellon University. The opinions expressed are those of the authors and do not represent views of the Institute or the U.S. Dept. of Education.
Some of the work reported here was written in papers with co-authors Emma Brunskill and Vincent Aleven.
References
Box, G. E. (1979). Robustness in the strategy of scientific model building. In Robustness in statistics (pp. 201-236).
Cen, H. (2009). Generalized learning factors analysis: improving cognitive models with machine learning (Doctoral dissertation). Carnegie Mellon University, Pittsburgh, PA.
Chi, M., VanLehn, K., Litman, D., & Jordan, P. (2011). Empirically evaluating the application of reinforcement learning to the induction of effective and adaptive pedagogical strategies. User Modeling and User-Adapted Interaction, 21(1-2), 137-180.
Cobb, P. (1990). A constructivist perspective on information-processing theories of mathematical activity. International Journal of Educational Research, 14(1), 67-92.
Corbett, A. T., & Anderson, J. R. (1994). Knowledge tracing: Modeling the acquisition of procedural knowledge. User modeling and user-adapted interaction, 4(4), 253-278.
Doroudi, S., & Brunskill, E. (2017, June). The misidentified identifiability problem of Bayesian Knowledge Tracing. In Proceedings of the 10th International Conference on Educational Data Mining. International Educational Data Mining Society.
References
Doroudi, S. & Brunskill, E. (2019, March). Fairer but not fair enough: On the equitability of knowledge tracing. To appear in Proceedings of the 9th International Learning Analytics & Knowledge Conference. ACM.
Doroudi, S., Aleven, V., & Brunskill, E. (2017, April). Robust evaluation matrix: Towards a more principled offline exploration of instructional policies. In Proceedings of the Fourth (2017) ACM Conference on Learning@ Scale (pp. 3-12). ACM.
Doroudi, S., Aleven, V. & Brunskill, E. (2018). Where's the reward? A review of reinforcement learning for instructional sequencing. Manuscript in submission.
Duncan, O. D. (1975). Introduction to structural equation models. Elsevier.
Greeno, J. G. (1998). The situativity of knowing, learning, and research. American psychologist, 53(1), 5.
Rowe, J. P., Mott, B. W., & Lester, J. C. (2014). Optimizing Player Experience in Interactive Narrative Planning: A Modular Reinforcement Learning Approach. AIIDE, 3, 2.
Backup Slides



Over 500,000 students/year
25 million active monthly users
~12 million active monthly users
Student
Model
Data








Model-Based Instructional Sequencing in 1960s
Photos from suppes-corpus.stanford.edu