All Student Models are Wrong
But Some are Useful

Shayan Doroudi
 

December 3, 2018

University of California, Irvine

Student
Model

Data

Instructional Policy

Activity

Response

Millions of students

Model-Based Instructional Sequencing

Over 500,000 students/year

25 million active monthly users

~12 million active monthly users

Student
Model

Data

Model-Based Instructional Sequencing in 1960s

Photos from suppes-corpus.stanford.edu

“We assume that a mathematical model of learning will provide an approximate description of the student's learning, and the task for a theory of instruction is then to settle the question of how the instructional sequence of concepts, skills, and facts should be organized to optimize for a given student his rate of learning.”

Suppes (1974)

The Place of Theory in Educational Research

AERA Presidential Address

“It would be my prediction that we will see increasingly sophisticated theories of instruction in the near future.”

Student
Model

Data

Instructional Policy

We haven’t seen “increasingly sophisticated theories of instruction”

Student
Model

Data

Instructional Policy

“All Models are Wrong
But Some are Useful”

George Box, 1979

Statistical Models of Student Learning

≠

How Students Learn

2. Relying on a wrong model can have adverse consequences for students.

1. Undesirable behaviors of student models can be explained by using a wrong model.

I will demonstrate...

Three Consequences of a Wrong Model

Misguided Inferences about Learning

Misguided Instructional Decisions

Inequitable Outcomes

All Student Models are Wrong

But Some are Useful

Data-Driven Models + Learning Theory

Misguided Instructional Decisions

Inequitable Outcomes

Misguided Inferences about Learning

Robustness to How Students Learn

Student Models

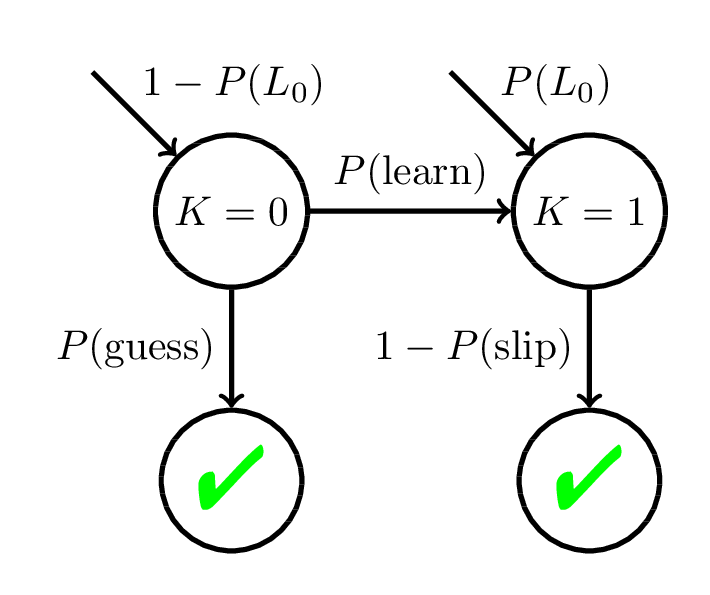
Bayesian Knowledge Tracing (BKT)

Corbett and Anderson, 1994

Bayesian Knowledge Tracing (BKT)

Data

Student A: 

Student B: 

Student C: 

...

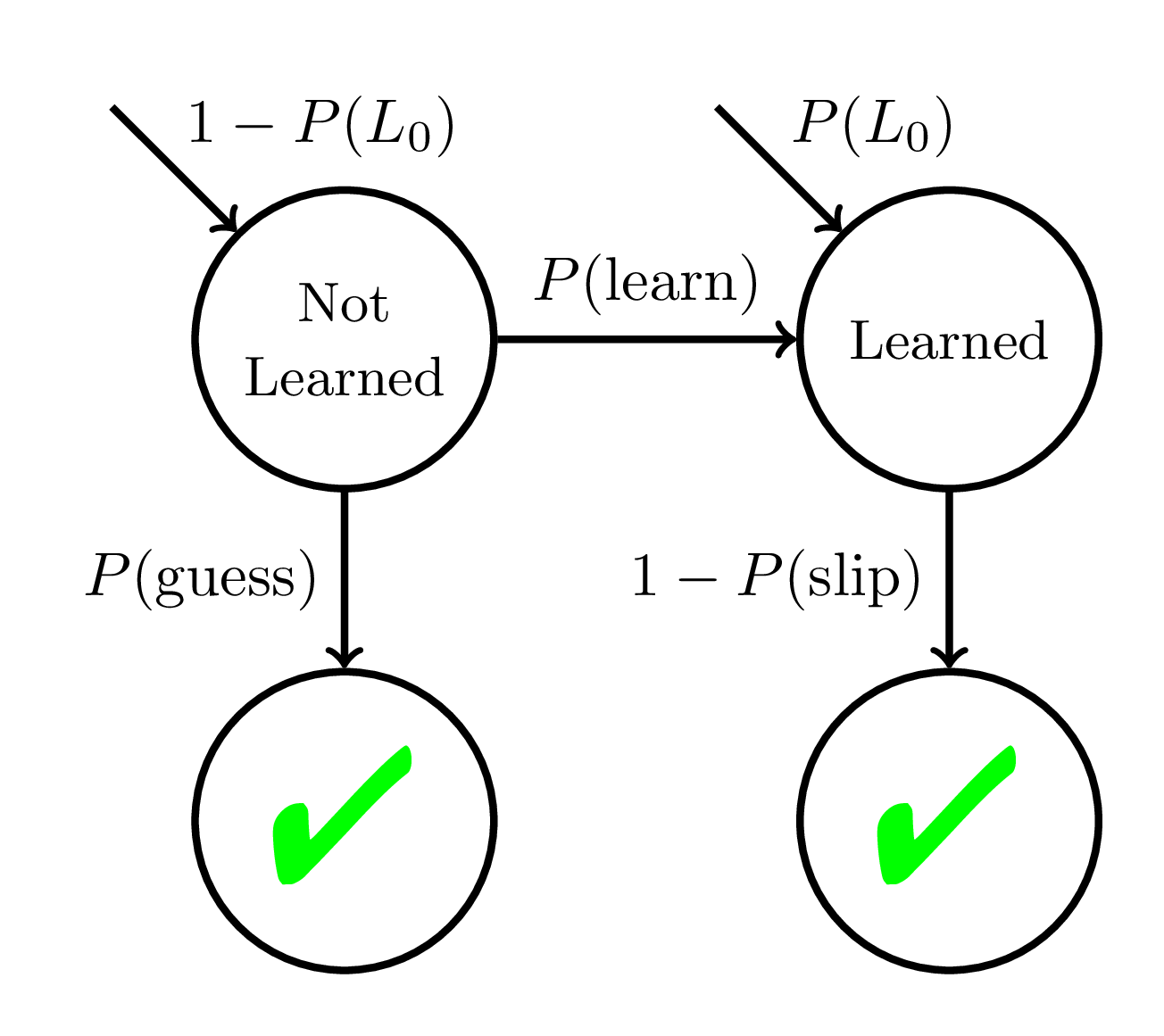
Bayesian Knowledge Tracing (BKT)

Data

Student A: 

Student B: 

Student C: 

...

Machine Learning

Bayesian Knowledge Tracing (BKT)

Addition

Subtraction

Multiplication

Mastery Learning

Keep giving practice opportunities on a skill/concept until student reaches mastery:

P(\text{Learned}) > 0.95

Then move onto the next skill/concept

Corbett and Anderson, 1994

Data

Mastery
Learning

Rosen et al., 2018

Ritter et al., 2007

Corbett and Anderson, 1994

Additive Factor Model (AFM)

Cen, 2009

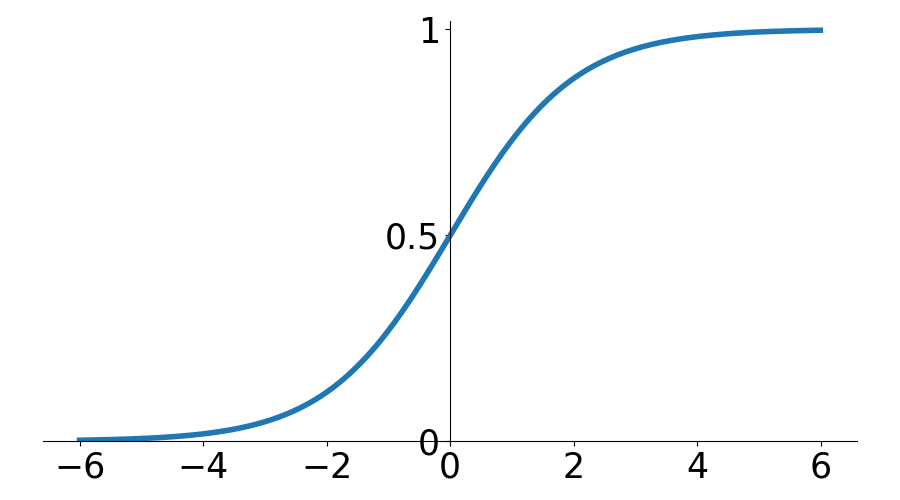
P(\text{Correct}) = \dfrac{1}{1 + \exp(-(\theta - \beta + \gamma t))}

\(\theta\) - Student Ability \(\sim \mathcal{N}(0, 1)\)

\(\beta\) - Item Difficulty

\(\gamma\) - Learning Rate

P(Correct)

\theta - \beta + \gamma t

All Student Models are Wrong

But Some are Useful

Data-Driven Models + Learning Theory

Misguided Instructional Decisions

Inequitable Outcomes

Misguided Inferences about Learning

Robustness to How Students Learn

Semantics of a BKT Model

75% of skills in a middle school mathematics tutoring system had P(guess) > 0.5 or P(slip) > 0.5

Baker, Corbett, and Aleven, 2008:

High guess and slip parameters are the result of BKT being unidentifiable.

Beck and Chang, 2007:

BKT Model actually is identifiable.

Semantics of a BKT Model

Doroudi and Brunskill, 2017:

High guess and slip parameters could be due to
fitting the wrong model.

Doroudi and Brunskill, Educational Data Mining 2017, Best Paper Nominee

Data

“Analysis of specification error relates to a rhetorical strategy in which we

suggest a model as the “true” one for sake of argument,

determine how our working model differs from it

and what the consequences of the difference(s) are,

and thereby get some sense of
how important the mistakes we will inevitably make may be.”

Otis Dudley Duncan, 1975

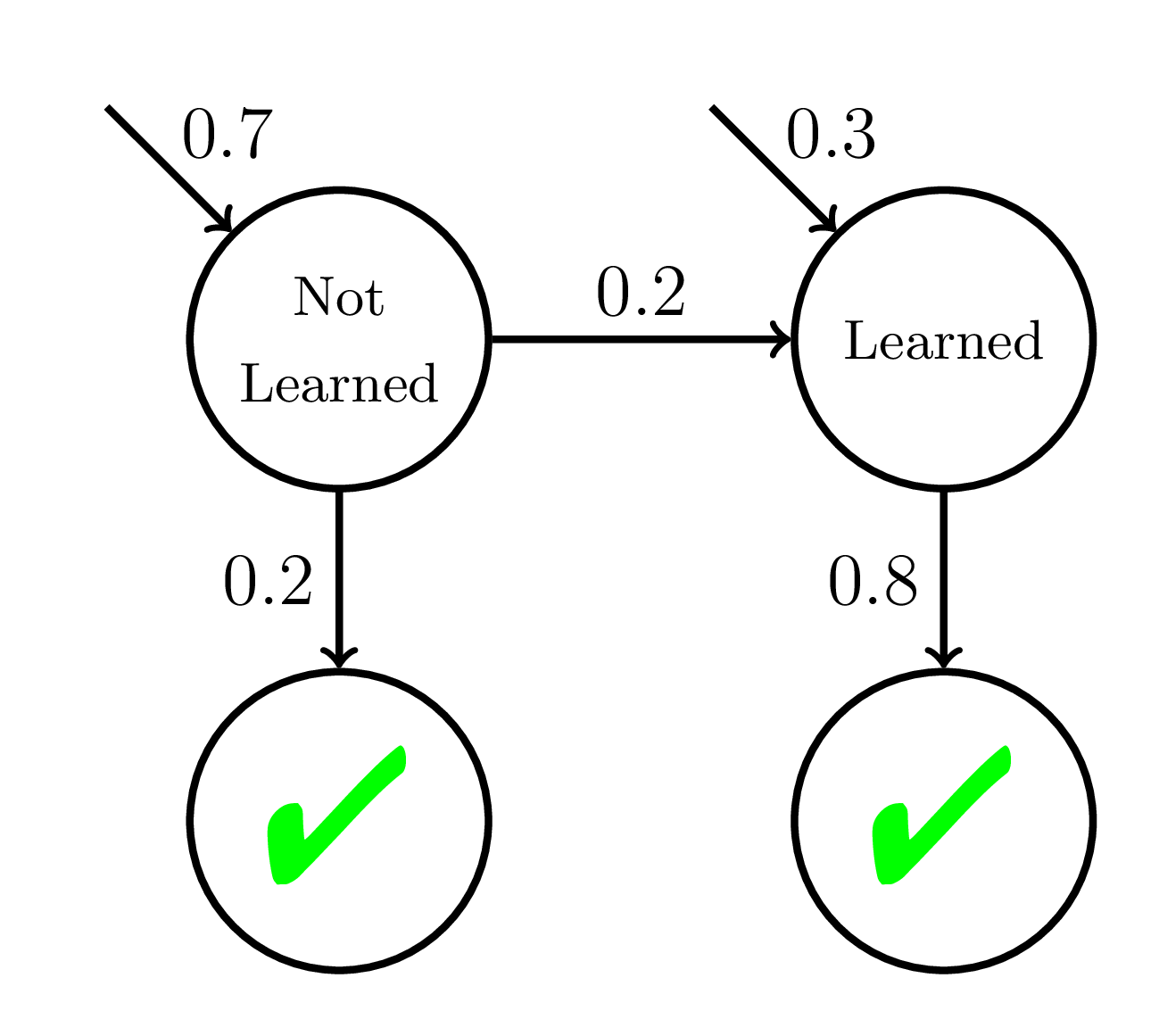
Semantics of a Wrong Model

P(\text{Correct}) = \dfrac{1}{1 + \exp(-(\theta - 2 + 0.1i))}
\theta \sim \mathcal{N}(0, 1)

P(Correct)

\theta - \beta + \gamma t

Doroudi and Brunskill, Educational Data Mining 2017, Best Paper Nominee

Semantics of a Wrong Model

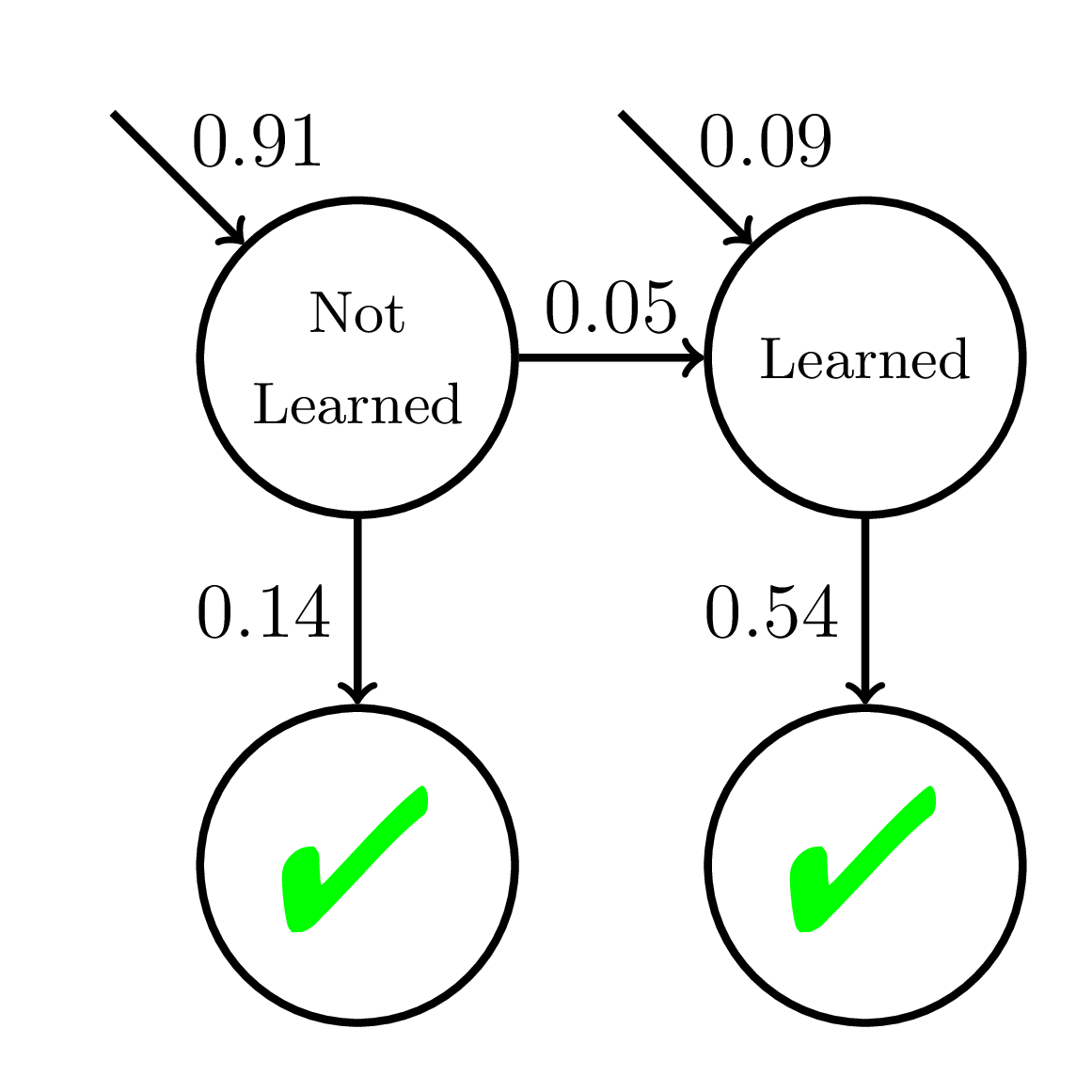
P(\text{Correct}) = \dfrac{1}{1 + \exp(-(\theta - 2 + 0.1i))}
\theta \sim \mathcal{N}(0, 1)

500 students

20 practice opportunities

High P(slip)!

P(Correct)

\theta - \beta + \gamma t

Doroudi and Brunskill, Educational Data Mining 2017, Best Paper Nominee

Not
Learned

Learned

Semantics of a Wrong Model

P(\text{Correct}) = \dfrac{1}{1 + \exp(-(\theta - 2 + 0.1i))}

100 students

200 practice opportunities

\theta \sim \mathcal{N}(0, 1)

High P(guess)!

Doroudi and Brunskill, Educational Data Mining 2017, Best Paper Nominee

P(Correct)

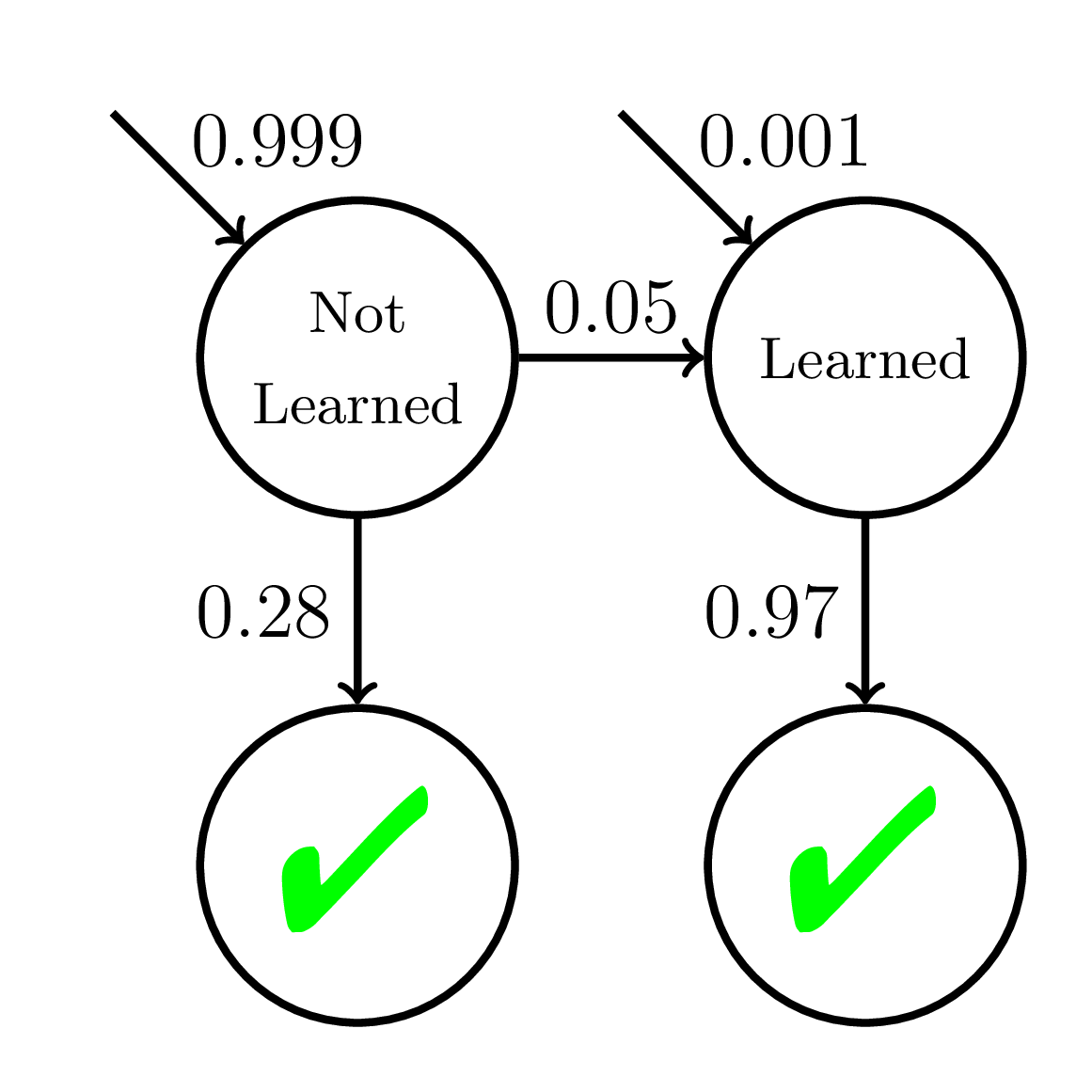
\theta - \beta + \gamma t

Not
Learned

Learned

Takeaway Message

Researcher

Incorrect inference

(e.g., throw out questions)

Data

Relying on the semantics of a wrong model can lead to incorrect inferences about student learning.

Takeaway Message

All Student Models are Wrong

But Some are Useful

Data-Driven Models + Learning Theory

Misguided Instructional Decisions

Inequitable Outcomes

Misguided Inferences about Learning

Robustness to How Students Learn

Data

Mastery
Learning

Misguided Notion of Mastery

P(\text{Correct}) = \dfrac{1}{1 + \exp(-(\theta - 2 + 0.1i))}
\theta \sim \mathcal{N}(0, 1)

Average P(Correct)
at Mastery:
0.54

P(Correct)

\theta - \beta + \gamma t

Mastery
Learning

Declare
Mastery

Data

Declare mastery early

Takeaway Message

Could have cascading effects that could impede on future learning.

Data

New Instructional Policy

Going Beyond Mastery Learning

New
Model

Fractions
Tutor

Fractions
Tutor

Around 1000 students

Data

New Instructional Policy

Experiment

New
Model

Fractions
Tutor

Fractions
Tutor

Fractions
Tutor

vs.

Baseline Policy

Doroudi, Aleven, and Brunskill, Learning @ Scale 2017

Simulated Experiment

New
Model

New
Model

Doroudi, Aleven, and Brunskill, Learning @ Scale 2017

Data

New Instructional Policy

New
Model

Fractions
Tutor

vs.

Baseline Policy

Baseline
Policy		 Adaptive Policy
Simulated Results 5.9 ± 0.9 9.1 ± 0.8

Doroudi, Aleven, and Brunskill, Learning @ Scale 2017

Posttest Scores (out of 16 points)

Simulation Results

Baseline
Policy		 Adaptive Policy
Simulated Results 5.9 ± 0.9 9.1 ± 0.8
Experimental Results 5.5 ± 2.6 4.9 ± 1.8

Posttest Scores (out of 16 points)

Doroudi, Aleven, and Brunskill, Learning @ Scale 2017

Experiment Results

Single Model Simulation

Fitted
Model

Fitted
Model

Chi et al., 2011
Rowe et al., 2014
Doroudi, Aleven, and Brunskill, Learning @ Scale 2017

Instructional
Policy

Robust Simulation

Fitted
Model

Instructional
Policy

“True”
Model

Doroudi, Aleven, and Brunskill, Learning @ Scale 2017

Robust Evaluation

Baseline
Policy		 Adaptive Policy
New Model 5.9 ± 0.9 9.1 ± 0.8

Doroudi, Aleven, and Brunskill, Learning @ Scale 2017

Posttest Scores (out of 16 points)

Robust Evaluation

Baseline
Policy		 Adaptive Policy
New Model 5.9 ± 0.9 9.1 ± 0.8
Bayesian Knowledge Tracing 6.5 ± 0.8 7.0 ± 1.0

Doroudi, Aleven, and Brunskill, Learning @ Scale 2017

Posttest Scores (out of 16 points)

Robust Evaluation

Baseline
Policy		 Adaptive Policy
New Model 5.9 ± 0.9 9.1 ± 0.8
Bayesian Knowledge Tracing 6.5 ± 0.8 7.0 ± 1.0
Deep Knowledge Tracing 9.9 ± 1.5 8.6 ± 2.1

Doroudi, Aleven, and Brunskill, Learning @ Scale 2017

Posttest Scores (out of 16 points)

Takeaway Message

Using a wrong student model can lead to incorrect inferences about the efficacy of an instructional policy.

All Student Models are Wrong

Semantics of a Wrong Model

But Some are Useful

Robust Models

Data-Driven Models + Learning Theory

Misguided Instructional Decisions

Inequitable Outcomes

Mastery learning intends to give each student
the right amount of instruction.

Equity of Mastery Learning

“The [BKT] model overestimates the true learning and performance parameters for below-average students who make many errors. While these students receive more remedial exercises than the above average students, they nevertheless receive less remedial practice than they need and perform worse on the test than expected.”

Corbett and Anderson, 1994

Corbett and Anderson, 1994

Equity of Mastery Learning

Corbett and Anderson, 1994
Doroudi and Brunskill, Learning Analytics & Knowledge 2019

Even after individualizing BKT parameters, they found that
low-performing students do worse on the test.

This inequity could be due to fitting the wrong model.

Doroudi and Brunskill, 2019:

Solution: Individualize BKT parameters for different students.

Corbett and Anderson, 1994

Equity of Mastery Learning

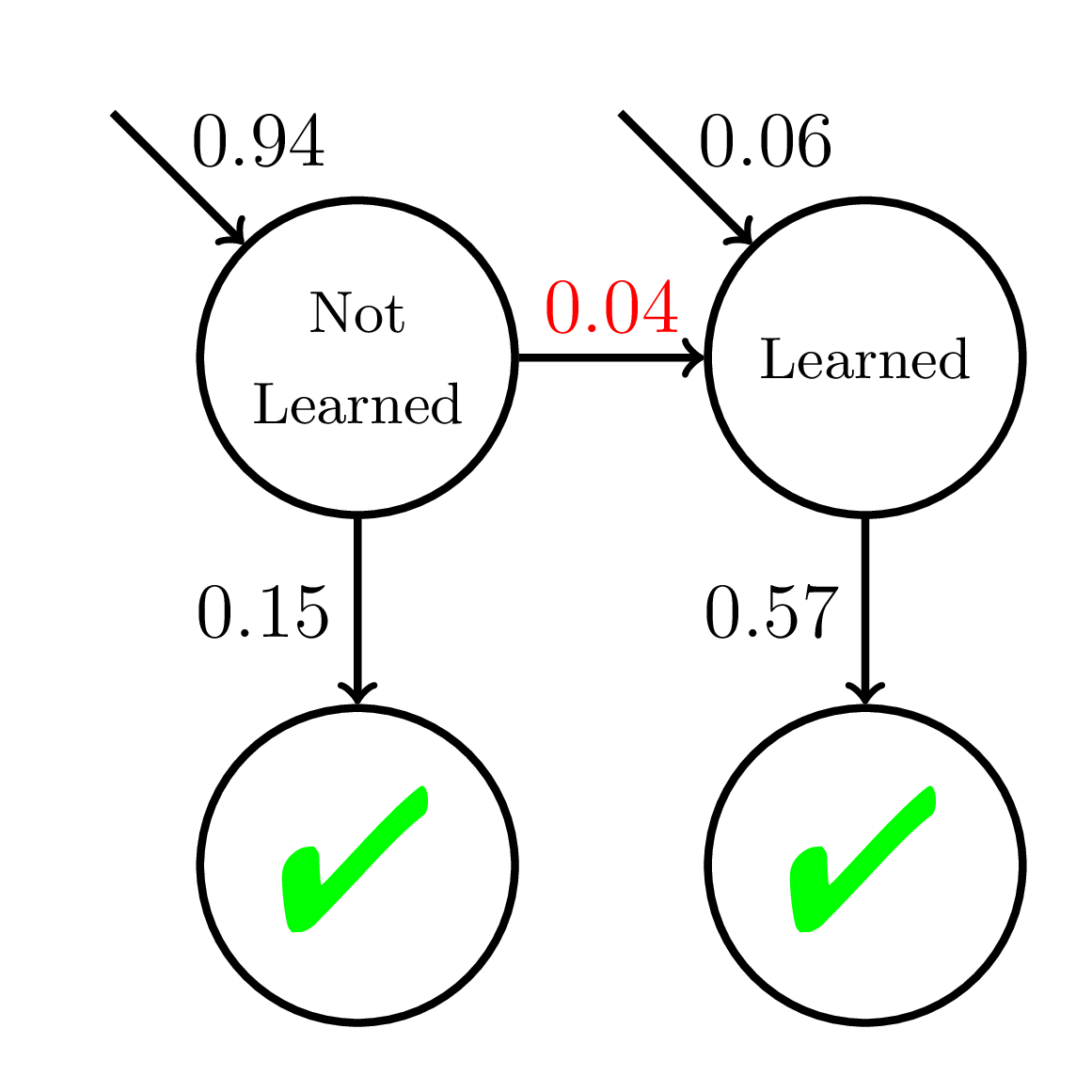
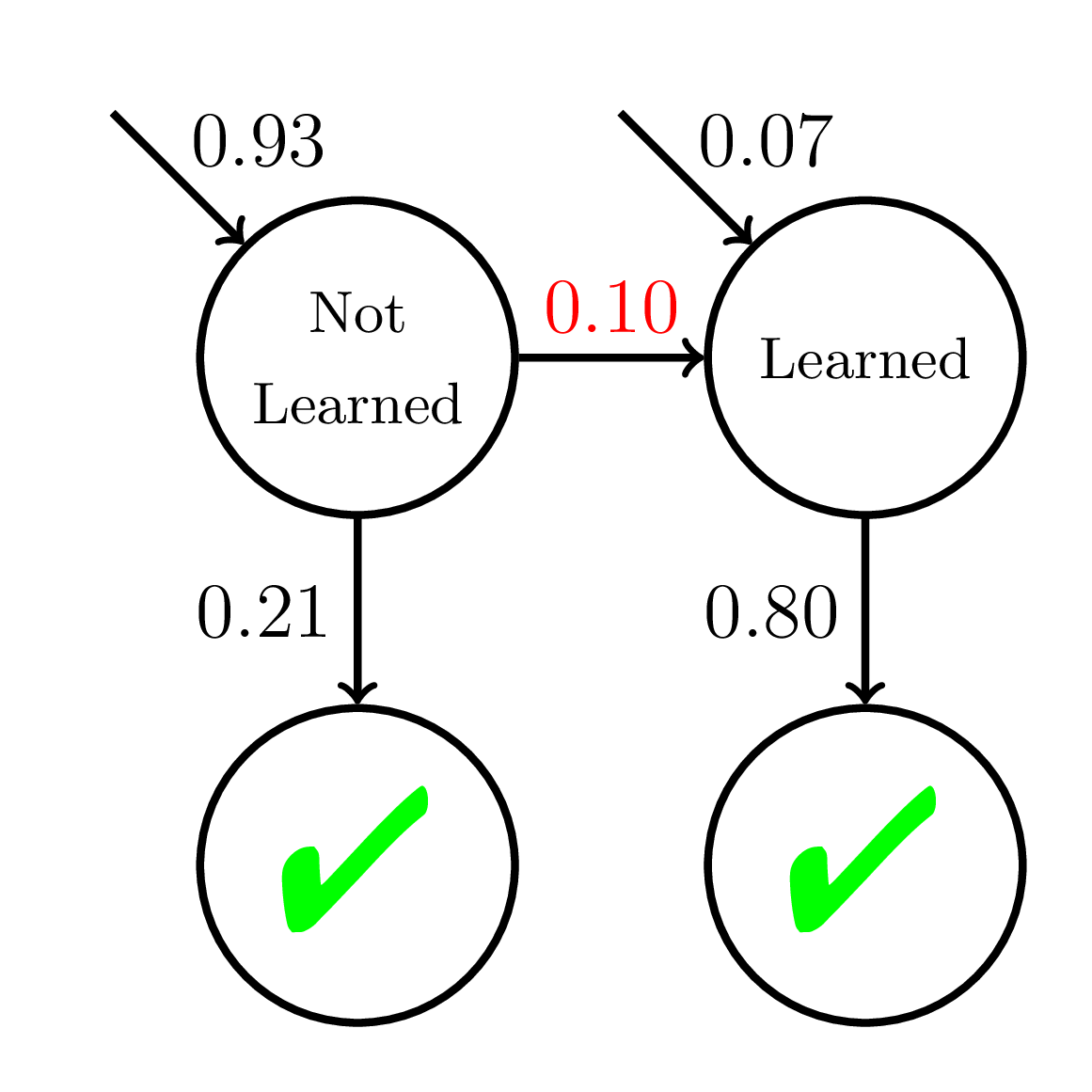
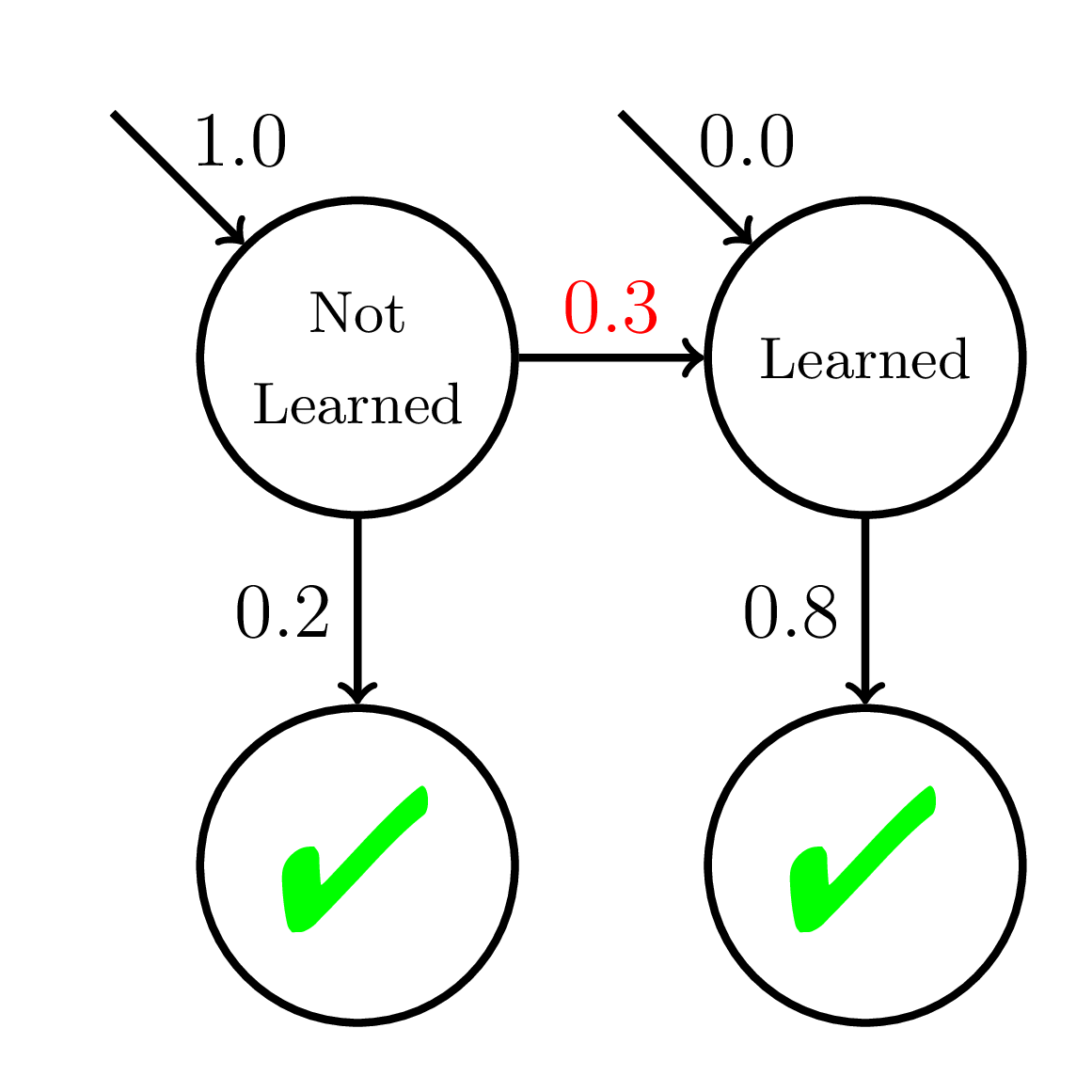
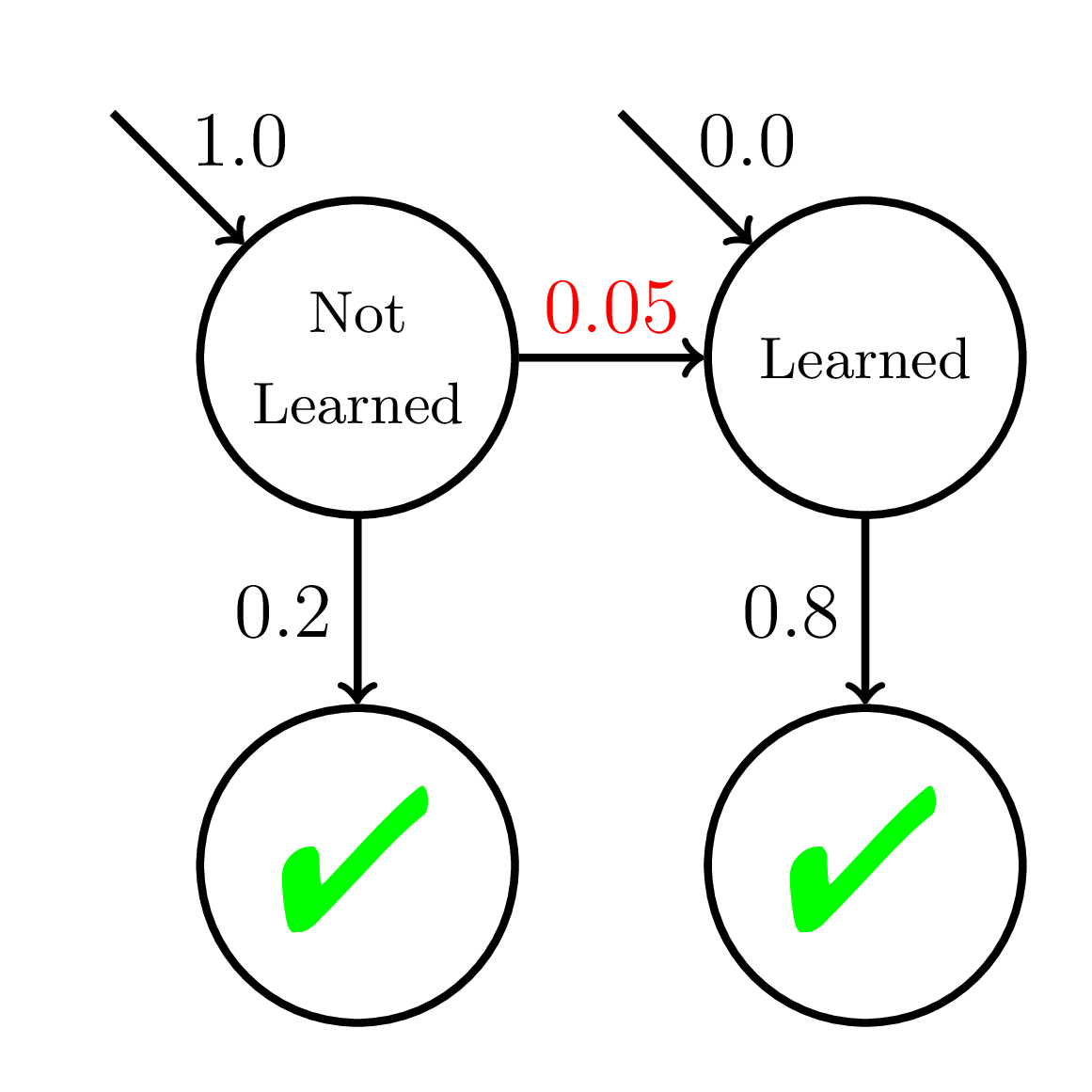
P(\text{Correct}) = \dfrac{1}{1 + \exp(-(\theta - 2 + {\color{red}{0.1}}t))}
\theta \sim \mathcal{N}(0, 1)

200 students

20 practice opportunities

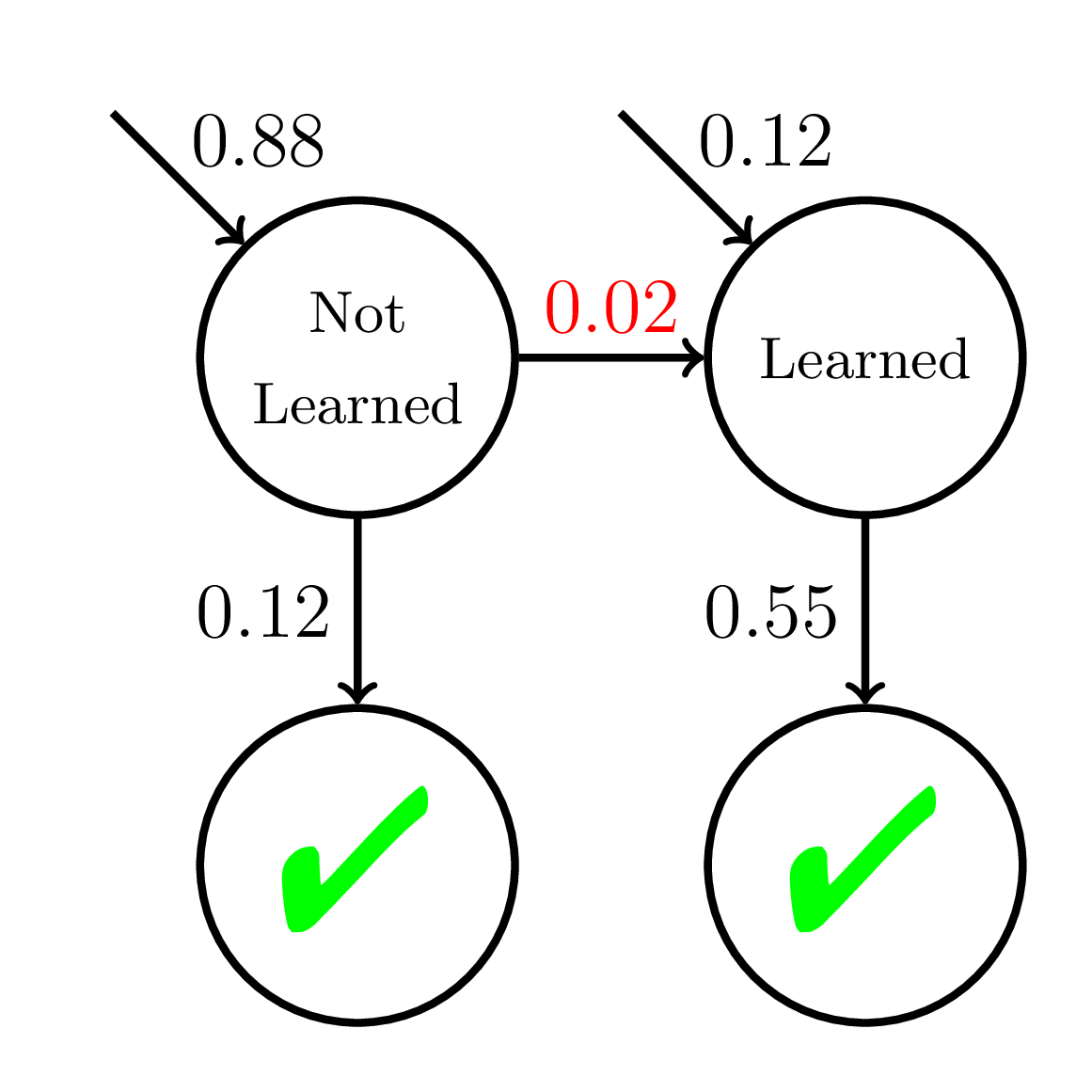
P(\text{Correct}) = \dfrac{1}{1 + \exp(-(\theta - 2 + {\color{red}{0.05}}t))}

200 students

20 practice opportunities

Fast Learners

Slow Learners

Doroudi and Brunskill, Learning Analytics & Knowledge 2019

Equity of Mastery Learning

P(\text{Correct}) = \dfrac{1}{1 + \exp(-(\theta - 2 + {\color{red}{0.1}}t))}
\theta \sim \mathcal{N}(0, 1)
P(\text{Correct}) = \dfrac{1}{1 + \exp(-(\theta - 2 + {\color{red}{0.05}}t))}

Average P(Correct)
at Mastery:
0.56

Average P(Correct) at Mastery:
0.45

Mastery
Learning

Mastery
Learning

Fast Learners

Slow Learners

Doroudi and Brunskill, Learning Analytics & Knowledge 2019

Consider how
(1) algorithms,
(2) machine learning,
(3) technology design, and
(4) socio-cultural forces
combine to affect equity in
learning technologies.  

Equity of Learning Technologies

All Student Models are Wrong

But Some are Useful

Data-Driven Models + Learning Theory

Misguided Instructional Decisions

Inequitable Outcomes

Misguided Inferences about Learning

Robustness to How Students Learn

Robust Evaluation Matrix

Doroudi, Aleven, and Brunskill, Learning @ Scale 2017

Student Models

Policy 1

Policy 2

Policy 3
Student Model 1
Student Model 2
Student Model 3

\(V_{SM_1,P_1}\)     \(V_{SM_1,P_2}\)     \(V_{SM_1,P_3}\)


\(V_{SM_2,P_1}\)     \(V_{SM_2,P_2}\)     \(V_{SM_2,P_3}\)


\(V_{SM_3,P_1}\)     \(V_{SM_3,P_2}\)     \(V_{SM_3,P_3}\)

Robust Evaluation Matrix

Student
Models		 Baseline
Policy		 Adaptive Policy
New Model 5.9 ± 0.9 9.1 ± 0.8
Bayesian Knowledge Tracing 6.5 ± 0.8 7.0 ± 1.0
Deep Knowledge Tracing 9.9 ± 1.5 8.6 ± 2.1

Doroudi, Aleven, and Brunskill, Learning @ Scale 2017

Posttest Scores (out of 16 points)

Robust Evaluation Matrix

Student
Models		 Baseline
Policy		 Adaptive Policy Awesome Policy
New Model 5.9 ± 0.9 9.1 ± 0.8 16
Bayesian Knowledge Tracing 6.5 ± 0.8 7.0 ± 1.0 16
Deep Knowledge Tracing 9.9 ± 1.5 8.6 ± 2.1 16

Doroudi, Aleven, and Brunskill, Learning @ Scale 2017

Posttest Scores (out of 16 points)

Robust Evaluation Matrix

Doroudi, Aleven, and Brunskill, Learning @ Scale 2017

Student Models

Policy 1

Policy 2

Policy 3
Demographic 1
Demographic 2
Demographic 3

\(V_{SM_1,P_1}\)     \(V_{SM_1,P_2}\)     \(V_{SM_1,P_3}\)


\(V_{SM_2,P_1}\)     \(V_{SM_2,P_2}\)     \(V_{SM_2,P_3}\)


\(V_{SM_3,P_1}\)     \(V_{SM_3,P_2}\)     \(V_{SM_3,P_3}\)

Can tell us which policies are equitable

Robust Evaluation Matrix


Student Models		 Mastery Learning
BKT
AFM - Fast Learners 56%
AFM - Slow Learners 45%

Doroudi and Brunskill, Learning Analytics & Knowledge 2019

Robust Evaluation Matrix


Student Models		 Mastery Learning
BKT
AFM - Fast Learners 56%
AFM - Slow Learners 45%
BKT - Fast Learners 98%*
BKT - Slow Learners 97.3%*

*Percent of students who are in learned state.

Doroudi and Brunskill, Learning Analytics & Knowledge 2019

Robust Evaluation Matrix


Student Models 		Mastery Learning
BKT 		Mastery Learning AFM
AFM - Fast Learners 56% 96%
AFM - Slow Learners 45% 95%
BKT - Fast Learners 98%*
BKT - Slow Learners 97.3%*

*Percent of students who are in learned state.

Doroudi and Brunskill, Learning Analytics & Knowledge 2019

Robust Evaluation Matrix


Student Models 		Mastery Learning
BKT 		Mastery Learning AFM
AFM - Fast Learners 56% 96%
AFM - Slow Learners 45% 95%
BKT - Fast Learners 98%* 99.8%*
BKT - Slow Learners 97.3%* 99.5%*

*Percent of students who are in learned state.

Doroudi and Brunskill, Learning Analytics & Knowledge 2019

All Student Models are Wrong

Misguided Inferences about Learning

But Some are Useful

Robustness to How Students Learn

Data-Driven Models + Learning Theory

Misguided Instructional Decisions

Inequitable Outcomes

Student
Model

Big
Data

Student
Model

Data

Theory

Doroudi, Aleven, and Brunskill, In Submission

Integrating Data with Theory

Cognitive
(Information Processing)

DistributedCognition

Constructivism

Socio-Cultural

Situated Cognition

 “It can be argued that there is a trade-off between accounting for the subjective experience of doing mathematics and the precision inherent in expressing models in the syntax of computer formalisms.”

Paul Cobb, 1987

“It is desirable to formulate situative models that are specific enough to implement them as simulation programs”

James Greeno, 1998

Theory-Model Gap

Socio-Cultural
Model

Cognitive
Model

Data

Robustness to Learning Theories

Policy 1

Policy 2

Policy 3
Cognitive Model
Constructivist Model
Socio-Cultural Model

Robustness to Learning Theories

\(V_{SM_1,P_1}\)     \(V_{SM_1,P_2}\)     \(V_{SM_1,P_3}\)


\(V_{SM_2,P_1}\)     \(V_{SM_2,P_2}\)     \(V_{SM_2,P_3}\)


\(V_{SM_3,P_1}\)     \(V_{SM_3,P_2}\)     \(V_{SM_3,P_3}\)

The Bigger Picture

Research Landscape

Properties of Models of Learning

Sequencing Instruction

Learner-Generated Content

Doroudi, Aleven, & Brunskill - L@S '17

Doroudi & Brunskill - LAK '19

Doroudi, Aleven, & Brunskill - In Submission

Doroudi et al. - EDM '15

Doroudi et al. -  EDM '16

Doroudi, Thomas, and Brunskill - UAI '17
*Best Paper*

Doroudi & Brunskill - EDM '17
*Best Paper Nominee*

Doroudi et al. - CHI '16

Doroudi et al. -  ICLS '18

Research Landscape

Properties of Models of Learning

Sequencing Instruction

Learner-Generated Content

Doroudi, Aleven, & Brunskill - L@S '17

Doroudi & Brunskill - LAK '19

Doroudi, Aleven, & Brunskill - In Submission

Doroudi et al. - EDM '15

Doroudi et al. -  EDM '16

Doroudi, Thomas, and Brunskill - UAI '17
*Best Paper*

Doroudi & Brunskill - EDM '17
*Best Paper Nominee*

Doroudi et al. - CHI '16

Doroudi et al. -  ICLS '18

This Talk

Assess the robustness of various student models and instructional policies

Future Directions

Study the equitability of learning technologies, including how algorithms interact with socio-cultural factors

Work with online education providers to study how the
consequences in this talk affect actual students

Build student models for settings that we care about
by bridging the theory-model gap

To build more robust data-driven learning technologies while advancing the science of learning

Vision

Acknowledgements

The research reported here was supported, in whole or in part, by the Institute of Education Sciences, U.S. Department of Education, through Grants R305A130215 and R305B150008 to Carnegie Mellon University. The opinions expressed are those of the authors and do not represent views of the Institute or the U.S. Dept. of Education.

Some of the work reported here was written in papers with co-authors Emma Brunskill and Vincent Aleven. I thank Emma Brunskill, Ken Holstein, and Petr Johanes for discussions that influenced this work.

References

Box, G. E. (1979). Robustness in the strategy of scientific model building. In Robustness in statistics (pp. 201-236).

 

Cen, H. (2009). Generalized learning factors analysis: improving cognitive models with machine learning (Doctoral dissertation). Carnegie Mellon University, Pittsburgh, PA.

 

Chi, M., VanLehn, K., Litman, D., & Jordan, P. (2011). Empirically evaluating the application of reinforcement learning to the induction of effective and adaptive pedagogical strategies. User Modeling and User-Adapted Interaction, 21(1-2), 137-180.

 

Cobb, P. (1990). A constructivist perspective on information-processing theories of mathematical activity. International Journal of Educational Research, 14(1), 67-92.

 

Corbett, A. T., & Anderson, J. R. (1994). Knowledge tracing: Modeling the acquisition of procedural knowledge. User modeling and user-adapted interaction, 4(4), 253-278.

 

Doroudi, S., & Brunskill, E. (2017, June). The misidentified identifiability problem of Bayesian Knowledge Tracing. In Proceedings of the 10th International Conference on Educational Data Mining. International Educational Data Mining Society.

References

Doroudi, S. & Brunskill, E. (2019, March). Fairer but not fair enough: On the equitability of knowledge tracing. To appear in Proceedings of the 9th International Learning Analytics & Knowledge Conference. ACM.

 

Doroudi, S., Aleven, V., & Brunskill, E. (2017, April). Robust evaluation matrix: Towards a more principled offline exploration of instructional policies. In Proceedings of the Fourth (2017) ACM Conference on Learning@ Scale (pp. 3-12). ACM.

 

Doroudi, S., Aleven, V. & Brunskill, E. (2018). Where's the reward? A review of reinforcement learning for instructional sequencing. Manuscript in submission.

 

Duncan, O. D. (1975). Introduction to structural equation models. Elsevier.

 

Greeno, J. G. (1998). The situativity of knowing, learning, and research. American psychologist, 53(1), 5.

 

Rowe, J. P., Mott, B. W., & Lester, J. C. (2014). Optimizing Player Experience in Interactive Narrative Planning: A Modular Reinforcement Learning Approach. AIIDE, 3, 2.

Backup Slides

Data

New Instructional Policy

Review of Data-Driven Instruction

Student
Model

vs.

Baseline Policy

Doroudi, Aleven, and Brunskill, In Submission

Better understand researchers' beliefs about learning and computational modeling via interviews (ongoing work).

Bridging the Theory-Model Gap

Use agent-based modeling and social simulation to model socio-cultural and situative theories.

Assess robustness of models under different conceptions of learning.

At least 95% of students learn the skill

Mastery
Learning

Four Clusters of Studies

Doroudi, Aleven, and Brunskill, In Submission

aprender

to learn

Paired-Association Tasks

Concept Learning Tasks

Sequencing Activity Types

Sequencing Interdependent Content

Four Clusters of Studies

Doroudi, Aleven, and Brunskill, In Submission

reading

Paired-Association Tasks

Concept Learning Tasks

Sequencing Activity Types

Sequencing Interdependent Content

Four Clusters of Studies

Doroudi, Aleven, and Brunskill, In Submission

Worked Example

Problem
Solving

\(x^2 - 4 = 12\)
Solve for \(x\):
\(x^2 - 4 = 12\)
\(x^2 = 4 + 12\)
\(x^2 = 16\)
\(x = \sqrt{16} = \pm4\)

\(x^2 - 4 = 12\)
Solve for \(x\):

Paired-Association Tasks

Concept Learning Tasks

Sequencing Activity Types

Sequencing Interdependent Content

Five Clusters of Studies

Doroudi, Aleven, and Brunskill, In Submission

Paired-Association Tasks

Concept Learning Tasks

Sequencing Activity Types

Sequencing Interdependent Content

Four Clusters of Studies

Doroudi, Aleven, and Brunskill, In Submission

Data-Driven Policy Outperformed Baseline
Mixed Results		 Data-Driven Policy Did Not
Outperform
Baseline
Paired-Association Tasks 10 0 3
Concept Learning Tasks 2 3 0
Sequencing Activity Types 4 4 0
Sequencing Interdependent Content 0 0 6

Four Clusters of Studies

Doroudi, Aleven, and Brunskill, In Submission

Paired-Association Tasks

Concept Learning Tasks

Sequencing Activity Types

Sequencing Interdependent Content

Use Psychologically-Inspired Models

Spacing Effect

Worked-Example Effect

Use Data-Driven
Models

We attempt to treat the same problem with several alternative models each with different simplifications but with a common...assumption. Then, if these models, despite their different assumptions, lead to similar results, we have what we can call a robust theorem that is relatively free of the details of the model.
Hence, our truth is the intersection of independent lies.

- Richard Levins, 1966

Importance Sampling

  • Estimator that gives unbiased and consistent estimates for a policy!

  • Can have very high variance when policy is different from prior data.

  • Example: Worked example or problem-solving?

    • 20 sequential decisions ⇒ need over 2^{20}$20\(2^{20}\) students!

  • Importance sampling can prefer the worse of two policies more often than not (Doroudi, Thomas, and Brunskill, 2017).

Doroudi, Thomas, and Brunskill, Uncertainty in Artificial Intelligence 2017, Best Paper

200 students

20 practice opportunities

Fast Learners

Slow Learners

Doroudi and Brunskill, Learning Analytics & Knowledge 2019