Pre-start

Announcements
- Homework 2 is up and "due" on 10/11. Good luck. Have fun.
- You should be able to do all of it other than evaluating Poisson models after today's lecture. It's mostly just data exploration and plotting (which may be challenging!)
- HW1
- Please submit soonish if you haven't. Ask if you need any help still! Submission has been reopened. Can't talk about it yet.
- Please look at feedback regardless of your grade! There were some algebra errors as well as slight conceptual confusions. Correct the latter and resubmit. The former isn't a big deal (-1).
Neural Signal Processing & Machine Learning
ELEC/BIOE 548 | ELEC 483
Fall 2022
Episode 10: Processing points pt 1
(Oh, right. The Poisson process. The Poisson process for Kuzco, the Poisson process chosen especially to kill Kuzco, Kuzco's Poisson process. That Poisson process?)


1
Introduction. Class & brains
2
Fundamental neurobiology. How do neurons fire? How/what do we record?
3
Modeling spike trains. First bit of analysis work and understanding firing properties of neurons.
5
Classification. Making machines learn. Which direction is a monkey trying to reach? Bayesian decoding.
4
Point processes. Continued modeling work of neurons.
6
Clustering/Mixture models. Making machines learn some more. Spike sorting.
Bi-weekly Schedule
7
Continuous decoding. Kalman filters. Machines continue to learn.
8
Spectral analysis? LFP interpretation in spectral domain. But also kinda in clustering.
Brain Signals!
-
How can we measure neural activity?
-
What info do neurons encode in trains of action potentials (“spike trains”)?
-
How can we model “statically” encoded information? (Wrap up this week!)
-
Estimation/”decoding”
-
How can we model/decode “dynamic” information? (filtering, Kalman, HMM)
-
Signal conditioning – “spike sorting” (PCA, Expectation-Maximization)
-
Beyond spike trains (LFP, EEG, imaging)
Recap
- Sequences & rates
- both are important
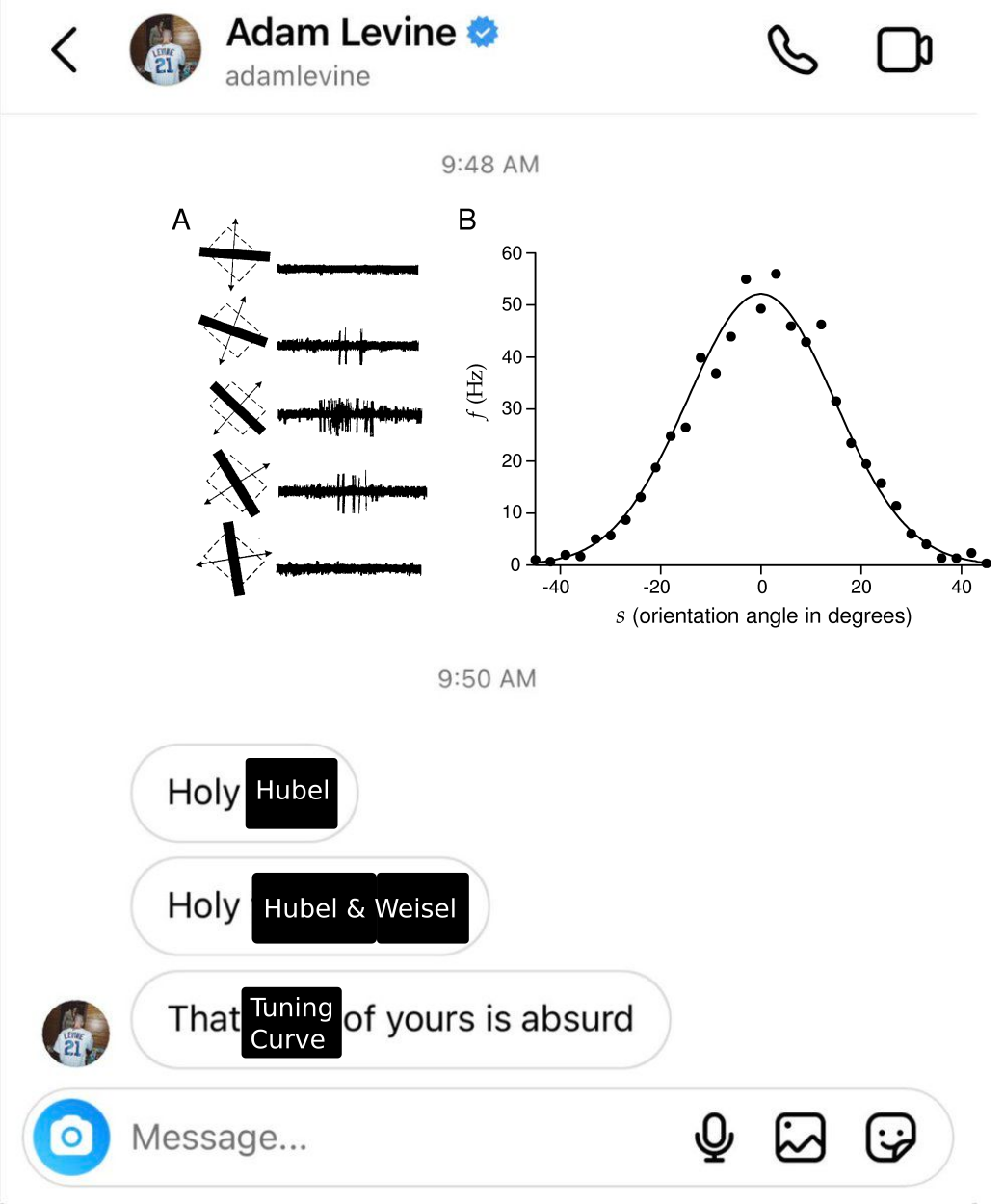
- Tuning curves
- multiple trials add to noise
- Artificially we account for noise and an infinite number of trials by modeling neural activity with some statistical distribution
Wrapping Up Poisson-ing on Ipad
If this all makes sense to everyone today I'm happy. Perhaps we'll end early if that happens quickly!
Next class will be evaluating models (very similar to ANTM :).