Pre-start


Announcements
- Homework 1 was "due"
- Does "due" make sense and "self grading" make sense?
- Thank y'all for making this a fun homework!!
- Thank y'all for the feedback!!!
- We'll start giving feedback from this weekend/next week.
- Homework 2 will be up this weekend! Take a look before class Tuesday please for any confusions in wordings or understanding!
Neural Signal Processing & Machine Learning
ELEC/BIOE 548 | ELEC 483
Fall 2022
Episode 9: Firing rates & spiking statistics pt 2
(FINALLY! MODELING! *hand model*)



1
Introduction. Class & brains
2
Fundamental neurobiology. How do neurons fire? How/what do we record?
3
Modeling spike trains. First bit of analysis work and understanding firing properties of neurons.
5
Classification. Making machines learn. Which direction is a monkey trying to reach? Bayesian decoding.
4
Point processes. Continued modeling work of neurons.
6
Clustering/Mixture models. Making machines learn some more. Spike sorting.
Bi-weekly Schedule
7
Continuous decoding. Kalman filters. Machines continue to learn.
8
Spectral analysis? LFP interpretation in spectral domain. But also kinda in clustering.
Brain Signals!
-
How can we measure neural activity?
-
What info do neurons encode in trains of action potentials (“spike trains”)?
-
How can we model “statically” encoded information?
-
Estimation/”decoding”
-
How can we model/decode “dynamic” information? (filtering, Kalman, HMM)
-
Signal conditioning – “spike sorting” (PCA, Expectation-Maximization)
-
Beyond spike trains (LFP, EEG, imaging)
Recap
- Neurons transmit information by firing sequences of spikes
- Neural encoding – the map from stimulus to neural response. (hard)
- Can measure how neurons respond to a wide variety of stimuli. Then construct models; attempt to predict responses to other stimuli.
- Neural decoding – the map from response to stimulus. (easy-ish)
- Attempt to reconstruct a stimulus, or certain aspects of that stimulus, from the spike sequence it evokes
- We will discuss decoding extensively in the rest of this course.
Recap: Population Codes!
How does a population of neurons (in motor cortex) encode, with spike times, where the arm will move next?
How is the actual arm movement encoded?

Recap: Time-Varying Firing Rates
Choo-choo(t)
Ways to approximate a time-varying firing rate from a spike train
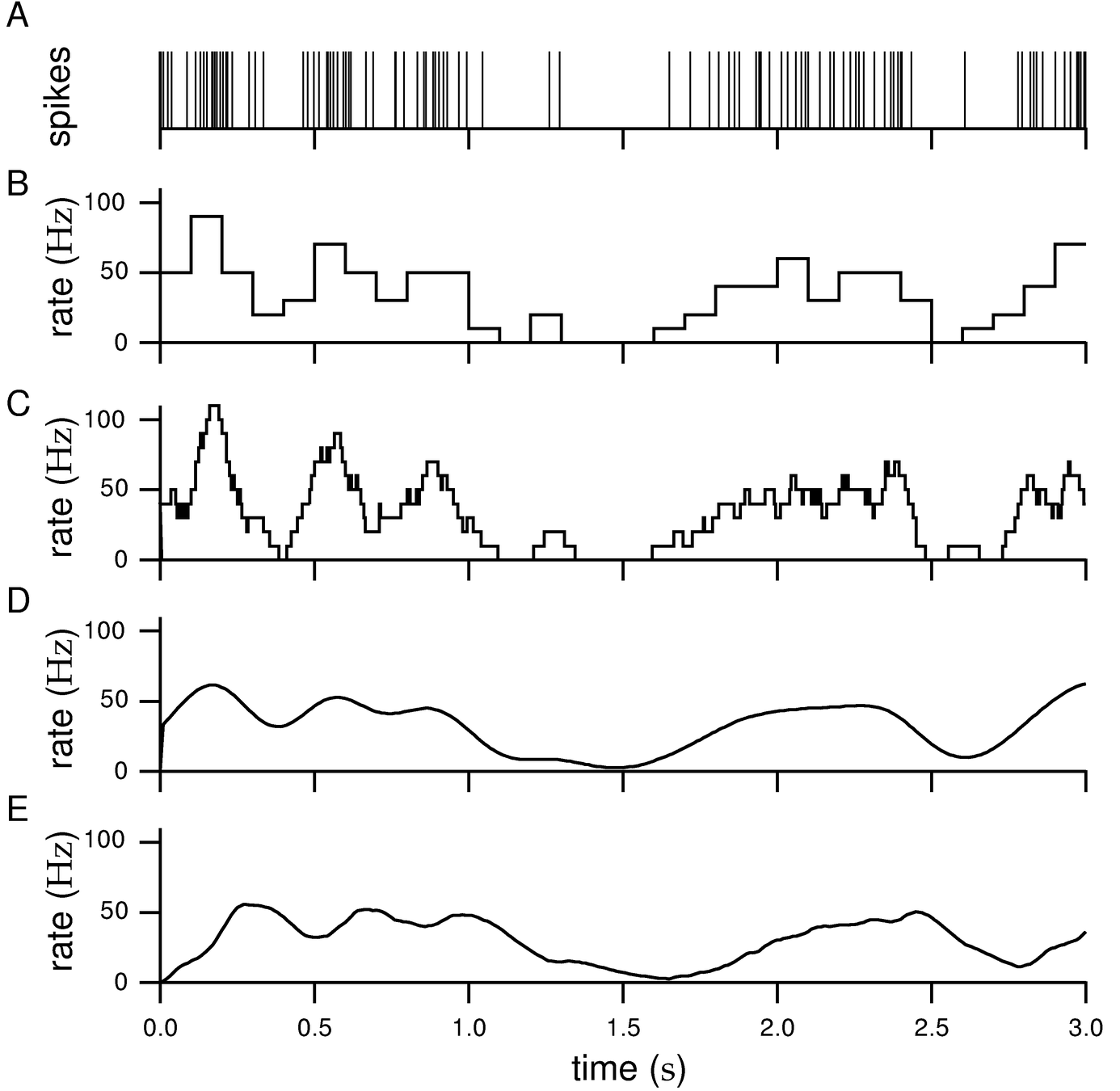
Raw spike train
Counts in 100 ms windows (non-overlapping)
Counts in 100 ms windows (sliding window)
Convolution with Gaussian (what's a good sigma??)
Convolution with one-sided exponential (why is this more realistic for real time??)
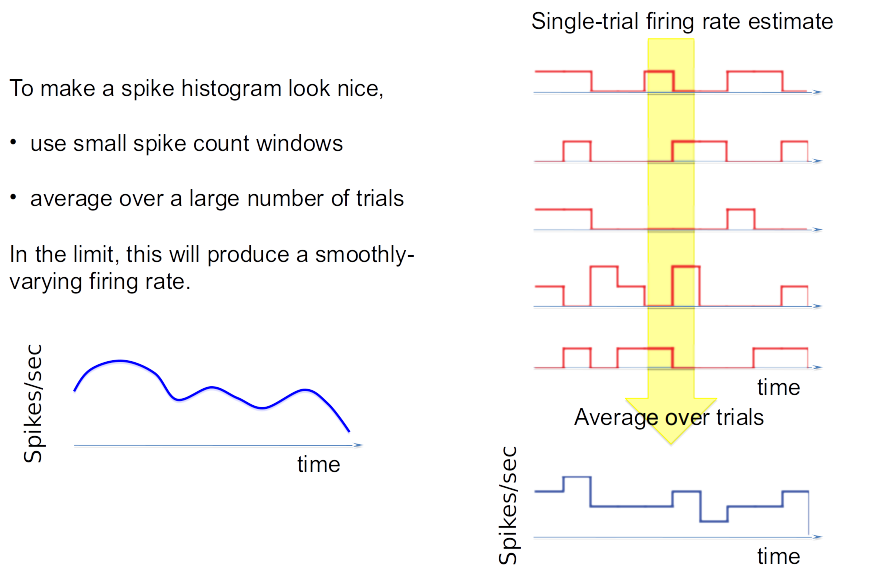
Recap: Trial-Averaged Firing Rates
choo-choo/(num(choo-choos))
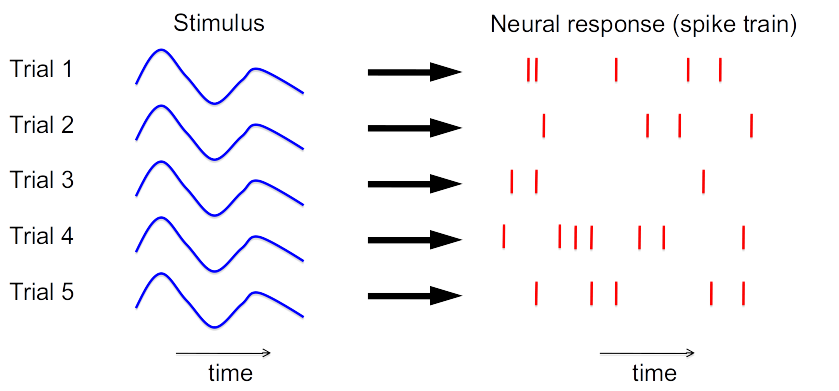
Recap: Trial-Averaged Firing Rates
choo-choo/(num(choo-choos))
Sequences vs Rates
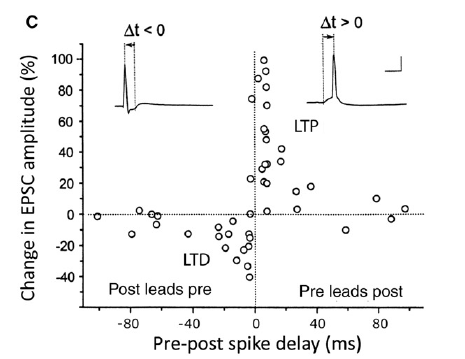
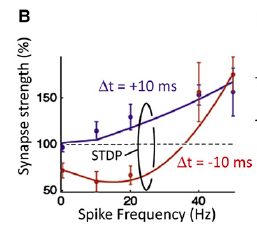
- Spike-timing dependent plasticity (we'll pick up from here next time!)
- THE TIME IS NOW!
- Rate at which neurons fire matter. Given what we've talked about what else could matter? Why?
- Hebbs rule: Neurons that fire together wire together
- Spike-time dependent plasticity

Neural Responses & Stimuli

Neural Responses & Stimuli
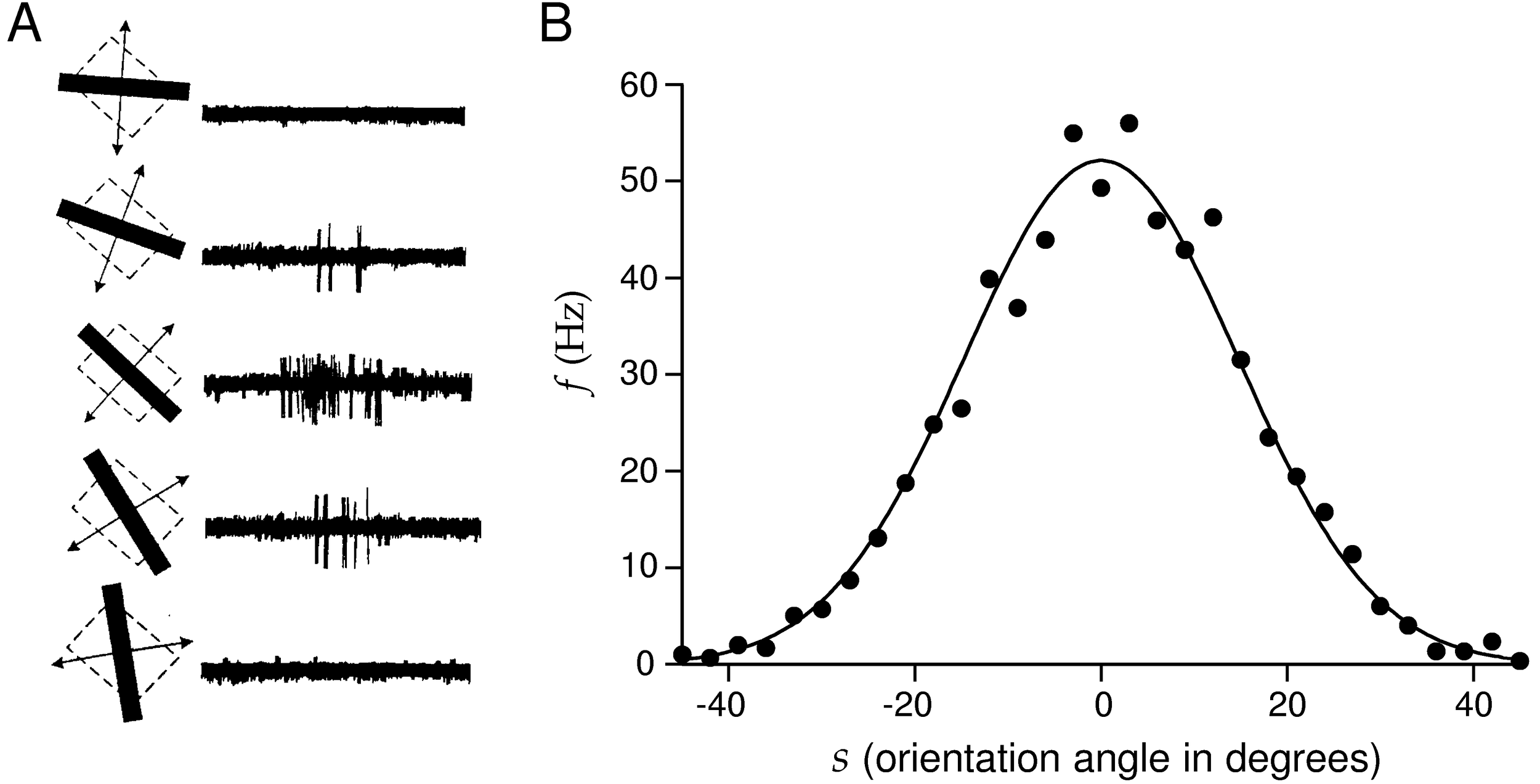
Tuning curves
- Neural responses typically depend on many stimulus properties, start with one.
- Simple approach
- Count the number of spikes fired during the presentation of a stimulus.
- Repeat stimulus presentation many times to better estimate the mean count
- Vary the stimulus attribute of interest, s
- Plot result and (optionally) fit parameterized function to data




Neural Responses & Stimuli
Tuning curves
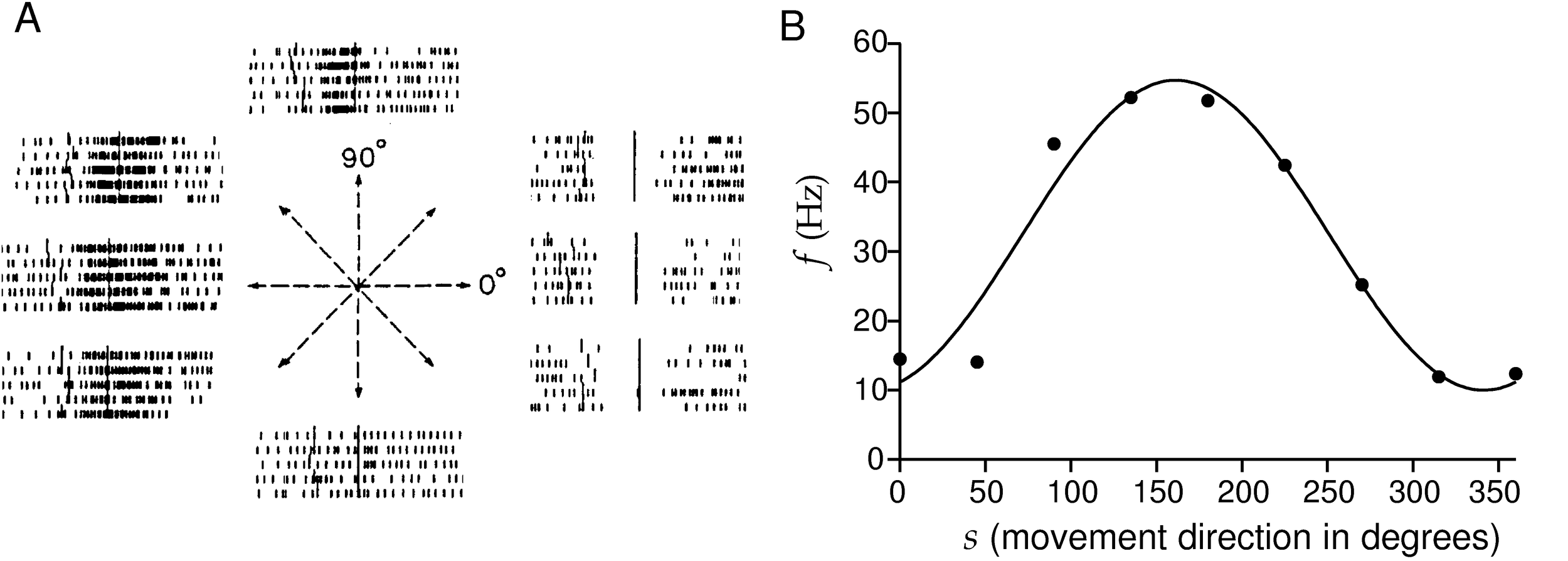
- Monkey motor cortex example from earlier task!
- Monkey trained to reach in different directions, s
- Count number of spikes during arm movement
- Repeat movement many times to better estimate the mean count

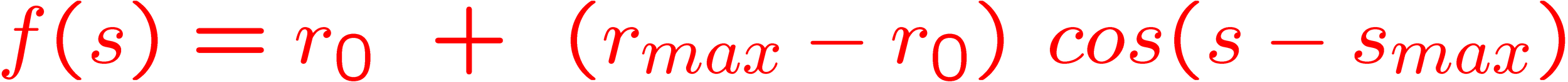



Neural Responses & Stimuli
Tuning curves

Neural Responses & Stimuli
Tuning curves (Noise)
- Tuning curves describe the MEAN FIRING RATE, given a stimulus
- They DO NOT describe how the firing rate varies from trial to trial
Neural Responses & Stimuli
Tuning curves (Noise)
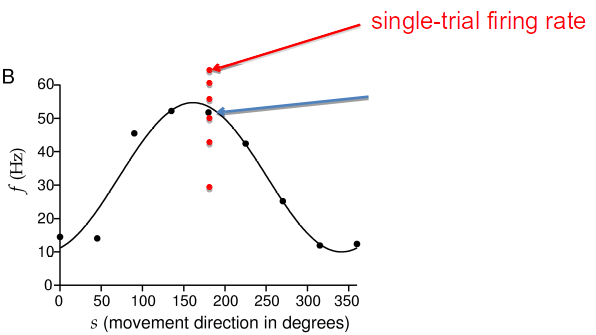
- Single-trial responses are probabilistic, not deterministic
- Noise models describe the probability distribution, representing the firing rate on any given trial, about the mean f(s).
- Standard deviation for the noise distribution can be
- Independent of the mean f(s) - additive noise
- Dependent of the mean e.g., Poisson noise
- We will soon discuss a stochastic spike generator model (Poisson) that will allow us to examine noise in finer detail
Problem with sequences
- A complete description of the stochastic relationship b/w a stimulus and a response would require us to know the probabilities corresponding to every sequence of spikes that can be evoked by the stimulus!
- However, the number of possible spike sequences is typically so large that determining or even roughly estimating all of their probabilities of occurrences is impossible
- Instead we must rely on some statistical model that allows us to estimate the probability of an arbitrary spike sequence!
- AND SO WE BEGIN MODELING!
Spike-Train Stats
- Point Process - stochastic process that generates a sequence of events, APs
- Renewal Process - point process where the probability of an event depends only on the immediately preceding event (intervals b/w successive events are independent)
- Poisson Process - point process where no dependence at all on preceding events (events are statistically independent)
The Poisson process is an extremely useful and widely used, approximation of stochastic neuronal firing.
SWITCH TO IPAD/PDF Notes!