

Lecture 10: Clustering
Shen Shen
November 8, 2024
Intro to Machine Learning

Outline
- Recap: Supervised learning and unsupervised learning
- \(k\)-means clustering:
- \(k\)-means objective
- \(k\)-means algorithm
- Initialization matters
- \(k\) matters
- Clustering vs. classification
- Clustering and related
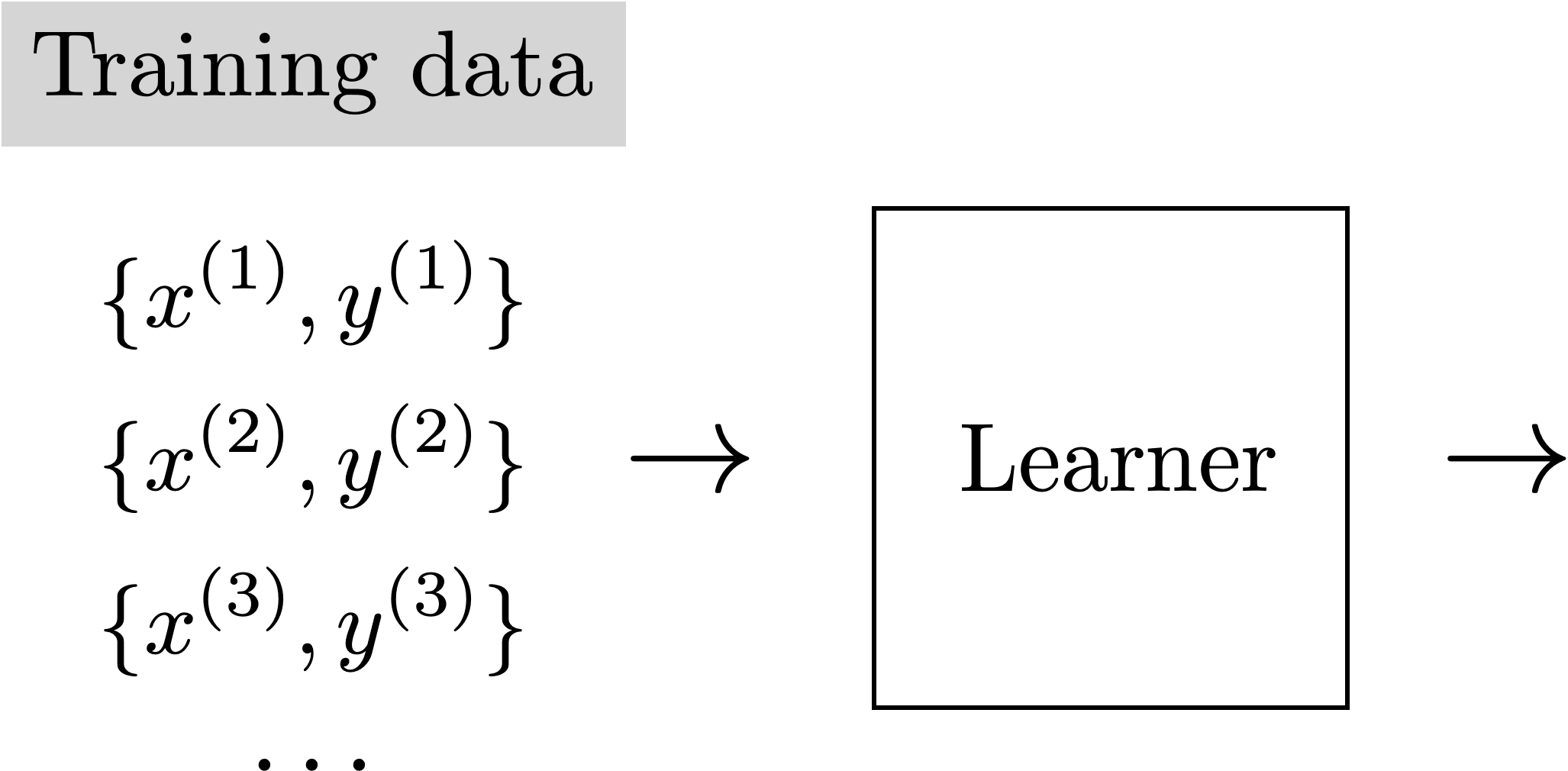
Recap: Supervised learning
- explicit supervision via labels \(y\).
- labels can be quite expensive to create.
"To date, the cleverest thinker of all time was Issac. "
feature
label
To date, the
cleverest
To date, the cleverest
thinker
To date, the cleverest thinker
was
To date, the cleverest thinker of all time was
Issac
Recap: Unsupervised/Self-supervised learning
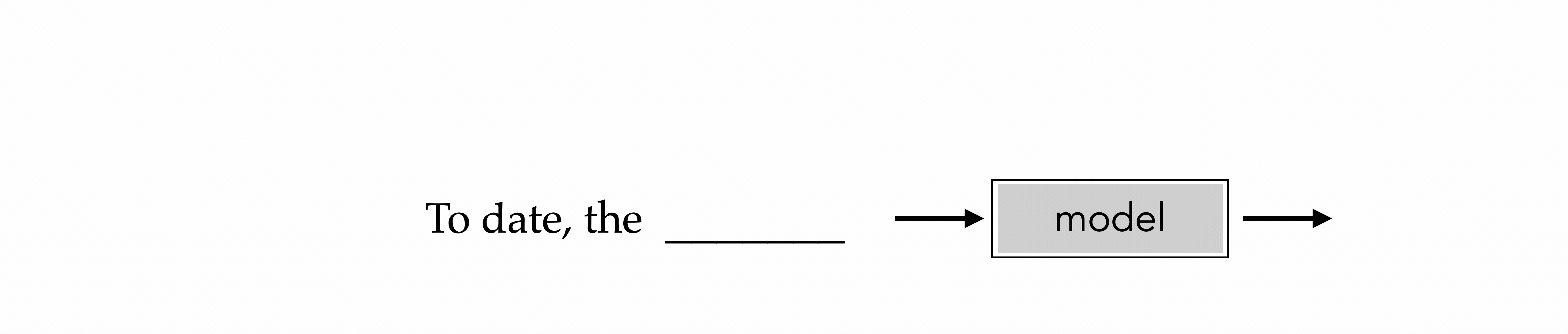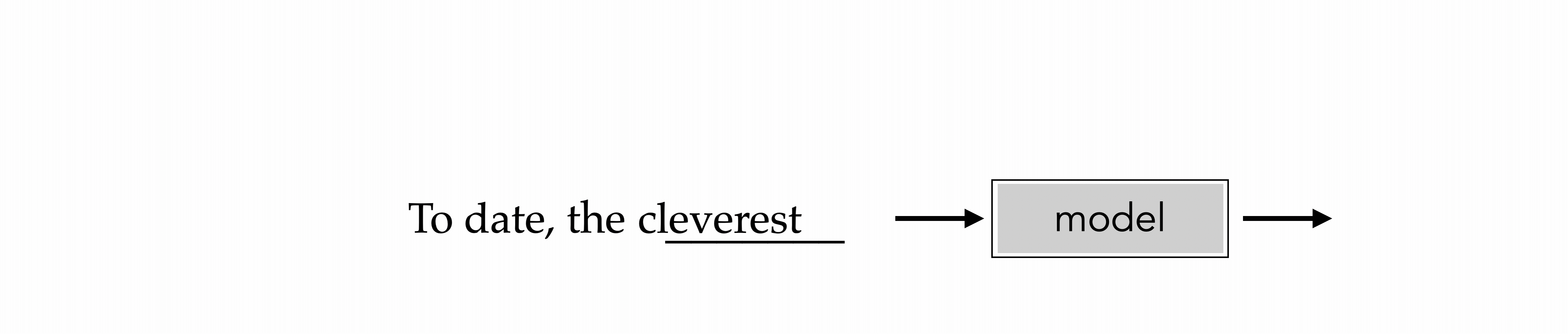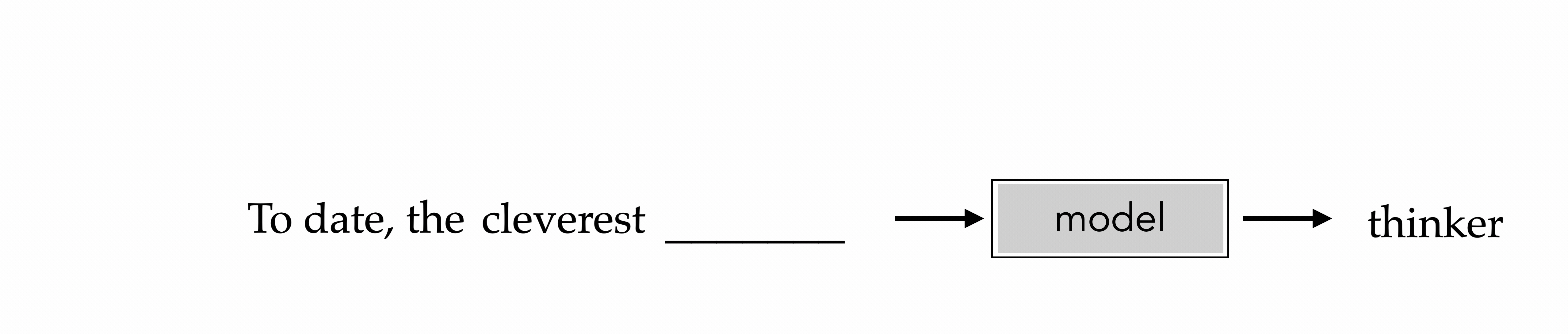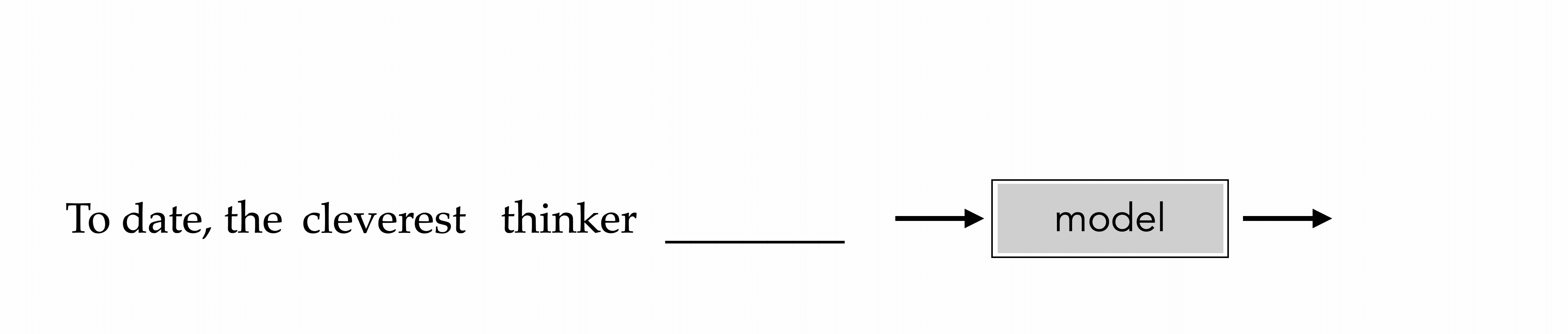
Auto-encoder
Training Data
loss/objective
hypothesis class
A model
\(f\)
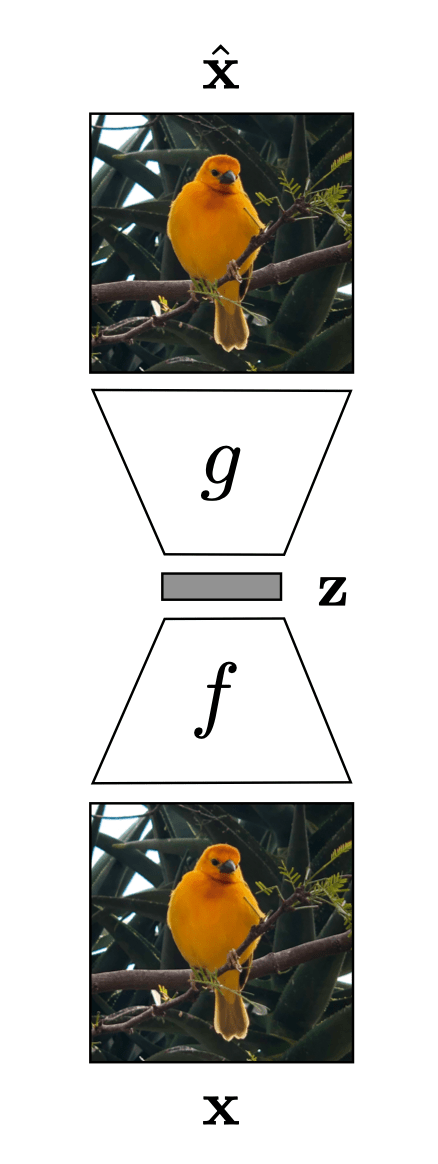
\(m<d\)
Recap: Unsupervised/Self-supervised learning
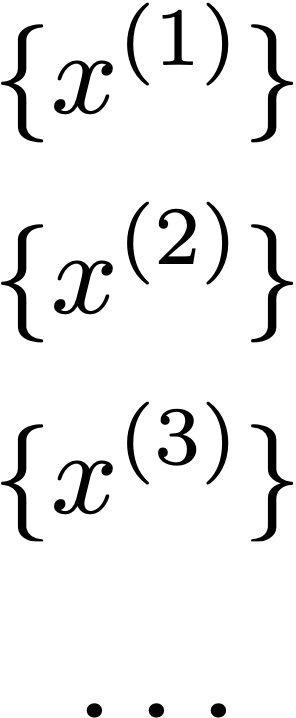

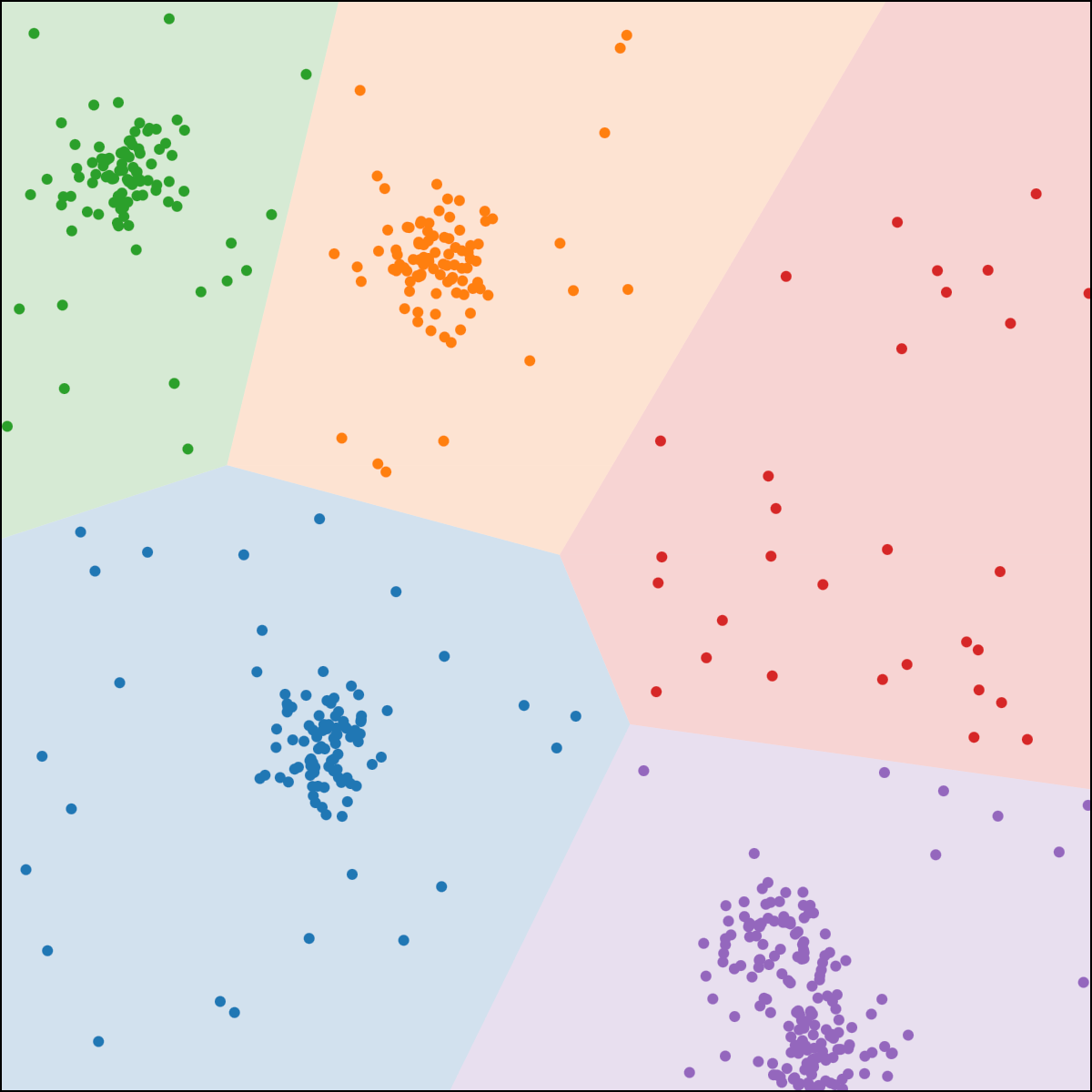
- \(x_1\): longitude, \(x_2\): latitude
- Person \(i\) location \(x^{(i)}\)

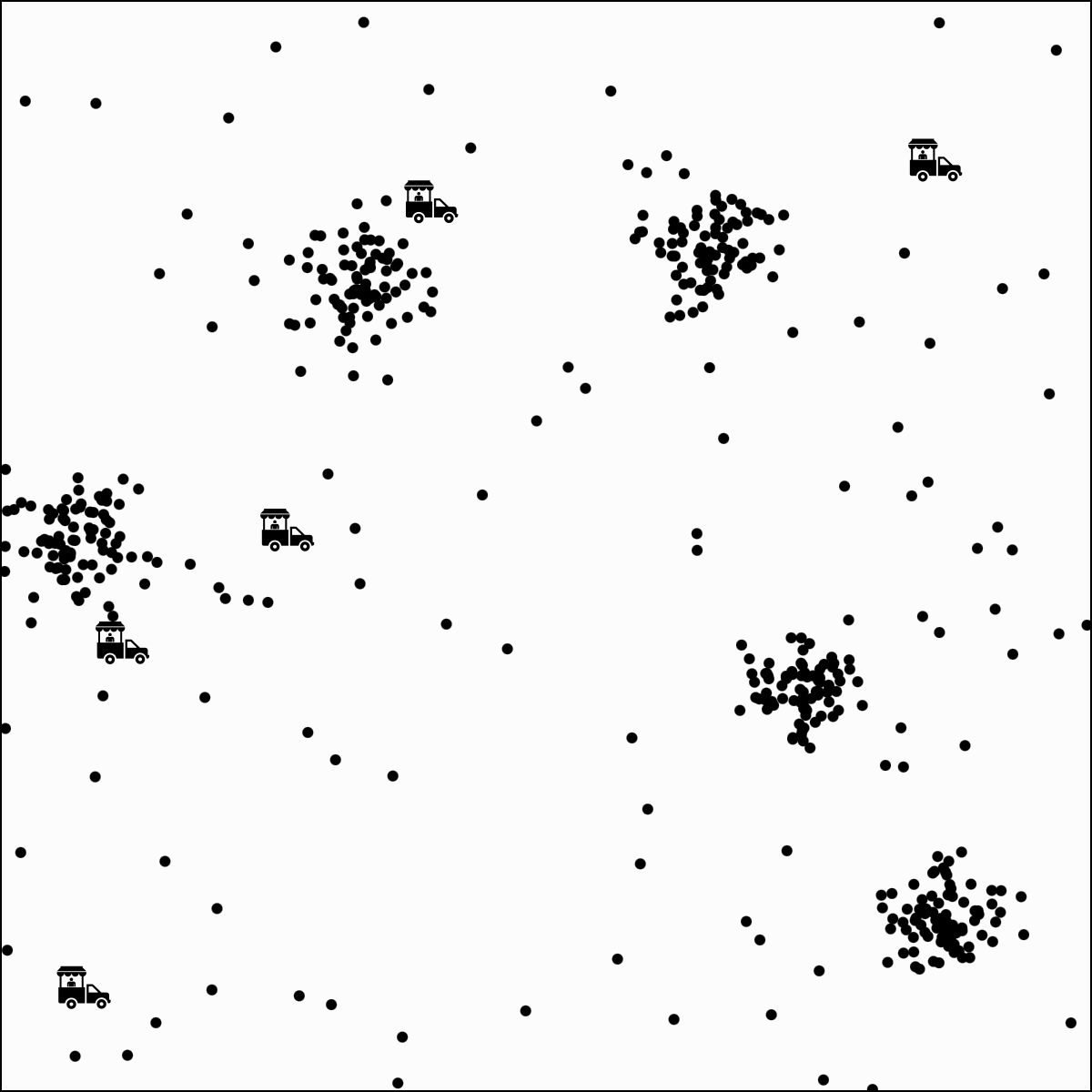
Food-truck placement
- \(x_1\): longitude, \(x_2\): latitude
- Person \(i\) location \(x^{(i)}\)
- Q: where should I have \(k\) food trucks park?
Food-truck placement

- \(x_1\): longitude, \(x_2\): latitude
- Person \(i\) location \(x^{(i)}\)
- Q: where should I have \(k\) food trucks park?
- Food truck \(j\) location \(\mu^{(j)}\)

Food-truck placement
- \(x_1\): longitude, \(x_2\): latitude
- Person \(i\) location \(x^{(i)}\)
- Q: where should I have \(k\) food trucks park?
- Food truck \(j\) location \(\mu^{(j)}\)
- Loss if \(i\) walks to truck \(j\) : \(\left\|x^{(i)}-\mu^{(j)}\right\|_2^2\)

Food-truck placement
- \(x_1\): longitude, \(x_2\): latitude
- Person \(i\) location \(x^{(i)}\)
- Q: where should I have \(k\) food trucks park?
- Food truck \(j\) location \(\mu^{(j)}\)
- Loss if \(i\) walks to truck \(j\) : \(\left\|x^{(i)}-\mu^{(j)}\right\|_2^2\)
- Index of the truck where person \(i\) walks: \(y^{(i)}\)
- Person \(i\) overall loss:
\(\sum_{j=1}^k \mathbf{1}\left\{y^{(i)}=j\right\}\left\|x^{(i)}-\mu^{(j)}\right\|_2^2\)

Food-truck placement
indicator function, 1 if person \(i\) is assigned to truck \(j,\) otherwise 0.
\( \sum_{j=1}^k \mathbf{1}\left\{y^{(i)}=j\right\}\left\|x^{(i)}-\mu^{(j)}\right\|_2^2\)
\(k\)-means objective
clustering membership
clustering centroid location
enumerates over cluster
enumerates over data
can switch the order = \(\sum_{j=1}^k \sum_{i=1}^n \mathbf{1}\left\{y^{(i)}=j\right\}\left\|x^{(i)}-\mu^{(j)}\right\|_2^2\)
what we learn
\(\sum_{i=1}^n\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
10 return \(\mu, y\)

3 \(y_{\text {old }} = y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
10 return \(\mu, y\)
3 \(y_{\text {old }} = y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
1 \(\mu, y=\) random initialization


2 for \(t=1\) to \(\tau\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
10 return \(\mu, y\)
3 \(y_{\text {old }} = y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)


1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
10 return \(\mu, y\)
3 \(y_{\text {old }} = y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)


1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
10 return \(\mu, y\)
3 \(y_{\text {old }} = y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)


1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
10 return \(\mu, y\)
3 \(y_{\text {old }} = y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
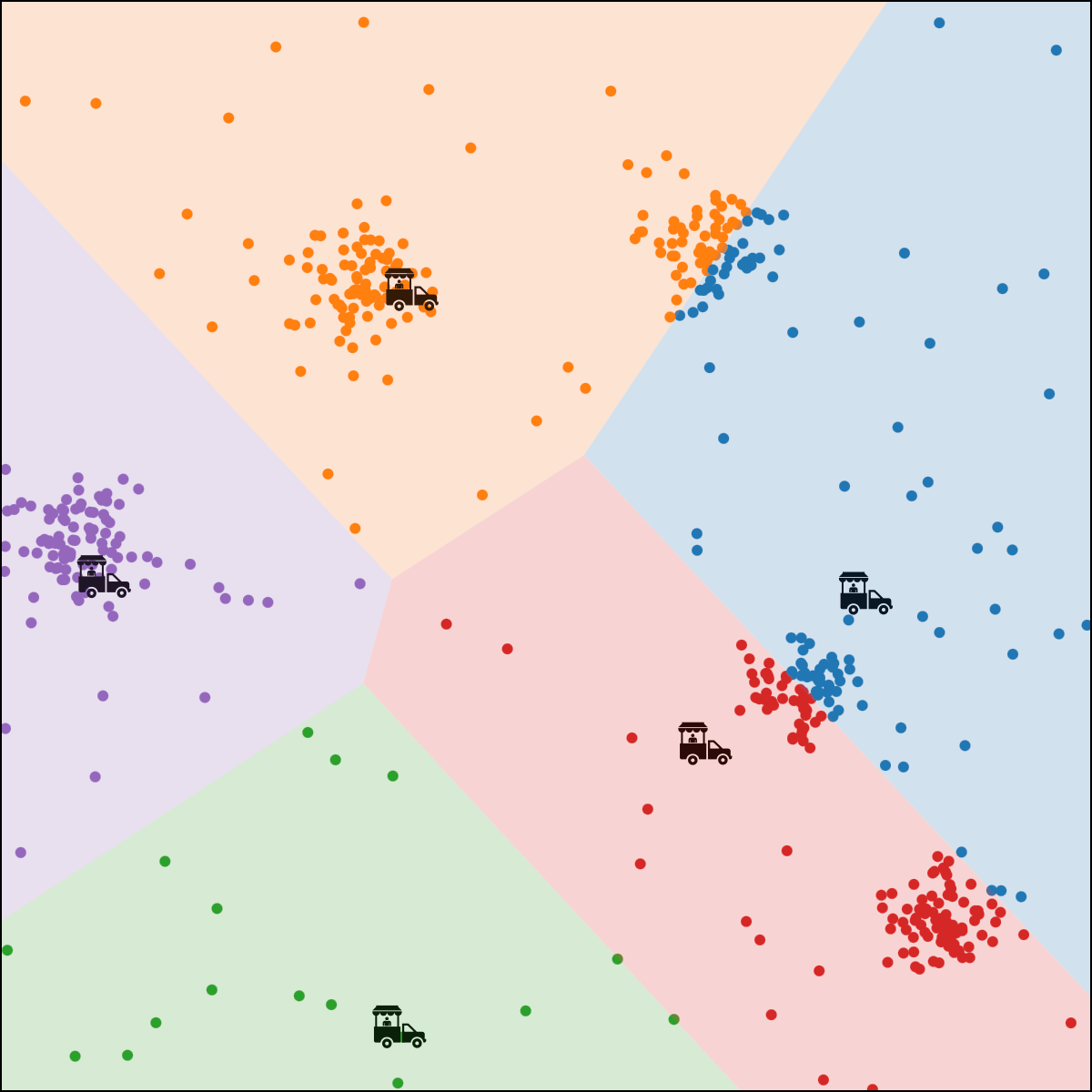
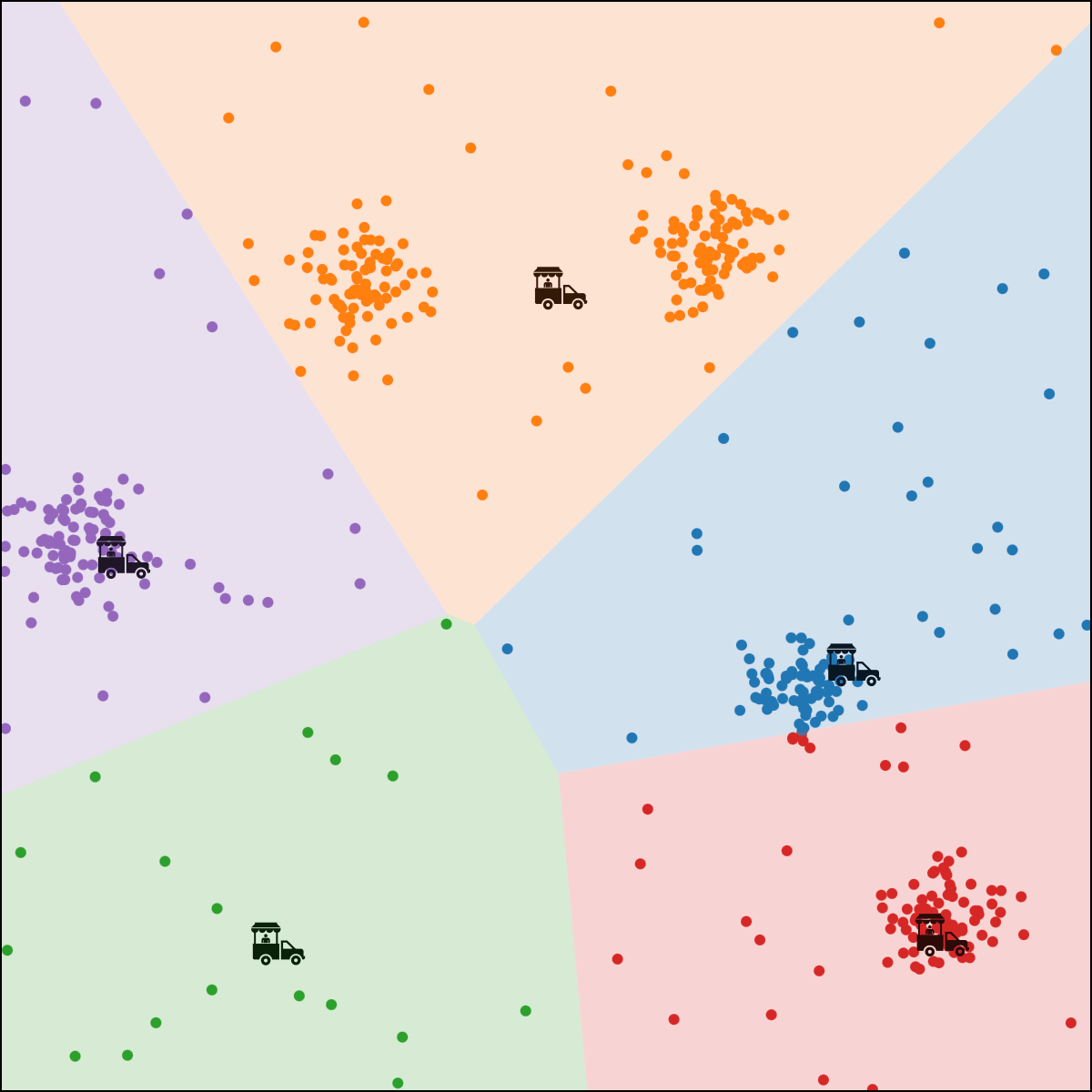
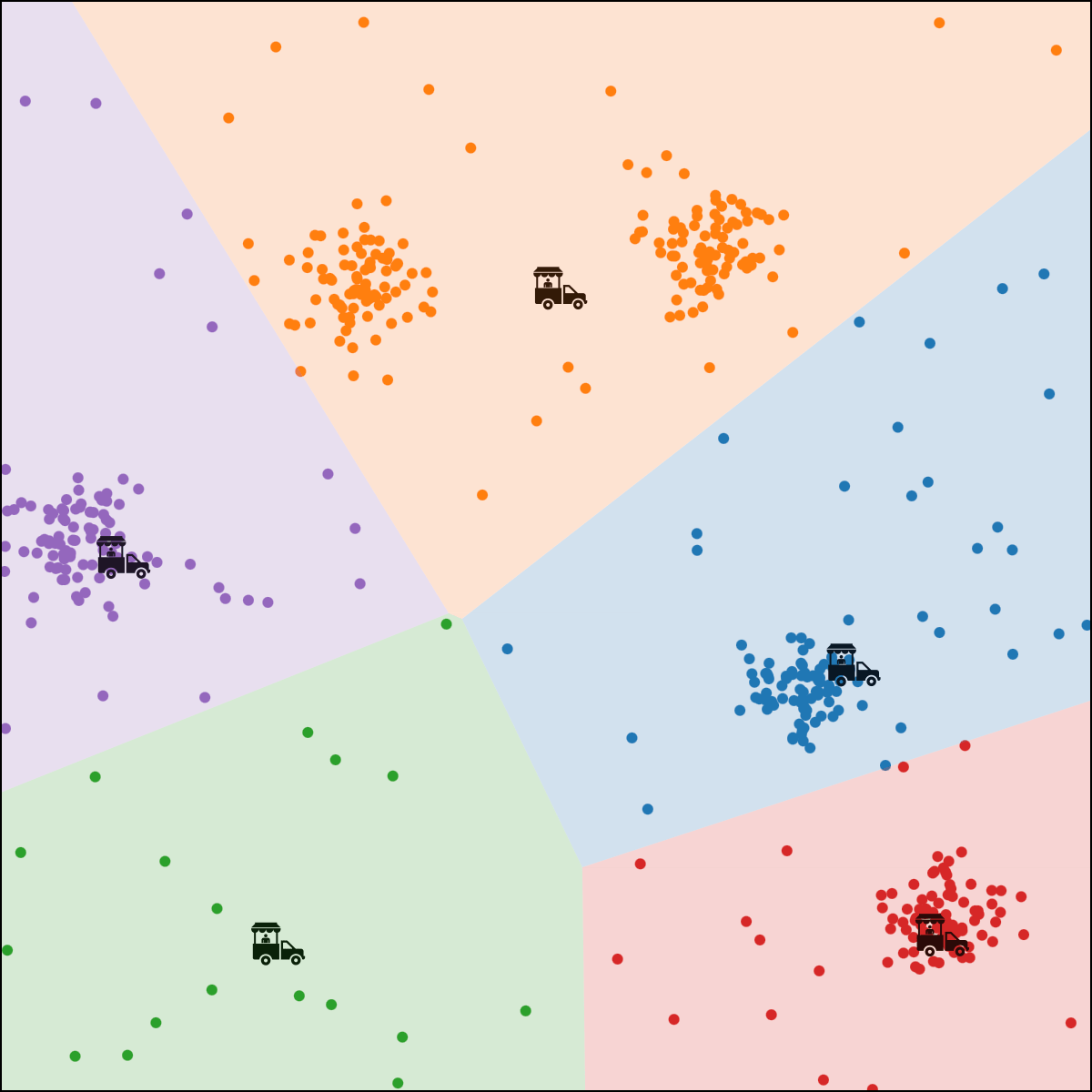
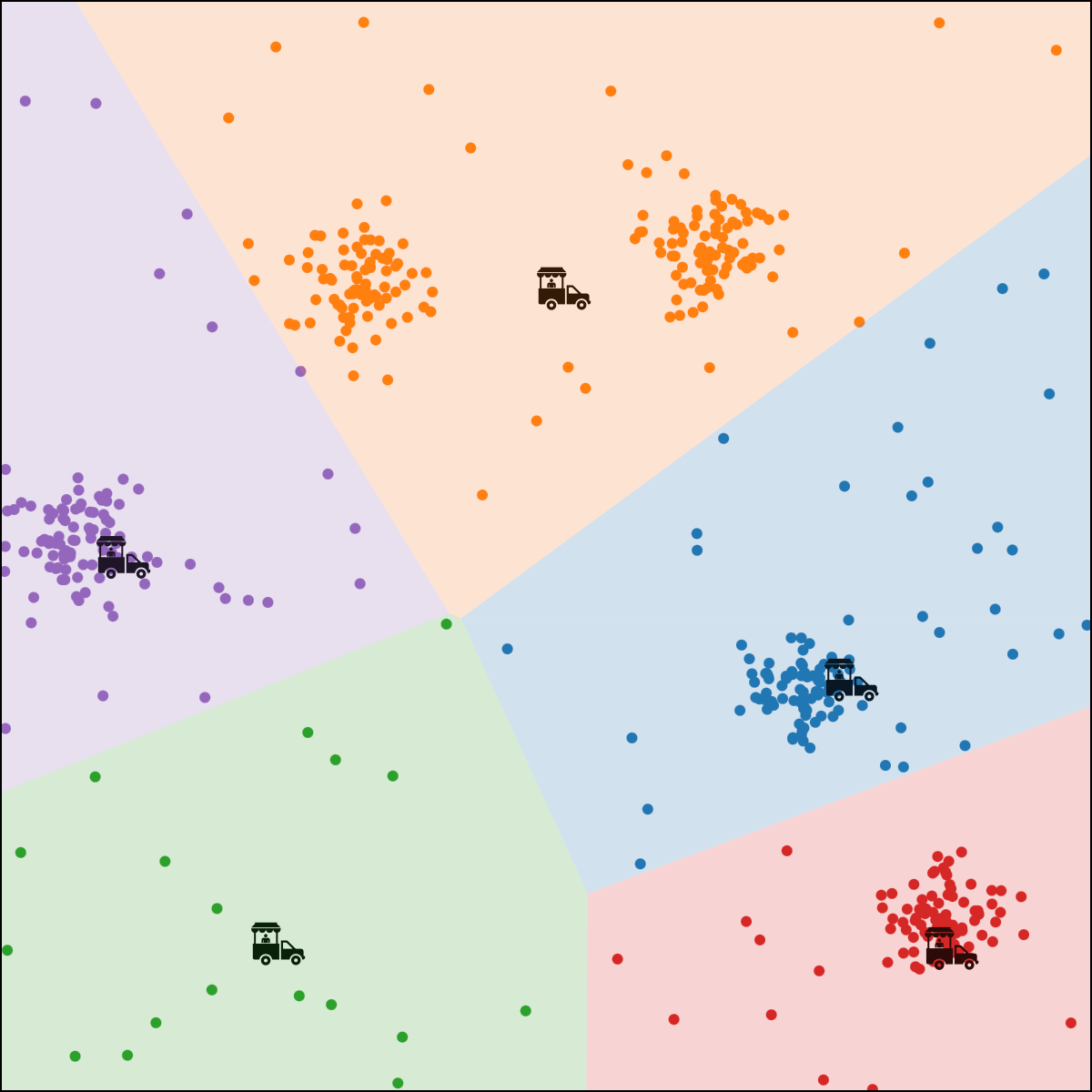
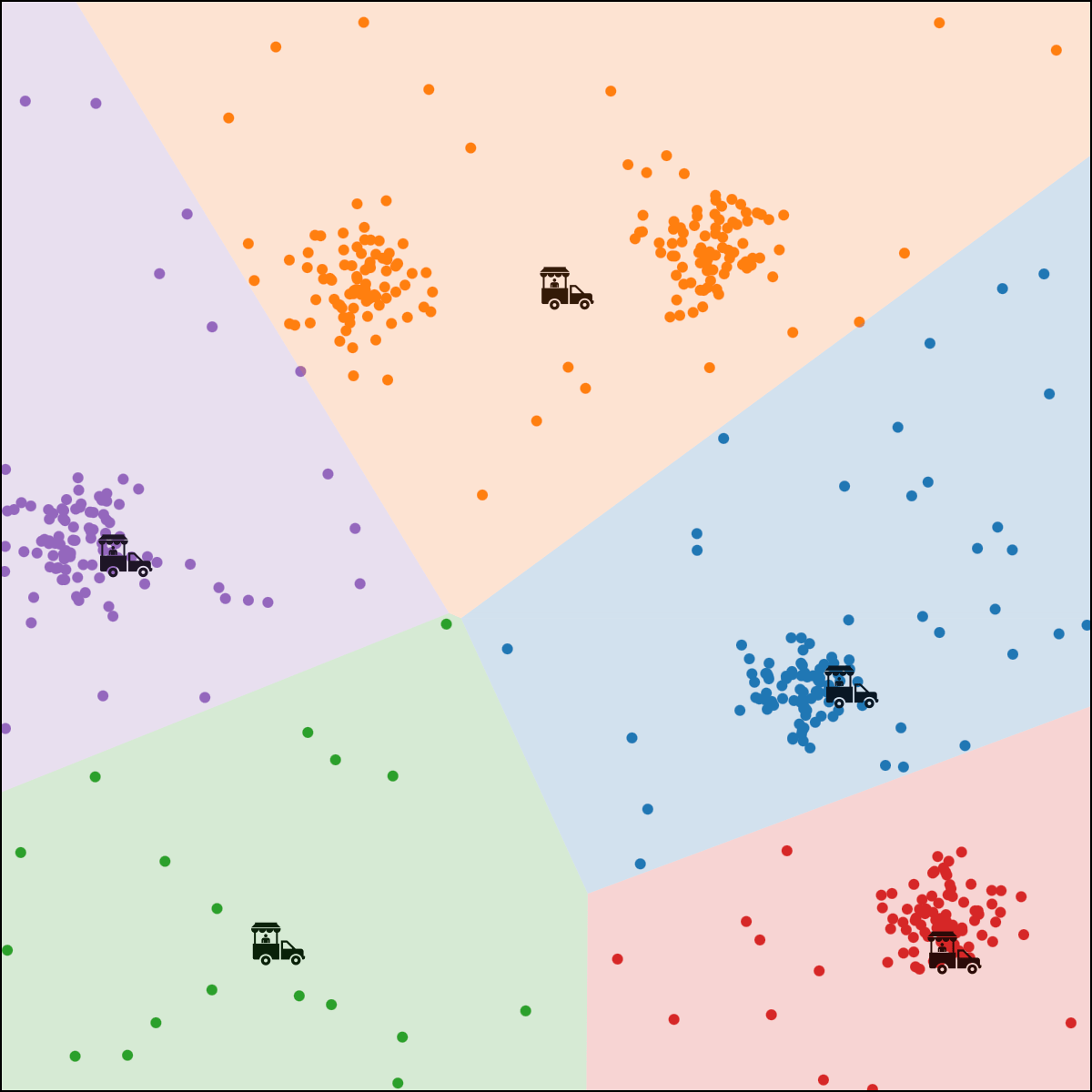
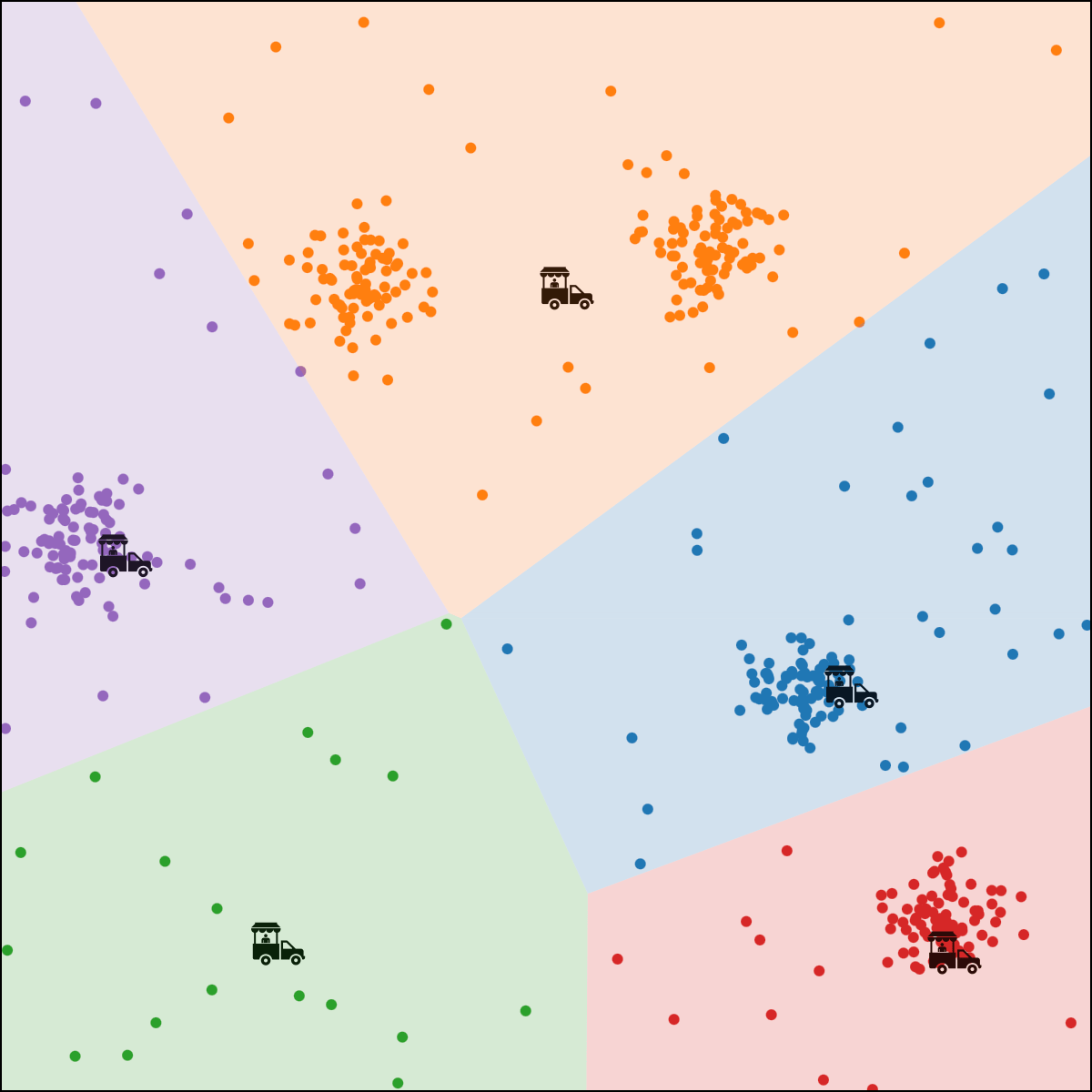
each person \(i\) gets assigned to food truck \(j\), color-coded.
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
\(\dots\)

3 \(y_{\text {old }} = y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)

3 \(y_{\text {old }} = y\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
\(N_j = \sum_{i=1}^n \mathbf{1}\left\{y^{(i)}=j\right\}\)
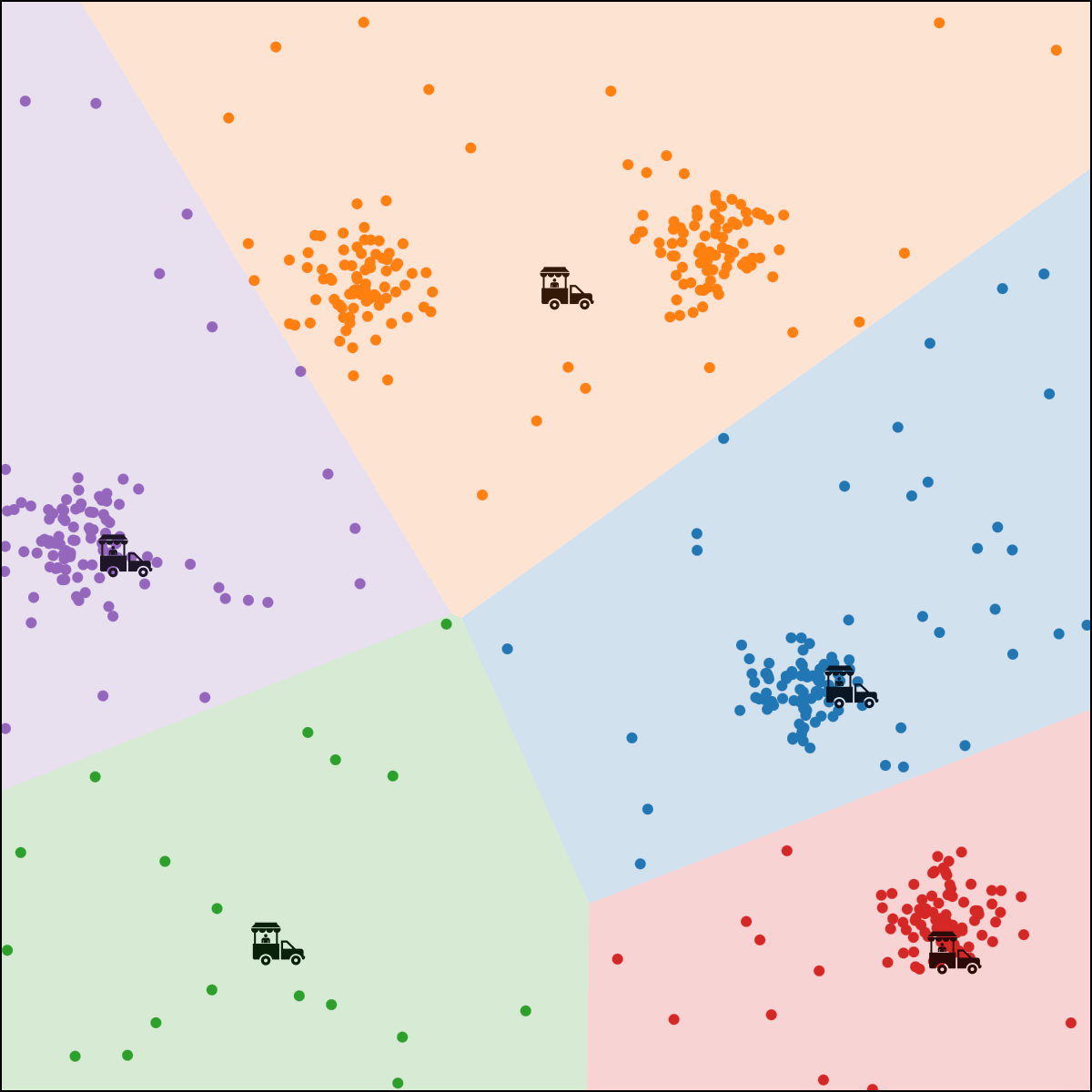
food truck \(j\) gets moved to the "central" location of all ppl assigned to it
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
\(\dots\)

3 \(y_{\text {old }} = y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
2 for \(t=1\) to \(\tau\)


3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
2 for \(t=1\) to \(\tau\)


3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
2 for \(t=1\) to \(\tau\)

3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)

3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break


3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break


3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break


3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)

K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
2 for \(t=1\) to \(\tau\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)

3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)

K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)

K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)

K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)

K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)

K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)

K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
3 \(y_{\text {old }} = y\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
10 return \(\mu, y\)
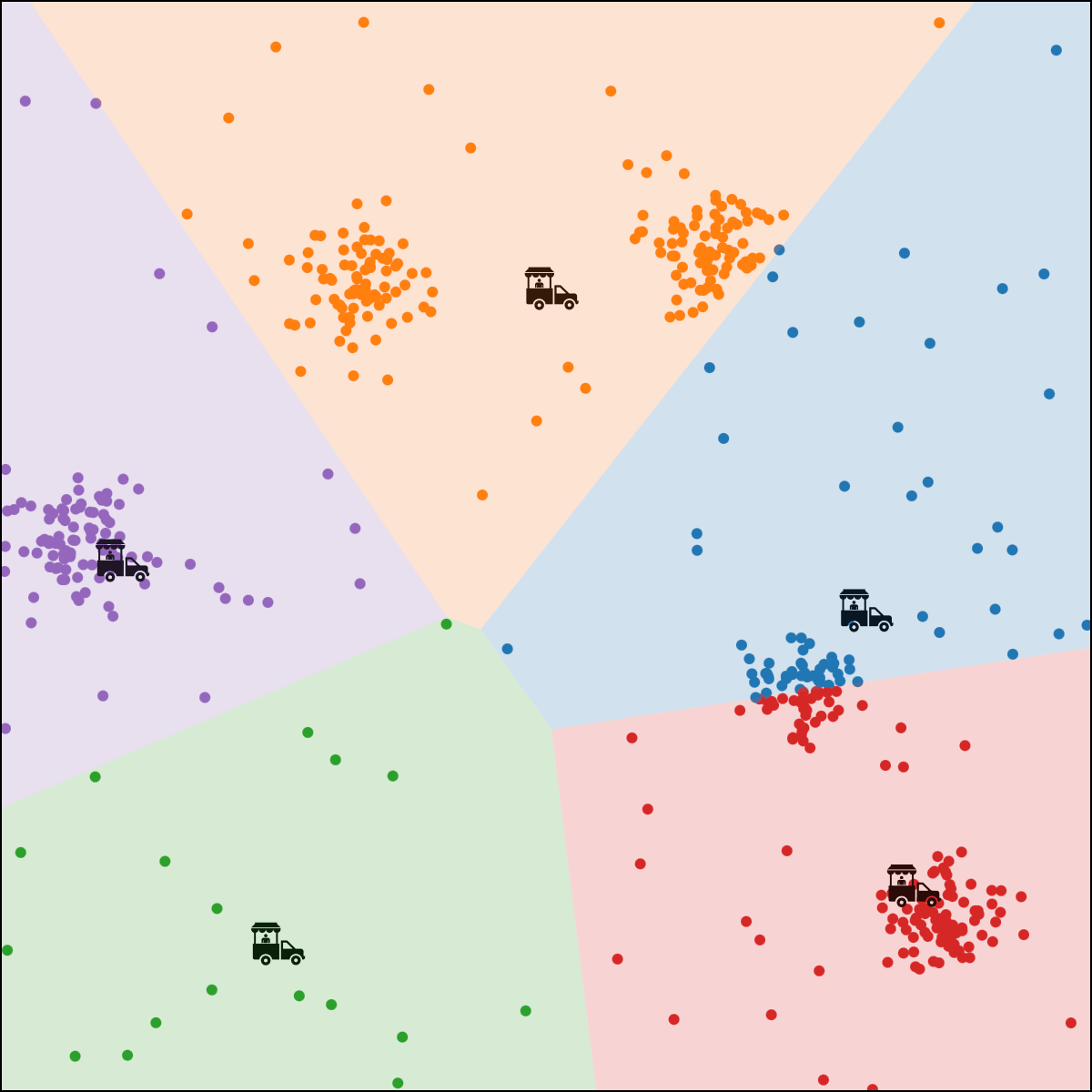
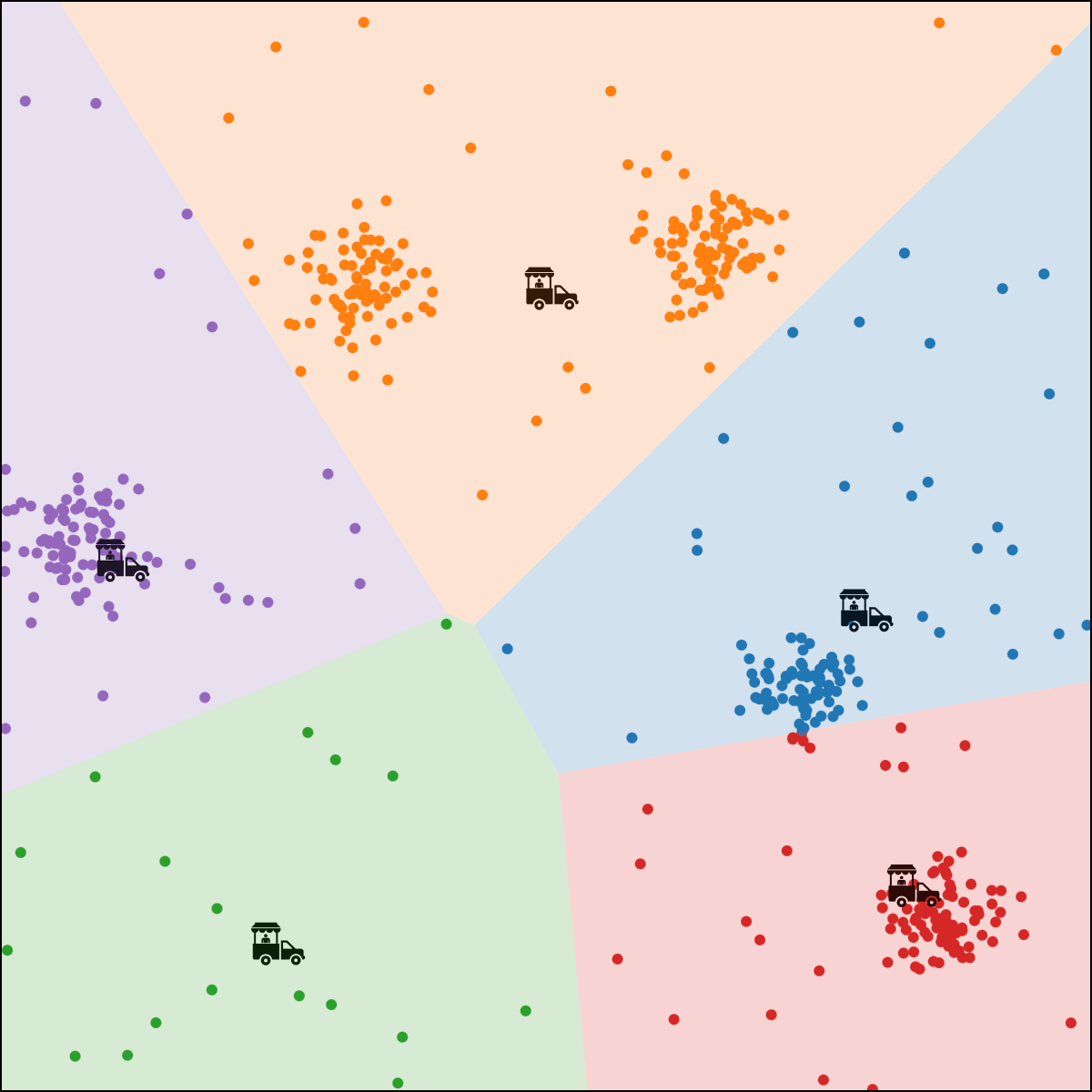
- if run for enough outer iterations, the algorithm will converge to a local minimum of the k-means objective.
- that local minimum could be "bad".
Effect of initialization

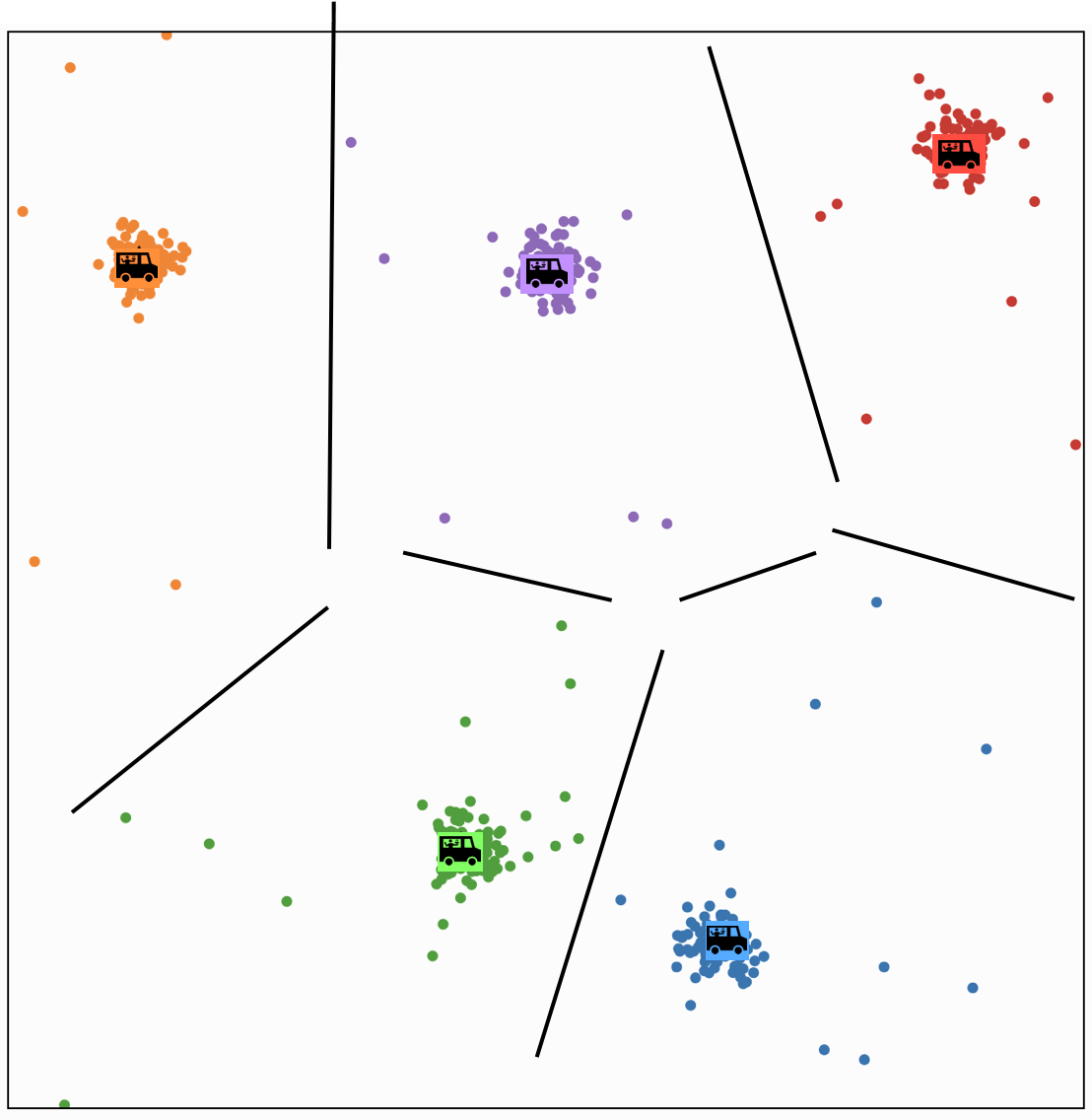
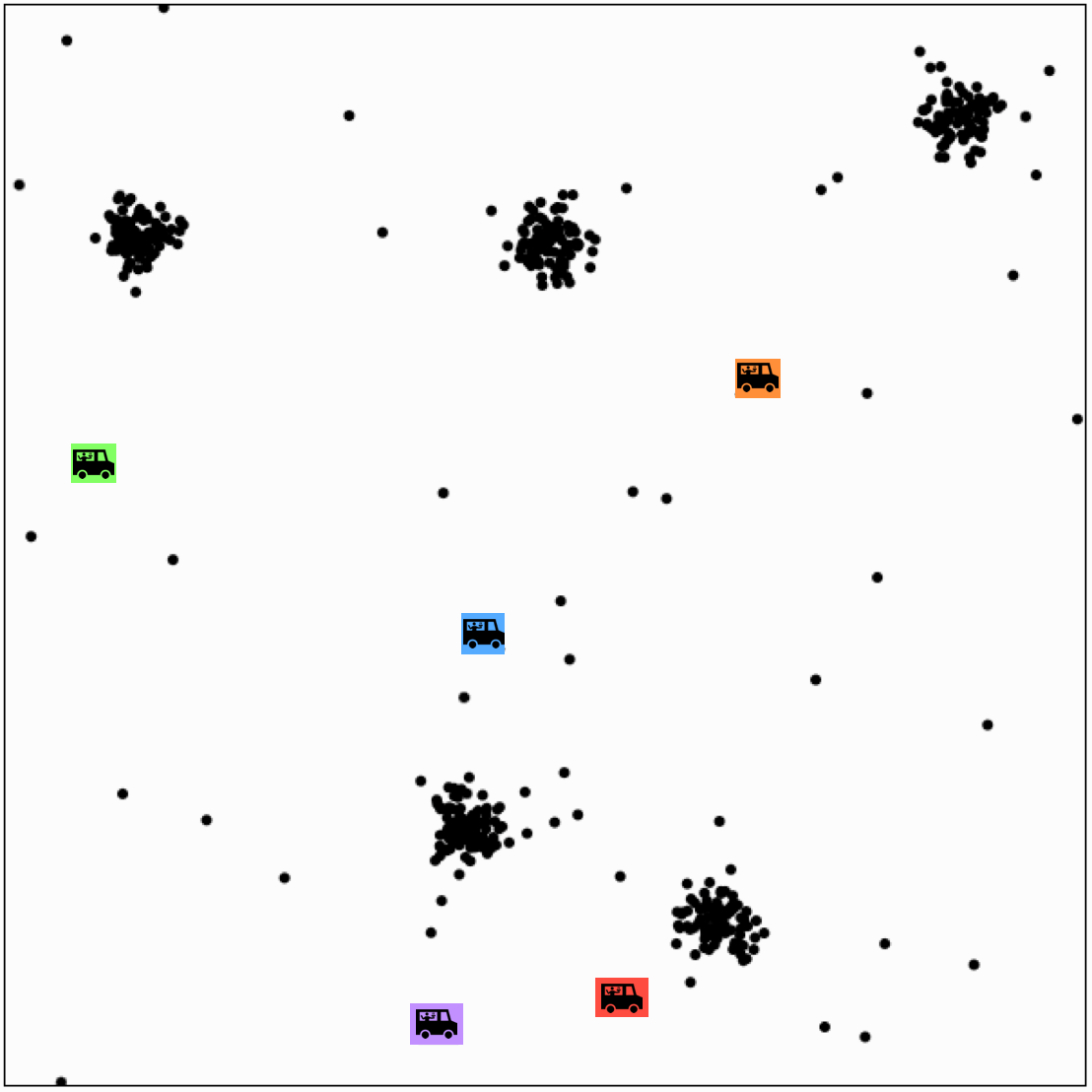

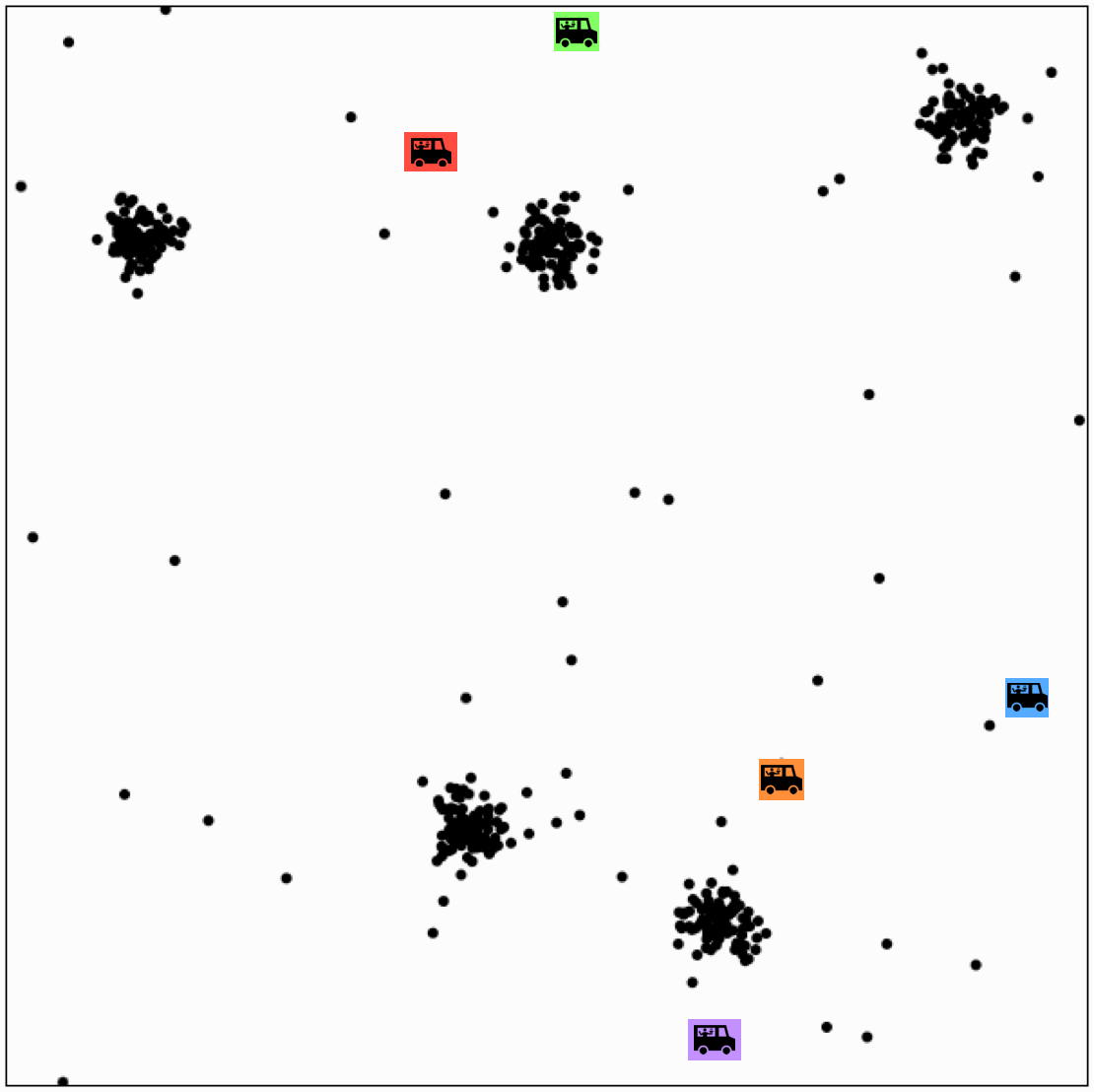
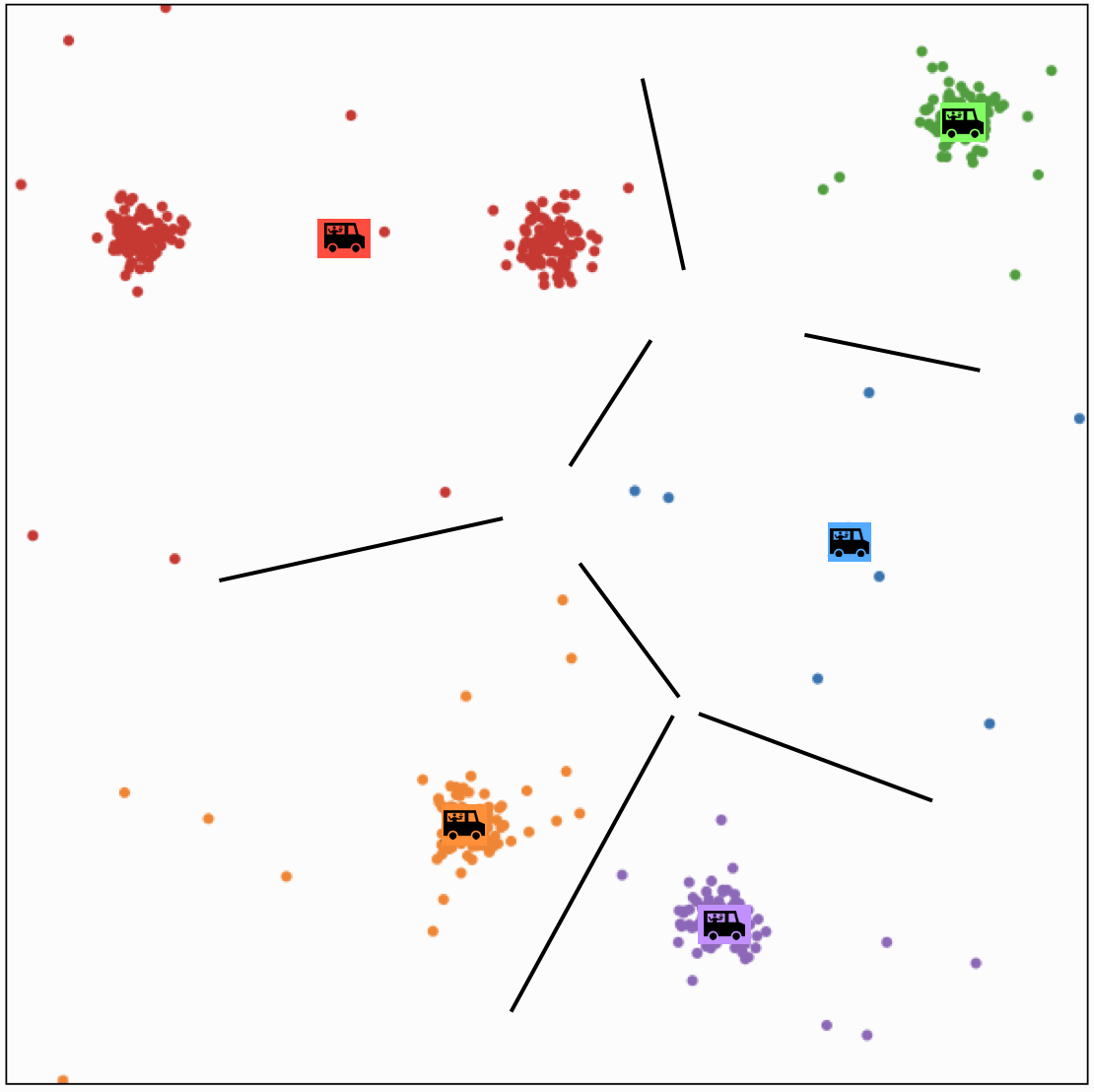
Effect of initialization - one remedy:



Run random initializations multiple times,
Compare their \(k\)-means objective values, choose the lowest one
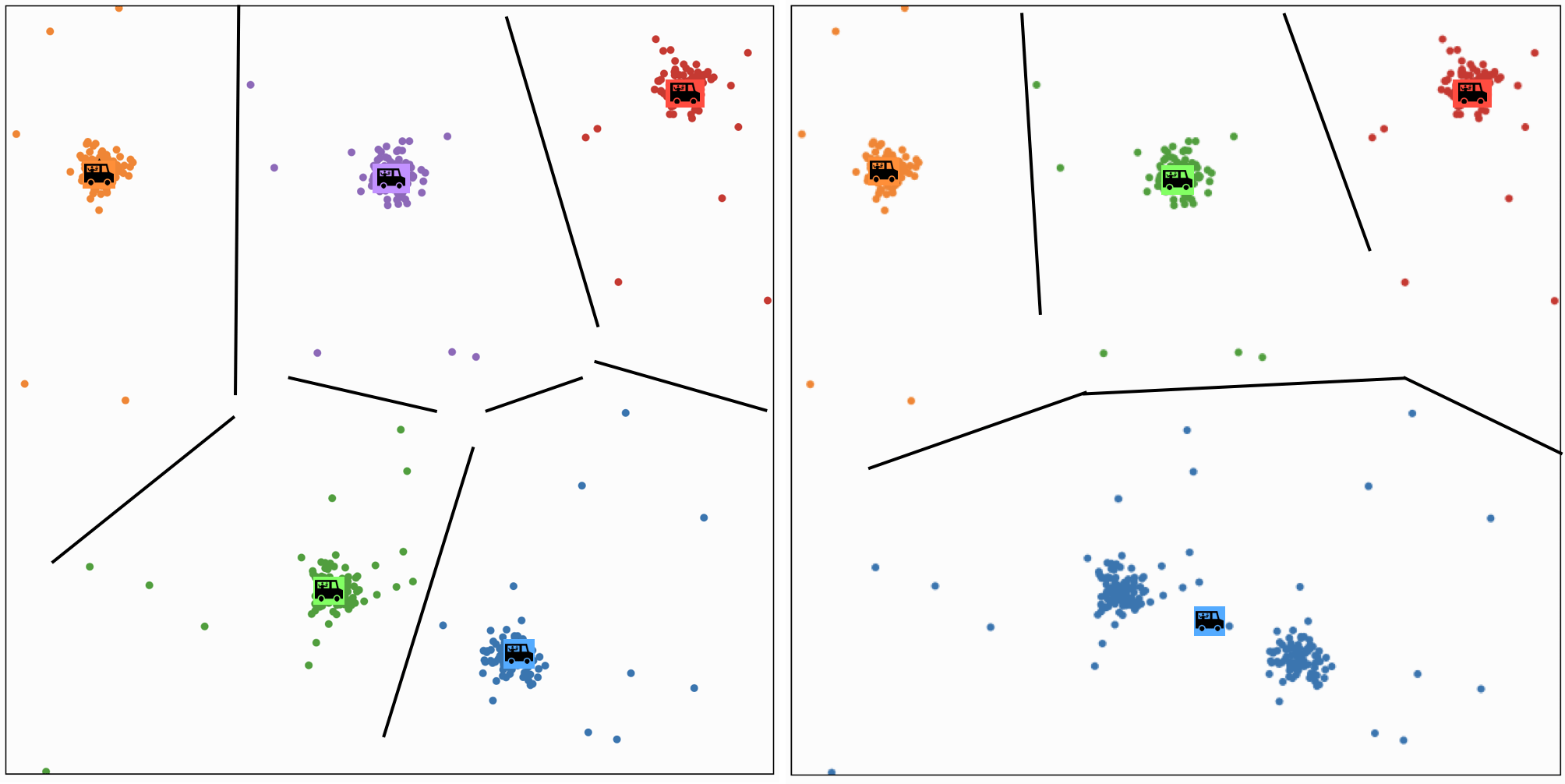
Effect of \(k\)
- Choosing of \(k\) is a judgment call. Cross-validation.
\(k\)-means
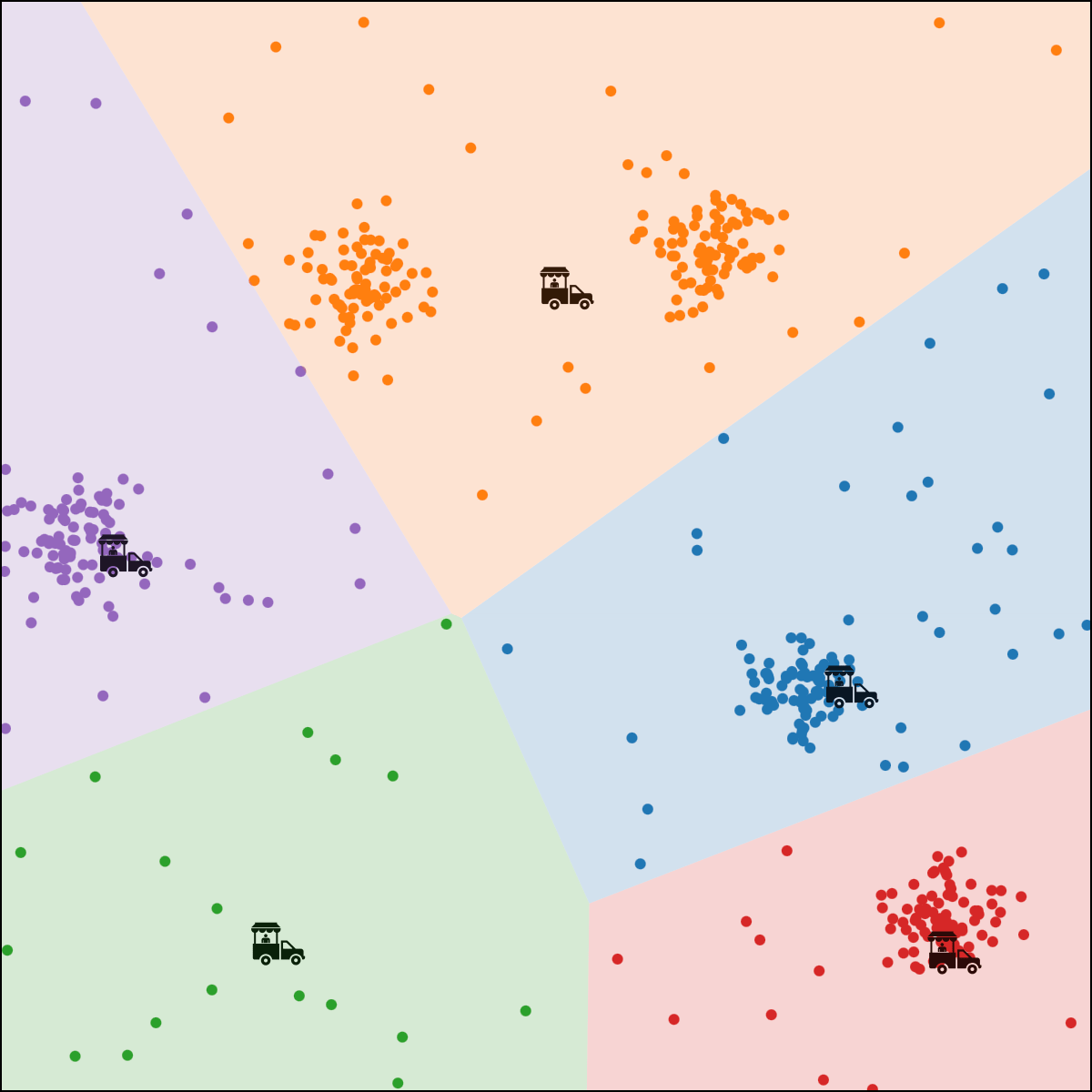

Compare to classification
Compare to classification
- Did we just do \(k\)-class classification?
- Looks like we assigned label \(y^{(i)}\), which takes \(k\) different values, to each feature vector \(x^{(i)}\)
- But we didn't use any labeled data
- The "labels" here don't have meaning; we could permute them and have the same result.
- Output is really a partition of the data/features.

- So what did we do?
- We clustered the data: we grouped the data by similarity
- Why not just plot the data? We should -- whenever we can!
- But also: Precision, big data, high dimensions, high volume.
- An example of unsupervised learning: no labeled data, and we're finding patterns.

Compare to classification

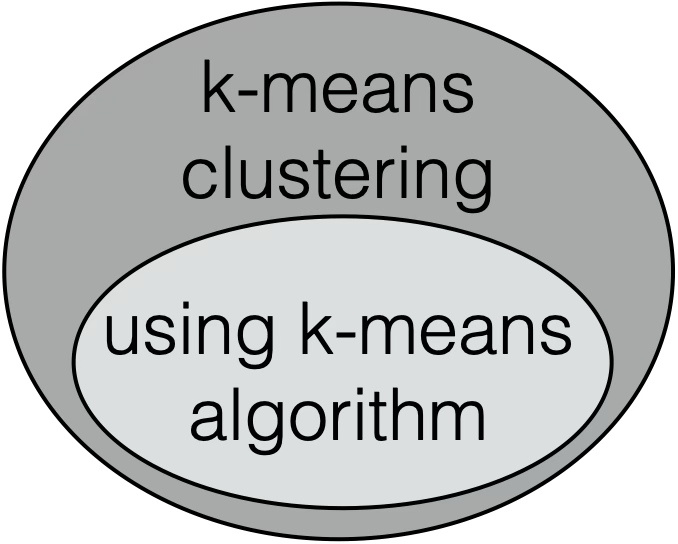
- \(k\)-means ++
- integre programming
- enumeration
- ...
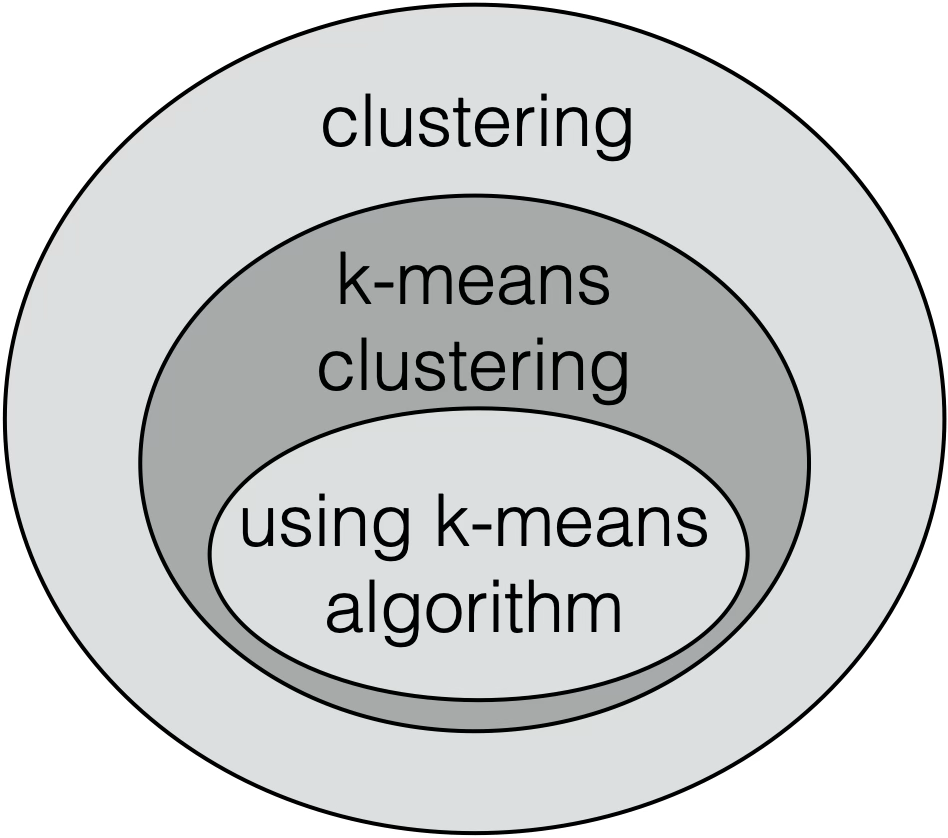

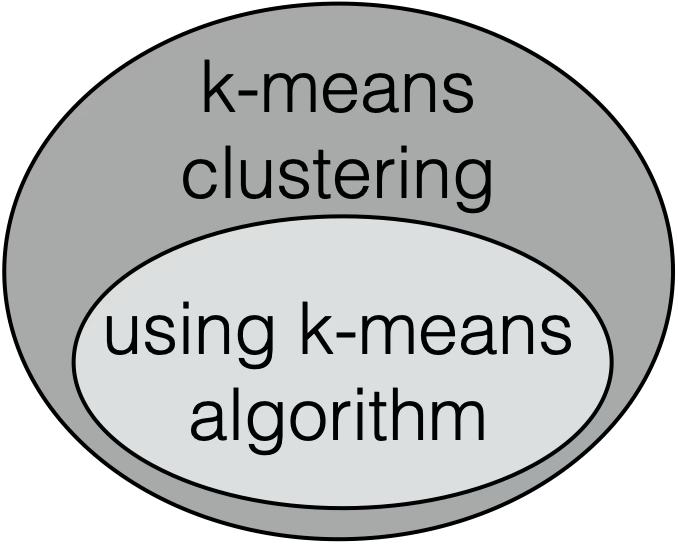
- Hierarchical Clustering
- Gaussian mixture model (GMMs)
- DBSCAN (Density-Based Spatial Clustering of Applications with Noise)



- More broadly, self-supervised learning
- Auto-encoder
- Variational auto-encoder
- Dimensionality reduction (PCA, t-SNE
- Rich world of generative models
...

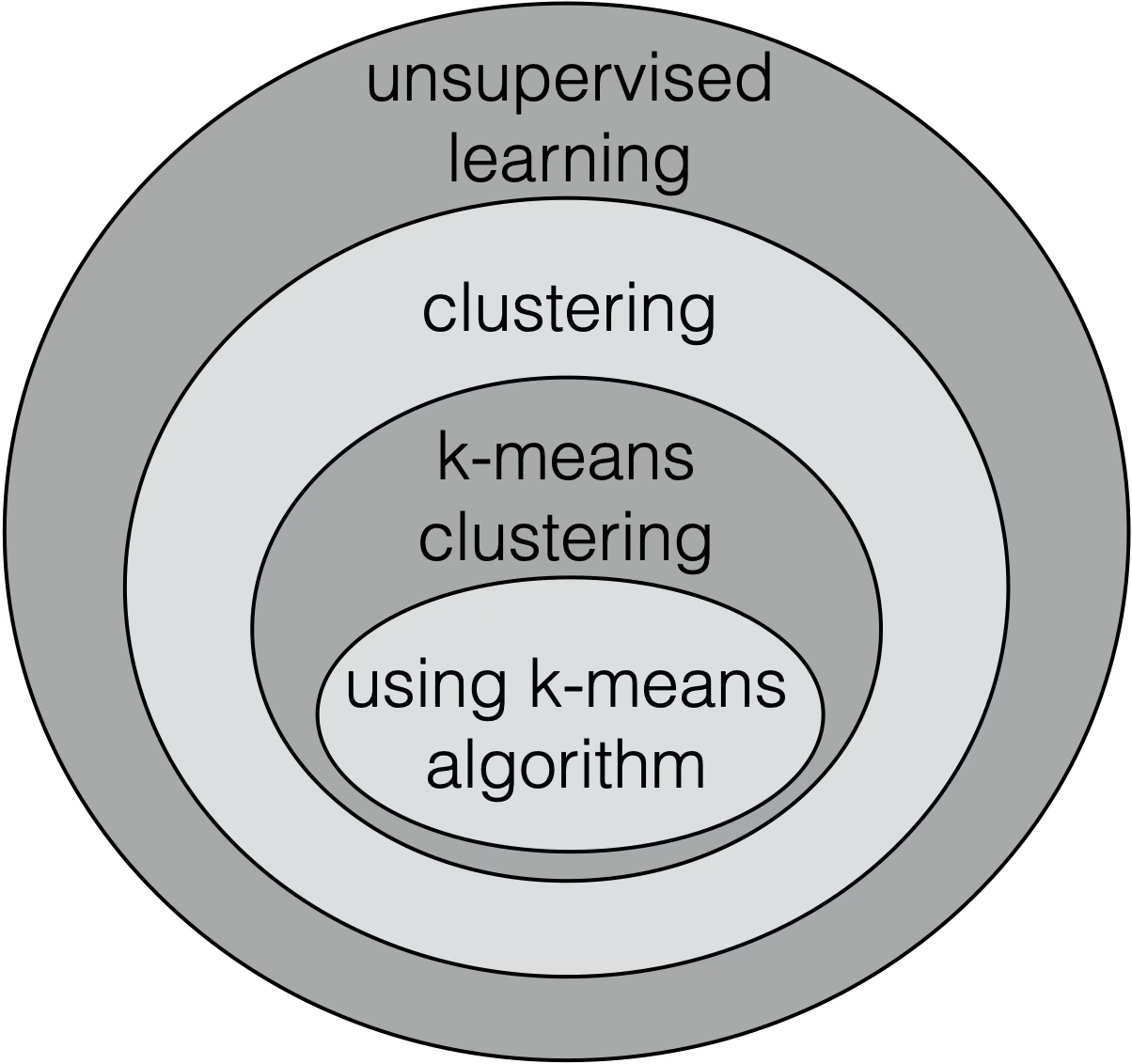
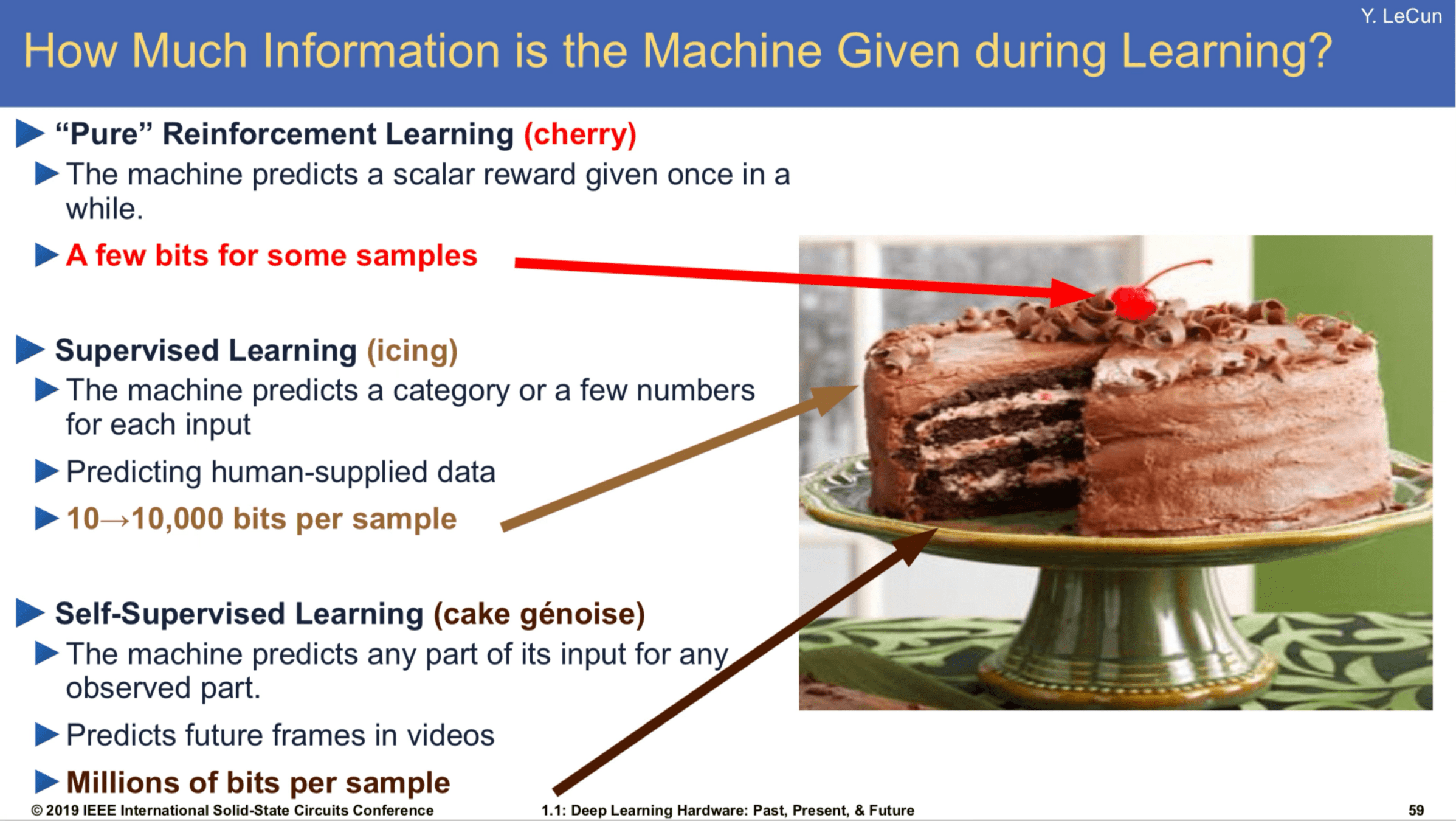
[Slide Credit: Yann LeCun]
Summary
- Clustering is an important kind of unsupervised learning in which we try to divide the x’s into a finite set of groups that are in some sense similar.
- A widely used clustering objective is the k-means. It also requires a distance metric on x’s.
- There’s a convenient special-purpose method for finding a local optimum: the k-means algorithm.
- The solution obtained by k-means algorithm is sensitive to initialization.
- The solution obtained by k-means algorithm is sensitive to the number of clusters chosen.
Thanks!
We'd love to hear your thoughts.
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
3 \(y_{o l d}=y\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbb{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
10 return \(\mu, y\)
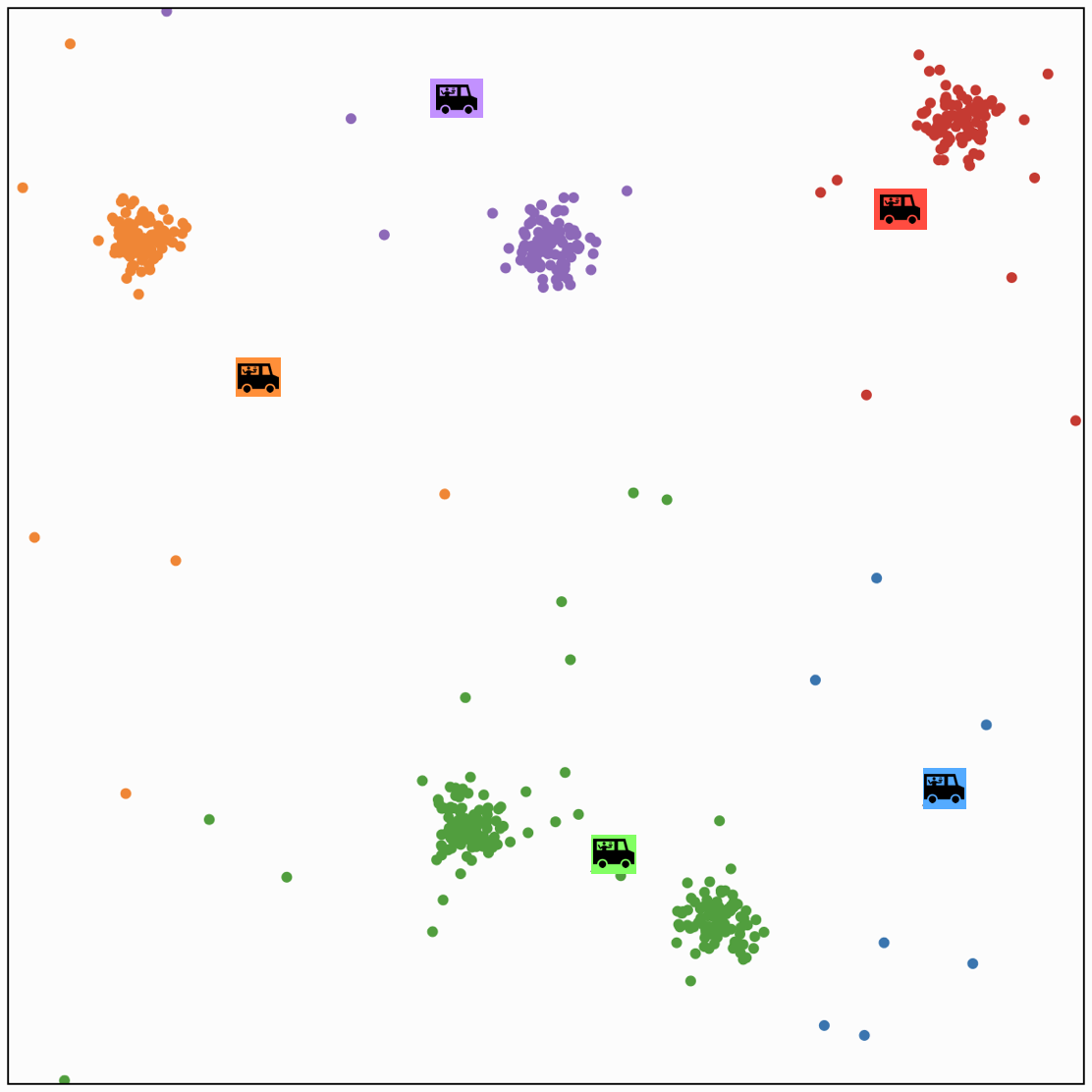

Food distribution placement
- \(x_1\): longitude, \(x_2\): latitude
- Person \(i\) location \(x^{(i)}\)
- Food truck \(j\) location \(\mu^{(j)}\)
- Q: where should I have my \(k\) food trucks park?
- want to minimize the "loss" of people we serve
- Loss if \(i\) walks to truck \(j\) : \(\left\|x^{(i)}-\mu^{(j)}\right\|_2^2\)
- Index of the truck where person \(i\) is chosen to walk to: \(y^{(i)}\)
(image credit: Tamara Broderick)