https://introml.mit.edu/

Lecture 3:  Gradient Descent Methods

 

Shen Shen

September 13, 2024

Intro to Machine Learning

  • Next Friday Sept 20, lecture will still be held at 12pm in 45-230, and live-streamed; But, it's a student holiday, attendance ultra not expected but always appreciated 😉
  • Lecture pages have centralized resources
  • Lecture recordings might be used for edX or beyond; pick a seat outside the camera/mic zone if you do not wish to participate.

Outline

  • Recap, motivation for gradient descent methods
  • Gradient descent algorithm (GD)
    • The gradient vector
    • GD algorithm
    • Gradient decent properties
      • convex functions, local vs global min 
  • Stochastic gradient descent (SGD)
    • SGD algorithm and setup
    • GD vs SGD comparison

Outline

  • Recap, motivation for gradient descent methods
  • Gradient descent algorithm (GD)
    • The gradient vector
    • GD algorithm
    • Gradient decent properties
      • convex functions, local vs global min 
  • Stochastic gradient descent (SGD)
    • SGD algorithm and setup
    • GD vs SGD comparison
Recall
  • A general ML approach
    • Collect data
    • Choose hypothesis class, hyperparameter, loss function
    • Train (optimize for) "good" hypothesis by minimizing loss. 

 

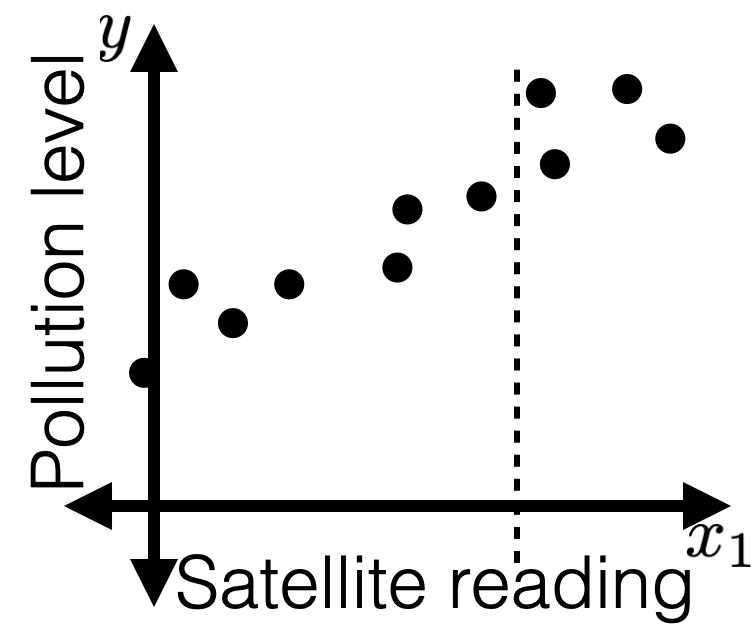
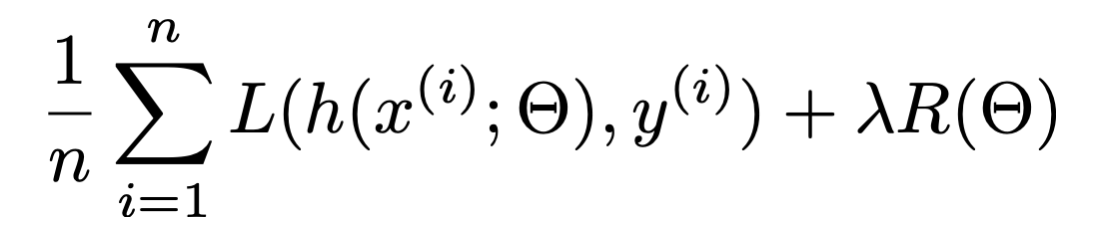
  • Limitations of a closed-form solution for objective minimizer
    • Don't always have closed-form solutions. (Recall, half-pipe cases.)
    • Ridge came to the rescue, but we don't always have such "savior".
    • Even when closed-form solutions exist, can be expensive to compute (recall, lab2, Q2.8)
  • Want a more general, efficient way! (=> GD methods today)

Outline

  • Recap, motivation for gradient descent methods
  • Gradient descent algorithm (GD)
    • The gradient vector
    • GD algorithm
    • Gradient decent properties
      • convex functions, local vs global min 
  • Stochastic gradient descent (SGD)
    • SGD algorithm and setup
    • GD vs SGD comparison

For \(f: \mathbb{R}^m \rightarrow \mathbb{R}\), its gradient \(\nabla f: \mathbb{R}^m \rightarrow \mathbb{R}^m\) is defined at the point \(p=\left(x_1, \ldots, x_m\right)\) in \(m\)-dimensional space as the vector

​

\nabla f(p)=\left[\begin{array}{c} \frac{\partial f}{\partial x_1}(p) \\ \vdots \\ \frac{\partial f}{\partial x_m}(p) \end{array}\right]
  1. Generalizes 1-dimensional derivatives.
  2. By construction, always has the same dimensionality as the function input.

(Aside: sometimes, the gradient doesn't exist, or doesn't behave nicely, as we'll see later in this course. For today, we have well-defined, nice, gradients.)

Gradient 

\nabla f(p)=\left[\begin{array}{c} \frac{\partial f}{\partial x_1}(p) \\ \vdots \\ \frac{\partial f}{\partial x_m}(p) \end{array}\right]
f(x, y, z) = x^2 + y^3 + z

another example

\nabla f(x, y, z) = \begin{bmatrix} 2x \\ 3y^2 \\ 1 \end{bmatrix}

a gradient can be the (symbolic) function

\nabla f(3, 2, 1) = \begin{bmatrix} 6\\ 12 \\ 1 \end{bmatrix}

one cute example:

exactly like how derivative can be both a function and a number.

or,

we can also evaluate the gradient function at a point and get (numerical) gradient vectors

\nabla f(p)=\left[\begin{array}{c} \frac{\partial f}{\partial x_1}(p) \\ \vdots \\ \frac{\partial f}{\partial x_m}(p) \end{array}\right]

3. the gradient points in the direction of the (steepest) increase in the function value.

 

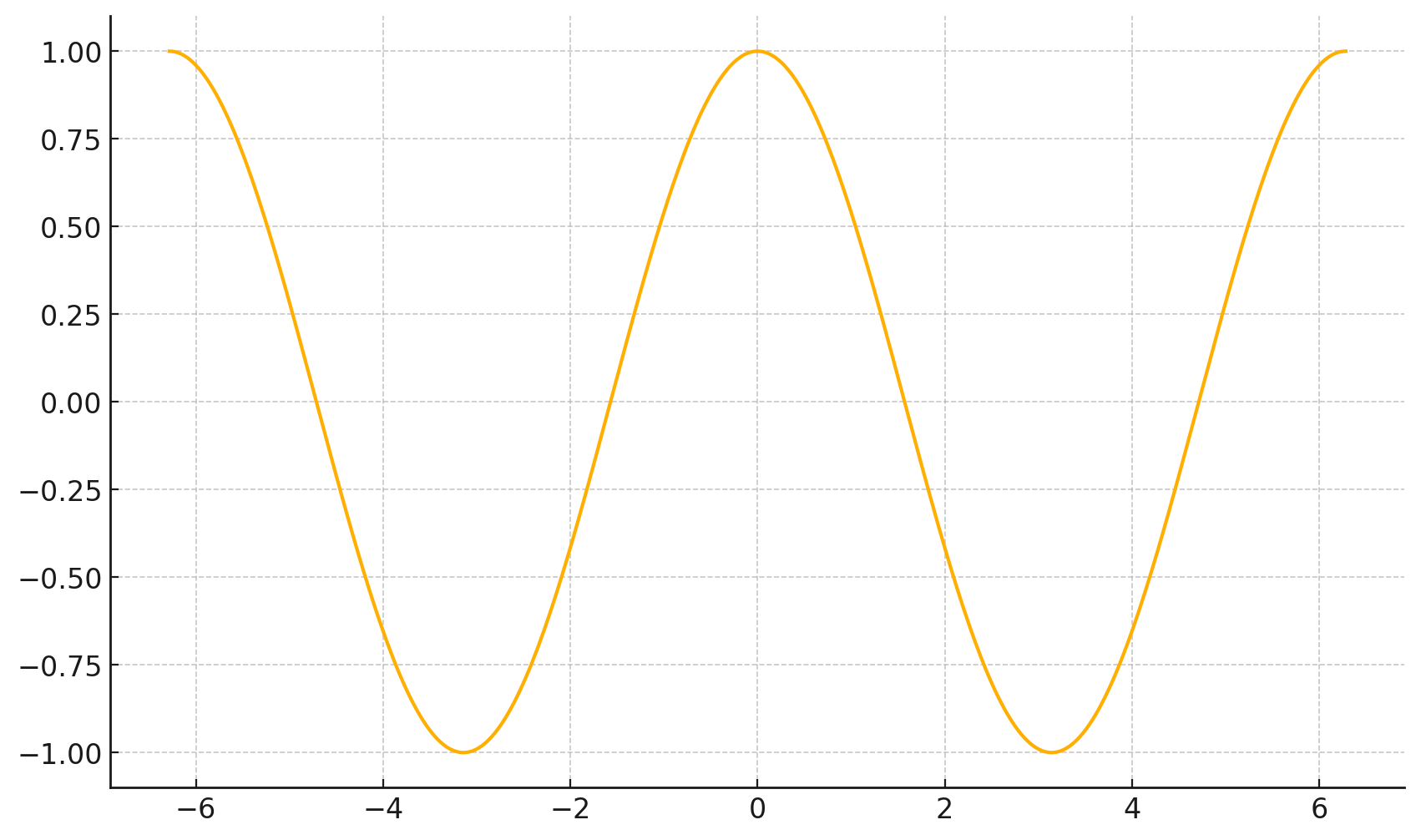
\(\frac{d}{dx} \cos(x) \bigg|_{x = -4} = -\sin(-4) \approx -0.7568\)

 

\(\frac{d}{dx} \cos(x) \bigg|_{x = 5} = -\sin(5) \approx 0.9589\)

Outline

  • Recap, motivation for gradient descent methods
  • Gradient descent algorithm (GD)
    • The gradient vector
    • GD algorithm
    • Gradient decent properties
      • convex functions, local vs global min 
  • Stochastic gradient descent (SGD)
    • SGD algorithm and setup
    • GD vs SGD comparison

hyperparameters

initial guess

of parameters

learning rate, 

aka, step size

precision

1

2

3

4

5

6

7

8

1

2

3

4

5

6

7

8

1

2

3

4

5

6

7

8

1

2

3

4

5

6

7

8

1

2

3

4

5

6

7

8

1

2

3

4

5

6

7

8

1

2

3

4

5

6

7

8

1

2

3

4

5

6

7

8

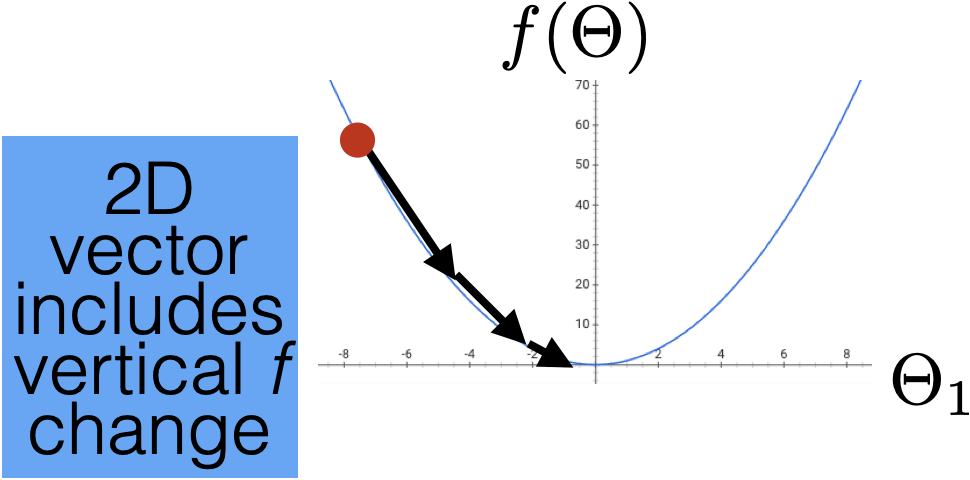
Q: if this condition is satisfied, what does it imply?

A: the gradient at the current parameter is almost zero.

1

2

3

4

5

6

7

8

Other possible stopping criteria for line 7:

  • Parameter norm change between iteration\(\left\|\Theta^{(t)}-\Theta^{(t-1)}\right\|<\epsilon\)
  • Gradient norm close to zero \(\left\|\nabla_{\Theta} f\left(\Theta^{(t)}\right)\right\|<\epsilon\)
  • Max number of iterations \(T\)

1

2

3

4

5

6

7

8

Outline

  • Recap, motivation for gradient descent methods
  • Gradient descent algorithm (GD)
    • The gradient vector
    • GD algorithm
    • Gradient decent properties
      • convex functions, local vs global min
  • Stochastic gradient descent (SGD)
    • SGD algorithm and setup
    • GD vs SGD comparison

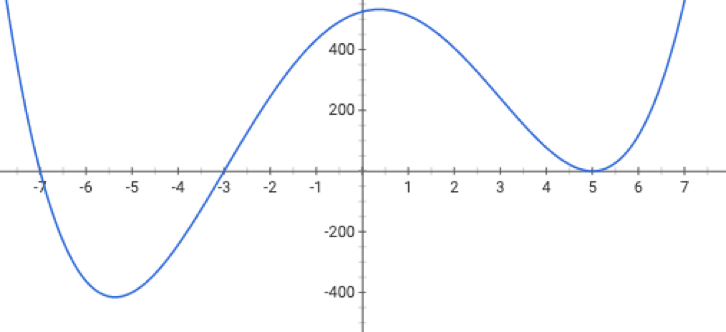
When minimizing a function, we'd hope to get to a global minimizer

 

At a global minimizer

the gradient vector is the zero vector

\(\Rightarrow\)

\(\nLeftarrow\)

When minimizing a function, we'd hope to get to a global minimizer

 

At a global minimizer

the gradient vector is the zero vector

\(\Leftarrow\)

the function is a convex function

\{

A function \(f\) is convex 

if any line segment connecting two points of the graph of \(f\) lies above or on the graph.

  • (\(f\) is concave if \(-f\) is convex.)
  • (one can say a lot about optimization convergence for convex functions.)

Some examples

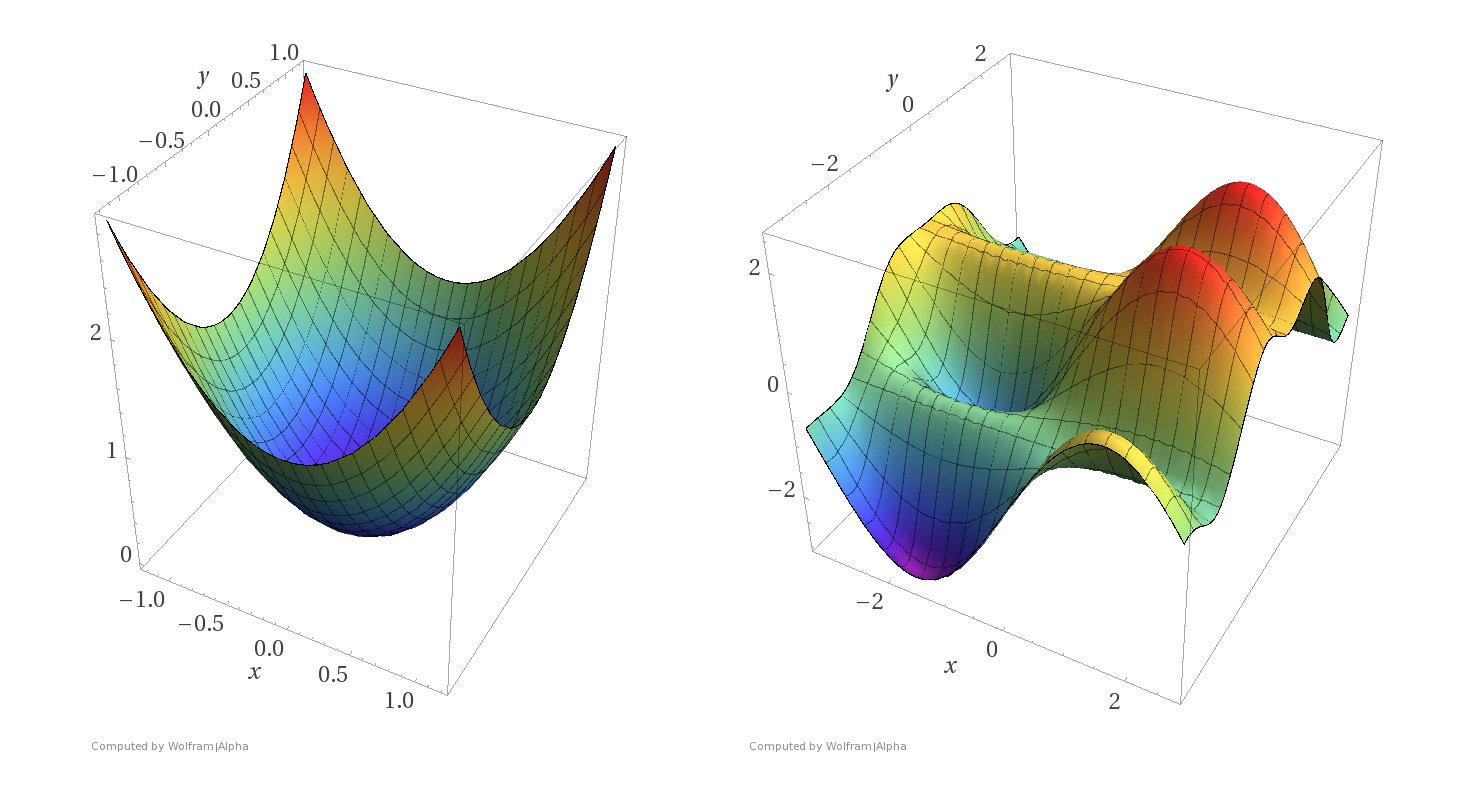
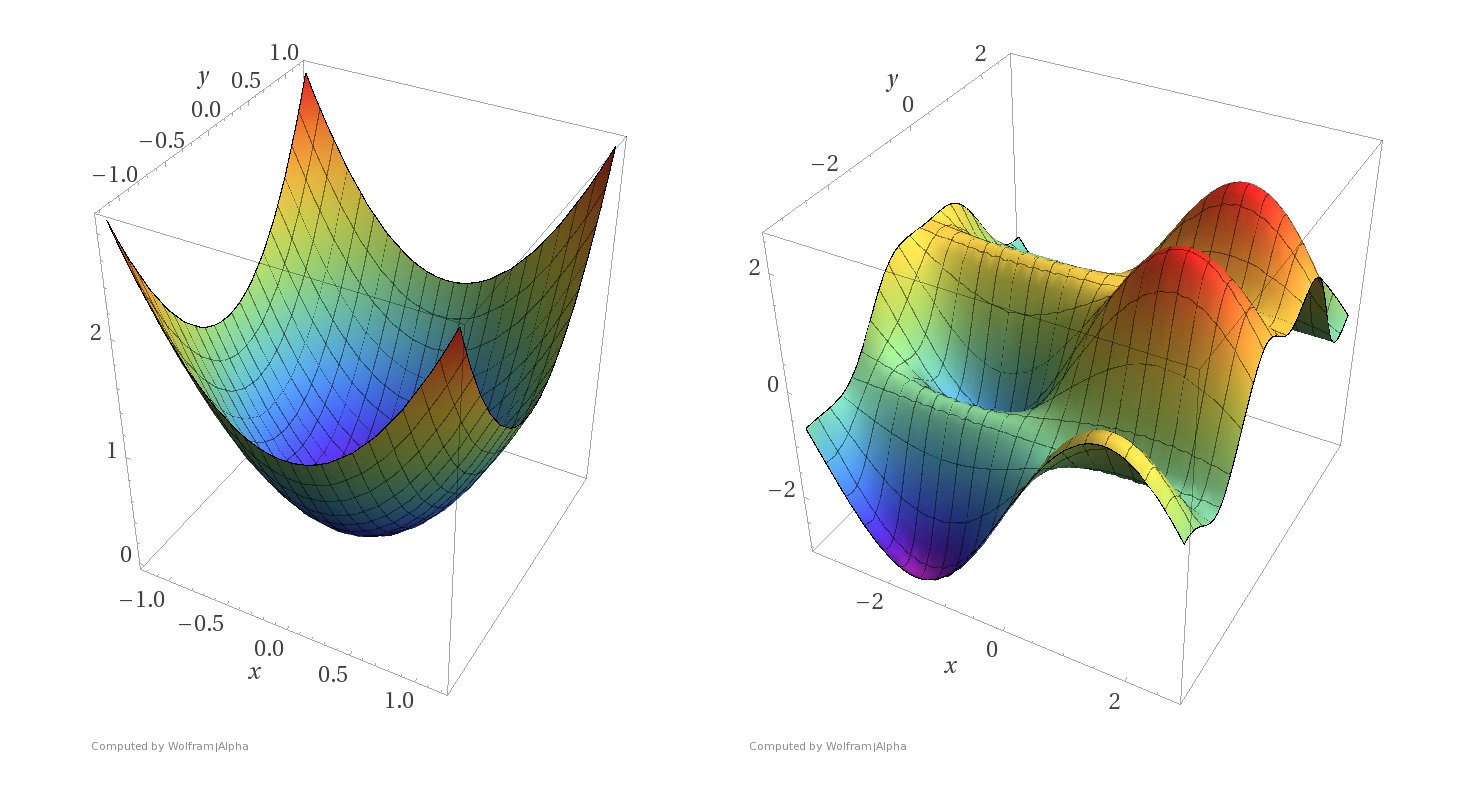
Convex functions

Non-convex functions

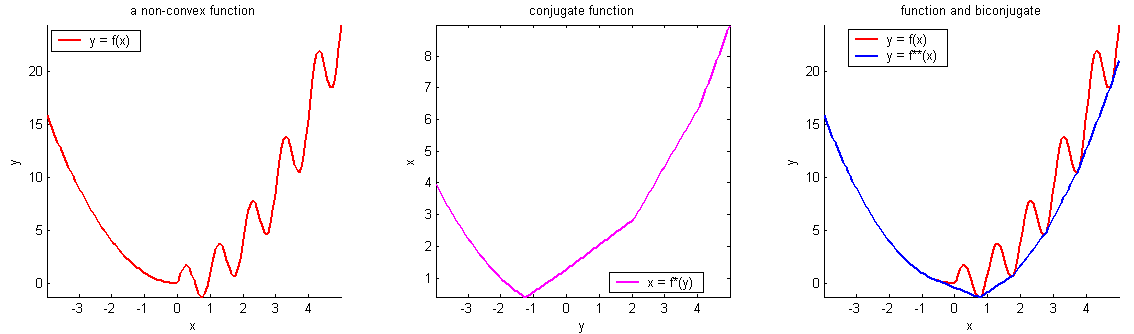
  • A function \(f\) on \(\mathbb{R}^m\) is convex if any line segment connecting two points of the graph of \(f\) lies above or on the graph.
  • For convex functions, all local minima are global minima.

What do we need to know:

  • Intuitive understanding of the definition
  • If given a function, can determine if it's convex. (We'll only ever give at most 2D, so visual understanding is enough)
  • Understand how gradient descent algorithms may "fail" without convexity.
  • Recognize that OLS loss function is convex, ridge regression loss is (strictly) convex, and later cross-entropy loss function is convex too.
  • Assumptions:
    • \(f\) is sufficiently "smooth" 
    • \(f\) has at least one global minimum
    • Run the algorithm long enough
    • \(\eta\) is sufficiently small
    • \(f\) is convex
  • Conclusion:
    • Gradient descent will return a parameter value within \(\tilde{\epsilon}\) of a global minimum (for any chosen \(\tilde{\epsilon}>0\) )

Gradient Descent Performance

if violated, may not have gradient,

can't run gradient descent

  • Assumptions:
    • \(f\) is sufficiently "smooth"
    • \(f\) has at least one global minimum
    • Run the algorithm long enough
    • \(\eta\) is sufficiently small
    • \(f\) is convex
  • Conclusion:
    • Gradient descent will return a parameter value within \(\tilde{\epsilon}\) of a global minimum (for any chosen \(\tilde{\epsilon}>0\) )

Gradient Descent Performance

if violated:

may not terminate/no minimum to converge to

  • Assumptions:
    • \(f\) is sufficiently "smooth" 
    • \(f\) has at least one global minimum
    • Run the algorithm long enough
    • \(\eta\) is sufficiently small
    • \(f\) is convex
  • Conclusion:
    • Gradient descent will return a parameter value within \(\tilde{\epsilon}\) of a global minimum (for any chosen \(\tilde{\epsilon}>0\) 

Gradient Descent Performance

if violated:

see demo on next slide, also lab/recitation/hw

  • Assumptions:
    • \(f\) is sufficiently "smooth" 
    • \(f\) has at least one global minimum
    • Run the algorithm long enough
    • \(\eta\) is sufficiently small
    • \(f\) is convex
  • Conclusion:
    • Gradient descent will return a parameter value within \(\tilde{\epsilon}\) of a global minimum (for any chosen \(\tilde{\epsilon}>0\) )

Gradient Descent Performance

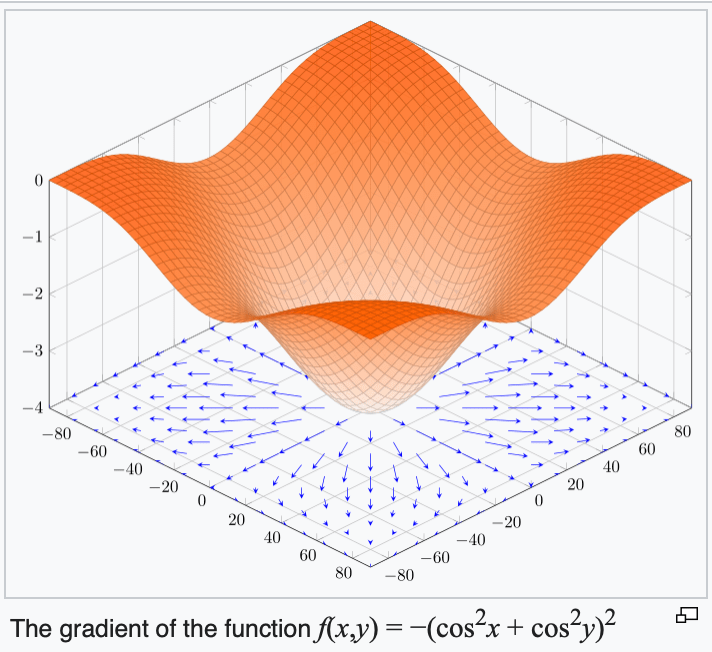
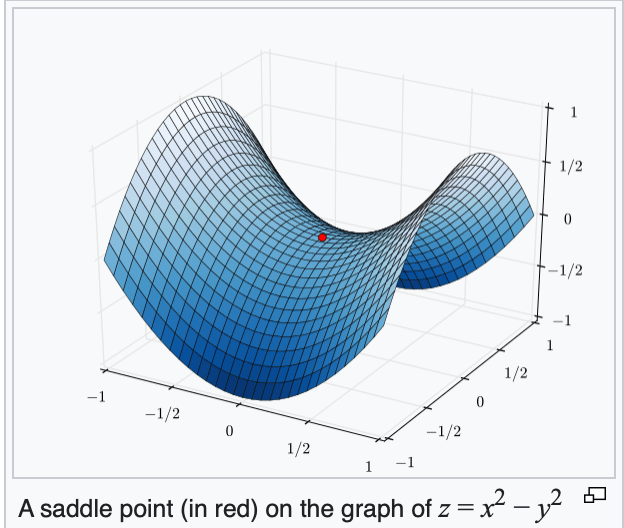
if violated, may get stuck at a saddle point

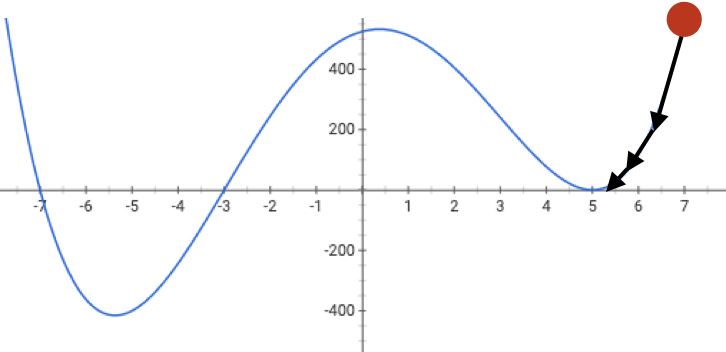
or a local minimum

Gradient descent performance

  • Assumptions:
    • \(f\) is sufficiently "smooth" 
    • \(f\) has at least one global minimum
    • Run the algorithm sufficiently "long"
    • \(\eta\) is sufficiently small
    • \(f\) is convex
  • Conclusion:
    • Gradient descent will return a parameter value within \(\tilde{\epsilon}\) of a global minimum (for any chosen \(\tilde{\epsilon}>0\) )

Outline

  • Recap, motivation for gradient descent methods
  • Gradient descent algorithm (GD)
    • The gradient vector
    • GD algorithm
    • Gradient decent properties
      • convex functions, local vs global min
  • Stochastic gradient descent (SGD)
    • SGD algorithm and setup
    • GD vs SGD comparison

Gradient of an ML objective

  • An ML objective function is a finite sum
  • the MSE of a linear hypothesis:
  • The gradient of an ML objective :
\nabla f(\Theta) = \nabla (\frac{1}{n} \sum_{i=1}^n f_i(\Theta))
\frac{2}{n} \sum_{i=1}^n\left(\theta^{\top} x^{(i)}-y^{(i)}\right) x^{(i)}
= \frac{1}{n} \sum_{i=1}^n \nabla f_i(\Theta)
  • and its gradient w.r.t. \(\theta\):

In general, 

For instance,

\frac{1}{n} \sum_{i=1}^n\left(\theta^{\top} x^{(i)}-y^{(i)}\right)^2
f(\Theta)=\frac{1}{n} \sum_{i=1}^n f_i(\Theta)

(gradient of the sum) = (sum of the gradient) 

👆

Concrete example

Three data points:

{(2,5), (3,6), (4,7)}

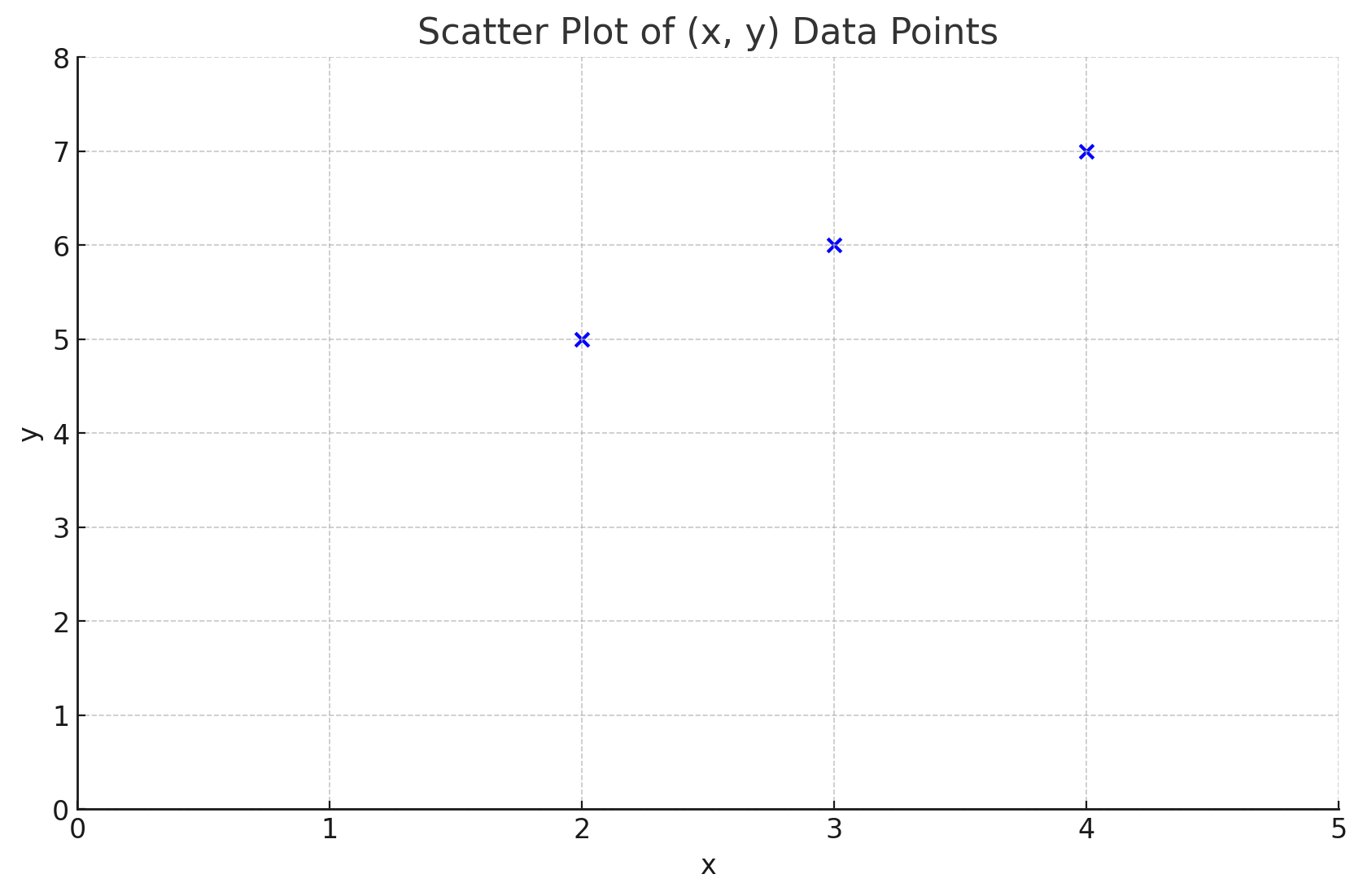
Fit a line (without offset) to the dataset, MSE: 

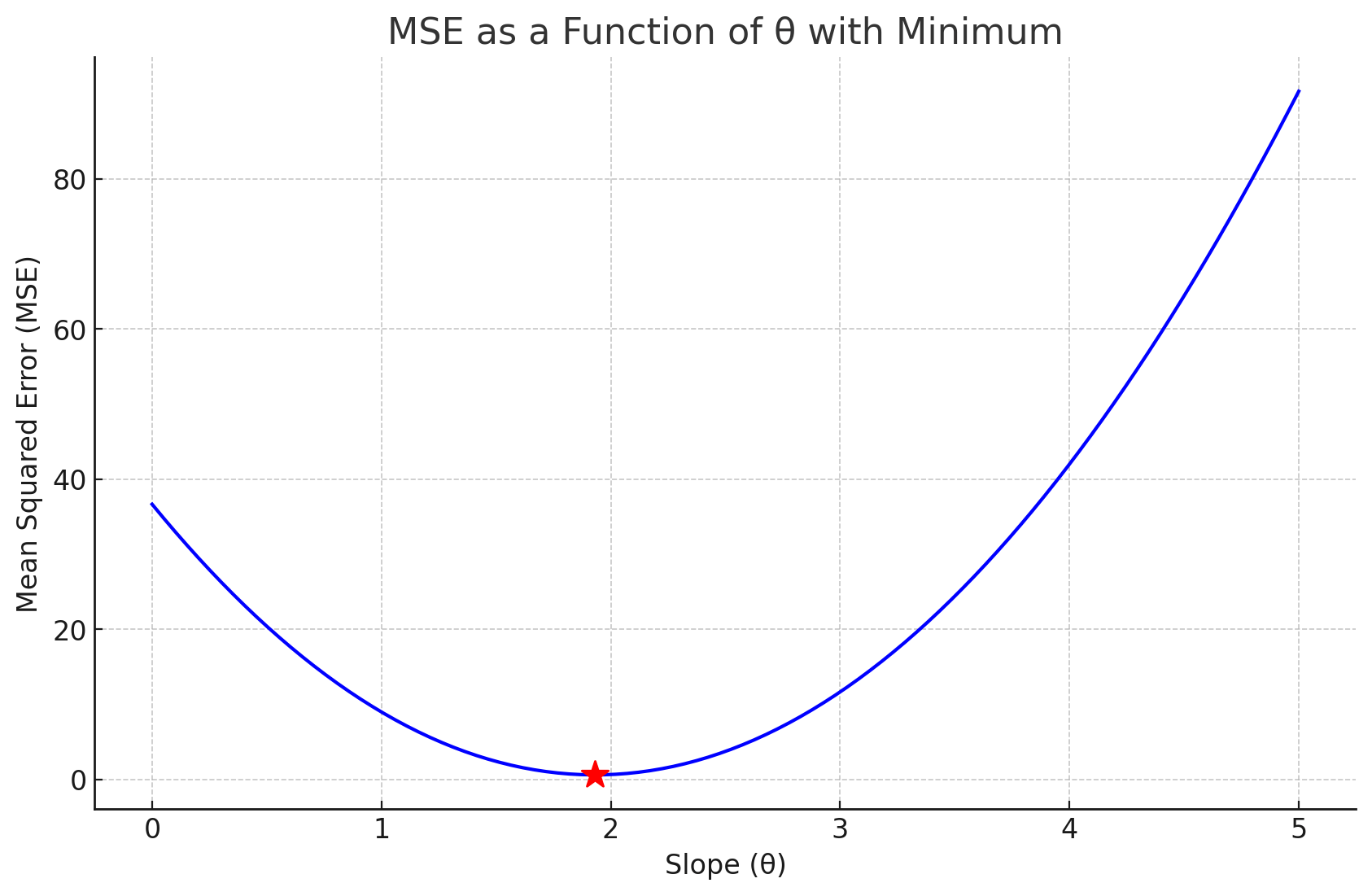
f(\theta) = \frac{1}{3}\left[(2 \theta-5)^2+(3 \theta-6)^{2}+(4 \theta-7)^2\right]
\nabla_\theta f = \frac{2}{3}[2(2 \theta-5)+3(3 \theta-6)+4(4 \theta-7)]

First data point's "pull"

Second data point 's "pull"

Third data point's "pull"

Stochastic gradient descent

\nabla f(\Theta)= \frac{1}{n} \sum_{i=1}^n \nabla f_i(\Theta)
\approx \nabla f_i(\Theta)

for a randomly picked data point \(i\)

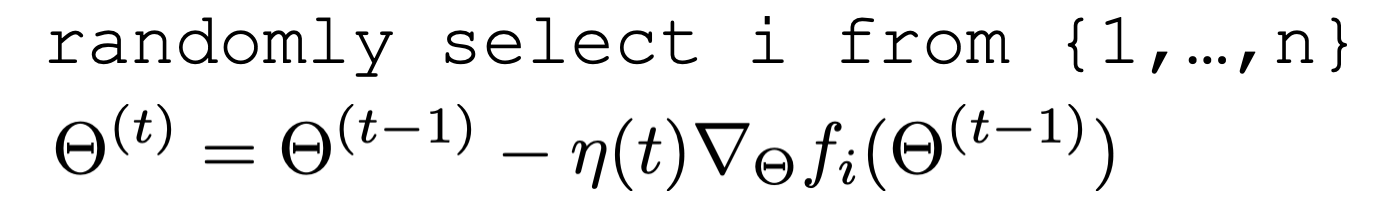
  • Assumptions:
    • \(f\) is sufficiently "smooth" 
    • \(f\) has at least one global minimum
    • Run the algorithm long enough
    • \(\eta\) is sufficiently small and satisfies additional "scheduling" condition
    • \(f\) is convex
  • Conclusion:
    • Stochastic gradient descent will return a parameter value within \(\tilde{\epsilon}\) of a global minimum with probability 1 (for any chosen \(\tilde{\epsilon}>0\) )

Stochastic gradient descent performance

\(\sum_{t=1}^{\infty} \eta(t)=\infty\) and \(\sum_{t=1}^{\infty} \eta(t)^2<\infty\)

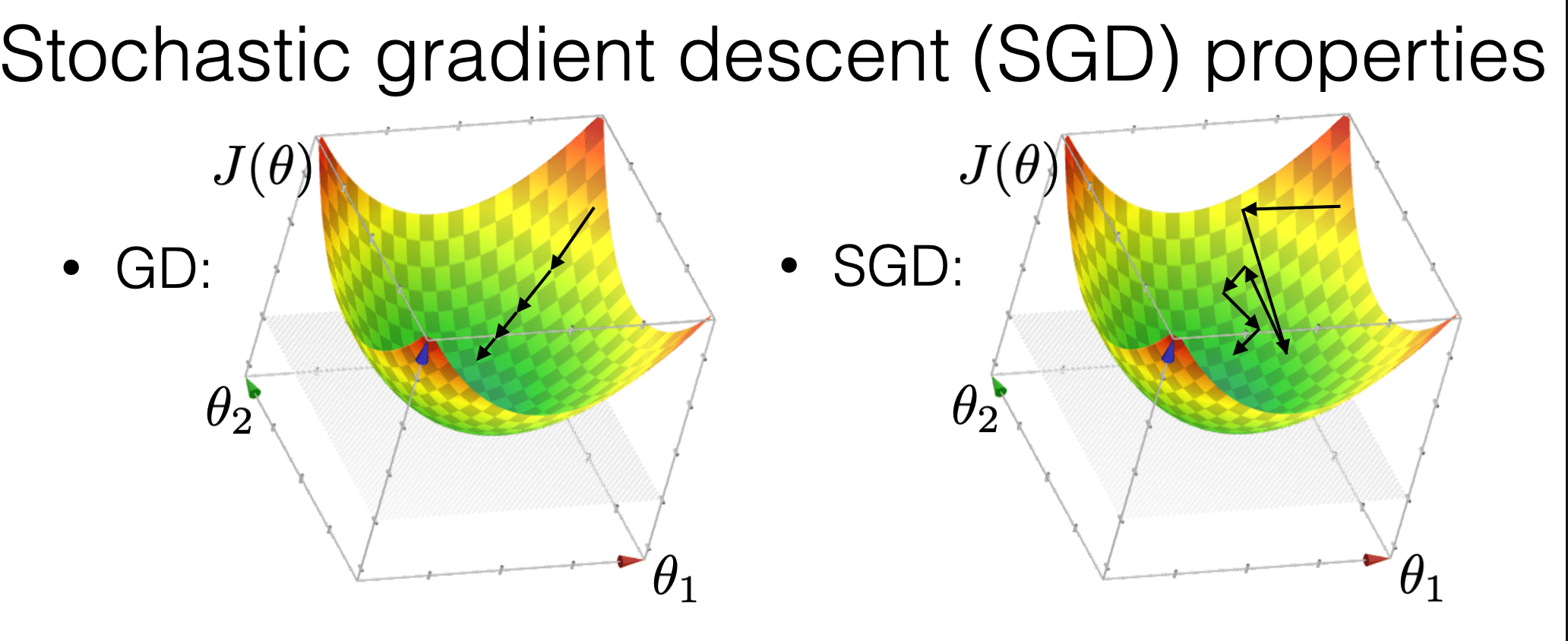
is more "random"

is more efficient 

may get us out of a local min

Compared with GD, SGD 

\nabla f(\Theta)= \frac{1}{n} \sum_{i=1}^n \nabla f_i(\Theta)
\approx \nabla f_i(\Theta)

Summary

  • Most ML methods can be formulated as optimization problems.

  • We won’t always be able to solve optimization problems analytically (in closed-form).

  • We won’t always be able to solve (for a global optimum) efficiently.

  • We can still use numerical algorithms to good effect.  Lots of sophisticated ones available.

  • Introduce the idea of gradient descent in 1D: only two directions!  But magnitude of step is important.

  • In higher dimensions the direction is very important as well as magnitude.

  • GD, under appropriate conditions (most notably, when objective function is convex), can guarantee convergence to a global minimum.

  • SGD: approximated GD, more efficient, more random, and less guarantees.

Thanks!

We'd love to hear your thoughts.