https://introml.mit.edu/

Lecture 6: Neural Networks

 

Shen Shen

Oct 4, 2024

Intro to Machine Learning

Outline

  • Recap, the leap from simple linear models
  • (Feedforward) Neural Networks Structure
    • Design choices
  • Forward pass
  • Backward pass
    • Back-propagation
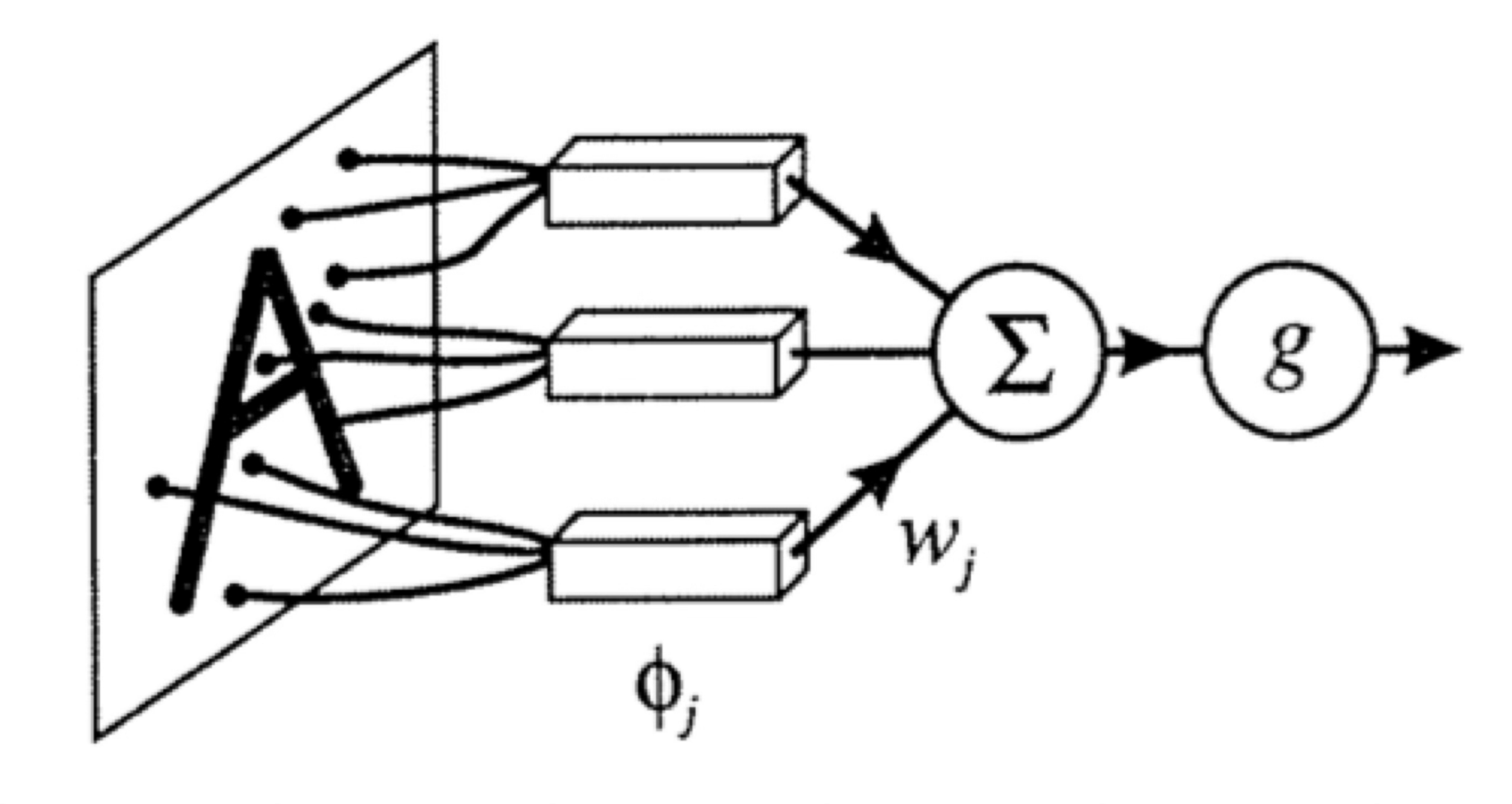
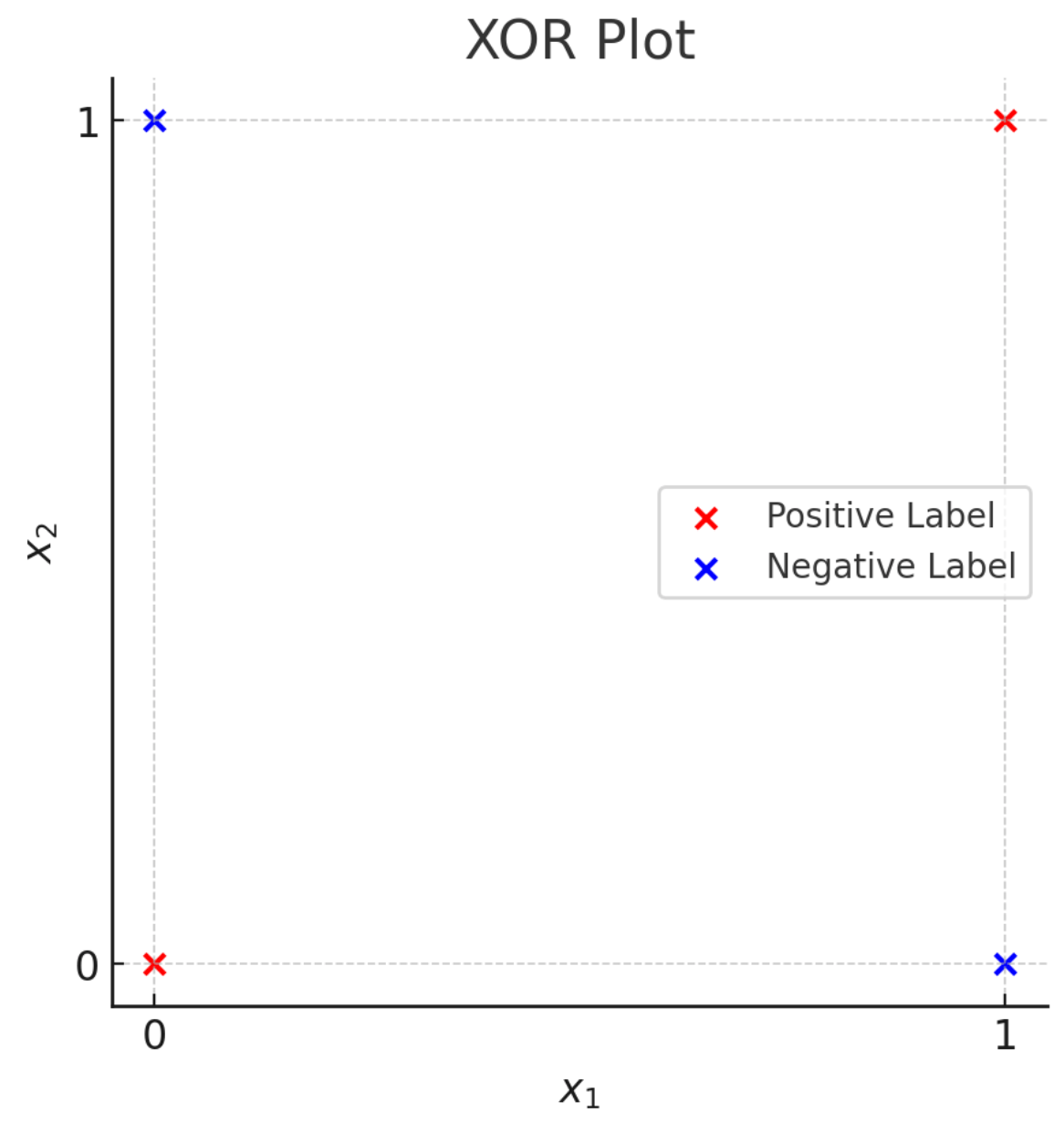
Recap:

leveraging  nonlinear transformations

👆

importantly, linear in \(\phi\), non-linear in \(x\)

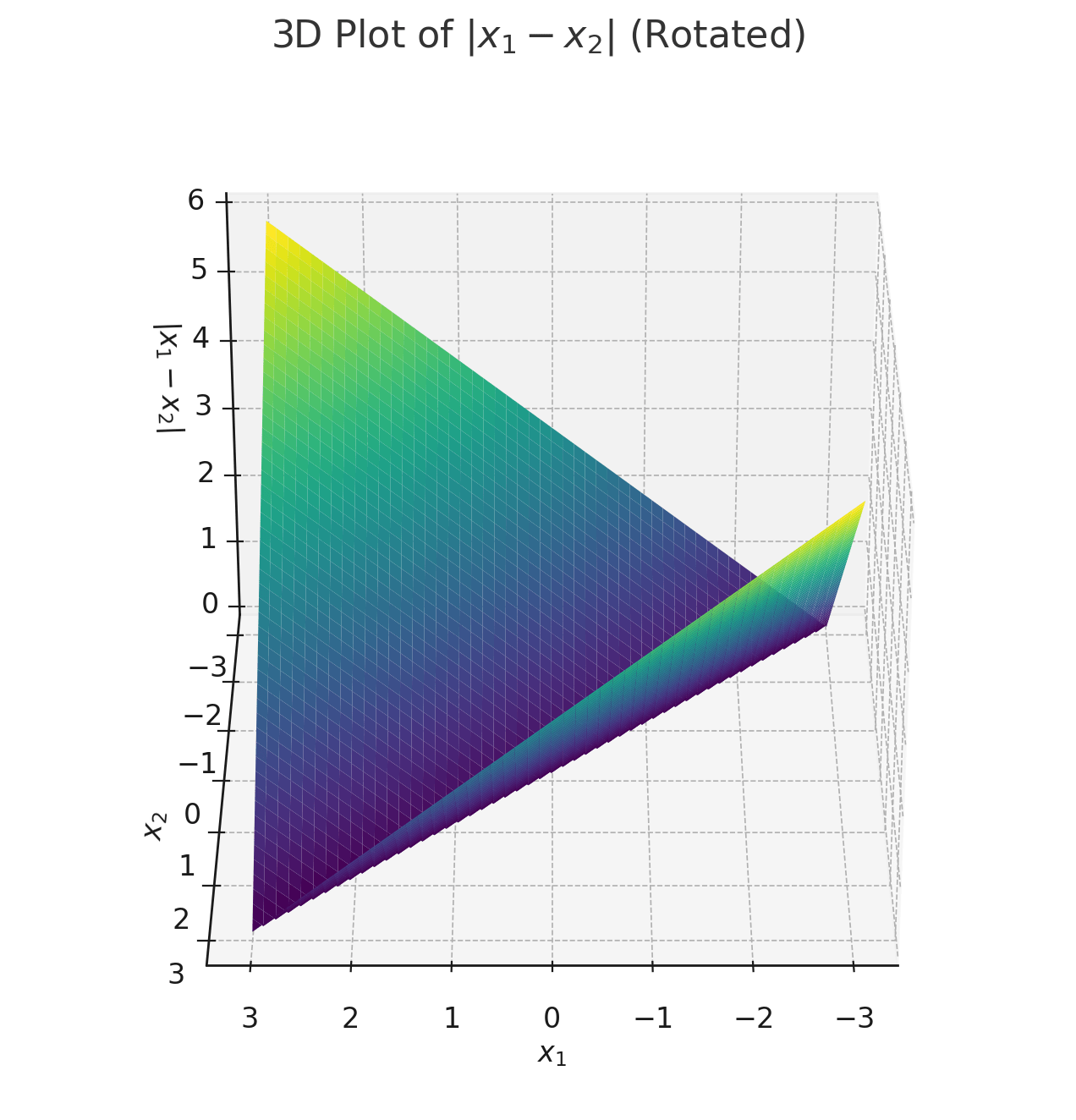
\phi\left(\left[x_1; x_2\right]\right)=\left[1;|x_1-x_2|\right]

transform via

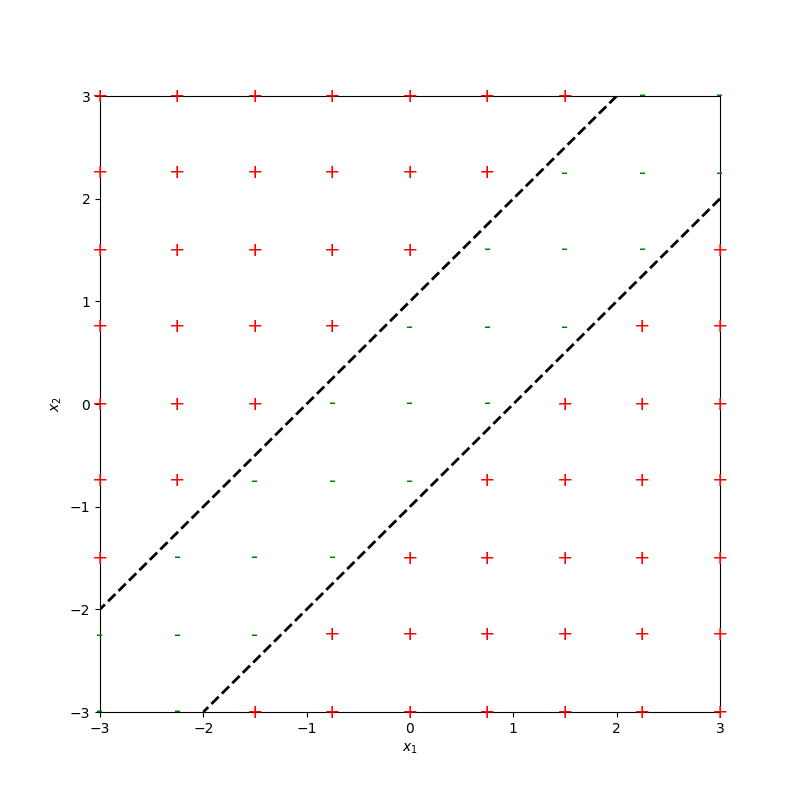
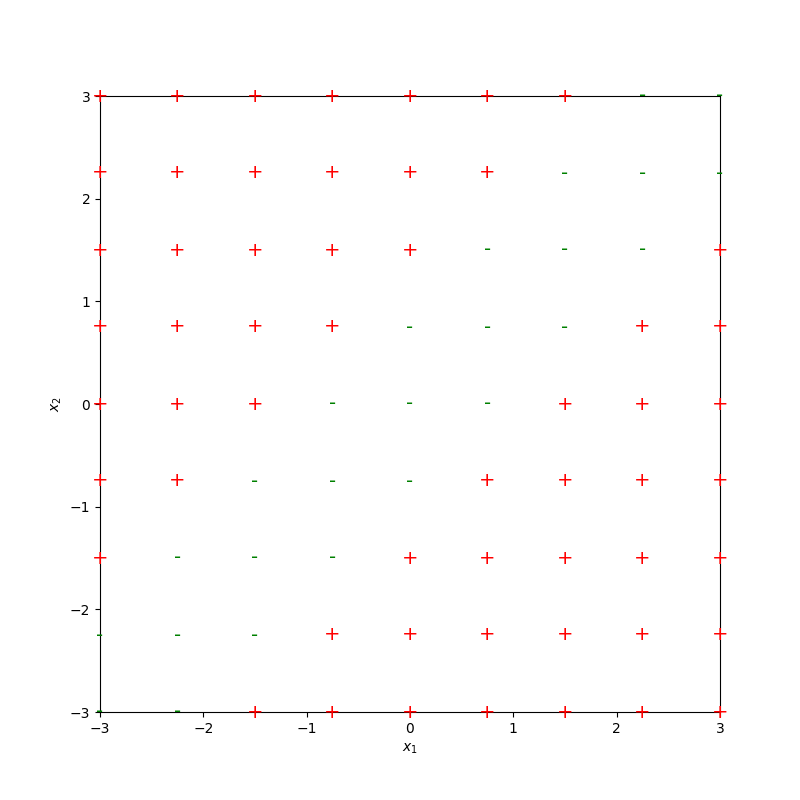
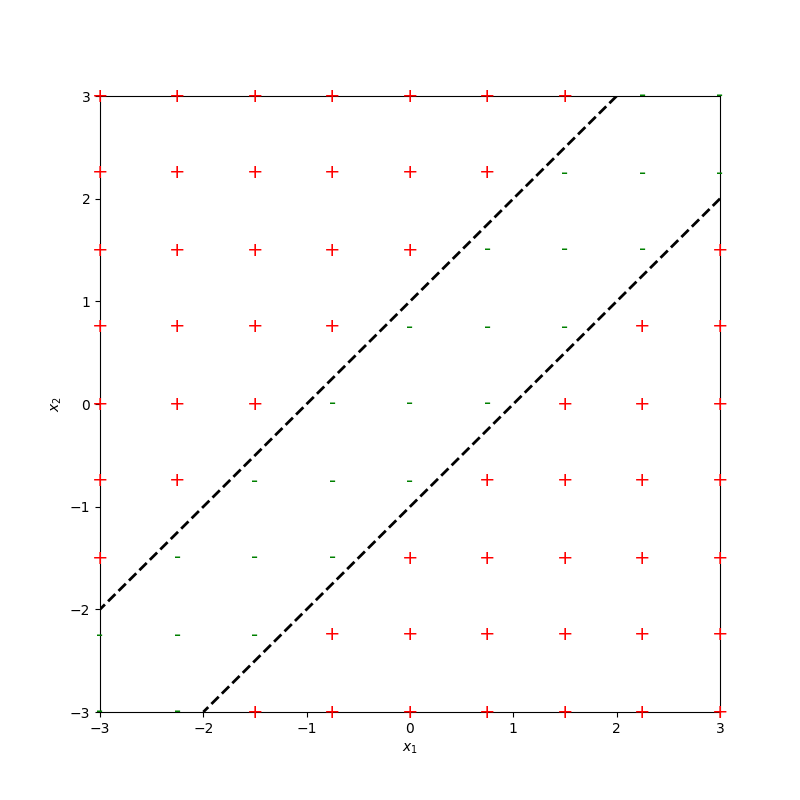
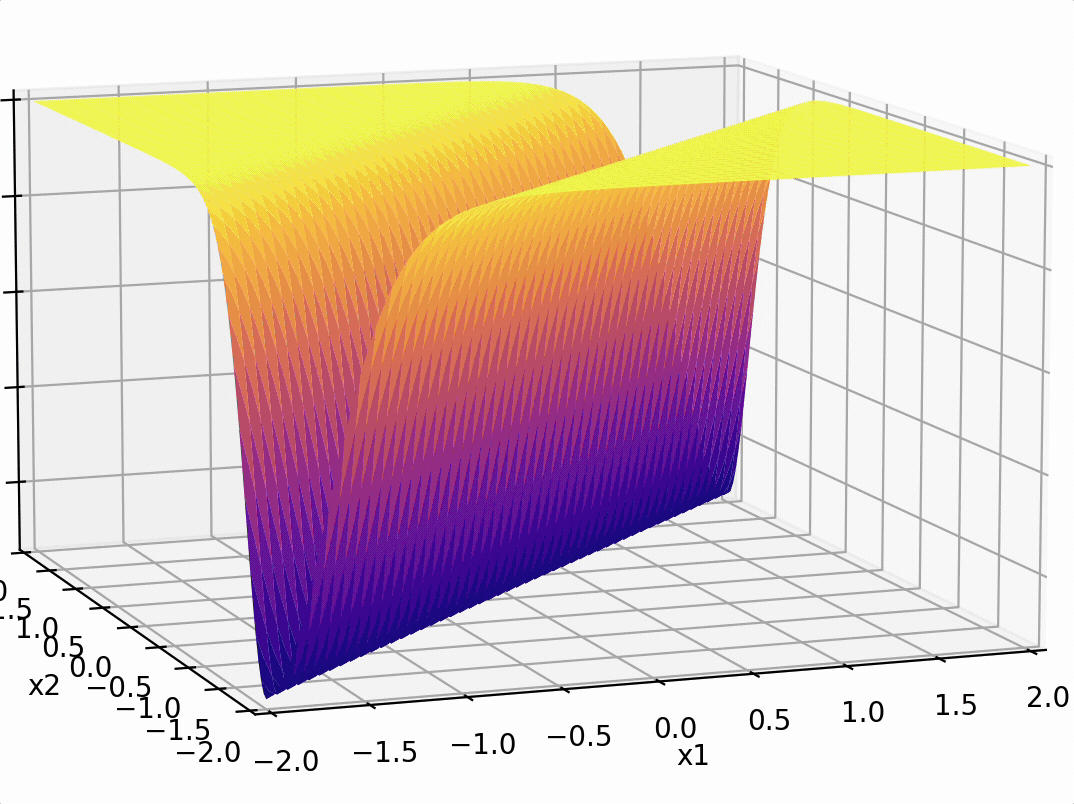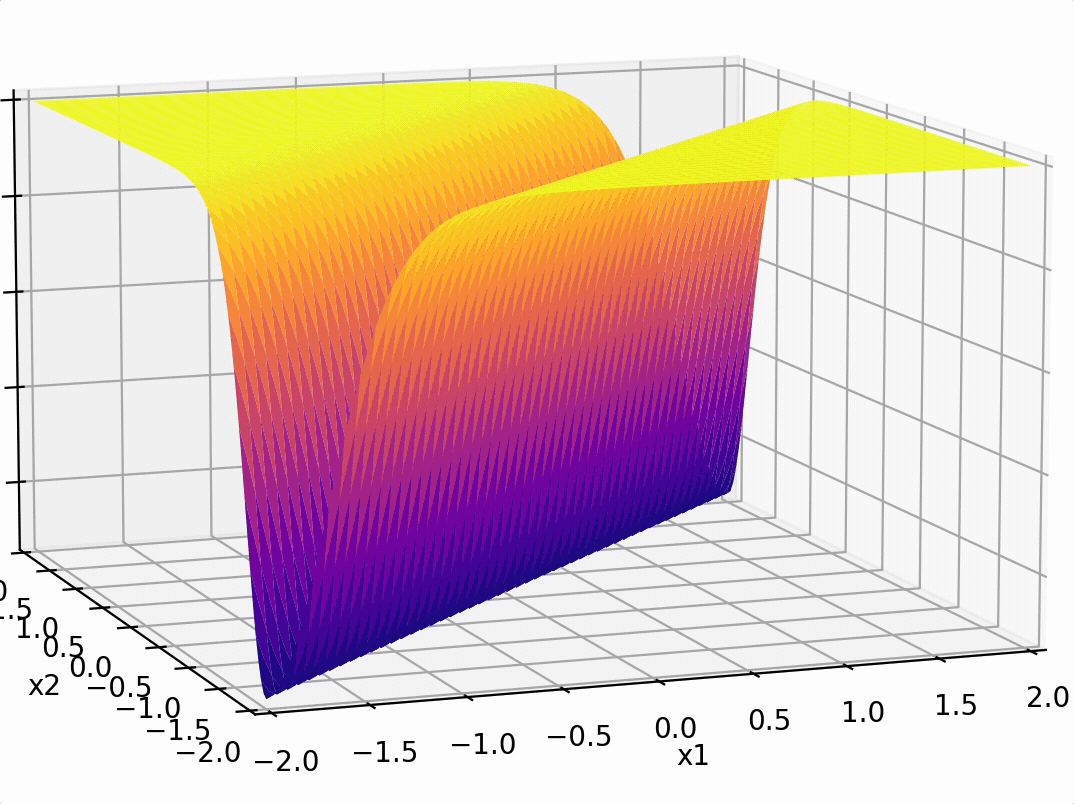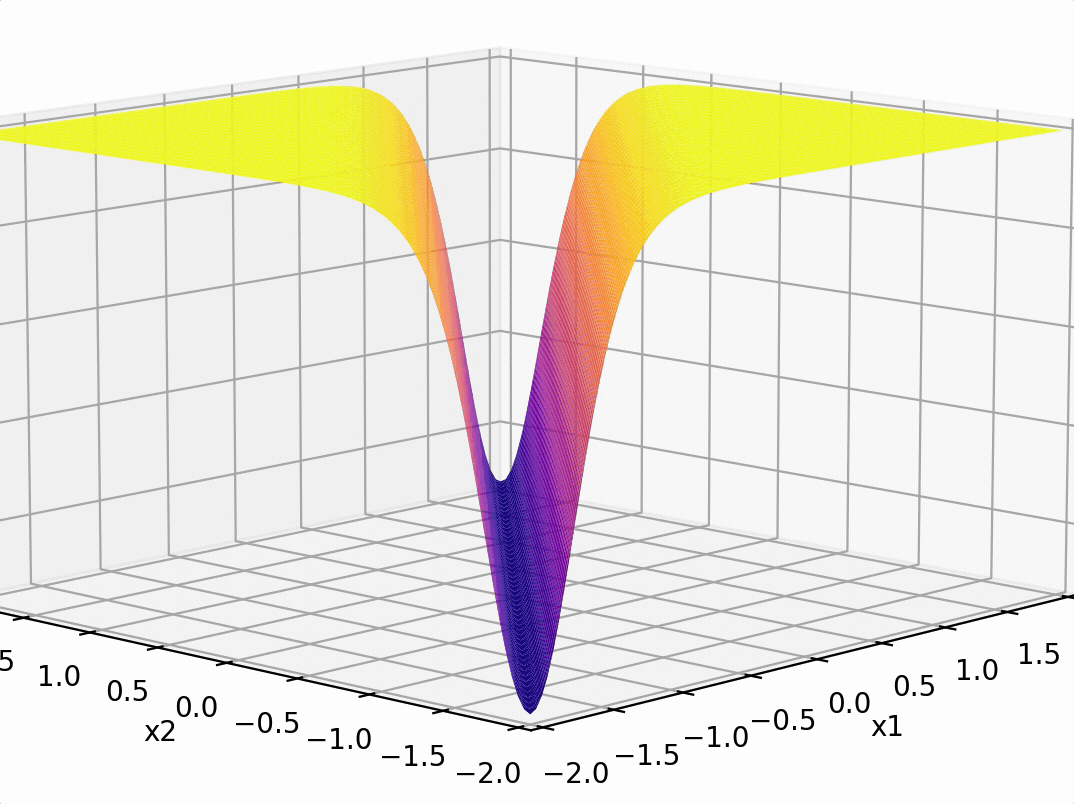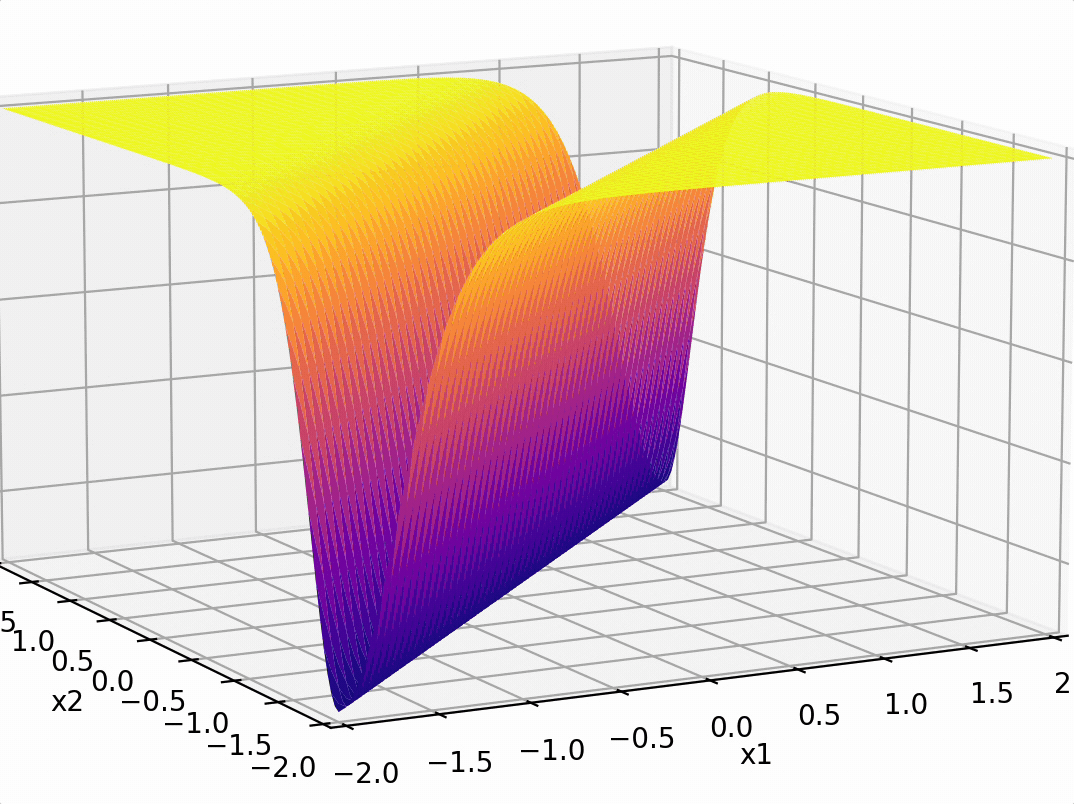
​Pointed out key ideas (enabling neural networks):

  • ​Nonlinear feature transformation
  • "Composing" simple transformations
  • Backpropagation 
\}

expressiveness

efficient training

\sigma_1 = \sigma(5 x_1 -5 x_2 + 1)
\sigma_2 = \sigma(-5 x_1 + 5 x_2 + 1)

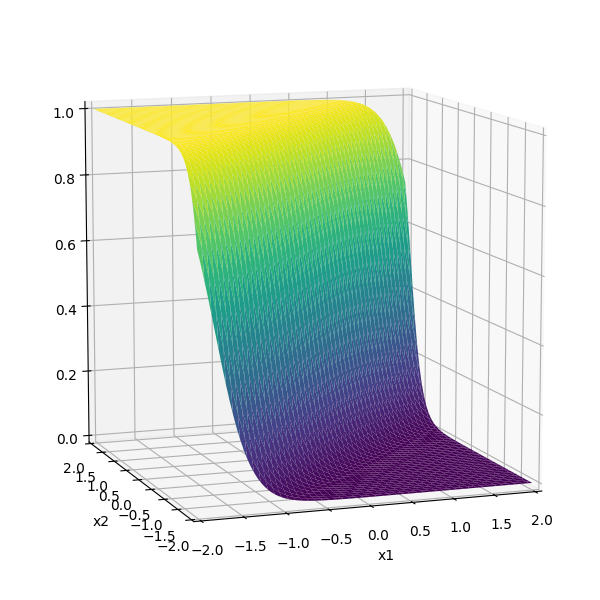
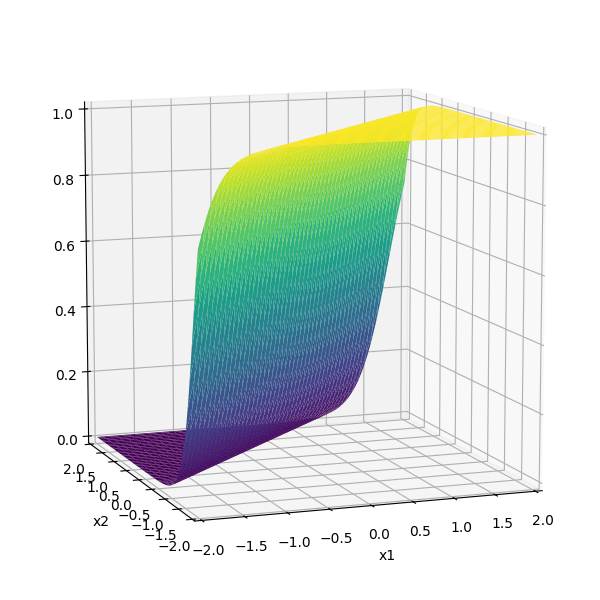
Two epiphanies:  

  • nonlinear transformation empowers linear tools
  • "composing" simple nonlinearities amplifies such effect

some appropriate weighted sum

Outline

  • Recap, the leap from simple linear models
  • (Feedforward) Neural Networks Structure
    • Design choices
  • Forward pass
  • Backward pass
    • Back-propagation

 

👋 heads-up, in this section, for simplicity:

all neural network diagrams focus on a single data point

A neuron:

\(w\): what the algorithm learns

  • \(x\): \(d\)-dimensional input
a = f(z)
\Sigma

A neuron:

  • \(a\): post-activation output
  • \(f\): activation function
  • \(w\): weights (i.e. parameters)
  • \(z\): pre-activation output

\(f\): what we engineers choose

\dots
x_1
x_2
x_d
x = \left[ \begin{array}{c} \\ \\ \\ \\ \\ \\ \\ \end{array} \right]
w_1
w_d
\dots
w_2
= w^Tx
z
f(\cdot)
= f(w^Tx)

\(z\): scalar

\(a\): scalar

Choose activation \(f(z)=z\)

learnable parameters (weights)

e.g. linear regressor represented as a computation graph

= z
= w^Tx
w_1
w_d
\dots
x_1
x_2
x_d
\dots
x = \left[ \begin{array}{c} \\ \\ \\ \\ \\ \\ \\ \end{array} \right]
w_2
\Sigma
f(\cdot)
g
z

Choose activation \(f(z)=\sigma(z)\)

learnable parameters (weights)

e.g. linear logistic classifier represented as a computation graph

= \sigma(z)
= w^Tx
w_1
w_d
\dots
x_1
x_2
x_d
\dots
w_2
\Sigma
f(\cdot)
g
z
x = \left[ \begin{array}{c} \\ \\ \\ \\ \\ \\ \\ \end{array} \right]
\dots

A layer:

learnable weights

A layer:

a^1
z^1
\Sigma
f(\cdot)
z^2
\Sigma
f(\cdot)
a^2
z^m
a^m
\Sigma
f(\cdot)
\dots
x_1
x_2
x_d
  • (# of neurons) = (layer's output dimension).
  • typically, all neurons in one layer use the same activation \(f\) (if not, uglier algebra).
  • typically fully connected, where all \(x_i\) are connected to all \(z_j,\) meaning each \(x_i\) influences every \(a_j\) eventually.
  • typically, no "cross-wiring", meaning e.g. \(z_1\) won't affect \(a^2.\) (the final layer may be an exception if softmax is used.)
\dots

layer

linear combo

activations

A (fully-connected, feed-forward) neural network: 

\dots
\dots

layer

\dots
x_1
x_2
x_d

input

\Sigma
f(\cdot)
\Sigma
f(\cdot)
\Sigma
f(\cdot)
\Sigma
f(\cdot)
\Sigma
f(\cdot)
\Sigma
f(\cdot)
\Sigma
f(\cdot)

neuron

learnable weights

We choose:

  • activation \(f\) in each layer
  • # of layers
  • # of neurons in each layer

hidden

output

Outline

  • Recap, the leap from simple linear models
  • (Feedforward) Neural Networks Structure
    • ​Design choices
  • ​Forward pass
  • Backward pass
    • Back-propagation
\sigma_1 = \sigma(5 x_1 + -5 x_2 + 1)
\sigma_2 = \sigma(-5 x_1 + 5 x_2 + 1)

some appropriate weighted sum

recall this example

x_1
x_2
1
\Sigma
f(\cdot)
\Sigma
f(\cdot)
\Sigma
f(\cdot)

\(f(\cdot) = \sigma(\cdot)\) 

\(f(\cdot) \) identity function

it can be represented as

Activation function \(f\) choices

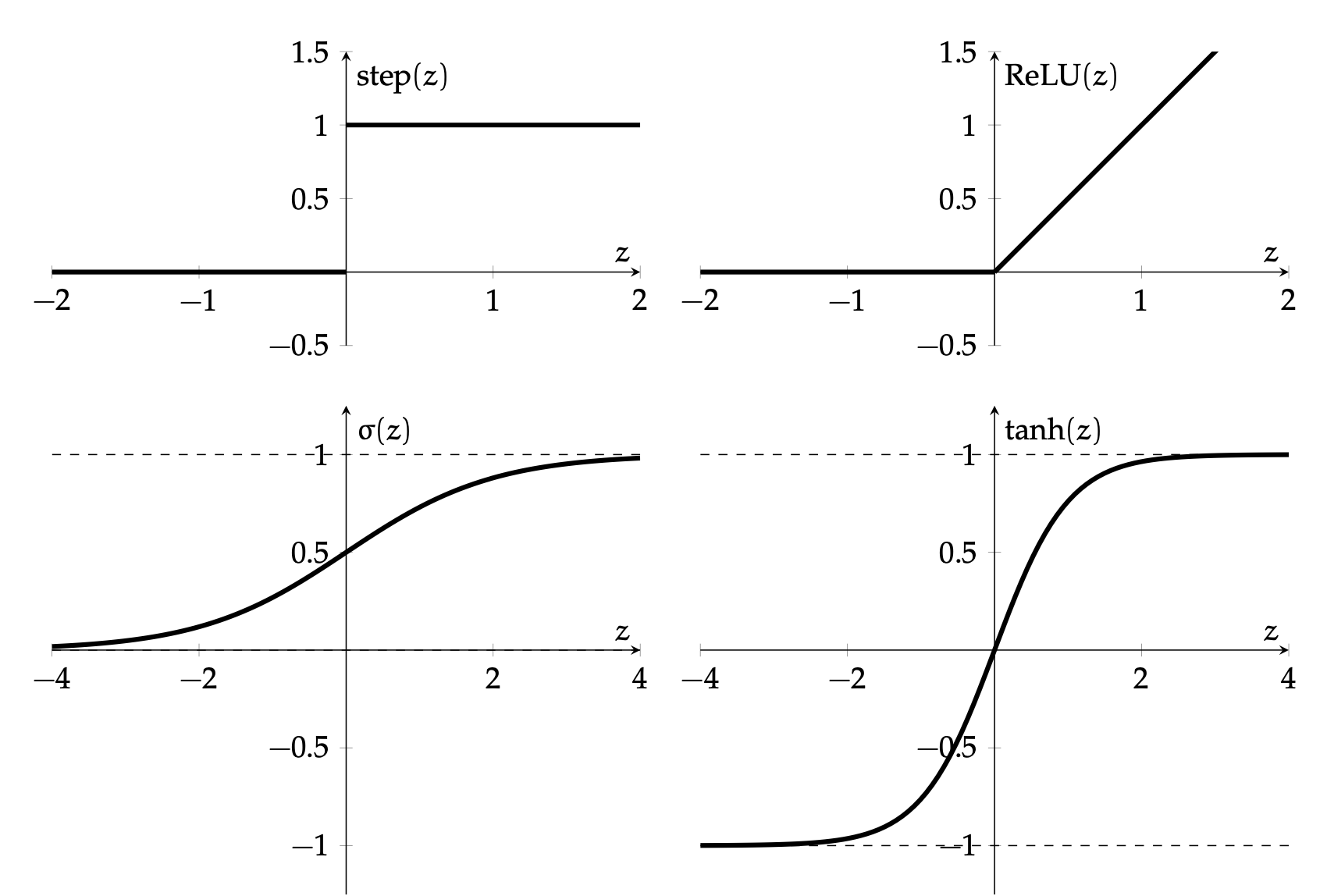
\(\sigma\) used to be the most popular

  • firing rate of a neuron
  • elegant gradient \(\sigma^{\prime}(z)=\sigma(z) \cdot(1-\sigma(z))\)
a = f(z)
\Sigma
\dots
x_1
x_2
x_d
x = \left[ \begin{array}{c} \\ \\ \\ \\ \\ \\ \\ \end{array} \right]
w_1
w_d
\dots
w_2
= w^Tx
z
f(\cdot)
= f(w^Tx)
  • default choice in hidden layers
  • very simple function form, so is the gradient.

 

 

 

 

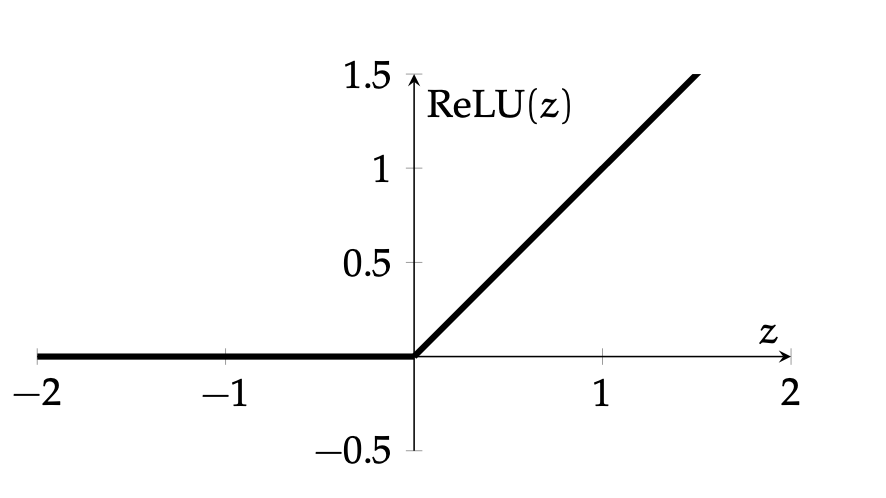
\operatorname{ReLU}(z)=\left\{\begin{array}{ll} 0 & \text { if } z<0 \\ z & \text { otherwise } \end{array}\\ \\ \right.
=\max (0, z)

nowadays

  • drawback: if strongly in negative region, a single ReLU can be "dead" (no gradient).
  • Luckily, typically we have lots of units, so not everyone is dead. 
\frac{\partial \text{ReLU}(z)}{\partial z}:=\left\{\begin{array}{lll} 0, & \text { if } \quad z<0 \\ 1, & \text { if } \quad \text{otherwise} \end{array}\right.

compositions of ReLU(s) can be quite expressive

in fact, asymptotically, can approximate any function!

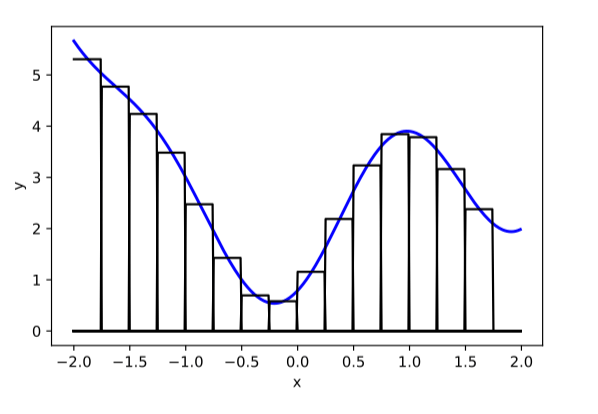
(image credit: Phillip Isola)

x_1
x_2

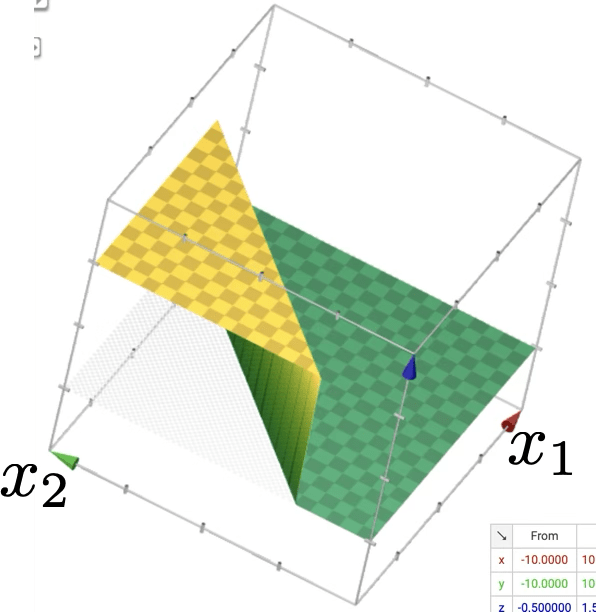
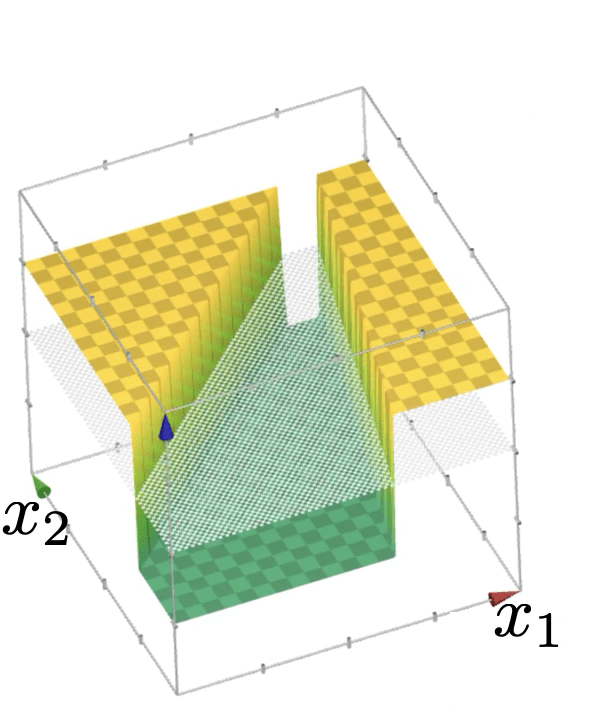
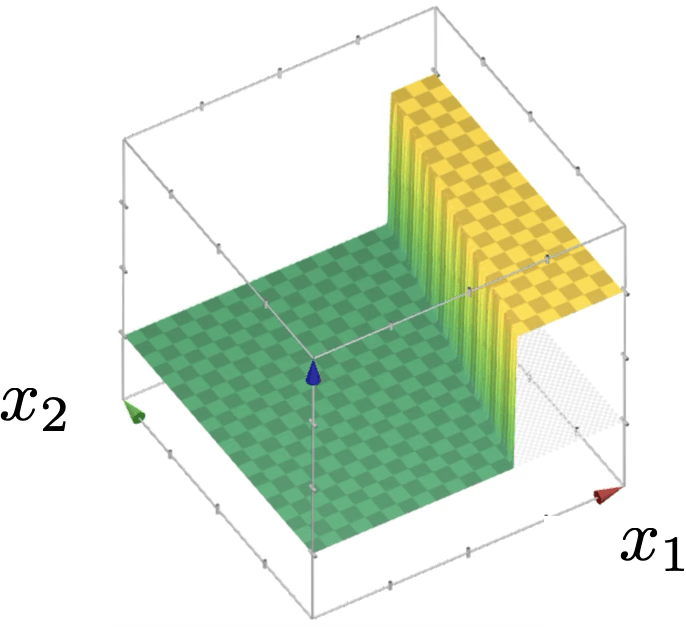
(image credit: Tamara Broderick)

or give arbitrary decision boundaries!

+
=

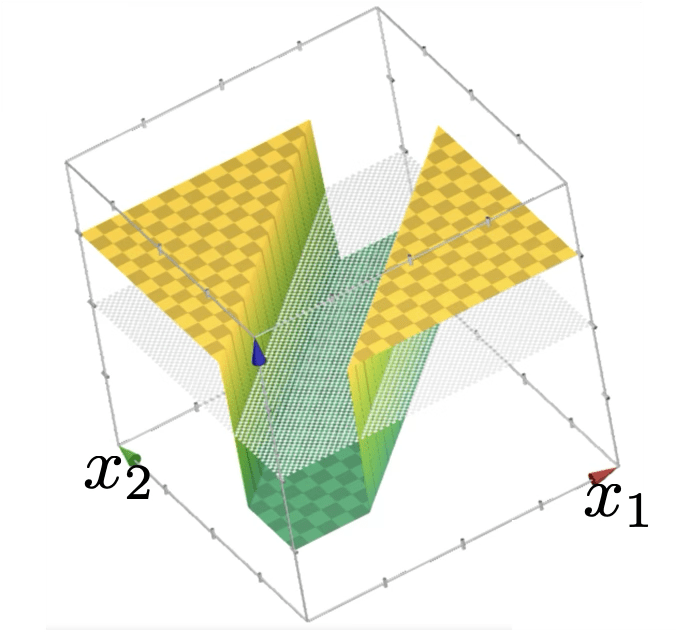
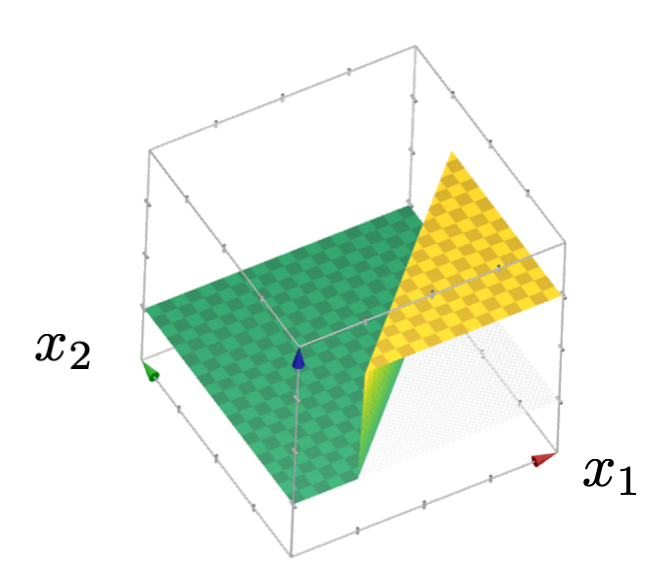
(image credit: Tamara Broderick)

+
=

output layer design choices

  • # neurons, activation, and loss depend on the high-level goal. 
  • typically straightforward.
  • Multi-class setup: if predict one and only one class out of \(K\) possibilities, then last layer: \(K\) neurons, softmax activation, cross-entropy loss

 

 

 

 

  • other multi-class settings, see discussion in lab.

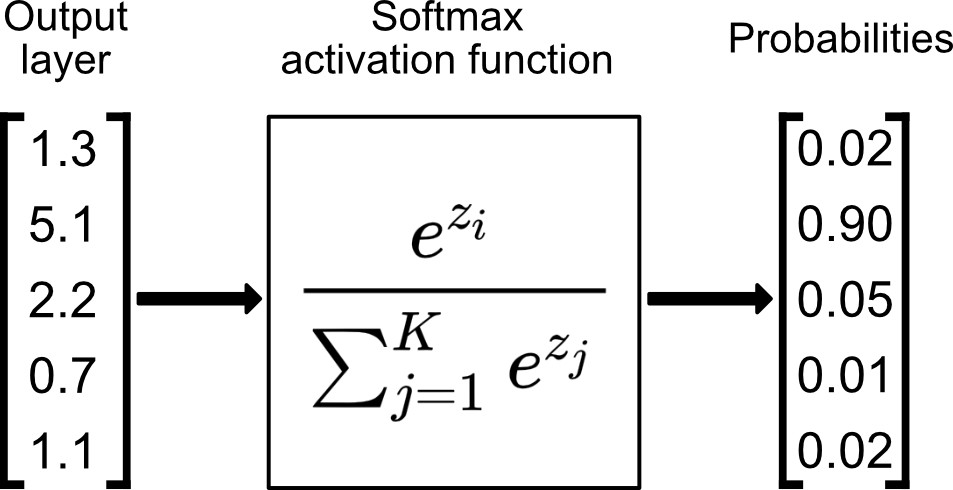
e.g., say \(K=5\) classes

input \(x\)

hidden layer(s)

\dots

output layer

  • Width: # of neurons in layers 
  • Depth: # of layers
  • More expressive if increasing either the width or depth.

 

  • The usual pitfall of overfitting (though in NN-land, it's also an active research topic.)

(The demo won't embed in PDF. But the direct link below works.)

Outline

  • Recap, the leap from simple linear models
  • (Feedforward) Neural Networks Structure
    • ​Design choices
  • ​Forward pass
  • Backward pass
    • Back-propagation
  • Evaluate the loss \(\mathcal{L} = (g-y)^2\)
  • Repeat for each data point, average the sum of \(n\) individual losses

e.g. forward-pass of a linear regressor

y^{(i)}
f(\cdot)
\mathcal{L}(g, y)
\mathcal{L}(g, y)
\underbrace{\quad \quad \quad } \\ n
\mathcal{L}(g, y)
\dots
= w^Tx
w_1
w_d
\dots
w_2
\Sigma
z
= z
g
\dots
x_1
x_2
x_d
x^{(i)} \quad = \left[ \begin{array}{c} \\ \\ \\ \\ \\ \\ \\ \end{array} \right]
\dots
\dots
  • Evaluate the loss \(\mathcal{L} = - [y \log g+\left(1-y\right) \log \left(1-g\right)]\)
  • Repeat for each data point, average the sum of \(n\) individual losses
f(\cdot)
\mathcal{L}(g, y)
\mathcal{L}(g, y)
\underbrace{\quad \quad \quad } \\ n
\mathcal{L}(g, y)
\dots
x_1
x_2
x_d
x^{(i)} \quad = \left[ \begin{array}{c} \\ \\ \\ \\ \\ \\ \\ \end{array} \right]
= w^Tx
w_1
w_d
\dots
w_2
\Sigma
z
= \sigma(z)
g

e.g. forward-pass of a linear logistic classifier

\dots
y^{(i)}
\dots
\dots
x^{(1)}
y^{(1)}
f^1

linear combination

nonlinear activation

\begin{aligned} & W^1 \\ \end{aligned}
\begin{aligned} & W^2 \\ \end{aligned}
\begin{aligned} & W^L \\ \end{aligned}
f^2
f^L
g^{(1)}

\(\dots\)

f^2\left(\hspace{2cm}; \mathbf{W}^2\right)
f^1(\mathbf{x}^{(i)}; \mathbf{W}^1)
f^L\left(\dots \hspace{3.5cm}; \dots \mathbf{W}^L\right)

Forward pass:

evaluate, given the current parameters,

  • the model output \(g^{(i)}\) =  
  • the loss incurred on the current data \(\mathcal{L}(g^{(i)}, y^{(i)})\)
  • the training error \(J = \frac{1}{n} \sum_{i=1}^{n}\mathcal{L}(g^{(i)}, y^{(i)})\)
\mathcal{L}(g^{(1)}, y^{(1)})
\mathcal{L}(g, y)
\mathcal{L}(g^{(n)}, y^{(n)})
\underbrace{\quad \quad \quad \quad \quad } \\ n
\dots
\dots
\dots

loss function

Outline

  • Recap, the leap from simple linear models
  • (Feedforward) Neural Networks Structure
    • Design choices
  • Forward pass
  • Backward pass
    • Back-propagation
  • Randomly pick a data point \((x^{(i)}, y^{(i)})\)
  • Evaluate the gradient \(\nabla_{W^2} \mathcal{L(g^{(i)},y^{(i)})}\) 
  • Update the weights \(W^2 \leftarrow W^2 - \eta \nabla_{W^2} \mathcal{L(g^{(i)},y^{(i)}})\) 
x^{(i)}
y^{(i)}
f^1
\begin{aligned} & W^1 \\ \end{aligned}
\begin{aligned} & W^2 \\ \end{aligned}
\begin{aligned} & W^L \\ \end{aligned}
f^2
f^L
g^{(i)}

\(\dots\)

\mathcal{L}(g^{(i)}, y^{(i)})
\mathcal{L}(g, y)
\mathcal{L}(g^{(n)}, y^{(n)})
\underbrace{\quad \quad \quad \quad \quad } \\ n
\dots
\dots
\dots

Backward pass:

Run SGD to update the parameters, e.g. to update \(W^2\)

\(\nabla_{W^2} \mathcal{L(g^{(i)},y^{(i)})}\)

x

\(\dots\)

y
f^1
\begin{aligned} & W^1 \\ \end{aligned}
\begin{aligned} & W^2 \\ \end{aligned}
\begin{aligned} & W^L \\ \end{aligned}
f^2
f^L
\mathcal{L}(g,y)
g

\(\nabla_{W^2} \mathcal{L(g,y)}\)

Backward pass:

Run SGD to update the parameters, e.g. to update \(W^2\)

Evaluate the gradient \(\nabla_{W^2} \mathcal{L(g^{(i)},y^{(i)})}\) 

Update the weights \(W^2 \leftarrow W^2 - \eta \nabla_{W^2} \mathcal{L(g^{(i)},y^{(i)}})\) 

x
y
f^1
\begin{aligned} & W^1 \\ \end{aligned}
\begin{aligned} & W^2 \\ \end{aligned}
\mathcal{L}(g,y)
g

How do we get these gradient though?

\(\nabla_{W^1} \mathcal{L(g,y)}\)

Backward pass:

Run SGD to update the parameters, e.g. to update \(W^1\)

Evaluate the gradient \(\nabla_{W^1} \mathcal{L(g^{(i)},y^{(i)})}\) 

Update the weights \(W^1 \leftarrow W^1 - \eta \nabla_{W^1} \mathcal{L(g^{(i)},y^{(i)}})\) 

\(\dots\)

\begin{aligned} & W^L \\ \end{aligned}
f^2
f^L

Outline

  • Recap, the leap from simple linear models
  • (Feedforward) Neural Networks Structure
    • Design choices
  • Forward pass
  • Backward pass
    • Back-propagation
\mathcal{L}(g, y)
\mathcal{L}(g, y)
\underbrace{\quad \quad \quad } \\ n
\mathcal{L}(g, y)
\dots
x_1
x_2
x_d
x^{(i)} \quad = \left[ \begin{array}{c} \\ \\ \\ \\ \\ \\ \\ \end{array} \right]

e.g. backward-pass of a linear regressor

\dots
y^{(i)}
\dots
\dots
  • Randomly pick a data point \((x^{(i)}, y^{(i)})\)
  • Evaluate the gradient \(\nabla_{w} \mathcal{L(g^{(i)},y^{(i)})}\) 
  • Update the weights \(w \leftarrow w - \eta \nabla_w \mathcal{L(g^{(i)},y^{(i)}})\) 
w
\left[ \begin{array}{c} \\ \\ \\ \\ \\ \\ \\ \end{array} \right]
= w^Tx
\Sigma
w_1
w_2
\dots
w_d
w_1
w_2
\dots
w_d
=
\nabla_{w} \mathcal{L(g^{(i)},y^{(i)})}
g
\mathcal{L}(g, y)
\dots
x_1
x_2
x_d
x \quad = \left[ \begin{array}{c} \\ \\ \\ \\ \\ \\ \\ \end{array} \right]

e.g. backward-pass of a linear regressor

y
\left[ \begin{array}{c} \\ \\ \\ \\ \\ \\ \\ \end{array} \right]
\Sigma
w_1
w_2
\dots
w_d
y \in \mathbb{R}
x \in \mathbb{R^d}
w \in \mathbb{R^d}
= \frac{\partial \mathcal{L}(g,y)}{\partial w}
\nabla_{w} \mathcal{L(g,y)}
= x \cdot 2(g - y)
\frac{\partial g}{\partial w}
= \frac{\partial[(g - y)^2] }{\partial w}
= \frac{\partial[(w^T x - y)^2] }{\partial w}
\nabla_{w} \mathcal{L(g,y)}
\frac{\partial \mathcal{L}}{\partial g}
w
=
\nabla_{w} \mathcal{L(g,y)}
= w^Tx
g
\text{ReLU}
\mathcal{L}(g, y)
\dots
x_1
x_2
x_d
x \quad = \left[ \begin{array}{c} \\ \\ \\ \\ \\ \\ \\ \end{array} \right]

e.g. backward-pass of a non-linear regressor

y
\left[ \begin{array}{c} \\ \\ \\ \\ \\ \\ \\ \end{array} \right]
= w^Tx
\Sigma
z
w_1
w_2
\dots
w_d
y \in \mathbb{R}
x \in \mathbb{R^d}
w \in \mathbb{R^d}
= \frac{\partial \mathcal{L}(g,y)}{\partial w}
\nabla_{w} \mathcal{L(g,y)}
= x \cdot \frac{\partial[(\text{ReLU}(z))] }{\partial z} \cdot 2(g - y)
\frac{\partial g}{\partial z}
\frac{\partial z}{\partial w}
= \frac{\partial[(g - y)^2] }{\partial w}
\nabla_{w} \mathcal{L(g,y)}
\frac{\partial \mathcal{L}}{\partial g}
w
=
\nabla_{w} \mathcal{L(g,y)}
g
= \text{ReLU}(z)
x

\(\dots\)

y
f^1
\begin{aligned} & W^1 \\ \end{aligned}
\begin{aligned} & W^2 \\ \end{aligned}
\begin{aligned} & W^L \\ \end{aligned}
f^2
f^L
\mathcal{L}(g,y)
g
\underbrace{\hspace{4.7cm}}

Now, back propagation: reuse of computation

Z^L
A^2
Z^2
A^1
Z^1
\frac{\partial \mathcal{L}(g,y)}{\partial W^2}
\frac{\partial \mathcal{L}(g,y)}{\partial g}
\frac{\partial g}{\partial Z^{L}}
\frac{\partial Z^3}{\partial A^{2}}\frac{\partial A^4}{\partial Z^{3}} \dots \frac{\partial Z^L}{\partial A^{L-1}}
\frac{\partial A^2}{\partial Z^{2}}
\frac{\partial Z^2}{\partial W^{2}}
\frac{\partial \mathcal{L}(g,y)}{\partial Z^2}
\underbrace{\hspace{4cm}}
\frac{\partial \mathcal{L}(g,y)}{\partial W^2}

how to find

?

\frac{\partial \mathcal{L}(g,y)}{\partial W^1}
x

\(\dots\)

y
f^1
\begin{aligned} & W^1 \\ \end{aligned}
\begin{aligned} & W^2 \\ \end{aligned}
\begin{aligned} & W^L \\ \end{aligned}
f^2
f^L
\mathcal{L}(g,y)
g
Z^L
A^2
Z^2
A^1
Z^1
\frac{\partial \mathcal{L}(g,y)}{\partial g}
\frac{\partial g}{\partial Z^{L}}
\frac{\partial Z^3}{\partial A^{2}}\frac{\partial A^4}{\partial Z^{3}} \dots \frac{\partial Z^L}{\partial A^{L-1}}
\frac{\partial A^2}{\partial Z^{2}}
\frac{\partial \mathcal{L}(g,y)}{\partial Z^2}
\underbrace{\hspace{4cm}}

back propagation: reuse of computation

\frac{\partial Z^2}{\partial W^{2}}
\underbrace{\hspace{4.7cm}}
\frac{\partial \mathcal{L}(g,y)}{\partial W^2}

how to find

?

\underbrace{\hspace{6.5cm}}
\frac{\partial \mathcal{L}(g,y)}{\partial W^1}
\frac{\partial Z^2}{\partial A^{1}}
\frac{\partial A^1}{\partial Z^{1}}
\frac{\partial Z^1}{\partial W^{1}}
x

\(\dots\)

y
f^1
\begin{aligned} & W^1 \\ \end{aligned}
\begin{aligned} & W^2 \\ \end{aligned}
\begin{aligned} & W^L \\ \end{aligned}
f^2
f^L
\mathcal{L}(g,y)
g
Z^L
A^2
Z^2
A^1
Z^1
\frac{\partial \mathcal{L}(g,y)}{\partial g}
\frac{\partial g}{\partial Z^{L}}
\frac{\partial Z^3}{\partial A^{2}}\frac{\partial A^4}{\partial Z^{3}} \dots \frac{\partial Z^L}{\partial A^{L-1}}
\frac{\partial A^2}{\partial Z^{2}}
\frac{\partial \mathcal{L}(g,y)}{\partial Z^2}
\underbrace{\hspace{4cm}}

back propagation: reuse of computation

how to find

\frac{\partial \mathcal{L}(g,y)}{\partial W^1}

?

Summary

  • We saw that introducing non-linear transformations of the inputs can substantially increase the power of linear tools. But it’s kind of difficult/tedious to select a good transformation by hand.
  • Multi-layer neural networks are a way to automatically find good transformations for us!
  • Standard NNs have layers that alternate between parametrized linear transformations and fixed non-linear transforms (but many other designs are possible.)
  • Typical non-linearities include sigmoid, tanh, relu, but mostly people use relu.
  • Typical output transformations for classification are as we've seen: sigmoid, or softmax.
  • There’s a systematic way to compute gradients via back-propagation, in order to update parameters.

Thanks!

We'd love to hear your thoughts.