https://introml.mit.edu/

Lecture 8: Convolutional Neural Networks

 

Shen Shen

October 25, 2024

Intro to Machine Learning

Outline

  • Recap, fully-connected net
  • Vision problem structure
  • Convolutional network structure 
  • Convolution
    • 1-dimensional and 2-dimensional convolution
    • 3-dimensional tensors
  • Max pooling
  • Case studies
\dots

layer

linear combo

activations

Recap:
\dots
\dots

layer

\dots
x_1
x_2
x_d

input

\Sigma
f(\cdot)
\Sigma
f(\cdot)
\Sigma
f(\cdot)
\Sigma
f(\cdot)
\Sigma
f(\cdot)
\Sigma
f(\cdot)
\Sigma
f(\cdot)

neuron

learnable weights

hidden

output

convolutional neural networks

  1. Why do we need a special network for images?

  2. Why is CNN (the) special network for images?

9

Why do we need a special net for images?

[video edited from 3b1b]

[video edited from 3b1b]

[video edited from 3b1b]

Q: Why do we need a specialized network?

Use the same small 2 hidden-layer network, need to learn ~3M parameters

 

For higher-resolution images (e.g. 1024-1024 already leads to 1-million dimensional as input), or more complex tasks, the number of parameters can just grow very fast. 

 

 

A:  fully-connected nets don't scale well for vision tasks

426-by-426 grayscale image

Underfitting

Appropriate model

Overfitting

k=1
k=2
k=10
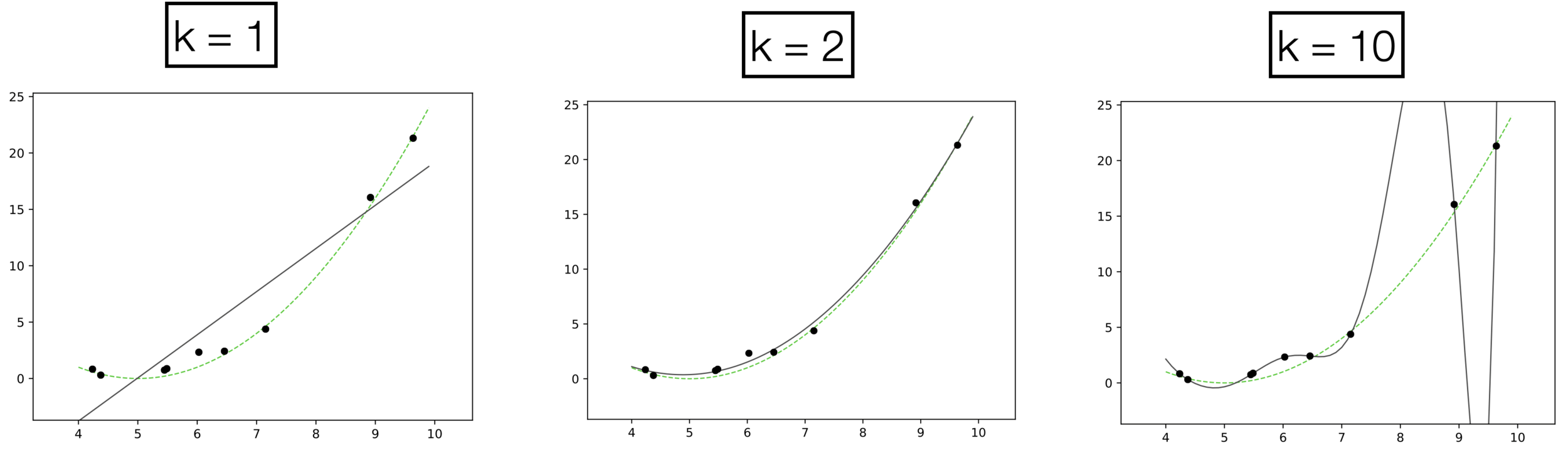
Recall, more powerful models also tend to overfitting

Why do we think

is 9?

Why do we think any of 

is 9?

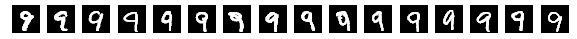
[video edited from 3b1b]

[video edited from 3b1b]

[video edited from 3b1b]

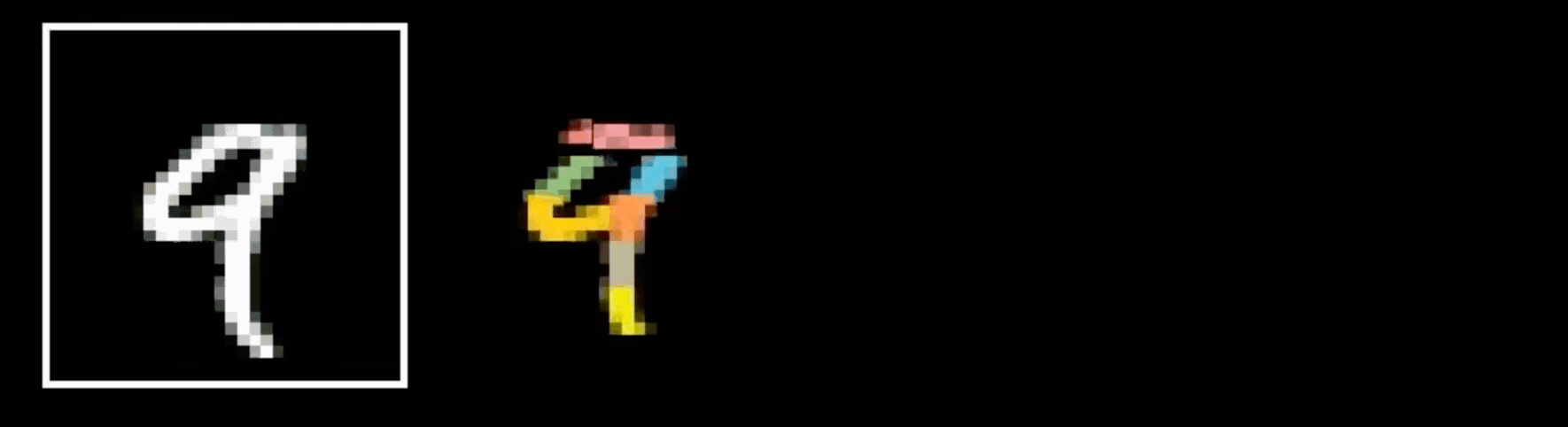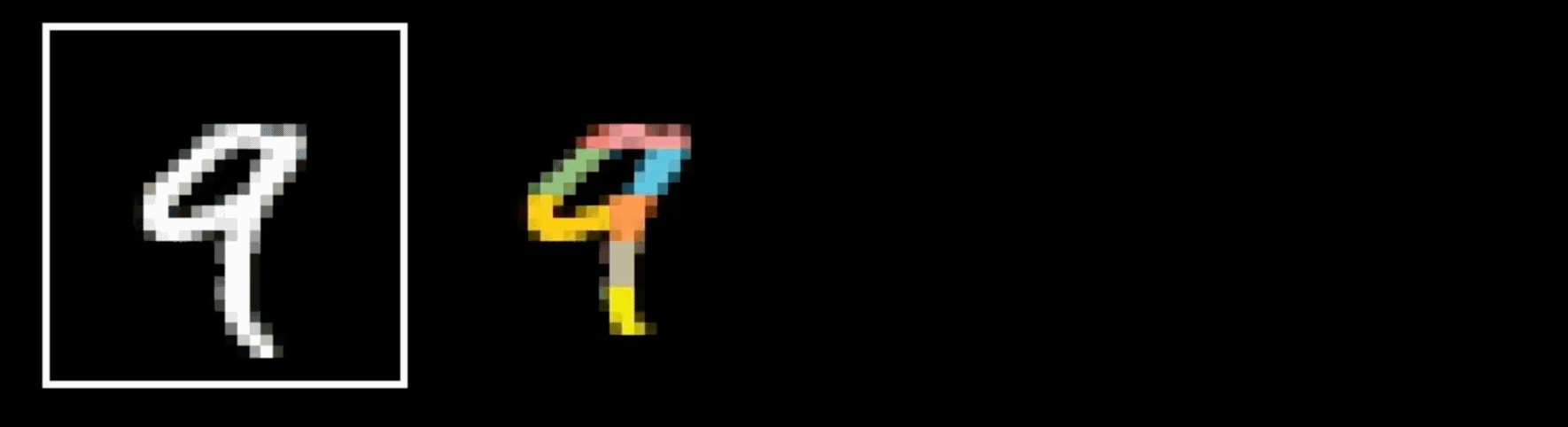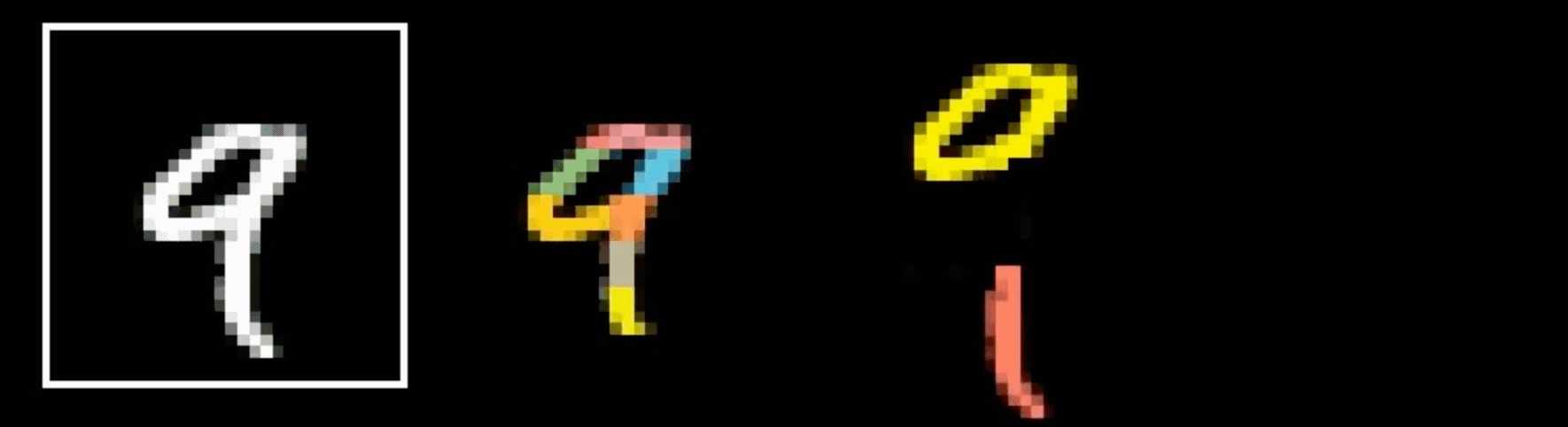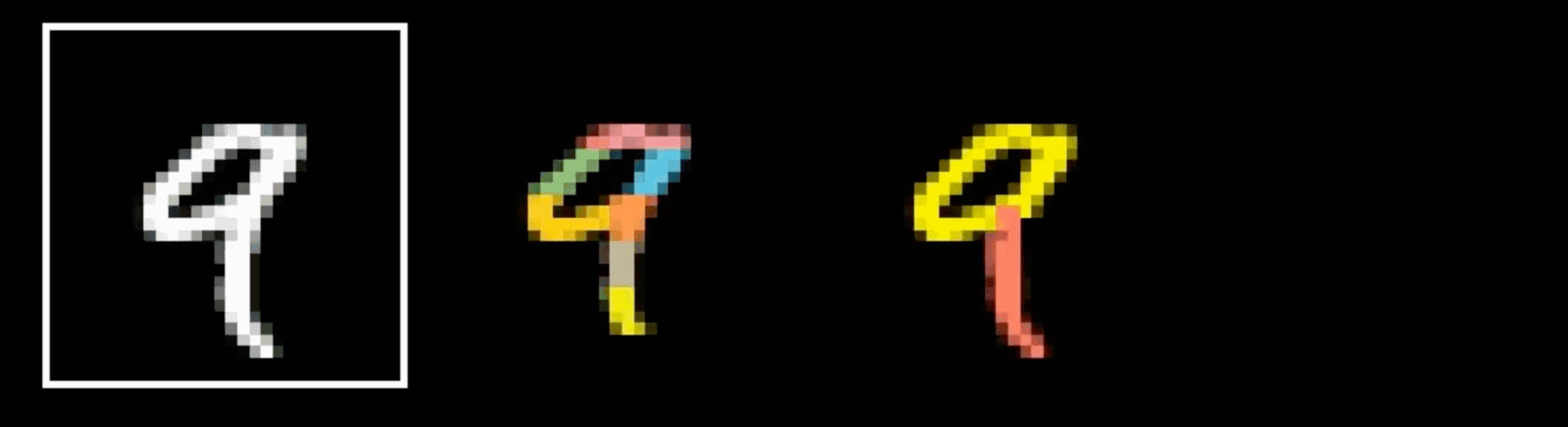
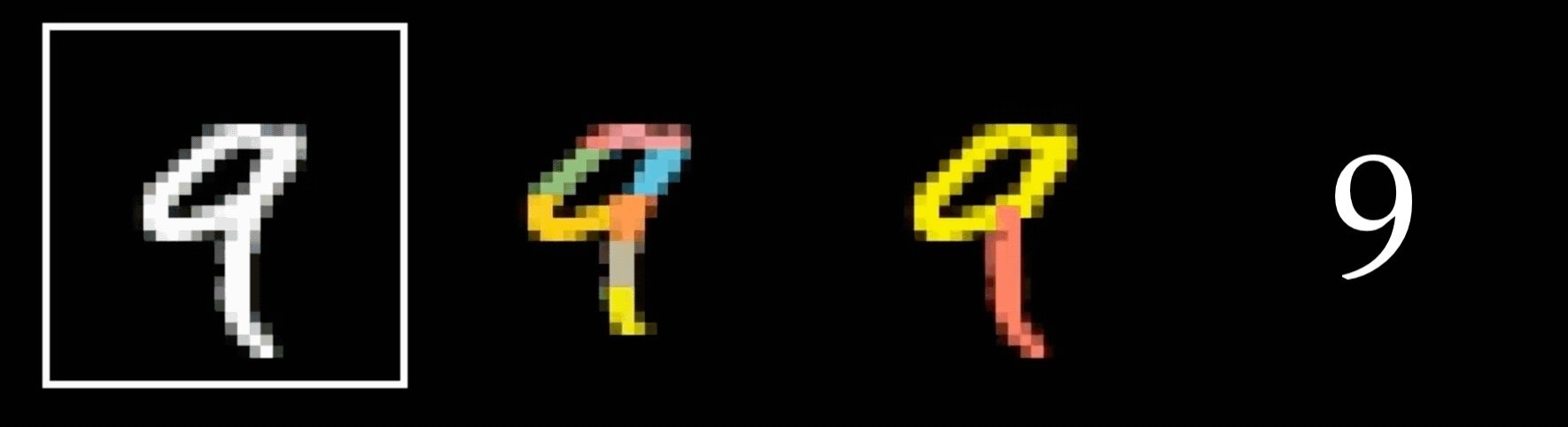
  • Visual hierarchy

layering is compatible with hierarchical structure

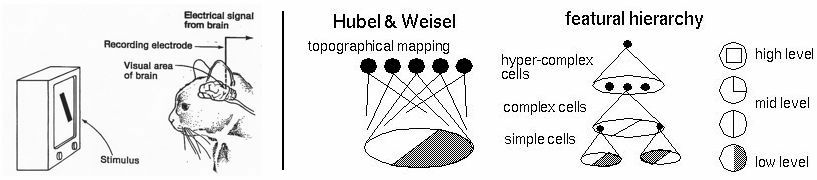
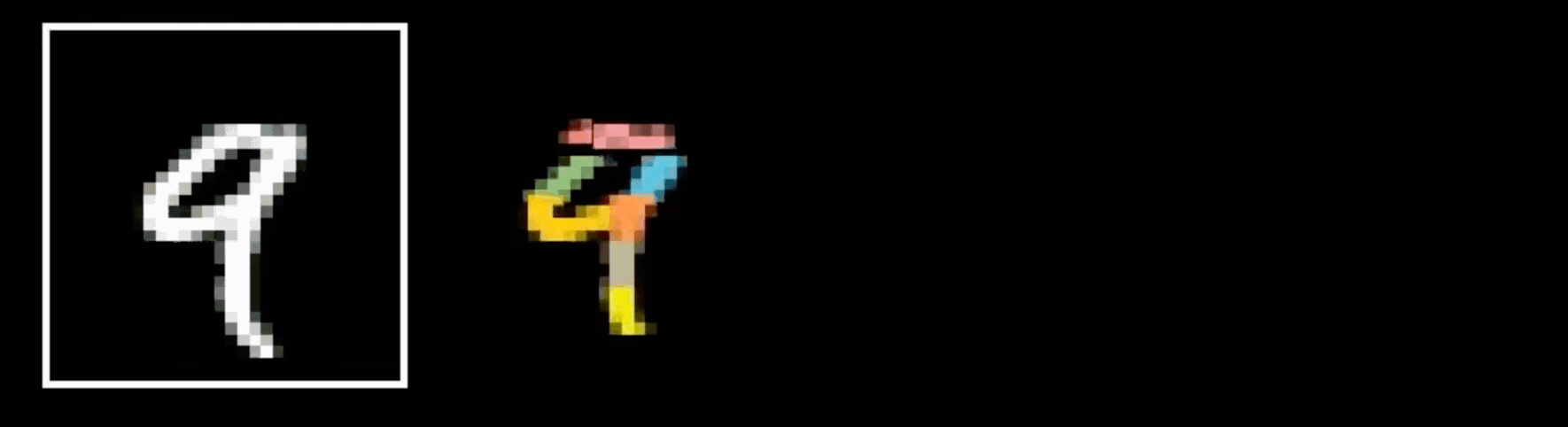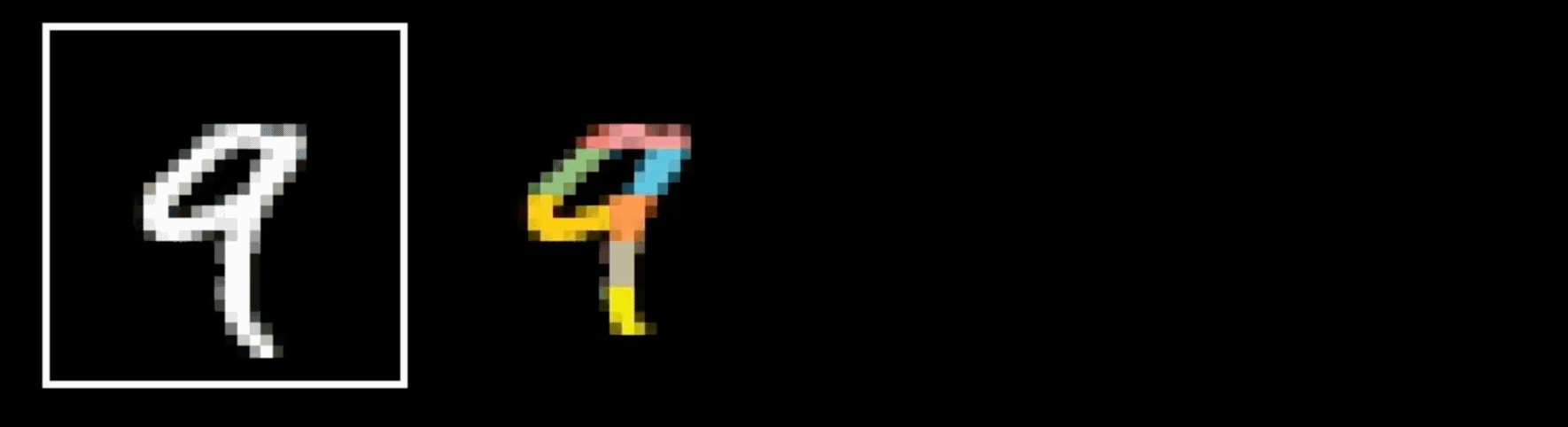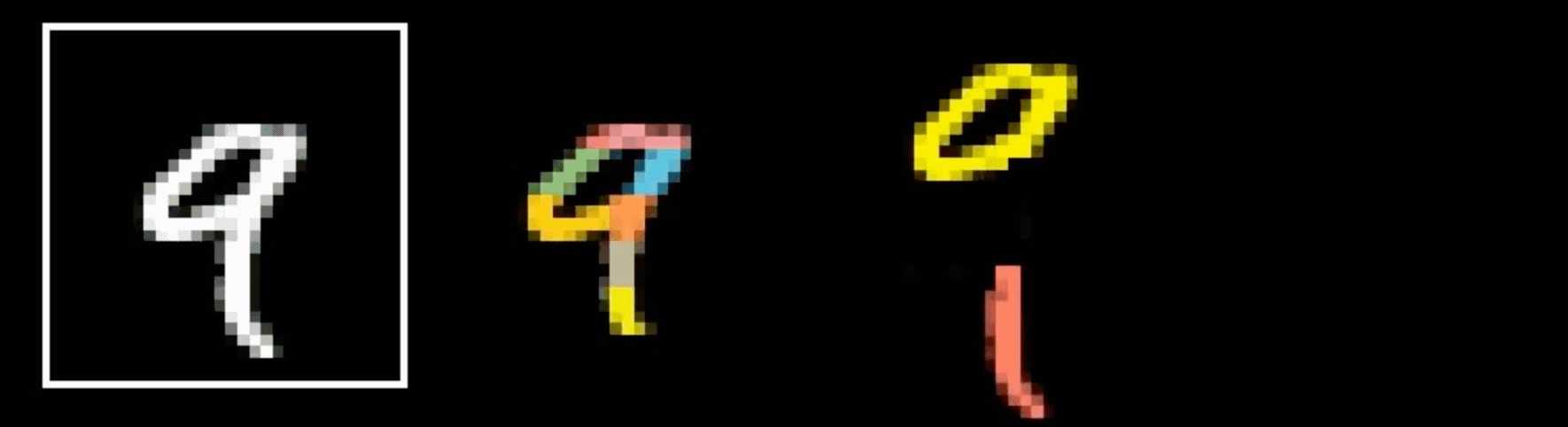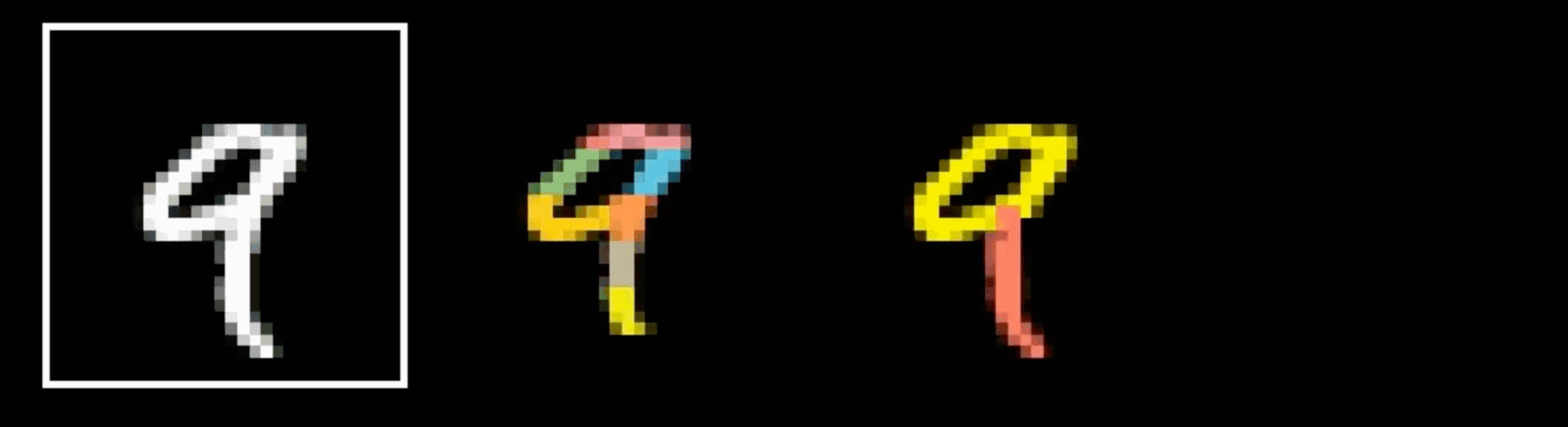
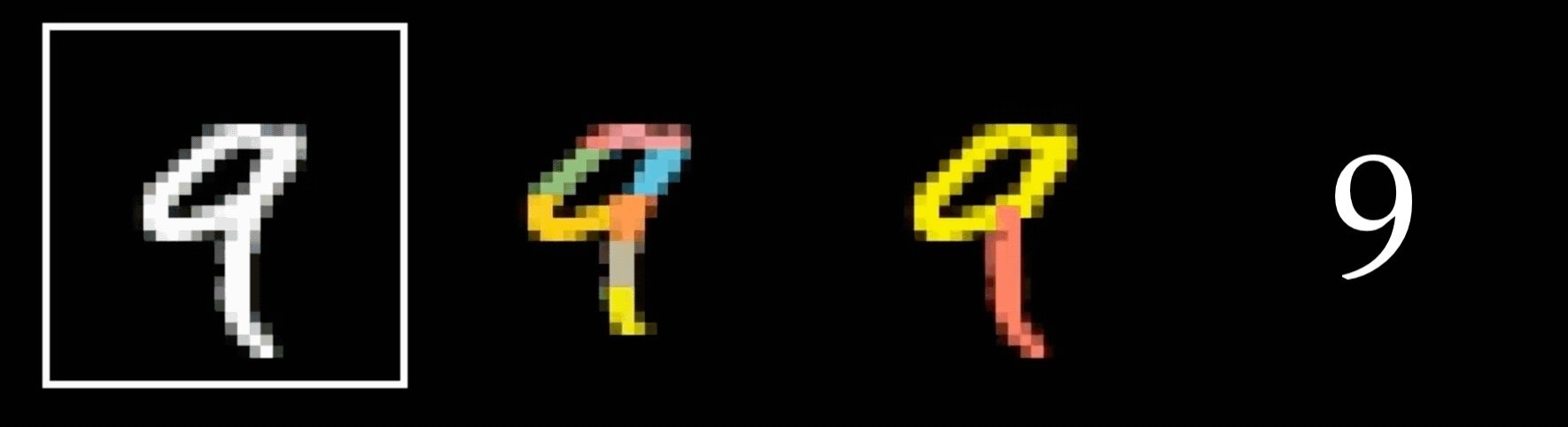
  • Visual hierarchy
  • Spatial locality
  • Translational invariance

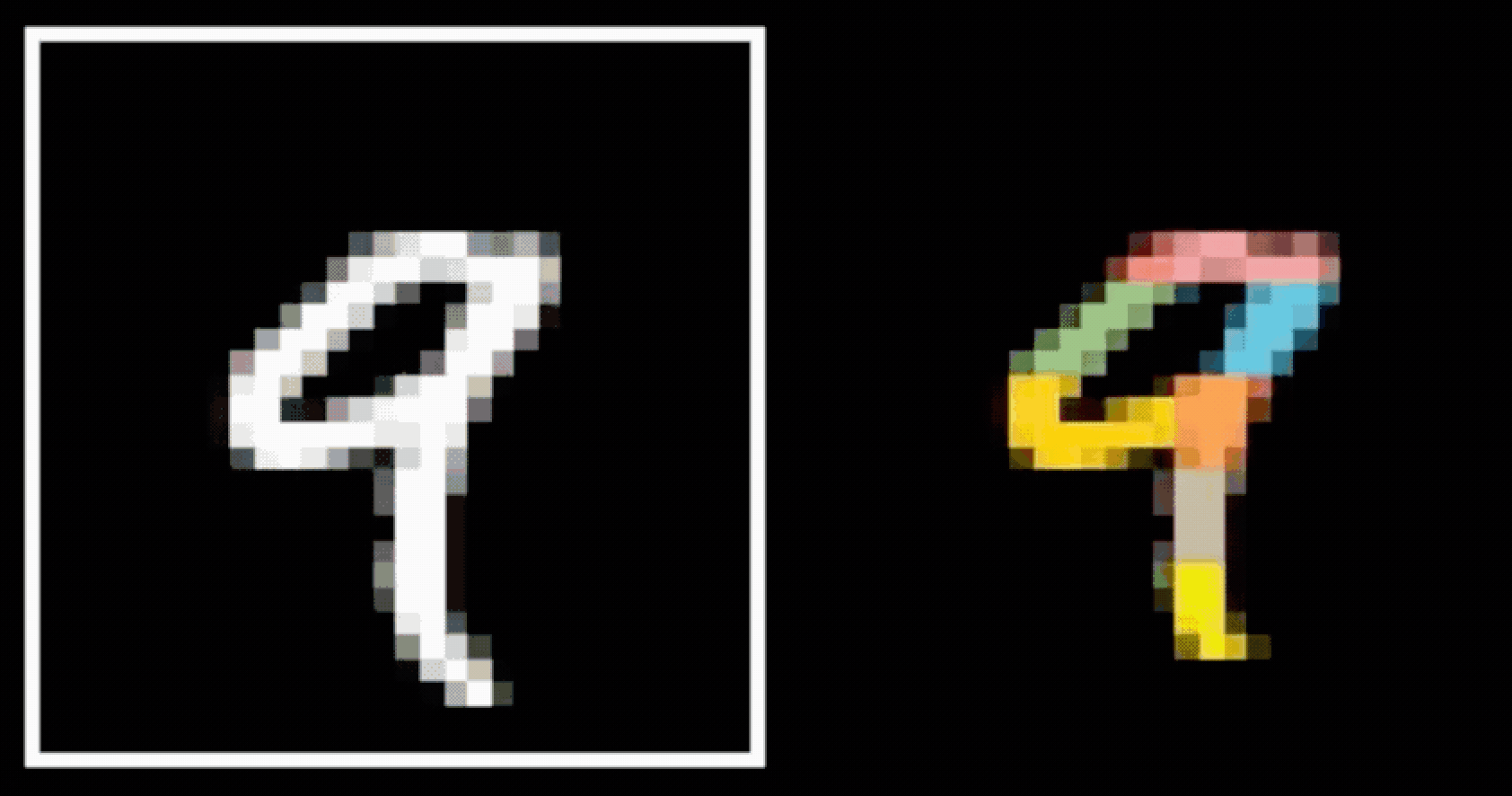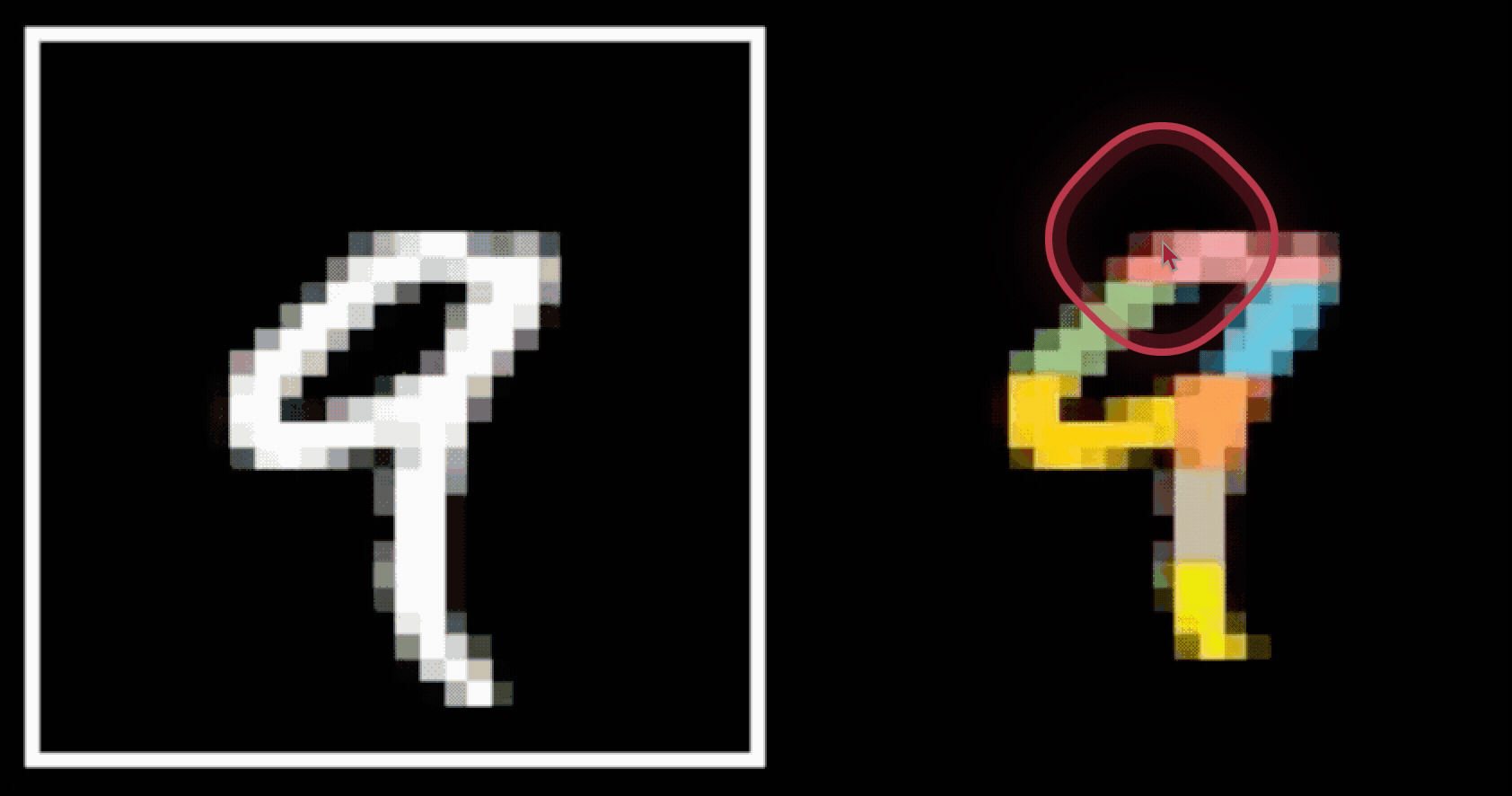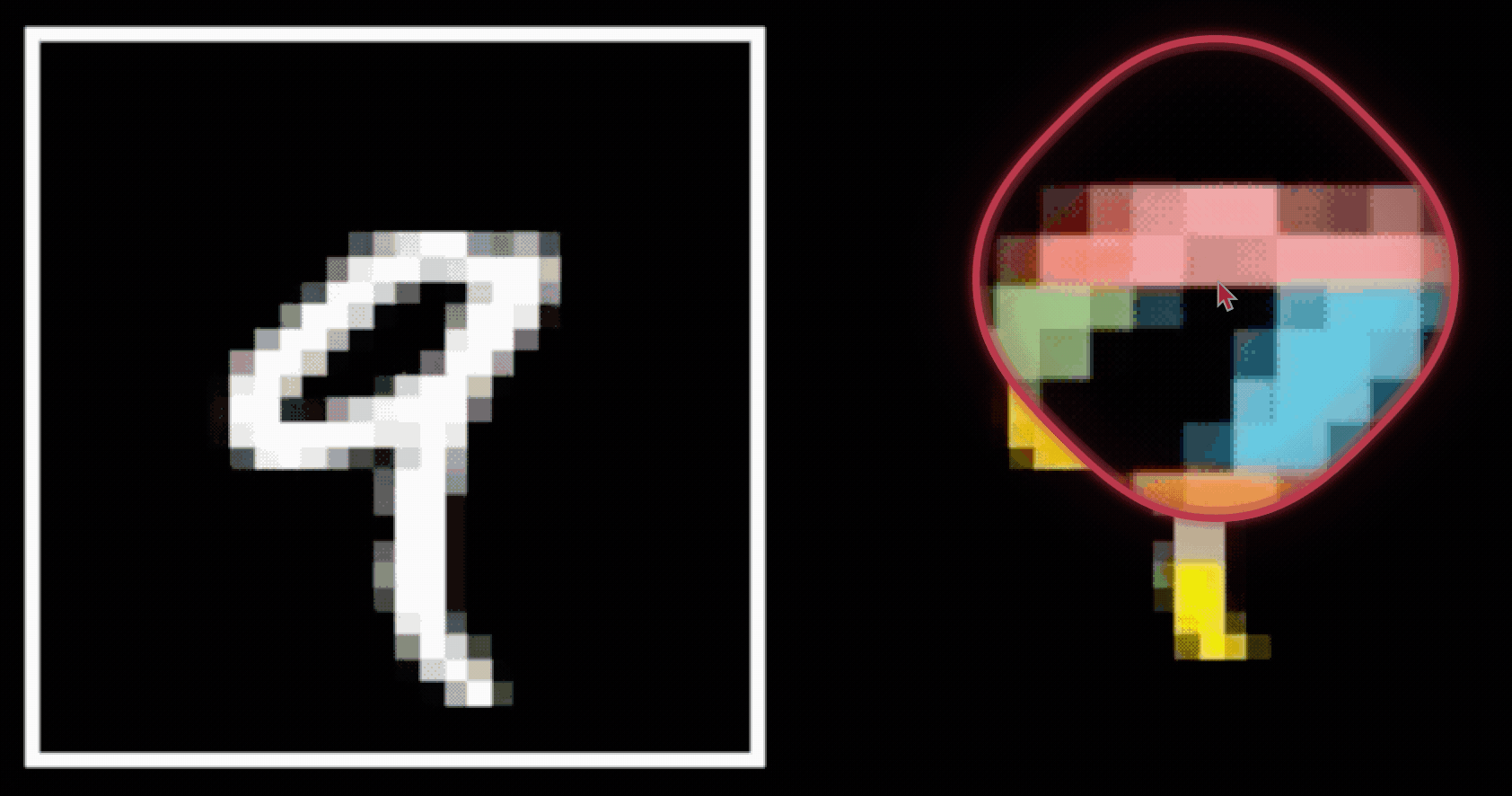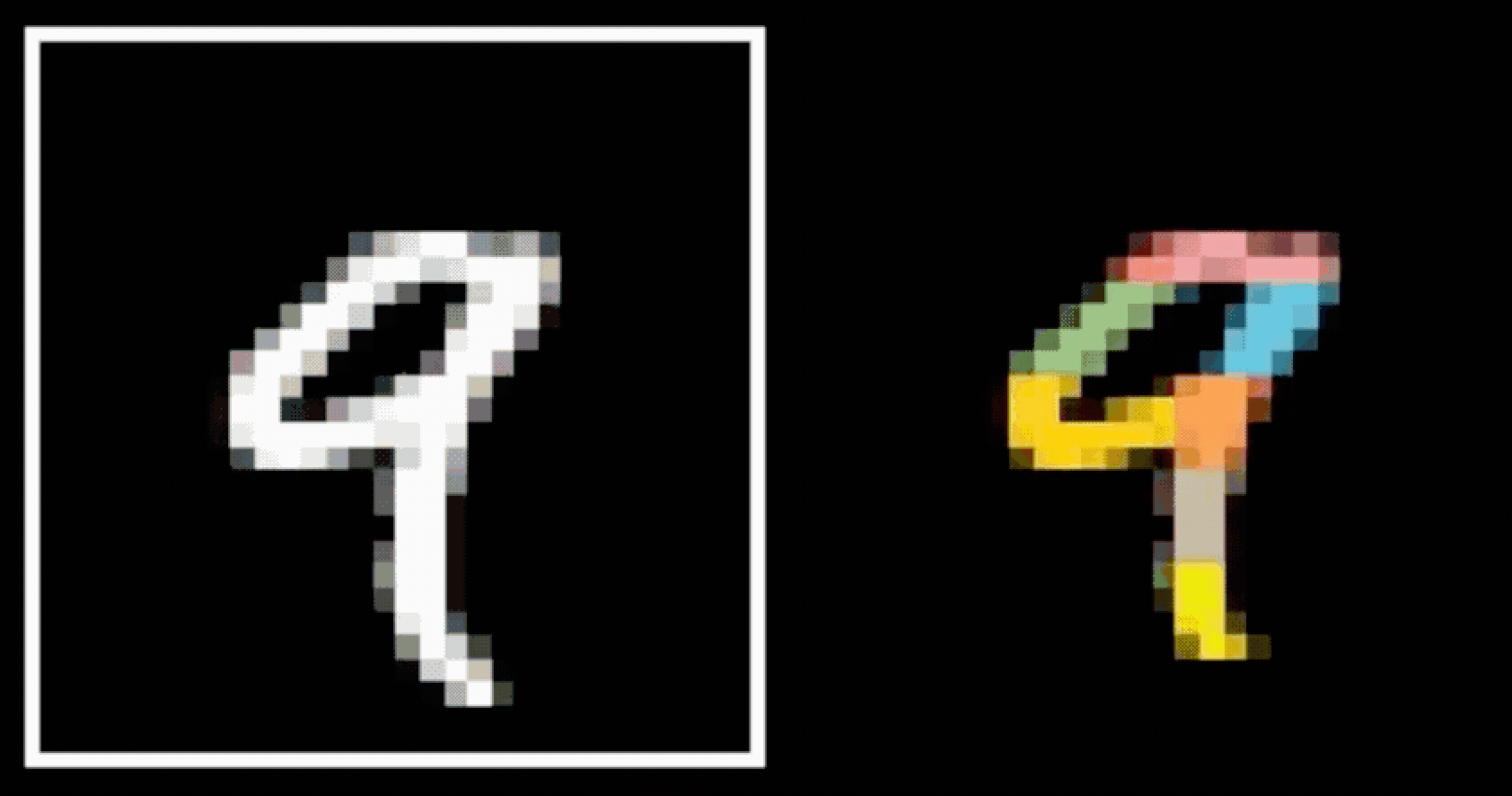
CNN cleverly exploits

to handle images efficiently and sensibly.

via

  • layering (with nonlinear activations) 
  • convolution
  • pooling
  • Visual hierarchy
  • Spatial locality
  • Translational invariance

Outline

  • Recap, fully-connected net
  • Vision problem structure
  • Convolutional network structure
  • Convolution
    • 1-dimensional and 2-dimensional convolution
    • 3-dimensional tensors
  • Max pooling
  • Case studies

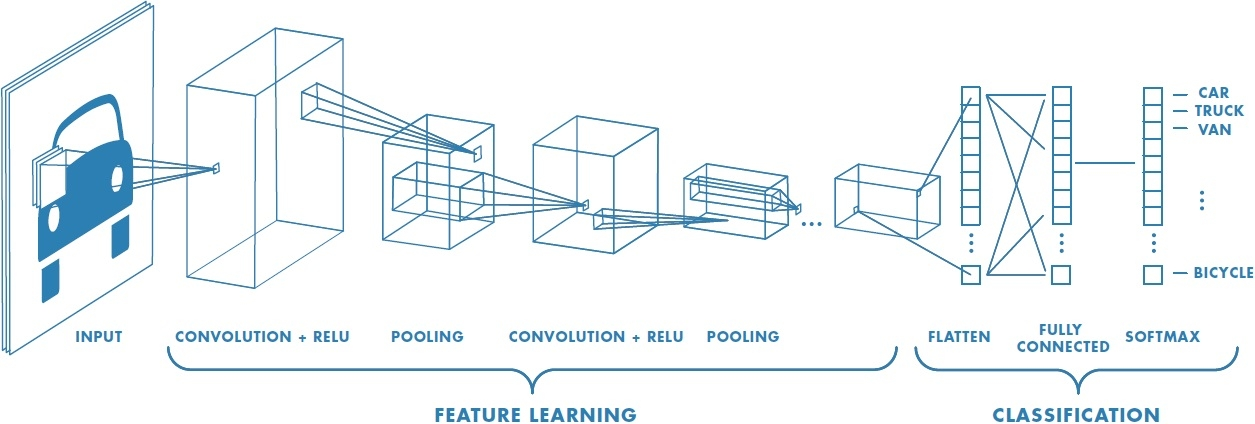
typical CNN structure for image classification

Outline

  • Recap, fully-connected net
  • Vision problem structure
  • Convolutional network structure
  • Convolution
    • 1-dimensional and 2-dimensional convolution
    • 3-dimensional tensors
  • Max pooling
  • Case studies

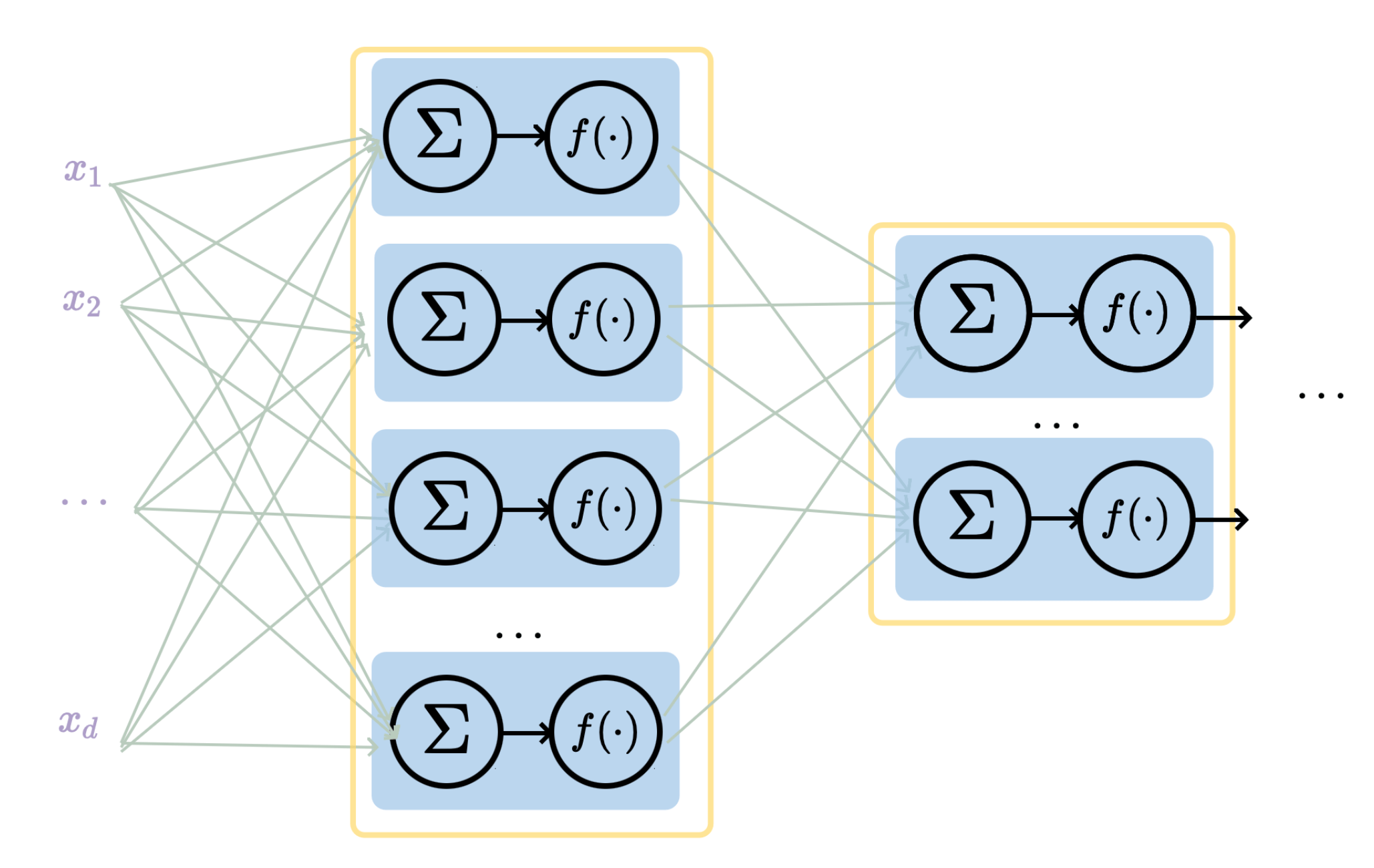
Convolutional layer might sound foreign, but it's very similar to fully connected layer

convolution with filters do these things:

Layer
fully-connected
convolutional

filter (kernels) weights

convolution

dot-product

Forward pass, do

Backward pass, learn

neuron weights

0

1

0

1

1

-1

1

input

filter

convolved output

1

(0*-1)+(1*1)=1

example: 1-dimensional convolution

0

1

0

1

1

-1

1

input

filter

convolved output

1

(1*-1)+(0*1)=-1

-1

example: 1-dimensional convolution

0

1

0

1

1

-1

1

input

filter

convolved output

1

1

example: 1-dimensional convolution

(0*-1)+(1*1)=1

-1

0

1

0

1

1

-1

1

input

filter

convolved output

1

1

-1

(1*-1)+(1*1)=0

0

example: 1-dimensional convolution

0

1

-1

1

1

-1

1

input

filter

convolved output

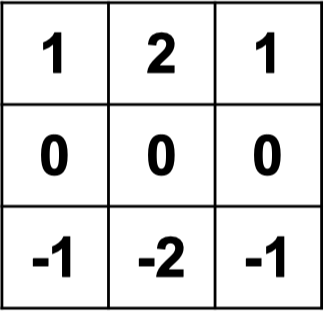
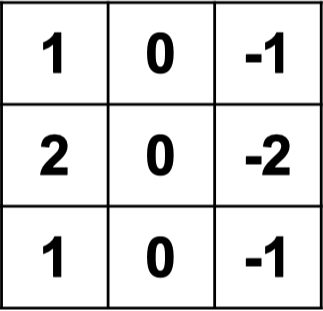
template matching

1

-2

2

0

convolution interpretation:

-1

 1

-1

 1

-1

 1

-1

 1

convolution interpretation:

0

1

-1

1

1

-1

1

input

filter

convolved output

1

-2

2

0

"look" locally

0

1

-1

1

1

-1

1

convolve with

=

dot product with

1

-2

2

0

1

0

0

0

0

-1

0

0

0

0

0

1

0

0

0

1

-1

0

1

-1

-1

convolution interpretation:

parameter sharing

0

1

0

1

1

convolve with

dot product with

0

1

0

1

1

?
?

1

I_{5\times5}
0 1

convolution interpretation:

input

filter

convolved output

0 1 0 1 0
1 0 1 0

translational equivariance 

hyperparameters

  • Zero-padding input
  • Filter size (e.g. we saw these two)
  • Stride

(e.g. stride of 2)

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

1

1

0

0

1

1

1

1

0

0

1

1

0

0

1

1

1

1

0

0

0

0

0

0

0

0

0

0

1

1

0

0

1

1

1

1

0

0

1

1

0

0

1

1

1

1

0

0

0

0

0

0

0

0

1

these weights are what CNN learn eventually

-1

1

0

0

0

0

1

1

1

1

0

0

0

0

1

1

1

1

1

1

1

1

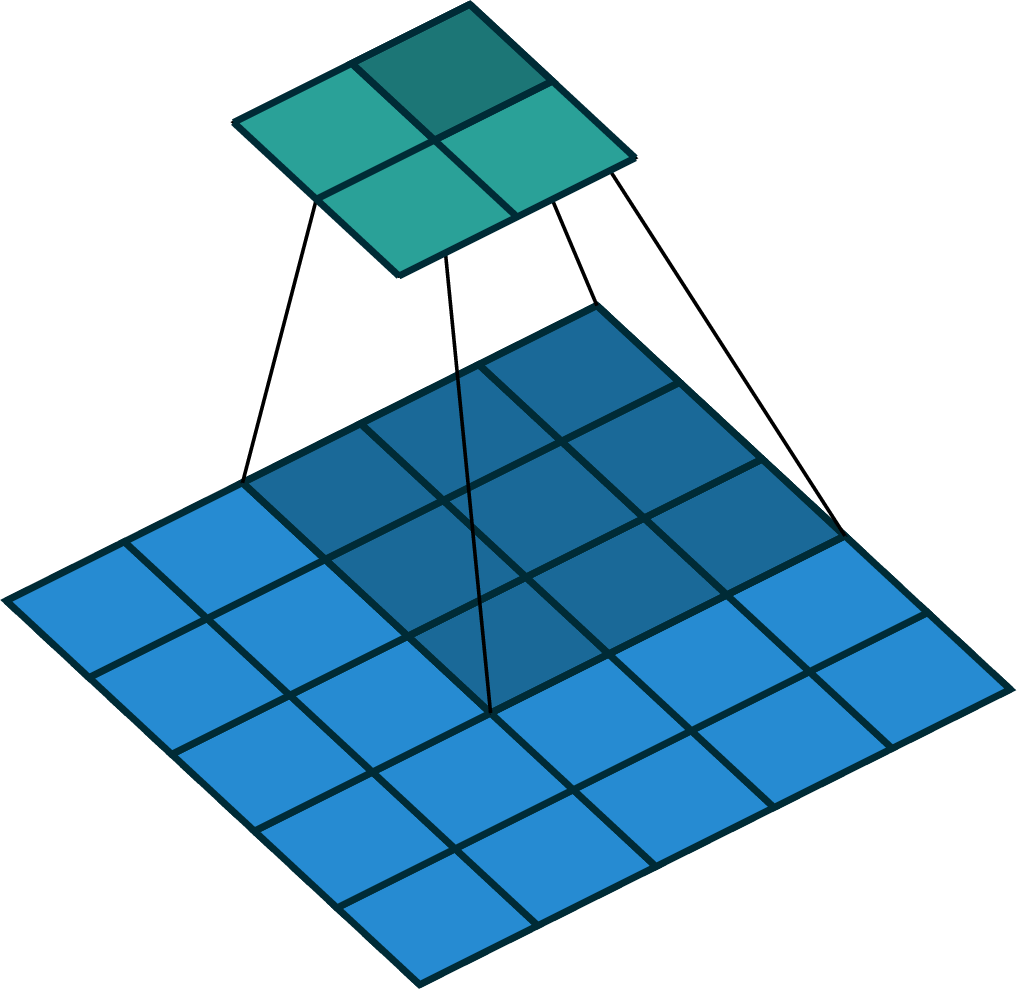
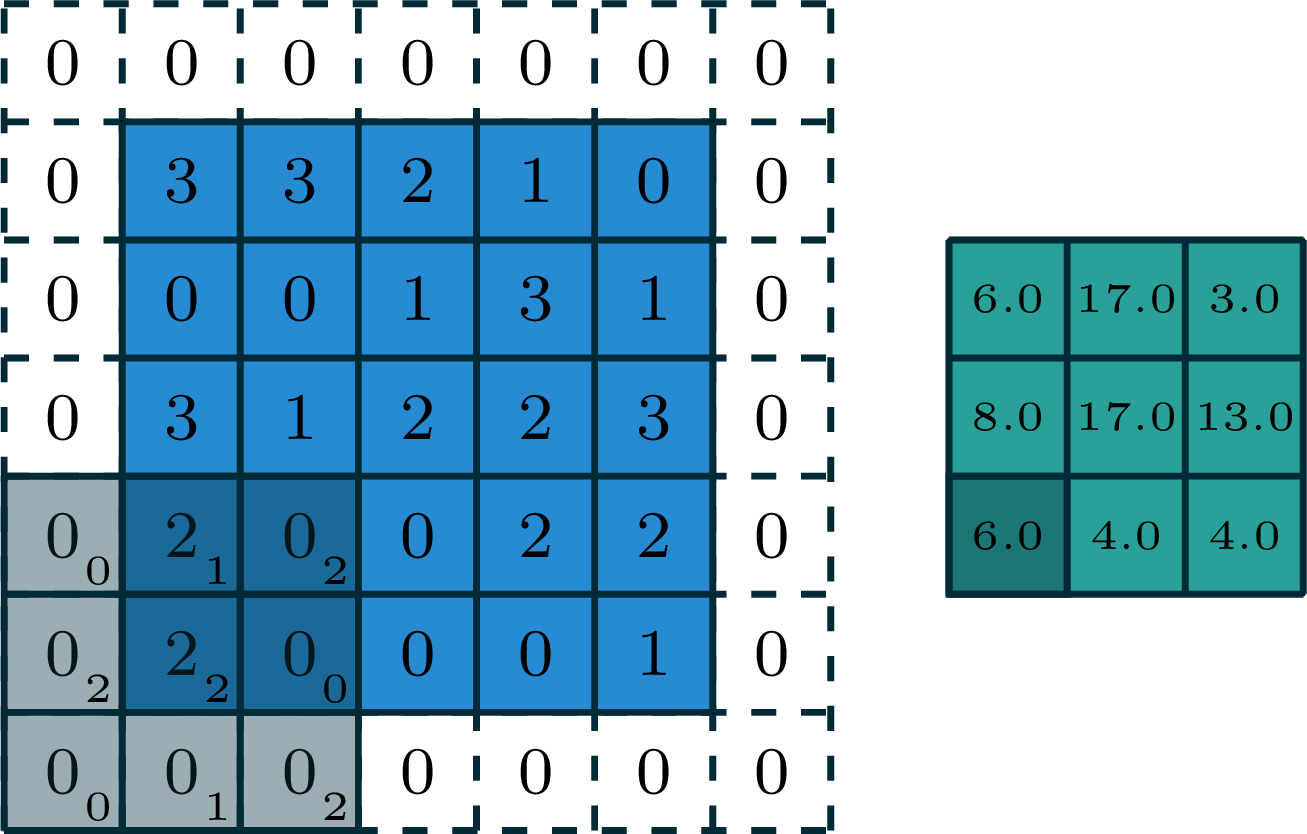
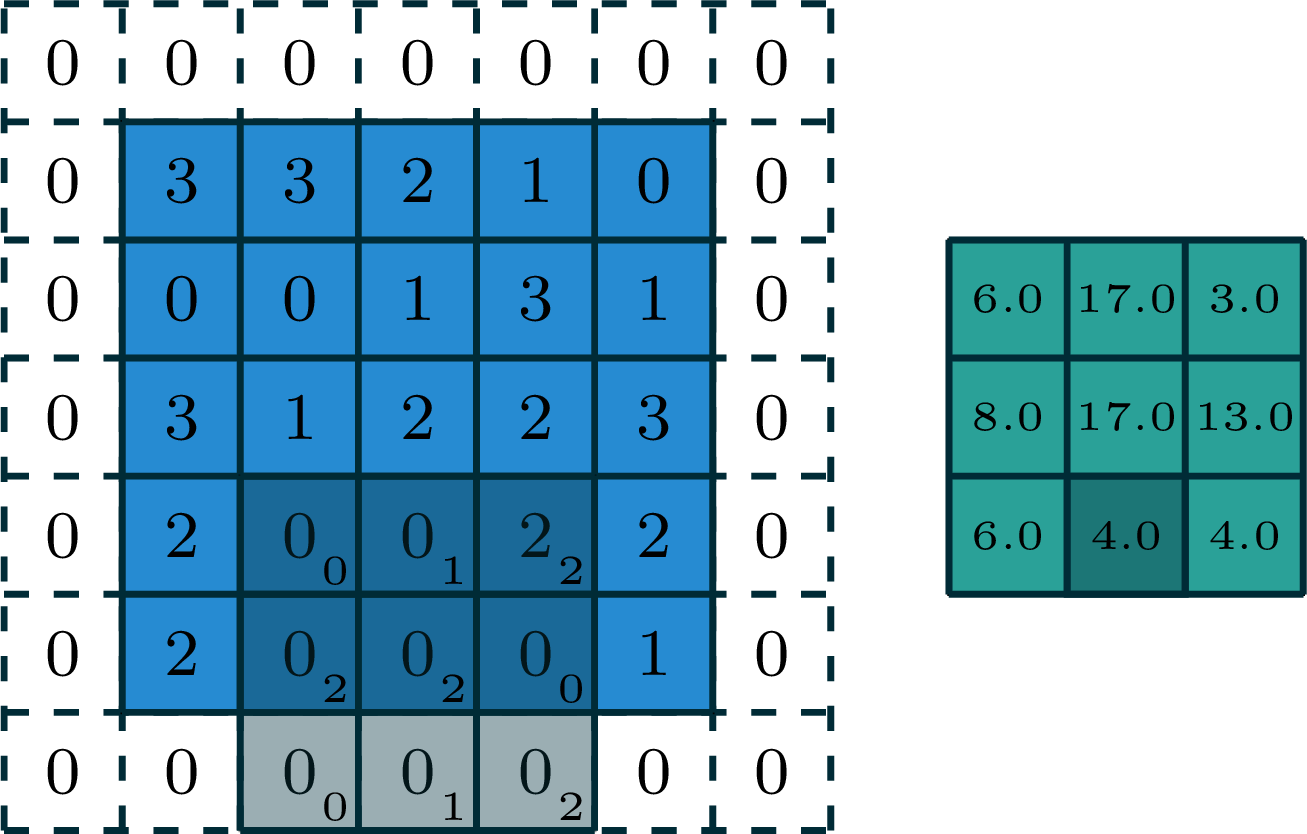
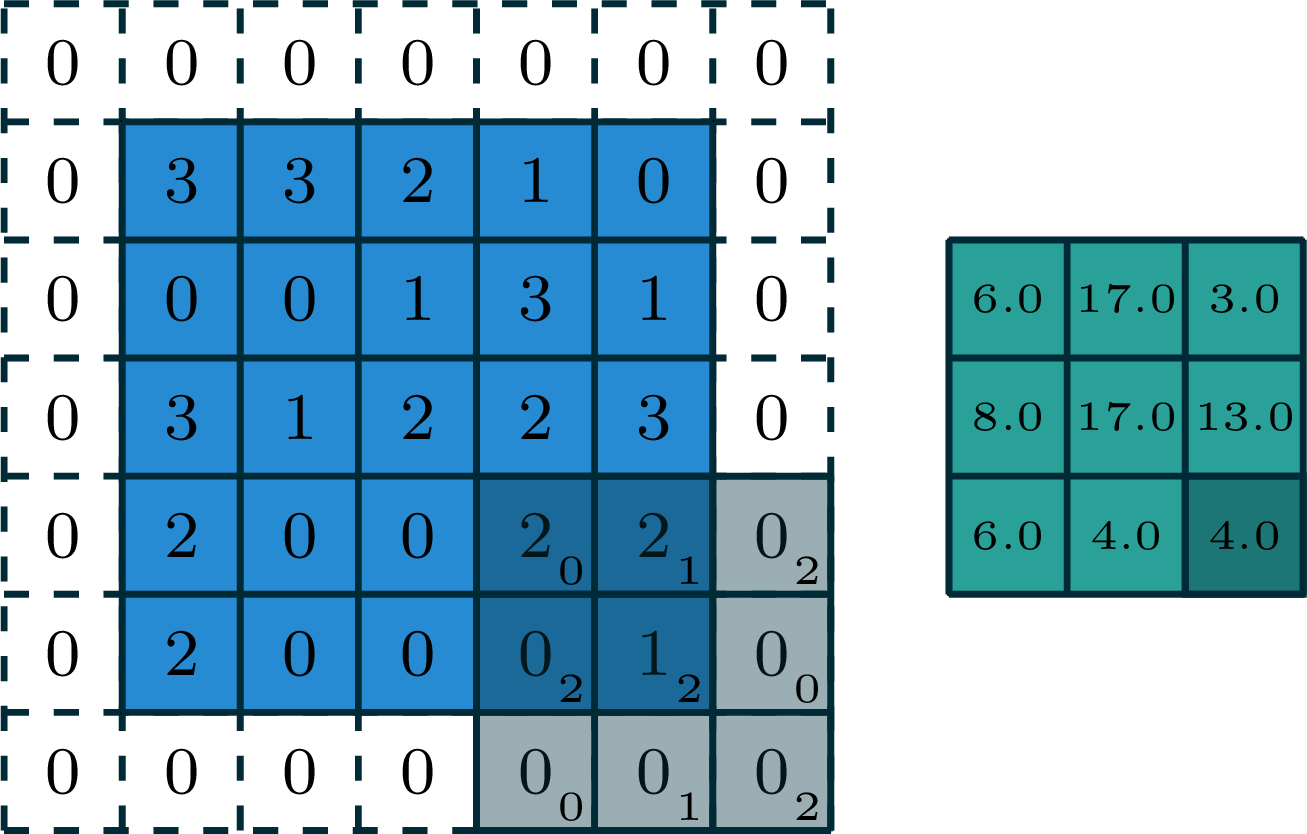
2-dimensional convolution

input

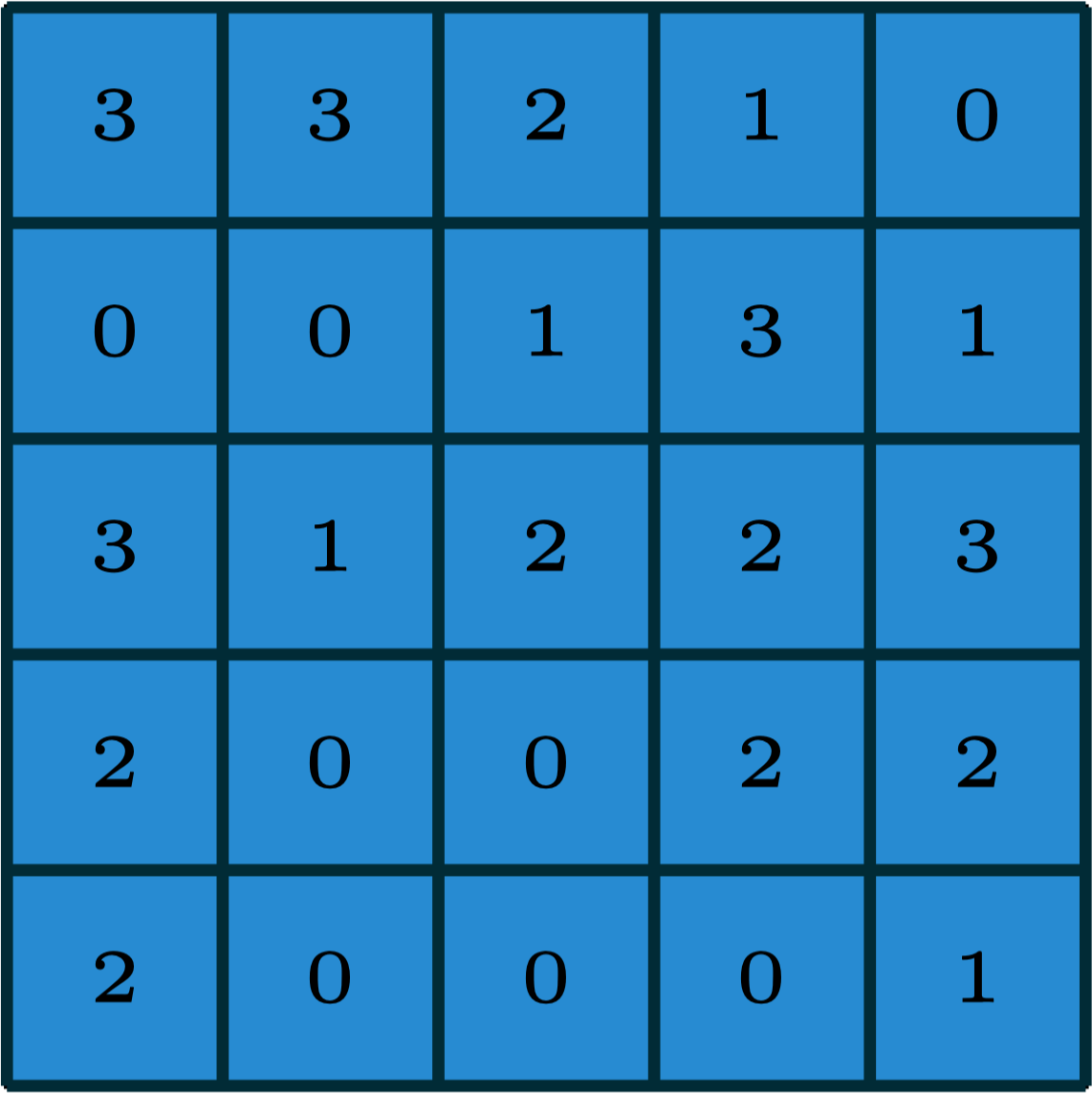
filter

[image edited from vdumoulin]

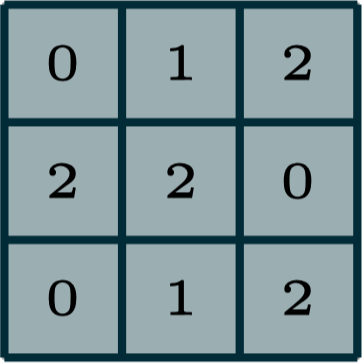
output

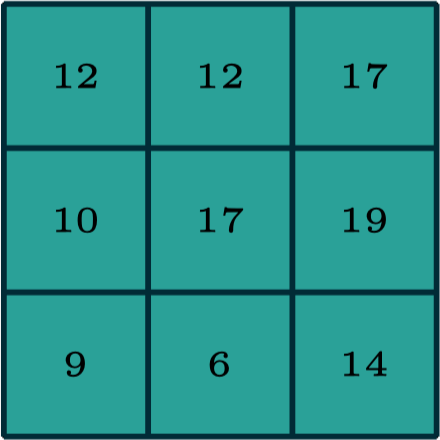
[image edited from vdumoulin]

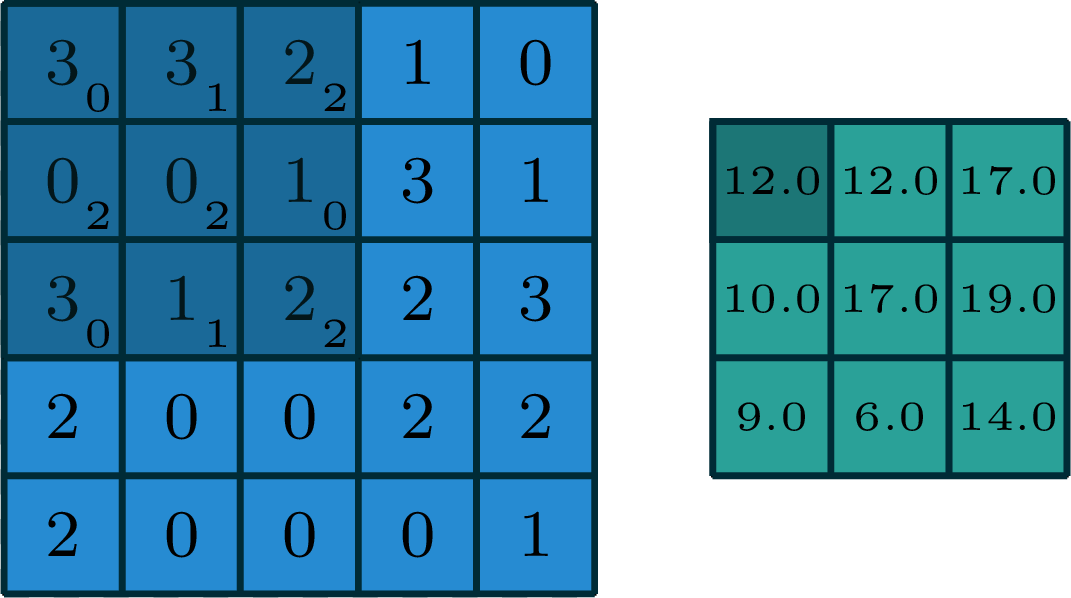
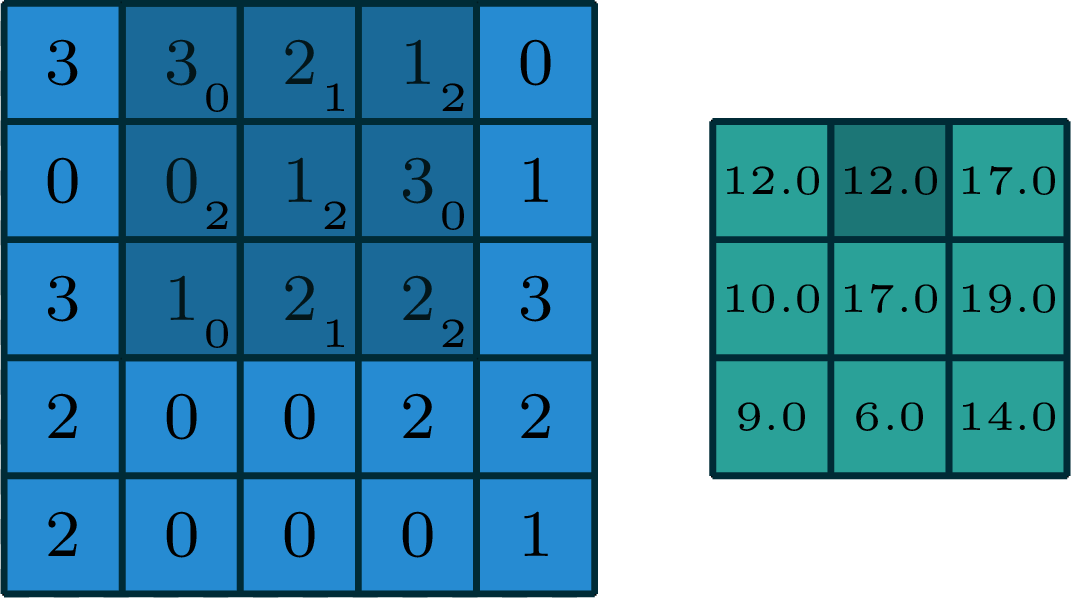
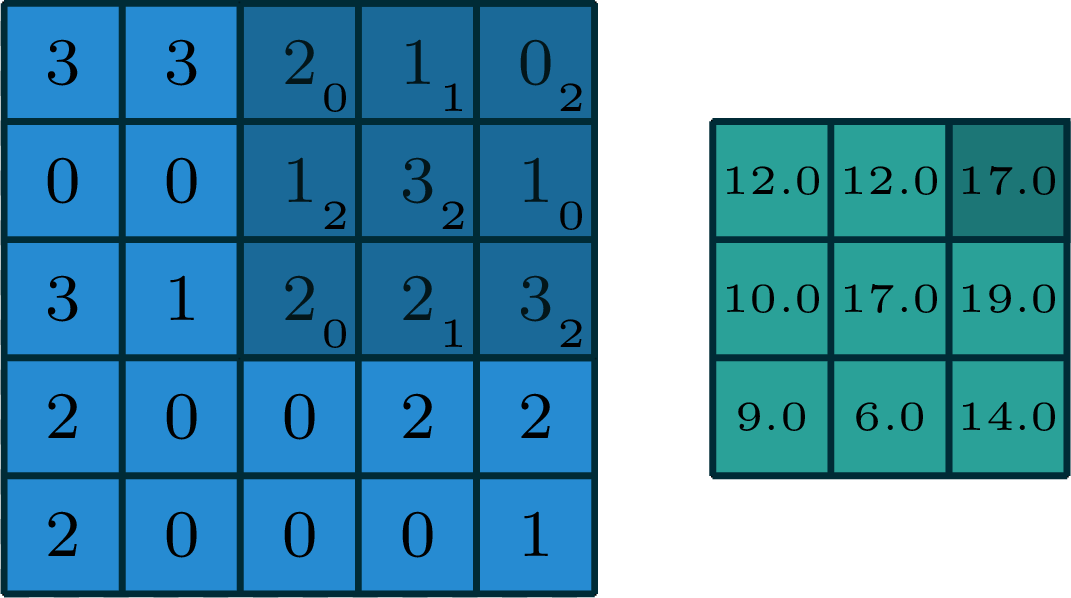
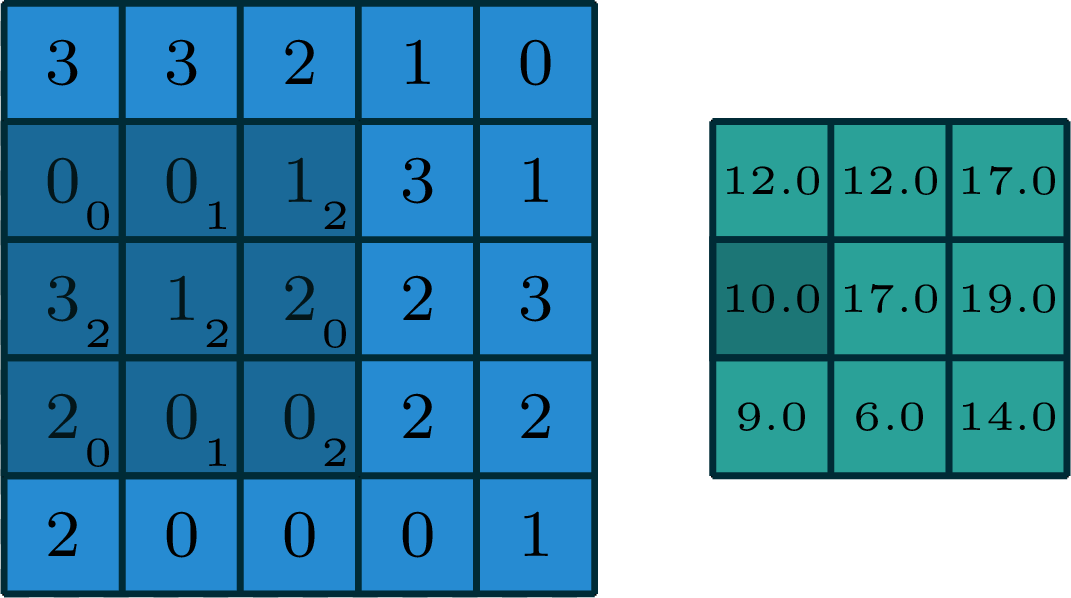
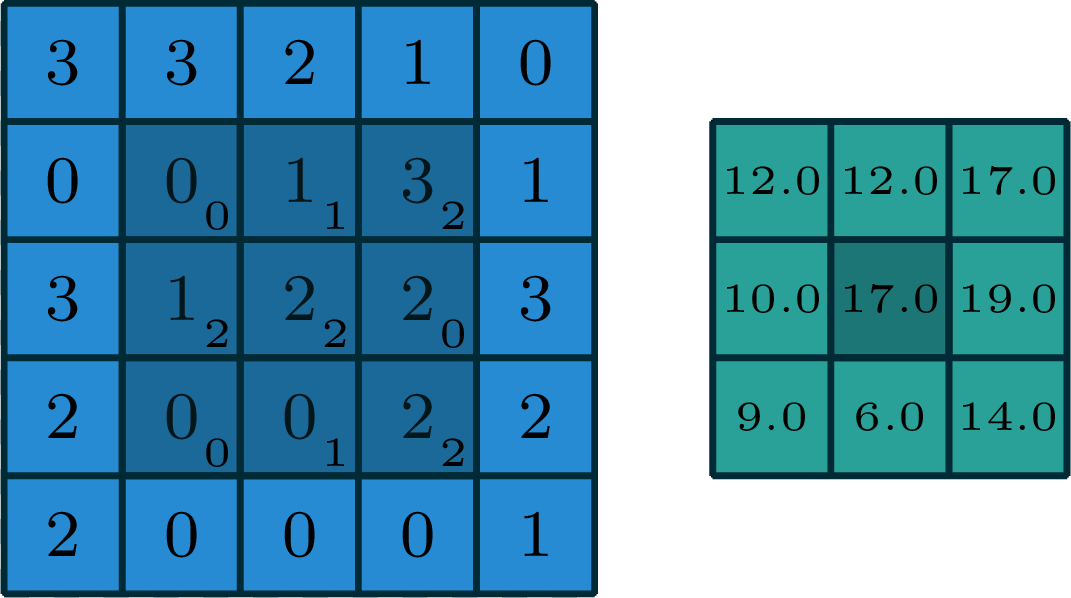
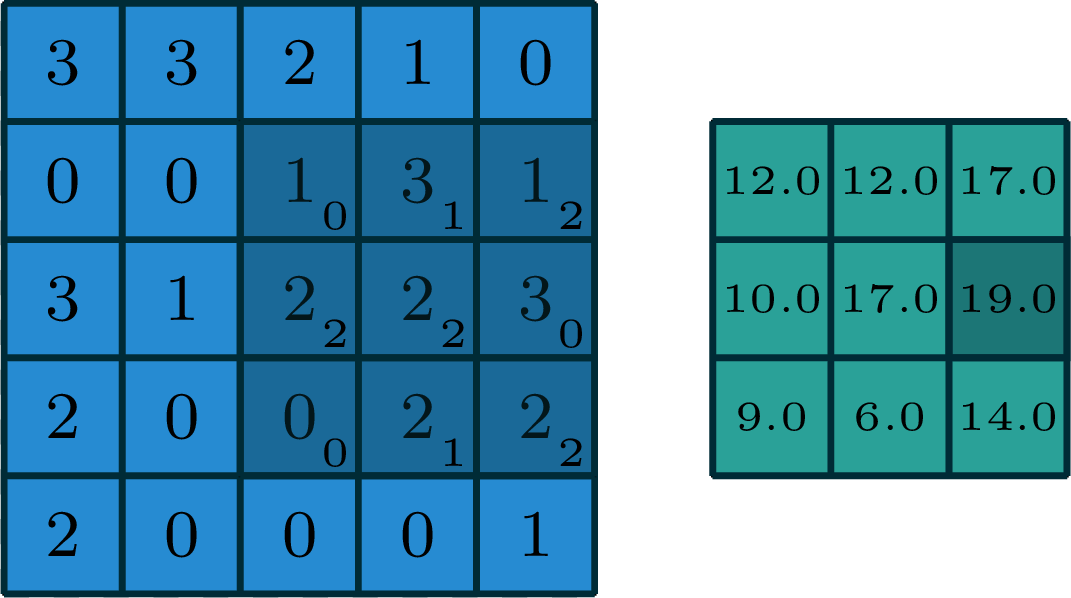
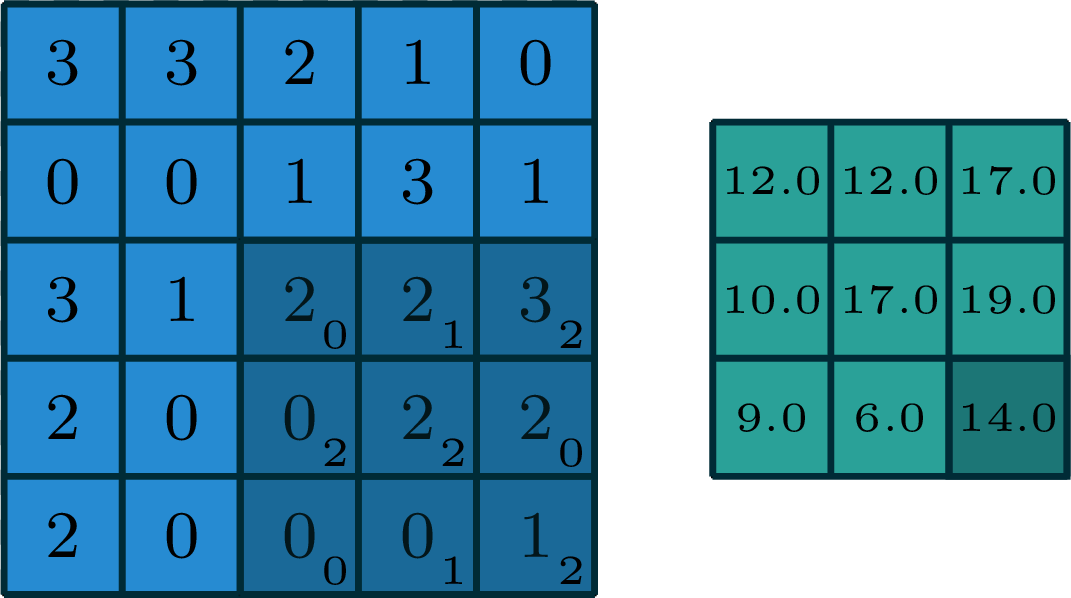
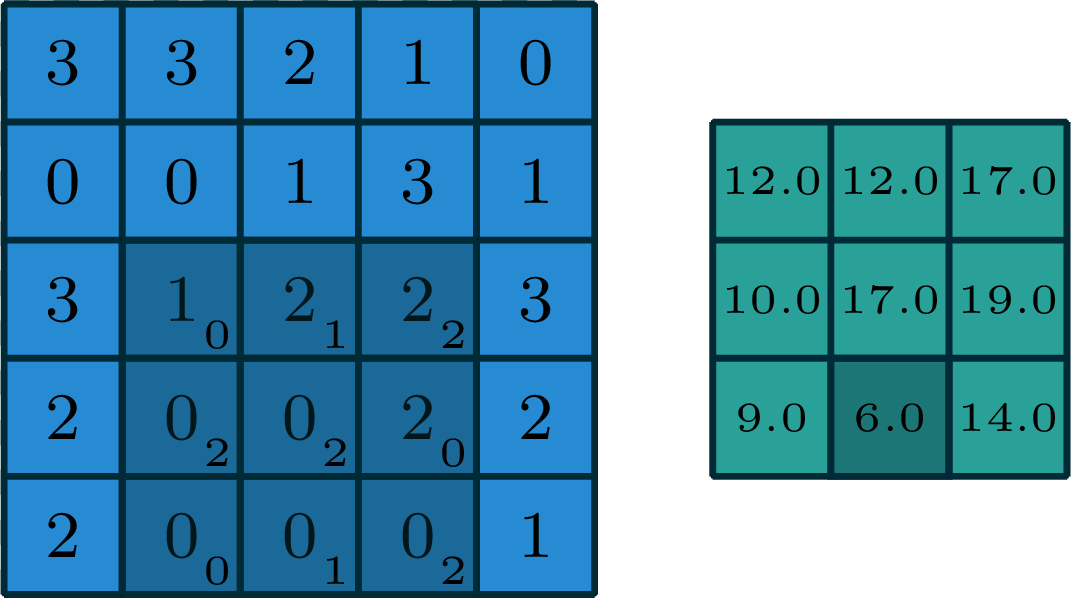
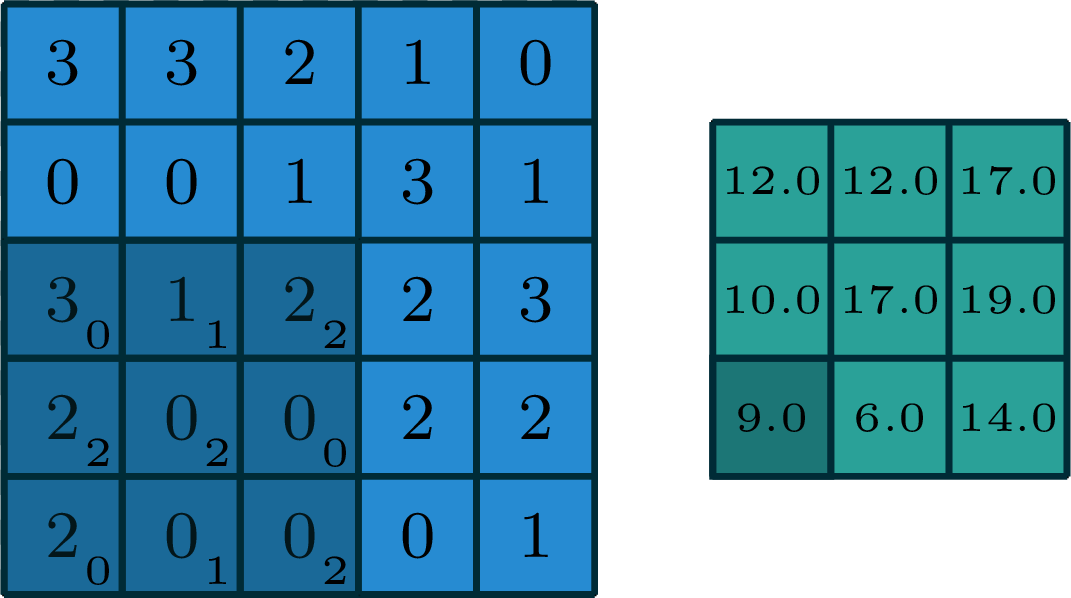
[image edited from vdumoulin]

stride of 2

input

filter

output

[image edited from vdumoulin]

stride of 2

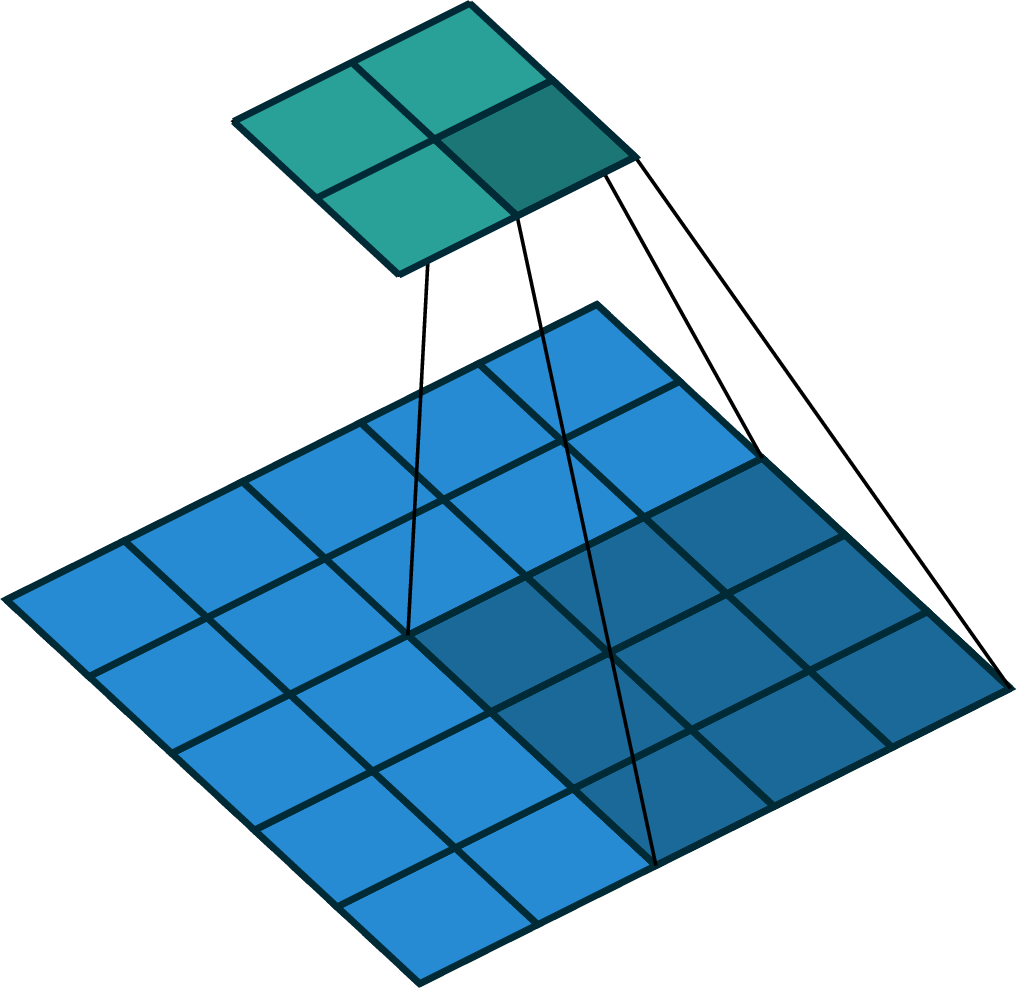
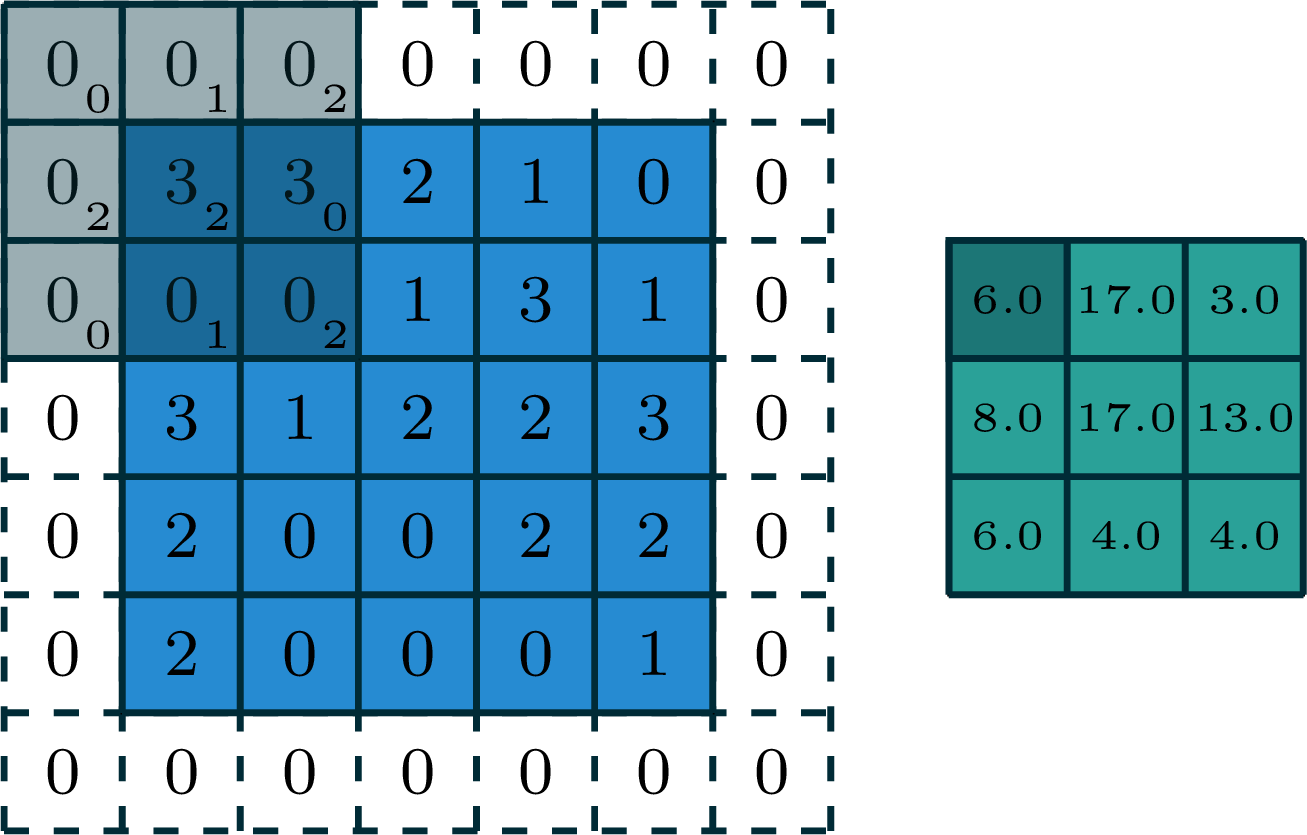
[image edited from vdumoulin]

stride of 2, with padding of size 1

input

filter

output

[image edited from vdumoulin]

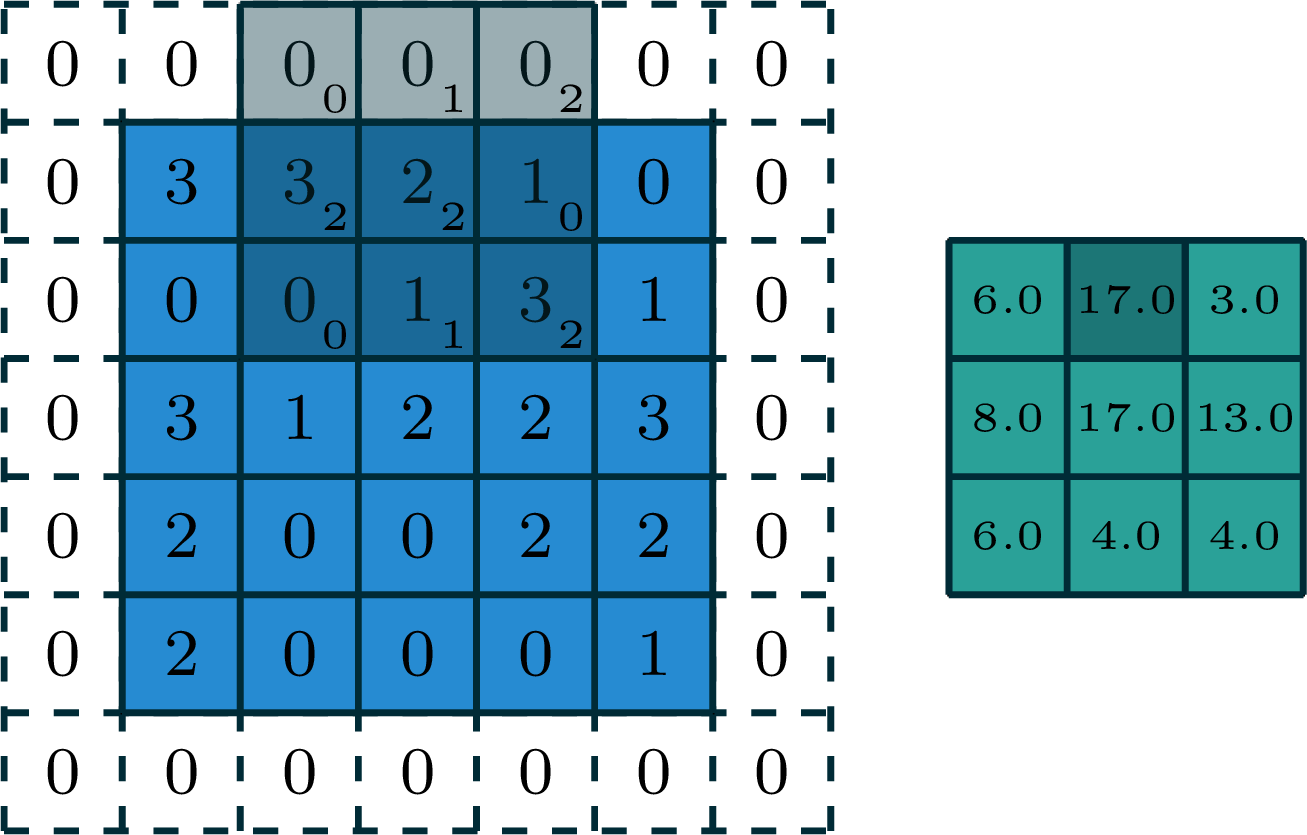
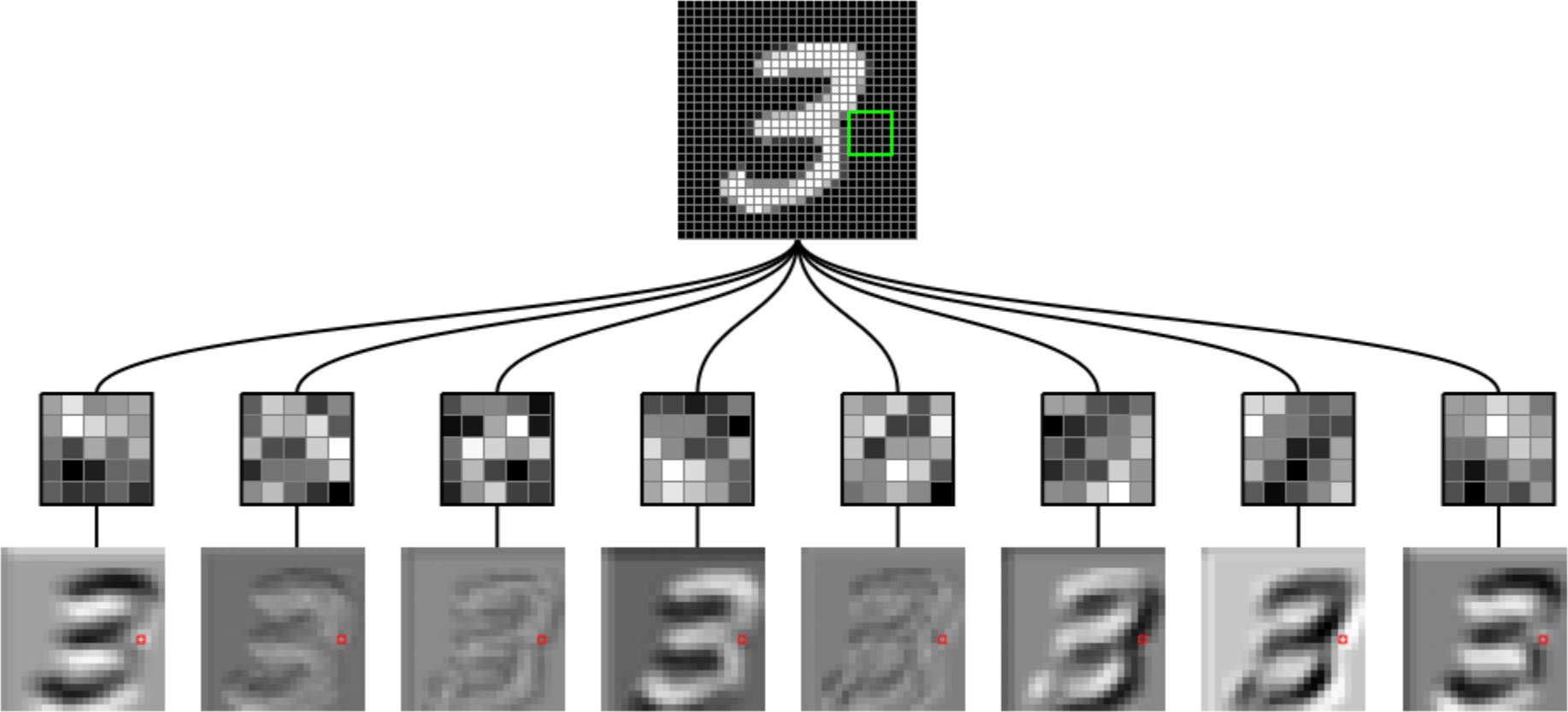
[video credit Lena Voita]

  • Looking locally
  • Parameter sharing
  • Template matching
  • Translational equivariance 

convolution interpretation:

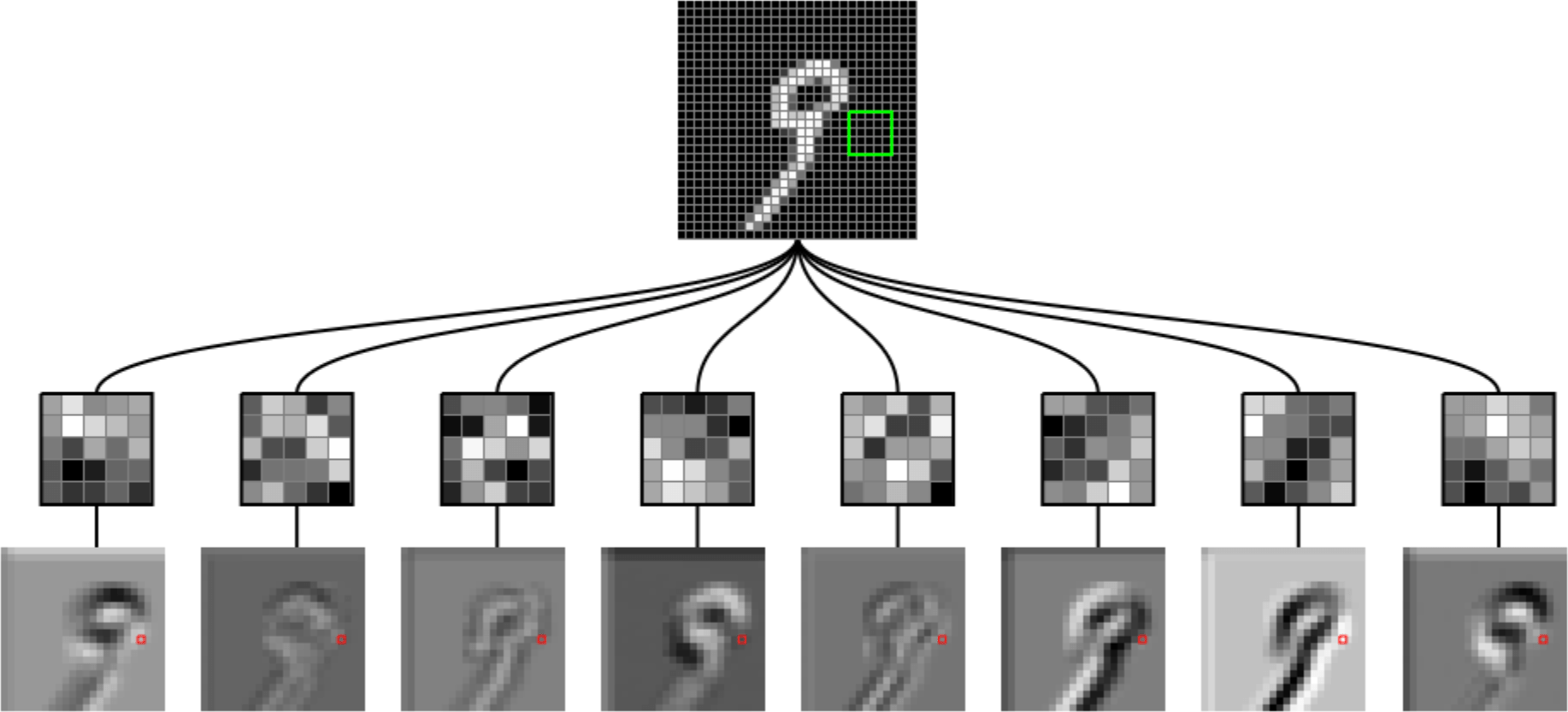
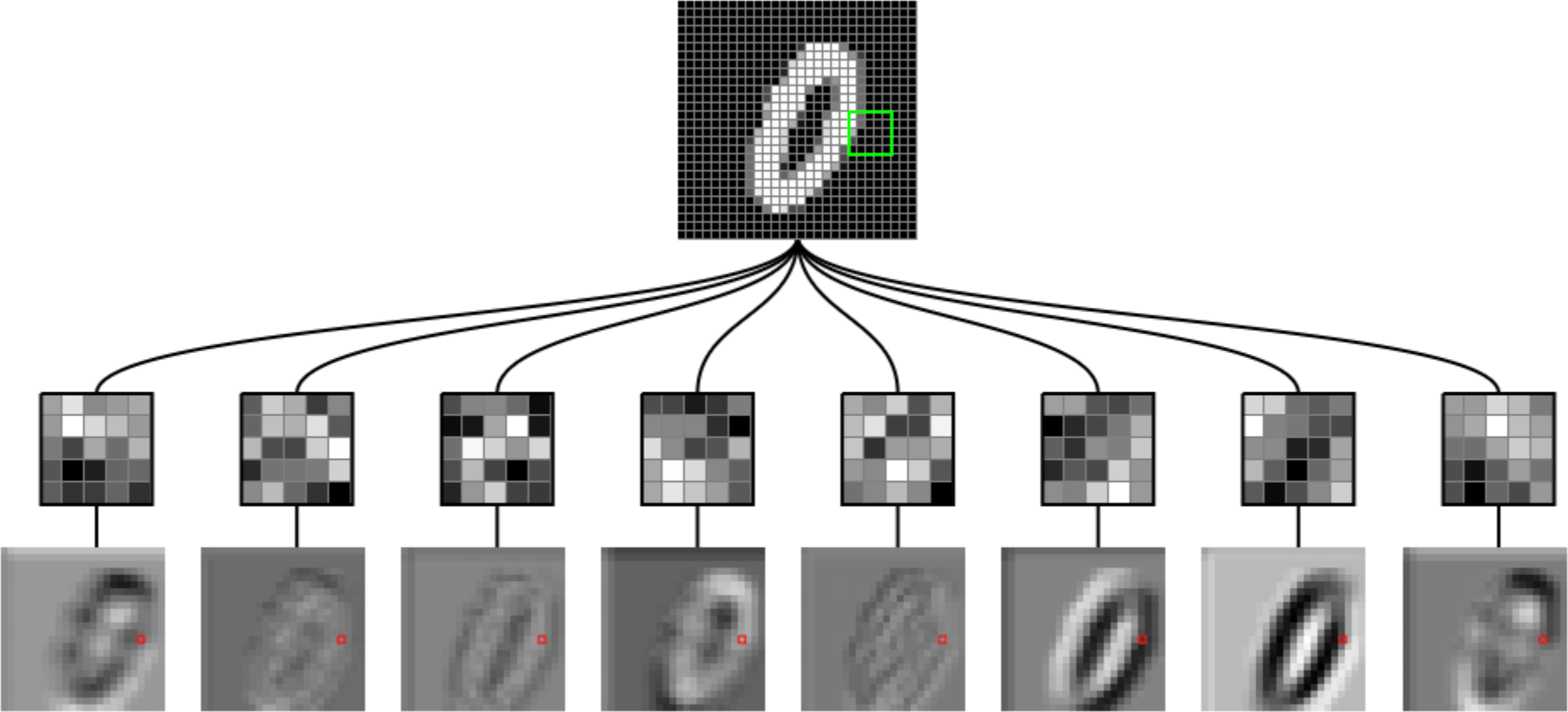
Outline

  • Recap, fully-connected net
  • Vision problem structure
  • Convolutional network structure
  • Convolution
    • 1-dimensional and 2-dimensional convolution
    • 3-dimensional tensors
  • Max pooling
  • Case studies

A tender intro to tensor:

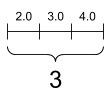
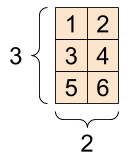
[image credit: tensorflow​]

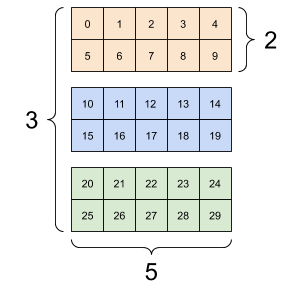
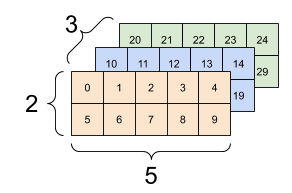
red

green

blue

[Photo by Zayn Shah, Unsplash]

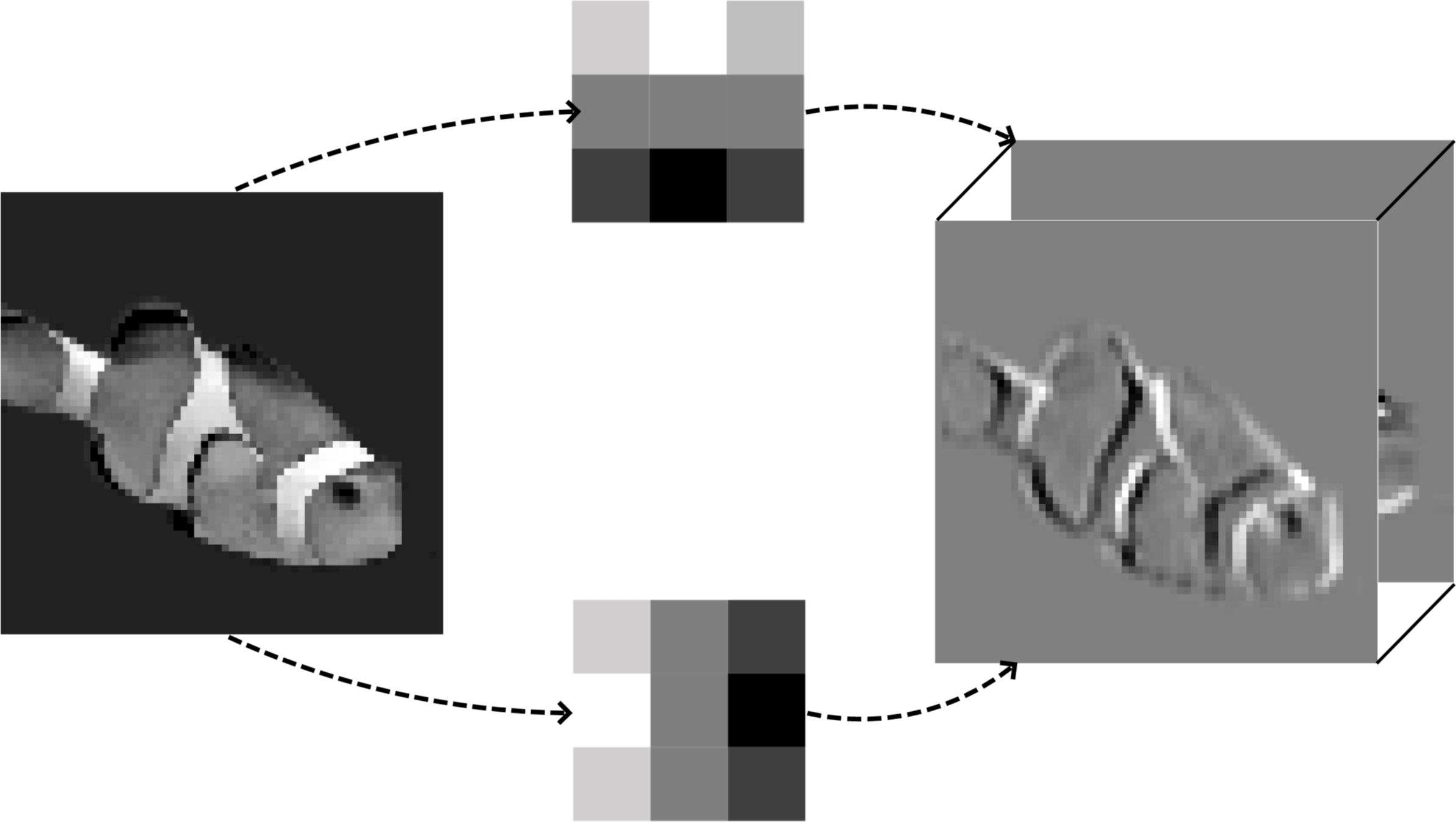
We'd encounter 3d tensor due to:

1. color input

image depth (channels)

image width

image

height

[Photo by Zayn Shah, Unsplash]

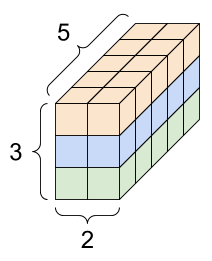
filter 1

filter 2

We'd encounter 3d tensor due to:

2. the use of multiple filters

filter 1

filter 2

image depth (channels)

\dots

We'd encounter 3d tensor due to:

2. the use of multiple filters

2. the use of multiple filters

image depth (channels)

image width

image

height

image depth (channels)

1. color input

We'd encounter 3d tensor due to

image width

image

height

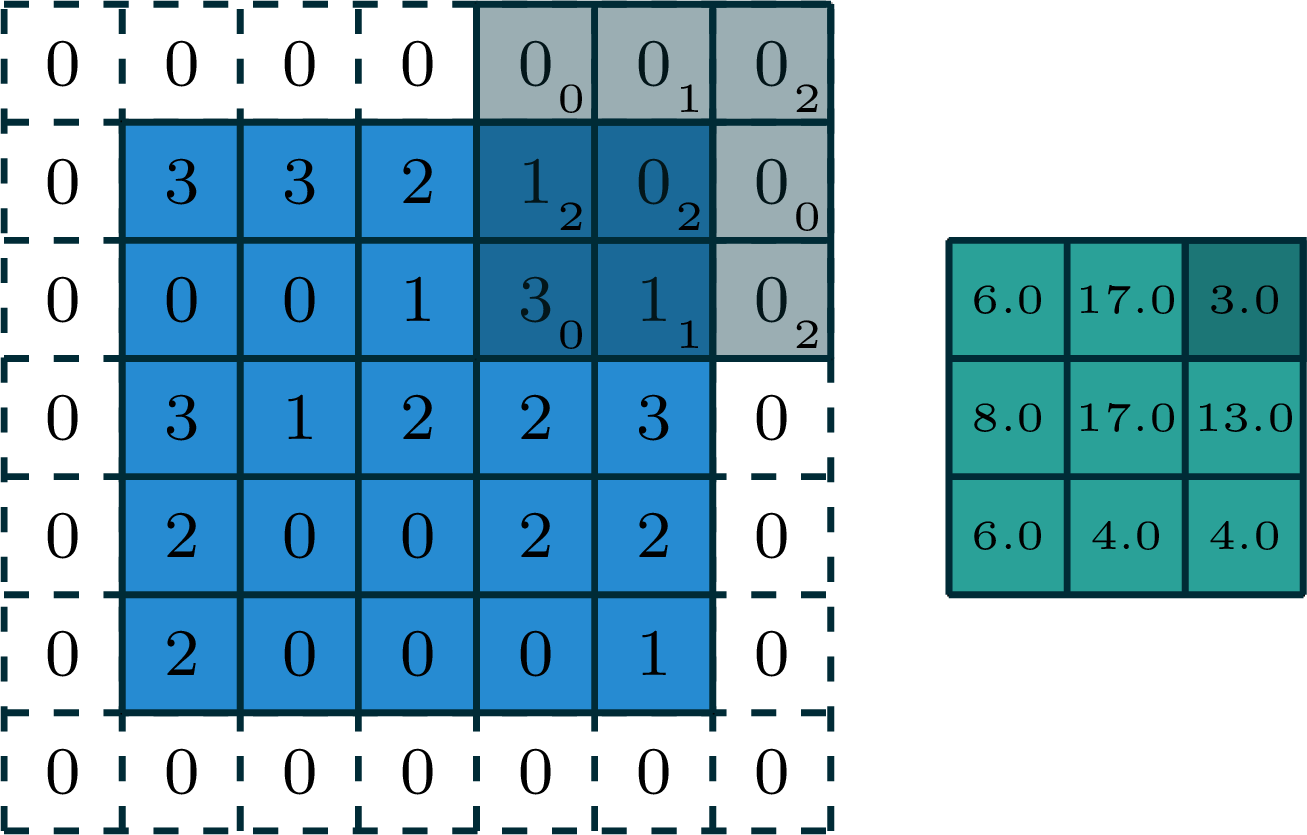
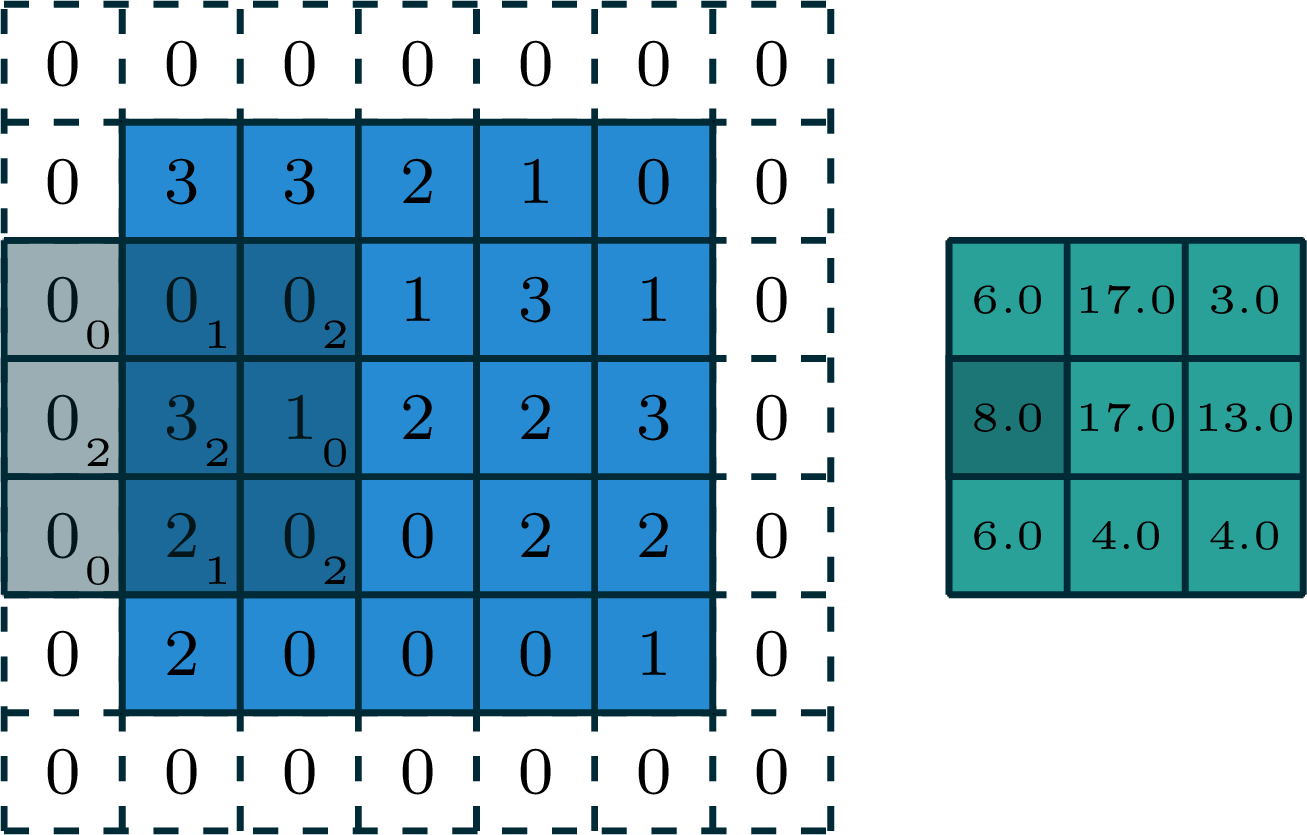
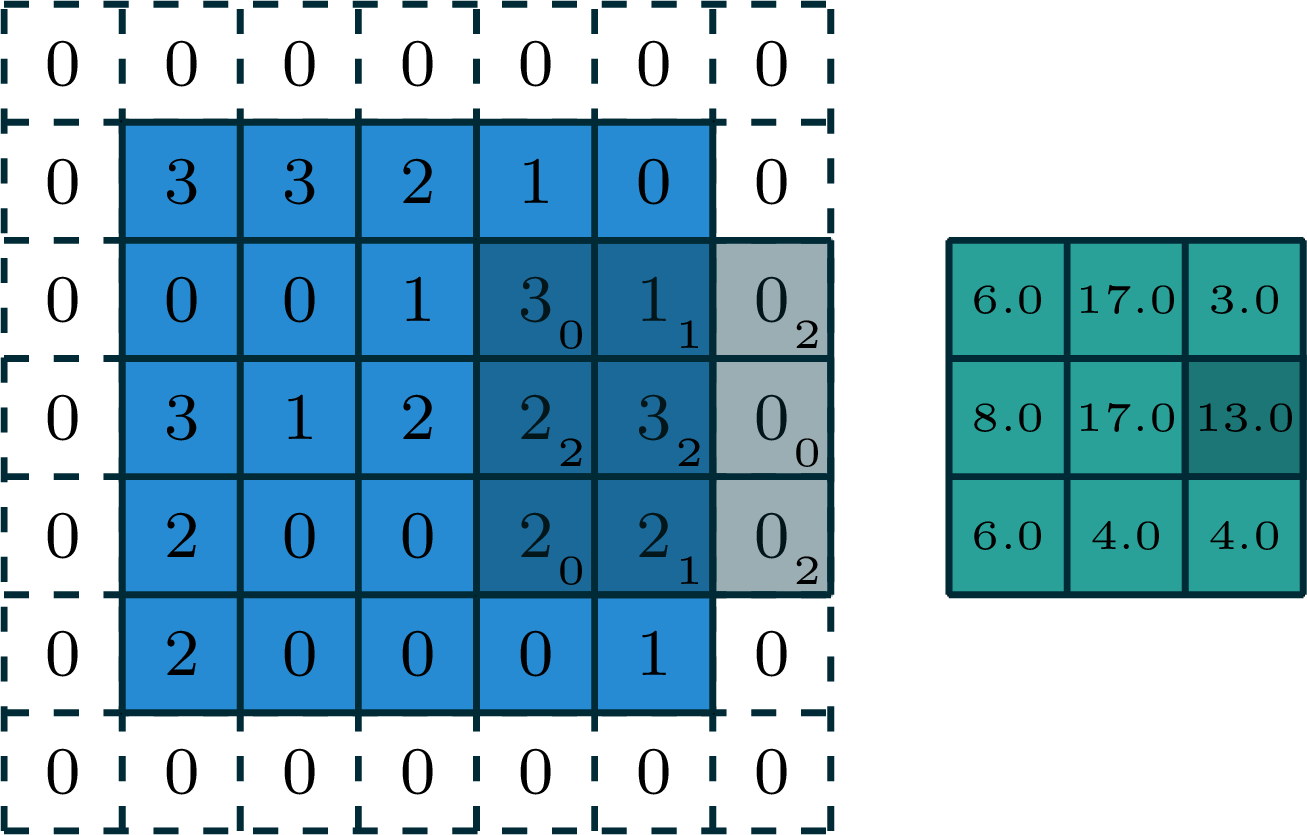
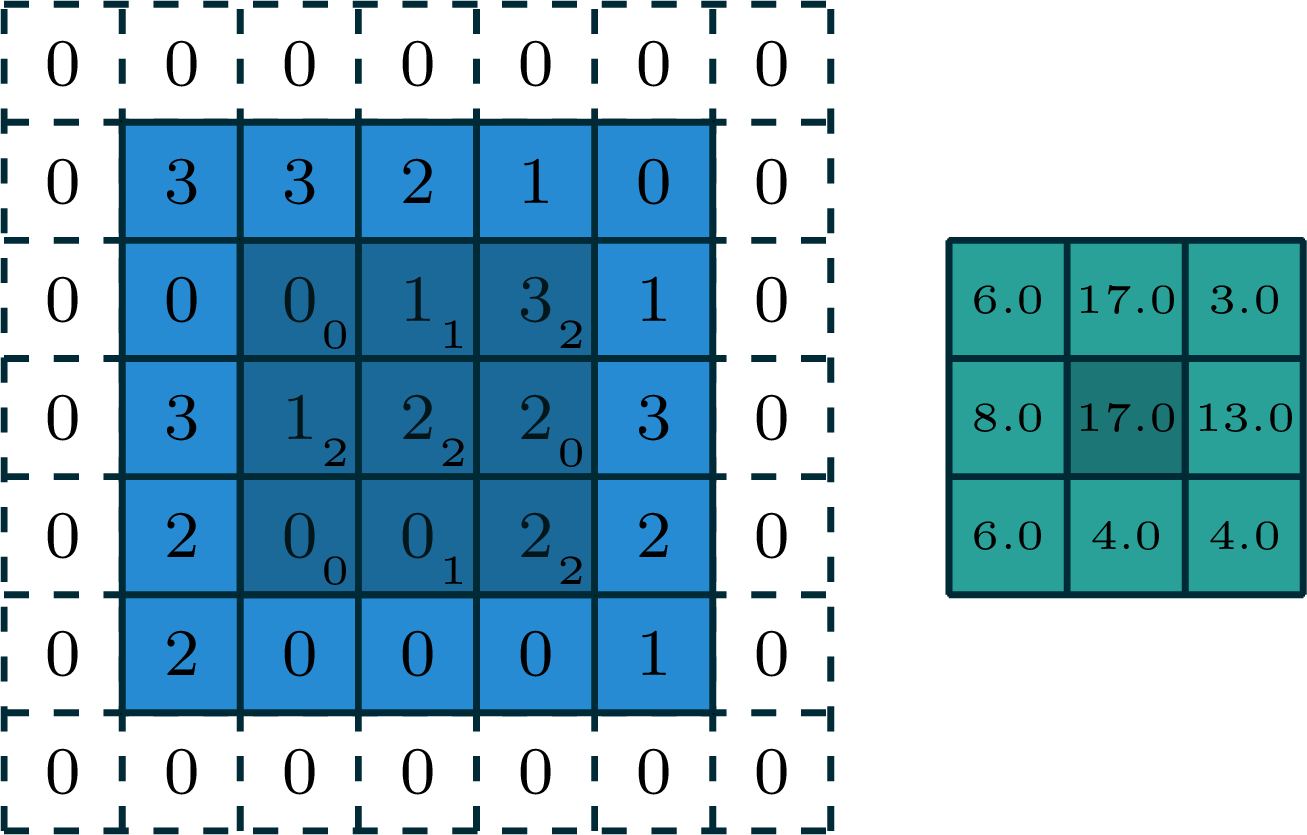
  • 2d convolution, 2d output

image depth (channels)

\Bigg\{
d
...
...
...
...
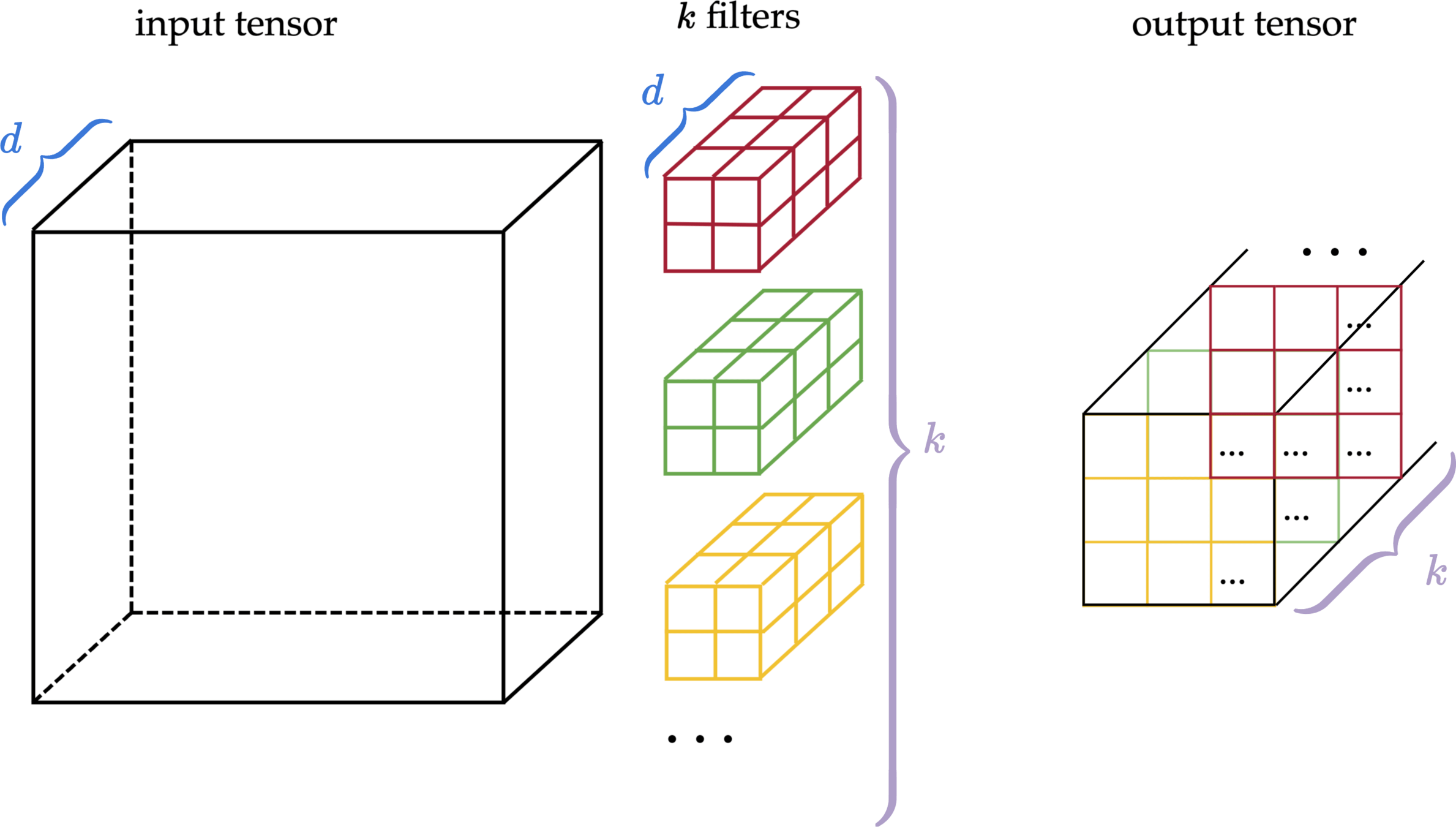
  • 3d tensor input, depth \(d\)
  • 3d tensor filter, depth \(d\)

output

But, we don't typically do 3-dimensional convolution. Instead:

We don't typically do 3-dimensional convolution, because

...
...
...

input tensor

one filter

2d output

  • 3d tensor input, depth \(d\)
  • 3d tensor filter, depth \(d\)
  • 2d tensor (matrix) output
...
...
... ... ...
...
...
... ... ...
...
...
... ... ...
\dots
\dots

input tensor

multiple filters

multiple output matrices

...
...

input tensor

\(k\) filters

output tensor

\dots
\dots
...
...
... ... ...
\Bigg\{
d
\Bigg\{
d
\left\{ \begin{array}{l} \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \end{array} \right.
k
\left\{ \begin{array}{l} \\ \\ \\ \end{array} \right.
k

2. the use of multiple filters 

1. color input

We'd encounter 3d tensor due to:

-- in doing 2-dimensional convolution

Outline

  • Recap, fully-connected net
  • Vision problem structure
  • Convolutional network structure
  • Convolution
    • 1-dimensional and 2-dimensional convolution
    • 3-dimensional tensors
  • Max pooling
  • Case studies
✅
✅
✅
✅
✅

convolution

max pooling

slide w. stride

slide w. stride

1-dimensional pooling

no learnable parameter

filter weights are the learnable parameter

ReLU

2-dimensional max pooling (example)

[image edited from vdumoulin]

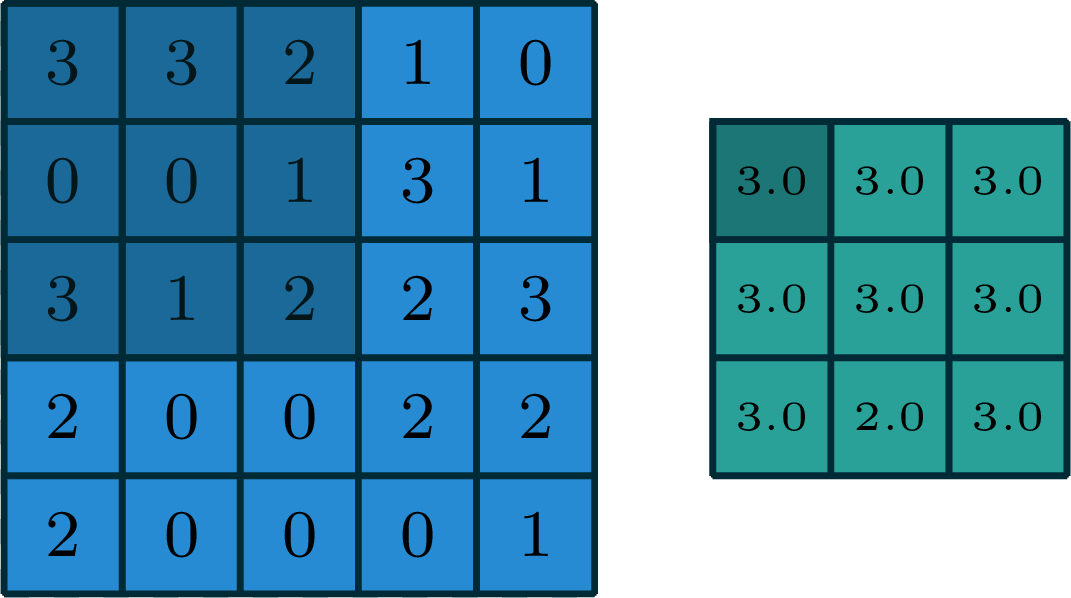
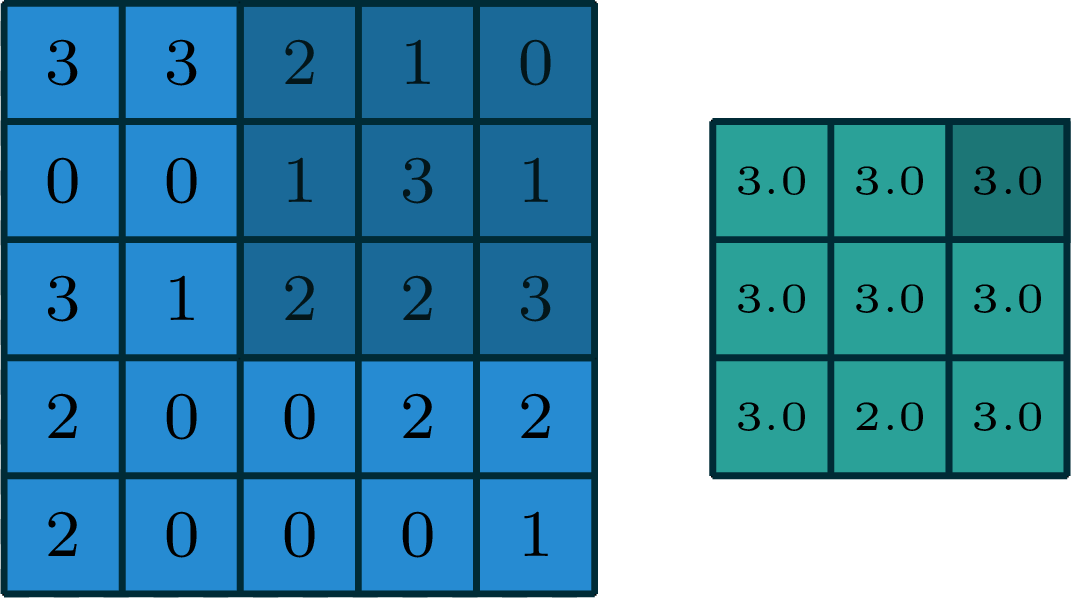
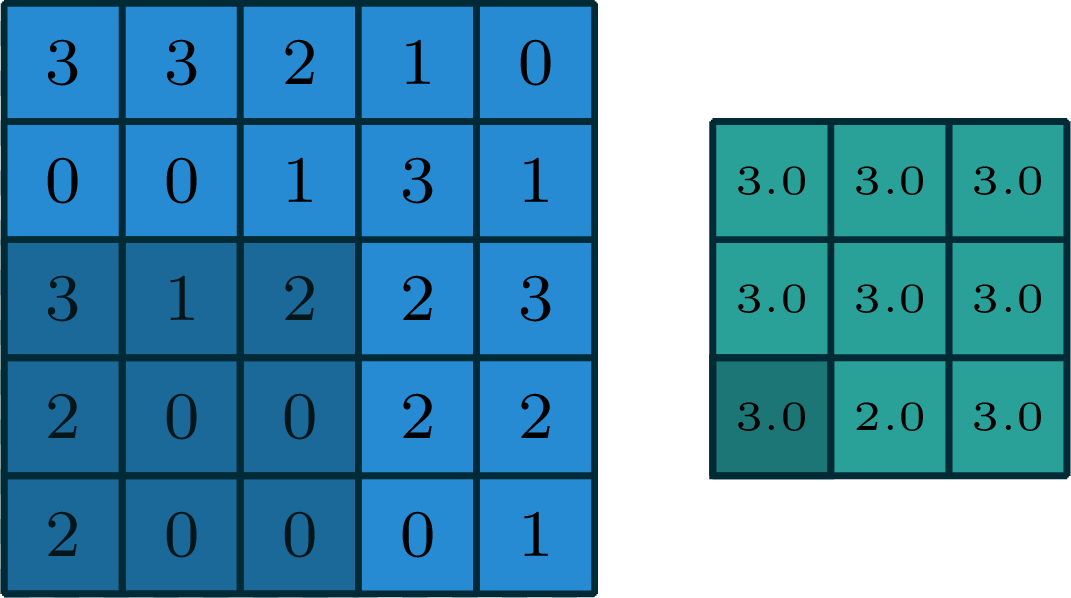
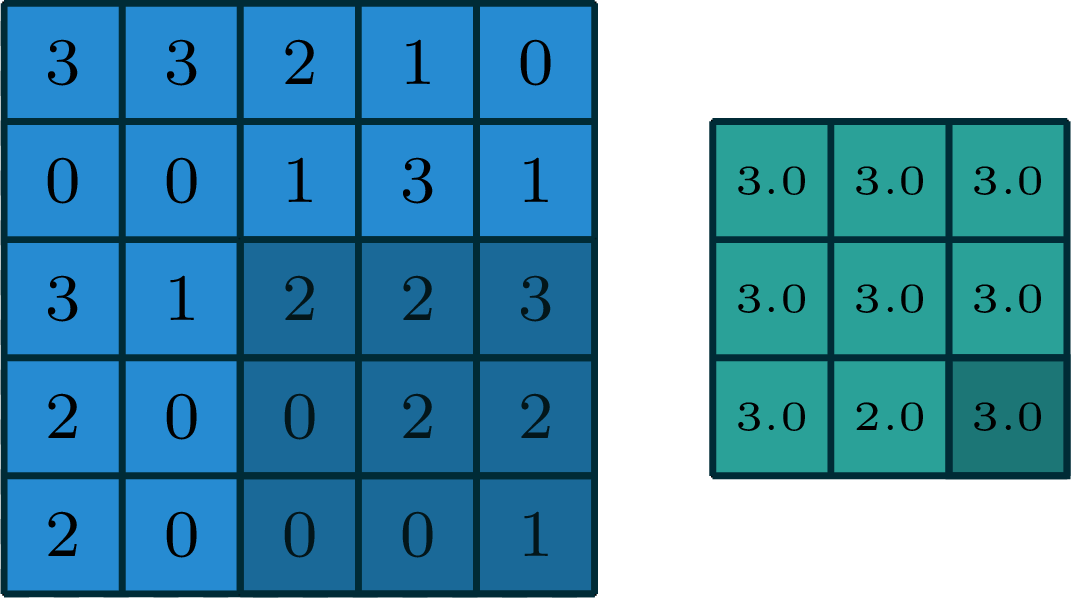
[gif adapted from demo source]

  • can choose filter size
  • typically choose to have no padding
  • typically a stride >1
  • reduces spatial dimension

2-dimensional max pooling (example)

Pooling across spatial locations achieves invariance w.r.t. small translations:

\Bigg\{ \begin{array}{l} \\ \\ \\ \\ \\ \end{array} \Bigg.
\Bigg\{ \begin{array}{l} \\ \\ \\ \\ \\ \end{array} \Bigg.
\{

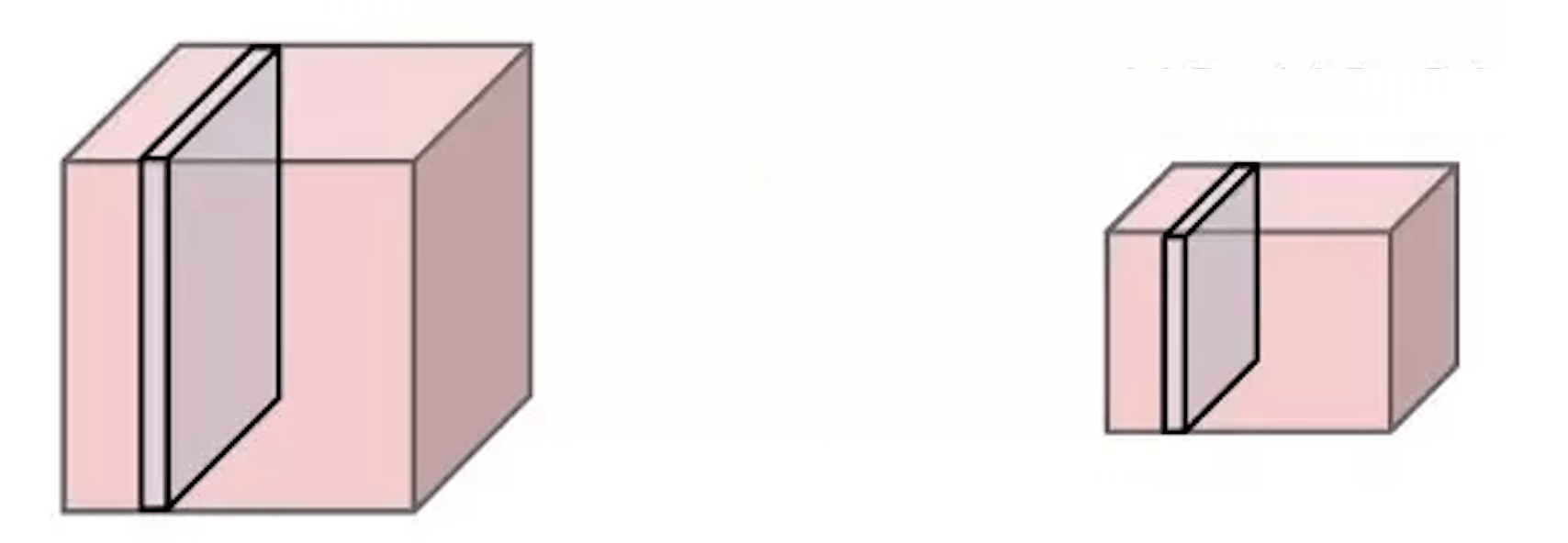
channel

channel

height

width

\{

width

height

\left\{ \begin{array}{l} \\ \\ \end{array} \right.
\Bigg\{ \begin{array}{l} \\ \\ \\ \\ \\ \end{array} \Bigg.

so the channel dimension remains unchanged after pooling.

pooling

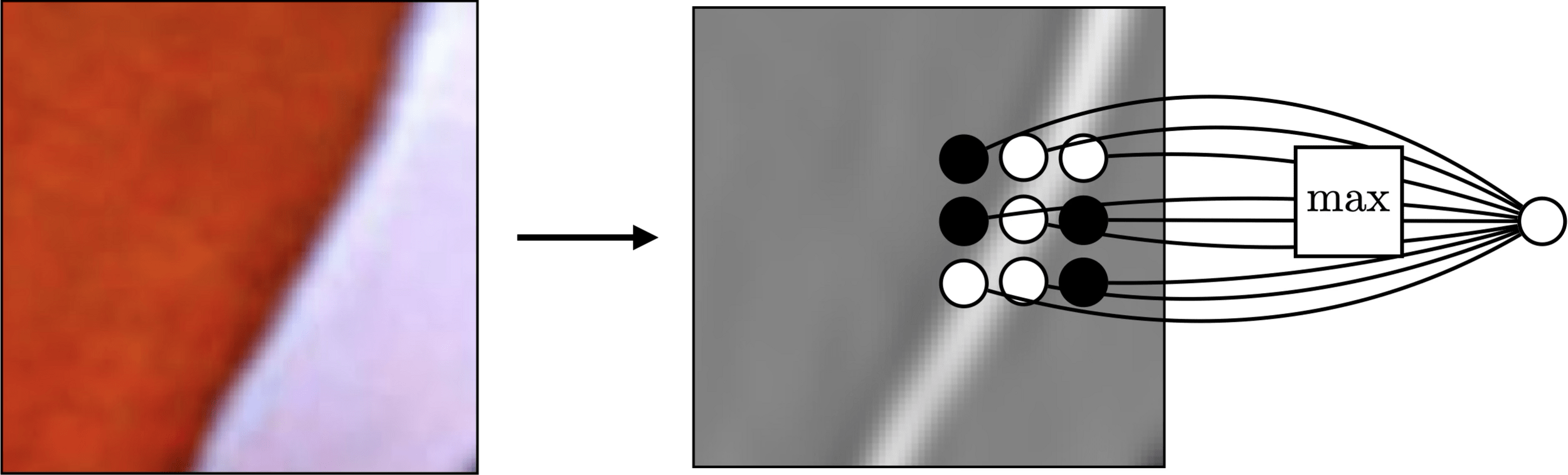
Pooling across spatial locations achieves invariance w.r.t. small translations:

[image credit Philip Isola]

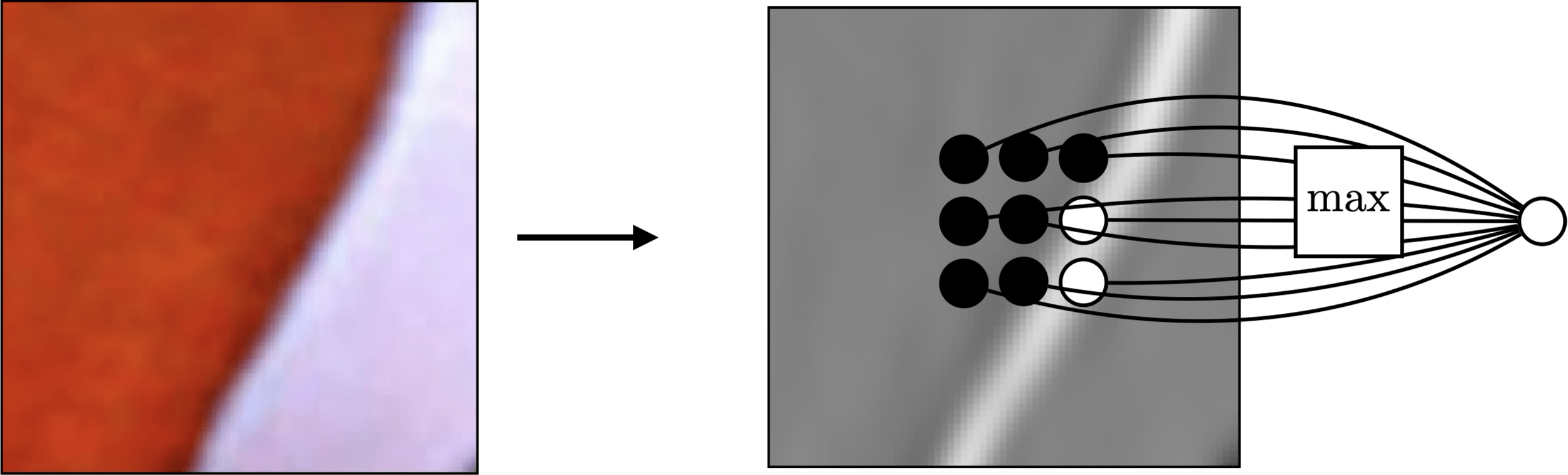
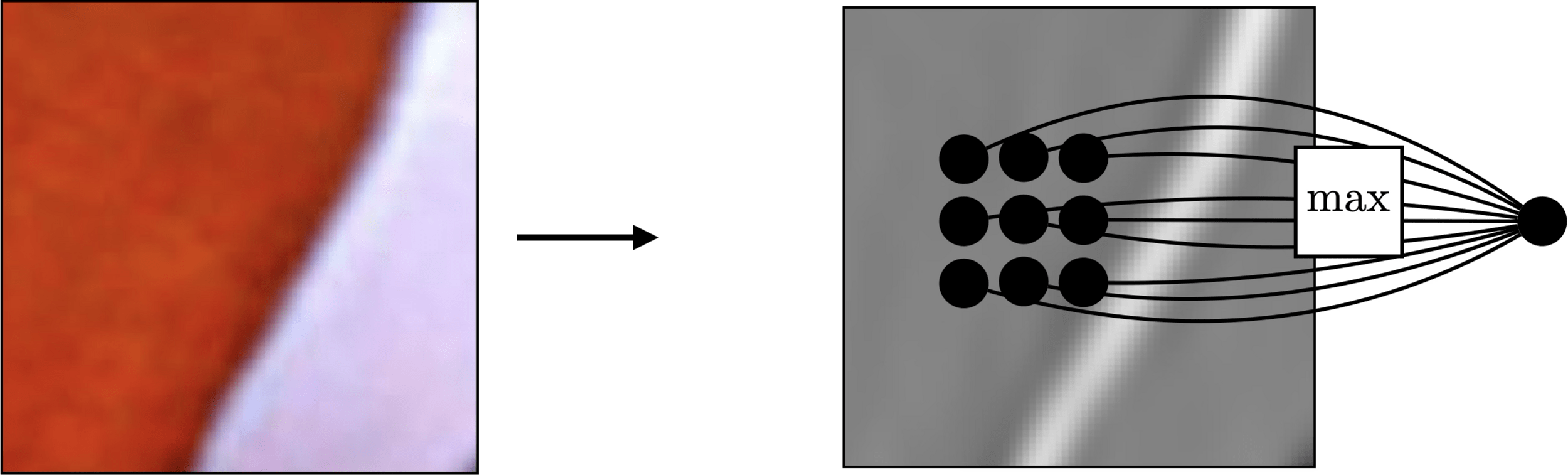
large response regardless of exact position of edge

Outline

  • Recap, fully-connected net
  • Vision problem structure
  • Convolutional network structure
  • Convolution
    • 1-dimensional and 2-dimensional convolution
    • 3-dimensional tensors
  • Max pooling
  • Case studies

[AlexNet paper]

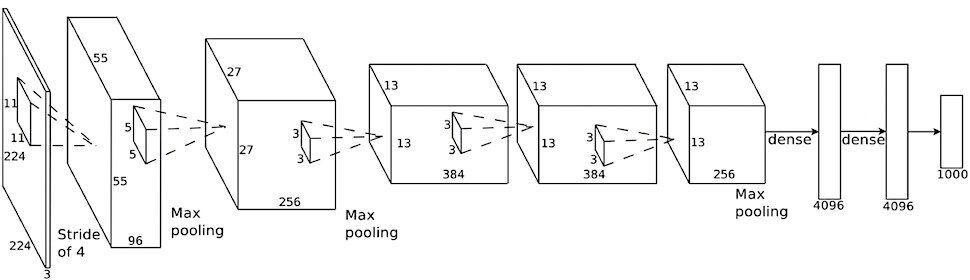
filter weights

fully-connected neuron weights

prediction, loss \(\mathcal{L}\)

\nabla \mathcal{L}

[image credit Philip Isola]

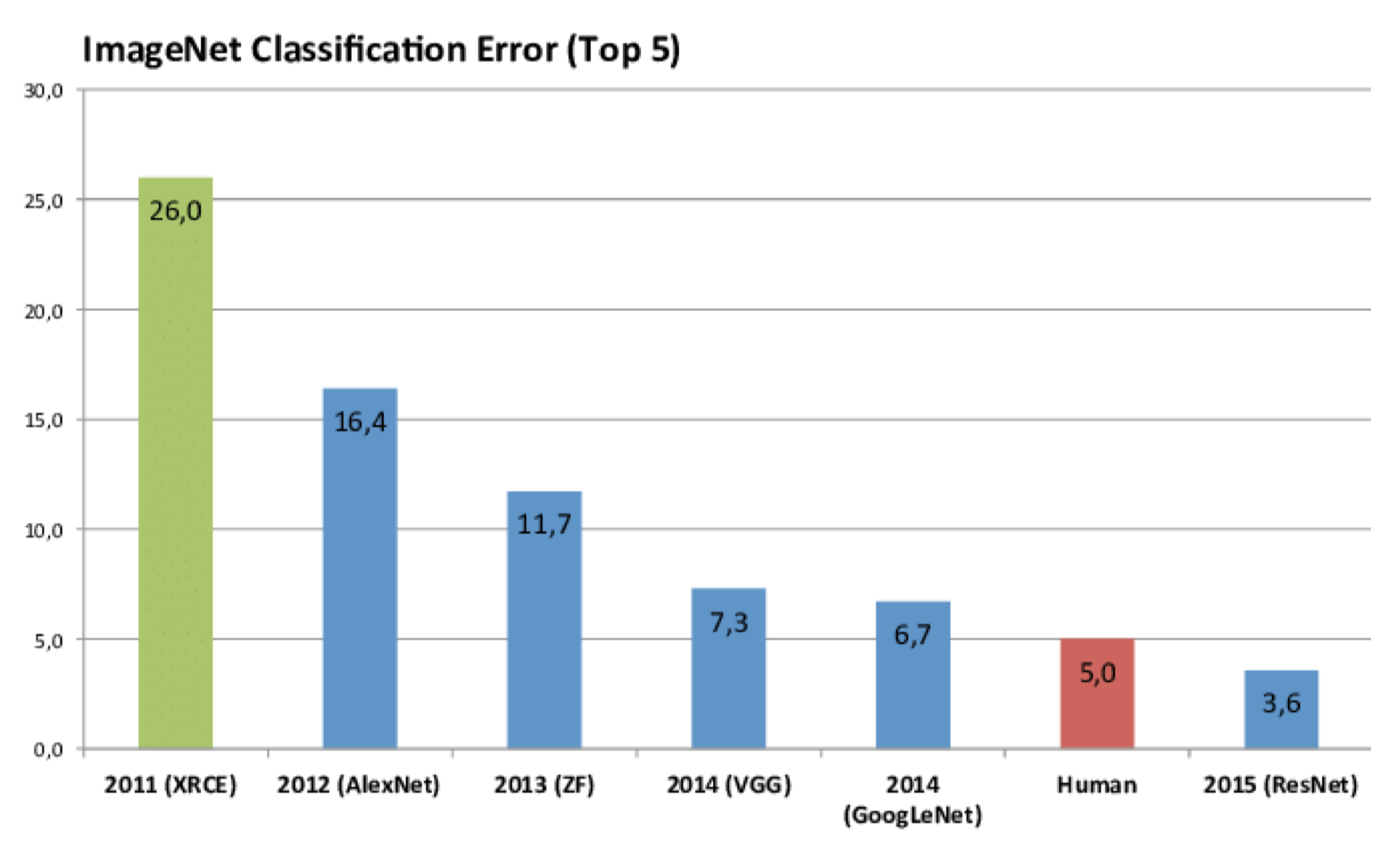
[image credit Philip Isola]

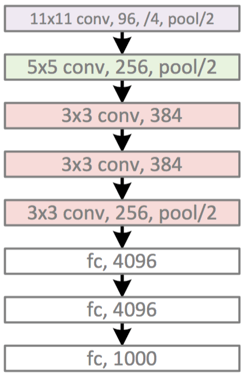
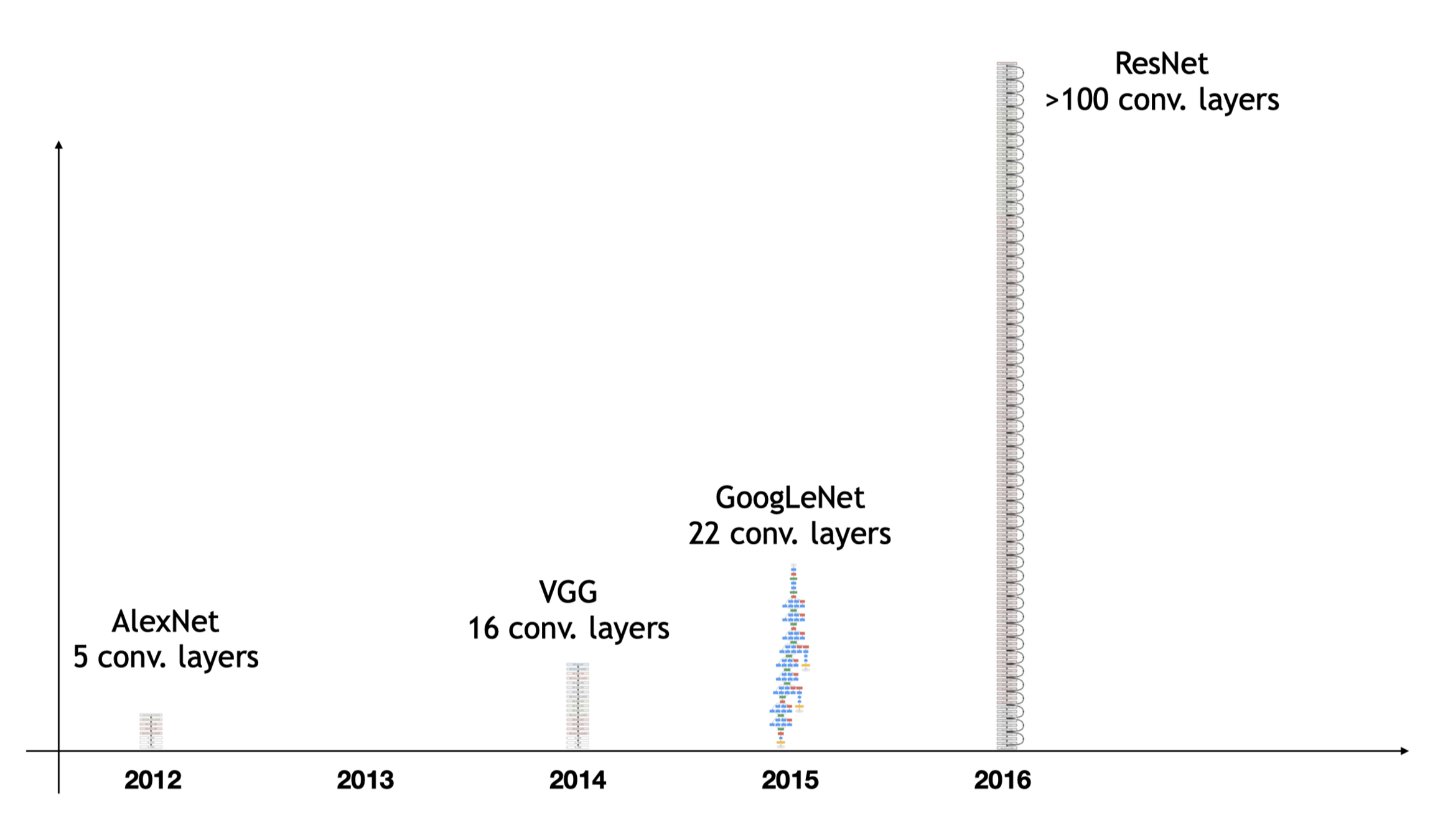
AlexNet '12

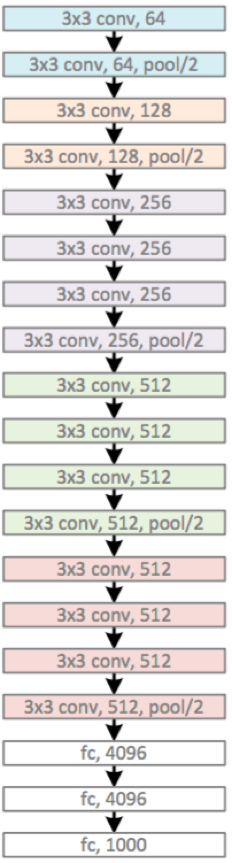
VGG '14

“Very Deep Convolutional Networks for Large-Scale Image Recognition”, Simonyan & Zisserman. ICLR 2015

[image credit Philip Isola and Kaiming He]

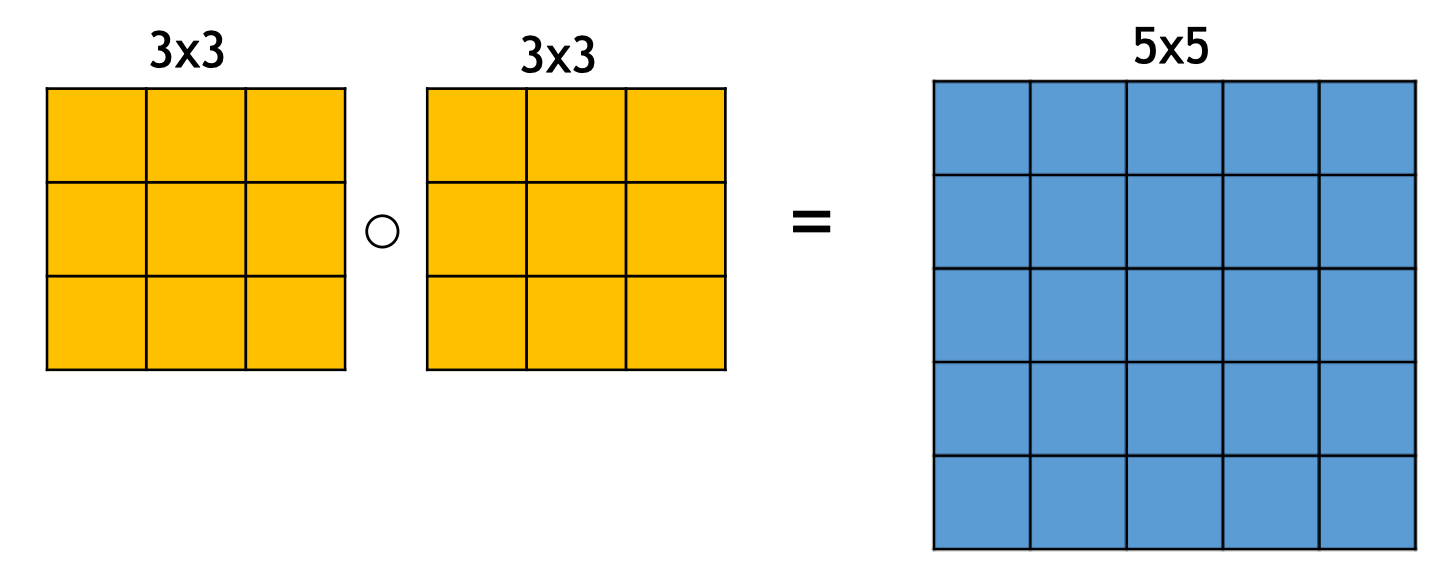
VGG '14

Main developments:

  • small convolutional kernels: only 3x3

 

 

 

 

 

 

 

  • increased depth: about 16 or 19 layers
  • stack the same modules

VGG '14

[He et al: Deep Residual Learning for Image Recognition, CVPR 2016]

[image credit Philip Isola and Kaiming He]

ResNet '16

 

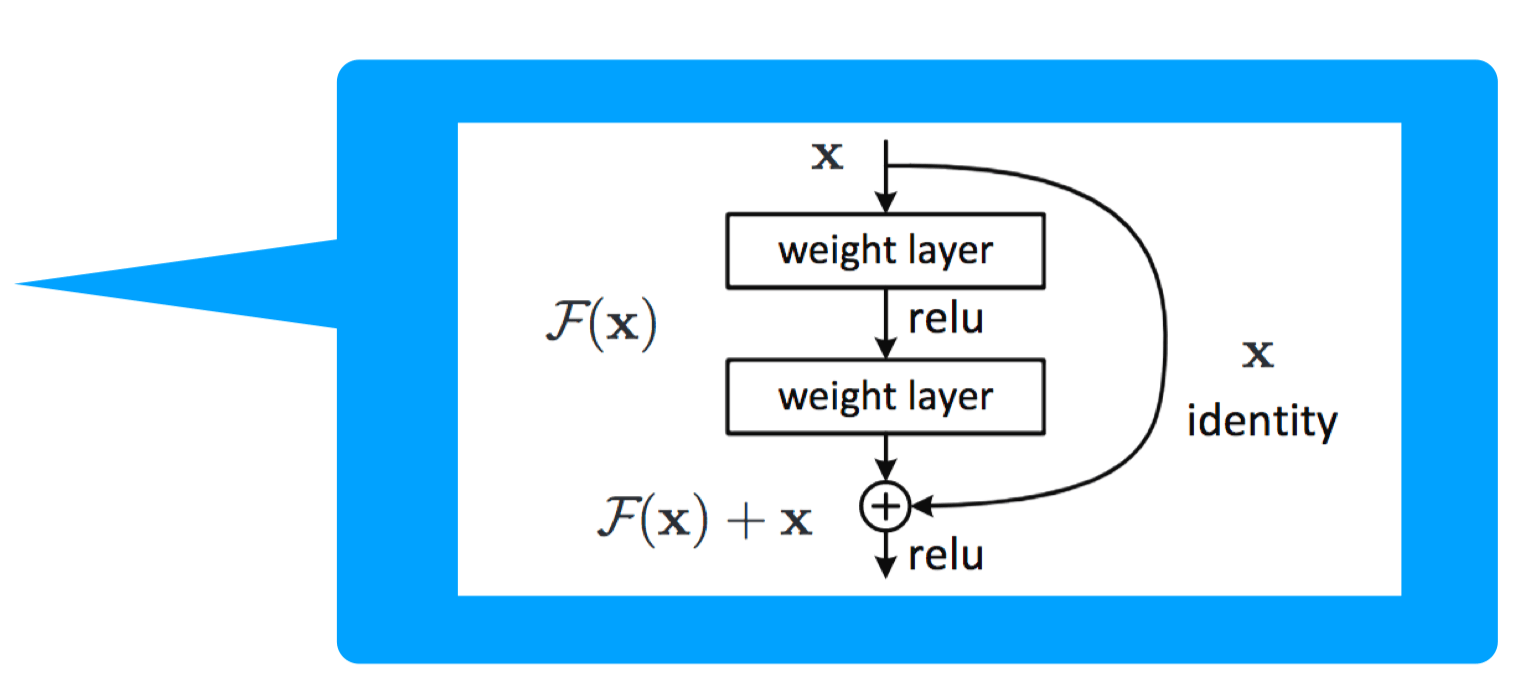
Main developments:

  • Residual block -- gradients can propagate faster (via the identity mapping)
  • increased depth: > 100 layers

Summary

  • Though NN are technically “universal approximators”, designing the NN structure so that it matches what we know about the underlying structure of the problem can substantially improve generalization ability and computational efficiency.
  • Images are a very important input type and they have important properties that we can take advantage of: visual hierarchy, translation invariance, spatial locality.
  • Convolution is an important image-processing technique that builds on these ideas. It can be interpreted as locally connected network, with weight-sharing.
  • Pooling layer helps aggregate local info effectively, achieving bigger receptive field.
  • We can train the parameters in a convolutional filtering function using backprop and combine convolutional filtering operations with other neural-network layers.

Thanks!

We'd love to hear your thoughts.