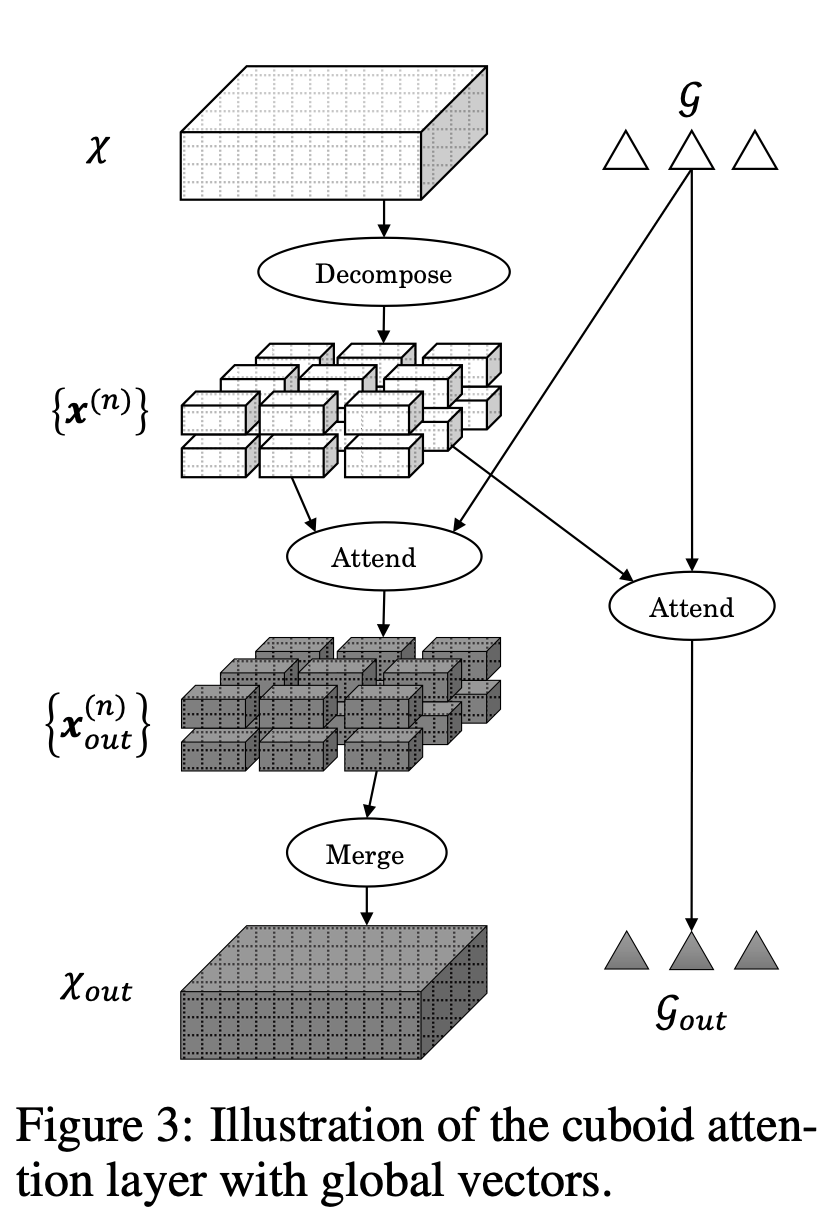
Lecture 9: Transformers
Intro to Machine Learning

Outline
- Transformers high-level intuition and architecture
- Attention mechanism
- Multi-head attention
- (Applications)
- Transformers high-level intuition and architecture
- Attention mechanism
- Multi-head attention
- (Applications)
[video edited from 3b1b]
Recap: Word embedding
this enables "soft" dictionary look-up:
dict_en2fr = {
"apple" : "pomme",
"banana": "banane",
"lemon" : "citron"}Good word-embeddings space is equipped with semantically meaningful vector arithmetic
Key
Value
apple
pomme
\(:\)
banane
banana
\(:\)
citron
lemon
\(:\)
dict_en2fr = {
"apple" : "pomme",
"banana": "banane",
"lemon" : "citron"}
query = "orange"
output = dict_en2fr[query]Python would complain. 🤯
orange
apple
pomme
banane
citron
banana
lemon
Key
Value
\(:\)
\(:\)
\(:\)
Query
Output
???
But we can probably see the rationale behind something like this:
Query
Key
Value
Output
orange
apple
\(:\)
pomme
banana
\(:\)
banane
lemon
\(:\)
citron
dict_en2fr = {
"apple" : "pomme",
"banana": "banane",
"lemon" : "citron"}
query = "orange"
output = dict_en2fr[query]0.1
pomme
0.1
banane
0.8
citron
+
+
0.1
pomme
0.1
banane
0.8
citron
+
+
via these mixing percentages [0.1 0.1 0.8] made sense
We put (query, key, value) in "good" embeddings in our human brain
such that mixing the values
Query
Key
Value
Output
orange
apple
\(:\)
pomme
0.1
pomme
0.1
banane
0.8
citron
banana
\(:\)
banane
lemon
\(:\)
citron
+
+
orange
orange
0.1
pomme
0.1
banane
0.8
citron
+
+
apple
banana
lemon
orange
0.8
0.1
0.1
pomme
banane
citron
+
+
very roughly, the attention mechanism in transformers automates this process.
apple
banana
lemon
orange
orange
orange
Query
Key
Value
Output
orange
apple
\(:\)
pomme
banana
\(:\)
banane
lemon
\(:\)
citron
orange
orange
pomme
banane
citron
0.1
pomme
0.1
banane
0.8
citron
+
+
0.1
pomme
0.1
banane
0.8
citron
+
+
dot-product similarity
softmax
0.1
0.1
0.8
a. compare query and key for merging percentages:
Query
Key
Value
Output
orange
apple
\(:\)
pomme
0.1
pomme
0.1
banane
0.8
citron
banana
\(:\)
banane
lemon
\(:\)
citron
+
+
orange
orange
pomme
banane
citron
+
+
0.8
0.1
0.1
pomme
banane
citron
+
+
b. then output mixed values
a. compare query and key for merging percentages:
Let's see how this intuition becomes a trainable mechanism.
apple
banana
lemon
orange
orange
orange
softmax
0.1
0.1
0.8
Outline
- Transformers high-level intuition and architecture
- Attention mechanism
- Multi-head attention
- (Applications)
- Transformers high-level intuition and architecture
- Attention mechanism
- Multi-head attention
- (Applications)
Large Language Models (LLMs) are trained in this self-supervised way

- Scrape the internet for plain texts.
- Cook up “labels” (prediction targets) from these texts.
- Convert “unsupervised” problem into “supervised” setup.
"To date, the cleverest thinker of all time was Issac. "
feature
label
To date, the
cleverest
To date, the cleverest
thinker
To date, the cleverest thinker
was
To date, the cleverest thinker of all time was
Issac
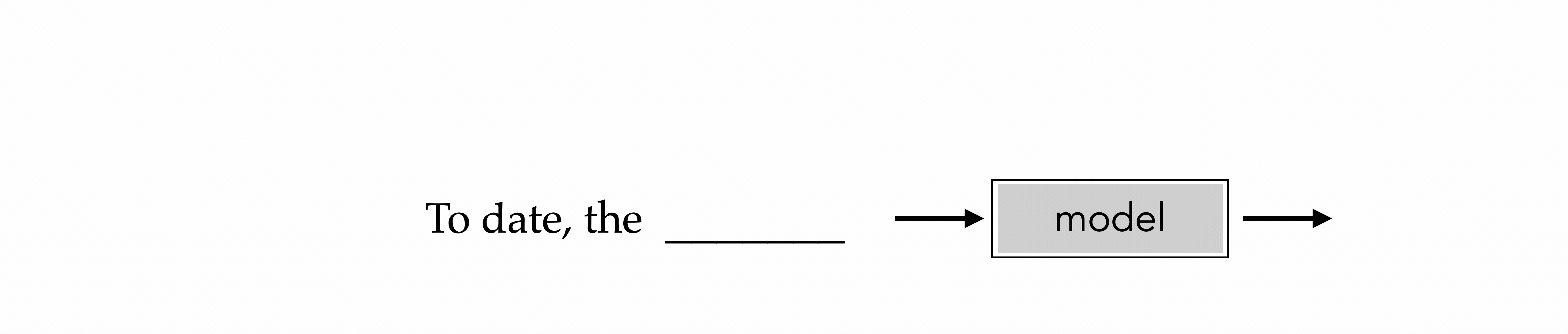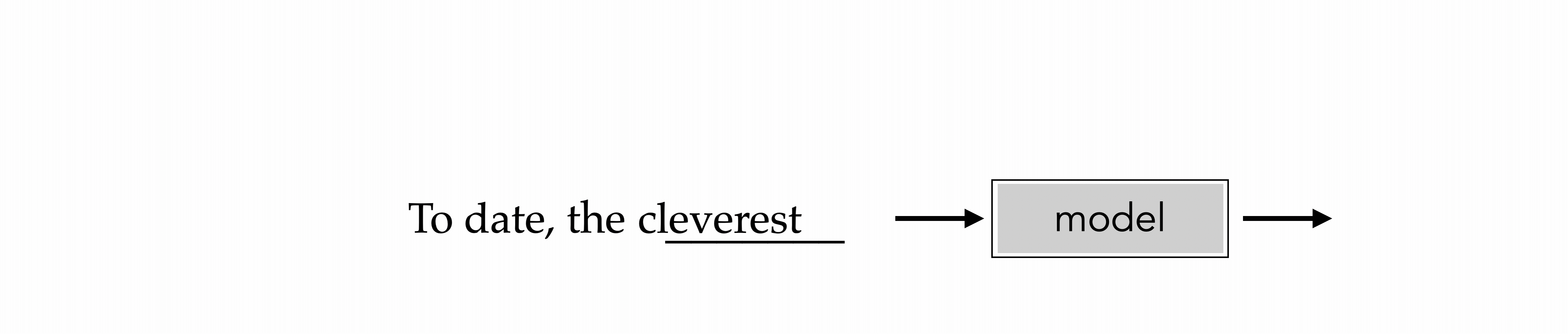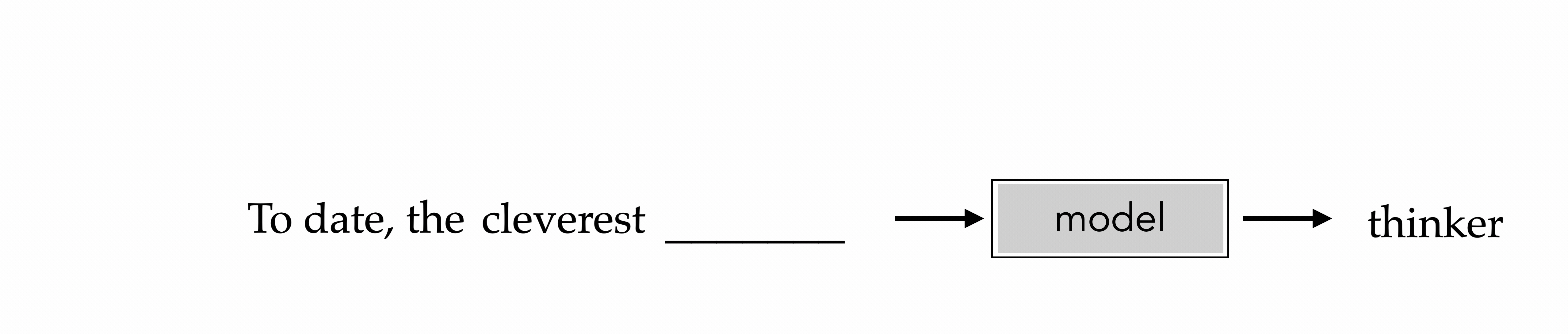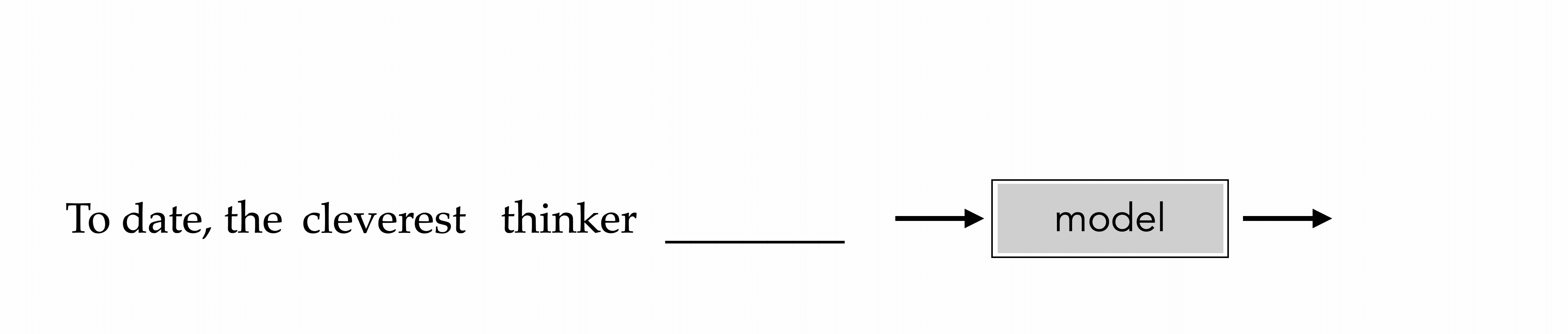
auto-regressive prediction
[video edited from 3b1b]
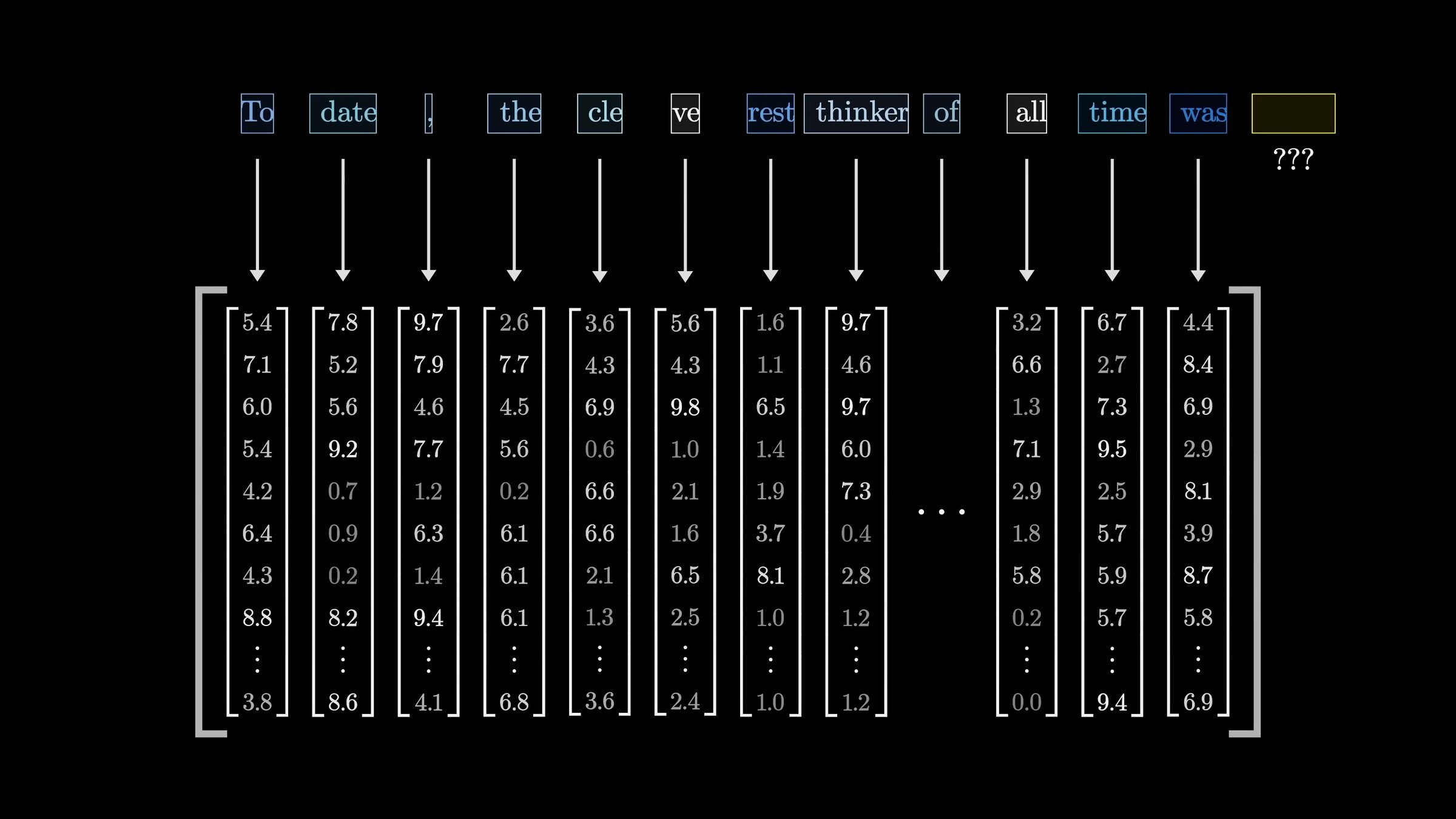
\(n\)
\(d\)
input embedding
[video edited from 3b1b]
[video edited from 3b1b]
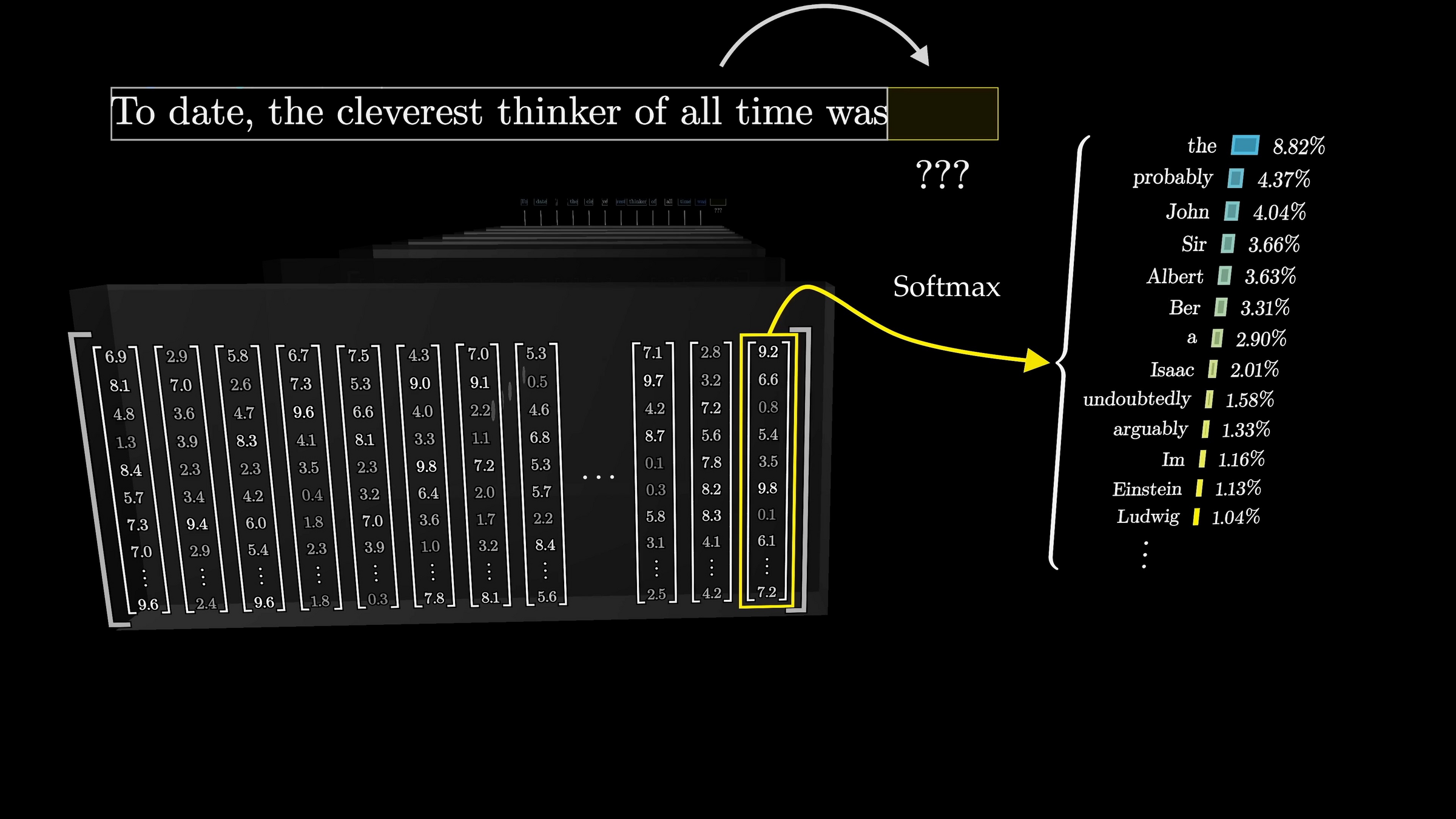
Cross-entropy loss encourages the internal weights update to push this probability higher
[video edited from 3b1b]
[video edited from 3b1b]
Transformer
"To date, the cleverest [thinker] of all time was Issac.
push for Prob("date") to be high
push for Prob("the") to be high
push for Prob("cleverest") to be high
push for Prob("thinker") to be high
distribution over the vocabulary
\(\dots\)
\(\dots\)
\(\dots\)
\(\dots\)
To
date
the
cleverest
input embedding
\(\dots\)
\(\dots\)
\(\dots\)
transformer block
transformer block
transformer block
\(L\) blocks
\(\dots\)
\(\dots\)
output embedding
To
date
the
cleverest
\(\dots\)
transformer block
transformer block
transformer block
A sequence of \(n\) tokens, each token in \(\mathbb{R}^{d}\)
\(\dots\)
\(\dots\)
\(\dots\)
\(\dots\)
output embedding
input embedding
input embedding
To
date
the
cleverest
input embedding
\(\dots\)
transformer block
output embedding
\(\dots\)
\(\dots\)
\(\dots\)
\(\dots\)
transformer block
transformer block
each of the \(n\) tokens transformed, block by block
within a shared \(d\)-dimensional word-embedding space.
To
date
the
cleverest
attention layer
MLP
\(\dots\)
\(\dots\)
\(\dots\)
\(\dots\)
neuron weights
input embedding
transformer block
output embedding
To
date
the
cleverest
attention layer
output projection
\((qkv)\) projection
attention mechanism
Most important bits in an attention layer:
- (query, key, value) projection
- attention mechanism
Why learning these projections:
- \(W_q\) learns how to ask
- \(W_k\) learns how to listen
- \(W_v\) learns how to speak
With learned projections, we frame \(x\) into:
- a query to be the questions
- a key to be compared
- a value to contribute
1. (query, key, value) projection
- \(W_q, W_k, W_v\), all in \(\mathbb{R}^{d \times d_k}\)
- project the \(d\)-dimensional word-embedding space to \(d_k\)-dimensional (\(qkv\)) space (typically \(d_k < d\))
- the query \(q_i = W_q^Tx_i, \forall i;\) similar weight sharing for keys and values
- parallel and structurally identical processing
1. (query, key, value) projection
To
date
the
cleverest
- Attention mechanism turns the projected \((q,k,v)\) into \(z\)
- Each \(z\) is context-aware: a mixture of everyone's values, weighted by relevance
2. Attention mechanism
attention mechanism
To
date
the
cleverest
Outline
- Transformers high-level intuition and architecture
- Attention mechanism
- Multi-head attention
- (Applications)
attention mechanism
To
date
the
cleverest
softmax
To
date
the
cleverest
softmax
To
date
the
cleverest
attention mechanism
To
date
the
cleverest
softmax
To
date
the
cleverest
softmax
To
date
the
cleverest
attention mechanism
To
date
the
cleverest
softmax
parallel and structurally identical processing
can calculate \(z_4\) without \(z_3\)
To
date
the
cleverest
softmax
To
date
the
cleverest
attention mechanism
To
date
the
cleverest
softmax
To
date
the
cleverest
softmax
To
date
the
cleverest
attention mechanism
Attention head
maps sequence of \(x\) to sequence of \(z\):
1. (query, key, value) projection
2. attention mechanism
parallel and structurally identical processing
attention mechanism
\((qkv)\) proj.
By stacking each individual vector in the sequence as a row
Attention head - compact matrix form
To
date
the
cleverest
input embedding
output embedding
\(\dots\)
transformer block
transformer block
transformer block
A sequence of \(n\) tokens, each token in \(\mathbb{R}^{d}\)
\(\dots\)
\(\dots\)
\(\dots\)
\(\dots\)
Stack each token as a row in the input
1. (query, key, value) projection
2a. dot-product similarity
compare \(q_i\) and \(k_j\)
assemble the \(n \times n\) similarities so rows correspond to query
2a. dot-product similarity
2a. dot-product similarity
2a. dot-product similarity
each row sums up to 1
softmax
softmax
softmax
softmax
softmax
row
\(A\)
2b. attention matrix
2c. attention-weighted values \(Z\)
softmax
row
attention mechanism
attention mechanism
attention mechanism
attention mechanism
attention mechanism
attention mechanism
Outline
- Transformers high-level intuition and architecture
- Attention mechanism
- Multi-head attention
- (Applications)
attention mechanism
attention mechanism
attention mechanism
attention mechanism
attention mechanism
attention mechanism
attention mechanism
attention mechanism
attention mechanism
attention mechanism
attention mechanism
attention mechanism
attention mechanism
In particular, each head:
- learns its own set of \(W_q, W_k, W_v\)
- creates its own projected sequence of \((q,k,v)\)
- computes its own sequence of \(z\)
- structurally identical processing
- for each token in the sequence:
- structurally identical processing
Parallel, and structurally identical processing across all heads and tokens.
Multi-head Attention
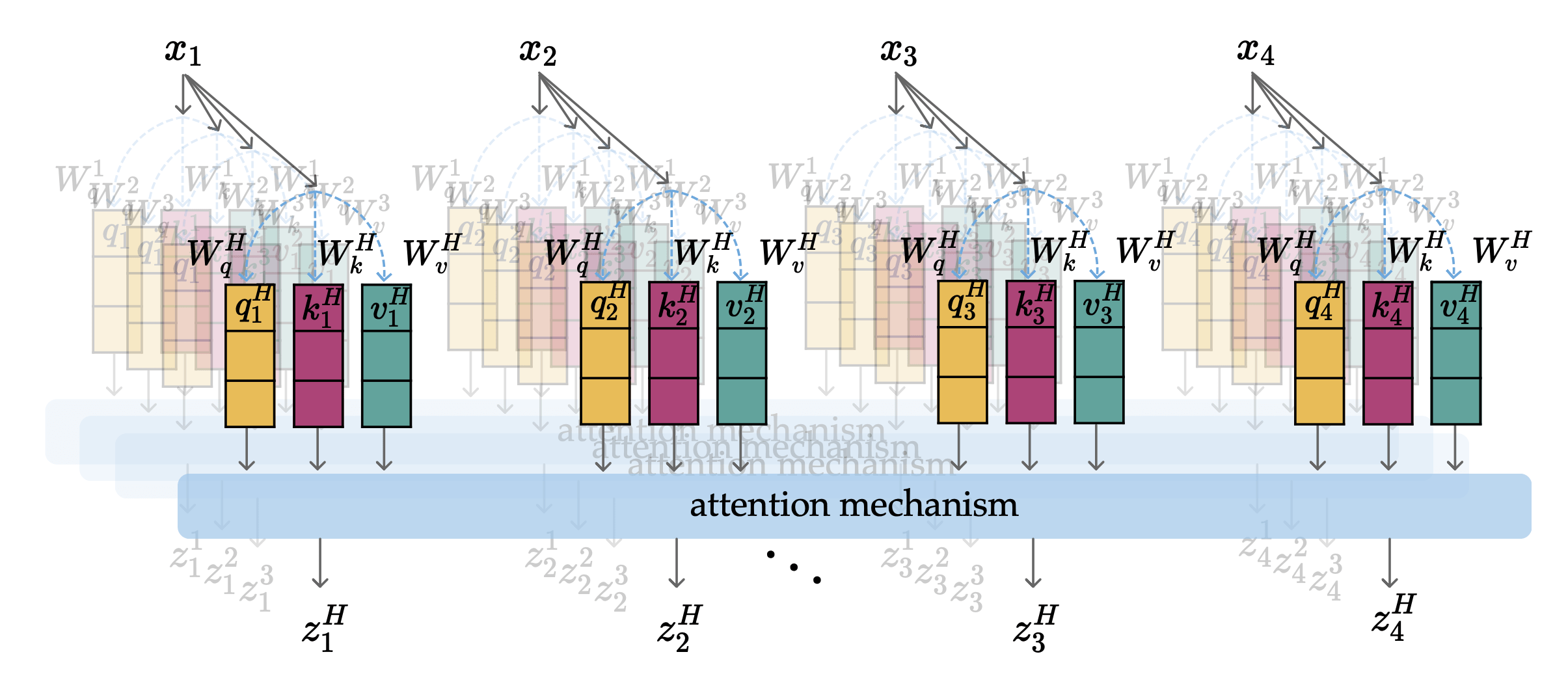
index along heads
index along sequence
attention mechanism
attention mechanism
attention mechanism
attention mechanism
multi-head attention
each concatenated \(z_i \in \mathbb{R}^{Hd_k}\)
concatenated \(z_1\)
concatenated \(z_2\)
concatenated \(z_3\)
concatenated \(z_4\)
attention mechanism
attention mechanism
attention mechanism
attention mechanism
multi-head attention
attention output projection
attention mechanism
attention mechanism
attention mechanism
attention mechanism
attention layer
all in \(\mathbb{R}^{d}\)
attention output projection
Shape Example
| num tokens | 2 | |
| input token dim | 4 | |
| embedding dim | 3 | |
| num heads | 5 |
$$n$$
$$d$$
$$d_k$$
$$H$$
learned
$$(qkv)$$
| query proj | |||
| key proj | |||
| value proj | |||
| output proj | |||
| input | |||
| query | |||
| key | |||
| value | |||
| attn matrix | |||
| attn head out | |||
| multi-head out | |||
| attn layer out |
$$W_q^h$$
$$W_k^h$$
$$W_v^h$$
$$W^o$$
$$Q^h$$
$$K^h$$
$$V^h$$
$$A^h$$
$$Z^h$$
$$d \times d_k$$
$$Hd_k\times d$$
$$n \times d$$
$$n \times d_k$$
$$n \times d_k$$
$$n \times d_k$$
$$n \times n$$
$$n \times d_k$$
$$n \times d$$
$$4 \times 3$$
$$15 \times 4$$
$$2 \times 4$$
$$2 \times 3$$
$$2 \times 3$$
$$2 \times 3$$
$$2 \times 2$$
$$2 \times 3$$
$$2 \times 4$$
$$d \times d_k$$
$$4 \times 3$$
$$d \times d_k$$
$$4 \times 3$$
$$X$$
$$Z_{\text{out}}$$
for a single attention head
$$\text {concat}(Z^1 \dots Z^H)$$
$$n \times Hd_k$$
$$2 \times 15$$
Some practical techniques commonly needed when training auto-regressive transformers:


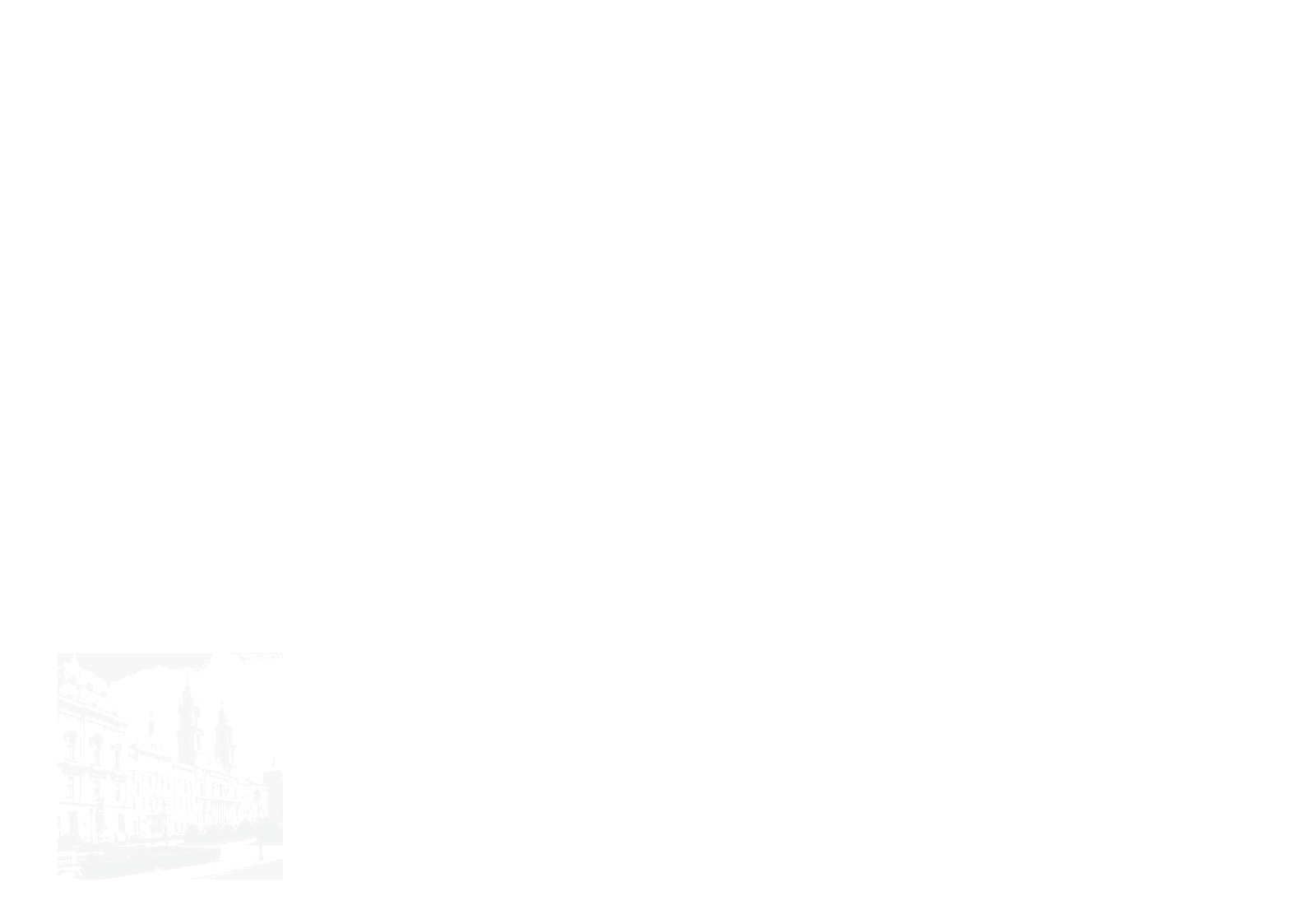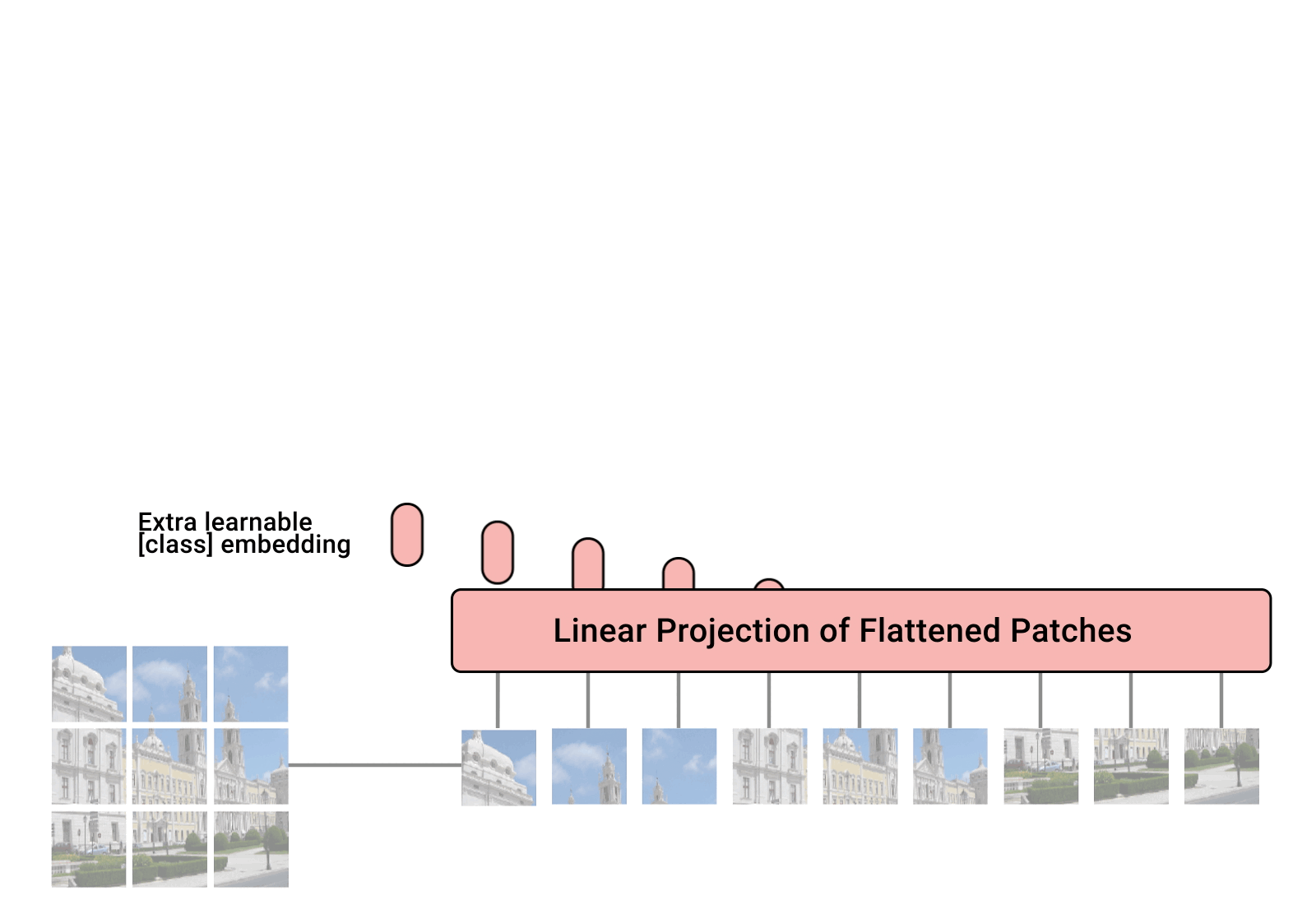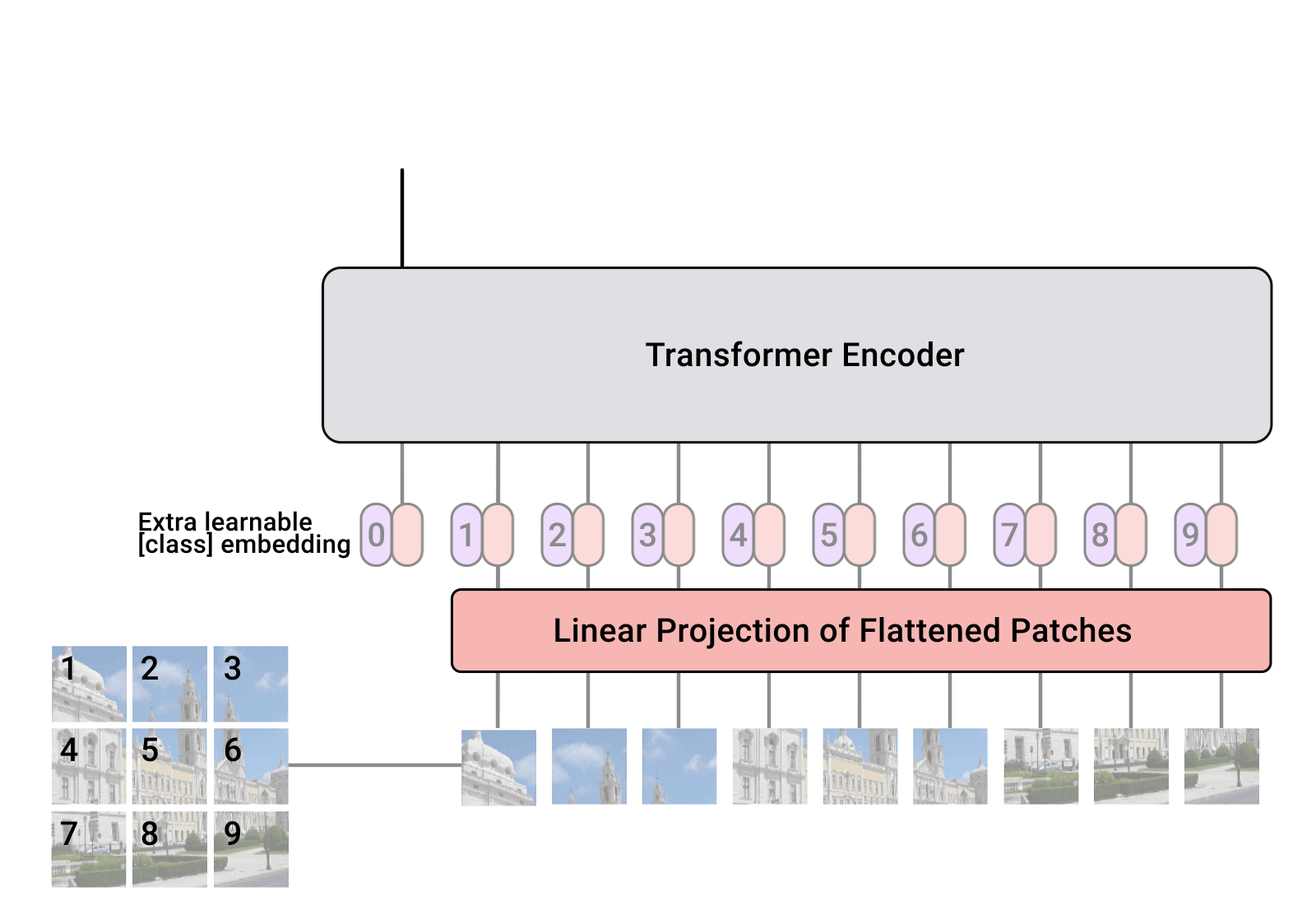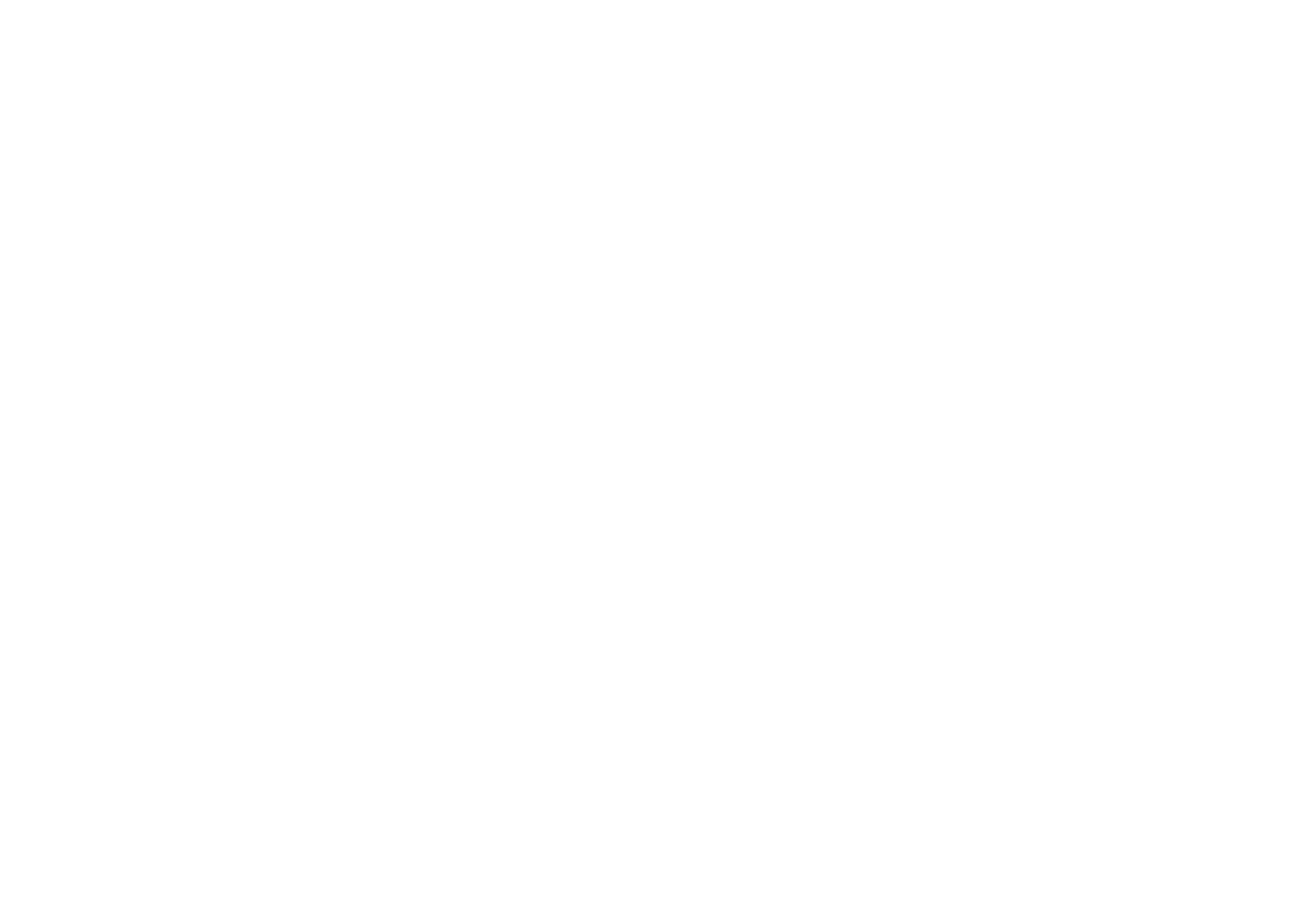
masking
Layer normlization
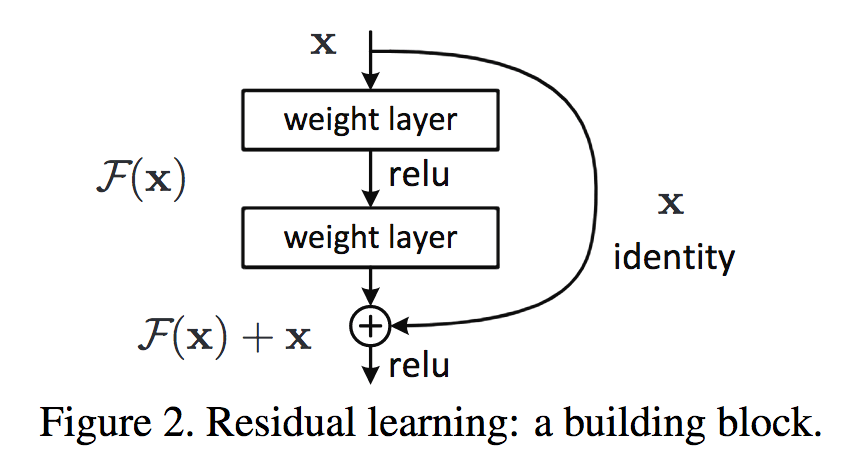
Residual connection
Positional encoding
Outline
- Transformers high-level intuition and architecture
- Attention mechanism
- Multi-head attention
- (Applications)
image credit: Nicholas Pfaff

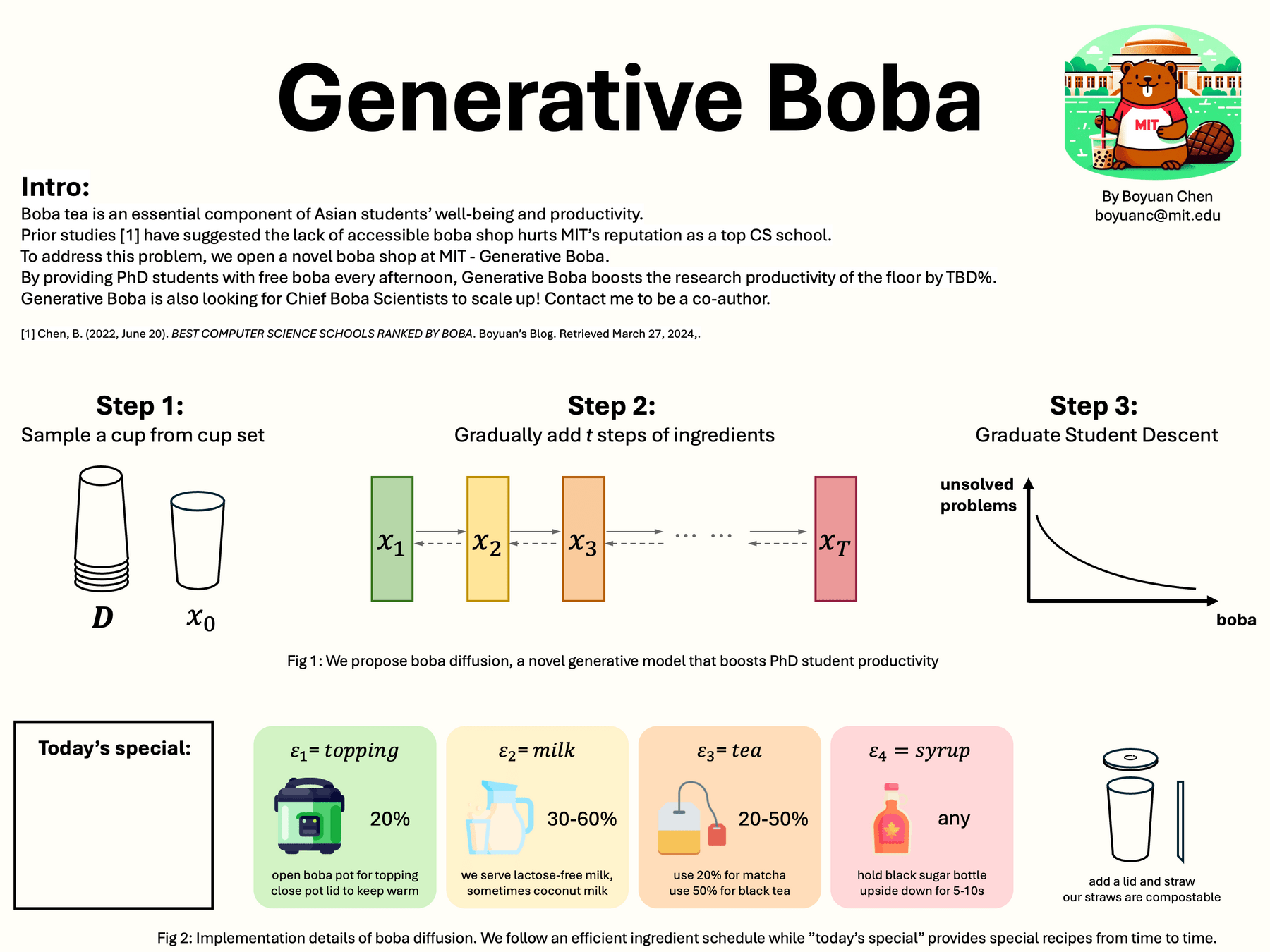
Generative Boba by Boyuan Chen in Bldg 45
😉
😉
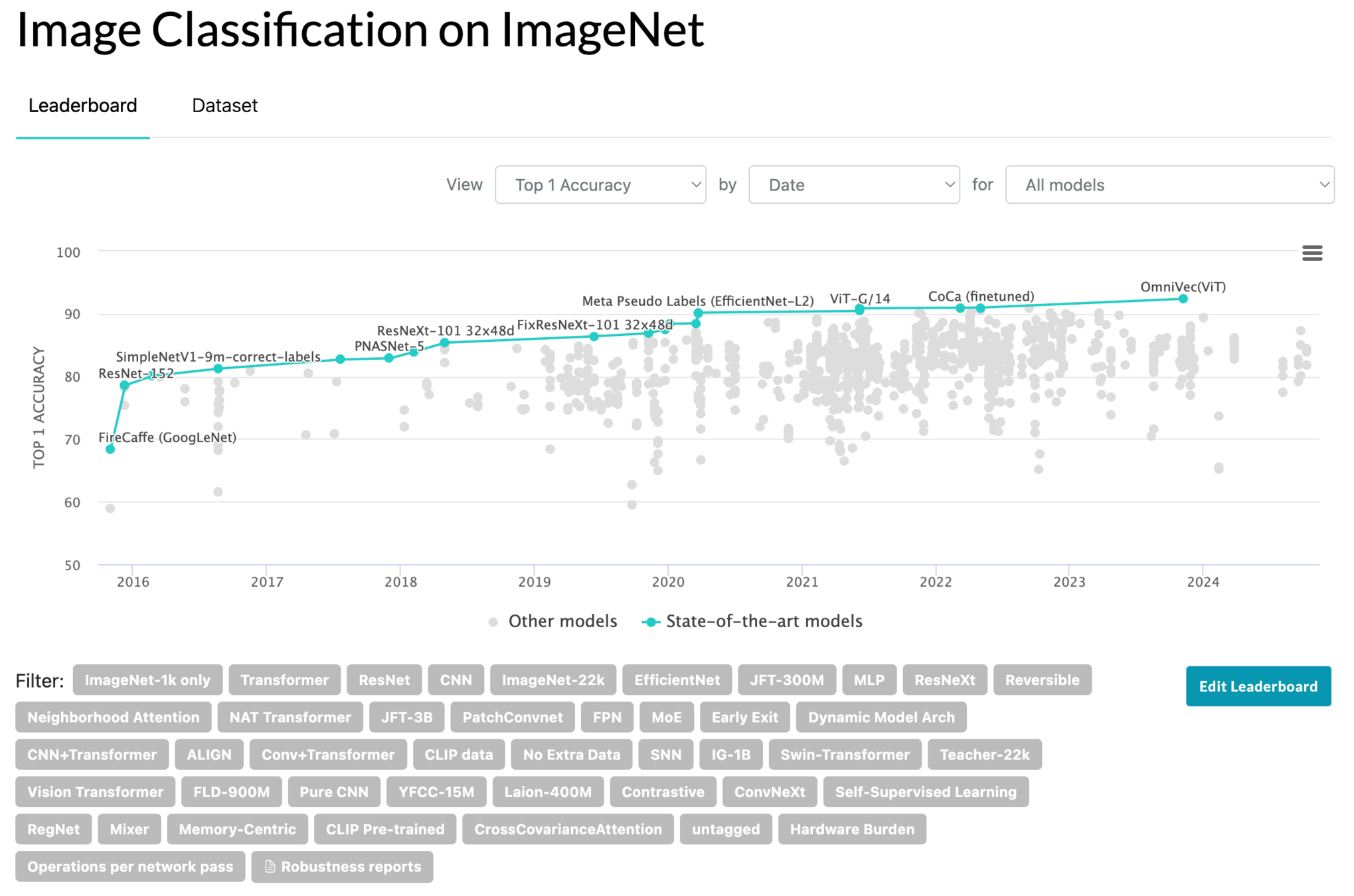
Transformers in Action: Performance across domains
Transformers in Action: Performance across domains
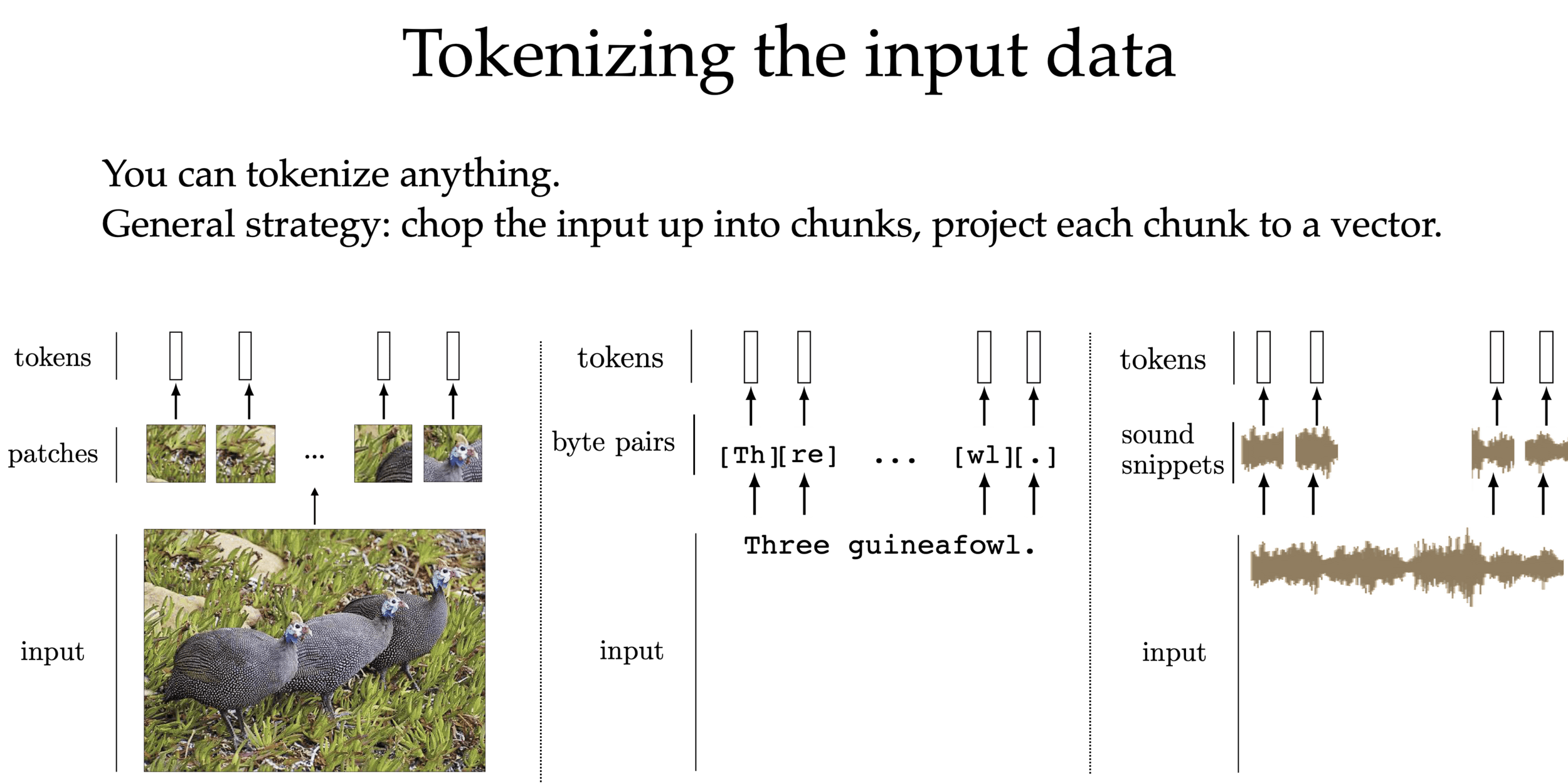
We can tokenize anything.
General strategy: chop the input up into chunks, project each chunk to an embedding
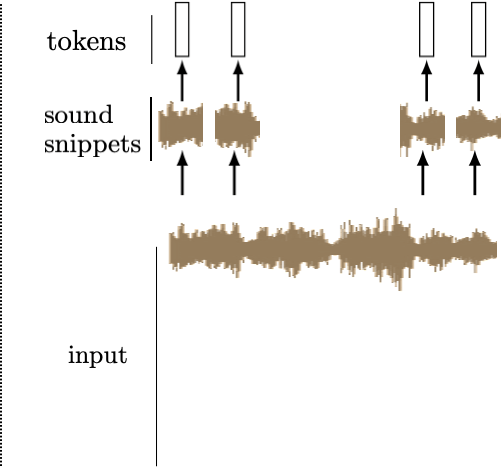
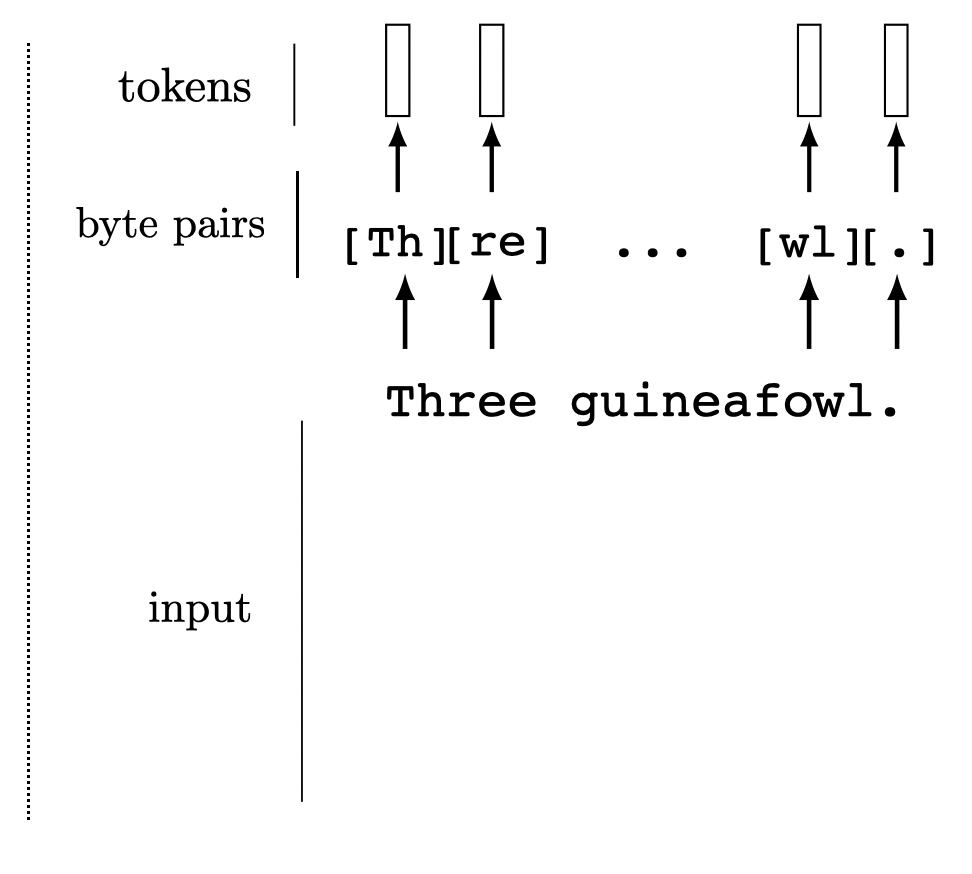
[images credit: visionbook.mit.edu]
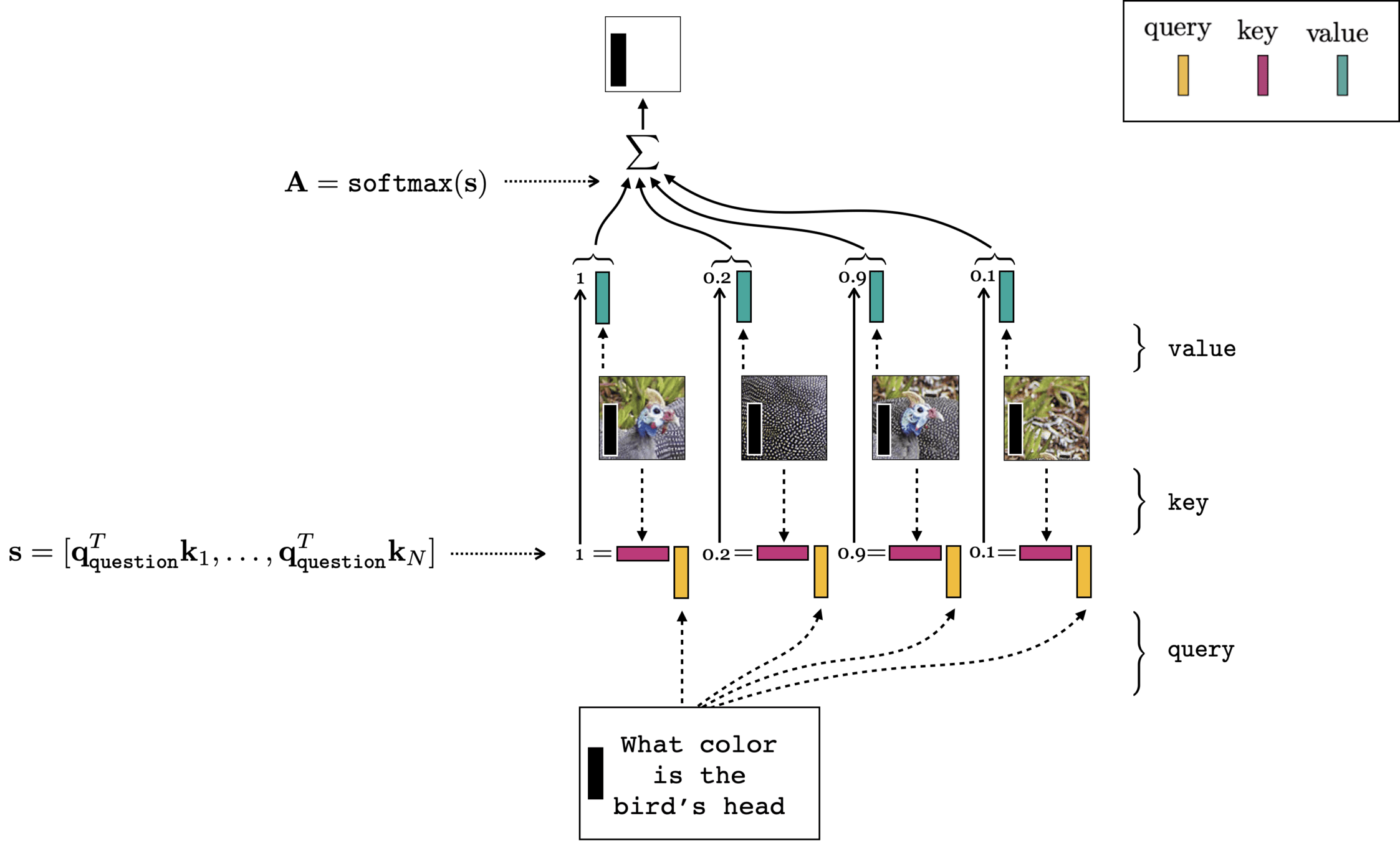
Multi-modality (image q&a)
- (query, key, value) come from different input modality
- cross-attention
[images credit: visionbook.mit.edu]

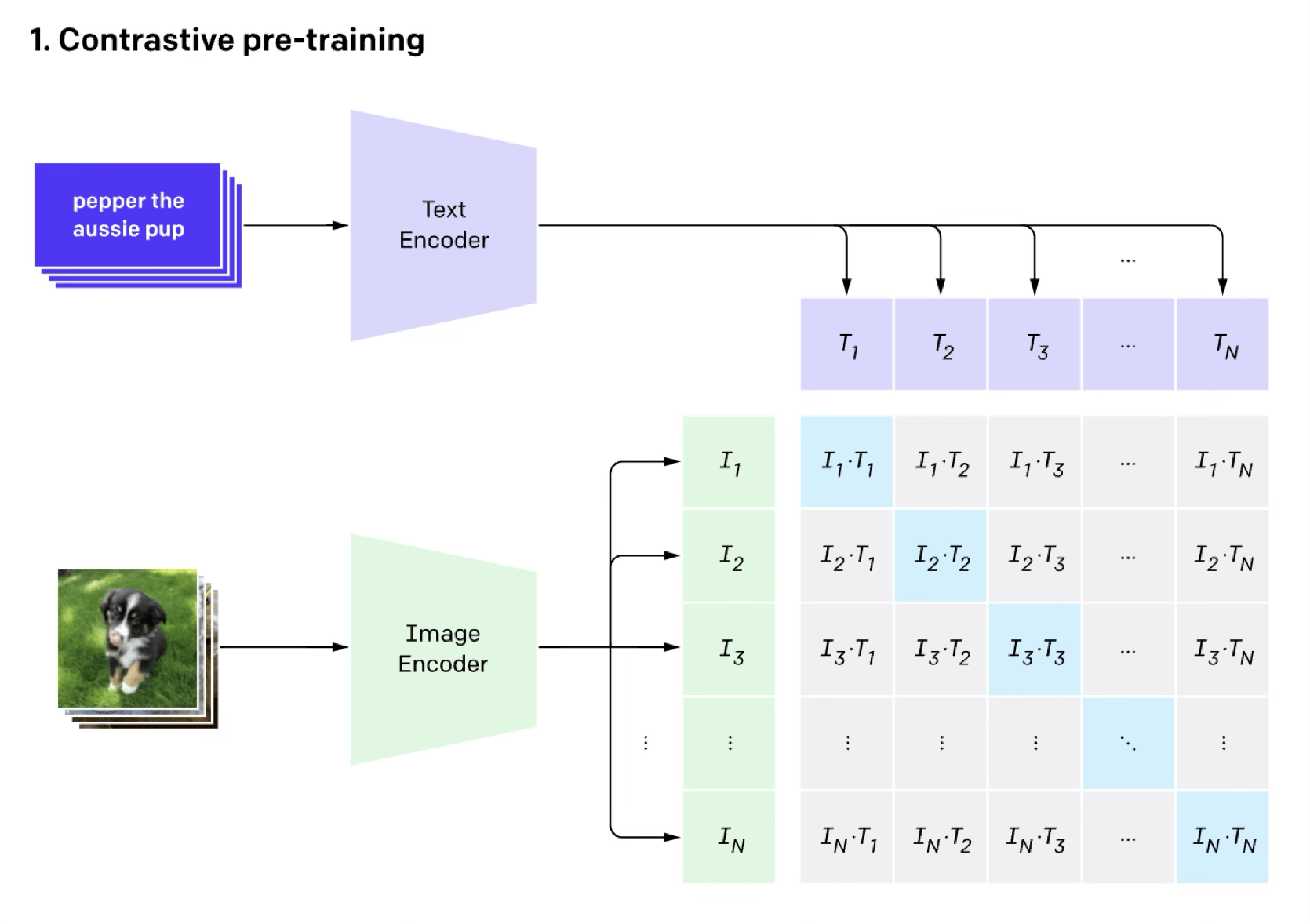
image classification (done in the contrastive way)
[Radford et al, Learning Transferable Visual Models From Natural Language Supervision, ICML, 2011]

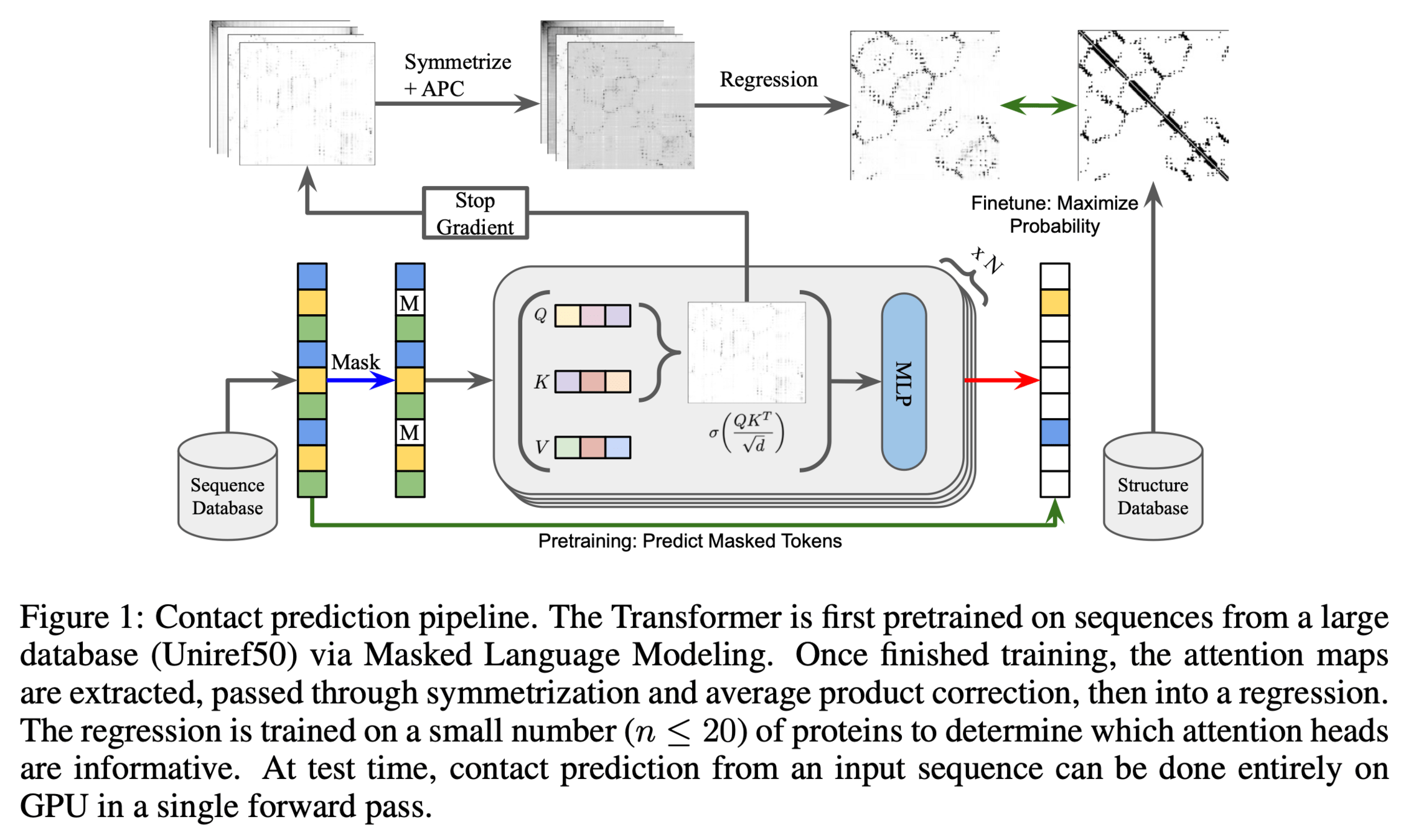





[“DINO”, Caron et all. 2021]
Success mode:
Success mode:
[Show, Attend and Tell: Neural Image Caption Generation with Visual Attention. Xu et al. CVPR (2016)]

Failure mode:

[Show, Attend and Tell: Neural Image Caption Generation with Visual Attention. Xu et al. CVPR (2016)]


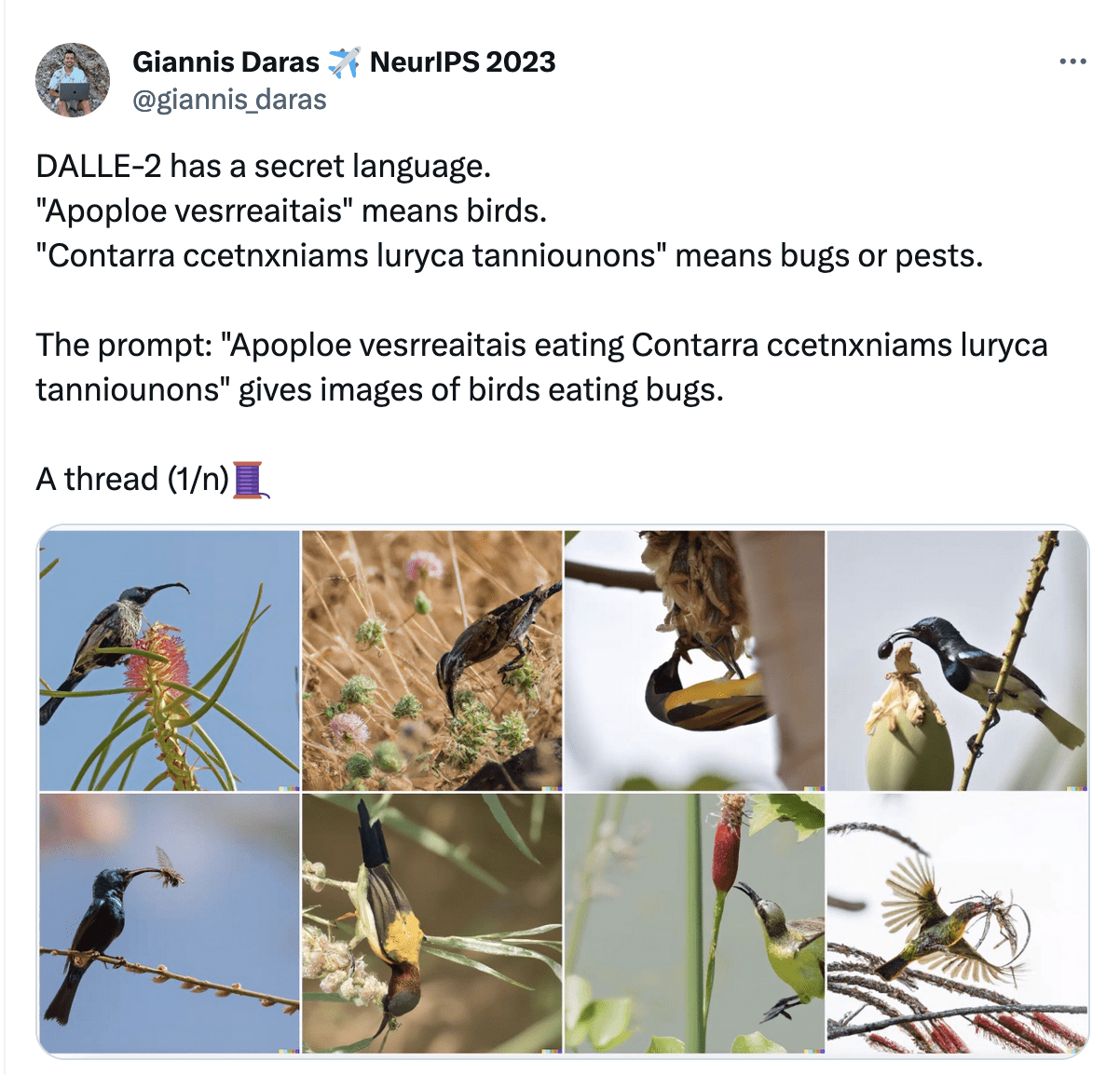
Success or Failure? mode:
Summary
- Transformers combine many of the best ideas from earlier architectures—patch-wise parallel processing (like convolution), relu nonlinearities, residual connections —with several new innovations, in particular, embedding and attention layers.
- Transformers start with some generic hard-coded embeddings, and block-by-block, creates better and better embeddings.
- Parallel processing everything in attention:
- each head is processed in parallel
- within each head, the \(q,k,v\) token sequence is created in parallel
- the attention scores are computed in parallel
- the attention output is computed in parallel.
Thanks!
for your attention!