

Lecture 10: Non-parametric Models
Intro to Machine Learning

Outline
- Non-parametric models overview
- Supervised learning non-parametric
- \(k\)-nearest neighbor
- Decision Tree
- Unsupervised learning non-parametric
- \(k\)-means clustering
Neural networks reason over billions of parameters, have incredible predictive power
Yet in many situations, we may not want to immediately fully commit to deep learning

A look at Mathurin's toolkit, which he keeps coming back to:
- Packages: scikit learn, pandas, numpy
- Frameworks: Keras, Tensorflow, Pytorch and Fastai
- Algorithms: lightgbm, xgboost, catboost
- AutoML tools: Prevision.io, h2o and other open sources such as TPOT, auto sklearn
- Cloud services: Google colab and kaggle kernels
"The choices were made to simplify the exposition and implementation: methods need to be transparent to be adopted as part of the election process and to inspire public confidence. [An alternative] might be more efficient, but because of its complexity would likely meet resistance from elections officials and voting rights groups." —Philip Stark, 2008


There’s more to machine learning than predictive power
- Interpretability — understanding why a model makes a decision.
- Adaptivity — updating to new data without retraining from scratch.
- Transparency & trust — explaining results to humans and stakeholders.
- Data exploration — learning structure before committing to a model.
- Efficiency — using the right model for the right data scale.
- Insight generation — discovering mechanisms, not just correlations.
Even if all we care about is vanilla predictive power, we
All ML models learn parameters — but not all are parametric.
Non-parametric doesn't mean no parameters
Instead, it means the model doesn't assumes a fixed functional form for \(h\)
- the model complexity grows with data
- usually fast to implement and train, and often effective as a baseline
| Electronic | Transistors, logic gates, amplifiers | |
| Chemical | Catalytic converters, enzyme reactions | |
| Biological | Vision, photosynthesis, DNA repair | |
| Computational | Algorithms, logic circuits, neural networks | |
| Social or economic | Market price formation, voting dynamics |
|
"Having parameters" ≠ "Being parametric,"
just as "Having mechanisms" ≠ "Being mechanical":
Outline
- Non-parametric models overview
-
Supervised learning non-parametric
- \(k\)-nearest neighbor
- Decision Tree
- Unsupervised learning non-parametric
- \(k\)-means clustering
-
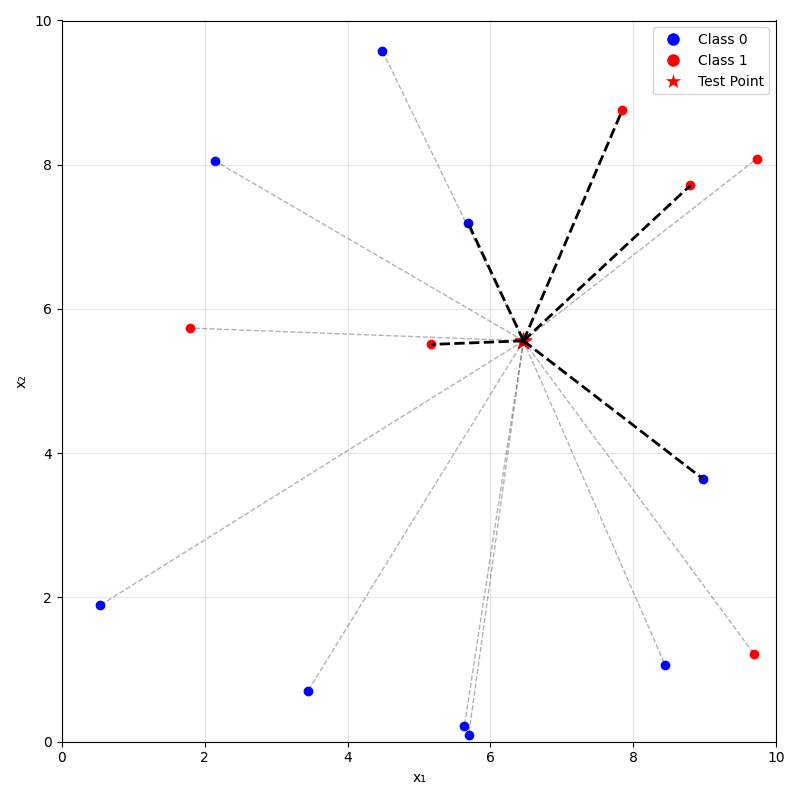
Predicting (inferencing, testing):
- For a new data point \(x_{\text{new}}\), take majority (class) or mean (regression) label of its \(k\) nearest neighbors.
- Training: None (just memorize the entire training data)
hyper-parameter:
- \(k:\) number of neighbors considered
- distance metric (typically Euclidean or Manhattan distance)
- tie-breaking scheme (typically at random)
When we can't fit an equation, we just remember examples.
parameters learned:
the entire training dataset's features and labels
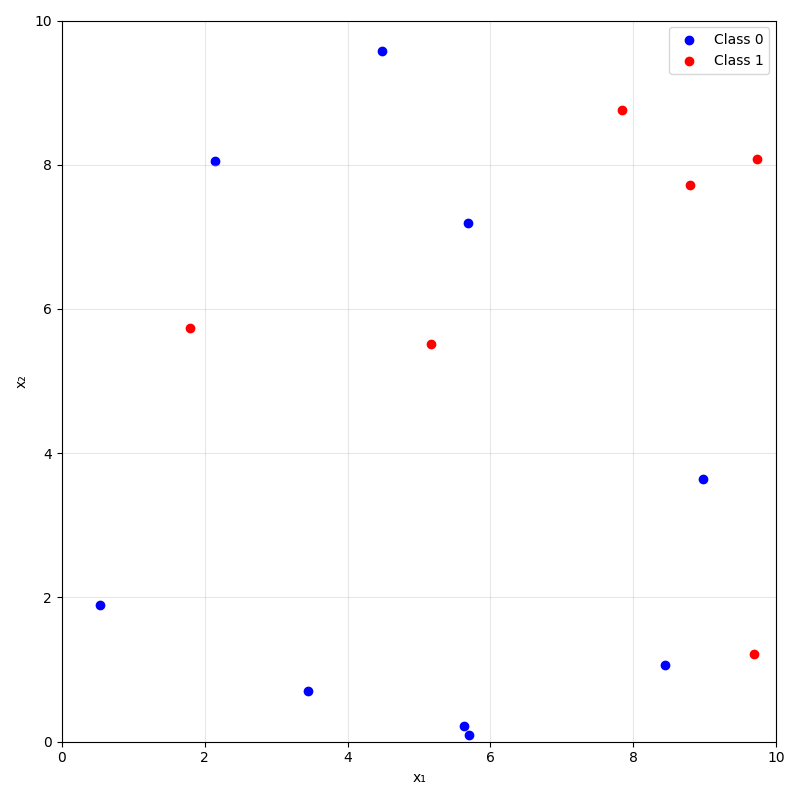
training data
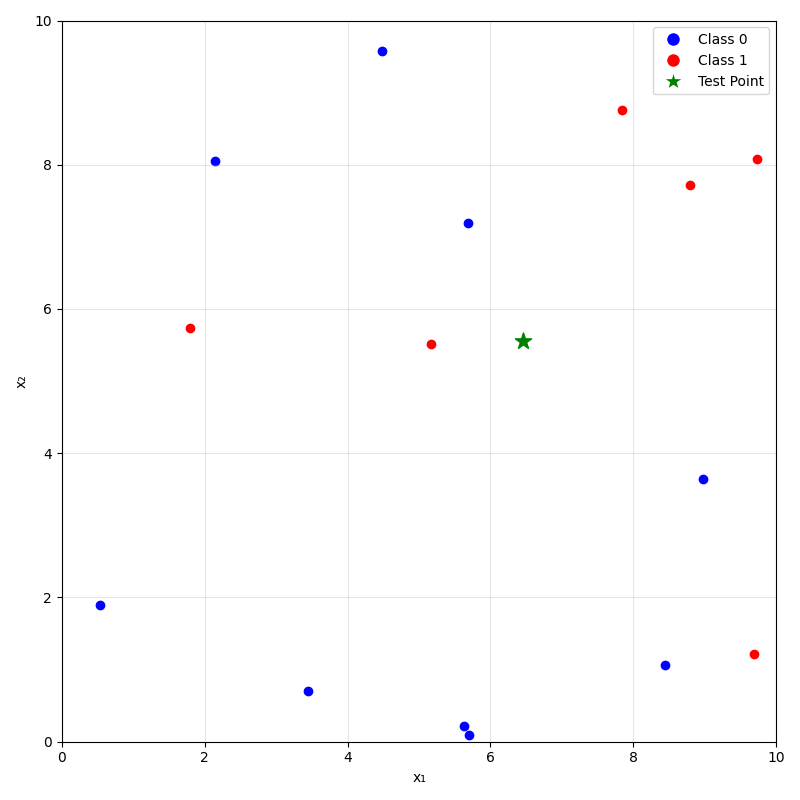
\(k=1\)
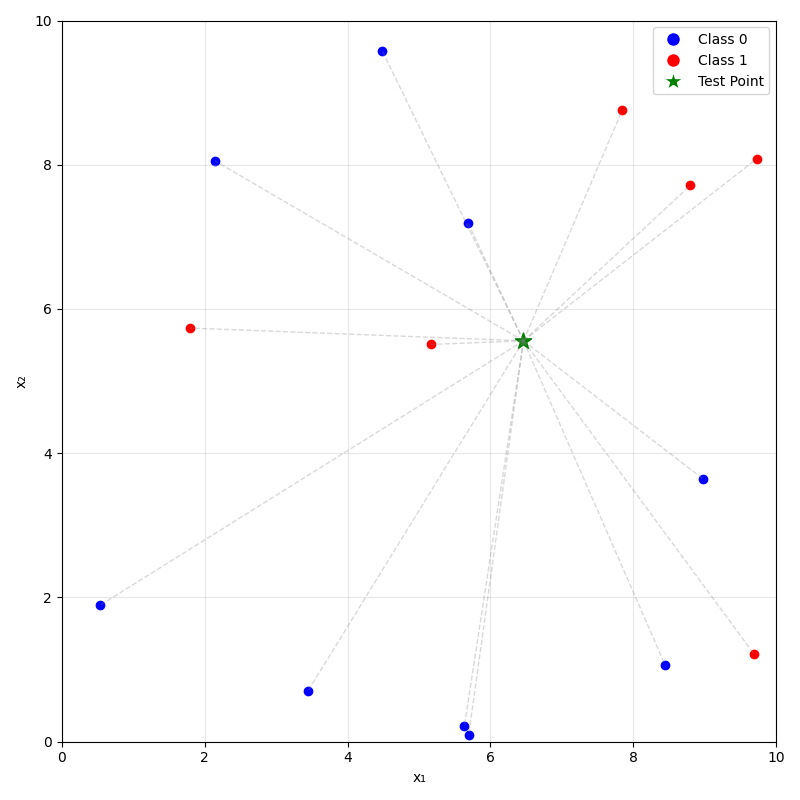

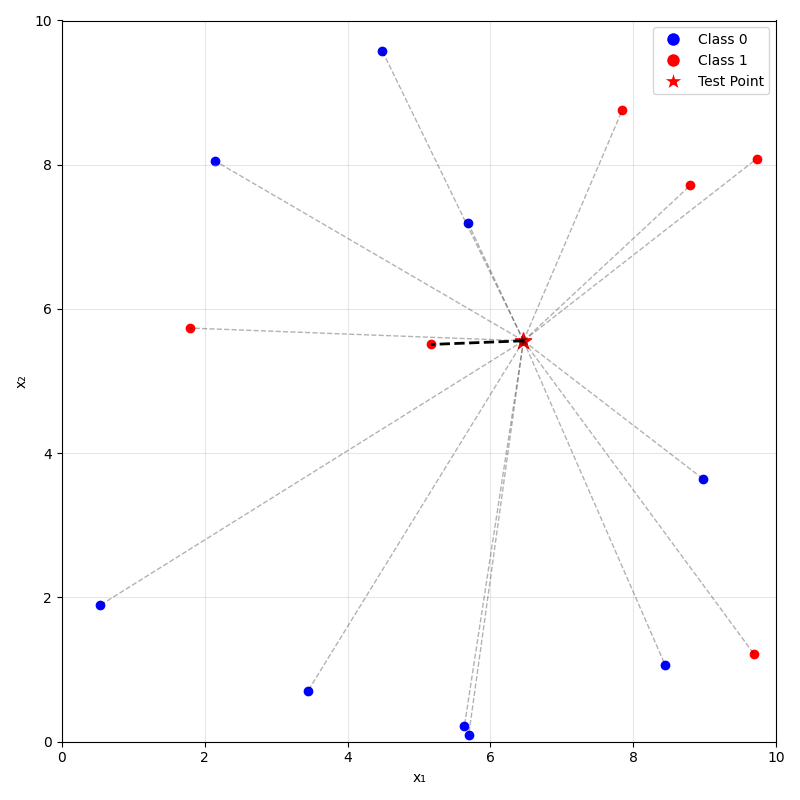
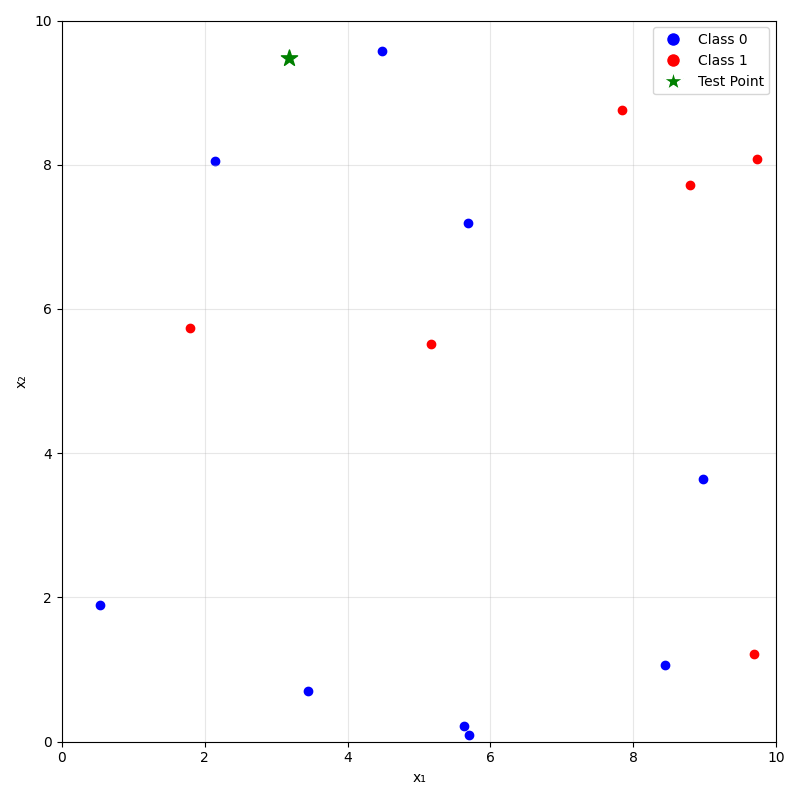
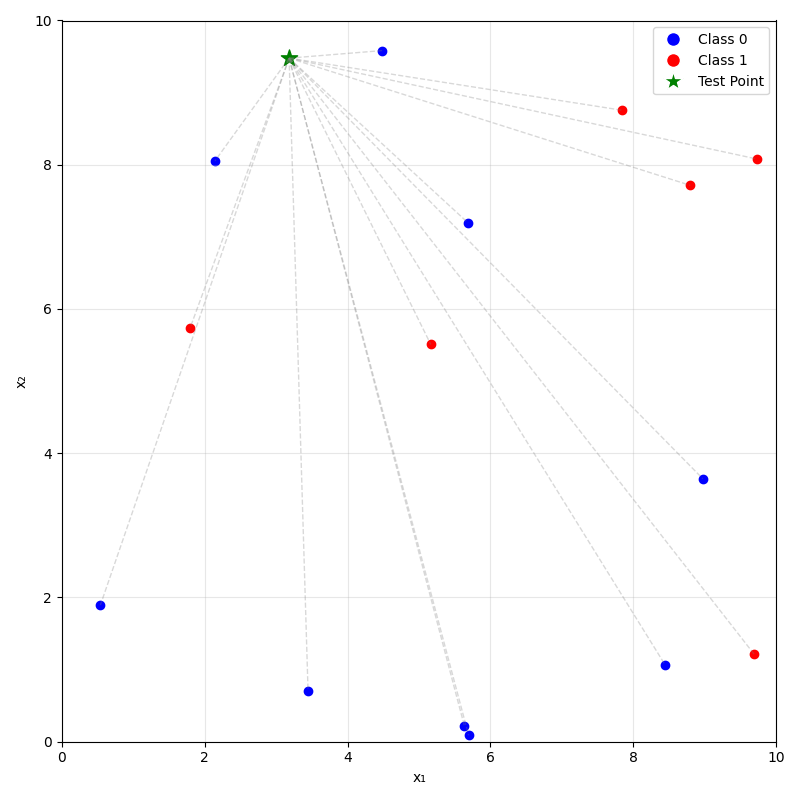
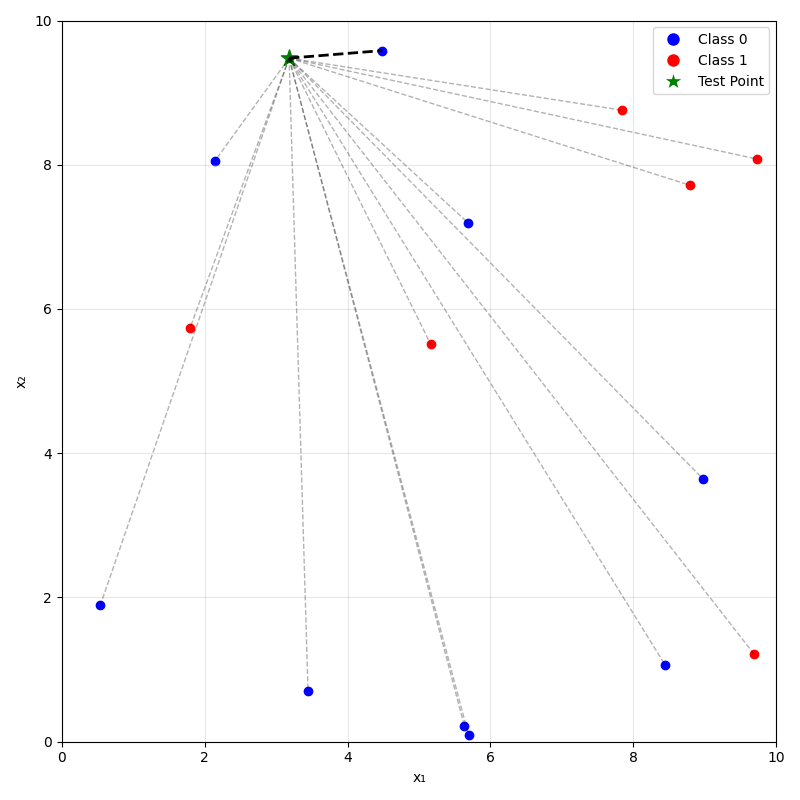
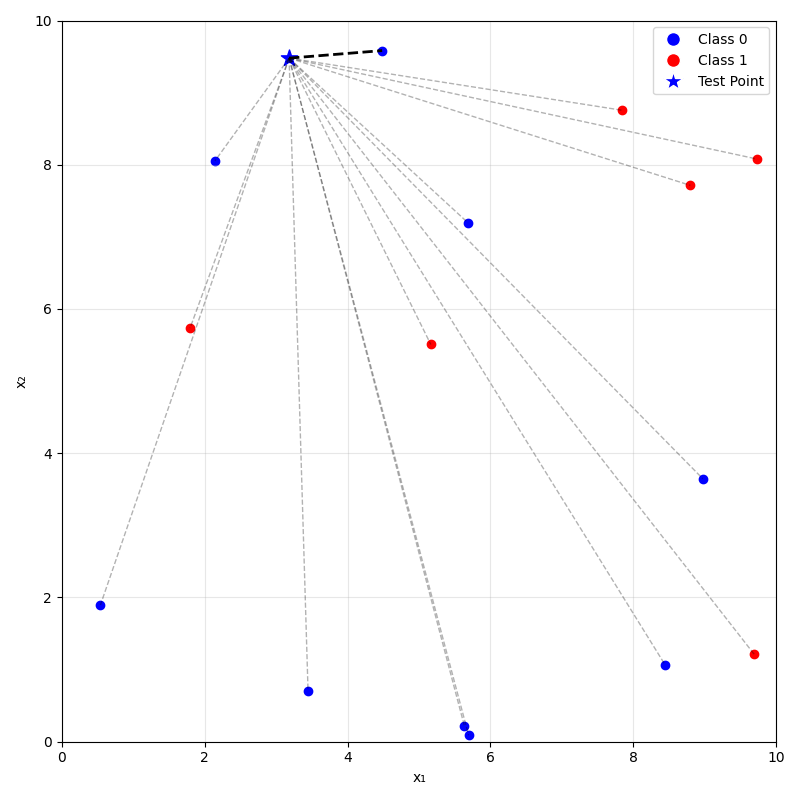
\(k=1\)
\(k=5\)
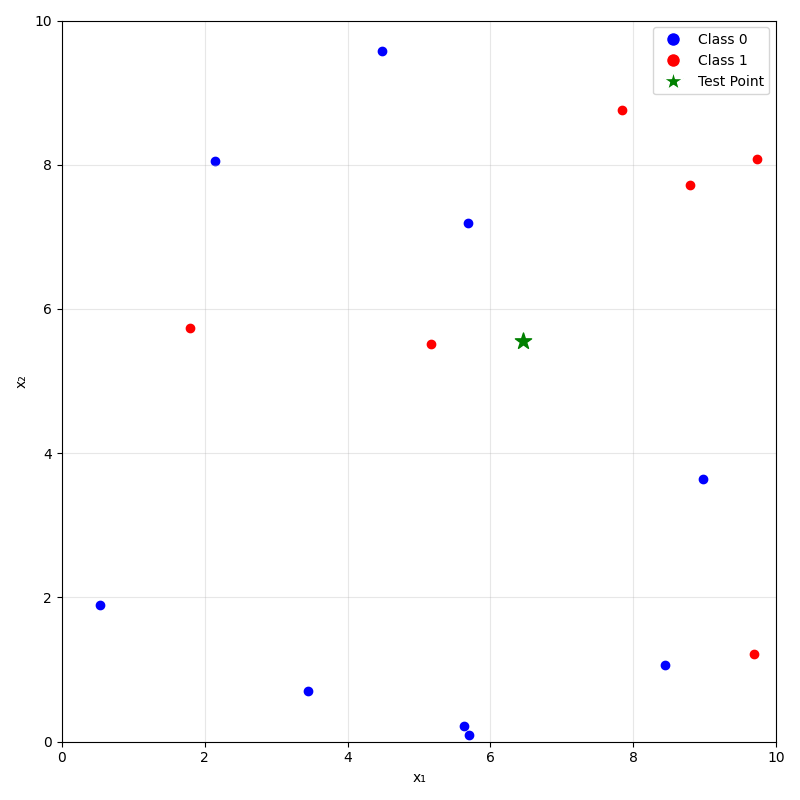
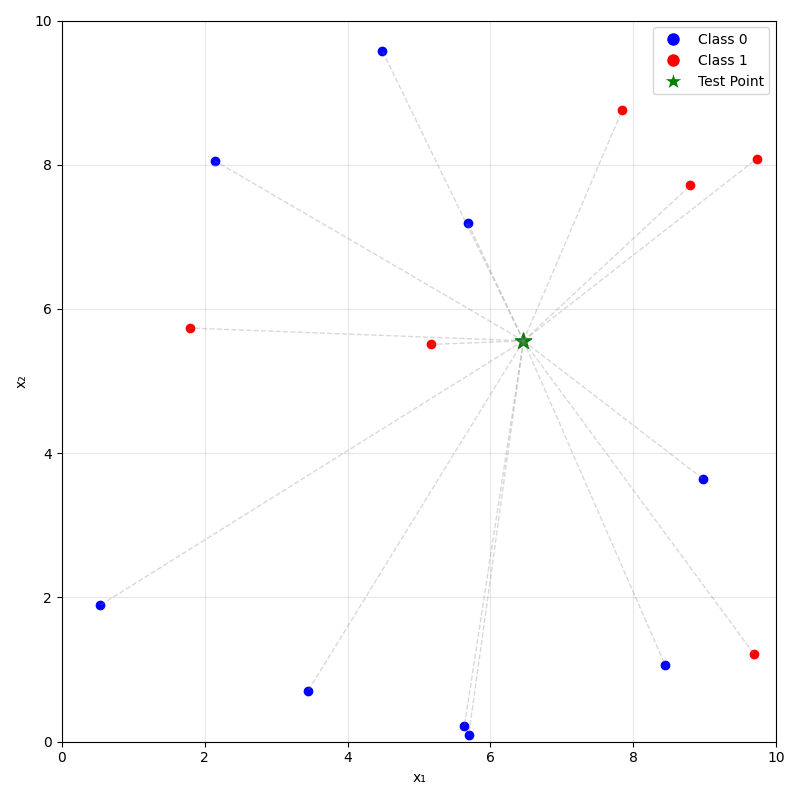
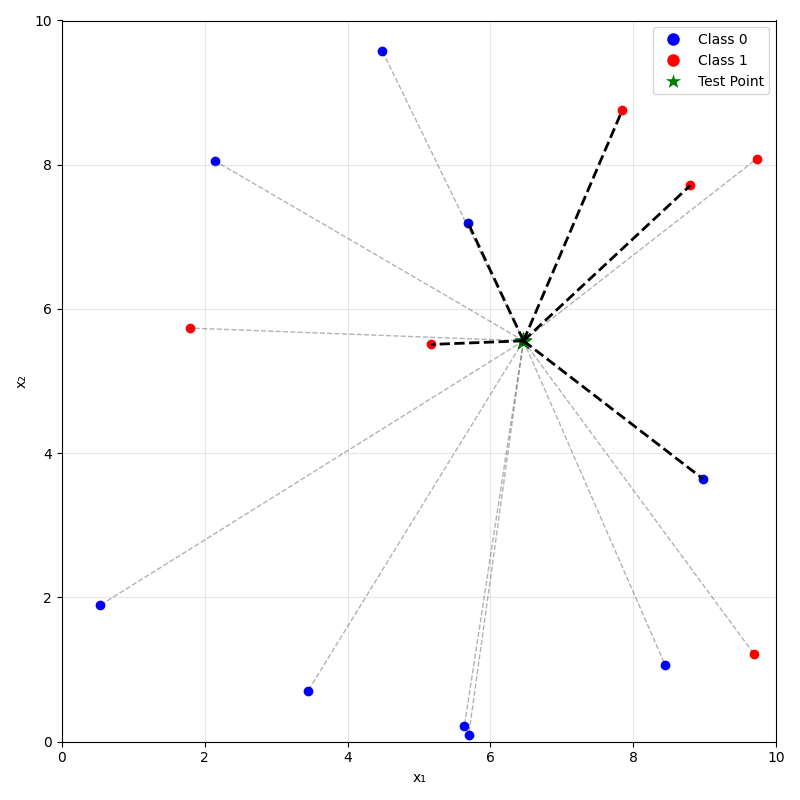
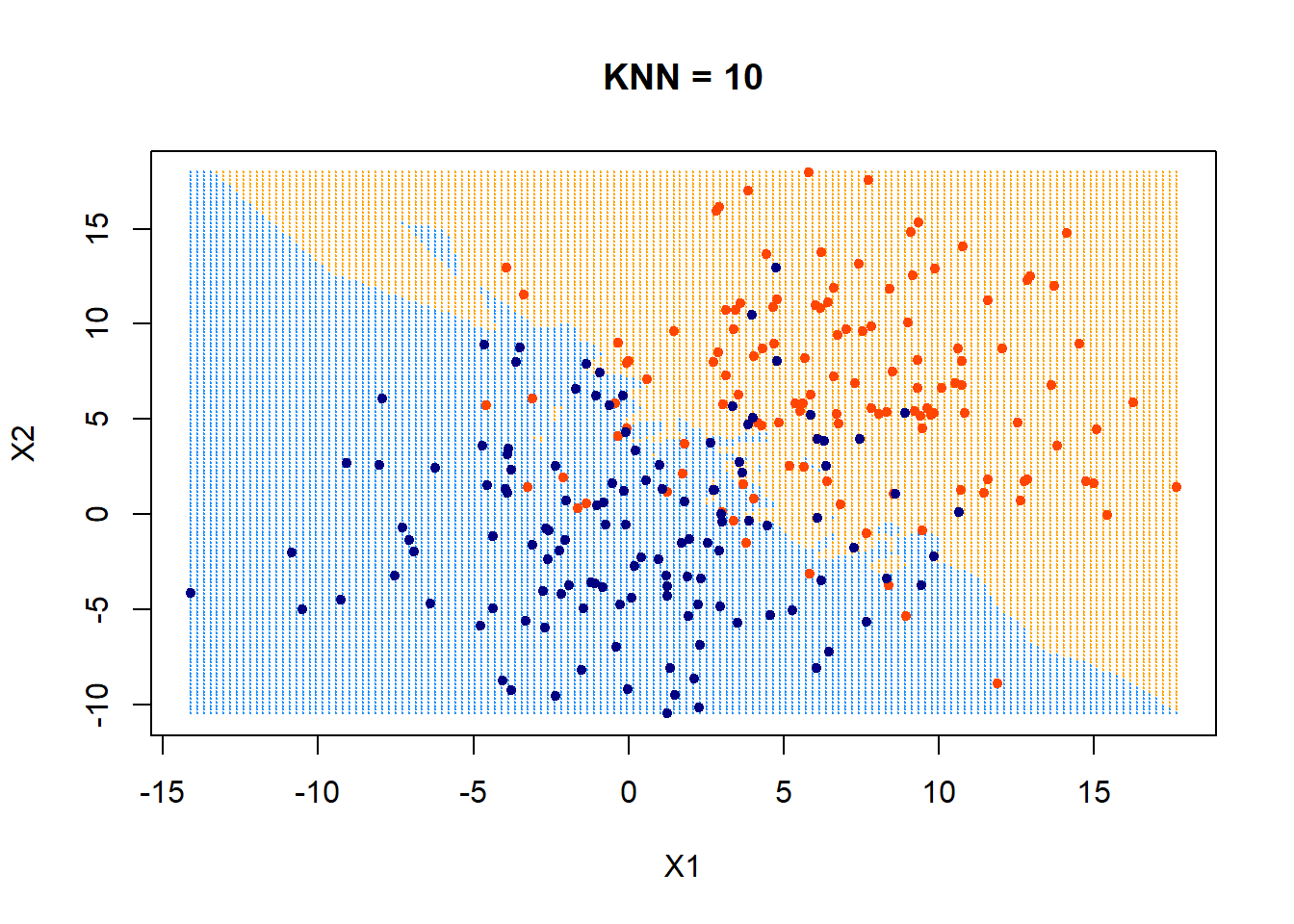
training data
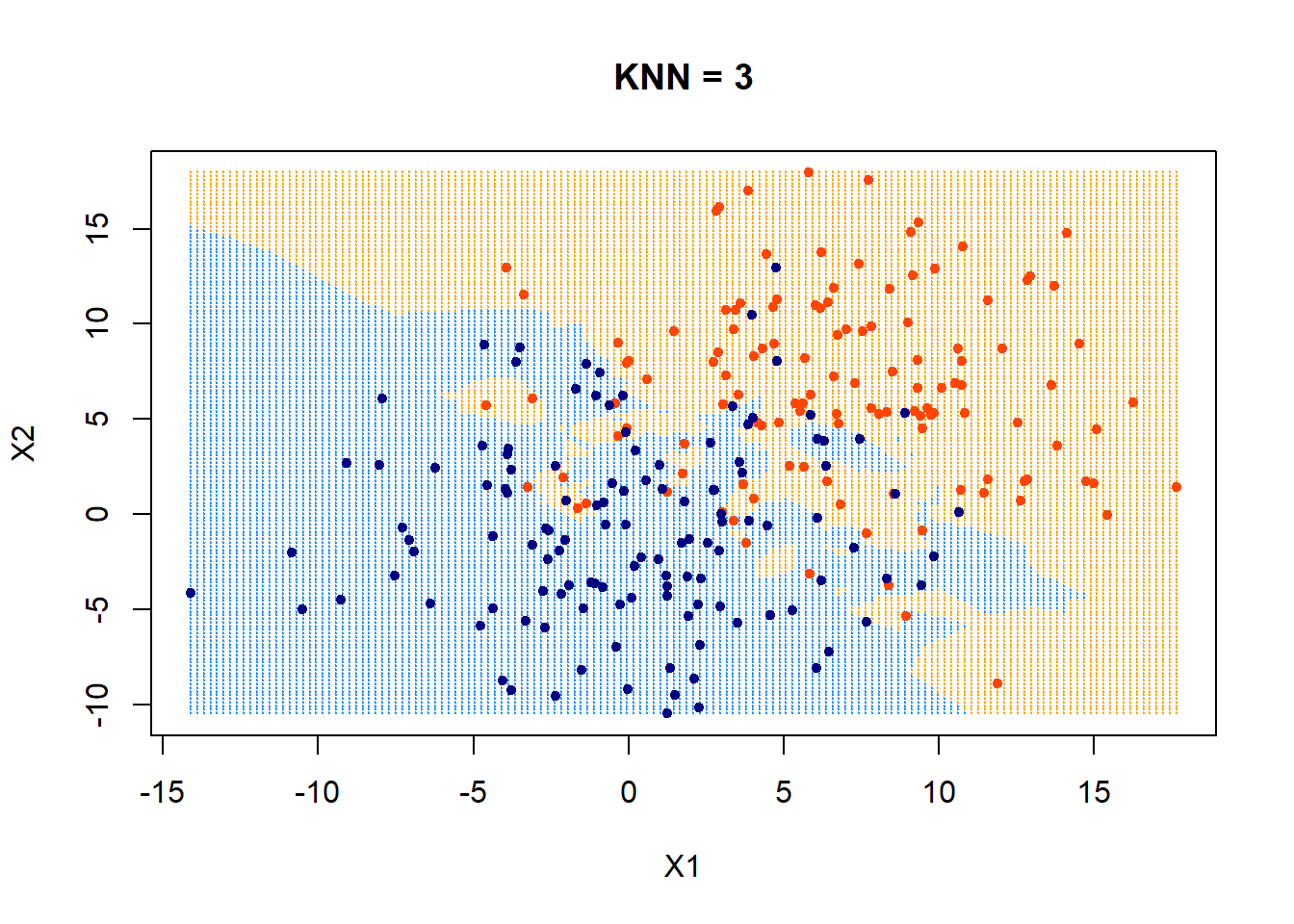
\(k=3\)
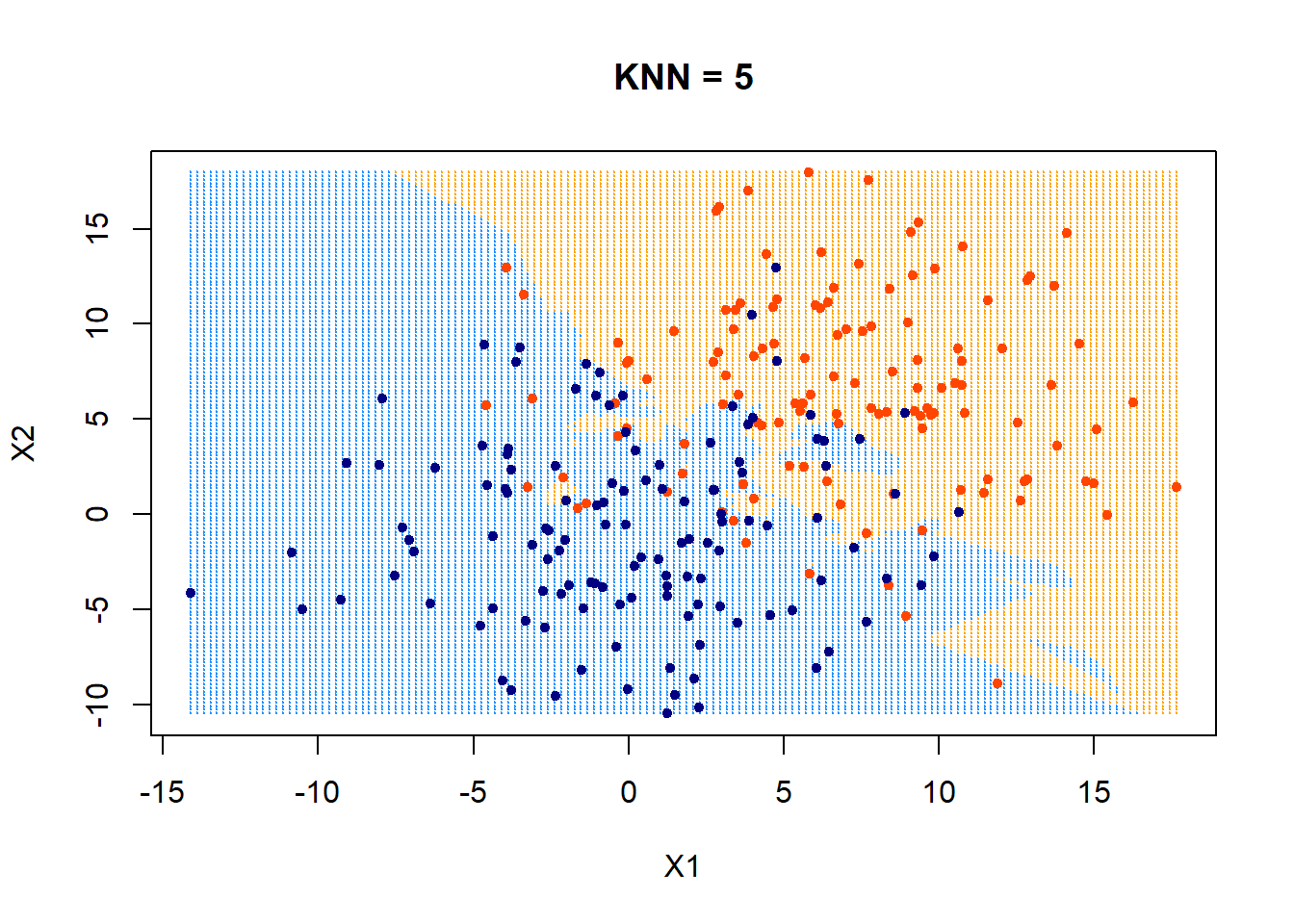
\(k=5\)
\(k=10\)
\(k\)-NN is a good choice when:
- Decision boundary is irregular / hard to parametrize.
- Dataset is small-to-medium (memory fits; latency acceptable).
Be cautious when:
- Very large \(n\) or \(d\) (naively needs all pair-wise distance calc, curse of dimensionality).
- Many irrelevant/noisy features (distance metric degrades).
- Features on different scales (must scale/normalize first).
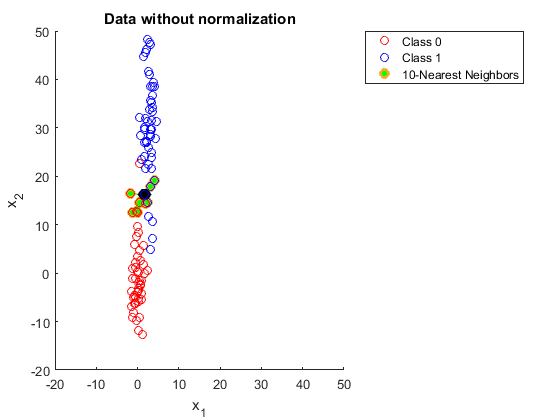
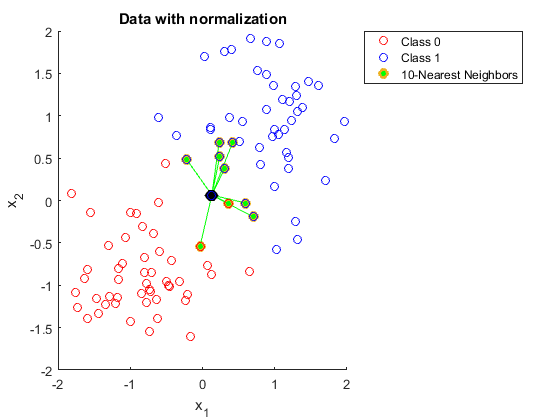
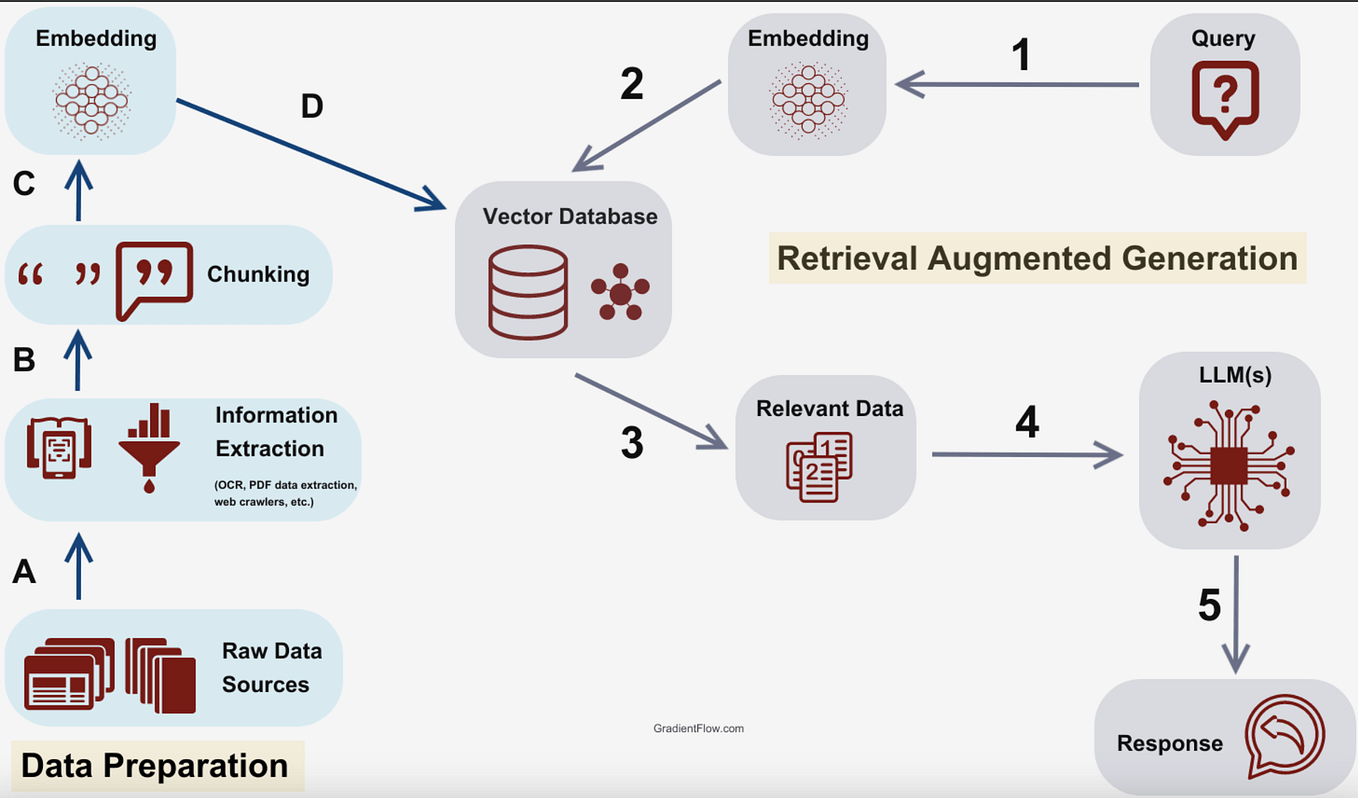
In a sense, it made modern language models non-parametric again.
Outline
- Non-parametric models overview
-
Supervised learning non-parametric
- \(k\)-nearest neighbor
- Decision Tree
- Unsupervised learning non-parametric
- \(k\)-means clustering
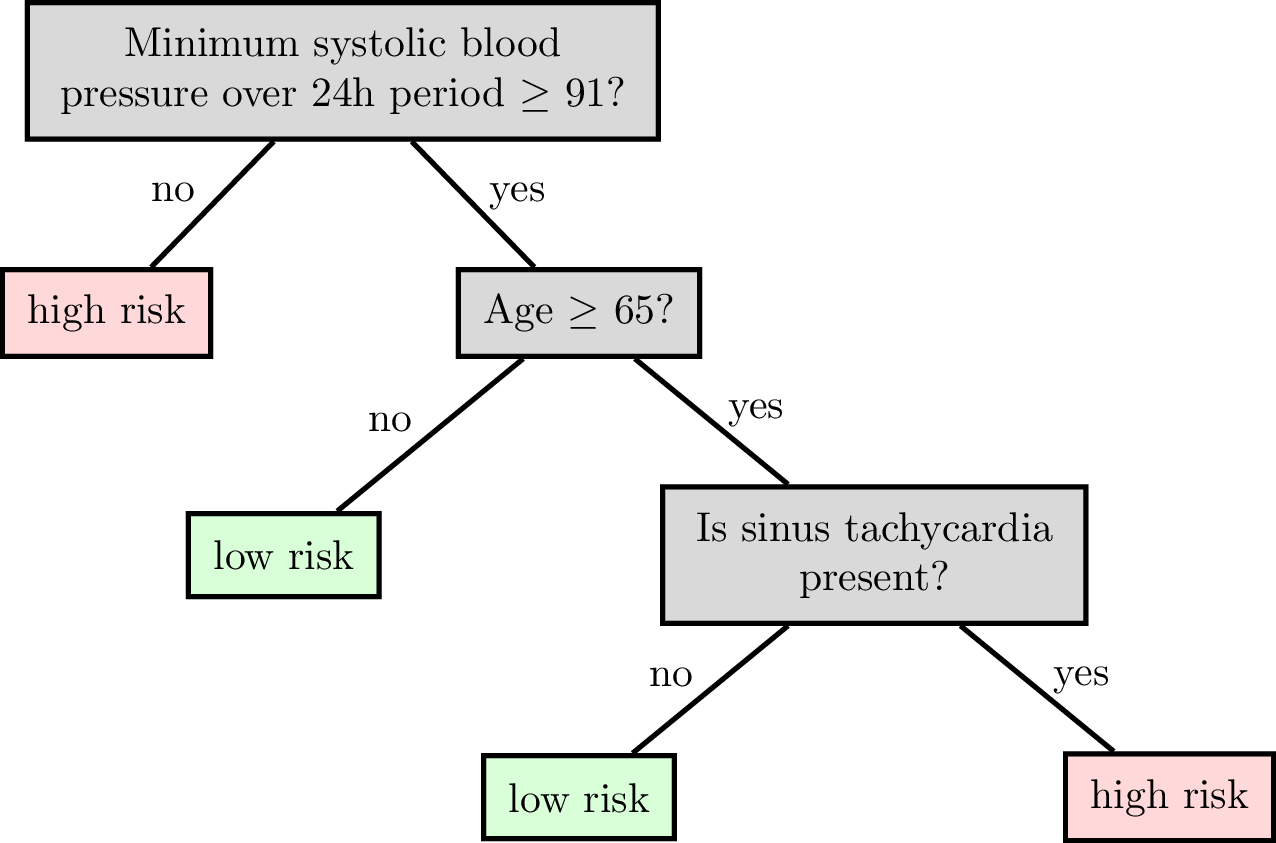
Reading a classification decision tree
features:
\(x_1\) : date
\(x_2\) : age
\(x_3\) : height
\(x_4\) : weight
\(x_5\) : sinus tachycardia?
\(x_6\) : min systolic bp, 24h
\(x_7\) : latest diastolic bp
labels \(y\) :
1: high risk
-1: low risk
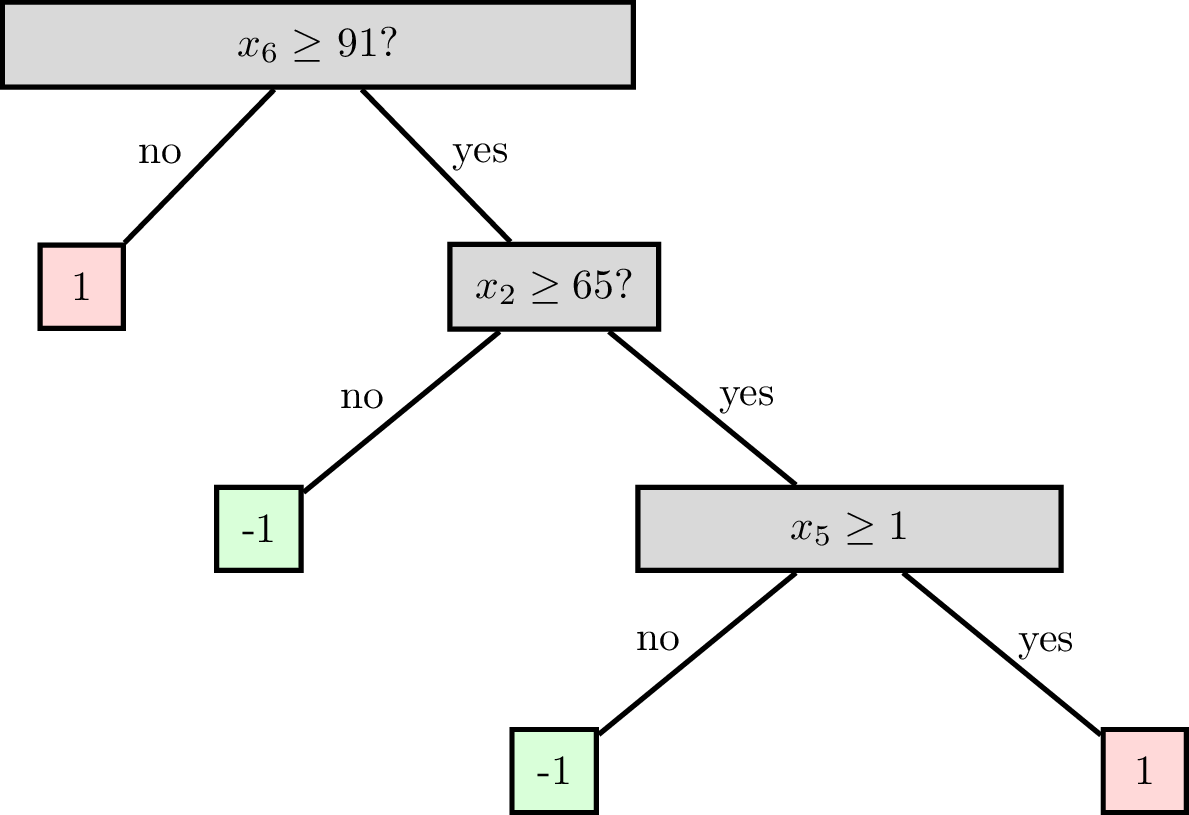
Node (root)
Leaf (terminal)
Node (internal)
Decision tree terminologies

Split dimension
Split value
A node can be specified by
Node(split dim, split value, left child, right child)
A leaf is specified by `Leaf(leaf_value)

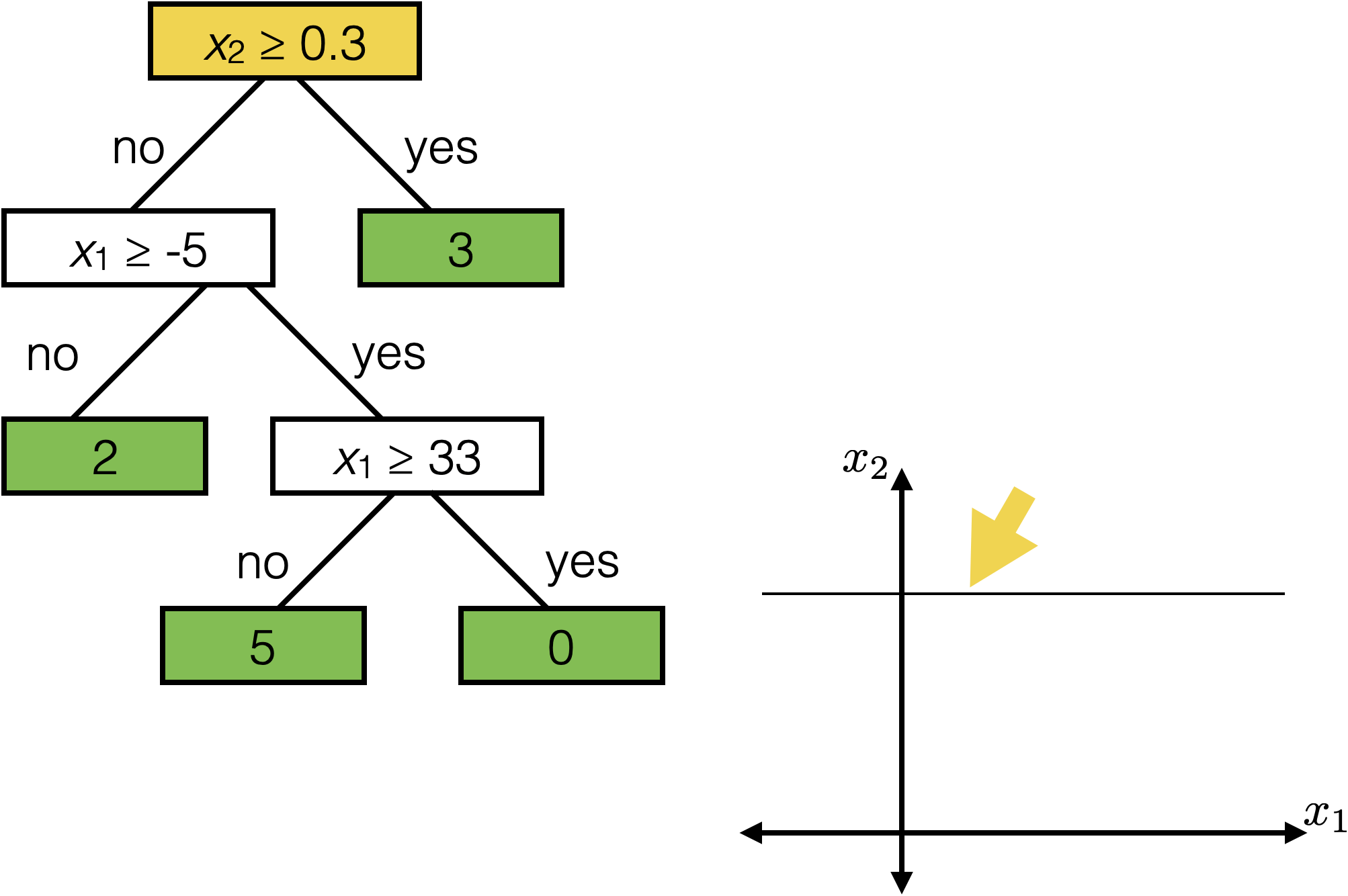
features:
- \(x_1\): temperature (deg C)
- \(x_2\): precipitation (cm/hr)
label: km run

Reading a regression decision tree
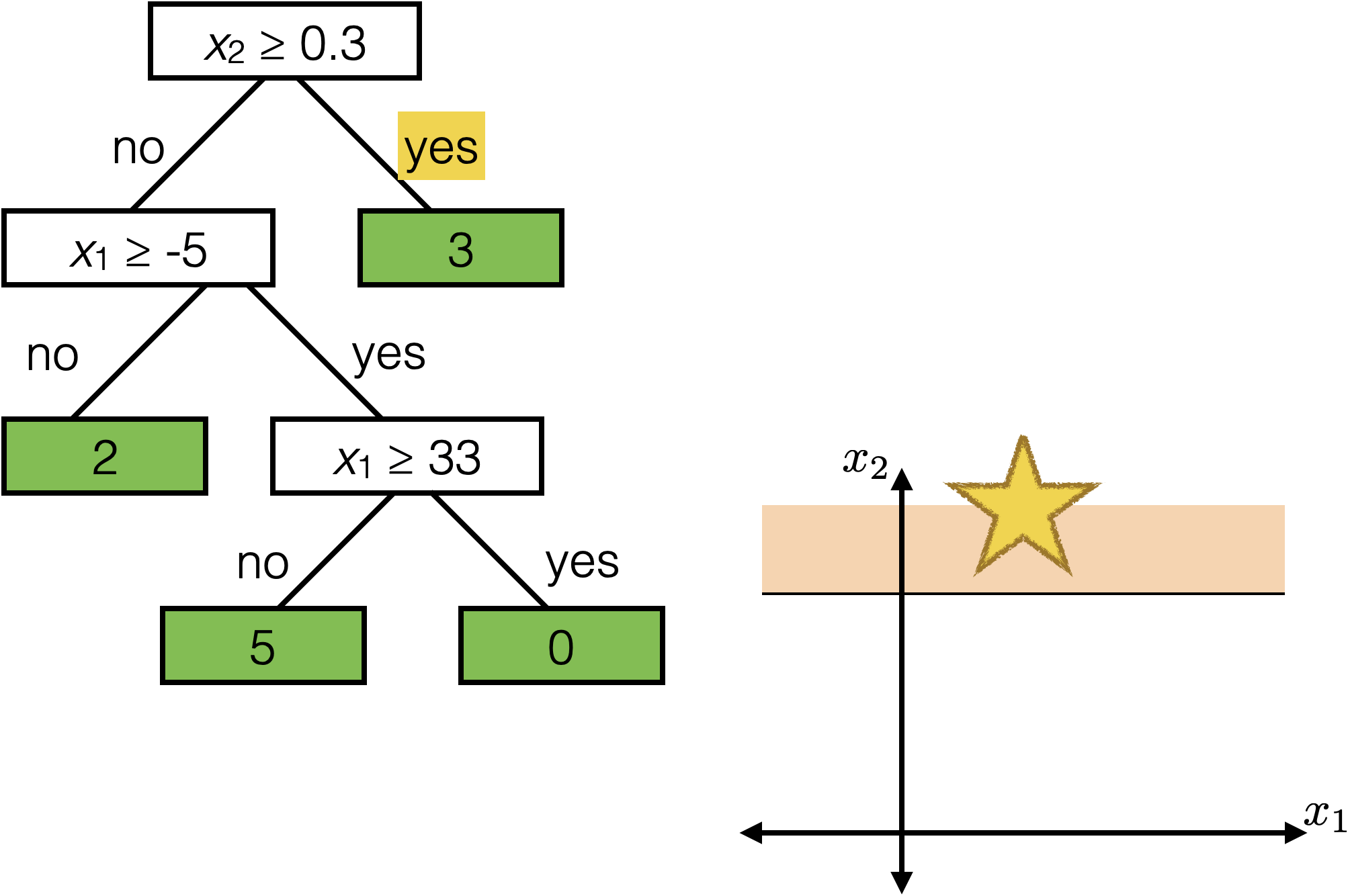
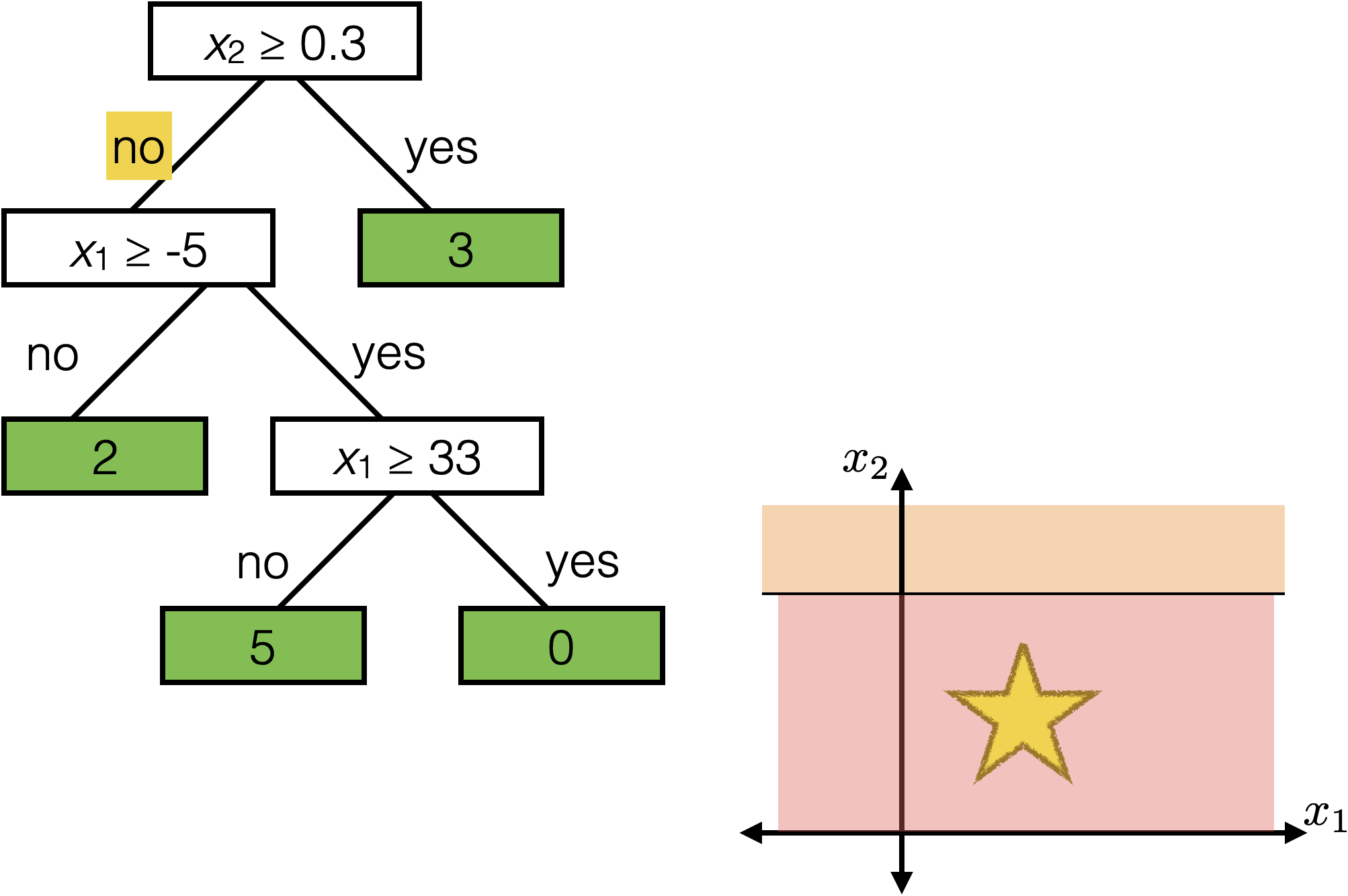

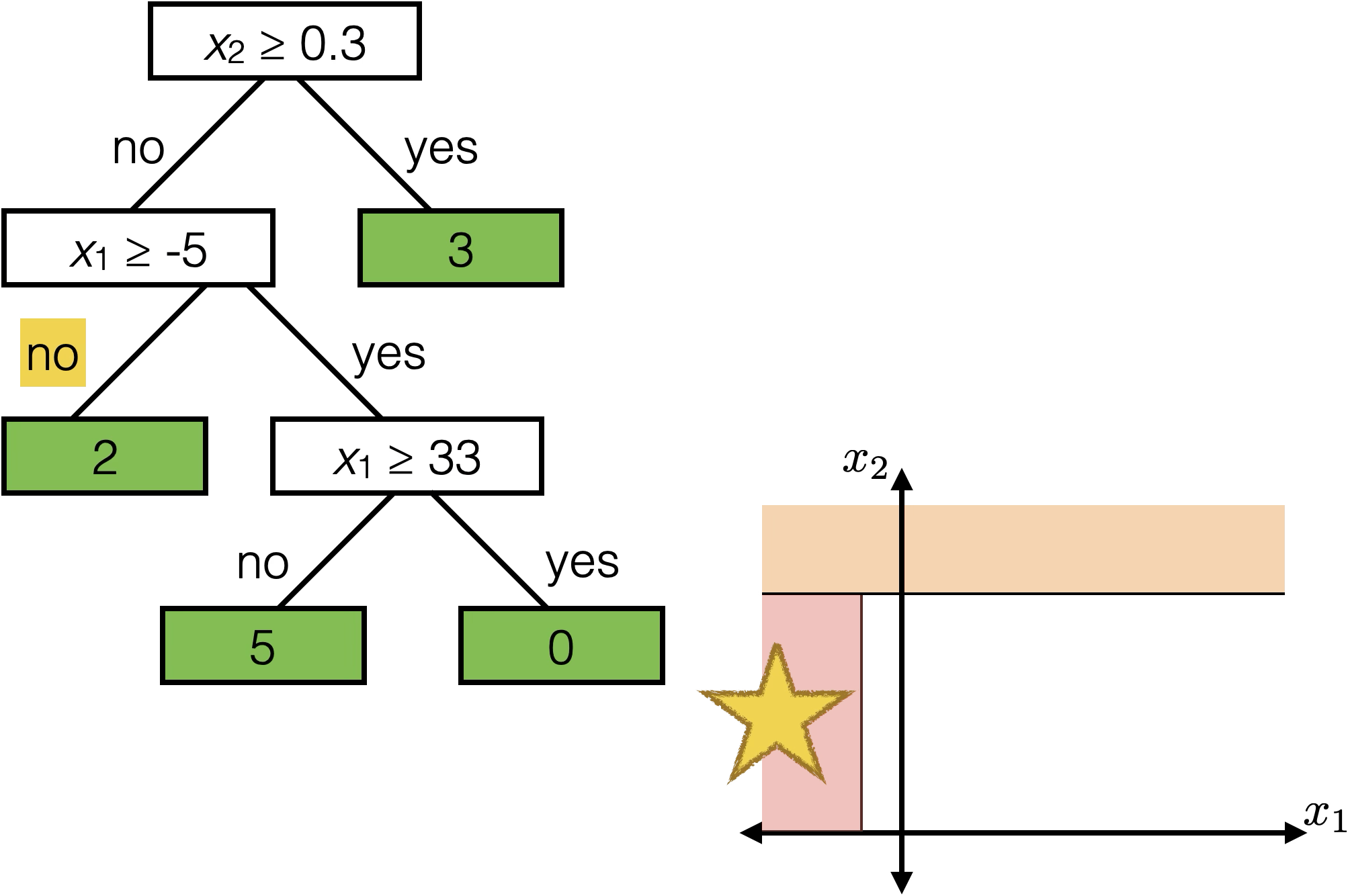
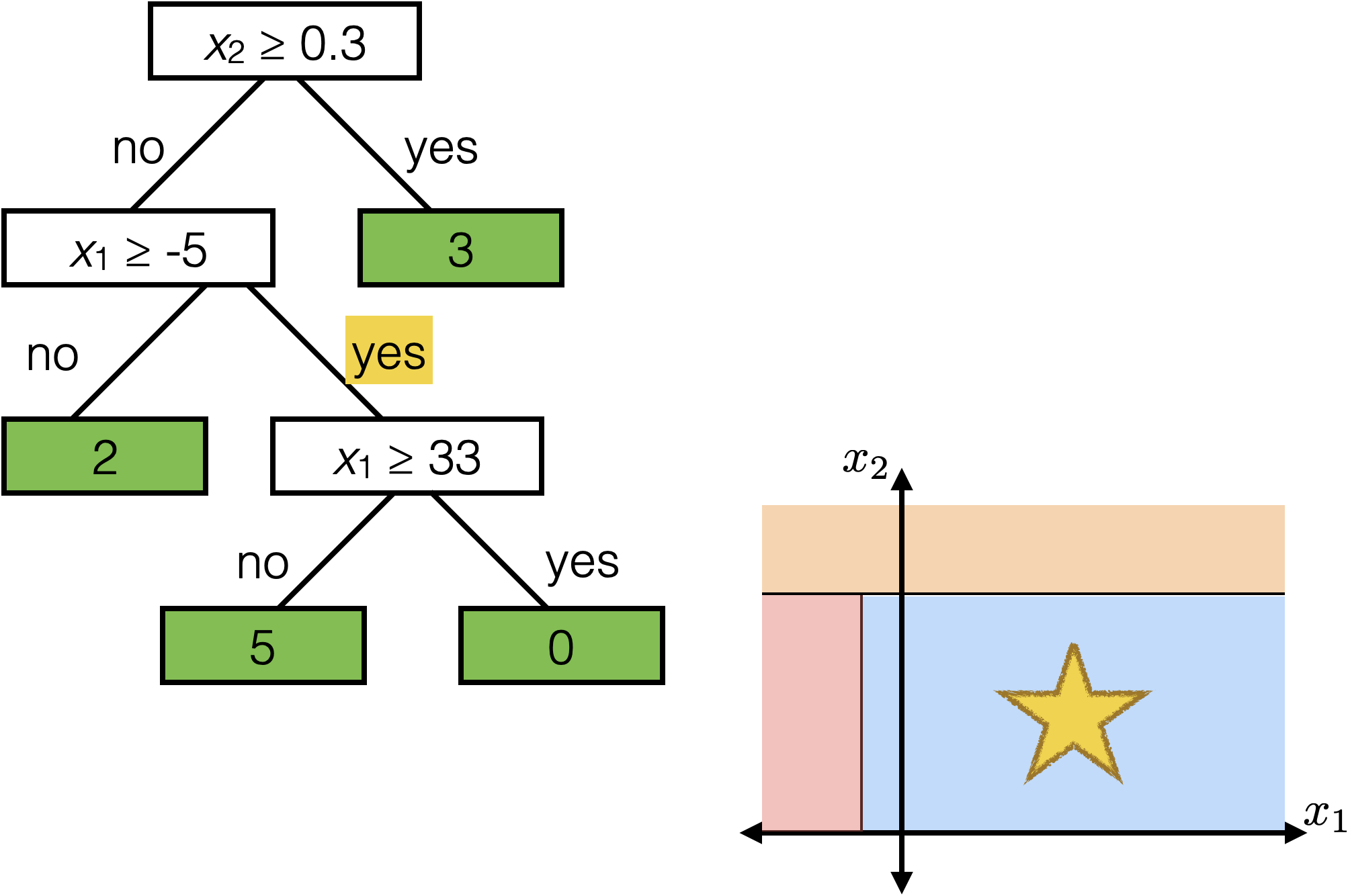
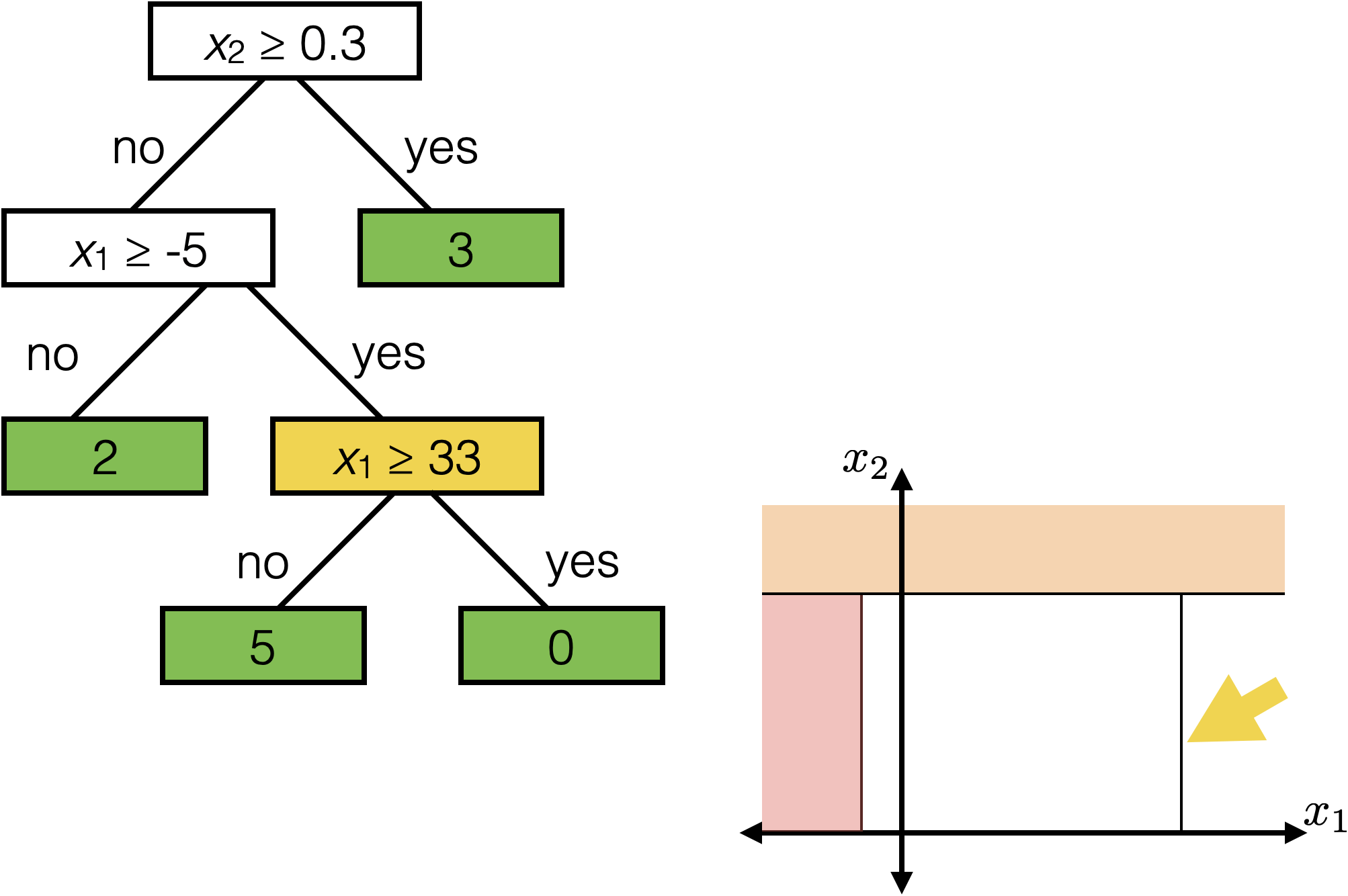
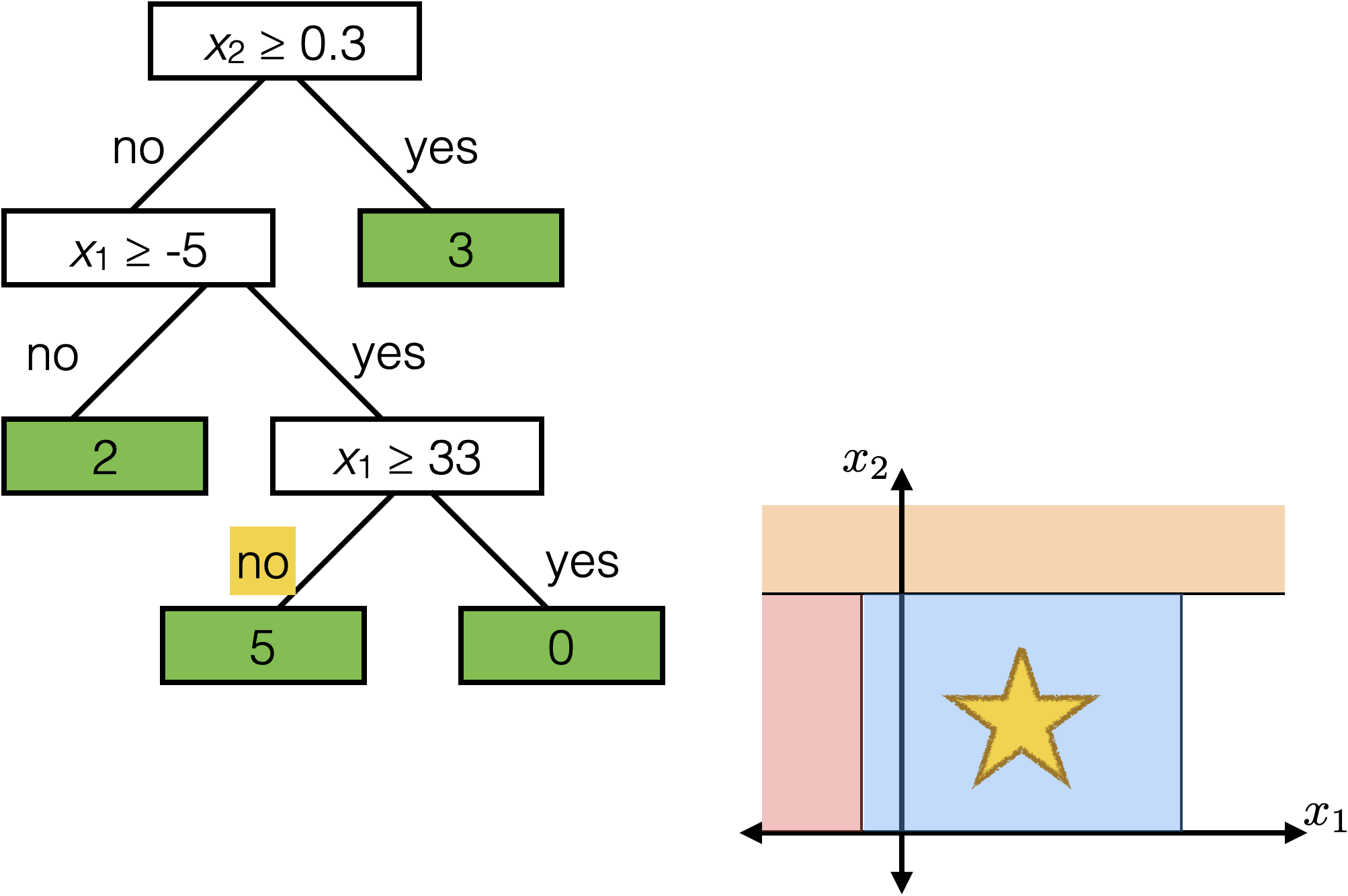
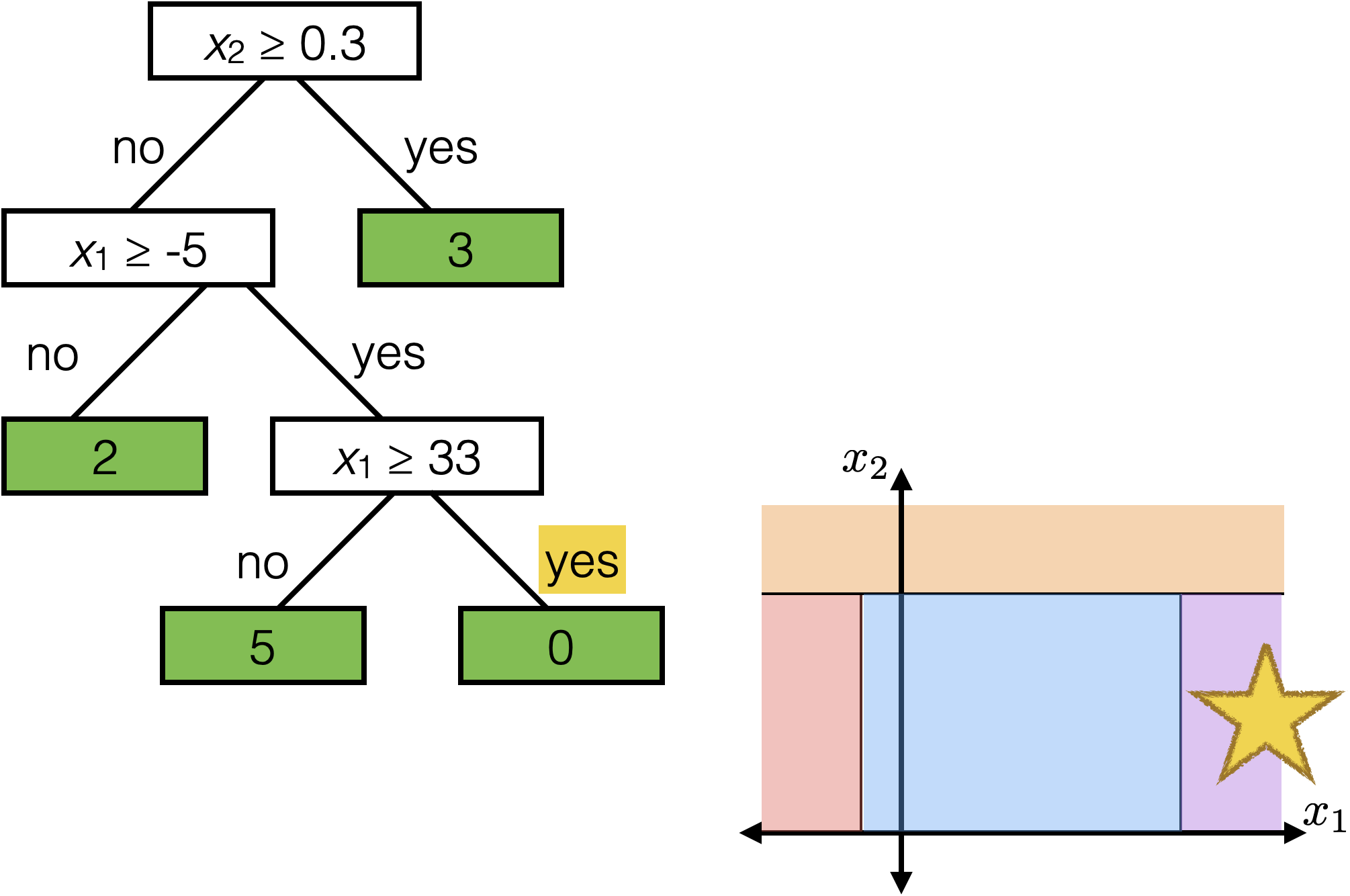
\(x_2 \geq 0.3\)
\(x_1 \geq -5 \)
\(x_1 \geq 33\)
2
3
0
5
temperature
precipitation
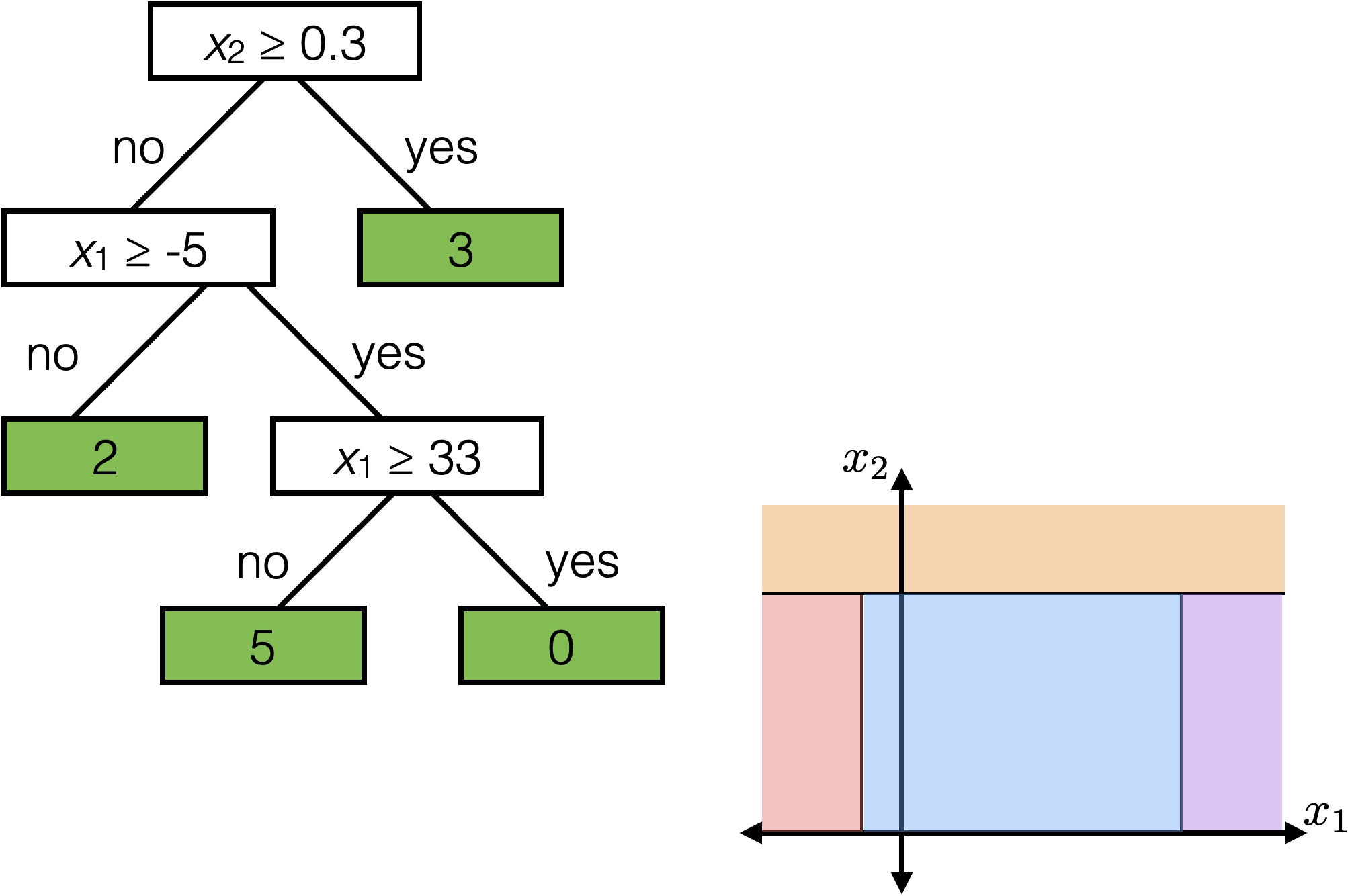
Each axis-aligned box in feature space shares one prediction
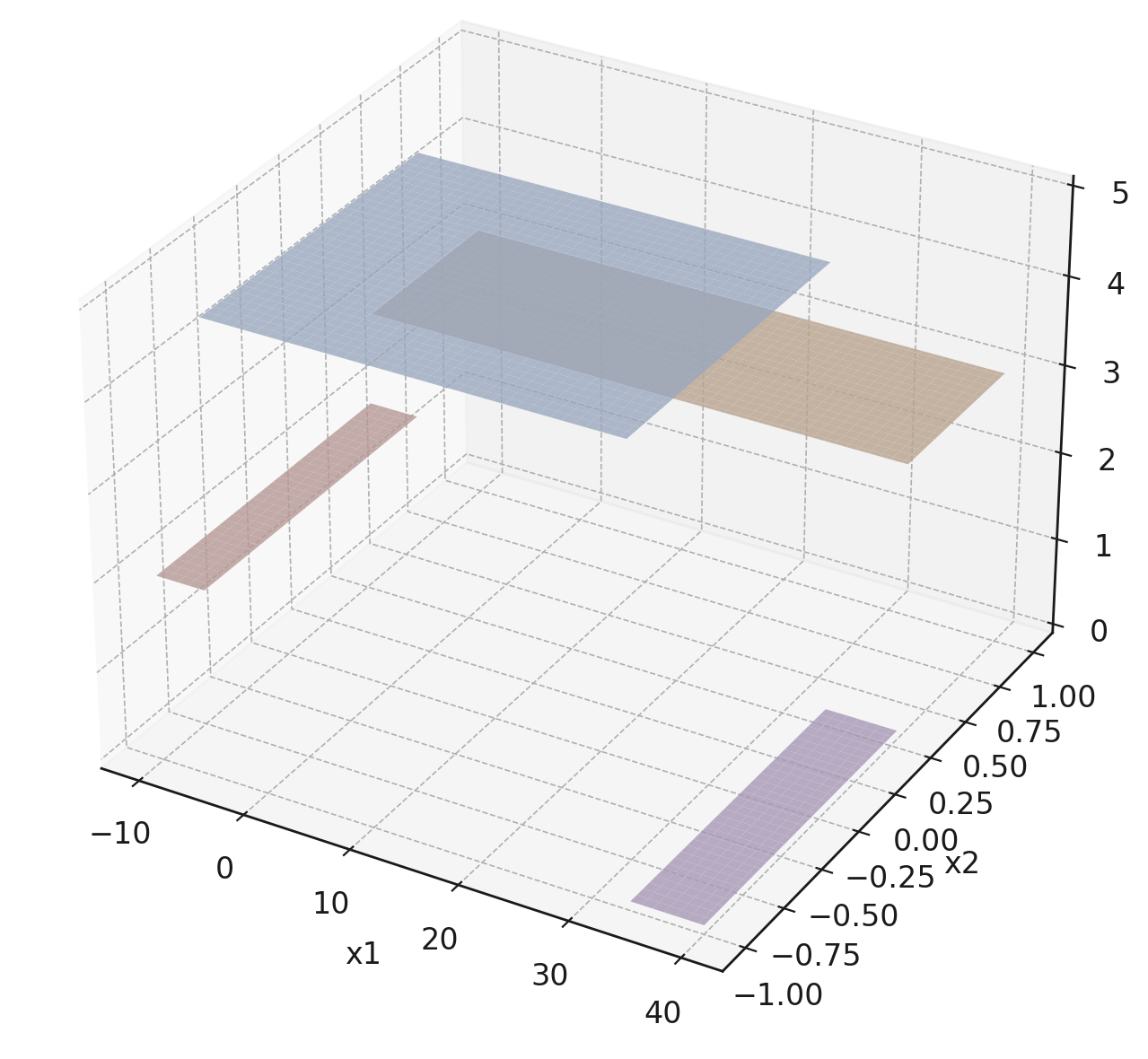
label: km run
temperature
precipitation
🌳 How to Grow a Regression Tree
The big idea:
-
Grow — start with all data at the root.
Try candidate splits along each feature. -
Split — pick the split that best reduces prediction error
(lowest weighted variance of target values). -
Stop — if a region is small or already consistent
(data within ≤ leaf size, or variance below a threshold), make it a leaf.
recursive partitioning: each split divides data into regions where the target values are more similar, and each leaf predicts by the average of its data points.
set of indices
hyper-parameter: largest leaf size
maximum number of training samples allowed in a leaf
\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
10. Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k, \mathcal{D}\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k, \mathcal{D}\right)\right)\)

- Choose \(k=2\)
- \(\operatorname{BuildTree}(\{1,2,3\};2)\)
- Line 1 true
\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
10. Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)

\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
10. Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
- For this fixed \((j, s)\)
- \(I_{j, s}^{+} = \{2,3\}\)
- \(I_{j, s}^{-} = \{1\}\)
- \(\hat{y}_{j, s}^{+} = 5\)
- \(\hat{y}_{j, s}^{-} = 0\)
- \(E_{j, s} =0\)

\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
10. Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
- For this fixed \((j, s)\)
- \(I_{j, s}^{+} = \{2,3\}\)
- \(I_{j, s}^{-} = \{1\}\)
- \(\hat{y}_{j, s}^{+} = 5\)
- \(\hat{y}_{j, s}^{-} = 0\)
- \(E_{j, s} =0\)

\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
10. Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
- Line 2: It suffices to consider a finite number of \((j, s)\) combo suffices (those that split in-between data points)

\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
10. Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
- Line 8: picks the "best" among these finite choices of \((j, s)\) combos (random tie-breaking).

\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
10. Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
Suppose line 8 sets this \((j^*,s^*)\),
say = \((j^*,s^*) = (1, 1.7)\)

\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
10. Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
Line 12 recursion
\(x_1 \geq 1.7\)

\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
10. Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
\(x_1 \geq 1.7\)

\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
10. Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
\(x_1 \geq 1.7\)
0

\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
10. Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
\(x_1 \geq 1.7\)
0

\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
10. Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
\(x_1 \geq 1.7\)
0
5
🌳 How to Grow a Classification Tree
The big idea:
-
Grow — start with all data at the root.
Try candidate splits along each feature. -
Split — pick the split that best separates the classes
(lowest weighted entropy or highest information gain). -
Stop — if a region is small or already pure
(data within ≤ leaf size, or most data share the same label), make it a leaf.
Recursive partitioning: each split divides data into regions that are more homogeneous in class labels, and each leaf predicts by the majority label of its data points.
entropy \(H:=-\sum_{\text {class }_c} \hat{P}_c (\log _2 \hat{P}_c)\)
(about 1.1)
for example: \(c\) iterates over 3 classes

\(\hat{P}_c:\)
\(H= -[\frac{4}{6} \log _2\left(\frac{4}{6}\right)+\frac{1}{6} \log _2\left(\frac{1}{6}\right)+\frac{1}{6} \log _2\left(\frac{1}{6}\right)]\)
(about 1.252)

\(\hat{P}_c:\)
\(H= -[\frac{3}{6} \log _2\left(\frac{3}{6}\right)+\frac{3}{6} \log _2\left(\frac{3}{6}\right)+ 0]\)

\(\hat{P}_c:\)
\(H= -[\frac{6}{6} \log _2\left(\frac{6}{6}\right)+ 0+ 0]\)
(= 0)
empirical probability
\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
10. Set \(\hat{y}=\) majority \(_{i \in I} y^{(i)}\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) majority \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) majority \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s} = \frac{\left|I_{j, s}^{-}\right|}{|I|} \cdot H\left(I_{j, s}^{-}\right)+\frac{\left|I_{j, s}^{+}\right|}{|I|} \cdot H\left(I_{j, s}^{+}\right)\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
weighted average entropy (WAE)
as performance metric
majority vote
as regional prediction
For classification
\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
10. Set \(\hat{y}=\) majority \(_{i \in I} y^{(i)}\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) majority \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) majority \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s} = \frac{\left|I_{j, s}^{-}\right|}{|I|} \cdot H\left(I_{j, s}^{-}\right)+\frac{\left|I_{j, s}^{+}\right|}{|I|} \cdot H\left(I_{j, s}^{+}\right)\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)

\( \frac{4}{6} \cdot H\left(I_{j, s}^{-}\right)+\frac{2}{6} \cdot H\left(I_{j, s}^{+}\right)\)
fraction of points to the left of the split
fraction of points to the right of the split
\(E_{j,s}= \)
\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
10. Set \(\hat{y}=\) majority \(_{i \in I} y^{(i)}\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) majority \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) majority \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s} = \frac{\left|I_{j, s}^{-}\right|}{|I|} \cdot H\left(I_{j, s}^{-}\right)+\frac{\left|I_{j, s}^{+}\right|}{|I|} \cdot H\left(I_{j, s}^{+}\right)\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)

\( -[\frac{3}{4} \log _2\left(\frac{3}{4}\right)+\frac{1}{4} \log _2\left(\frac{1}{4}\right)+0] \approx 0.811\)
\( \frac{4}{6} \cdot H\left(I_{j, s}^{-}\right)+\frac{2}{6} \cdot H\left(I_{j, s}^{+}\right)\)
\(\hat{P}_c:\)
\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
10. Set \(\hat{y}=\) majority \(_{i \in I} y^{(i)}\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) majority \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) majority \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s} = \frac{\left|I_{j, s}^{-}\right|}{|I|} \cdot H\left(I_{j, s}^{-}\right)+\frac{\left|I_{j, s}^{+}\right|}{|I|} \cdot H\left(I_{j, s}^{+}\right)\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)

\( \frac{4}{6} \cdot H\left(I_{j, s}^{-}\right)+\frac{2}{6} \cdot H\left(I_{j, s}^{+}\right)\)
\(\approx 0.811\)
\( -[\frac{1}{2} \log _2\left(\frac{1}{2}\right)+\frac{1}{2} \log _2\left(\frac{1}{2}\right)+0] = 1\)
\(\hat{P}_c:\)
\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
10. Set \(\hat{y}=\) majority \(_{i \in I} y^{(i)}\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) majority \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) majority \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s} = \frac{\left|I_{j, s}^{-}\right|}{|I|} \cdot H\left(I_{j, s}^{-}\right)+\frac{\left|I_{j, s}^{+}\right|}{|I|} \cdot H\left(I_{j, s}^{+}\right)\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)

\( \frac{4}{6} \cdot H\left(I_{j, s}^{-}\right)+\frac{2}{6} \cdot H\left(I_{j, s}^{+}\right)\)
\(\approx 0.811\)
\( = 1\)
(for this split choice, line 7 \(E_{j, s}\approx\) 0.874)
\(\approx \frac{4}{6}\cdot0.811+\frac{2}{6}\cdot 1\)
\(= 0.874\)
\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
10. Set \(\hat{y}=\) majority \(_{i \in I} y^{(i)}\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) majority \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) majority \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s} = \frac{\left|I_{j, s}^{-}\right|}{|I|} \cdot H\left(I_{j, s}^{-}\right)+\frac{\left|I_{j, s}^{+}\right|}{|I|} \cdot H\left(I_{j, s}^{+}\right)\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)

\( \frac{5}{6} \cdot H\left(I_{j, s}^{-}\right)+\frac{1}{6} \cdot H\left(I_{j, s}^{+}\right)\)
\( -[\frac{4}{5} \log _2\left(\frac{4}{5}\right)+\frac{1}{5} \log _2\left(\frac{1}{5}\right)+0] \approx 0.722\)
\( -[1 \log _2\left(1\right)+0+0] = 0\)
(line 7, overall \(E_{j, s}\approx\) 0.602)
\(\operatorname{BuildTree}(I, k, \mathcal{D})\)
10. Set \(\hat{y}=\) majority \(_{i \in I} y^{(i)}\)
1. if \(|I| > k\)
2. for each split dim \(j\) and split value \(s\)
3. Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
4. Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
5. Set \(\hat{y}_{j, s}^{+}=\) majority \(_{i \in I_{j, s}^{+}} y^{(i)}\)
6. Set \(\hat{y}_{j, s}^{-}=\) majority \(_{i \in I_{j, s}^{-}} y^{(i)}\)
7. Set \(E_{j, s} = \frac{\left|I_{j, s}^{-}\right|}{|I|} \cdot H\left(I_{j, s}^{-}\right)+\frac{\left|I_{j, s}^{+}\right|}{|I|} \cdot H\left(I_{j, s}^{+}\right)\)
8. Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
9. else
11. return \(\operatorname{Leaf}\)(leave_value=\(\hat{y})\)
12. return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)

this split \(E_{j, s}\approx\) 0.602
this split \(E_{j, s}\approx\) 0.874
line 8, set the better \((j, s)\)
Key takeaway:
Entropy measures impurity → the best split minimizes the weighted entropy.
(Weighted = each branch's entropy weighted by how many samples fall there.)
🪓 In classification decision trees, we keep "cutting" where uncertainty drops the most.




Ensemble
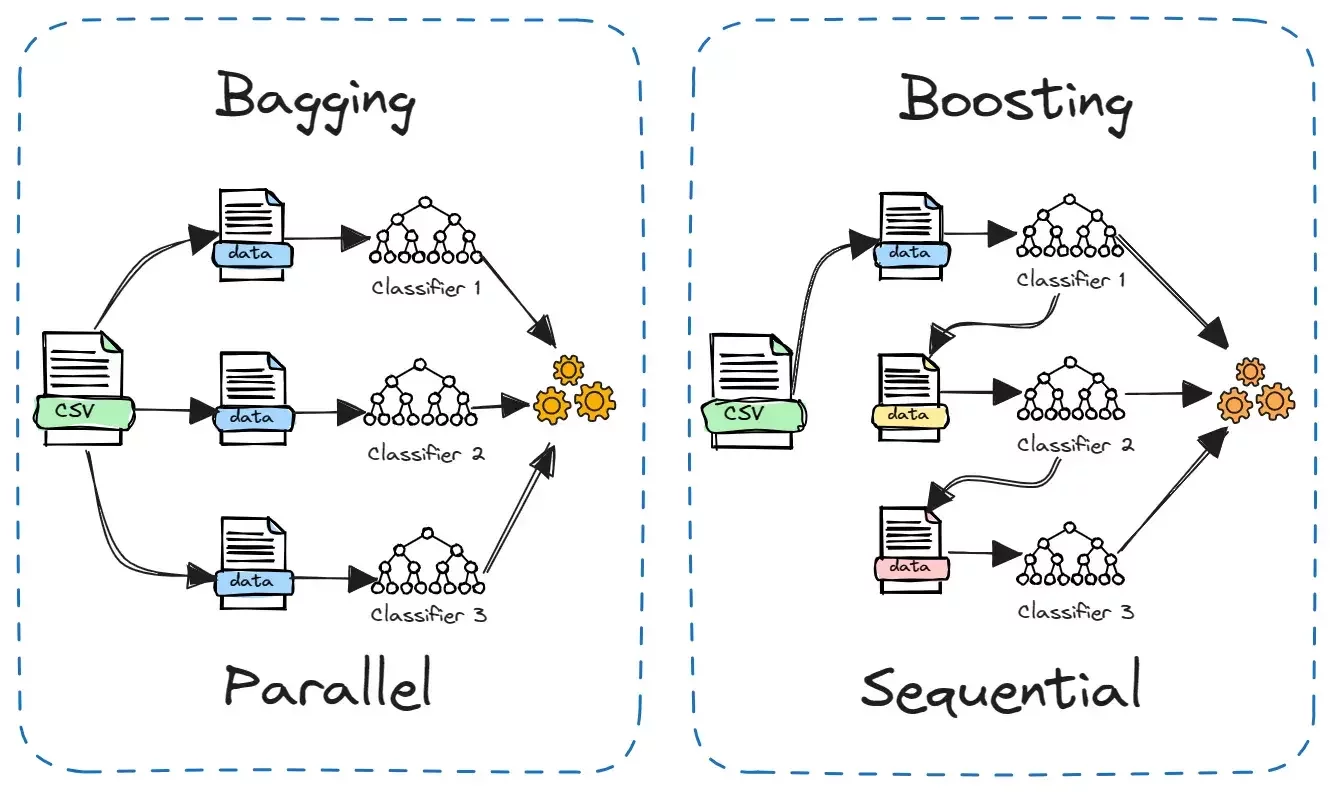
- One of multiple ways to make and use an ensemble
- Bagging = Bootstrap aggregating
Bagging
Bagging
Draw with replacement from \(\mathcal{D}_n,\) create \(B\) new data sets of size \(n\)
\(\tilde{\mathcal{D}}_n^{(1)}\)
\(\tilde{x}^{(1)}, \tilde{y}^{(1)}\)
\(\tilde{x}^{(2)}, \tilde{y}^{(2)}\)
\(\tilde{x}^{(4)}, \tilde{y}^{(4)}\)
\(\tilde{x}^{(3)}, \tilde{y}^{(3)}\)
\(\tilde{\mathcal{D}}_n^{(2)}\)
\(\tilde{x}^{(1)}, \tilde{y}^{(1)}\)
\(\tilde{x}^{(2)}, \tilde{y}^{(2)}\)
\(\tilde{x}^{(4)}, \tilde{y}^{(4)}\)
\(\tilde{x}^{(3)}, \tilde{y}^{(3)}\)
\(\left(x^{(2)}, y^{(2)}\right)\)
\(\tilde{\mathcal{D}}_n^{(B)}\)
\(\tilde{x}^{(4)}, \tilde{y}^{(4)}\)
\(\tilde{x}^{(3)}, \tilde{y}^{(3)}\)
\(\tilde{x}^{(1)}, \tilde{y}^{(1)}\)
Training data \(\mathcal{D}_n\)
\(\left(x^{(1)}, y^{(1)}\right)\)
\(\left(x^{(2)}, y^{(2)}\right)\)
\(\left(x^{(3)}, y^{(3)}\right)\)
\(\left(x^{(4)}, y^{(4)}\right)\)
\(\hat{h}^{(B)}\)
\(\hat{h}^{(1)}\)
\(\hat{h}^{(2)}\)
for regression, average; for classification, vote
\(\hat{h}_{\text {bag }}(x)\)
(boosting)
Outline
- Non-parametric models overview
- Supervised learning non-parametric
- \(k\)-nearest neighbor
- Decision Tree (read a tree, BuildTree, Bagging)
-
Unsupervised learning non-parametric
- \(k\)-means clustering

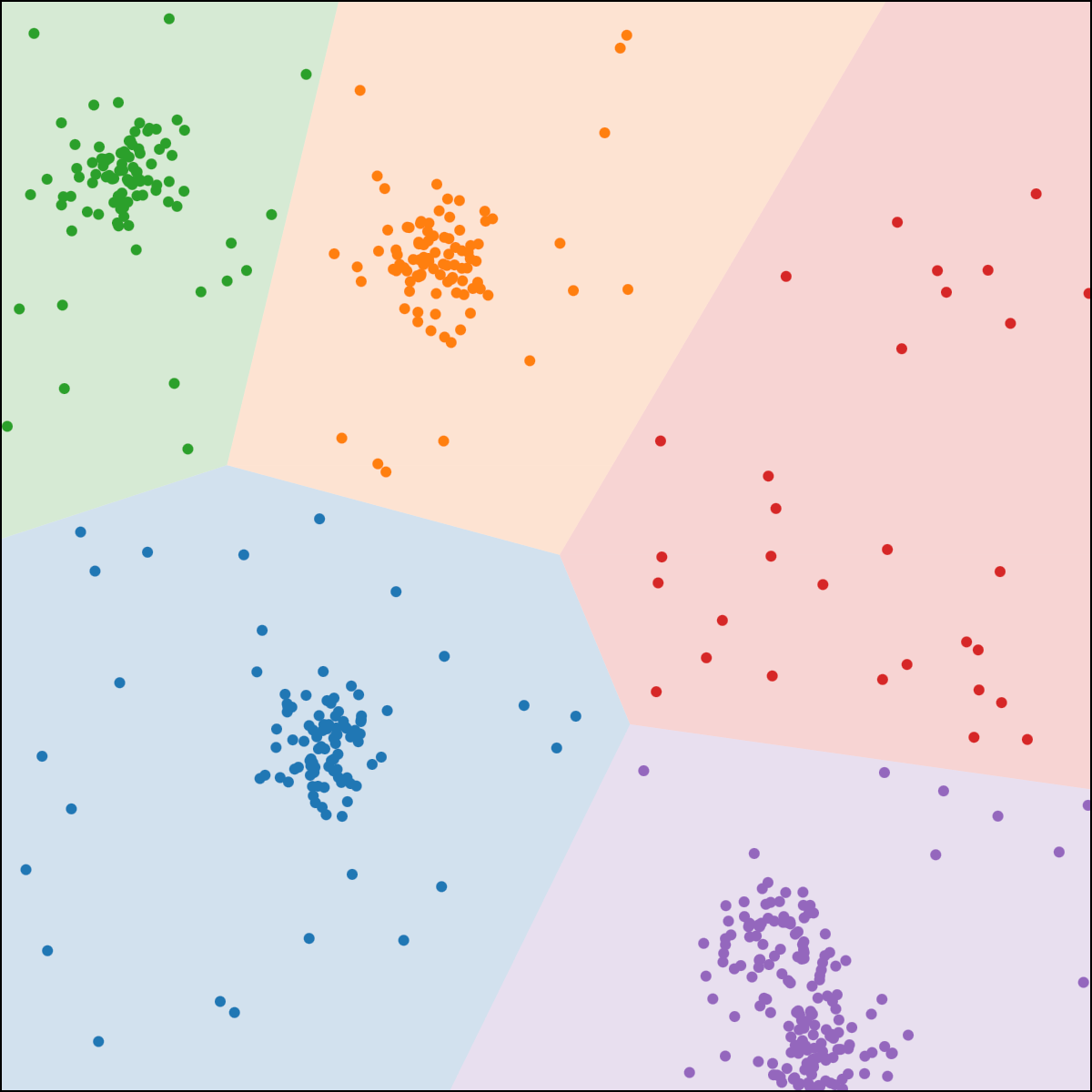
\(k\)-means clustering
structure discovery without labels
- \(x_1\): longitude, \(x_2\): latitude
- \(n\) person, person \(i\) location \(x^{(i)}\)

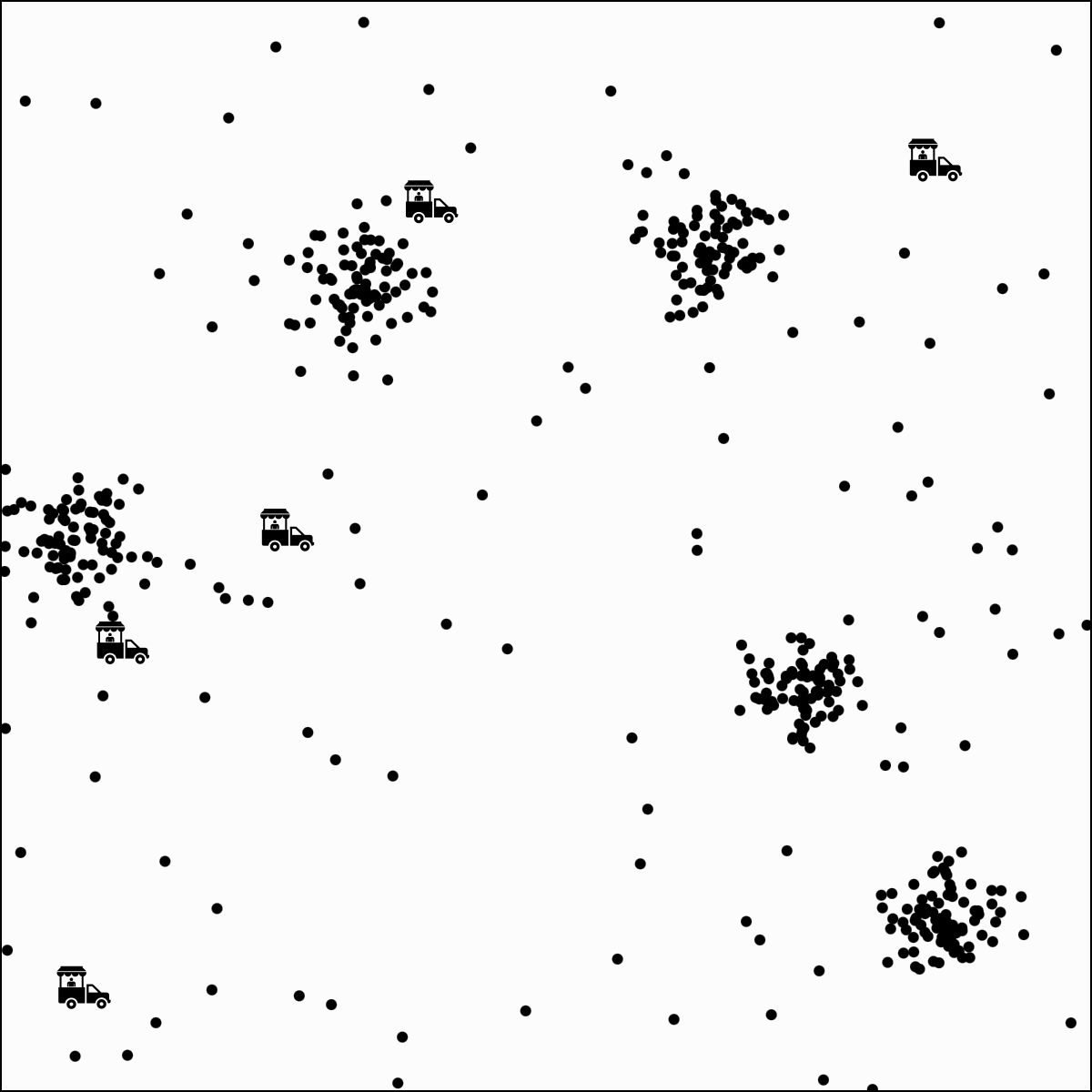
Food-truck placement
- \(x_1\): longitude, \(x_2\): latitude
- \(n\) person, person \(i\) location \(x^{(i)}\)
- \(k\) food trucks, say \(k=5\)
Food-truck placement

- \(x_1\): longitude, \(x_2\): latitude
- \(n\) person, person \(i\) location \(x^{(i)}\)
- \(k\) food trucks, say \(k=5\)
- Food truck \(j\) location \(\mu^{(j)}\)

Food-truck placement
- \(x_1\): longitude, \(x_2\): latitude
- \(n\) person, person \(i\) location \(x^{(i)}\)
- \(k\) food trucks, say \(k=5\)
- Food truck \(j\) location \(\mu^{(j)}\)
- Loss for \(i\) to walk to truck \(j\) : \(\left\|x^{(i)}-\mu^{(j)}\right\|^2\)

Food-truck placement
- \(x_1\): longitude, \(x_2\): latitude
- \(n\) person, person \(i\) location \(x^{(i)}\)
- \(k\) food trucks, say \(k=5\)
- Food truck \(j\) location \(\mu^{(j)}\)
- Loss for \(i\) to walk to truck \(j\) : \(\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
- Index of the truck to which \(i\) walks: \(y^{(i)}\)
- Person \(i\) overall loss:
\(\sum_{j=1}^k \mathbf{1}\left\{y^{(i)}=j\right\}\left\|x^{(i)}-\mu^{(j)}\right\|_2^2\)

indicator function
1 if person \(i\) is assigned to truck \(j,\) 0 o/w.
Food-truck placement
\( \sum_{j=1}^k \mathbf{1}\left\{y^{(i)}=j\right\}\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
\(k\)-means objective
clustering membership
clustering centroid location
sum over cluster
sum over data points
can switch the order = \(\sum_{j=1}^k \sum_{i=1}^n \mathbf{1}\left\{y^{(i)}=j\right\}\left\|x^{(i)}-\mu^{(j)}\right\|_2^2\)
what we learn
\(\sum_{i=1}^n\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
10 return \(\mu, y\)

3 \(y_{\text {old }} = y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
10 return \(\mu, y\)
3 \(y_{\text {old }} = y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
1 \(\mu, y=\) random initialization


2 for \(t=1\) to \(\tau\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
10 return \(\mu, y\)
3 \(y_{\text {old }} = y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)


1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
10 return \(\mu, y\)
3 \(y_{\text {old }} = y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)


1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
10 return \(\mu, y\)
3 \(y_{\text {old }} = y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)


1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
10 return \(\mu, y\)
3 \(y_{\text {old }} = y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
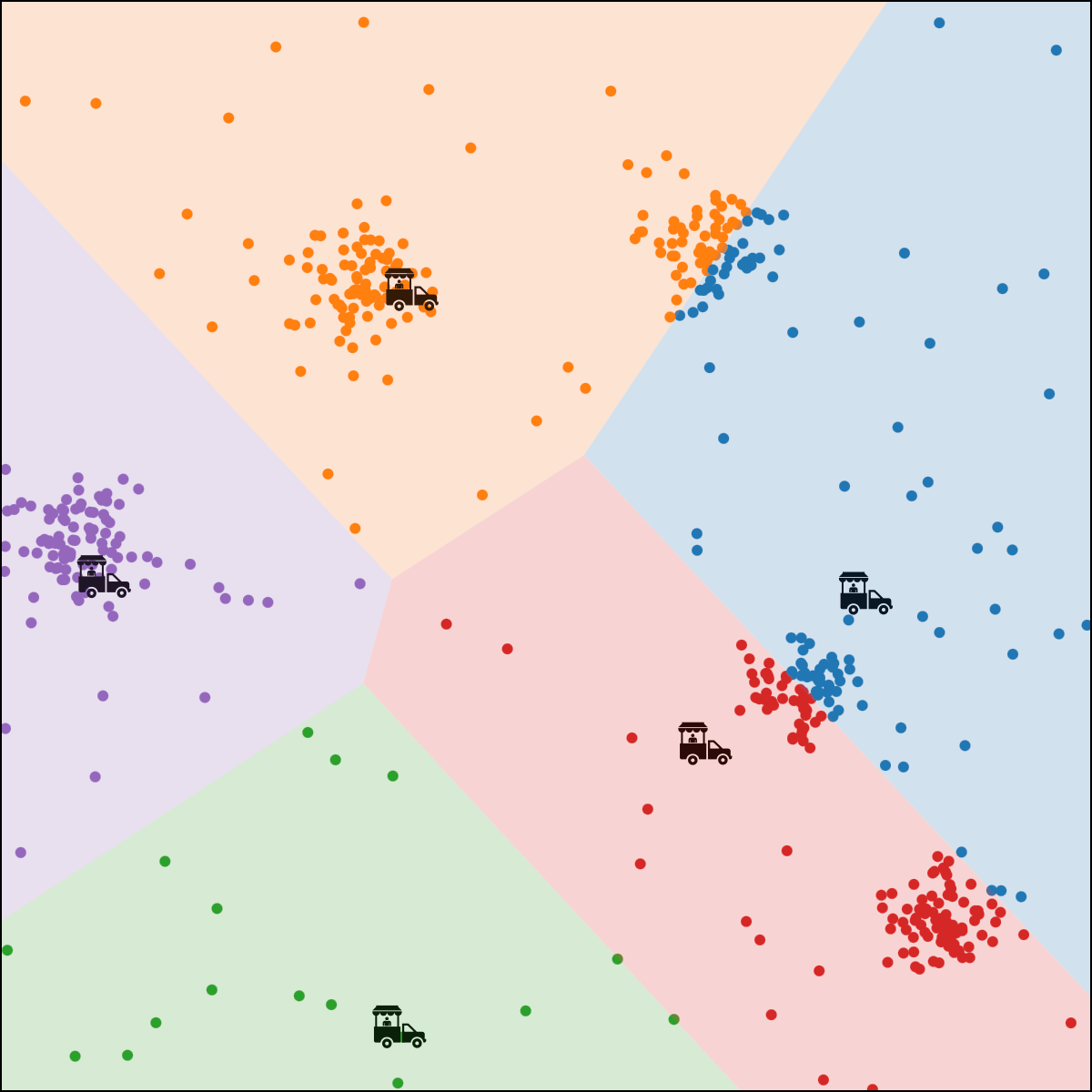
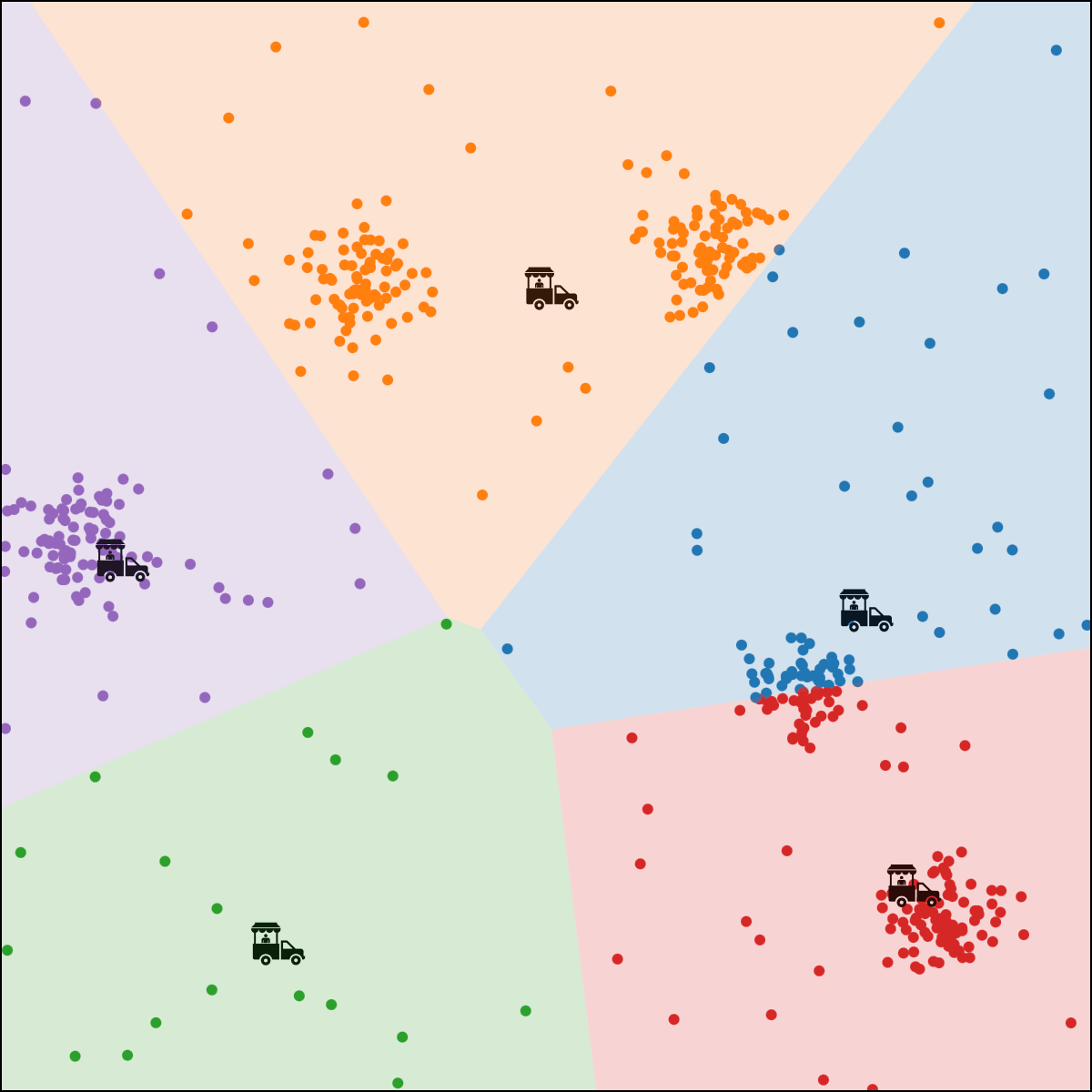
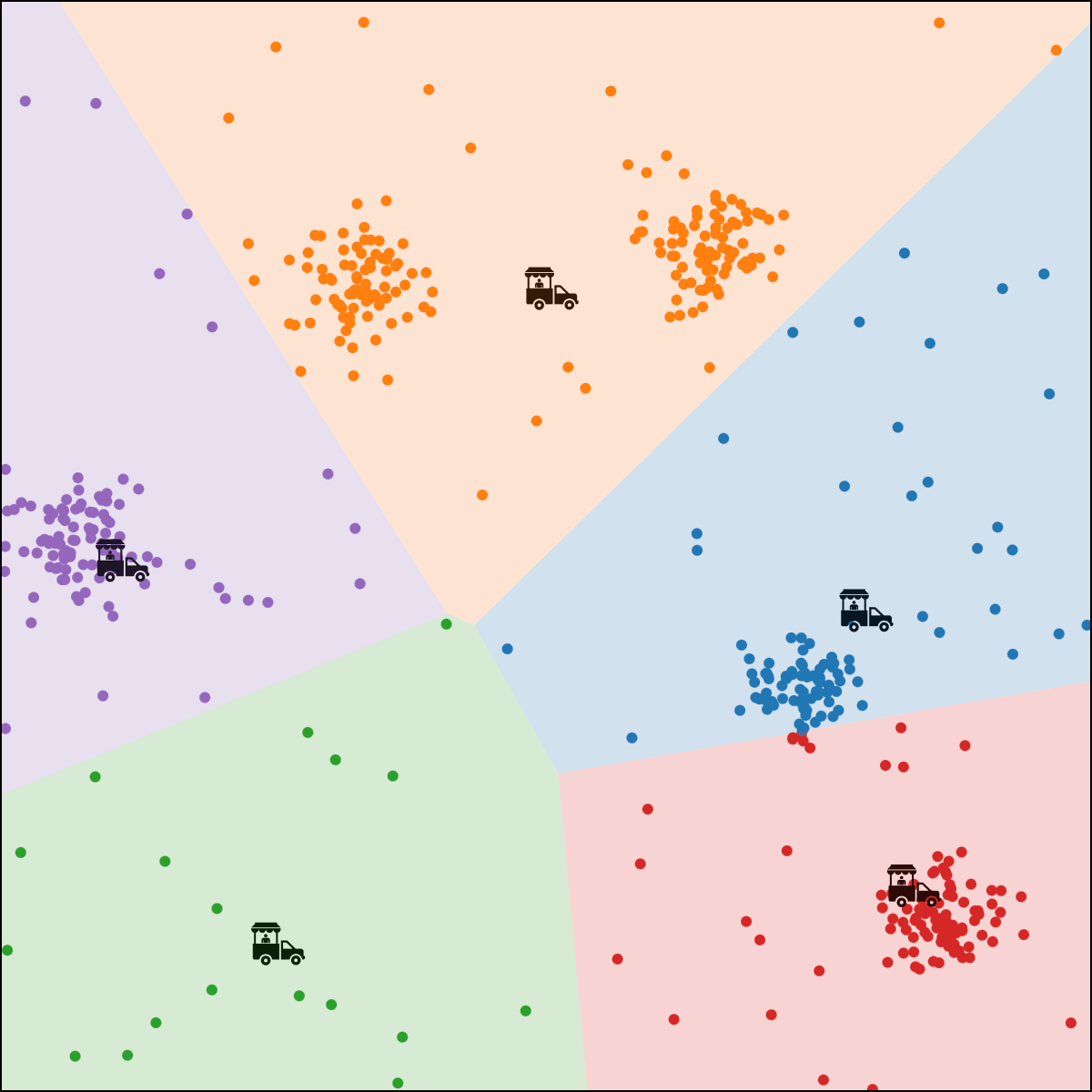
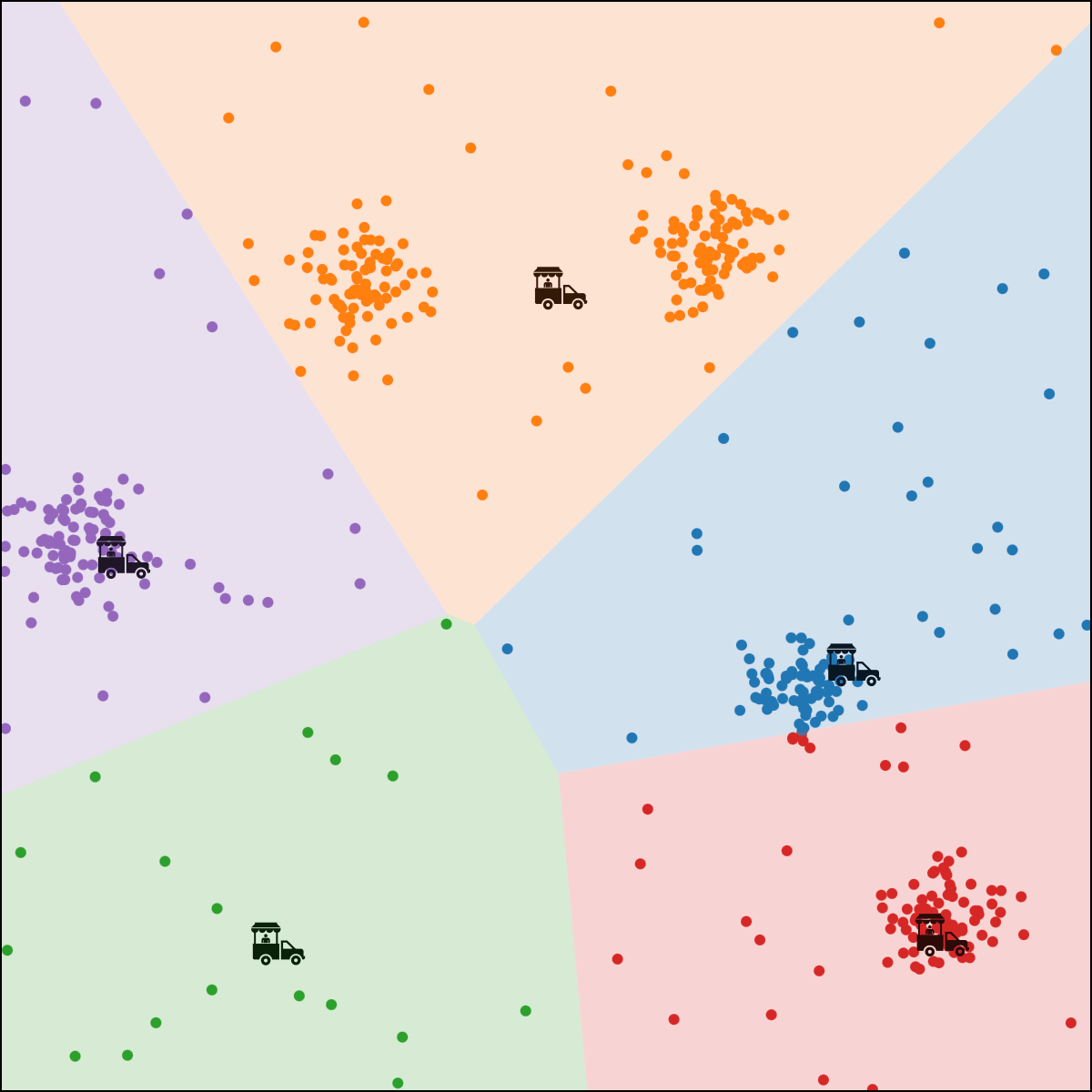
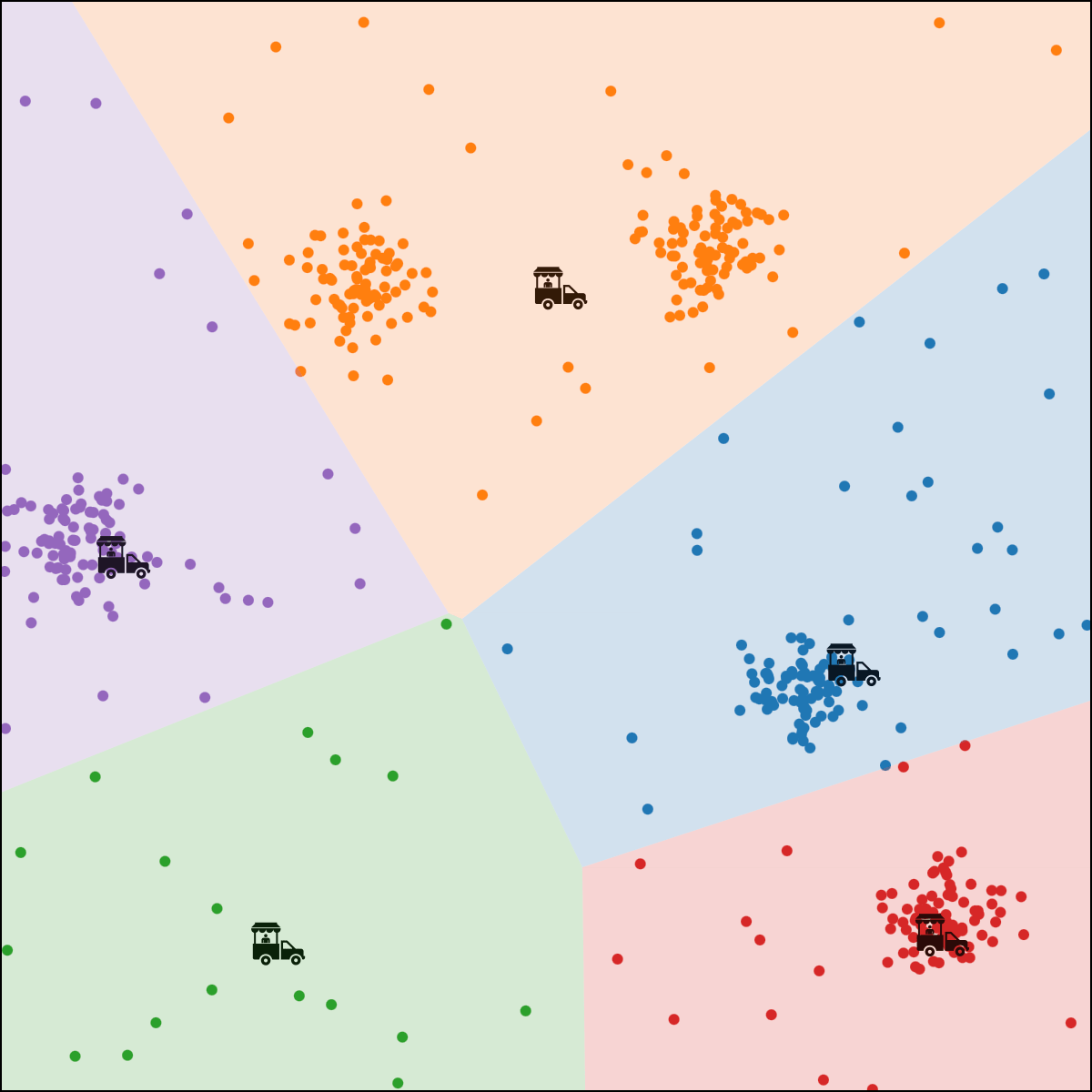
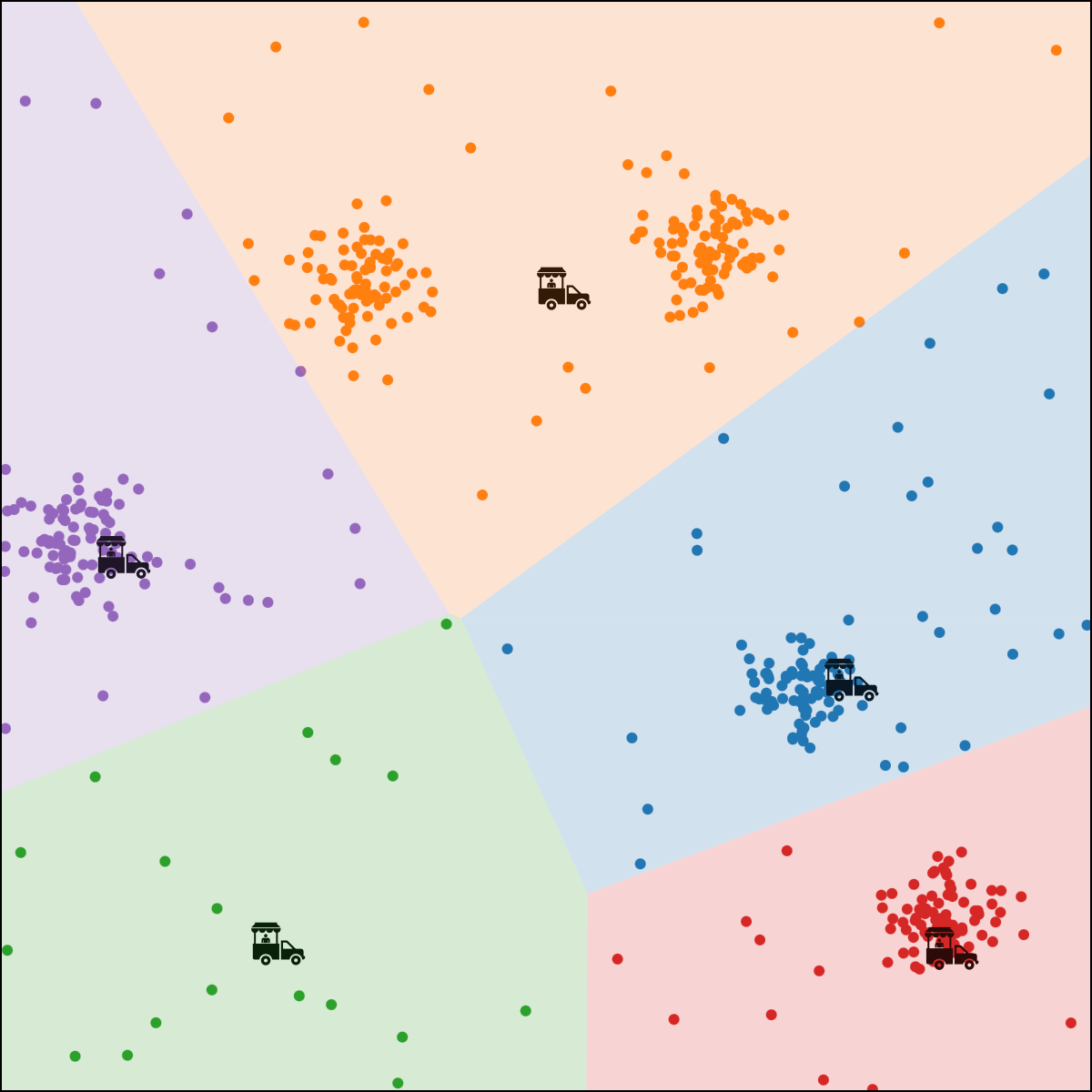
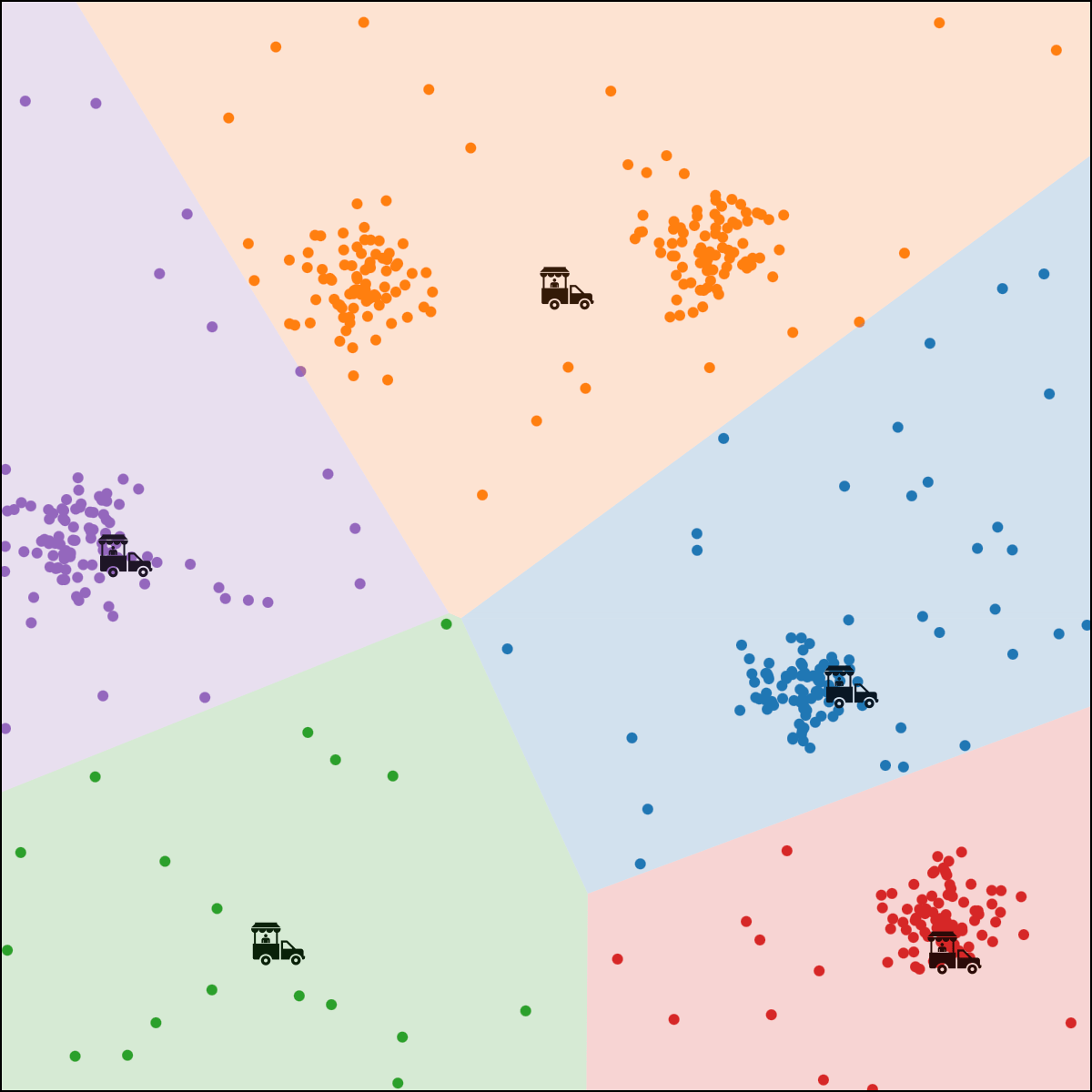
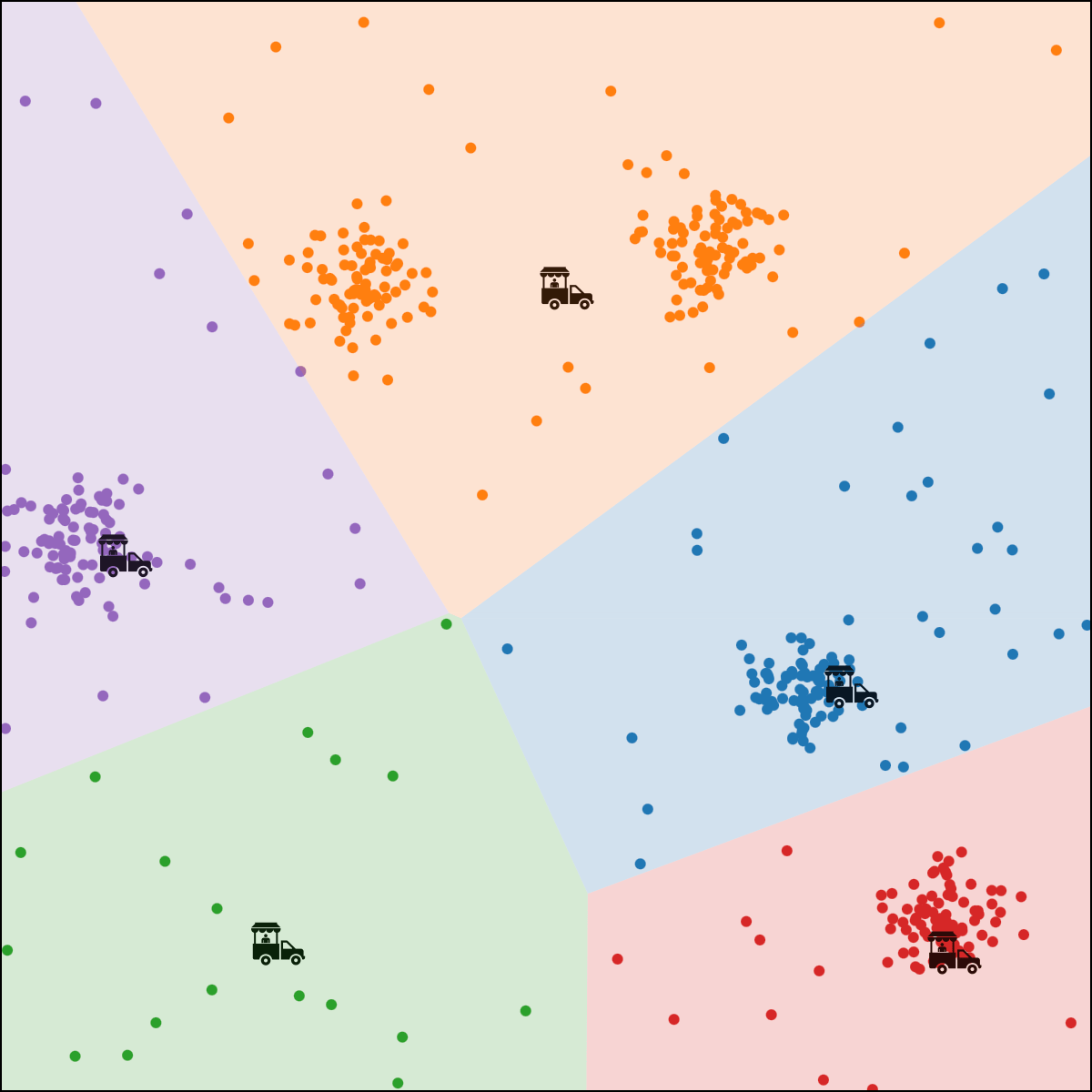
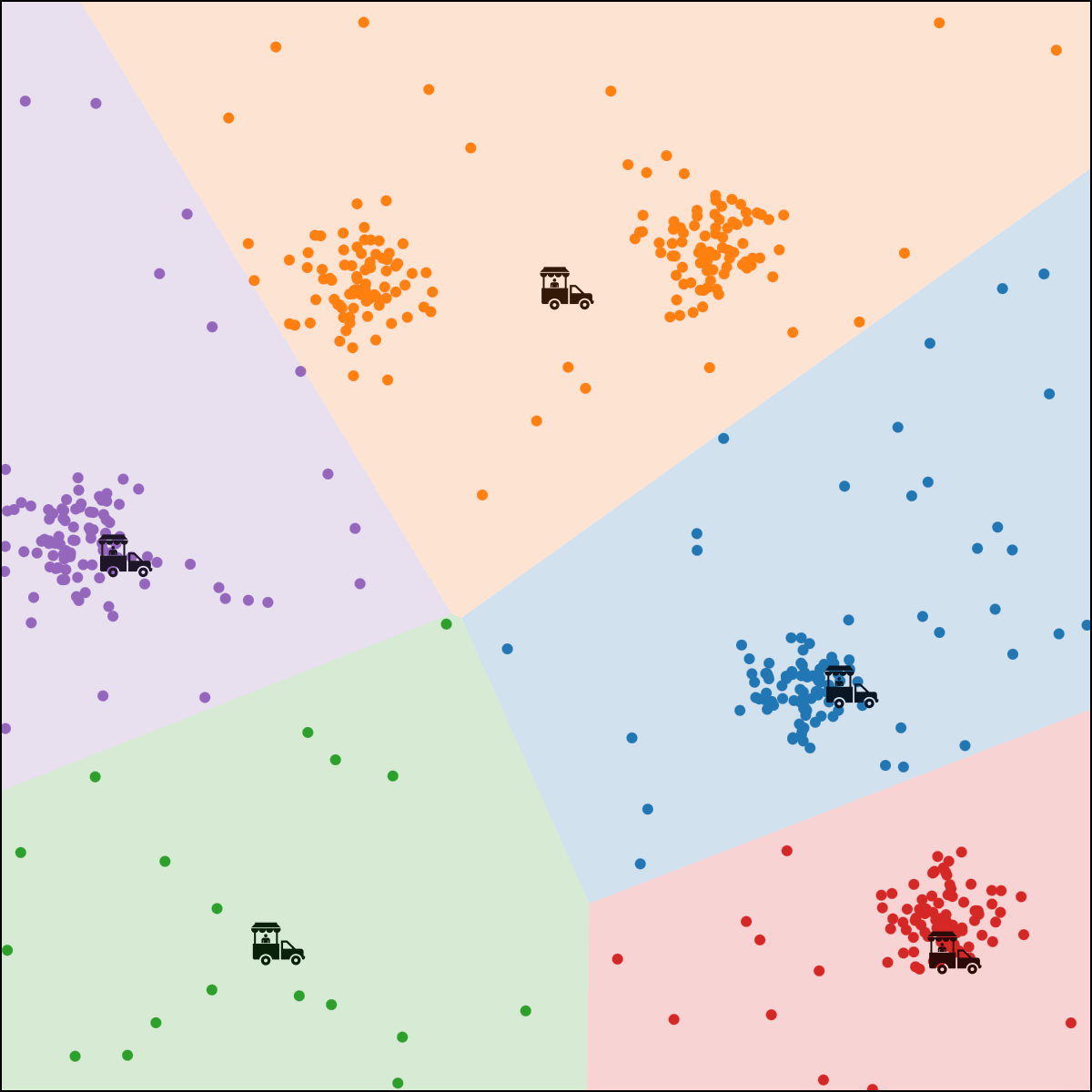
person \(i\) assigned to food truck \(j\), feature space partition color-coded.
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
\(\dots\)

3 \(y_{\text {old }} = y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)

3 \(y_{\text {old }} = y\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
\(N_j = \sum_{i=1}^n \mathbf{1}\left\{y^{(i)}=j\right\}\)
move food truck \(j\) to the central location of all people assigned to it.
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
\(\dots\)

3 \(y_{\text {old }} = y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
2 for \(t=1\) to \(\tau\)


3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
2 for \(t=1\) to \(\tau\)


3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
2 for \(t=1\) to \(\tau\)

3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)

3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break


3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break


3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break


3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)

K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
2 for \(t=1\) to \(\tau\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)

3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)

K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)

K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)

K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)

K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)

K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbf{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
3 \(y_{\text {old }} = y\)
10 return \(\mu, y\)

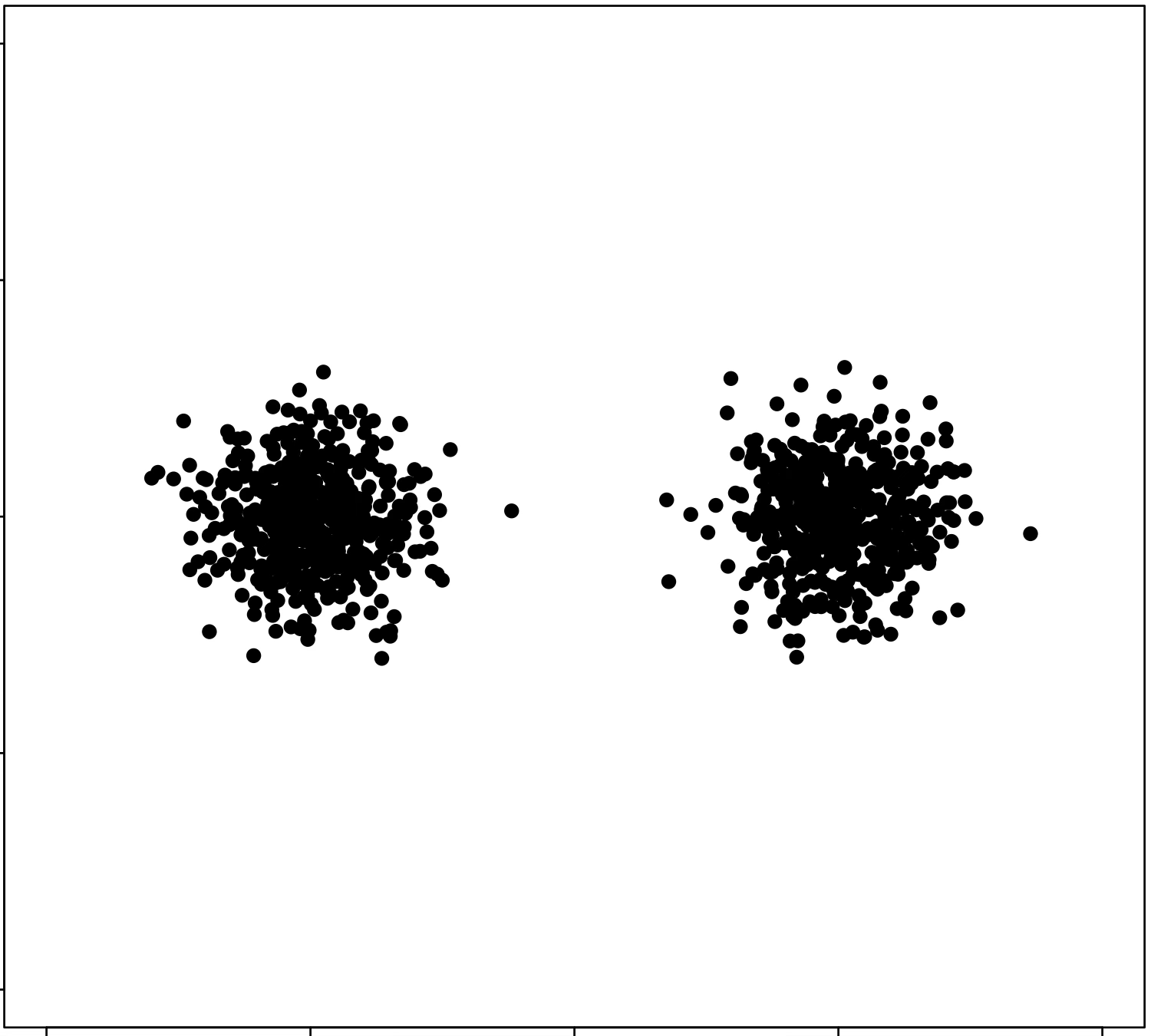
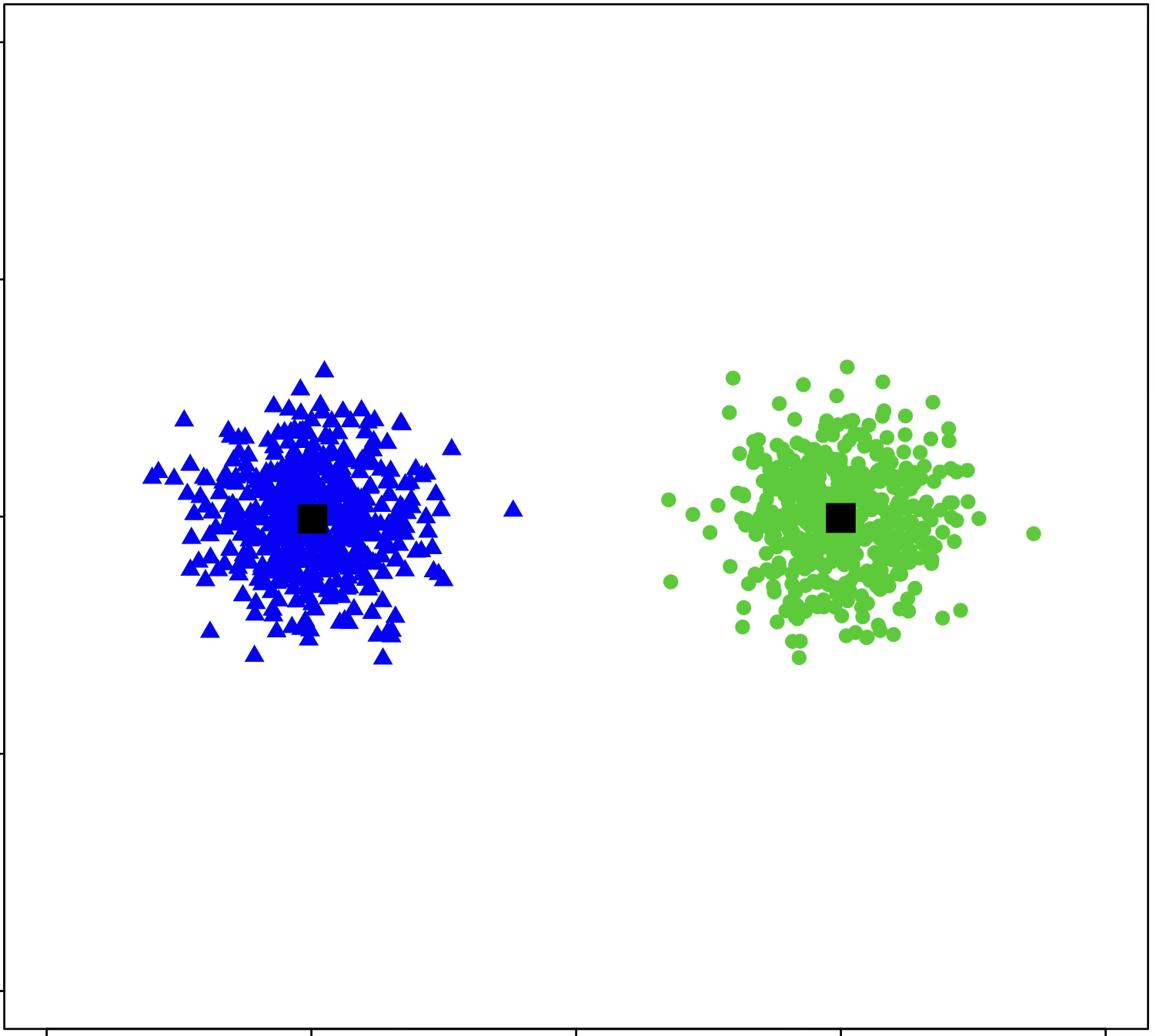
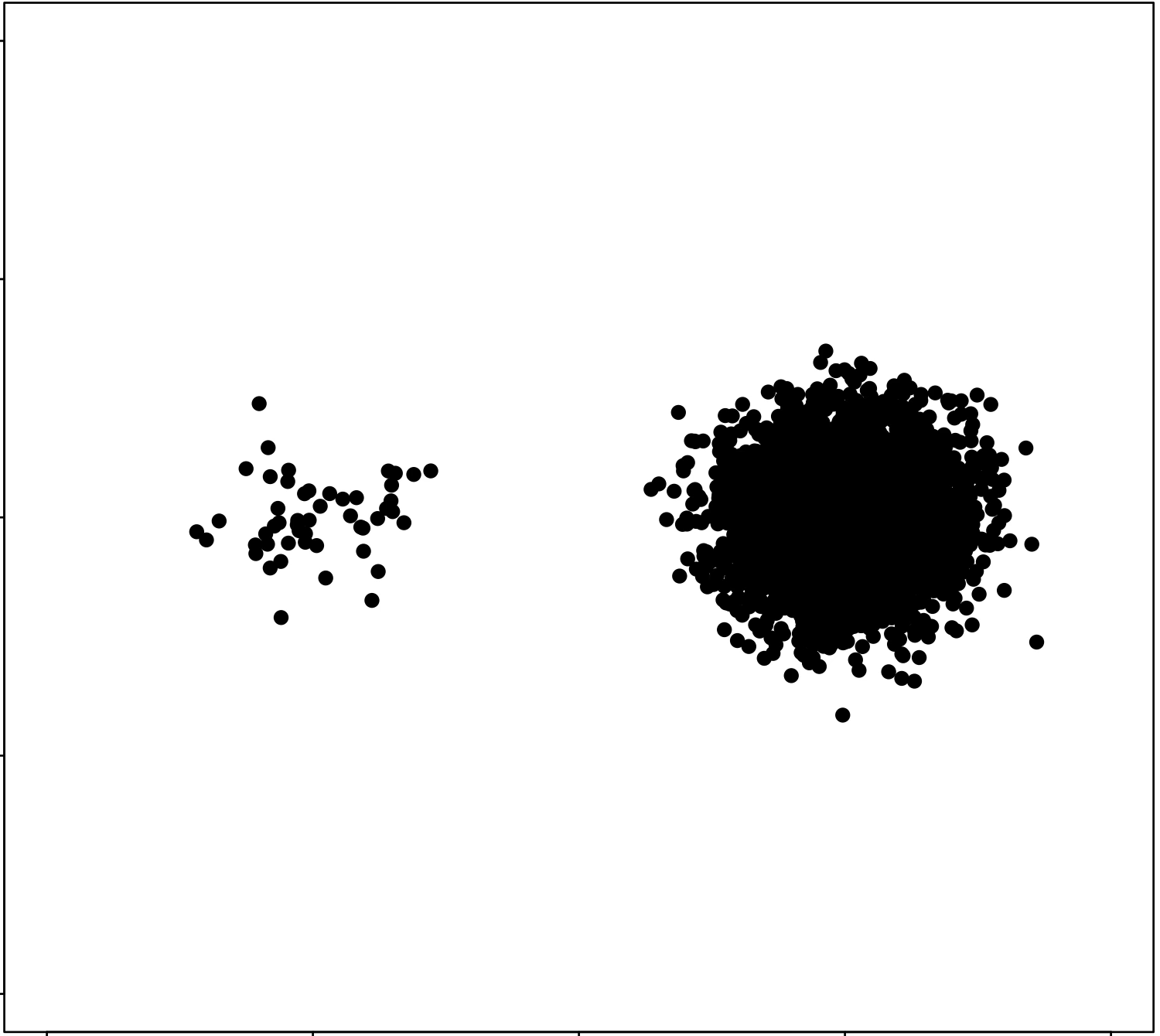
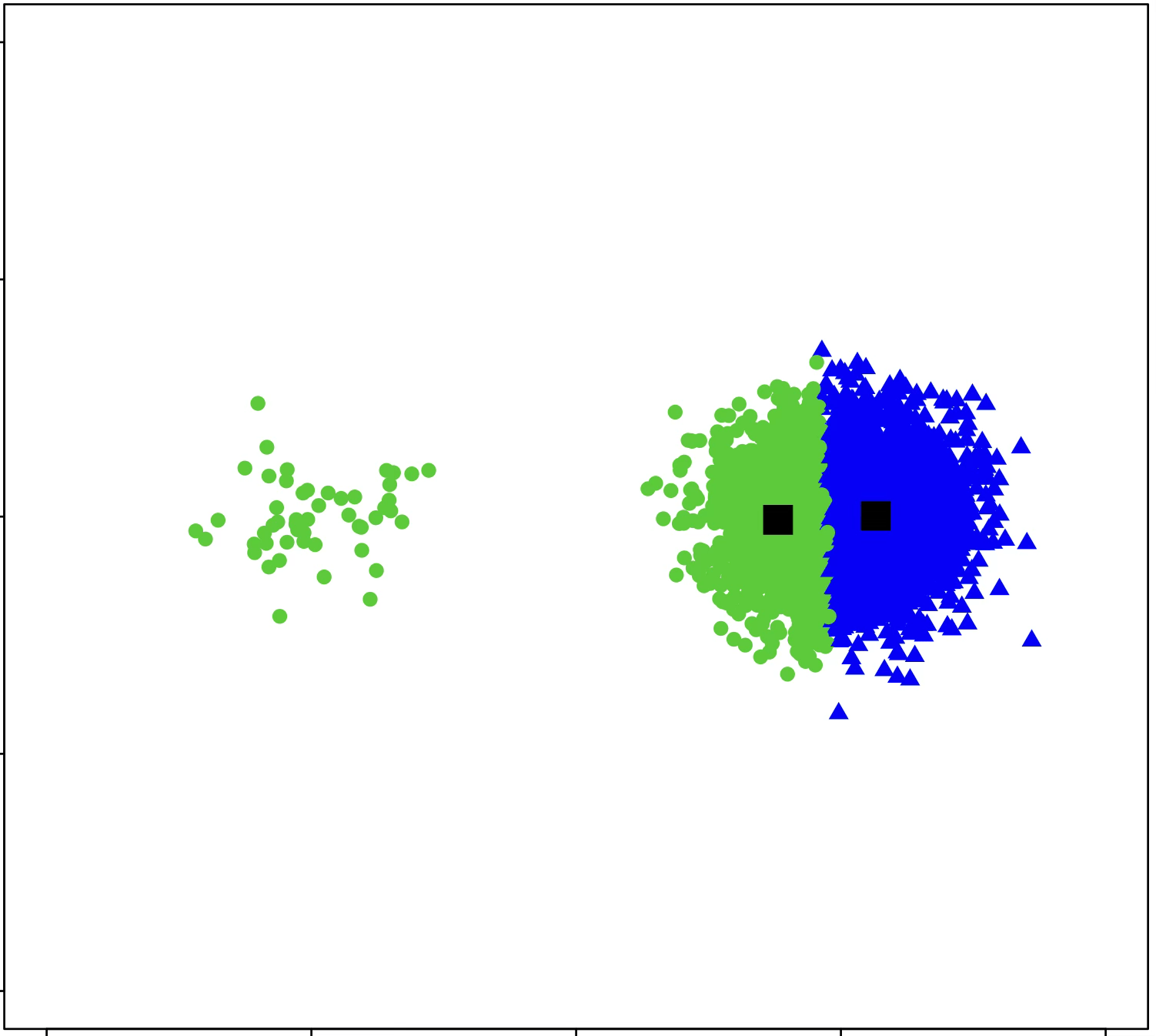
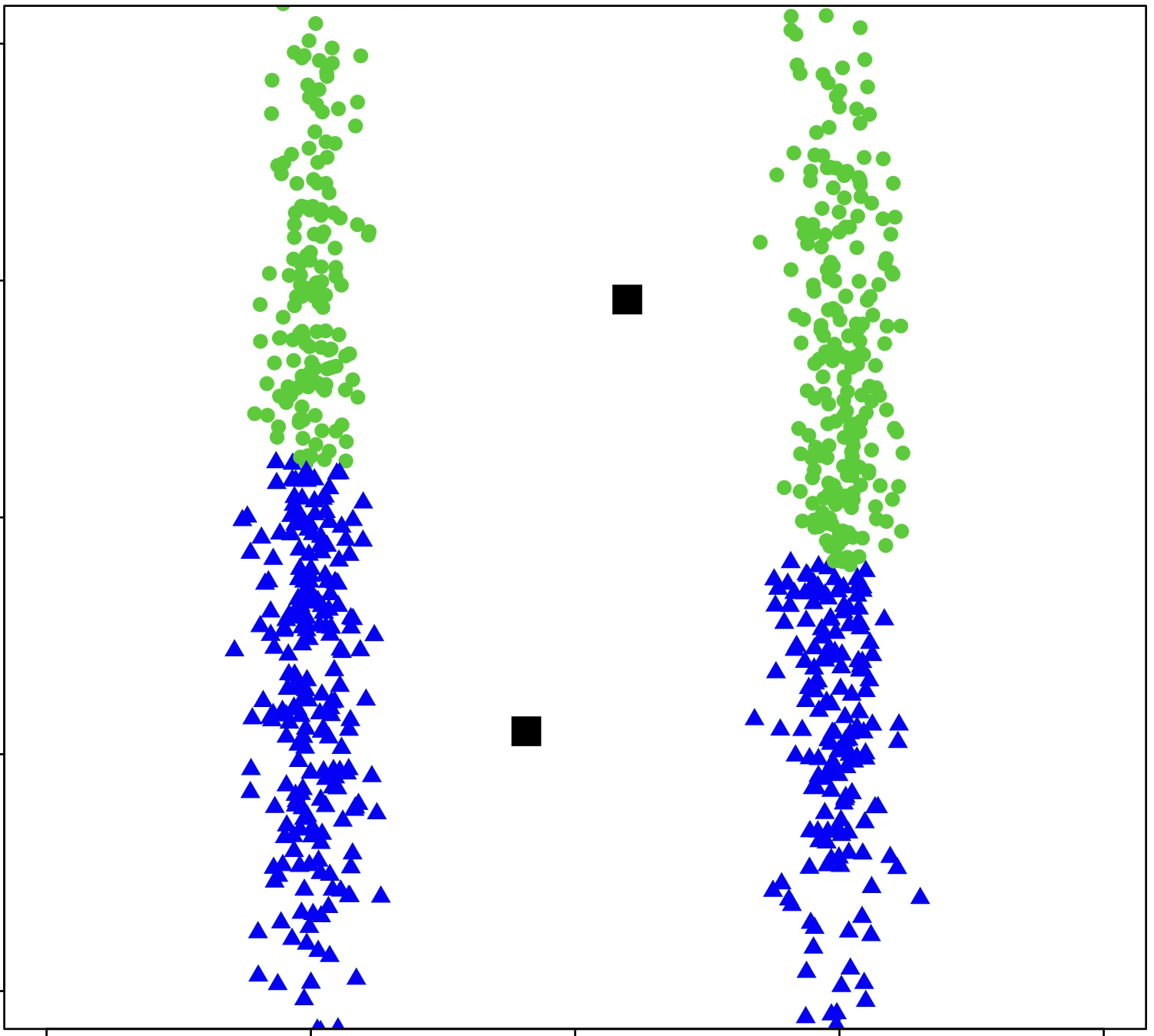
\(k\)-means algorithm is sensitive to initialization
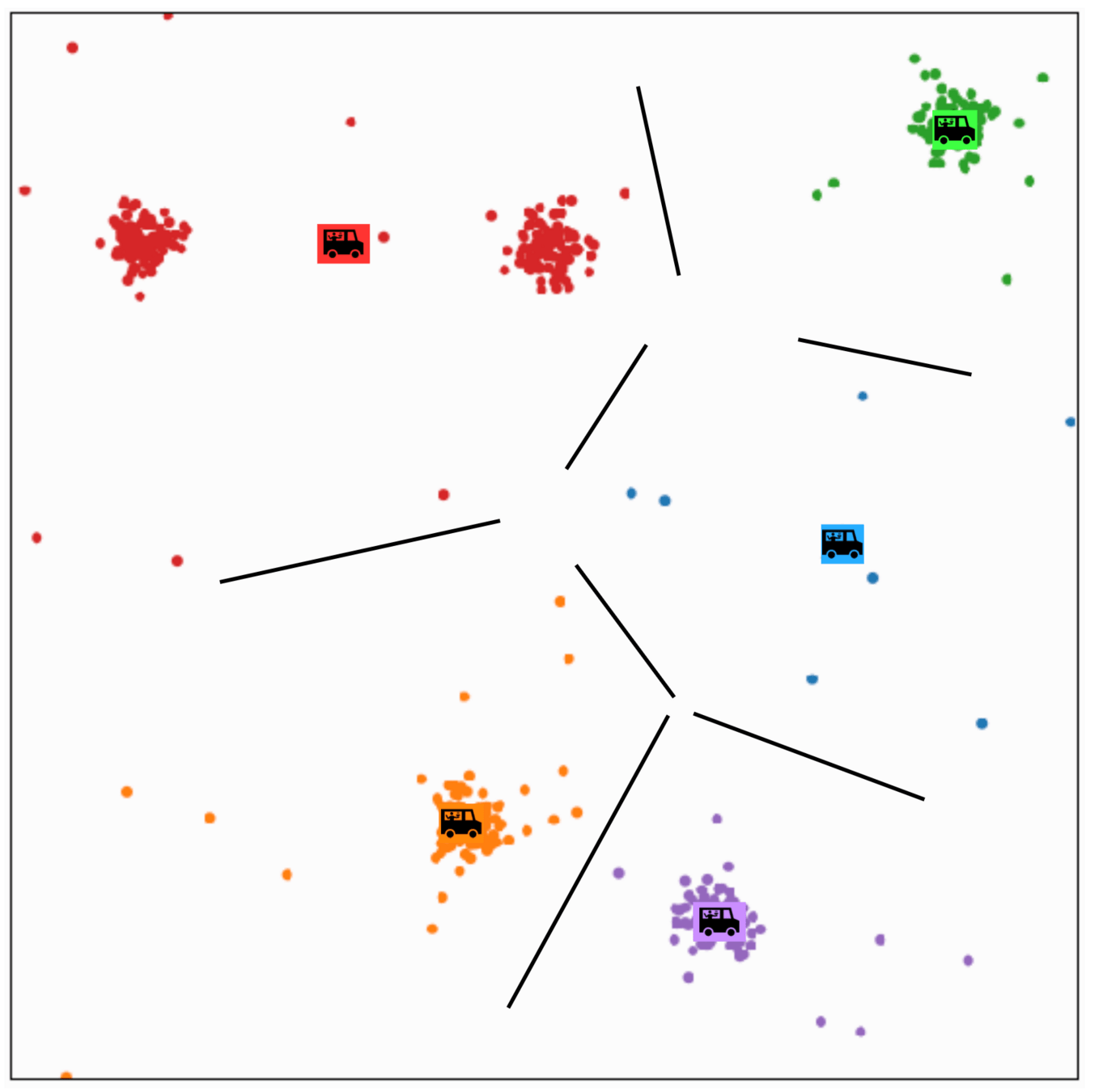
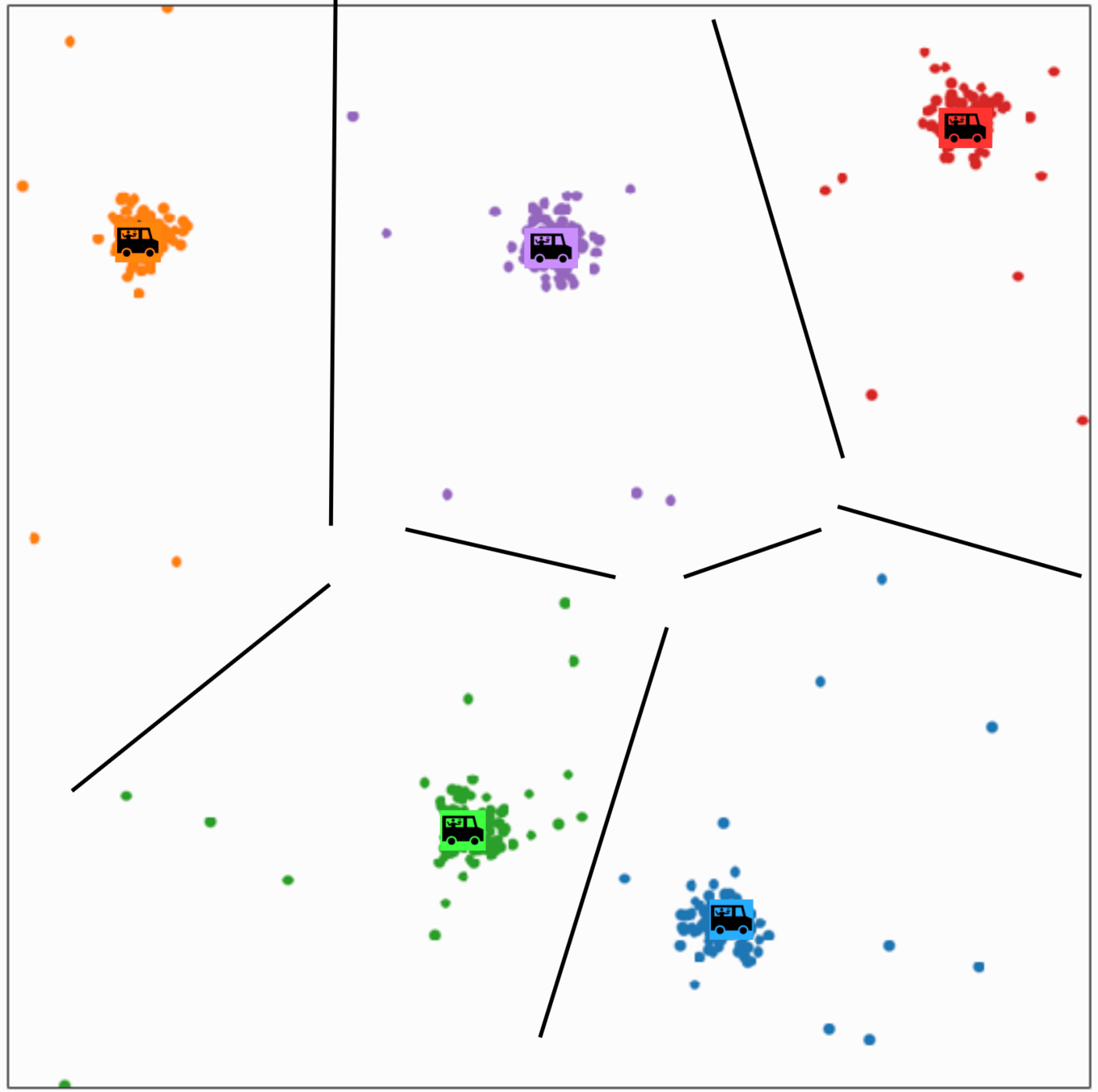
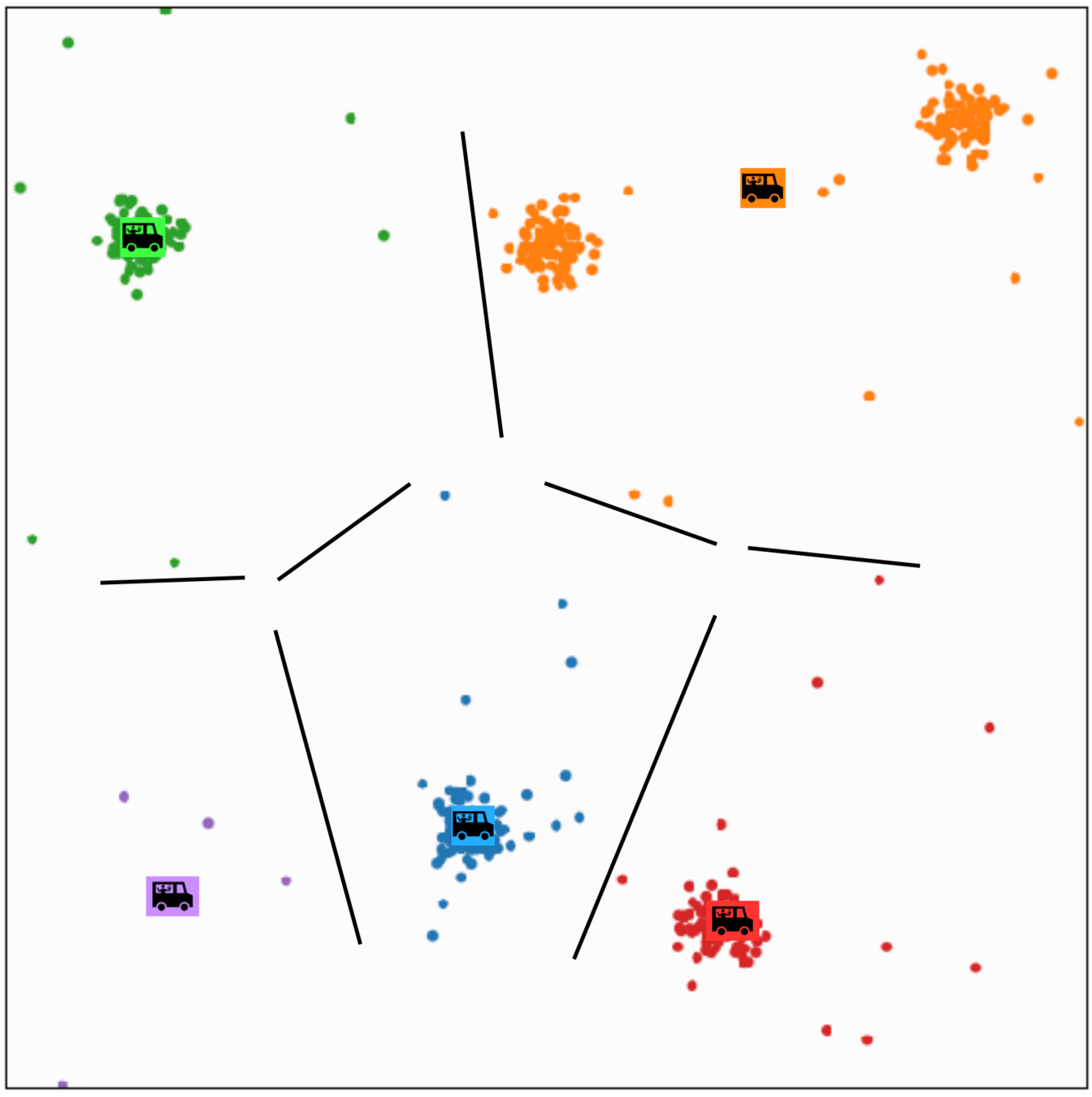
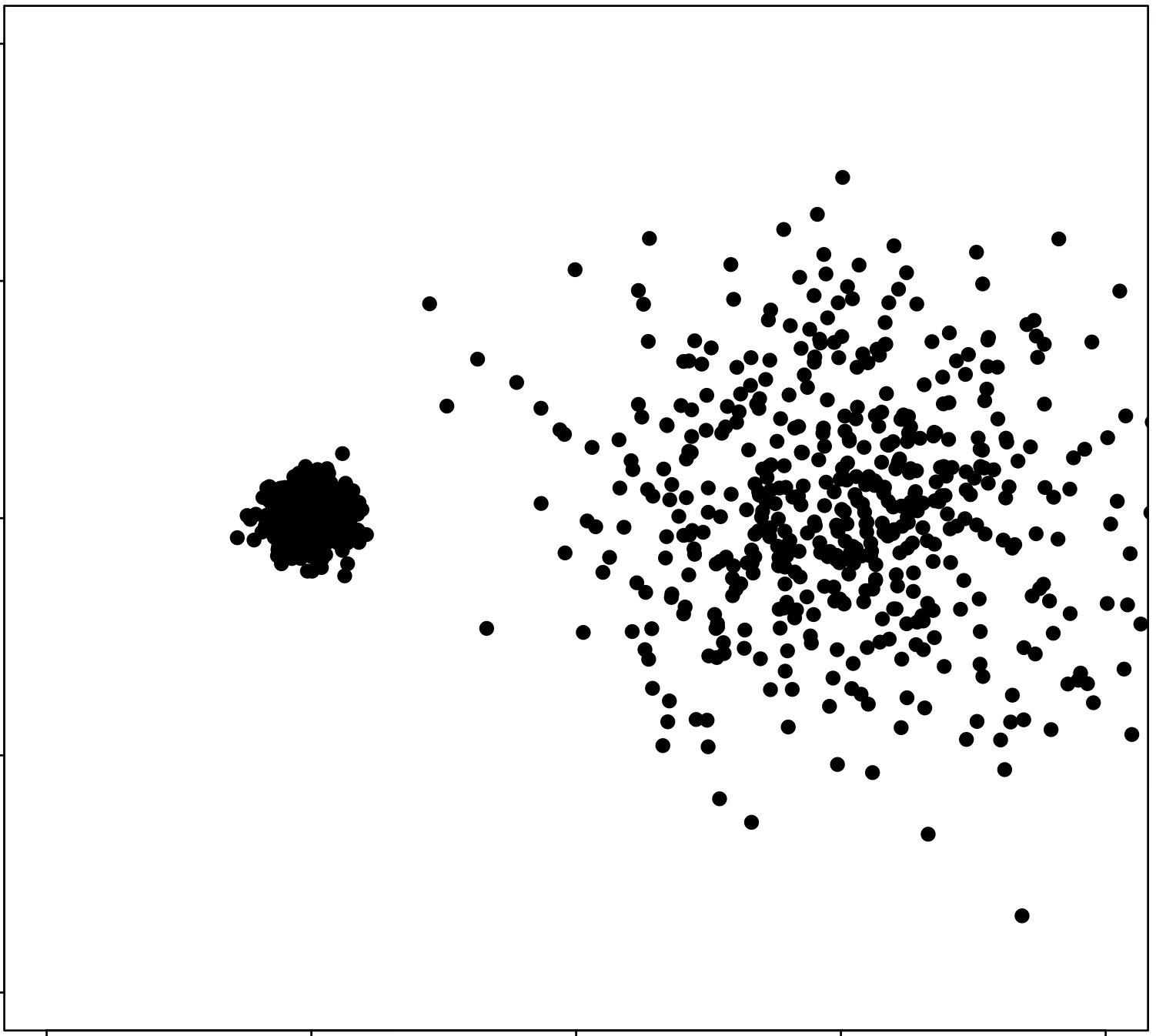
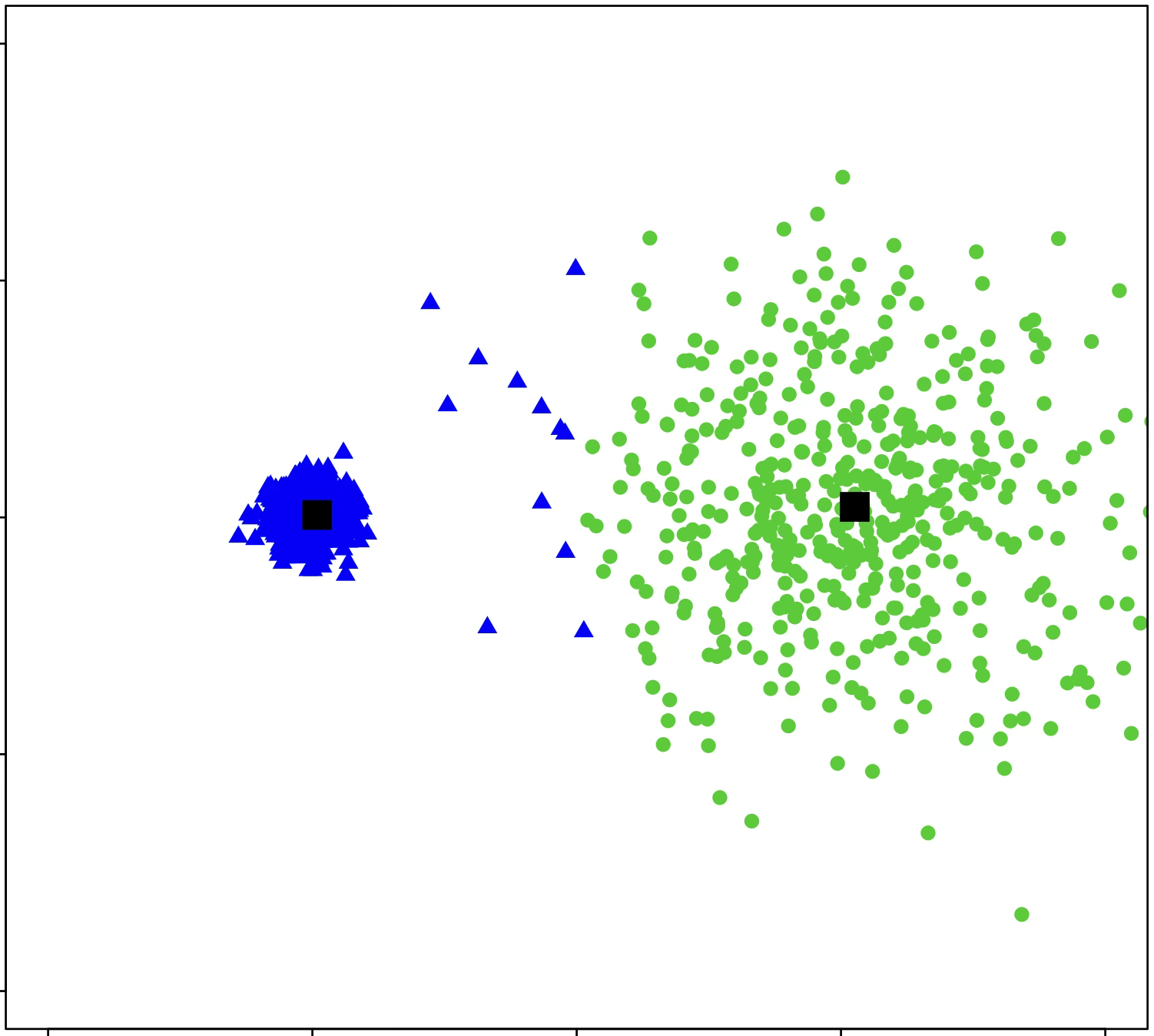
\(k\)-means algorithm is sensitive to \(k\)

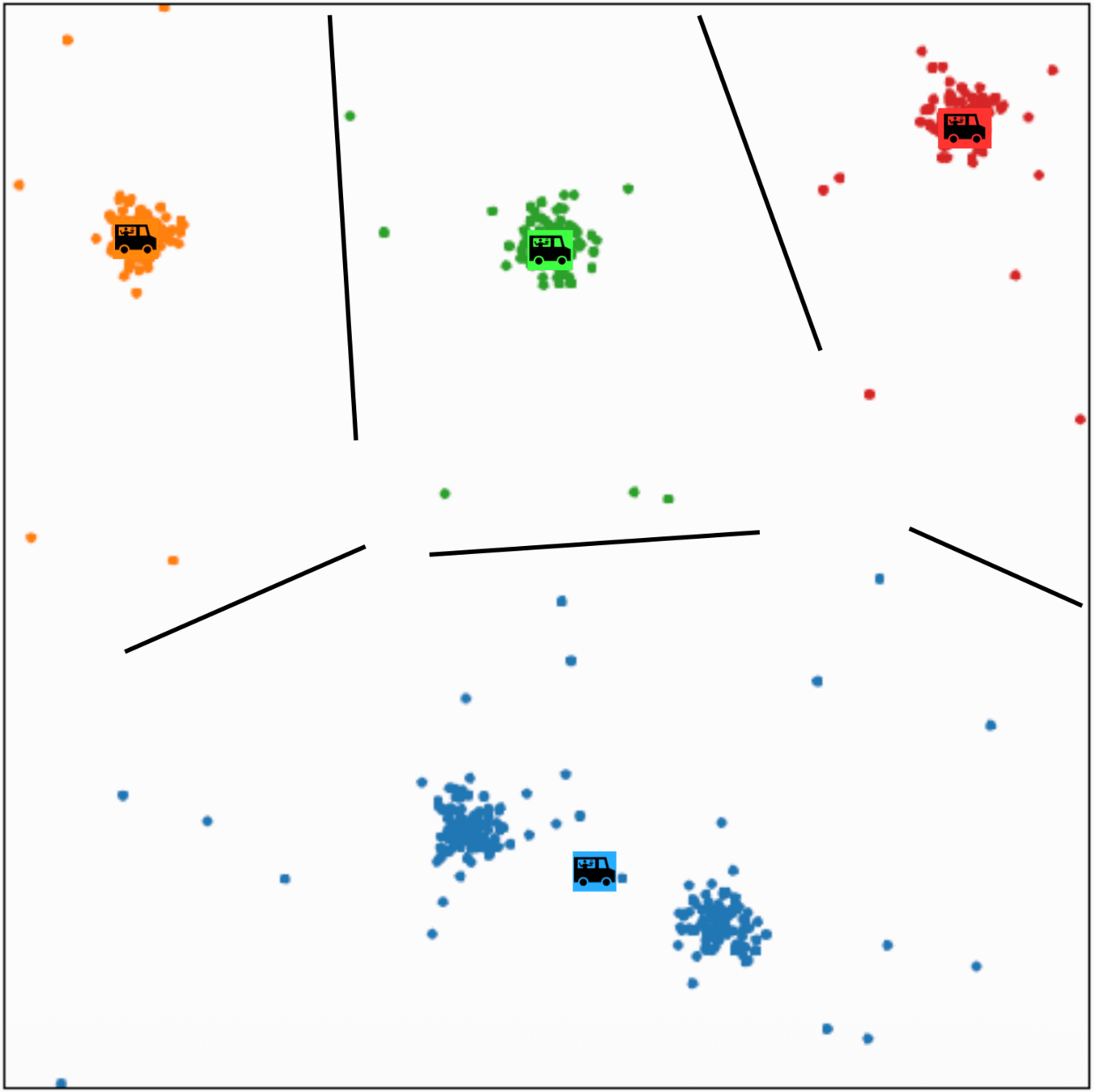
(\(k\)-means works well for well-separated circular clusters of the same size)
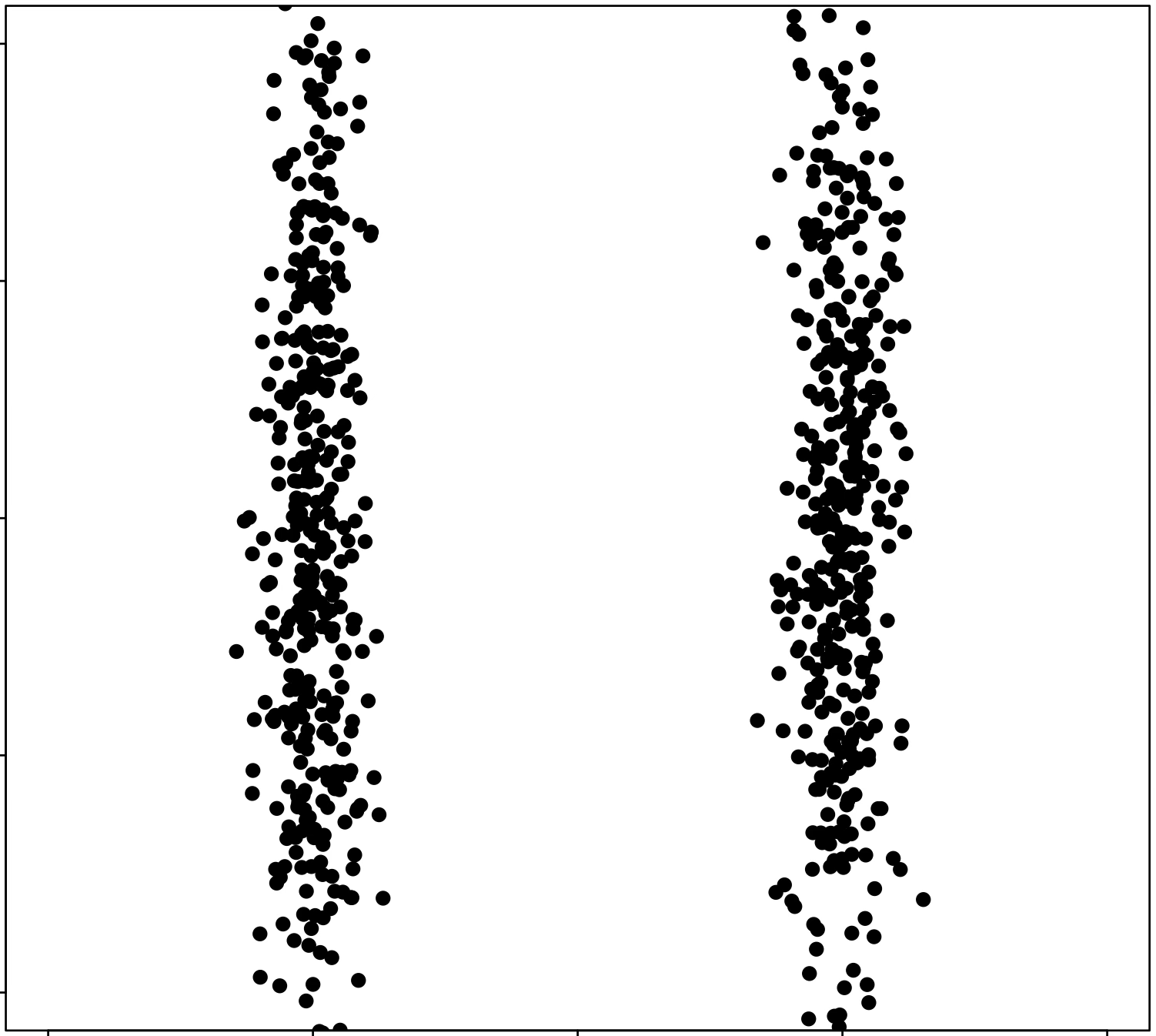
(\(k\)-means can be thought of as performing special auto-encodering)
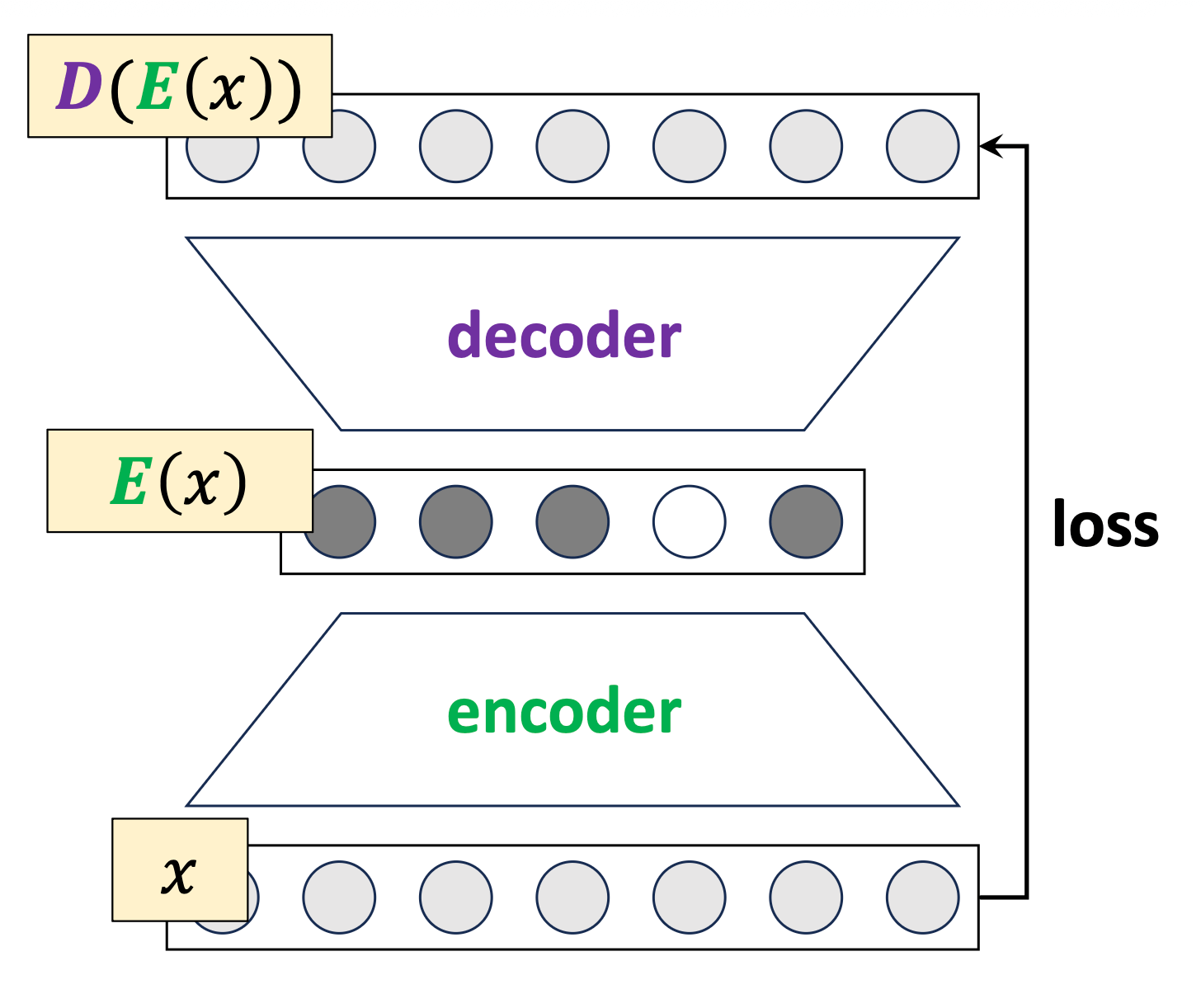
encoder 𝑬: map 𝑥 to a (one-hot) code
decoder 𝑫: map a code to a center
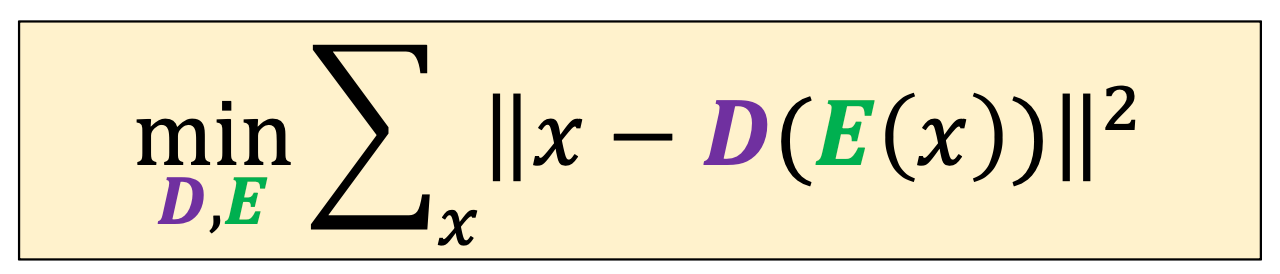
(cluster center are prototypes)
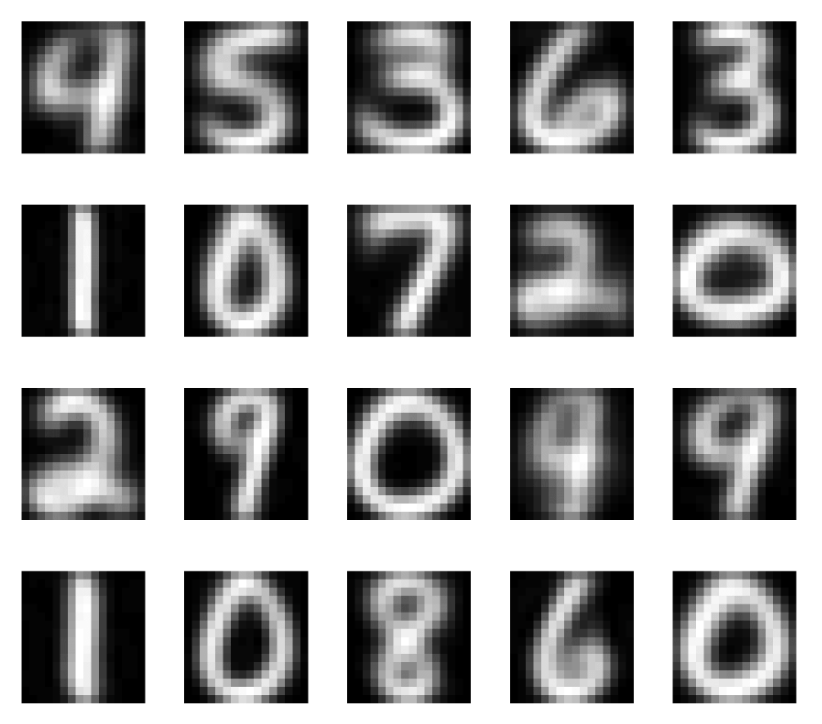
not actual data points MNIST However, they clearly show that MNIST has strong cluster structure defined by the different digit types.
learned representations
Summary
- Non-parametric models let data define structure — balancing flexibility, interpretability, and intuition. Complexity grows with data; make few assumptions about functional form.
- \(k\)-Nearest Neighbors (kNN): Predict by looking at nearby training points; depends on chosen distance metric. Works well for small, low-dim data but costly in high dimensions.
- Decision Trees: Learn interpretable, flow-chart-like rules by recursively splitting data. Regularize by growing deep trees, then pruning to simplify. Ensembles: Combine many simple models so they can vote → stronger, more stable predictors.
- \(k\)-Means Clustering: Unsupervised grouping of similar data using a distance measure. The k-means algorithm is sensitive to initialization and the choice of \(k\).
- kNN ↔ local averaging, Trees ↔ adaptive partition, Ensembles ↔ aggregation, k-Means ↔ unsupervised structure.
Thanks!
We'd love to hear your thoughts.
Bagging
Training data \(\mathcal{D}_n\)
\(\left(x^{(1)}, y^{(1)}\right)\)
\(\left(x^{(2)}, y^{(2)}\right)\)
\(\left(x^{(3)}, y^{(3)}\right)\)
\(\left(x^{(4)}, y^{(4)}\right)\)
\(\left(x^{(5)}, y^{(5)}\right)\)
\(\tilde{\mathcal{D}}_n^{(1)}\)
\(\tilde{x}^{(1)}, \tilde{y}^{(1)}\)
\(\tilde{x}^{(2)}, \tilde{y}^{(2)}\)
\(\tilde{x}^{(4)}, \tilde{y}^{(4)}\)
\(\tilde{x}^{(3)}, \tilde{y}^{(3)}\)
\(\tilde{x}^{(5)}, \tilde{y}^{(5)}\)
- Training data \(\mathcal{D}_n\)
- For \(b=1, \ldots, B\)
- Draw a new "data set" \(\tilde{\mathcal{D}}_n^{(b)}\) of size \(n\) by sampling with replacement from \(\mathcal{D}_n\)