Intro to Machine Learning

https://introml.mit.edu/

Lecture 11: Reinforcement Learning

Shen Shen

April 26, 2024

Outline

  • Recap: Markov Decision Processes
  • Reinforcement Learning Setup
    • What's changed from MDP?
  • Model-based methods
  • Model-free methods
    • (tabular) Q-learning
      • \(\epsilon\)-greedy action selection
      • exploration vs. exploitation
    • (neural network) Q-learning
  • RL setup again
    • What's changed from supervised learning?

MDP Definition and Goal

  • \(\mathcal{S}\) : state space, contains all possible states \(s\).
  • \(\mathcal{A}\) : action space, contains all possible actions \(a\).
  • \(\mathrm{T}\left(s, a, s^{\prime}\right)\) : the probability of transition from state \(s\) to \(s^{\prime}\) when action \(a\) is taken.
  • \(\mathrm{R}(s, a)\) : a function that takes in the (state, action) and returns a reward.
  • \(\gamma \in [0,1]\): discount factor, a scalar.
  • \(\pi{(s)}\) : policy, takes in a state and returns an action.

Ultimate goal of an MDP: Find the "best" policy \(\pi\).

State \(s\)

Action \(a\)

Reward \(r\)

\dots

Policy \(\pi(s)\)

Transition \(\mathrm{T}\left(s, a, s^{\prime}\right)\)

Reward \(\mathrm{R}(s, a)\)

time

a trajectory (aka an experience or rollout) \(\quad \tau=\left(s_0, a_0, r_0, s_1, a_1, r_1, \ldots\right)\)

r_0 = \\ \mathrm{R}(s_0, a_0)
r_1 = \\ \mathrm{R}(s_1, a_1)
r_2 = \\ \mathrm{R}(s_2, a_2)
r_4 = \\ \mathrm{R}(s_4, a_4)
r_5 = \\ \mathrm{R}(s_5, a_5)
r_6 = \\ \mathrm{R}(s_6, a_6)
r_7 = \\ \mathrm{R}(s_7, a_7)
\dots
r_3 = \\ \mathrm{R}(s_3, a_3)

how "good" is a trajectory?

\mathrm{R}(s_0, a_0)
\gamma \mathrm{R}(s_1, a_1)
\gamma^3\mathrm{R}(s_3, a_3)
\gamma^2 \mathrm{R}(s_2, a_2)
\gamma^4\mathrm{R}(s_4, a_4)
\gamma^5\mathrm{R}(s_5, a_5)
\gamma^6\mathrm{R}(s_6, a_6)
\gamma^7\mathrm{R}(s_7, a_7)
\dots
+
+
+
+
+
+
+
  • almost all transitions are deterministic:

    • Normally, actions take Mario to the “intended” state.

      • E.g., in state (7), action “↑” gets to state (4)

    • If an action would've taken us out of this world, stay put

      • E.g., in state (9), action “→” gets back to state (9)

    • except, in state (6), action “↑” leads to two possibilities:

      • 20% chance ends in (2)

      • 80% chance ends in (3)

1
2
9
8
7
5
4
3
6
80\%
20\%

Running example: Mario in a grid-world 

  • 9 possible states
  • 4 possible actions: {Up ↑, Down ↓, Left ←, Right →}
1
2
9
8
7
5
4
3
6
80\%
20\%

example cont'd

1
1
1
1
-10
-10
-10
-10
  • (state, action) pair can get Mario rewards:
  • Any other (state, action) pairs get reward 0
  • In state (6), any action gets reward -10
  • In state (3), any action gets reward +1

actions: {Up ↑, Down ↓, Left ←, Right →}

  • goal is to find a gameplay policy strategy for Mario, to get maximum expected sum of discounted rewards, with a discount facotor \(\gamma = 0.9\) 
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
-10
V_{\pi}^0(s)
V_{\pi}^1(s)
V_{\pi}^2(s)
0
0
-9
0
0
0
0
1.9
-9.28

Now, let's think about \(V_\pi^3(6)\)

1
2
9
8
7
5
4
3
6
80\%
20\%

Recall:

 

 

 

 

 

 

\(\pi(s) =  ``\uparrow",\  \forall s\)

\(\mathrm{R}(3, \uparrow) = 1\)

\(\mathrm{R}(6, \uparrow) = -10\)

\(\gamma = 0.9\)

2

3

action \(\uparrow\)

action \(\uparrow\)

\mathrm{R}(3, \uparrow)
\mathrm{R}(2, \uparrow)
\gamma^2
\gamma^2
\gamma^2
\mathrm{R}(2, \uparrow)
\mathrm{R}(3, \uparrow)
\gamma^2

6

action \(\uparrow\)

\mathrm{R}(6, \uparrow)
\mathrm{R}(6, \uparrow)
\gamma
\gamma
\mathrm{R}(2, \uparrow)
\mathrm{R}(2, \uparrow)
20\%
20\%

2

action \(\uparrow\)

3

80\%
80\%

action \(\uparrow\)

\gamma
\gamma
\mathrm{R}(3, \uparrow)
\mathrm{R}(3, \uparrow)
+
\mathrm{R}(2, \uparrow)
\gamma
\gamma
\mathrm{R}(2, \uparrow)
20\%
[
+
]
\mathrm{R}(6, \uparrow)
=
\mathrm{R}(3, \uparrow)
\gamma
\mathrm{R}(3, \uparrow)
80\%
[
+
+
]
\gamma
V_\pi^3(6)=
\mathrm{R}(6, \uparrow)
\mathrm{R}(2, \uparrow)
\gamma
\gamma^2
\mathrm{R}(2, \uparrow)
20\%
[
+
+
]
\mathrm{R}(3, \uparrow)
\gamma
\mathrm{R}(3, \uparrow)
\gamma^2
80\%
[
+
+
]
\mathrm{R}(6, \uparrow)
=
\gamma
20\%
+
V_\pi^2(2)
\gamma
80\%
+
V_\pi^2(3)
\pi(s)
V_{\pi}^h(s)

MDP

Policy evaluation

finite-horizon policy evaluation 

infinite-horizon policy evaluation

\(\gamma\) is now necessarily <1 for convergence too in general 

Bellman equation

  • \(|\mathcal{S}|\) many linear equations

For any given policy \(\pi(s),\) the infinite-horizon (state) value functions are
\(V_\pi(s):=\mathbb{E}\left[\sum_{t=0}^{\infty} \gamma^t \mathrm{R}\left(s_t, \pi\left(s_t\right)\right) \mid s_0=s, \pi\right], \forall s\)

V_\pi(s)= \mathrm{R}(s, \pi(s))+ \gamma \sum_{s^{\prime}} \mathrm{T}\left(s, \pi(s), s^{\prime}\right) V_\pi\left(s^{\prime}\right), \forall s

For a given policy \(\pi(s),\) the finite-horizon horizon-\(h\) (state) value functions are:
\(V^h_\pi(s):=\mathbb{E}\left[\sum_{t=0}^{h-1} \gamma^t \mathrm{R}\left(s_t, \pi\left(s_t\right)\right) \mid s_0=s, \pi\right], \forall s\)

Bellman recursion

V^{h}_\pi(s)= \mathrm{R}(s, \pi(s))+ \gamma \sum_{s^{\prime}} \mathrm{T}\left(s, \pi(s), s^{\prime}\right) V^{h-1}_\pi\left(s^{\prime}\right), \forall s
1
2
9
8
7
5
4
3
6
80\%
20\%

Recall:

example: recursively finding \(Q^h(s, a)\)

\(\gamma = 0.9\)

\(Q^h(s, a)\) is the expected sum of discounted rewards for

1
1
1
1
-10
-10
-10
-10

States and one special transition:

\(\mathrm{R}(s,a)\)

  • starting in state \(s\),
  • take action \(a\), for one step
  • act optimally there afterwards for the remaining \((h-1)\) steps
Q^1(s, a)
0
0
0
0
0
1
0
-10
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
-10
1
-10
-10
Q^0(s, a)
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
2
9
8
7
5
4
3
6
80\%
20\%

Recall:

\(\gamma = 0.9\)

\(Q^h(s, a)\) is the expected sum of discounted rewards for

  • starting in state \(s\),
  • take action \(a\), for one step
  • act optimally there afterwards for the remaining \((h-1)\) steps
Q^1(s, a) = \mathrm{R}(s,a)

States and one special transition:

0
0
0
1
0
-10
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
-10
1
-10
-10
0
0
Q^2(s, a)
  • act optimally for one more timestep, at the next state \(s^{\prime}\) 
0
0
0
0
1.9
1.9
1
-8
  • 20% chance, \(s'\) = 2, act optimally, receive \(\max _{a^{\prime}} Q^{1}\left(2, a^{\prime}\right)\)
  • 80% chance, \(s'\) = 3, act optimally, receive \(\max _{a^{\prime}} Q^{1}\left(3, a^{\prime}\right)\)
-9.28

Let's consider \(Q^2(6, \uparrow)\)

\(= -10 + .9 [.2*0+ .8*1] = -9.28\)

\(=\mathrm{R}(6,\uparrow)  + \gamma[.2 \max _{a^{\prime}} Q^{1}\left(2, a^{\prime}\right)+ .8\max _{a^{\prime}} Q^{1}\left(3, a^{\prime}\right)] \)

  • receive \(\mathrm{R}(6,\uparrow)\)
1
2
9
8
7
5
4
3
6
80\%
20\%

Recall:

\(\gamma = 0.9\)

\(Q^h(s, a)\) is the expected sum of discounted rewards for

  • starting in state \(s\),
  • take action \(a\), for one step
  • act optimally there afterwards for the remaining \((h-1)\) steps
Q^1(s, a)

States and one special transition:

0
0
0
1
0
-10
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
-10
1
-10
-10
0
0
Q^2(s, a)
0
0
0
0
1.9
1.9
1
-8
-9.28

\(Q^2(6, \uparrow) =\mathrm{R}(6,\uparrow)  + \gamma[.2 \max _{a^{\prime}} Q^{1}\left(2, a^{\prime}\right)+ .8\max _{a^{\prime}} Q^{1}\left(3, a^{\prime}\right)] \)

Q^h (s, a)=\mathrm{R}(s, a)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, a, s^{\prime} \right) \max _{a^{\prime}} Q^{h-1}\left(s^{\prime}, a^{\prime}\right), \forall s,a
=\mathrm{R}(s, a)

in general 

1
2
9
8
7
5
4
3
6
80\%
20\%

Recall:

\(\gamma = 0.9\)

\(Q^h(s, a)\) is the expected sum of discounted rewards for

  • starting in state \(s\),
  • take action \(a\), for one step
  • act optimally there afterwards for the remaining \((h-1)\) steps
Q^1(s, a)

States and one special transition:

0
0
0
1
0
-10
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
-10
1
-10
-10
0
0
Q^2(s, a)
0
0
0
0
1.9
1.9
1
-8
-9.28
\pi_h^*(s)=\arg \max _a Q^h(s, a), \forall s, h

what's the optimal action in state 3, with horizon 2, given by \(\pi_2^*(3)=?\)

 

in general 

either up or right 

Given the finite horizon recursion

Q(s, a)=\mathrm{R}(s, a)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, a, s^{\prime} \right) \max _{a^{\prime}} Q \left(s^{\prime}, a^{\prime}\right)
  1. for \(s \in \mathcal{S}, a \in \mathcal{A}\) :
  2.       \(\mathrm{Q}_{\text {old }}(\mathrm{s}, \mathrm{a})=0\)
  3. while True:
  4.       for \(s \in \mathcal{S}, a \in \mathcal{A}\) :
  5.             \(\mathrm{Q}_{\text {new }}(s, a) \leftarrow \mathrm{R}(s, a)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, a, s^{\prime}\right) \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)\)
  6.       if \(\max _{s, a}\left|Q_{\text {old }}(s, a)-Q_{\text {new }}(s, a)\right|<\epsilon:\)
  7.             return \(\mathrm{Q}_{\text {new }}\)
  8.       \(\mathrm{Q}_{\text {old }} \leftarrow \mathrm{Q}_{\text {new }}\)
Q^h (s, a)=\mathrm{R}(s, a)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, a, s^{\prime} \right) \max _{a^{\prime}} Q^{h-1}\left(s^{\prime}, a^{\prime}\right)

We should easily be convinced of the infinite horizon equation

Infinite-horizon Value Iteration

Outline

  • Recap: Markov Decision Processes
  • Reinforcement Learning Setup
    • What's changed from MDP?
  • Model-based methods
  • Model-free methods
    • (tabular) Q-learning
      • \(\epsilon\)-greedy action selection
      • exploration vs. exploitation
    • (neural network) Q-learning
  • RL setup again
    • What's changed from supervised learning?
  • all transitions probabilities are unknown.

Running example: Mario in a grid-world (the Reinforcement-Learning Setup)

  • 9 possible states
  • 4 possible actions: {Up ↑, Down ↓, Left ←, Right →}
  • (state, action) pair gets Mario unknown rewards.
  • goal is to find a gameplay policy strategy for Mario, to get maximum expected sum of discounted rewards, with a discount facotor \(\gamma = 0.9\) 
?
?
?
\dots
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
1
2
9
8
7
5
4
3
6

MDP Definition and Goal

  • \(\mathcal{S}\) : state space, contains all possible states \(s\).
  • \(\mathcal{A}\) : action space, contains all possible actions \(a\).
  • \(\mathrm{T}\left(s, a, s^{\prime}\right)\) : the probability of transition from state \(s\) to \(s^{\prime}\) when action \(a\) is taken.
  • \(\mathrm{R}(s, a)\) : a function that takes in the (state, action) and returns a reward.
  • \(\gamma \in [0,1]\): discount factor, a scalar.
  • \(\pi{(s)}\) : policy, takes in a state and returns an action.

Ultimate goal of an MDP: Find the "best" policy \(\pi\).

RL

RL:

Outline

  • Recap: Markov Decision Processes
  • Reinforcement Learning Setup
    • What's changed from MDP?
  • Model-based methods
  • Model-free methods
    • (tabular) Q-learning
      • \(\epsilon\)-greedy action selection
      • exploration vs. exploitation
    • (neural network) Q-learning
  • RL setup again
    • What's changed from supervised learning?

Model-Based Methods

Keep playing the game to approximate the unknown rewards and transitions.

e.g. by observing what reward \(r\) received from being in state 6 and take \(\uparrow\) action, we know \(\mathrm{R}(6,\uparrow)\)

Transitions are a bit more involved but still simple:

Rewards are particularly easy:

     e.g. play the game 1000 times, count the # of times (we started in state 6, take \(\uparrow\) action, end in state 2), then, roughly, \(\mathrm{T}(6,\uparrow, 2 ) = (\text{that count}/1000) \)

(MDP)-

Now, with \(\mathrm{R}, \mathrm{T}\) estimated, we're back in MDP setting.

(for solving RL)

In Reinforcement Learning:

  • Model typically means MDP tuple \(\langle\mathcal{S}, \mathcal{A}, \mathrm{T}, \mathrm{R}, \gamma\rangle\)
  • The learning objective is not referred to as hypothesis explicitly, we simply just call it the policy.

Outline

  • Recap: Markov Decision Processes
  • Reinforcement Learning Setup
    • What's changed from MDP?
  • Model-based methods
  • Model-free methods
    • (tabular) Q-learning
      • \(\epsilon\)-greedy action selection
      • exploration vs. exploitation
    • (neural network) Q-learning
  • RL setup again
    • What's changed from supervised learning?

How do we learn a good policy without learning transition or rewards explicitly? 

We kinda already know a way: Q functions!

So once we have "good" Q values, we can find optimal policy easily. 

(Recall from MDP lab)

But didn't we calculate this Q-table via value iteration using transition and rewards explicitly?

Indeed, recall that, in MDP:

Q(s, a)=\mathrm{R}(s, a)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, a, s^{\prime} \right) \max _{a^{\prime}} Q \left(s^{\prime}, a^{\prime}\right)
  1. for \(s \in \mathcal{S}, a \in \mathcal{A}\) :
  2.       \(\mathrm{Q}_{\text {old }}(\mathrm{s}, \mathrm{a})=0\)
  3. while True:
  4.       for \(s \in \mathcal{S}, a \in \mathcal{A}\) :
  5.             \(\mathrm{Q}_{\text {new }}(s, a) \leftarrow \mathrm{R}(s, a)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, a, s^{\prime}\right) \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)\)
  6.       if \(\max _{s, a}\left|Q_{\text {old }}(s, a)-Q_{\text {new }}(s, a)\right|<\epsilon:\)
  7.             return \(\mathrm{Q}_{\text {new }}\)
  8.       \(\mathrm{Q}_{\text {old }} \leftarrow \mathrm{Q}_{\text {new }}\)
Q^h (s, a)=\mathrm{R}(s, a)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, a, s^{\prime} \right) \max _{a^{\prime}} Q^{h-1}\left(s^{\prime}, a^{\prime}\right)
  • Infinite horizon equation
  • Infinite-horizon Value Iteration
  • Finite horizon recursion
\mathrm{Q}_{\text {new }}(s, a) \leftarrow \mathrm{R}(s, a)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, a, s^{\prime}\right) \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)
  • value iteration relied on having full access to \(\mathrm{R}\) and \(\mathrm{T}\)
  • BUT, this is basically saying the realized \(s'\) is the only possible next state; pretty rough! We'd override any previous "learned" Q values.
  • hmm... perhaps, we could simulate \((s,a)\), observe \(r\) and \(s'\), and just use
r
+\ \gamma \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)
  • better way is to smoothly keep track of what's our old belief with new evidence:
\mathrm{Q}_{\text {new }}(6, \uparrow) \leftarrow -10 +\gamma \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(2, a^{\prime}\right)
\mathrm{Q}_{\text {new }}(6, \uparrow) \leftarrow -10 +\gamma \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(3, a^{\prime}\right)

e.g.

as the proxy for the r.h.s. assignment?

\mathrm{Q}_{\text {new }}(s, a) \leftarrow(1-\alpha) \mathrm{Q}_{\text {old }}(s, a)+\alpha\left(r+\gamma \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)\right)

target

old belief

learning rate

 

  1. for \(s \in \mathcal{S}, a \in \mathcal{A}\) :
  2.       \(\mathrm{Q}_{\text {old }}(\mathrm{s}, \mathrm{a})=0\)
  3. while True:
  4.       for \(s \in \mathcal{S}, a \in \mathcal{A}\) :
  5.             \(\mathrm{Q}_{\text {new }}(s, a) \leftarrow \mathrm{R}(s, a)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, a, s^{\prime}\right) \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)\)
  6.       if \(\max _{s, a}\left|Q_{\text {old }}(s, a)-Q_{\text {new }}(s, a)\right|<\epsilon:\)
  7.             return \(\mathrm{Q}_{\text {new }}\)
  8.       \(\mathrm{Q}_{\text {old }} \leftarrow \mathrm{Q}_{\text {new }}\)

VALUE-ITERATION \((\mathcal{S}, \mathcal{A}, \mathrm{T}, \mathrm{R}, \gamma, \epsilon)\)

Q-LEARNING \(\left(\mathcal{S}, \mathcal{A}, \gamma, \mathrm{s}_0,\alpha\right)\)

 

  1. for \(s \in \mathcal{S}, a \in \mathcal{A}\) :
  2.       \(\mathrm{Q}_{\text {old }}(\mathrm{s}, \mathrm{a})=0\)
  3. \(s \leftarrow s_0\)
  4. while True:​
  5.       \(a \leftarrow \) select_action \(\left(s, Q_{\text{old}}(s, a)\right)\)
  6.       \(r, s^{\prime}=\operatorname{execute}(a)\)
  7.       \(\mathrm{Q}_{\text {new}}(s, a) \leftarrow(1-\alpha) \mathrm{Q}_{\text {old }}(s, a)+\alpha\left(r+\gamma \max _{a^{\prime}} \mathrm{Q}_{\text {old}}(s', a')\right)\)
  8.       \(s \leftarrow s^{\prime}\)
  9.       if \(\max _{s, a}\left|Q_{\text {old }}(s, a)-Q_{\text {new }}(s, a)\right|<\epsilon:\)
  10.             return \(\mathrm{Q}_{\text {new }}\)
  11.       \(\mathrm{Q}_{\text {old }} \leftarrow \mathrm{Q}_{\text {new }}\)

"calculating"

"estimating"

Q-LEARNING \(\left(\mathcal{S}, \mathcal{A}, \gamma, \mathrm{s}_0,\alpha\right)\)

 

  1. for \(s \in \mathcal{S}, a \in \mathcal{A}\) :
  2.       \(\mathrm{Q}_{\text {old }}(\mathrm{s}, \mathrm{a})=0\)
  3. \(s \leftarrow s_0\)
  4. while True:​
  5.       \(a \leftarrow \) select_action \(\left(s, Q_{\text{old}}(s, a)\right)\)
  6.       \(r, s^{\prime}=\operatorname{execute}(a)\)
  7.       \(\mathrm{Q}_{\text {new}}(s, a) \leftarrow(1-\alpha) \mathrm{Q}_{\text {old }}(s, a)+\alpha\left(r+\gamma \max _{a^{\prime}} \mathrm{Q}_{\text {old}}(s', a')\right)\)
  8.       \(s \leftarrow s^{\prime}\)
  9.       if \(\max _{s, a}\left|Q_{\text {old }}(s, a)-Q_{\text {new }}(s, a)\right|<\epsilon:\)
  10.             return \(\mathrm{Q}_{\text {new }}\)
  11.       \(\mathrm{Q}_{\text {old }} \leftarrow \mathrm{Q}_{\text {new }}\)
  • Remarkably, still can converge. (So long \(\mathcal{S}, \mathcal{A}\) are finite; we visit every state and action infinity-many times; and \(\alpha\) decays.
  • Line 7 :

\(\mathrm{Q}_{\text {new}}(s, a) \leftarrow\mathrm{Q}_{\text {old }}(s, a)+\alpha\left([r+\gamma \max _{a^{\prime}} \mathrm{Q}_{\text {old}}(s', a')] - \mathrm{Q}_{\text {old }}(s, a)\right)\)

\mathrm{Q}_{\text {new }}(s, a) \leftarrow(1-\alpha) \mathrm{Q}_{\text {old }}(s, a)+\alpha\left(r+\gamma \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)\right)

is equivalently:

)
+
(
-

old belief

learning

rate

target

old belief

  • Line 5, a sub-routine.

pretty similar to SGD.

  • \(\epsilon\)-greedy action selection strategy:
    • with probability \(1-\epsilon\), choose \(\arg \max _{\mathrm{a}} \mathrm{Q}(s, \mathrm{a})\)
    • with probability \(\epsilon\), choose an action \(a \in \mathcal{A}\) uniformly at random
  • If our \(Q\) values are estimated quite accurately (nearly converged to the true \(Q\) values), then should act greedily
    • \(\arg \max _a Q^h(s, a),\) as we did in MDP.
  • During learning, especially in early stages, we'd like to explore.
  • Benefit: get to observe more diverse (s,a) consequences.
  • exploration vs. exploitation.

Outline

  • Recap: Markov Decision Processes
  • Reinforcement Learning Setup
    • What's changed from MDP?
  • Model-based methods
  • Model-free methods
    • (tabular) Q-learning
      • \(\epsilon\)-greedy action selection
      • exploration vs. exploitation
    • (neural network) Q-learning
  • RL setup again
    • What's changed from supervised learning?
  • Q-learning only is kinda sensible for tabular setting. 
  • What do we do if \(\mathcal{S}\) and/or \(\mathcal{A}\) are large (or continuous)?
  • Recall from Q-learning algorithm, key line 7 :
\mathrm{Q}_{\text {new }}(s, a) \leftarrow(1-\alpha) \mathrm{Q}_{\text {old }}(s, a)+\alpha\left(r+\gamma \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)\right)

is equivalently:

\(\mathrm{Q}_{\text {new}}(s, a) \leftarrow\mathrm{Q}_{\text {old }}(s, a)+\alpha\left([r+\gamma \max _{a^{\prime}} \mathrm{Q}_{\text {old}}(s', a')] - \mathrm{Q}_{\text {old }}(s, a)\right)\)

learning

rate

old belief

+

target

(
-

old belief

)
  • Can be interpreted as we're minimizing:

\(\left(Q(s, a)-\left(r+\gamma \max _{a^{\prime}} Q\left(s^{\prime}, a^{\prime}\right)\right)\right)^2\)

via gradient method!

Outline

  • Recap: Markov Decision Processes
  • Reinforcement Learning Setup
    • What's changed from MDP?
  • Model-based methods
  • Model-free methods
    • (tabular) Q-learning
      • \(\epsilon\)-greedy action selection
      • exploration vs. exploitation
    • (neural network) Q-learning
  • RL setup again
    • What's changed from supervised learning?

Supervised learning

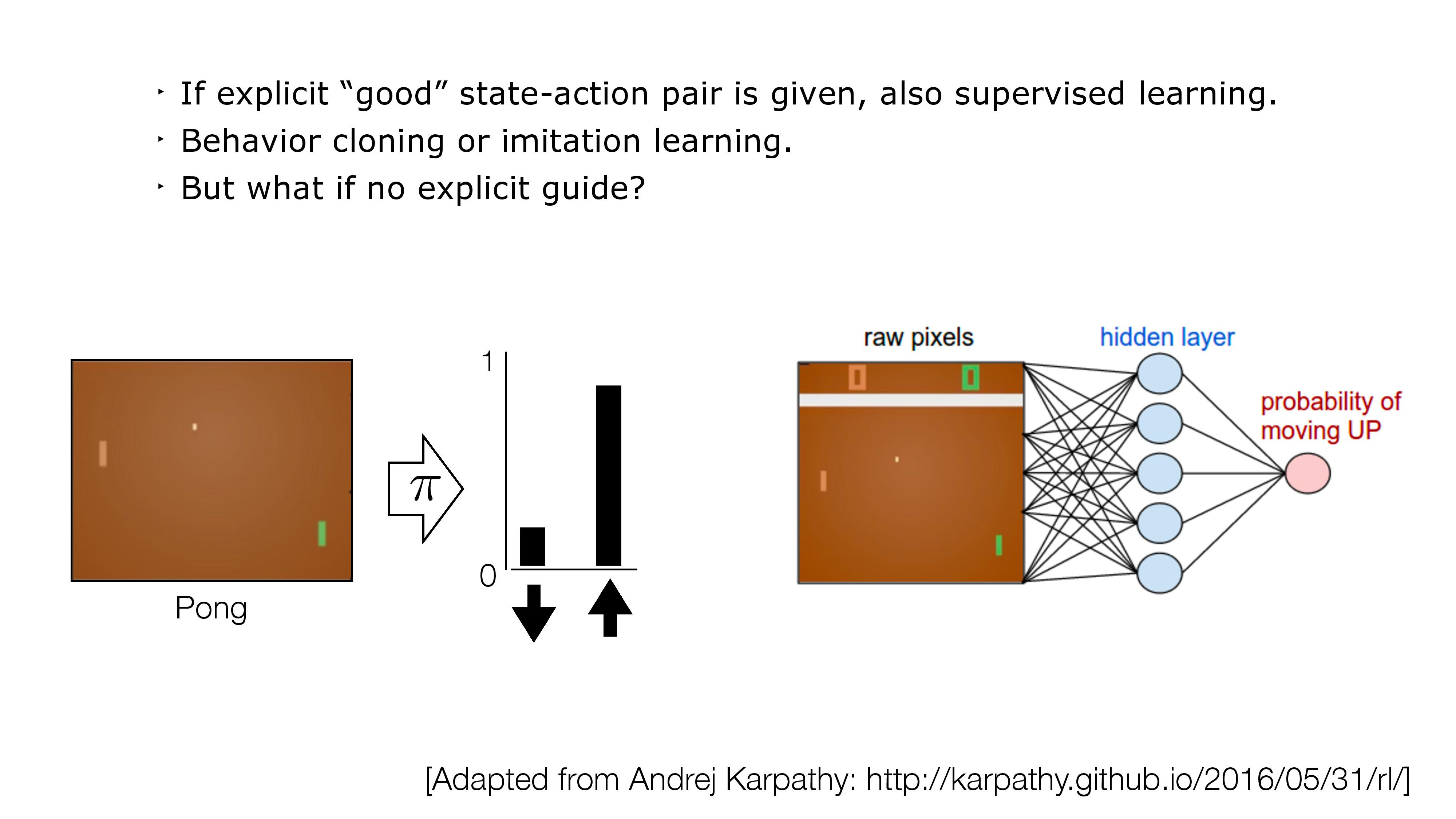
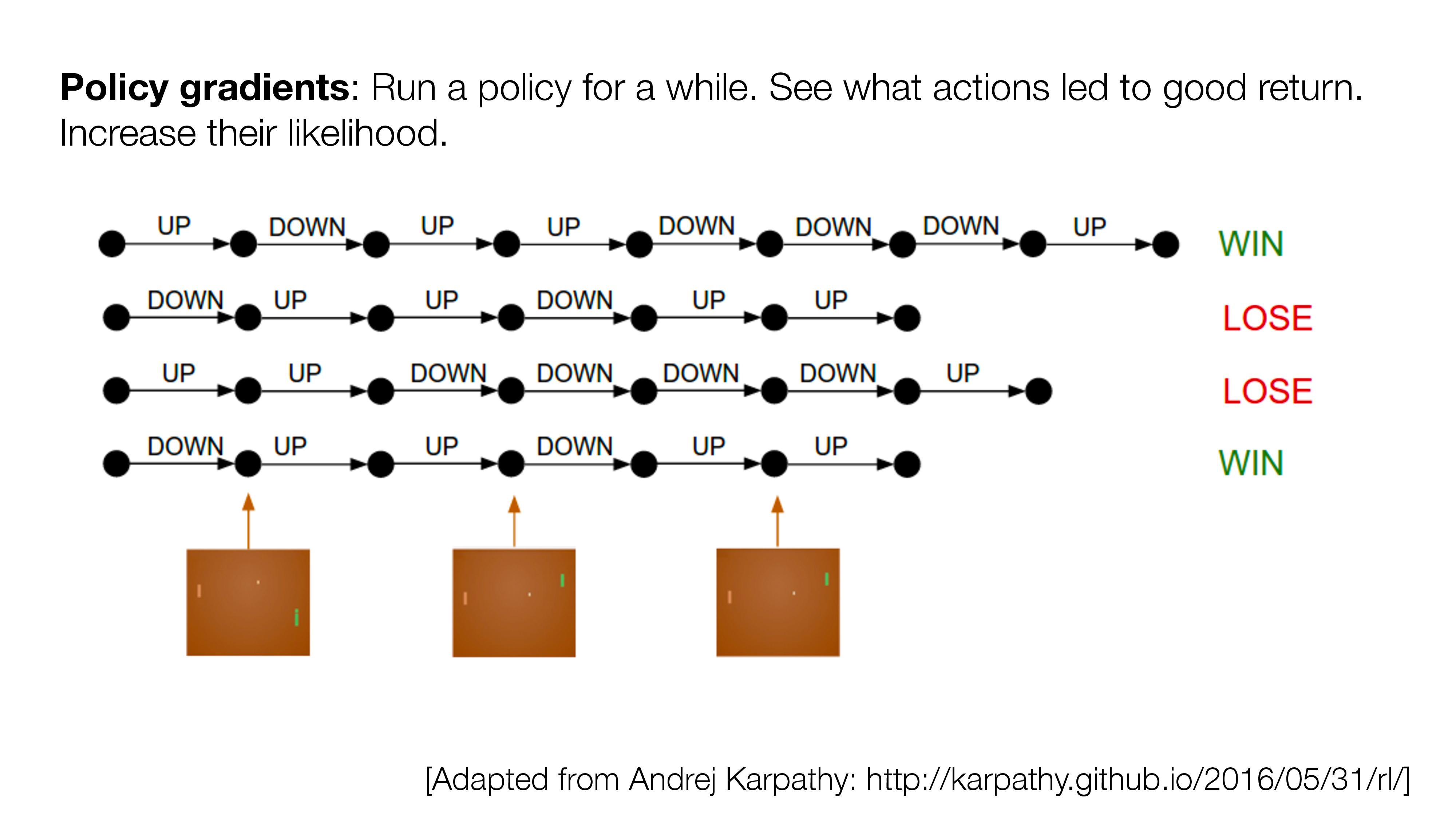
  • If no direct supervision is available?
  • Strictly RL setting. Interact, observe and get data. Use rewards/value as "coy" supervision signal.

Thanks!

We'd appreciate your feedback on the lecture.