Intro to Machine Learning
Lecture 4: Linear Classification (Logistic Regression)
Shen Shen
Feb 23, 2024
(some slides adapted from Tamara Broderick and Phillip Isola)
Outline
- Recap (ML pipeline, regression, regularization, GD)
- Classification General Setup
- (vanilla) Linear Classifier
- Understand a given linear classifier
- Linear separator: geometric intuition
- Learn a linear classifier via 0-1 loss?
- Linear Logistic Regression
- Sigmoid function
- Cross-entropy (negative log likelihood) loss
- Optimizing the loss via gradient descent
- Regularization, cross-validation still matter
- Multi-class classification
ML algorithm
Hypothesis class
Hyperparameters
If/how to add regularization
Objective (loss) functions
Compute/optimize
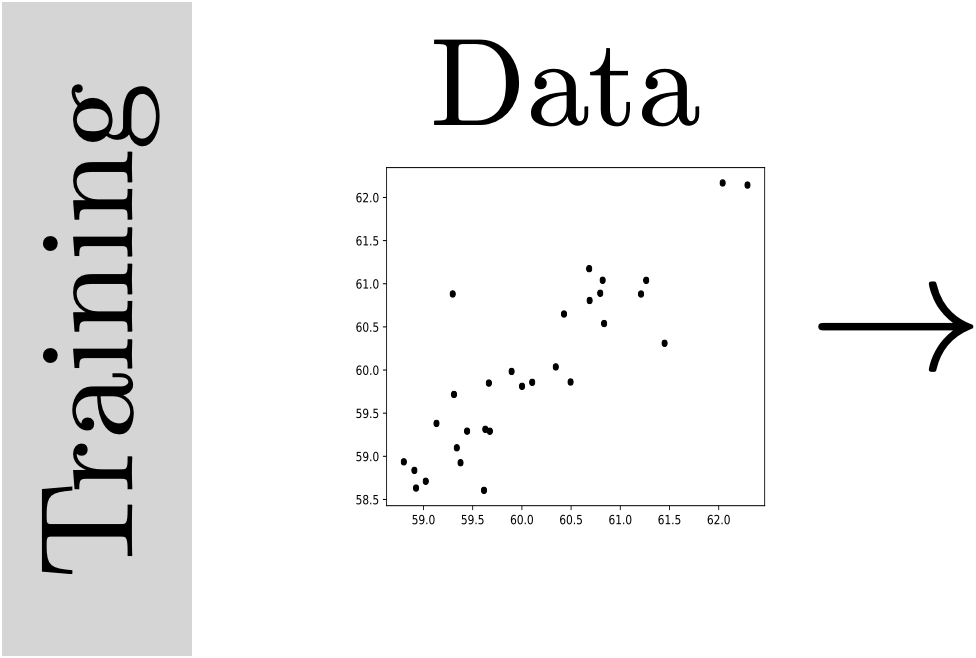
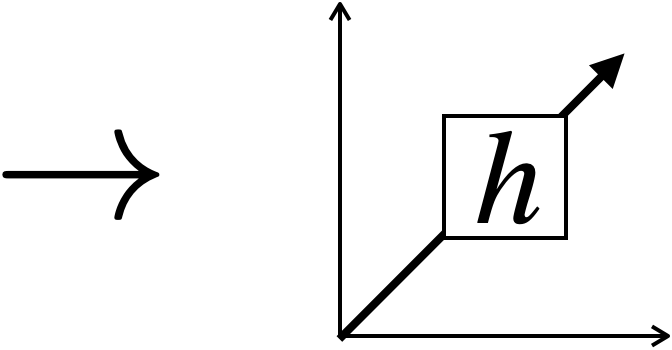
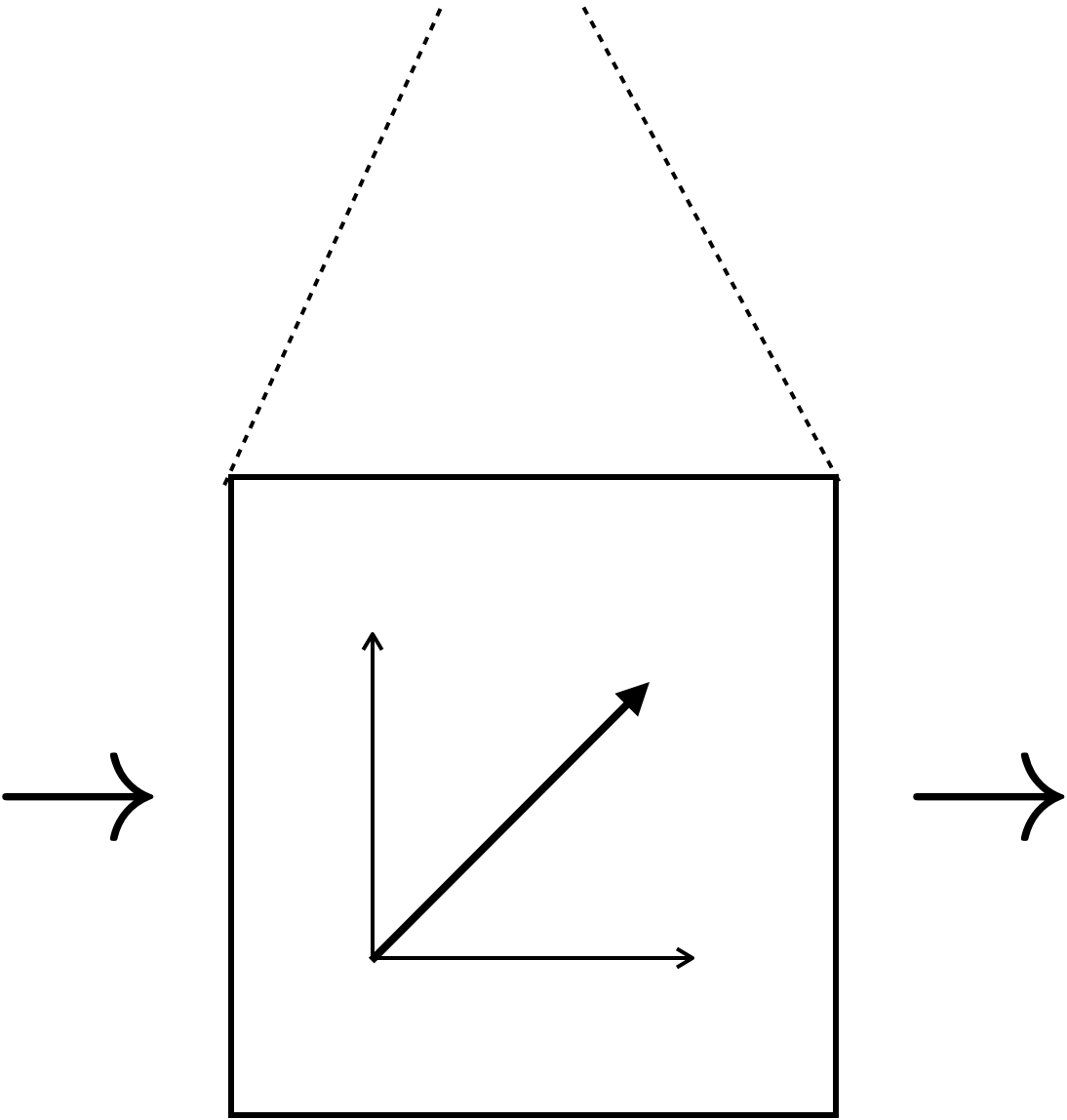
new
input \(x\)
new
prediction \(y\)
Testing
(predicting)
Recap:
- OLS can have analytical formula and "easy" prediction mechanism
- Regularization
- Cross-validation
- Gradient descent
Outline
- Recap (ML pipeline, regression, regularization, GD)
- Classification General Setup
- (vanilla) Linear Classifier
- Understand a given linear classifier
- Linear separator: geometric intuition
- Learn a linear classifier via 0-1 loss?
- Linear Logistic Regression
- Sigmoid function
- Cross-entropy (negative log likelihood) loss
- Optimizing the loss via gradient descent
- Regularization, cross-validation still matter
- Multi-class classification
Classification Setup
- General setup: Labels (and predictions) are in a discrete set
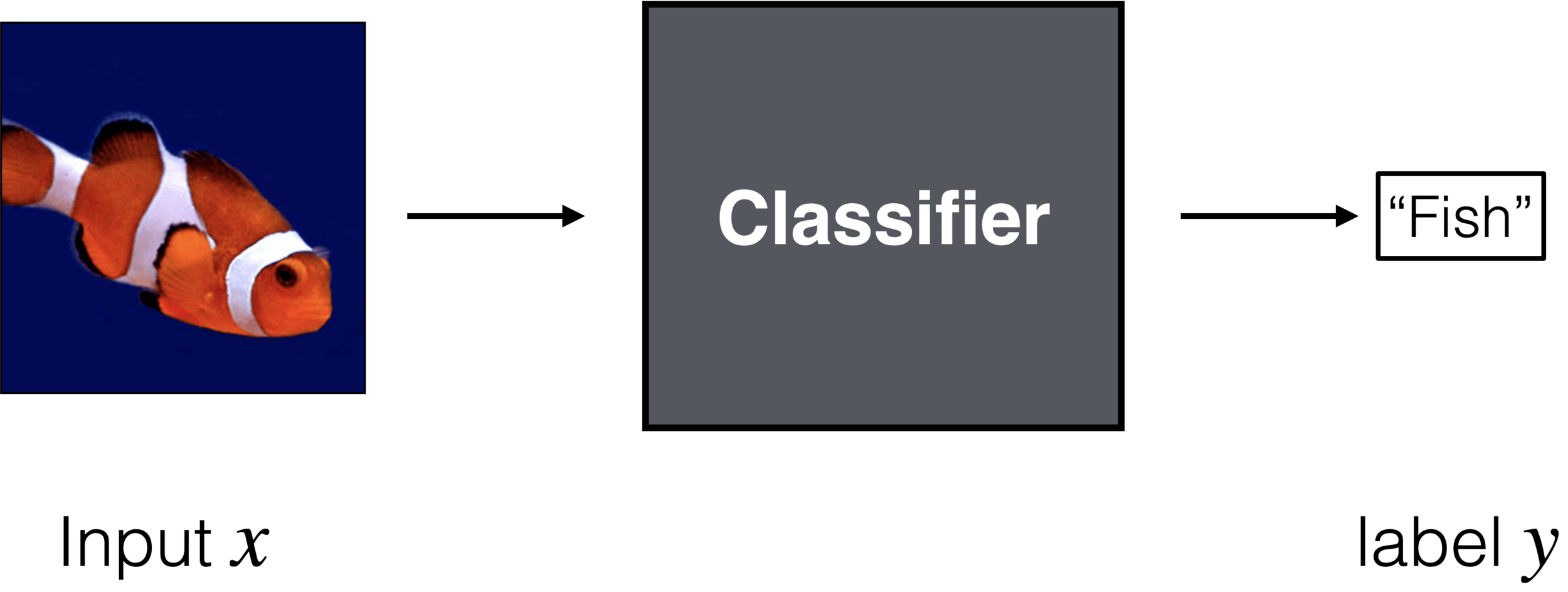
Classification Setup
- General setup: Labels (and predictions) are in a discrete set
Outline
- Recap (ML pipeline, regression, regularization, GD)
- Classification General Setup
- (vanilla) Linear Classifier
- Understand a given linear classifier
- Linear separator: geometric intuition
- Learn a linear classifier via 0-1 loss?
- Linear Logistic Regression
- Sigmoid function
- Cross-entropy (negative log likelihood) loss
- Optimizing the loss via gradient descent
- Regularization, cross-validation still matter
- Multi-class classification
(vanilla) Linear Classifier
- General setup: Labels (and predictions) are in a discrete set
- Simplest setup: linear binary classification. that is, two possible labels, e.g.\(y \in\){positive, negative} (or {dog, cat}, {pizza, not pizza}, {+1, 0}...)
- given a data point with features \(x_1, x_2, \dots x_d\)
- do some linear combination, calculate \(z =(\theta_1x_1 + \theta_2x_2 + \dots + \theta_dx_d) + \theta_0\)
- make a prediction: predict positive class if \(z>0\) otherwise negative class.
- We need to understand what are:
- Linear separator
- Normal vector
- Linear separability
(The demo won't embed in PDF. But the direct link below works.)
0-1 loss
\mathcal{L}_{01}(g, a)=\left\{\begin{array}{ll}
0 & \text { if } \text{guess} = \text{actual} \\
1 & \text { otherwise }
\end{array}\right .
- 😊 Very intuitive
- 😊 Easy to evaluate
- 🥺 Very hard to optimize (NP-hard)
- "Flat" almost everywhere (those local gradient=0, not helpful)
- Has "jumps" elsewhere (don't have gradient there)
(The demo won't embed in PDF. But the direct link below works.)
Outline
- Recap (ML pipeline, regression, regularization, GD)
- Classification General Setup
- (vanilla) Linear Classifier
- Understand a given linear classifier
- Linear separator: geometric intuition
- Learn a linear classifier via 0-1 loss?
- Linear Logistic Regression
- Sigmoid function
- Cross-entropy (negative log likelihood) loss
- Optimizing the loss via gradient descent
- Regularization, cross-validation still matter
- Multi-class classification
Linear Logistic Regression
- Despite regression in the name, really a hypothesis class for classification
- Mainly motivated to solve the non-"smooth" issue of "vanilla" linear classifier (where we used sign() function and 0-1 loss)
- But has nice probabilistic interpretation too
- Concretely, we need to know:
- Sigmoid function
- Cross-entropy (negative log likelihood) loss
- Optimizing the loss via gradient descent
- Regularization, cross-validation still matter
Recall: (Vanilla) Linear Classifier
- calculate \(z =(\theta_1x_1 + \theta_2x_2 + \dots + \theta_dx_d) + \theta_0\)
- predict positive class if \(z>0\) otherwise negative class.
Linear Logistic Regression
- calculate \(z =(\theta_1x_1 + \theta_2x_2 + \dots +\theta_dx_d) + \theta_0\)
- "squish" \(z\) with a sigmoid/logistic function: \[g = \sigma(z)=\frac{1}{1+\exp (-z)}\]
- predict positive class if \(g>0.5,\) otherwise, negative class.
- with some appropriate \(\theta\), \(\theta_0\) can horizontally flip, squeezing, expanding, shift
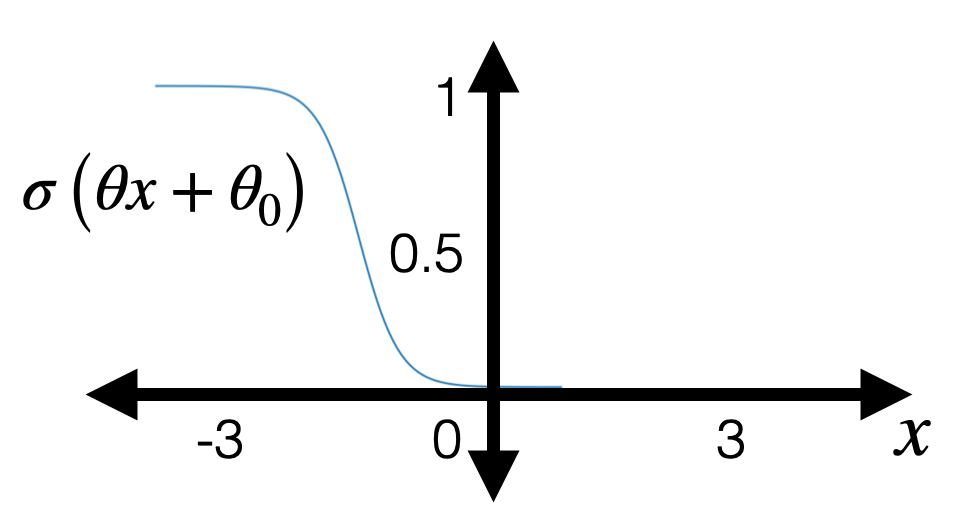
- vertically always monotonically "sandwiched" between 0 and 1 (and never quite get to either 0 or 1)
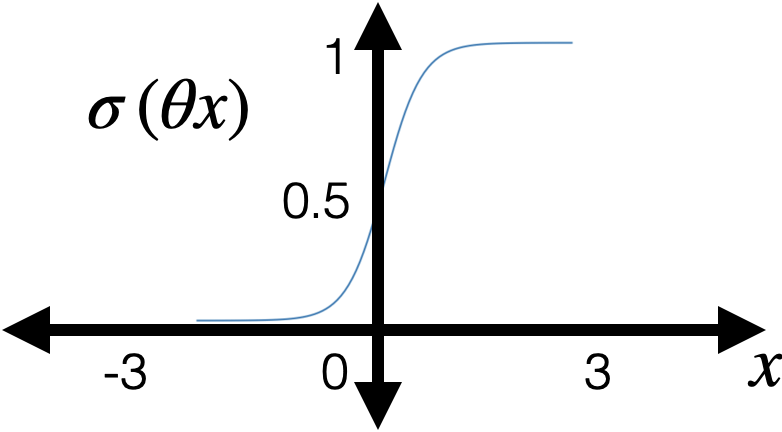
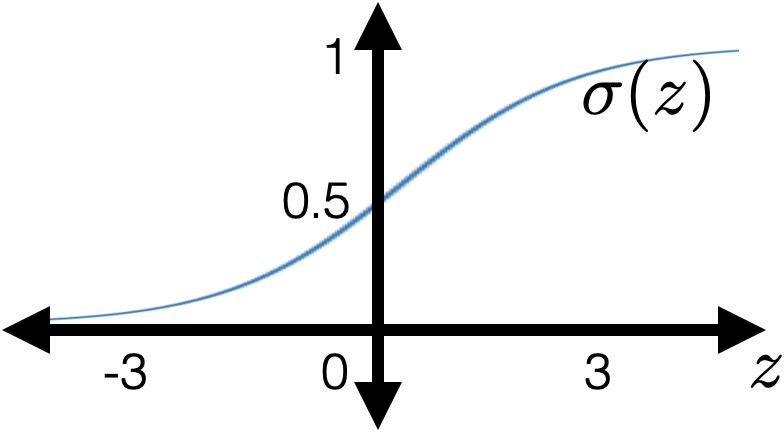
- very nice/elegant gradient
-
probabilistic interpretation
Comments about sigmoid
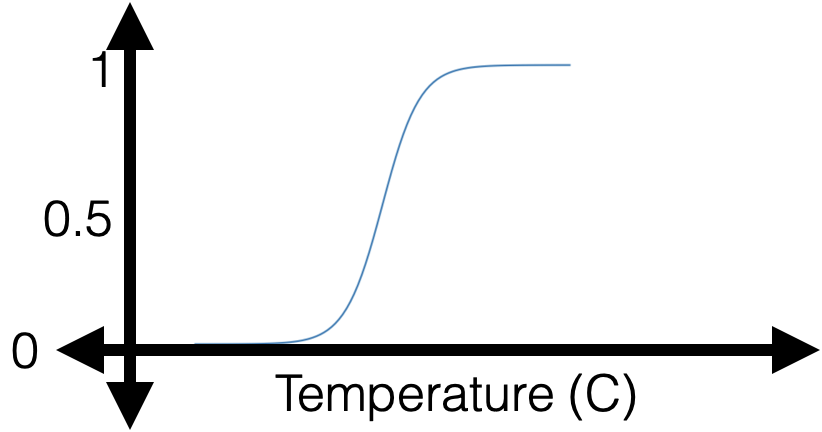
e.g. suppose, wanna predict whether to bike to school.
with given parameters, how do I make prediction?
1 feature:
\begin{aligned}
g(x) & =\sigma\left(\theta x+\theta_0\right) \\
& =\frac{1}{1+\exp \left\{-\left(\theta x+\theta_0\right)\right\}}
\end{aligned}
2 features:
\begin{aligned}
g(x) & =\sigma\left(\theta^{\top} x+\theta_0\right) \\
& =\frac{1}{1+\exp \left\{-\left(\theta^{\top} x+\theta_0\right)\right\}}
\end{aligned}
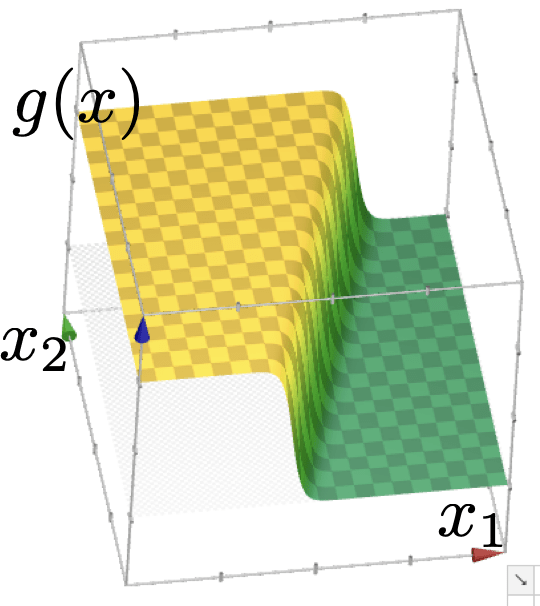
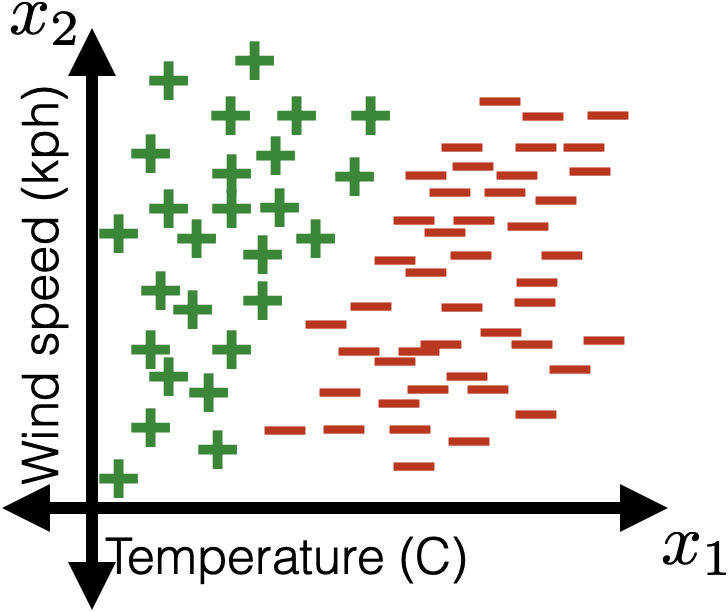
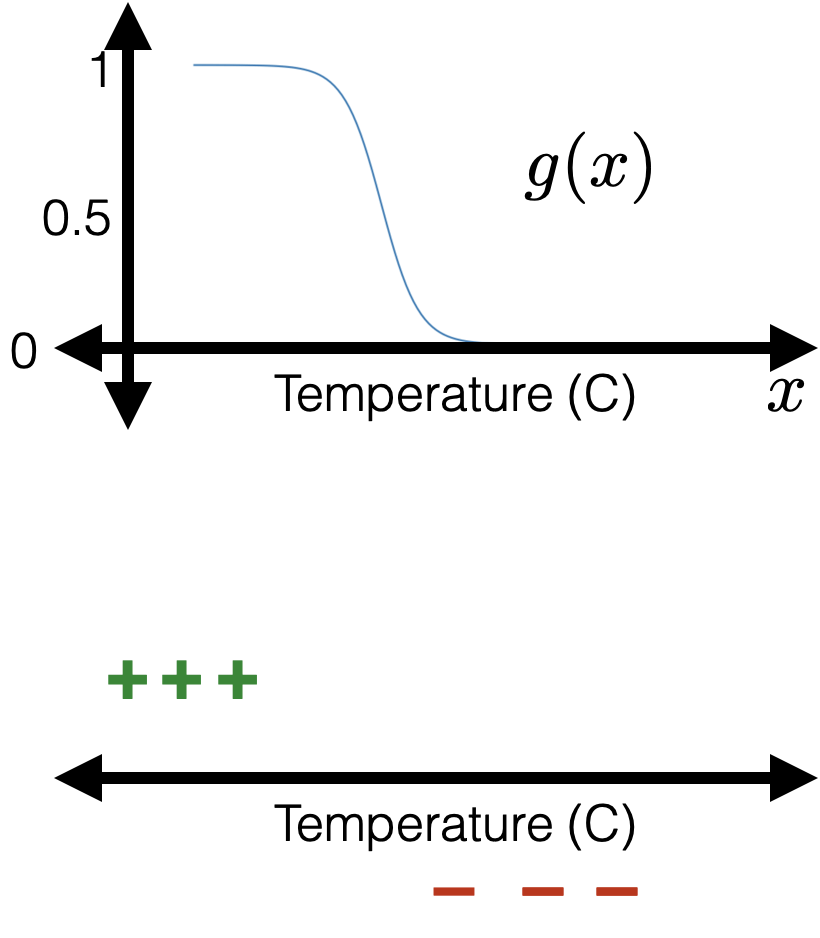
Learning a logistic regression classifier
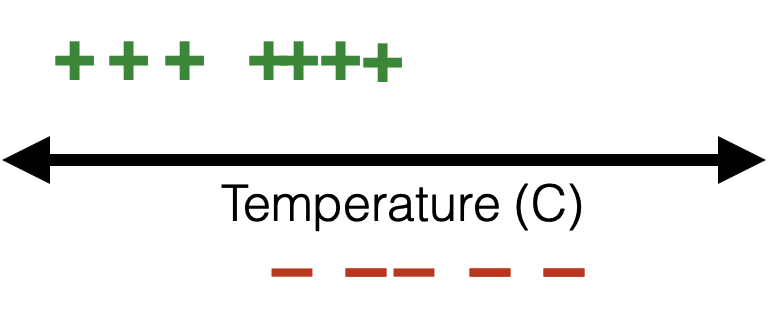
training data:
😍
🥺
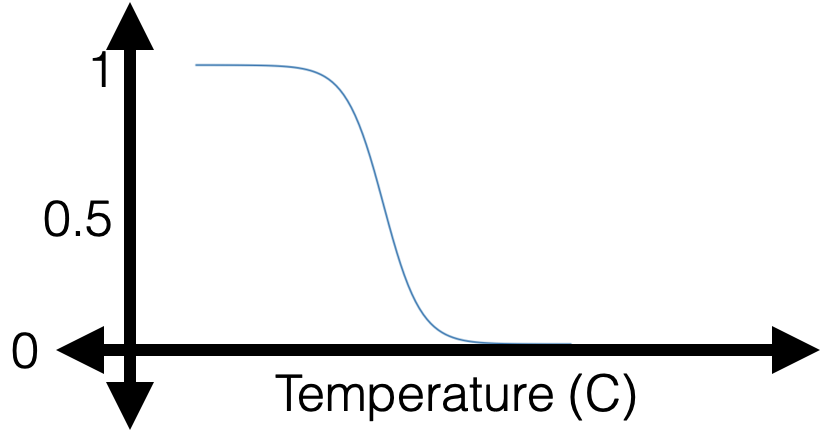
- Suppose labels \(y \in \{+1,0\}\)
- When see a training datum \(i\) with \(y^{(i)}=1\), would like \(g^{(i)}\) be high
- When see a training datum \(i\) with \(y^{(i)}=0\), would like \(1 - g^{(i)}\) be high
- i.e. for \(i\)th training data point, want this probability (likelihood) \[\begin{cases}g^{(i)} & \text { if } y^{(i)}=1 \\ 1-g^{(i)} & \text { if } y^{(i)}=0 \end{cases}\] to be high.
- or, equivalently, want \(g^{(i) y^{(i)}}\left(1-g^{(i)}\right)^{1-y^{(i)}}\) to be high
g(x)=\sigma\left(\theta x+\theta_0\right)
Learning a logistic regression classifier
training data:
😍
🥺
- Suppose labels \(y \in \{+1,0\}\)
- For training data point \(i,\) would like \(g^{(i) y^{(i)}}\left(1-g^{(i)}\right)^{1-y^{(i)}}\) to be high
- As logarithm is monotonic, would like \(y^{(i)} \log g^{(i)}+\left(1-y^{(i)}\right) \log \left(1-g^{(i)}\right)\) to be high
- Add a negative sign, to turn the above into a loss \[\mathcal{L}_{\text {nll }}(g^{(i)}, y^{(i)}) = \mathcal{L}_{\text {nll }}(\text { guess, actual })=\\-(\text { actual } \cdot \log (\text { guess })+(1-\text { actual }) \cdot \log (1-\text { guess }))\]
- Want the above to be low for all data points, under i.i.d. assumption, equivalently, wanna minimize \(J_{lr} =\frac{1}{n}\sum_{i=1}^n \mathcal{L}_{\text {nll }}\left(g^{(i)}, y^{(i)}\right) =\frac{1}{n} \sum_{i=1}^n \mathcal{L}_{\text {nll }}\left(\sigma\left(\theta^{\top} x^{(i)}+\theta_0\right), y^{(i)}\right)\)
g(x)=\sigma\left(\theta x+\theta_0\right)
Comments about \(J_{lr} = \frac{1}{n} \sum_{i=1}^n \mathcal{L}_{\text {nll }}\left(\sigma\left(\theta^{\top} x^{(i)}+\theta_0\right), y^{(i)}\right)\)
- Also called cross-entropy loss
- Convex, differentiable with nice (elegant) gradients
- Doesn't have a closed-form solution
- Can still run gradient descent
- But, a gotcha: when training data is linearly separable
g(x)=\sigma\left(\theta^T x+\theta_0\right)
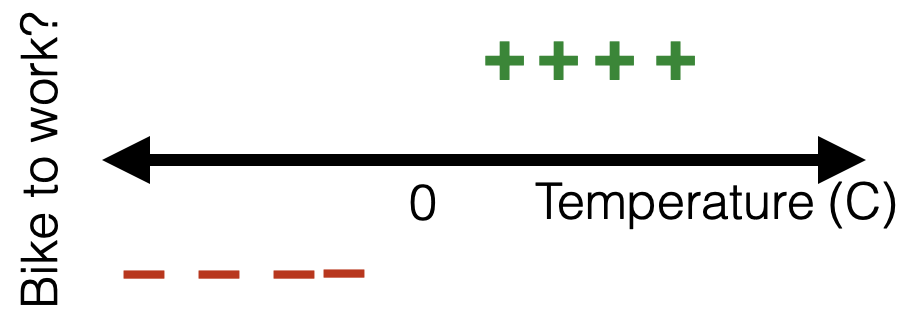
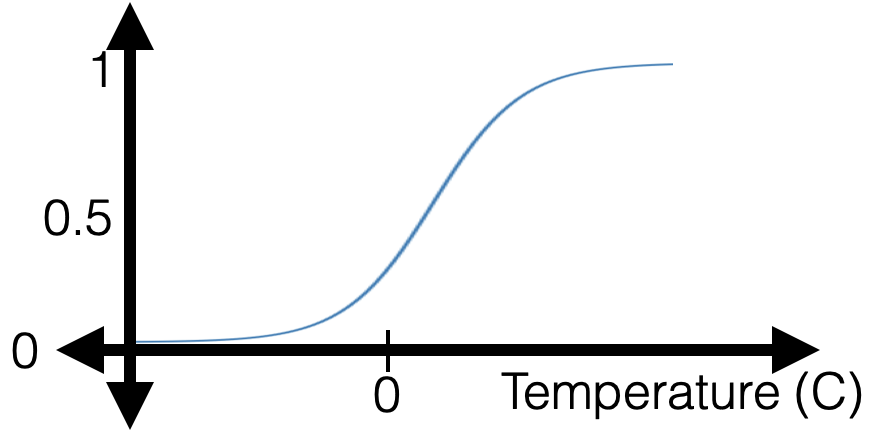
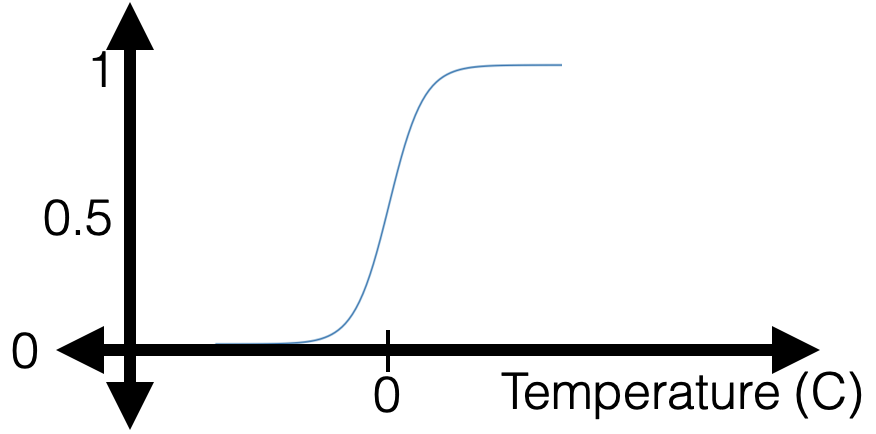
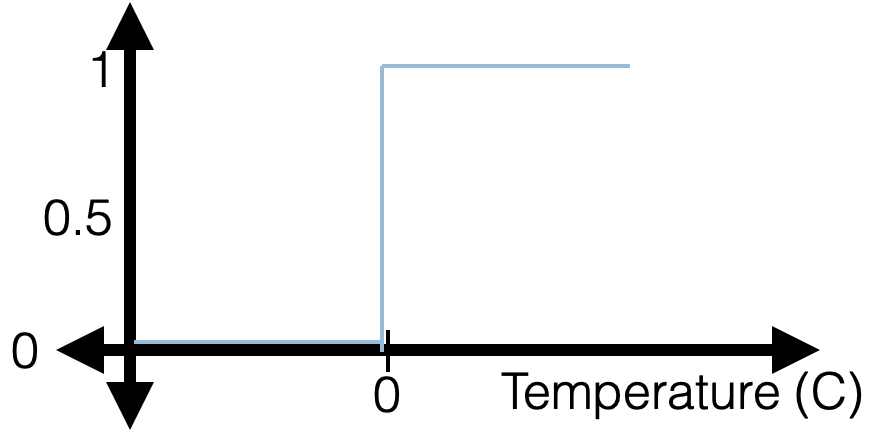
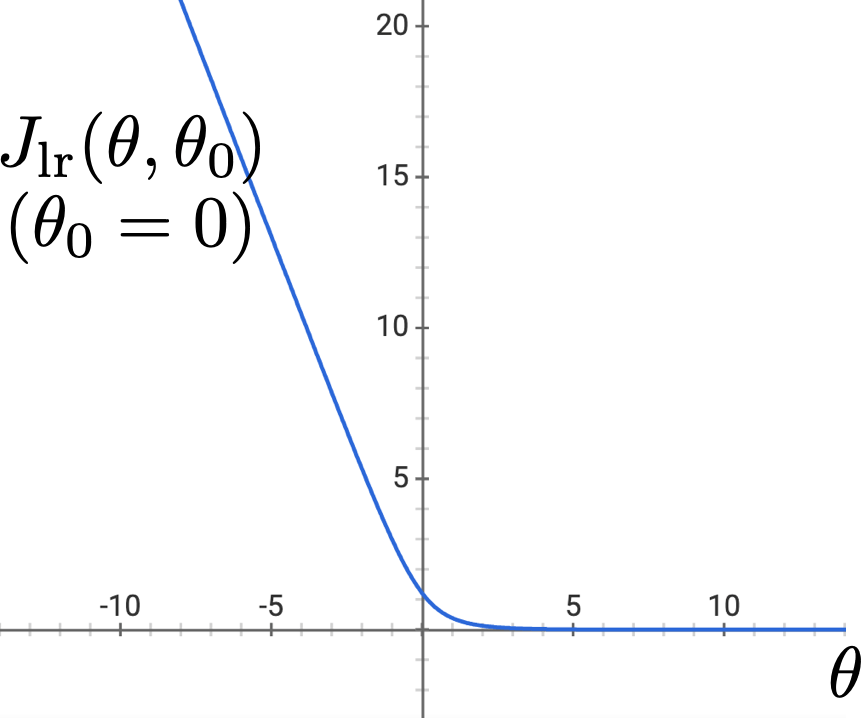
Regularization for Logistic Regression
\mathrm{J}_{\operatorname{lr}}\left(\theta, \theta_0 ; \mathcal{D}\right)=\left(\frac{1}{n} \sum_{i=1}^n \mathcal{L}_{\mathrm{nll}}\left(\sigma\left(\theta^{\top} x^{(i)}+\theta_0\right), y^{(i)}\right)\right)+\lambda\|\theta\|^2
- \(\lambda \geq 0\)
- No regularizing \(\theta_0\) (think: why?)
- Penalizes being overly certain
- Objective is still differentiable & convex (gradient descent)
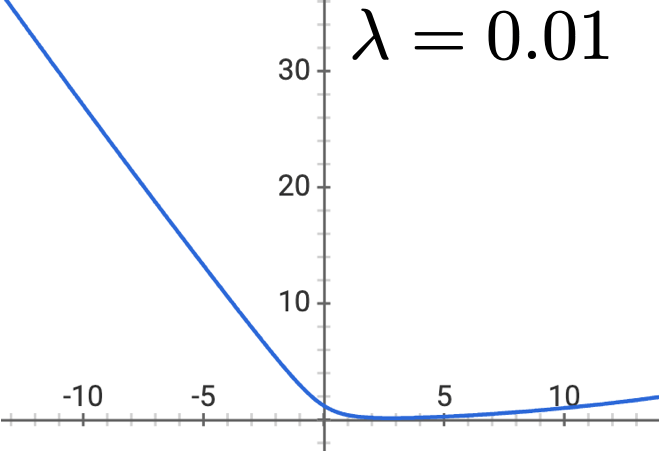
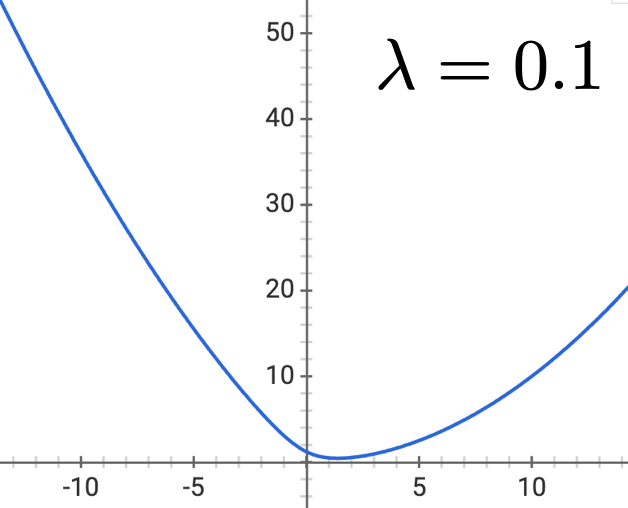
Outline
- Recap (ML pipeline, regression, regularization, GD)
- Classification General Setup
- (vanilla) Linear Classifier
- Understand a given linear classifier
- Linear separator: geometric intuition
- Learn a linear classifier via 0-1 loss?
- Linear Logistic Regression
- Sigmoid function
- Cross-entropy (negative log likelihood) loss
- Optimizing the loss via gradient descent
- Regularization, cross-validation still matter
- Multi-class classification
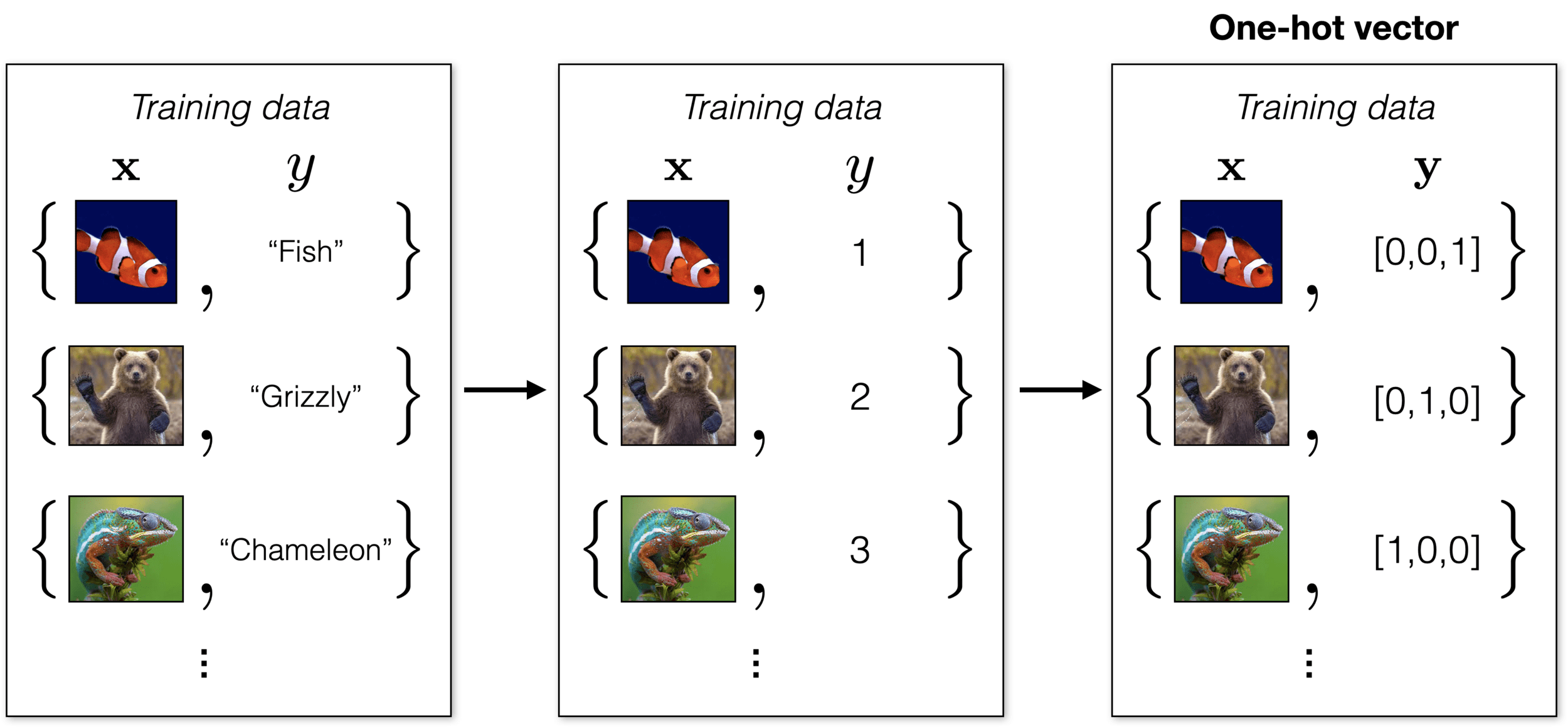
How to represent class labels?
Suppose \(K\) classes, then it's convenient to let y be a \(K\)-dimensional one-hot vector
Generalize sigmoid to softmax
Generalize NLL to NLL multi-class (NLLM, or just cross-entropy)
Every data point incur a scalar loss:
z=\theta^{\top} x+\theta_0
z=\theta^{\top} x+\theta_0
g = \sigma(z)=\frac{1}{1+\exp (-z)}
two classes
\(K\) classes
g =\operatorname{softmax}(z)=\left[\begin{array}{c}
\exp \left(z_1\right) / \sum_i \exp \left(z_i\right) \\
\vdots \\
\exp \left(z_K\right) / \sum_i \exp \left(z_i\right)
\end{array}\right]
scalar
\mathcal{L}_{\mathrm{nllm}}(\mathrm{g}, \mathrm{y})=-\sum_{\mathrm{k}=1}^{\mathrm{K}} \mathrm{y}_{\mathrm{k}} \cdot \log \left(\mathrm{g}_{\mathrm{k}}\right)
\mathcal{L}_{\mathrm{nll}}(\mathrm{g}, \mathrm{y})= - \left(y \log g +\left(1-y \right) \log \left(1-g \right)\right)
scalar
\(K\)-by-1
\(K\)-by-1
\mathcal{L}_{\mathrm{nllm}}(\mathrm{g}, \mathrm{y})=-\sum_{\mathrm{k}=1}^{\mathrm{K}} \mathrm{y}_{\mathrm{k}} \cdot \log \left(\mathrm{g}_{\mathrm{k}}\right)
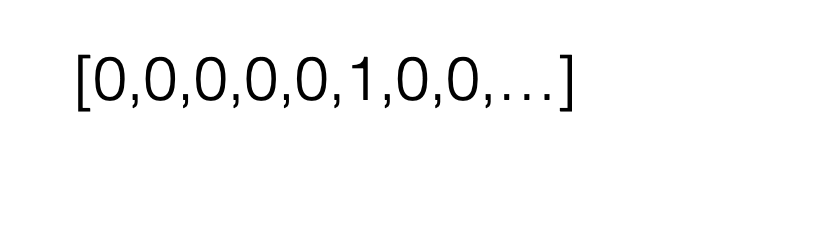
Summary
- Classification is a supervised learning problem, similar to regression, but where the output/label is in a discrete set
- Binary classification: only two possible label values
- Linear binary classification: think of theta and theta-0 as defining a d-1 dimensional hyperplane that cuts the d-dimensional input space into two half-spaces. (This is hard conceptually!)
- 0-1 loss is a natural loss function for classification, BUT, hard to optimize. (Non-smooth; zero-gradient)
- NLL is smoother and has nice probabilistic motivations. We can optimize using gradient descent!
- Regularization is still important.
- Generalizes to multi-class.
Thanks!
We'd love it for you to share some lecture feedback.