
Intro to Machine Learning


Lecture 9: Non-parametric Models
Shen Shen
April 12, 2024
(many slides adapted from Tamara Broderick)
Outline
- Recap (transforermers)
- Non-parametric models
- interpretability
- ease of use/simplicity
- Decision tree
- Terminologies
- Learn via the BuildTree algorithm
- Regression
- Classification
- Nearest neighbor
Outline
- Recap (transforermers)
- Non-parametric models
- interpretability
- ease of use/simplicity
- Decision tree
- Terminologies
- Learn via the BuildTree algorithm
- Regression
- Classification
- Nearest neighbor

Enduring principles:
- Chop up signal into patches (divide and conquer)
- Process each patch identically (and in parallel)
Lessons from CNNs

CNN
- Importantly, all these learned projection weights \(W\) are shared along the token sequence.
- Same "operation" repeated.
命








運
我




操




縱




Transformers

Interpretability
Outline
- Recap (transforermers)
- Non-parametric models
- interpretability
- ease of use/simplicity
- Decision tree
- Terminologies
- Learn via the BuildTree algorithm
- Regression
- Classification
- Nearest neighbor
- does not mean "no parameters"
- there are still parameters to be learned to build a hypothesis/model.
- just that, the model/hypothesis does not have a fixed parameterization.
- (e.g. even the number of parameters can change.)
Non-parametric models
- Decision trees and
- Nearest neighbor
are the classical examples of non-parametric models
Outline
- Recap (transforermers)
- Non-parametric models
- interpretability
- ease of use/simplicity
- Decision tree
- Terminologies
- Learn via the BuildTree algorithm
- Regression
- Classification
- Nearest neighbor
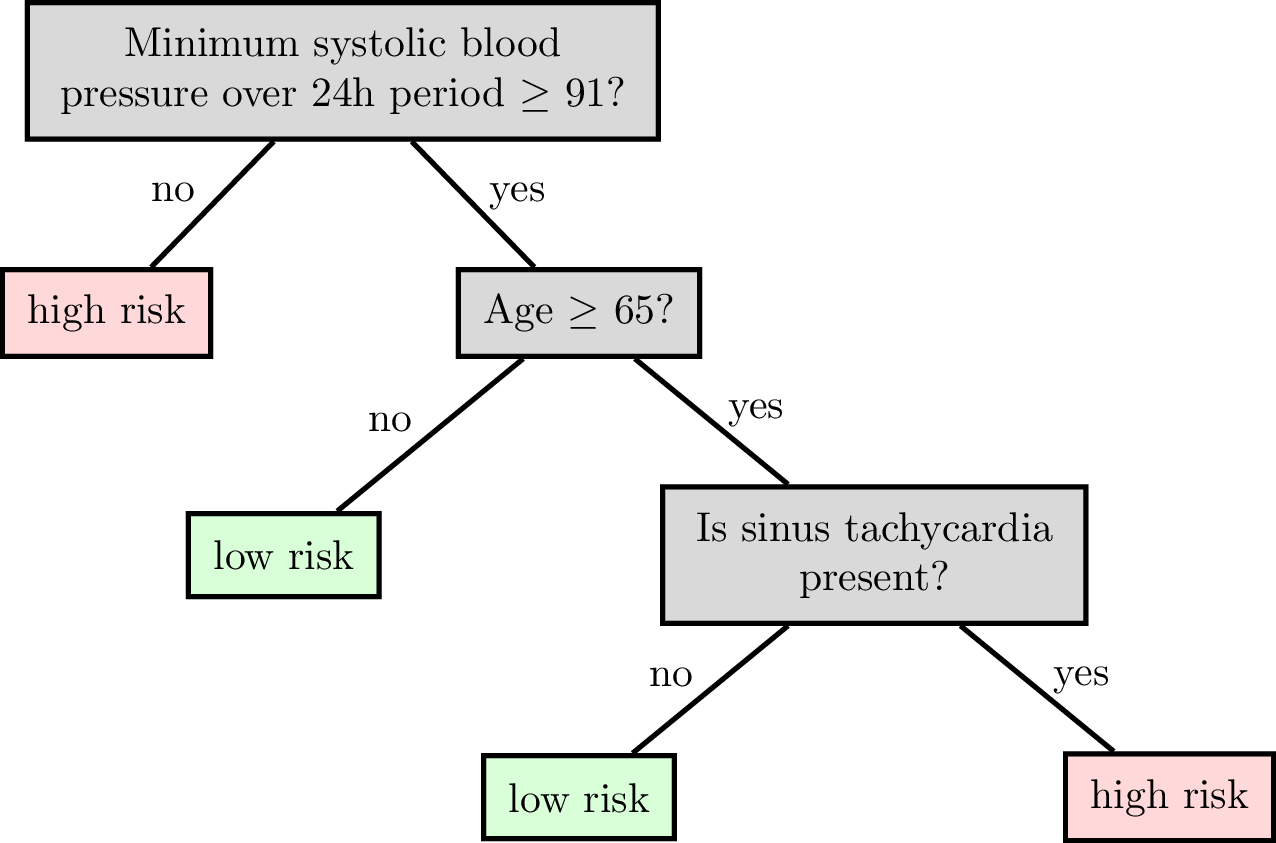
features:
\(x_1\): date
\(x_2\): age
\(x_3\): height
\(x_4\): weight
\(x_5\): sinus tachycardia?
\(x_6\): min systolic bp, 24h
\(x_7\): latest diastolic bp
labels:
1: high risk
-1: low risk
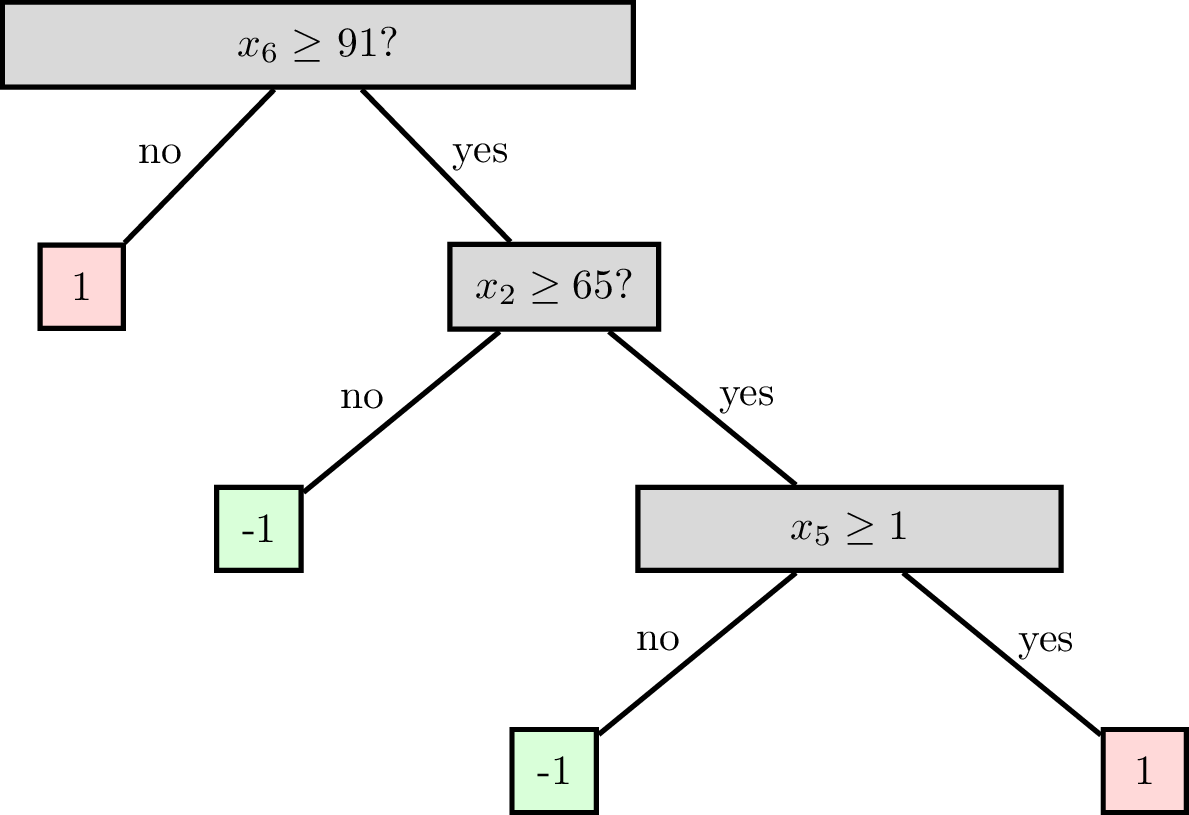
Root node
Internal (decision) node
Leaf (terminal) node

Split dimension
Split value
A node can be specified by
Node(split dim, split value, left child, right child)

A leaf can be specified by
Leaf(leaf value)
features:
- \(x_1\): temperature (deg C)
- \(x_2\): precipitation (cm/hr)
labels:
\(y\): km run
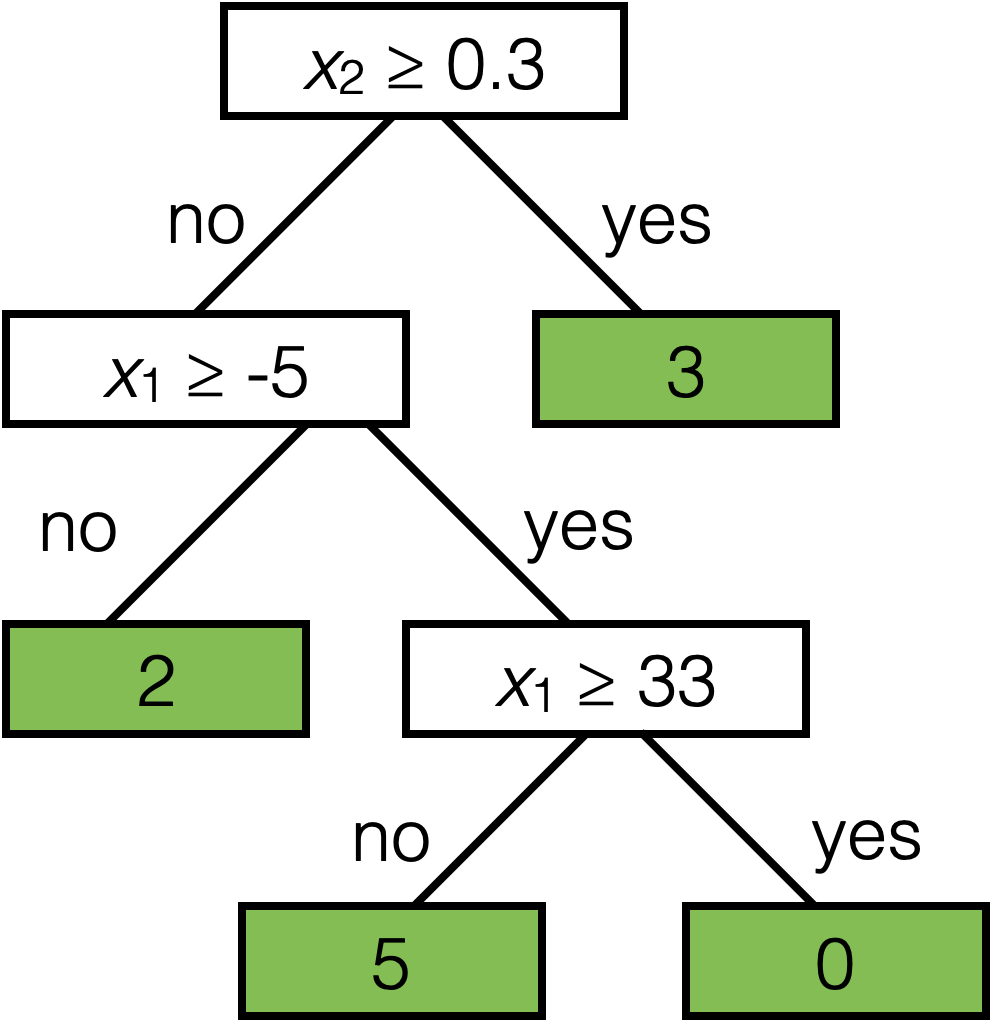
Tree defines an axis-aligned “partition” of the feature space:
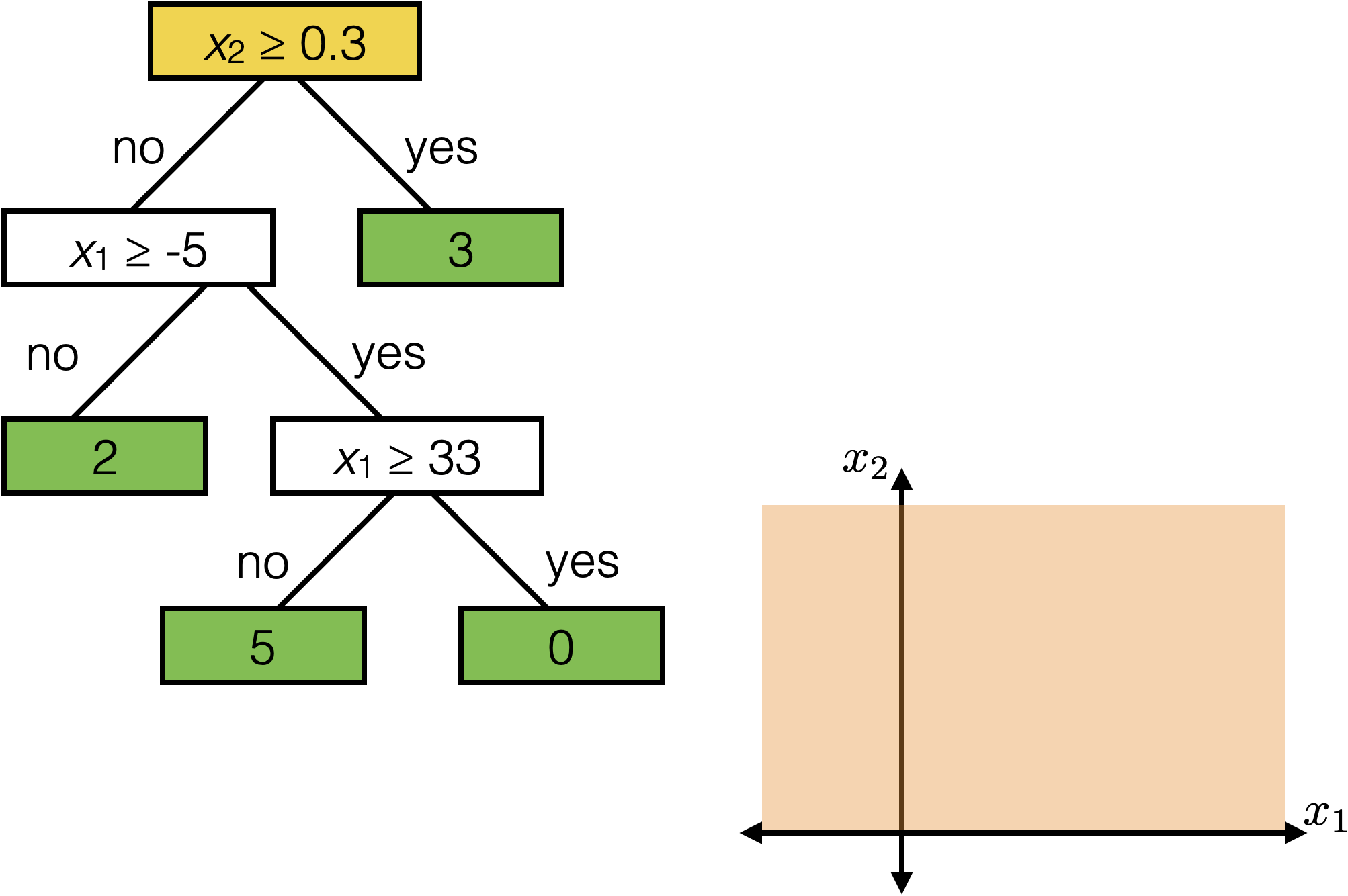
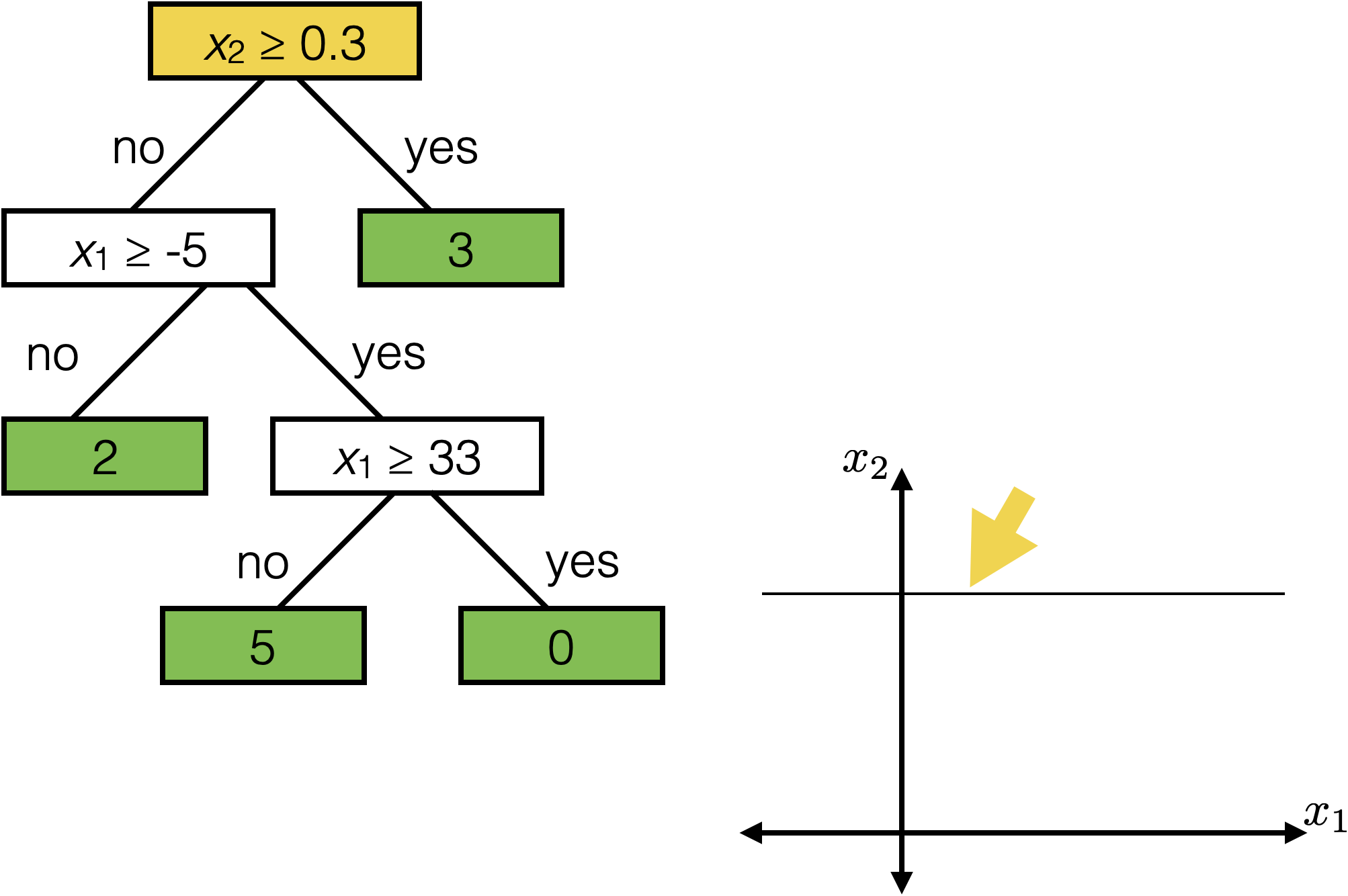
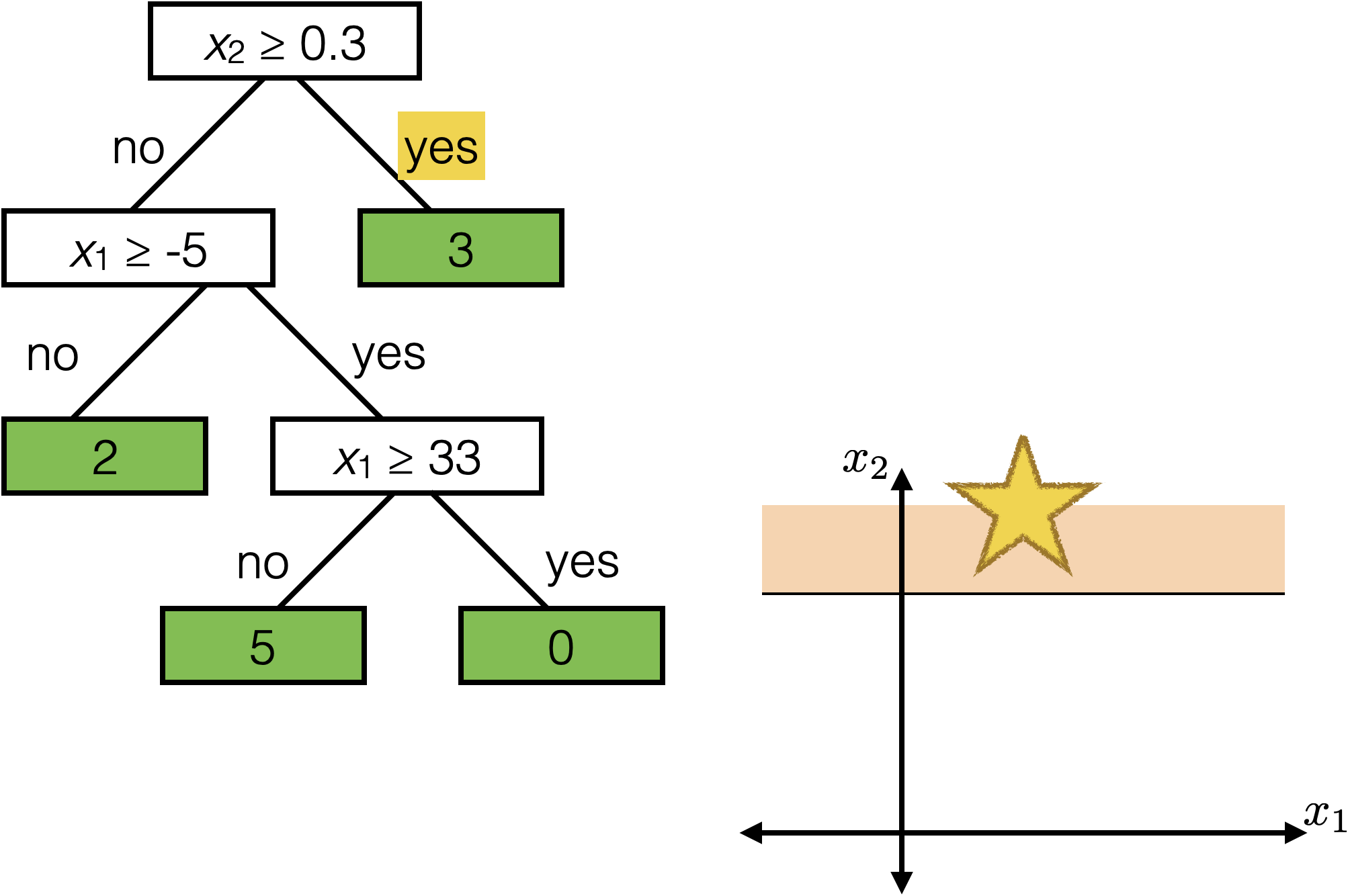
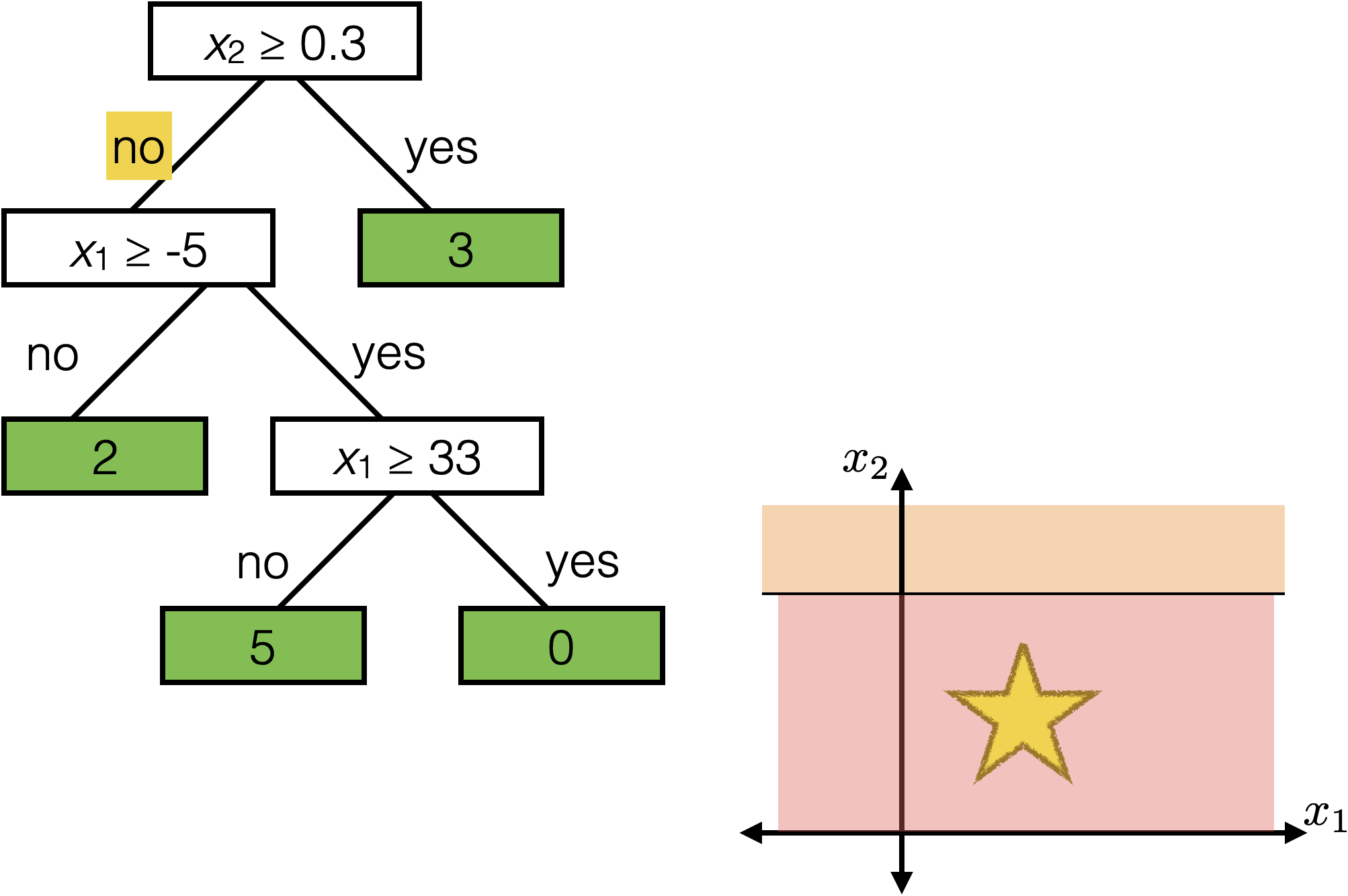

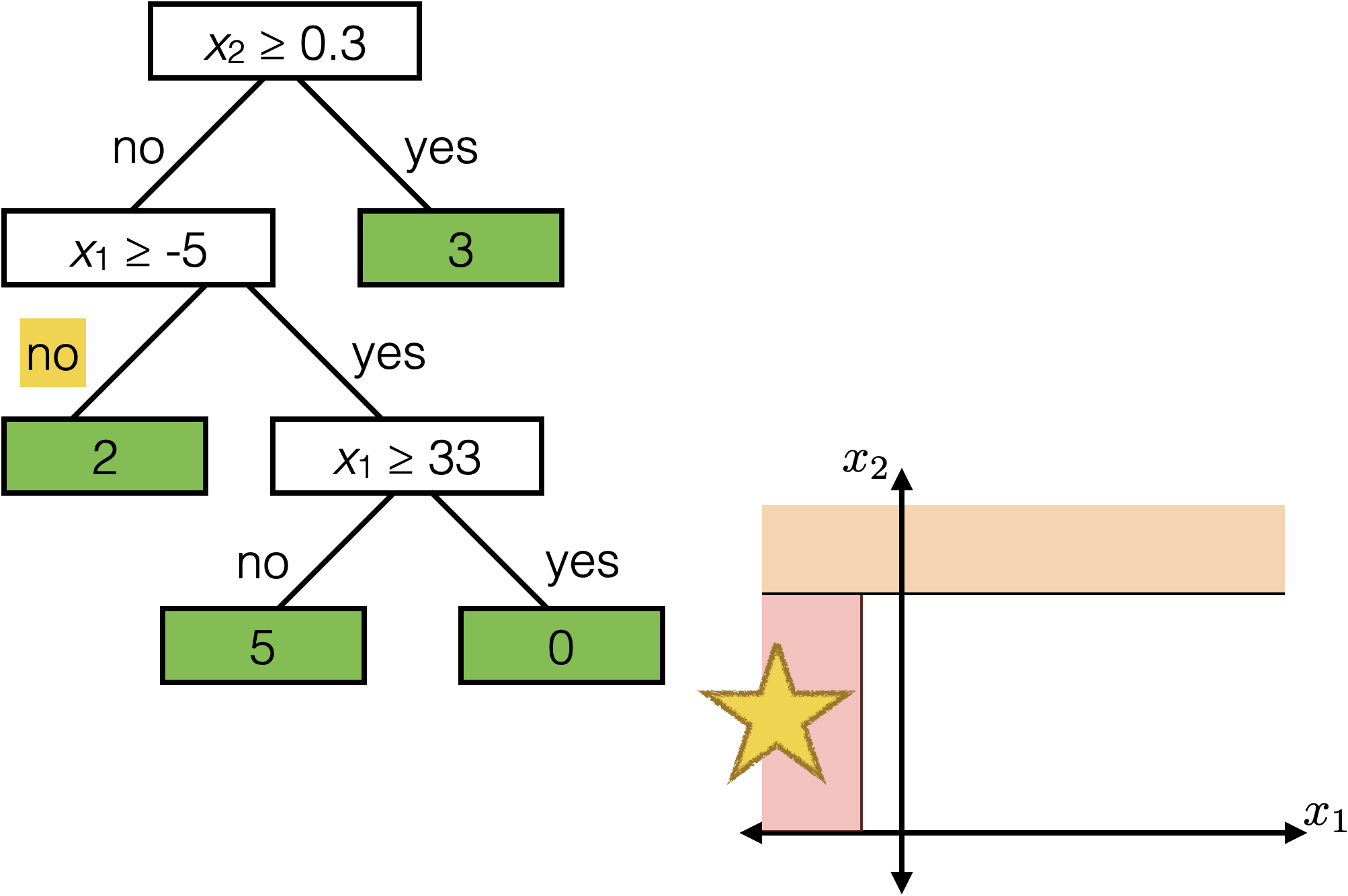
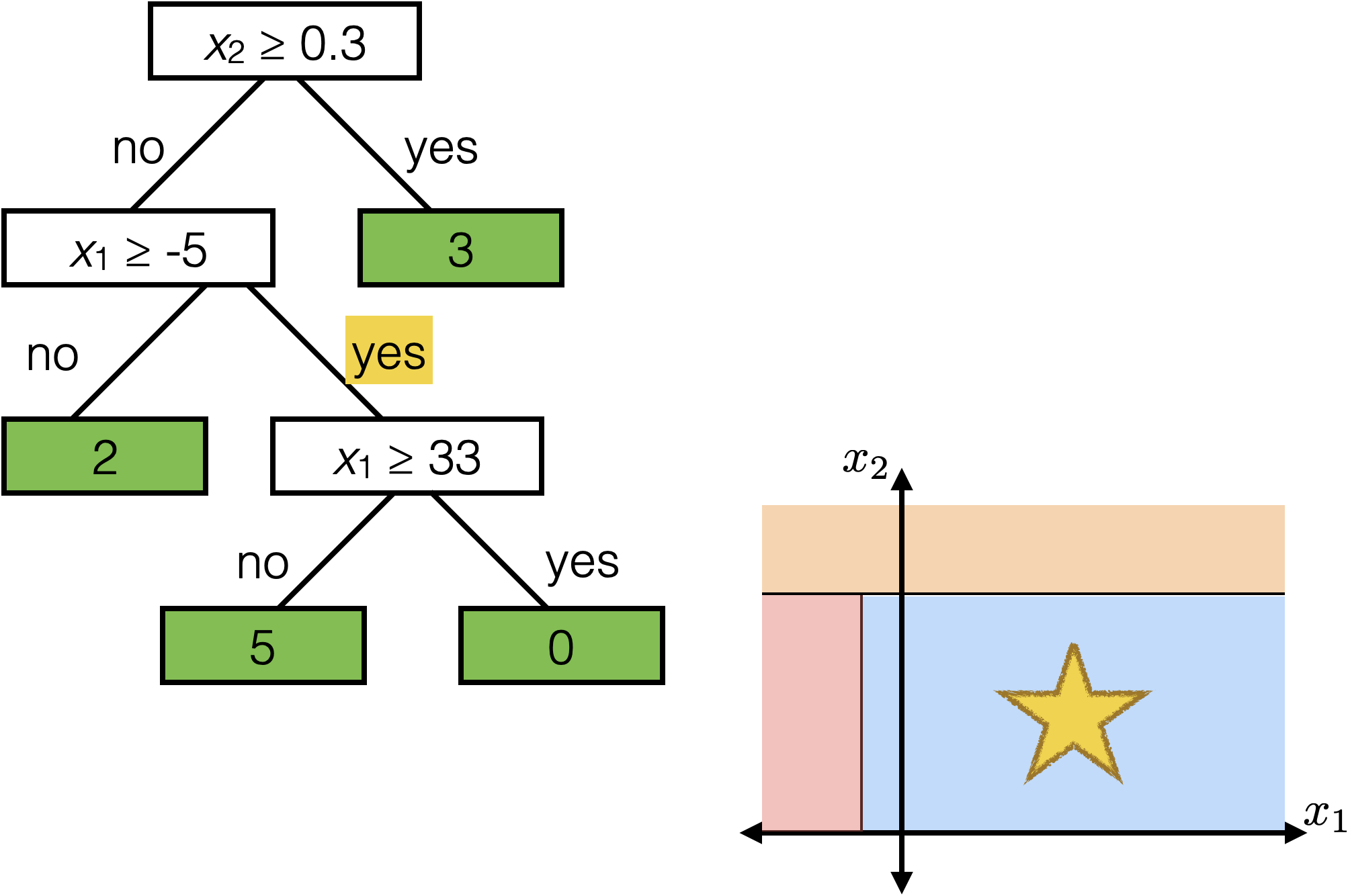
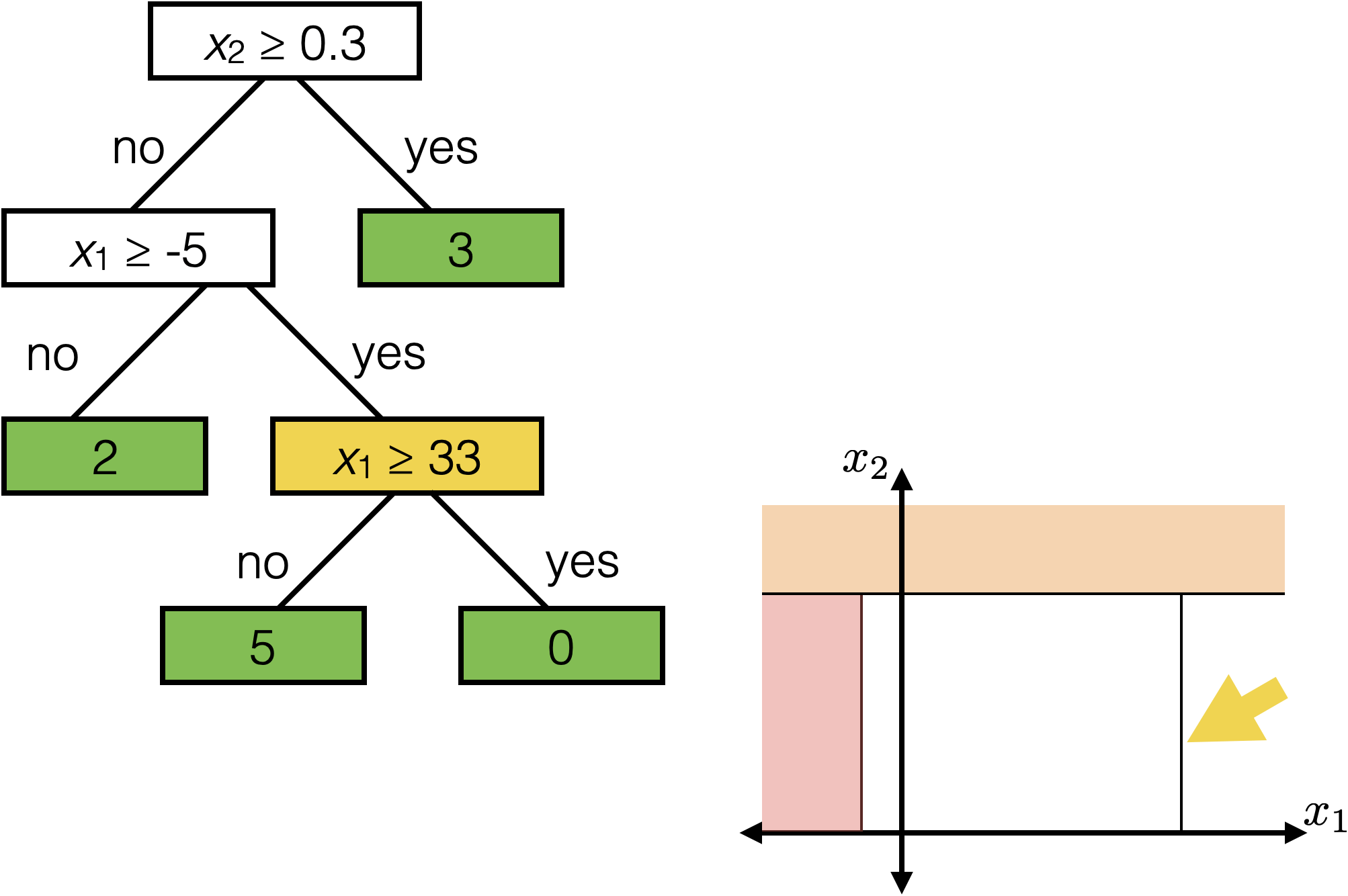
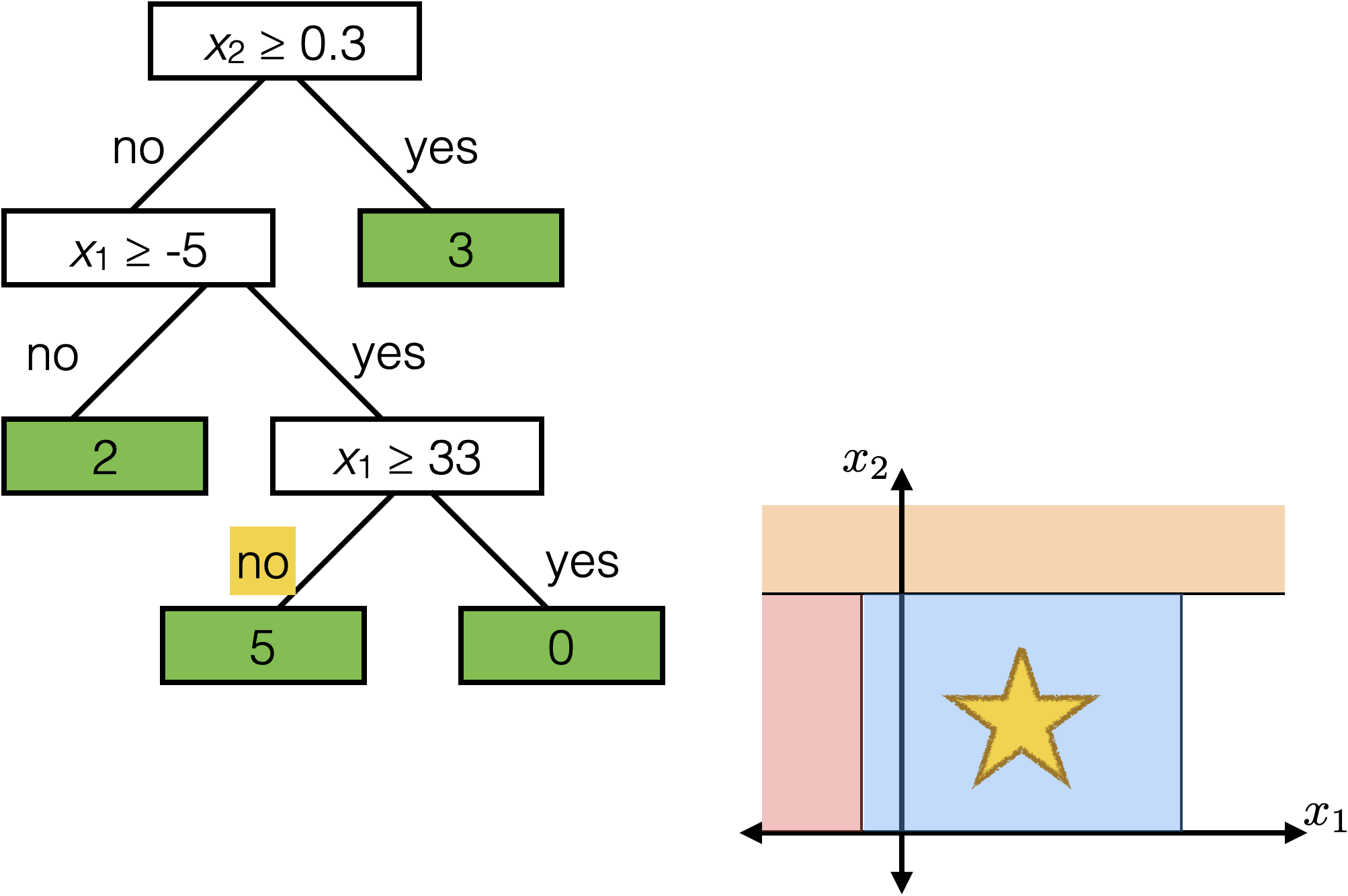
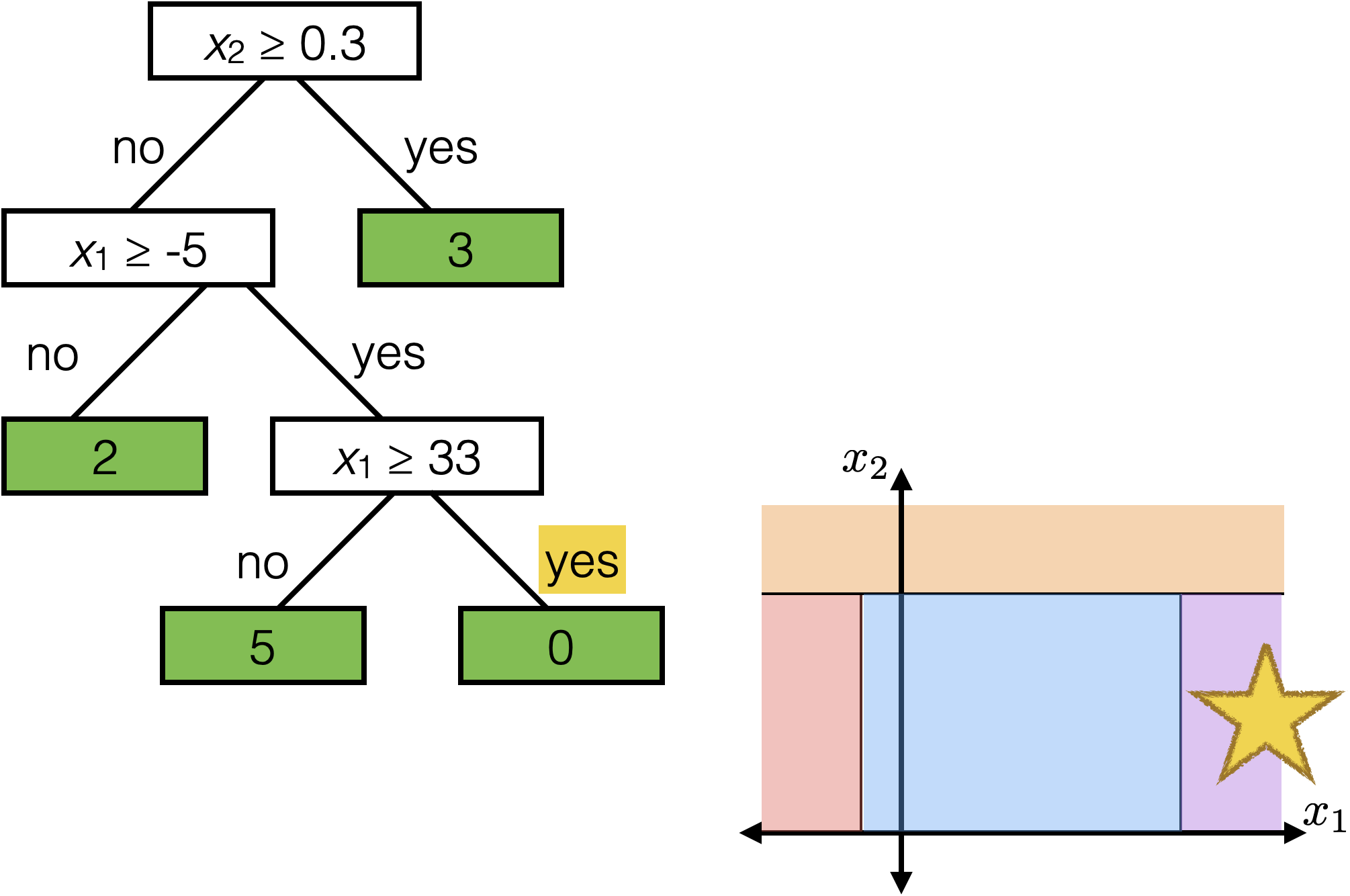
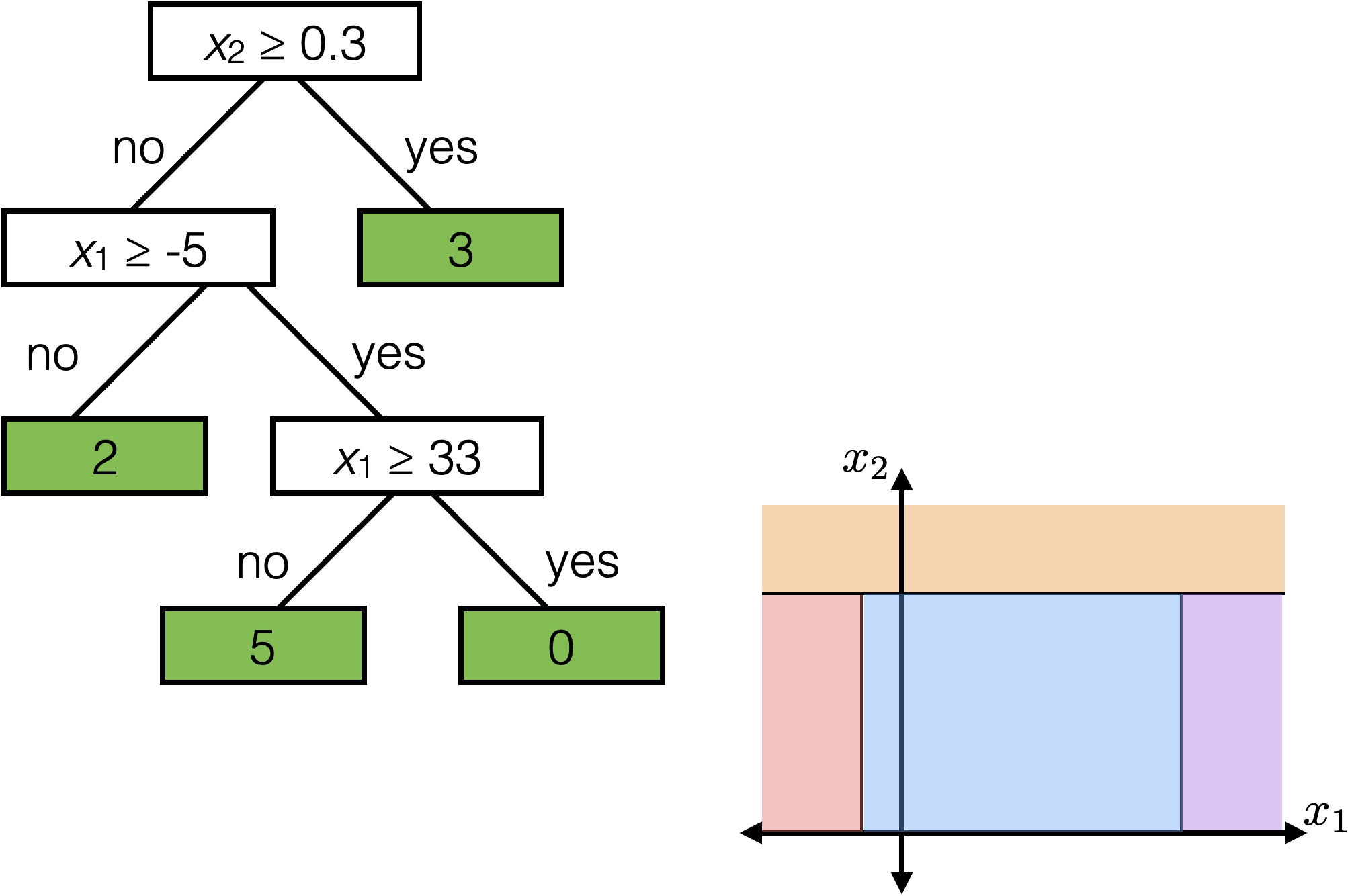

How to learn a tree?
Recall: familiar "recipe"
- Choose how to predict label (given features & parameters)
- Choose a loss (between guess & actual label)
- Choose parameters by trying to minimize the training loss
Here, we need:
- For each internal node:
- split dimension
- split value
- child nodes
- For each leaf node:
- label
- input \(I\): set of indices
- \(k\): hyper-parameter, maximum leaf "size", i.e. how many training data ended in that leaf node.
- \(\hat y\): (intermediate) prediction
\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
- \(j\): split dimension
- \(s\): split value


\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
- Choose \(k=2\)
- \(\operatorname{BuildTree}(\{1,2,3\};2)\)
- Line 1 true
- Consider a fixed \((j, s)\)
- \(I_{j, s}^{+} = \{2,3\}\)
- \(I_{j, s}^{-} = \{1\}\)
- \(\hat{y}_{j, s}^{+} = 5\)
- \(\hat{y}_{j, s}^{-} = 0\)
- \(E_{j, s} =0\)


\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
- Choose \(k=2\)
- \(\operatorname{BuildTree}(\{1,2,3\};2)\)
- Line 1 true
- Consider a fixed \((j, s)\)
- \(I_{j, s}^{+} = \{2,3\}\)
- \(I_{j, s}^{-} = \{1\}\)
- \(\hat{y}_{j, s}^{+} = 5\)
- \(\hat{y}_{j, s}^{-} = 0\)
- \(E_{j, s} =0\)
\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)

- So for line 2: a finite number of \((j, s)\) combo suffices (those splits in-between data points)
- Line 8 picks the "best" among these finite combos. (random tie-breaking)


\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
Suppose line 8 sets this \((j^*,s^*) = (1, 1.7)\)
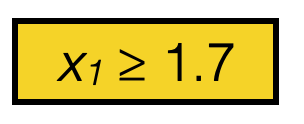
then 12 recursion


\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
Line 8 sets this \((j^*,s^*)\)
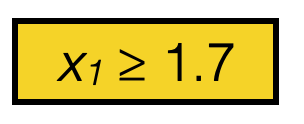
Line 12 recursion





\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
Line 8 sets this \((j^*,s^*)\)
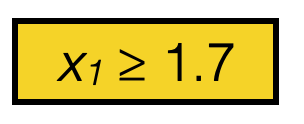
Line 12 recursion






\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
Line 8 sets this \((j^*,s^*)\)
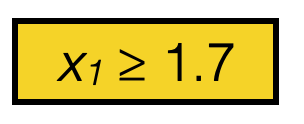
Line 12 recursion






\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
Line 8 sets this \((j^*,s^*)\)
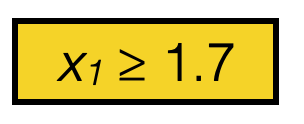
Line 12 recursion







\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)




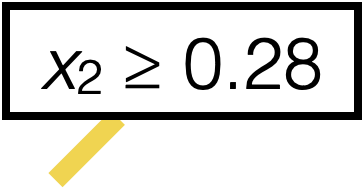
\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)
\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set. \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)



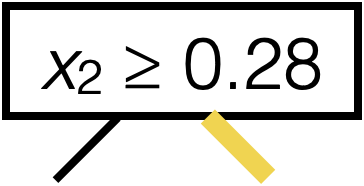
\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set. \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)




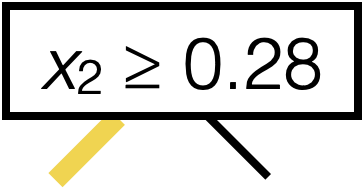
\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set. \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)



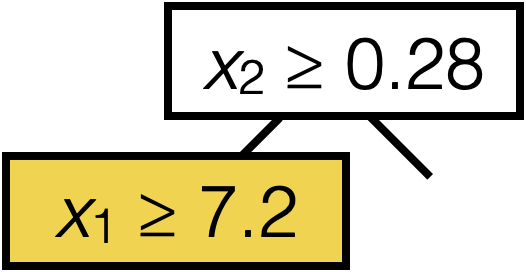

\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set. \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)


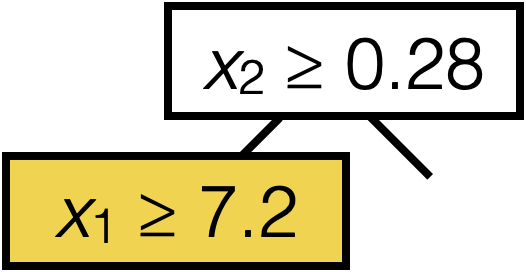

\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set. \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)




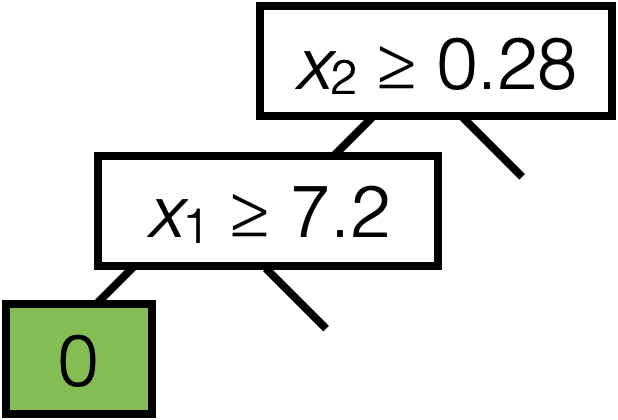
\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set. \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)



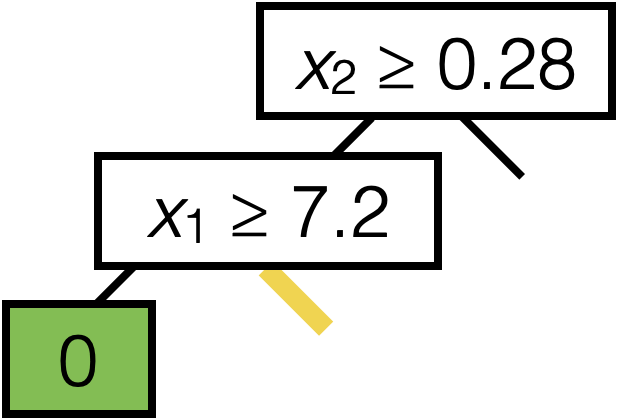
\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set. \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)


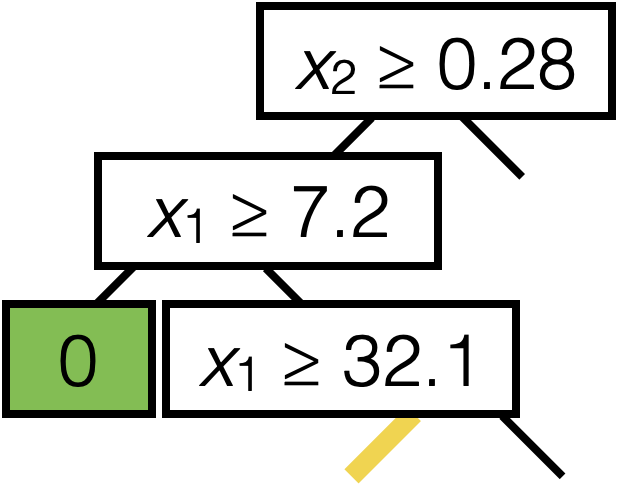

\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set. \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)


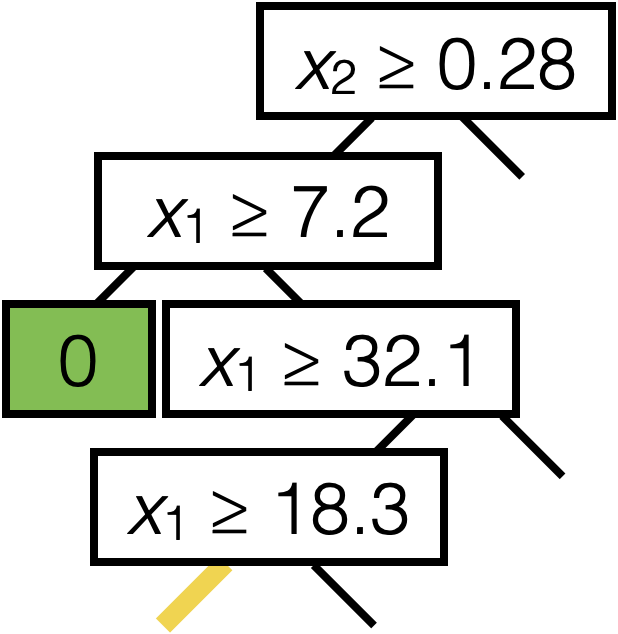

\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set. \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)




\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set. \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)



\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set. \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)



\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)




\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set \(\hat{y}_{j, s}^{+}=\)average \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\)average \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s}=\sum_{i \in I_{j, s}^{+}}\left(y^{(i)}-\hat{y}_{j, s}^{+}\right)^2+\sum_{i \in I_{j, s}^{-}}\left(y^{(i)}-\hat{y}_{j, s}^{-}\right)^2\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) average \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}, k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}, k\right)\right)\)



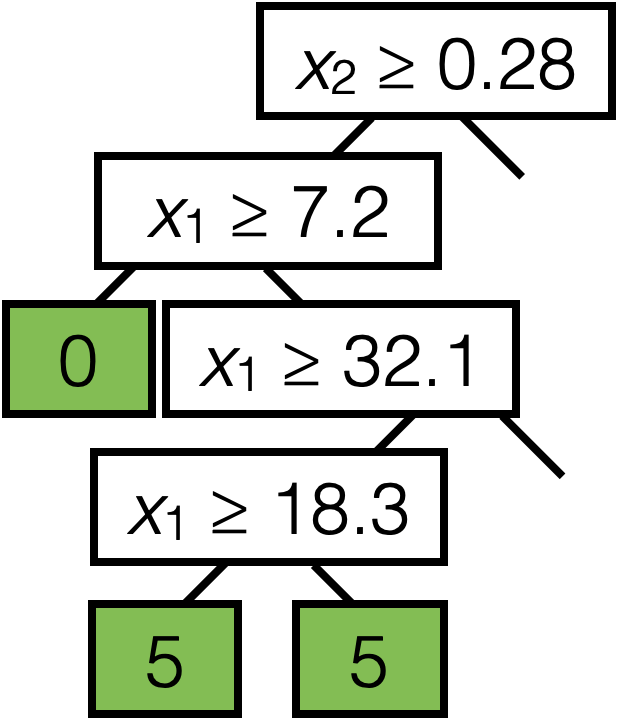
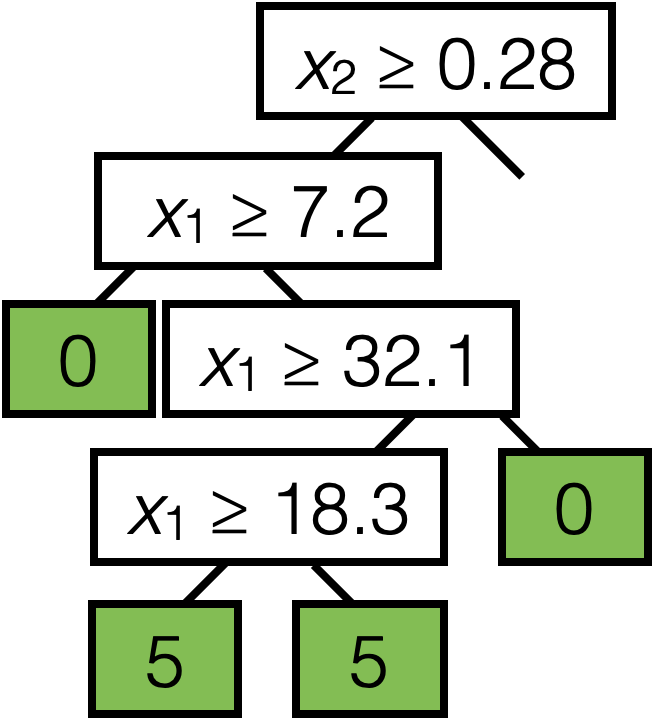
\(\operatorname{BuildTree}(I;k)\)
- if \(|I| > k\)
- for each split dim \(j\) and split value \(s\)
- Set \(I_{j, s}^{+}=\left\{i \in I \mid x_j^{(i)} \geq s\right\}\)
- Set \(I_{j, s}^{-}=\left\{i \in I \mid x_j^{(i)}<s\right\}\)
- Set \(\hat{y}_{j, s}^{+}=\) majority \(_{i \in I_{j, s}^{+}} y^{(i)}\)
- Set \(\hat{y}_{j, s}^{-}=\) majority \(_{i \in I_{j, s}^{-}} y^{(i)}\)
- Set \(E_{j, s} = \frac{\left|I_{j, s}^{-}\right|}{|I|} \cdot H\left(I_{j, s}^{-}\right)+\frac{\left|I_{j, s}^{+}\right|}{|I|} \cdot H\left(I_{j, s}^{+}\right)\)
- Set \(\left(j^*, s^*\right)=\arg \min _{j, s} E_{j, s}\)
- else
- Set \(\hat{y}=\) majority \(_{i \in I} y^{(i)}\)
- return \(\operatorname{LEAF}\)(leave_value=\(\hat{y})\)
- return \(\operatorname{Node}\left(j^*, s^*, \operatorname{BuildTree}\left(I_{j^*, s^*}^{-}; k\right), \operatorname{BuildTree}\left(I_{j^*, s^*}^{+}; k\right)\right)\)
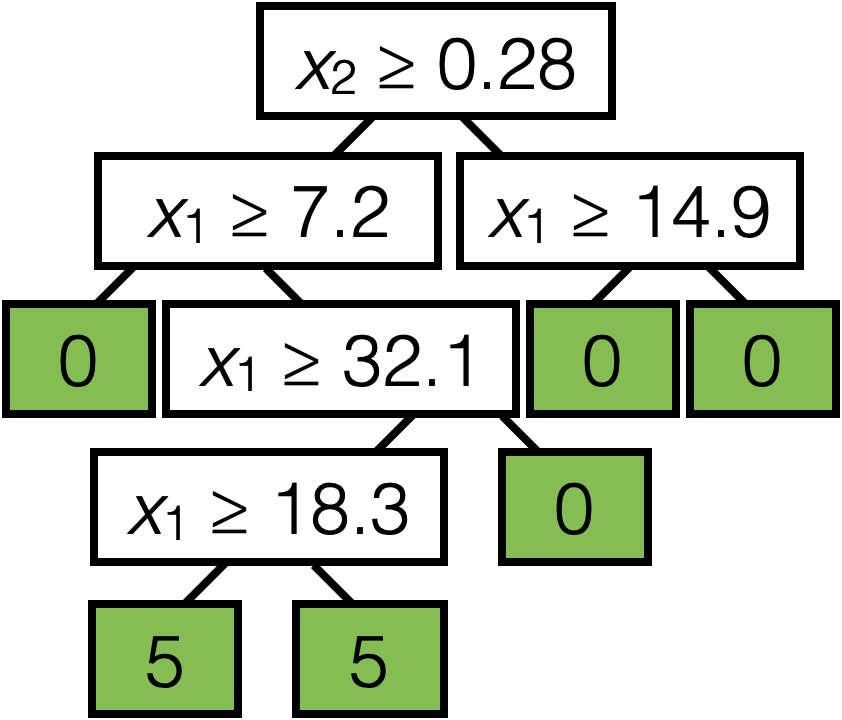
The only change from regression to classification:
- Line 5, 6, 10, average becomes majority vote
- Line 7 error more involved
\(E_{j, s} = \frac{\left|I_{j, s}^{-}\right|}{|I|} \cdot H\left(I_{j, s}^{-}\right)+\frac{\left|I_{j, s}^{+}\right|}{|I|} \cdot H\left(I_{j, s}^{+}\right)\)
- \({I}\) = 9, \(\left|I_{j, s}^{-}\right|\) = 6, \(\left|I_{j, s}^{+}\right|\) = 3
- So, \(E_{j, s} = \frac{6}{9} H\left(I_{j, s}^{-}\right) +\frac{3}{9} H\left(I_{j, s}^{-}\right)\)
\(H\left(I_{j, s}^{-}\right) = -[\frac{3}{6} \log _2\left(\frac{3}{6}\right)+\frac{2}{6} \log _2\left(\frac{2}{6}\right)+\frac{1}{6} \log _2\left(\frac{1}{6}\right)]\)
\(H\left(I_{j, s}^{+}\right) = -[\frac{1}{3} \log \left(\frac{1}{3}\right)+\frac{0}{3} \log _2\left(\frac{0}{3}\right)+\frac{2}{3} \log _2\left(\frac{2}{3}\right)]\)
\(H=-\sum_{\text {class }_c} \hat{P}_c (\log _2 \hat{P}_c)\)





- One of multiple ways to make and use an ensemble
- Bagging = Bootstrap aggregating
- Training data \(\mathcal{D}_n\)
Bagging


- One of multiple ways to make and use an ensemble
- Bagging = Bootstrap aggregating
- Training data \(\mathcal{D}_n\)
- For \(b=1, \ldots, B\)
- Draw a new "data set" \(\tilde{\mathcal{D}}_n^{(b)}\) of size \(n\) by sampling with replacement from \(\mathcal{D}_n\)
- Train a predictor \(\hat{f}^{(b)}\) on \(\tilde{\mathcal{D}}_n^{(b)}\)
- Return
- For regression: \(\hat{f}_{\text {bag }}(x)=\frac{1}{B} \sum_{b=1}^B \hat{f}^{(b)}(x)\)
- For classification: predictor at a point is class with highest vote count at that point
Bagging

Outline
- Recap (transforermers)
- Non-parametric models
- interpretability
- ease of use/simplicity
- Decision tree
- Terminologies
- Learn via the BuildTree algorithm
- Regression
- Classification
- Nearest neighbor
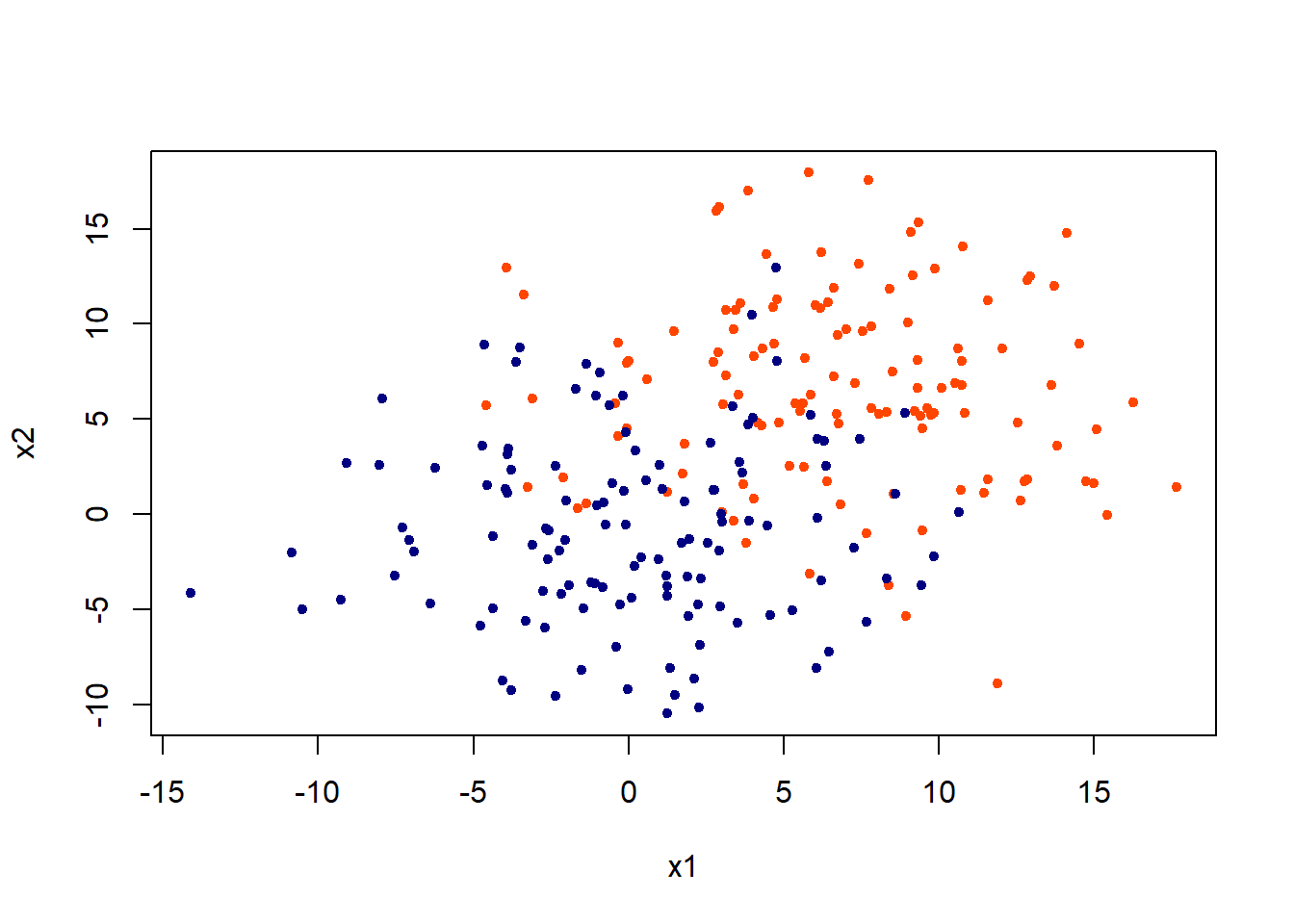
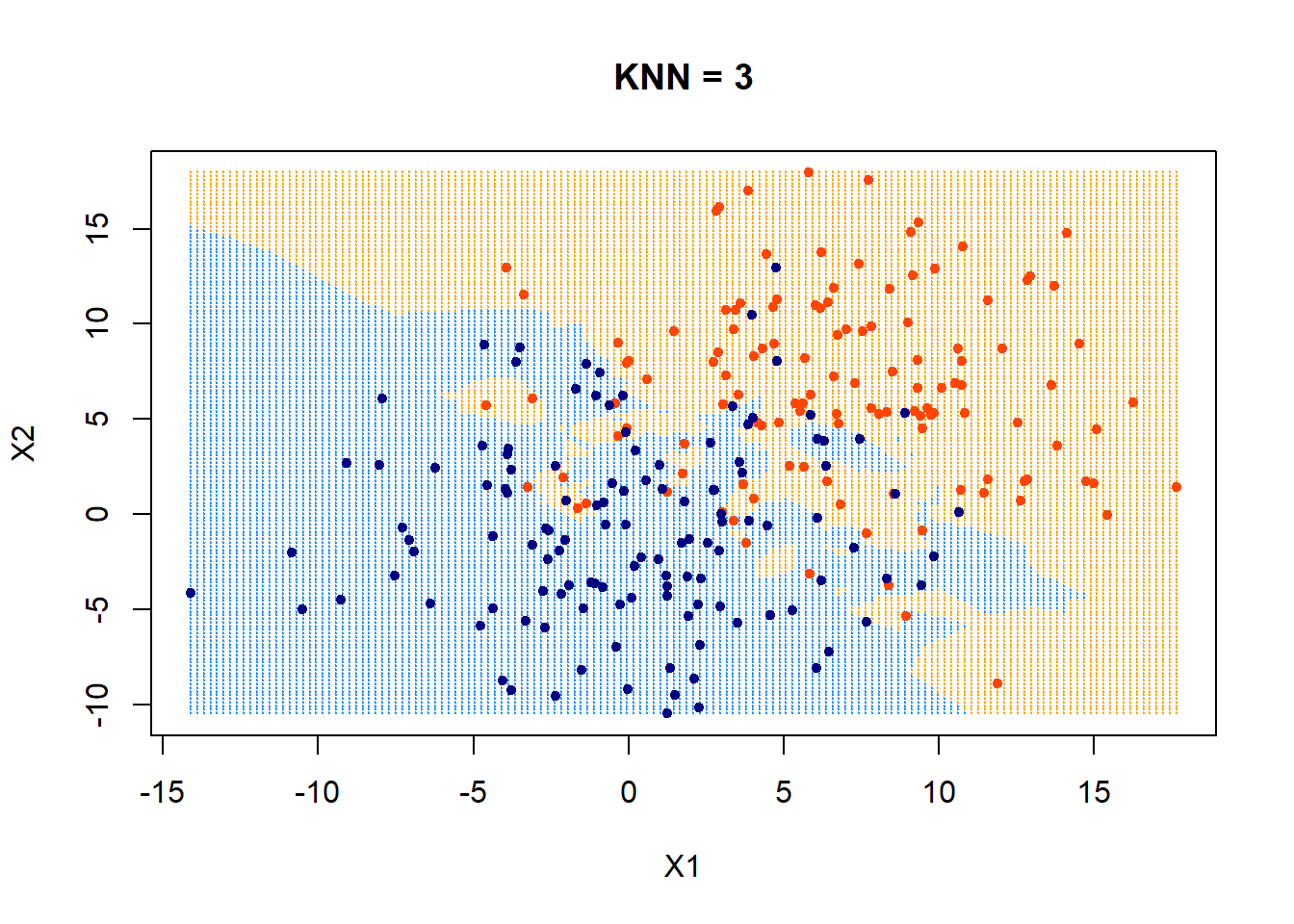
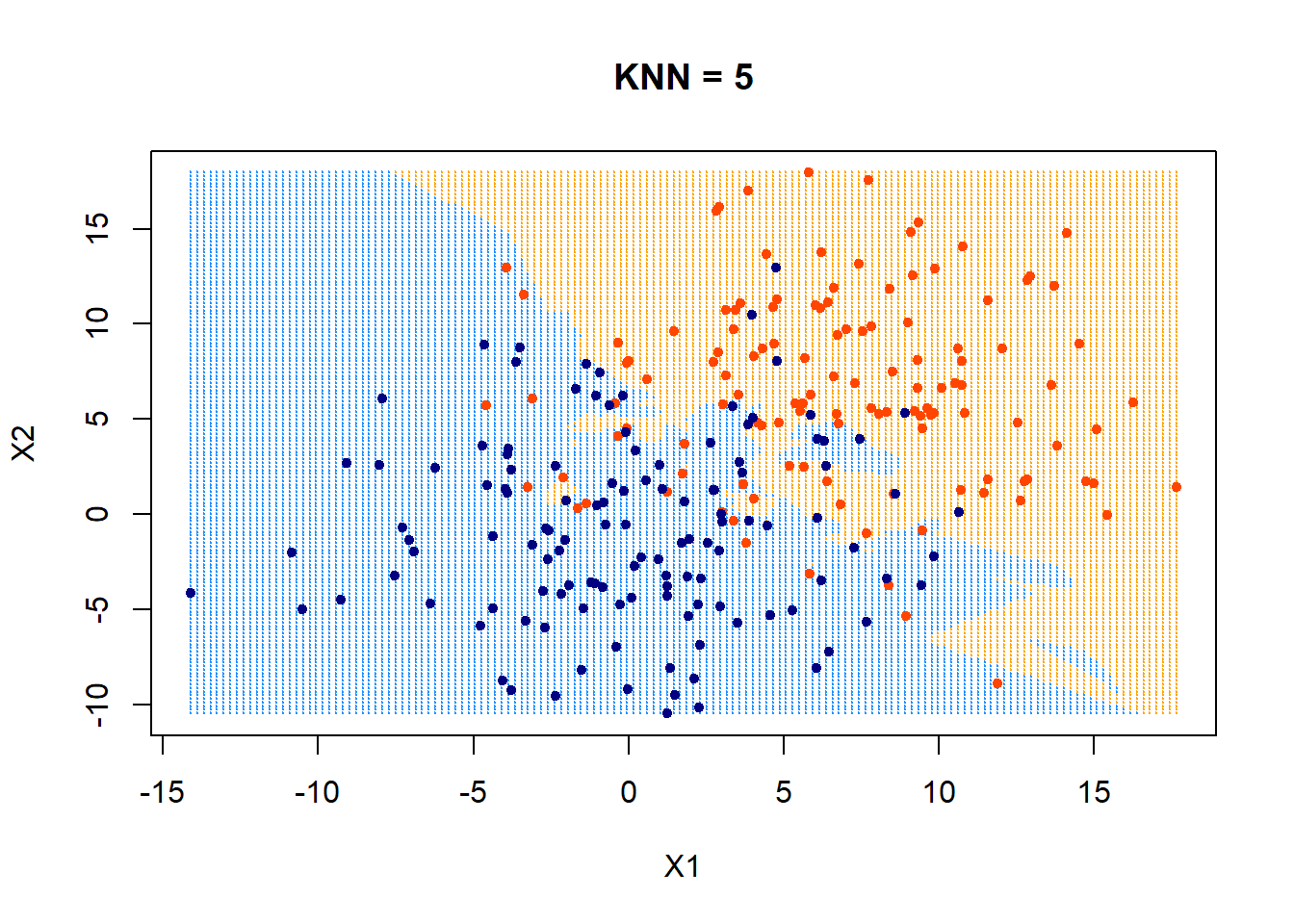
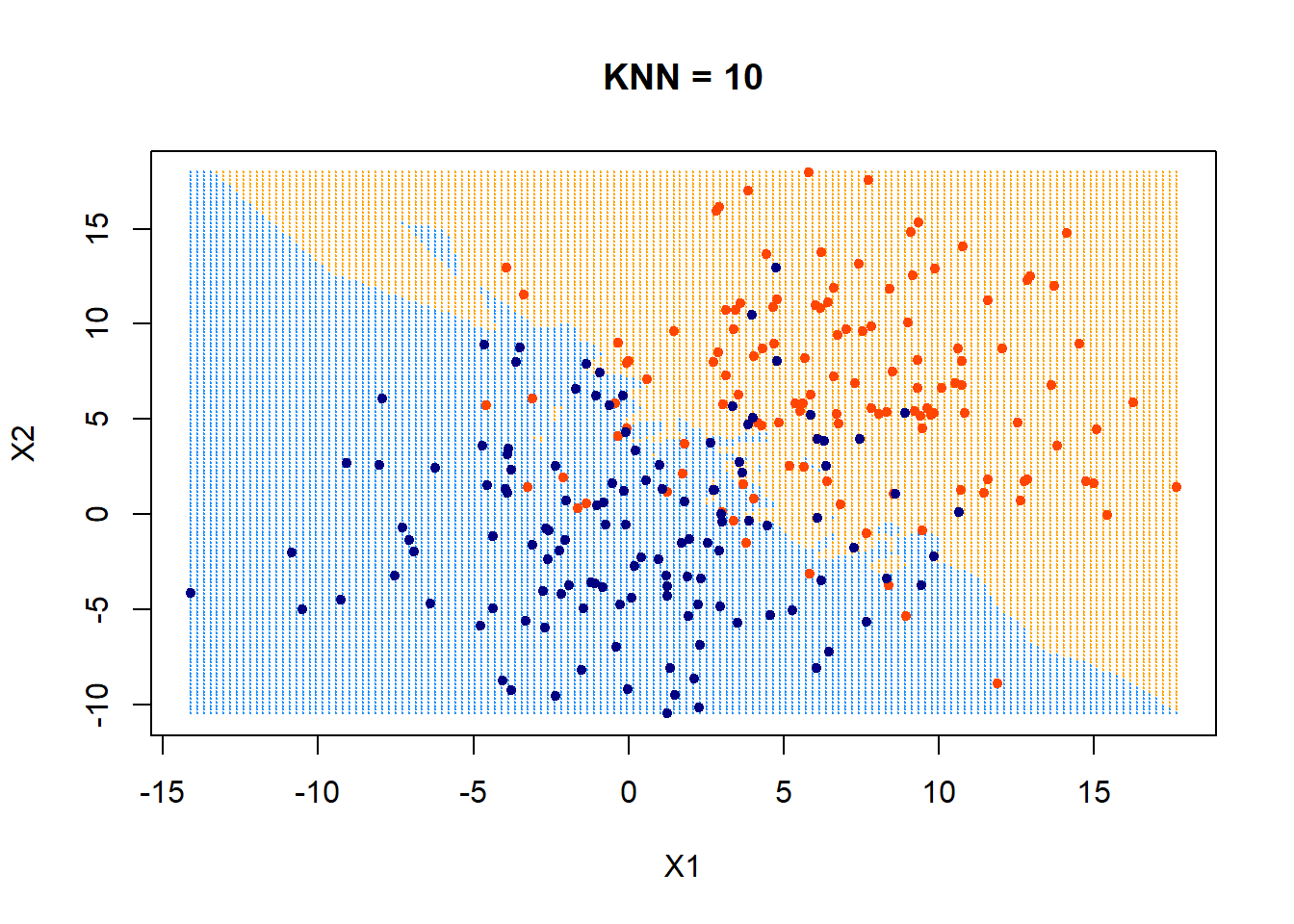
Nearest neighbor classifier
Training: None (or rather: memorize the entire training data)
Predicting/testing:
- for a new data point \(x_{new}\) do:
- find the \(k\) points in training data nearest to \(x_{new}\)
- For classification: predict label \(\hat{y_{new}}\) for \(x_{new}\) by taking a majority vote of the \(k\) neighbors's labels \(y\)
- For regression: predict label \(\hat{y_{new}}\) for \(x_{new}\) by taking an average over the \(k\) neighbors' labels \(y\)
- find the \(k\) points in training data nearest to \(x_{new}\)
- Hyperparameter: \(k\)
- Also need
- Distance metric (typically Euclidean or Manhattan distance)
- A tie-breaking scheme (typically at random)
Thanks!
We'd love it for you to share some lecture feedback.