https://introml.mit.edu/

Lecture 11: Reinforcement Learning 

 

Shen Shen

April 25, 2025

11am, Room 10-250

Intro to Machine Learning

Outline

  • Recap: Markov decision processes
  • Reinforcement learning setup
  • Model-based methods
  • Model-free methods
    • (tabular) Q-learning
      • \(\epsilon\)-greedy action selection
      • exploration vs. exploitation
    • (neural network) Q-learning
  • Reinforcement learning setup again
  • \(\mathcal{S}\) : state space, contains all possible states \(s\).
  • \(\mathcal{A}\) : action space, contains all possible actions \(a\).
  • \(\mathrm{T}\left(s, a, s^{\prime}\right)\) : the probability of transition from state \(s\) to \(s^{\prime}\) when action \(a\) is taken.
  • \(\mathrm{R}(s, a)\) : reward, takes in a (state, action) pair and returns a reward.
  • \(\gamma \in [0,1]\): discount factor, a scalar.
  • \(\pi{(s)}\) : policy, takes in a state and returns an action.

The goal of an MDP is to find a "good" policy.

Markov Decision Processes - Definition and terminologies

In 6.390,

  • \(\mathcal{S}\) and \(\mathcal{A}\) are small discrete sets, unless otherwise specified.
  • \(s^{\prime}\) and \(a^{\prime}\) are short-hand for the next-timestep
  • \(\mathrm{R}(s, a)\) is deterministic and bounded.
  • \(\pi(s)\) is deterministic.
\mathrm{V}_h^\pi(s)=\mathrm{R}\left(s, \pi(s)\right)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, \pi(s), s^{\prime}\right) \mathrm{V}_{h-1}^\pi\left(s^{\prime}\right)

the immediate reward for taking the policy-prescribed action \(\pi(s)\) in state \(s\).

horizon-\(h\) value in state \(s\): the expected sum of discounted rewards, starting in state \(s\) and following policy \(\pi\) for \(h\) steps.

\((h-1)\) horizon future values at a next state \(s^{\prime}\)

sum up future values weighted by the probability of getting to that next state \(s^{\prime}\) 

discounted by \(\gamma\) 

finite-horizon Bellman recursions 

infinite-horizon Bellman equations 

\mathrm{V}^\pi_{\infty}(s)= \mathrm{R}(s, \pi(s))+ \gamma \sum_{s^{\prime}} \mathrm{T}\left(s, \pi(s), s^{\prime}\right) \mathrm{V}^\pi_{\infty}\left(s^{\prime}\right), \forall s
\mathrm{V}_{h}^\pi(s)= \mathrm{R}(s, \pi(s))+ \gamma \sum_{s^{\prime}} \mathrm{T}\left(s, \pi(s), s^{\prime}\right) \mathrm{V}_{h-1}^\pi\left(s^{\prime}\right), \forall s

Recall: For a given policy \(\pi(s),\) the (state) value functions
\(\mathrm{V}_h^\pi(s):=\mathbb{E}\left[\sum_{t=0}^{h-1} \gamma^t \mathrm{R}\left(s_t, \pi\left(s_t\right)\right) \mid s_0=s, \pi\right], \forall s, h\)

\pi(s)
\mathrm{V}^{\pi}_{h}(s)

MDP

Policy evaluation

1. By summing \(h\) terms:

2. By leveraging structure:

Given the recursion

\mathrm{Q}^*_{\infty}(s, a)=\mathrm{R}(s, a)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, a, s^{\prime} \right) \max _{a^{\prime}} \mathrm{Q}^*_{\infty}\left(s^{\prime}, a^{\prime}\right)
  1. for \(s \in \mathcal{S}, a \in \mathcal{A}\) :
  2.       \(\mathrm{Q}_{\text {old }}(\mathrm{s}, \mathrm{a})=0\)
  3. while True:
  4.       for \(s \in \mathcal{S}, a \in \mathcal{A}\) :
  5.             \(\mathrm{Q}_{\text {new }}(s, a) \leftarrow \mathrm{R}(s, a)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, a, s^{\prime}\right) \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)\)
  6.       if \(\max _{s, a}\left|Q_{\text {old }}(s, a)-Q_{\text {new }}(s, a)\right|<\epsilon:\)
  7.             return \(\mathrm{Q}_{\text {new }}\)
  8.       \(\mathrm{Q}_{\text {old }} \leftarrow \mathrm{Q}_{\text {new }}\)
\mathrm{Q}^*_h (s, a)=\mathrm{R}(s, a)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, a, s^{\prime} \right) \max _{a^{\prime}} \mathrm{Q}^*_{h-1}\left(s^{\prime}, a^{\prime}\right)

we can have an infinite-horizon equation 

Value Iteration

if run this block \(h\) times and break, then the returns are exactly \(\mathrm{Q}^*_h\)

\{

\(\mathrm{Q}^*_{\infty}(s, a)\)

Outline

  • Recap: Markov decision processes
  • Reinforcement learning setup
  • Model-based methods
  • Model-free methods
    • (tabular) Q-learning
      • \(\epsilon\)-greedy action selection
      • exploration vs. exploitation
    • (neural network) Q-learning
  • Reinforcement learning setup again
  • (state, action) results in a transition into a next state:

    • Normally, we get to the “intended” state;

      • E.g., in state (7), action “↑” gets to state (4)

    • If an action would take Mario out of the grid world, stay put;

      • E.g., in state (9), “→” gets back to state (9)

    • In state (6), action “↑” leads to two possibilities:

      • 20% chance to (2)

      • 80% chance to (3)

80\%
20\%

Running example: Mario in a grid-world

  • 9 possible states
  • 4 possible actions: {Up ↑, Down ↓, Left ←, Right →}
1
2
9
8
7
5
4
3
6
Recall
1
1
1
1
-10
-10
-10
-10

reward of (3, \(\downarrow\))

reward of \((3,\uparrow\))

reward of \((6, \downarrow\))

reward of \((6,\rightarrow\))

  • (state, action) pairs give out rewards:
    • in state 3, any action gives reward 1
    • in state 6, any action gives reward -10
    • any other (state, action) pair gives reward 0
  • discount factor: a scalar of 0.9 that reduces the "worth" of rewards, depending on the timing we receive them.
    • e.g., for (3, \(\leftarrow\)) pair, we receive a reward of 1 at the start of the game; at the 2nd time step, we receive a discounted reward of 0.9; at the 3rd time step, it is further discounted to \((0.9)^2\), and so on.

Mario in a grid-world, cont'd

  • transition probabilities are unknown

Running example: Mario in a grid-world

Reinforcement learning setup

  • 9 possible states
  • 4 possible actions: {Up ↑, Down ↓, Left ←, Right →}
  • rewards unknown
  • discount factor \(\gamma = 0.9\) 
Now
?
?
?
\dots
?
  • \(\mathcal{S}\) : state space, contains all possible states \(s\).
  • \(\mathcal{A}\) : action space, contains all possible actions \(a\).
  • \(\mathrm{T}\left(s, a, s^{\prime}\right)\) : the probability of transition from state \(s\) to \(s^{\prime}\) when action \(a\) is taken.
  • \(\mathrm{R}(s, a)\) : reward, takes in a (state, action) pair and returns a reward.
  • \(\gamma \in [0,1]\): discount factor, a scalar.
  • \(\pi{(s)}\) : policy, takes in a state and returns an action.

The goal of an MDP problem is to find a "good" policy.

Markov Decision Processes - Definition and terminologies

Reinforcement Learning

RL

Reinforcement learning is very general:

robotics

games

social sciences

chatbot (RLHF)

health care

...

Outline

  • Recap: Markov decision processes
  • Reinforcement learning setup
  • Model-based methods
  • Model-free methods
    • (tabular) Q-learning
      • \(\epsilon\)-greedy action selection
      • exploration vs. exploitation
    • (neural network) Q-learning
  • Reinforcement learning setup again

Model-Based Methods

Keep playing the game to approximate the unknown rewards and transitions.

e.g. observe what reward \(r\) is received from taking the \((6, \uparrow)\) pair, we get \(\mathrm{R}(6,\uparrow)\)

  • Transitions are a bit more involved but still simple:
  • Rewards are particularly easy:

     e.g. play the game 1000 times, count the # of times that (start in state 6, take \(\uparrow\) action, end in state 2), then, roughly, \(\mathrm{T}(6,\uparrow, 2 )  = (\text{that count}/1000) \)

MDP-

Now, with \(\mathrm{R}\) and \(\mathrm{T}\) estimated, we're back in MDP setting.

(for solving RL)

In Reinforcement Learning:

  • Model typically means the MDP tuple \(\langle\mathcal{S}, \mathcal{A}, \mathrm{T}, \mathrm{R}, \gamma\rangle\)
  • What's being learned is not usually called a hypothesis—we simply refer to it as the value or policy.

[A non-exhaustive, but useful taxonomy of algorithms in modern RL. Source]

We will focus on (tabular) Q-learning,

and to a lesser extent touch on deep/fitted Q-learning like DQN.

Outline

  • Recap: Markov decision processes
  • Reinforcement learning setup
  • Model-based methods
  • Model-free methods
    • (tabular) Q-learning
      • \(\epsilon\)-greedy action selection
      • exploration vs. exploitation
    • (neural network) Q-learning
  • Reinforcement learning setup again

Is it possible to get an optimal policy without learning transition or rewards explicitly? 

We kinda know a way already:

With \(\mathrm{Q}^*\), we can back out \(\pi^*\) easily (greedily \(\arg\max \mathrm{Q}^*,\) no need of transition or rewards)

(Recall, from the MDP lab)

But...

didn't we arrive at \(\mathrm{Q}^*\) by value iteration; 

and didn't value iteration rely on transition and rewards explicitly?

\(\mathrm{Q}_{\text {new }}(s, a) \leftarrow \mathrm{R}(s, a)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, a, s^{\prime}\right) \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)\)

Value Iteration

  1. for \(s \in \mathcal{S}, a \in \mathcal{A}\) :
  2.       \(\mathrm{Q}_{\text {old }}(\mathrm{s}, \mathrm{a})=0\)
  3. while True:
  4.       for \(s \in \mathcal{S}, a \in \mathcal{A}\) :
  5.             \(\mathrm{Q}_{\text {new }}(s, a) \leftarrow \mathrm{R}(s, a)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, a, s^{\prime}\right) \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)\)
  6.       if \(\max _{s, a}\left|Q_{\text {old }}(s, a)-Q_{\text {new }}(s, a)\right|<\epsilon:\)
  7.             return \(\mathrm{Q}_{\text {new }}\)
  8.       \(\mathrm{Q}_{\text {old }} \leftarrow \mathrm{Q}_{\text {new }}\)
  • Indeed, value iteration relied on having full access to \(\mathrm{R}\) and \(\mathrm{T}\)
  • Without \(\mathrm{R}\) and \(\mathrm{T}\), how about we approximate like so:
    • pick an \((s,a)\) pair
    • execute \((s,a)\)
    • observe \(r\) and \(s'\)
    • update:

target

(we will see this idea has issues)

\[\mathrm{Q}_{\text {new }}(s, a) \leftarrow \mathrm{R}(s, a)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, a, s^{\prime}\right) \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)\]

\mathrm{Q}_{\text {new }}(s, a) \leftarrow ~ r +\gamma \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)

\(\gamma = 0.9\)

Let's try

\(\mathrm{Q}_\text{old}(s, a)\)

execute \((3, \uparrow)\), observe a reward \(r=1\)

\(\mathrm{Q}_{\text{new}}(s, a)\)

\mathrm{Q}_{\text {new }}(s, a) \leftarrow r +\gamma \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)

States & unknown transition:

unknown rewards:

?
?
?
\dots
?
  • execute \((6, \uparrow)\)
  • update \(\mathrm{Q}(6, \uparrow)\) as:

\(-10 + 0.9 \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(3, a^{\prime}\right)\)

-9.1

= -10 + 0.9 = -9.1

To update the estimate of \(\mathrm{Q}(6, \uparrow)\):

  • observe reward \(r=-10\), next state \(s'=3\)

\(\gamma = 0.9\) 

\(\mathrm{Q}_\text{old}(s, a)\)

\mathrm{Q}_{\text {new }}(s, a) \leftarrow r +\gamma \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)

\(\mathrm{Q}_{\text{new}}(s, a)\)

Let's try

?
?
?
\dots
?

rewards now known

  • execute \((6, \uparrow)\)
  • update \(\mathrm{Q}(6, \uparrow)\) as:

\(-10 + 0.9 \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(2, a^{\prime}\right)\)

-10

= -10 + 0 = -10

To update the estimate of \(\mathrm{Q}(6, \uparrow)\):

  • observe reward \(r=-10\), next state \(s'=2\)

\(\gamma = 0.9\) 

\(\mathrm{Q}_\text{old}(s, a)\)

\mathrm{Q}_{\text {new }}(s, a) \leftarrow r +\gamma \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)

\(\mathrm{Q}_{\text{new}}(s, a)\)

Let's try

?
?
?
\dots
?

rewards now known

  • execute \((6, \uparrow)\)
  • update \(\mathrm{Q}(6, \uparrow)\) as:

\(-10 + 0.9 \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(3, a^{\prime}\right)\)

-9.1

= -10 + 0.9 = -9.1

To update the estimate of \(\mathrm{Q}(6, \uparrow)\):

  • observe reward \(r=-10\), next state \(s'=3\)

\(\gamma = 0.9\) 

\(\mathrm{Q}_\text{old}(s, a)\)

\mathrm{Q}_{\text {new }}(s, a) \leftarrow r +\gamma \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)

\(\mathrm{Q}_{\text{new}}(s, a)\)

Let's try

?
?
?
\dots
?

rewards now known

  • execute \((6, \uparrow)\)
  • update \(\mathrm{Q}(6, \uparrow)\) as:

\(-10 + 0.9 \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(2, a^{\prime}\right)\)

-10

= -10 + 0 = -10

To update the estimate of \(\mathrm{Q}(6, \uparrow)\):

  • observe reward \(r=-10\), next state \(s'=2\)

\(\gamma = 0.9\) 

\(\mathrm{Q}_\text{old}(s, a)\)

\mathrm{Q}_{\text {new }}(s, a) \leftarrow r +\gamma \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)

\(\mathrm{Q}_{\text{new}}(s, a)\)

Let's try

?
?
?
\dots
?

rewards now known

  • execute \((6, \uparrow)\)
  • update \(\mathrm{Q}(6, \uparrow)\) as:

\(-10 + 0.9 \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(3, a^{\prime}\right)\)

-9.1

= -10 + 0.9 = -9.1

To update the estimate of \(\mathrm{Q}(6, \uparrow)\):

  • observe reward \(r=-10\), next state \(s'=3\)

\(\gamma = 0.9\) 

\(\mathrm{Q}_\text{old}(s, a)\)

\mathrm{Q}_{\text {new }}(s, a) \leftarrow r +\gamma \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)

\(\mathrm{Q}_{\text{new}}(s, a)\)

Let's try

?
?
?
\dots
?

rewards now known

\mathrm{Q}_{\text {new }}(s, a) \leftarrow \mathrm{R}(s, a)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, a, s^{\prime}\right) \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)
  • Value iteration relies on having full access to \(\mathrm{R}\) and \(\mathrm{T}\)
  • Without \(\mathrm{R}\) and \(\mathrm{T}\), perhaps we could execute \((s,a)\), observe \(r\) and \(s'\)

but the target keeps "washing away" the old progress.

🥺

r
+\ \gamma \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)

target

\mathrm{Q}_{\text {new }}(s, a)
\leftarrow
\mathrm{Q}_{\text {new }}(s, a) \leftarrow \mathrm{R}(s, a)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, a, s^{\prime}\right) \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)
(1-\alpha)
\mathrm{Q}_{\text {old }}(s, a)
\Bigg(
\Bigg)

old belief

learning rate

😍

core update rule of Q-learning

target

+
\alpha
r
+\ \gamma \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)
\leftarrow
\mathrm{Q}_{\text {new }}(s, a)
  • Value iteration relies on having full access to \(\mathrm{R}\) and \(\mathrm{T}\)
  • Without \(\mathrm{R}\) and \(\mathrm{T}\), perhaps we could execute \((s,a)\), observe \(r\) and \(s'\)

Outline

  • Recap: Markov decision processes
  • Reinforcement learning setup
  • Model-based methods
  • Model-free methods
    • (tabular) Q-learning
      • \(\epsilon\)-greedy action selection
      • exploration vs. exploitation
    • (neural network) Q-learning
  • Reinforcement learning setup again
  • execute \((6, \uparrow)\)
  • update \(\mathrm{Q}(6, \uparrow)\) as:
-9.55

To update the estimate of \(\mathrm{Q}(6, \uparrow)\):

  • observe reward \(r=-10\), next state \(s'=3\)

\(\gamma = 0.9\) 

\(\mathrm{Q}_\text{old}(s, a)\)

\(\mathrm{Q}_{\text{new}}(s, a)\)

?
?
?
\dots
?

rewards now known

\mathrm{Q}_{\text {new }}(s, a) \leftarrow (1-\alpha) \mathrm{Q}_{\text {old }}(s, a)+\alpha\left(r+\gamma \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)\right)

e.g. pick \(\alpha =0.5\)

\((-10 + \)

= -5 + 0.5(-10 + 0.9)= - 9.55

+ 0.5 

(1-0.5) * -10 

 \(0.9 \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(3, a^{\prime}\right))\)

Q-learning update

  • execute \((6, \uparrow)\)
  • update \(\mathrm{Q}(6, \uparrow)\) as:
-9.775

To update the estimate of \(\mathrm{Q}(6, \uparrow)\):

  • observe reward \(r=-10\), next state \(s'=2\)

\(\gamma = 0.9\) 

\(\mathrm{Q}_\text{old}(s, a)\)

\(\mathrm{Q}_{\text{new}}(s, a)\)

?
?
?
\dots
?

rewards now known

\mathrm{Q}_{\text {new }}(s, a) \leftarrow (1-\alpha) \mathrm{Q}_{\text {old }}(s, a)+\alpha\left(r+\gamma \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)\right)

e.g. pick \(\alpha =0.5\)

\((-10 + \)

= -4.775 + 0.5(-10 + 0)= - 9.775

+ 0.5 

(1-0.5) * -9.55 

 \(0.9 \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(2, a^{\prime}\right))\)

Q-learning update

  • execute \((6, \uparrow)\)
  • update \(\mathrm{Q}(6, \uparrow)\) as:
-9.8875

To update the estimate of \(\mathrm{Q}(6, \uparrow)\):

  • observe reward \(r=-10\), next state \(s'=2\)

\(\gamma = 0.9\) 

\(\mathrm{Q}_\text{old}(s, a)\)

\(\mathrm{Q}_{\text{new}}(s, a)\)

?
?
?
\dots
?

rewards now known

\mathrm{Q}_{\text {new }}(s, a) \leftarrow (1-\alpha) \mathrm{Q}_{\text {old }}(s, a)+\alpha\left(r+\gamma \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)\right)

e.g. pick \(\alpha =0.5\)

\((-10 + \)

= -4.8875 + 0.5(-10 + 0)= - 9.8875

+ 0.5 

(1-0.5) * -9.775 

 \(0.9 \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(2, a^{\prime}\right))\)

Q-learning update

 

  1. for \(s \in \mathcal{S}, a \in \mathcal{A}\) :
  2.       \(\mathrm{Q}_{\text {old }}(\mathrm{s}, \mathrm{a})=0\)
  3. while True:
  4.       for \(s \in \mathcal{S}, a \in \mathcal{A}\) :
  5.             \(\mathrm{Q}_{\text {new }}(s, a) \leftarrow \mathrm{R}(s, a)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, a, s^{\prime}\right) \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)\)
  6.       if \(\max _{s, a}\left|Q_{\text {old }}(s, a)-Q_{\text {new }}(s, a)\right|<\epsilon:\)
  7.             return \(\mathrm{Q}_{\text {new }}\)
  8.       \(\mathrm{Q}_{\text {old }} \leftarrow \mathrm{Q}_{\text {new }}\)

Value Iteration\((\mathcal{S}, \mathcal{A}, \mathrm{T}, \mathrm{R}, \gamma, \epsilon)\)

"calculating"

"learning" (estimating)

Q-Learning \(\left(\mathcal{S}, \mathcal{A}, \gamma, \alpha, s_0\right. \text{max-iter})\)

1. \(i=0\)
2. for \(s \in \mathcal{S}, a \in \mathcal{A}:\)
3.       \({\mathrm{Q}_\text{old}}(s, a) = 0\)
4. \(s \leftarrow s_0\)
5. while \(i < \text{max-iter}:\)
6.       \(a \gets \text{select}\_\text{action}(s, {\mathrm{Q}_\text{old}}(s, a))\)
7.       \(r,s' \gets \text{execute}(a)\)
8.      \({\mathrm{Q}}_{\text{new}}(s, a)  \leftarrow (1-\alpha){\mathrm{Q}}_{\text{old}}(s, a) + \alpha(r + \gamma \max_{a'}{\mathrm{Q}}_{\text{old}}(s', a'))\)
9.      \(s  \leftarrow s'\)
10.    \(i  \leftarrow (i+1)\)
11.      \(\mathrm{Q}_{\text{old}}  \leftarrow \mathrm{Q}_{\text{new}}\)
12. return \(\mathrm{Q}_{\text{new}}\)

"learning"

Q-Learning \(\left(\mathcal{S}, \mathcal{A}, \gamma, \alpha, s_0\right. \text{max-iter})\)

1. \(i=0\)
2. for \(s \in \mathcal{S}, a \in \mathcal{A}:\)
3.       \({\mathrm{Q}_\text{old}}(s, a) = 0\)
4. \(s \leftarrow s_0\)
5. while \(i < \text{max-iter}:\)
6.       \(a \gets \text{select}\_\text{action}(s, {\mathrm{Q}_\text{old}}(s, a))\)
7.       \(r,s' \gets \text{execute}(a)\)
8.      \({\mathrm{Q}}_{\text{new}}(s, a)  \leftarrow (1-\alpha){\mathrm{Q}}_{\text{old}}(s, a) + \alpha(r + \gamma \max_{a'}{\mathrm{Q}}_{\text{old}}(s', a'))\)
9.      \(s  \leftarrow s'\)
10.    \(i  \leftarrow (i+1)\)
11.      \(\mathrm{Q}_{\text{old}}  \leftarrow \mathrm{Q}_{\text{new}}\)
12. return \(\mathrm{Q}_{\text{new}}\)

  • Remarkably, 👈 can converge to the true infinite-horizon \(\mathrm{Q}^*\)-values\(^1\). 

\(^1\) given we visit all \(s,a\) infinitely often, and satisfy a decaying condition on the learning rate \(\alpha\).

  • Once converged, act greedily w.r.t \(\mathrm{Q}^*\) again.
  • We also only ever update an \((s,a)\) entry by "playing" it.
  • But convergence can be extremely slow;
  • What if we are impatient, or resource constrained? 

"learning"

Q-Learning \(\left(\mathcal{S}, \mathcal{A}, \gamma, \alpha, s_0\right. \text{max-iter})\)

1. \(i=0\)
2. for \(s \in \mathcal{S}, a \in \mathcal{A}:\)
3.       \({\mathrm{Q}_\text{old}}(s, a) = 0\)
4. \(s \leftarrow s_0\)
5. while \(i < \text{max-iter}:\)
6.       \(a \gets \text{select}\_\text{action}(s, {\mathrm{Q}_\text{old}}(s, a))\)
7.       \(r,s' \gets \text{execute}(a)\)
8.      \({\mathrm{Q}}_{\text{new}}(s, a)  \leftarrow (1-\alpha){\mathrm{Q}}_{\text{old}}(s, a) + \alpha(r + \gamma \max_{a'}{\mathrm{Q}}_{\text{old}}(s', a'))\)
9.      \(s  \leftarrow s'\)
10.    \(i  \leftarrow (i+1)\)
11.      \(\mathrm{Q}_{\text{old}}  \leftarrow \mathrm{Q}_{\text{new}}\)
12. return \(\mathrm{Q}_{\text{new}}\)

  • During learning, especially in early stages, we'd like to explore, and observe diverse \((s,a\)) consequences.
  • During later stages, can act more greedily w.r.t. the estimated Q values
  • \(\epsilon\)-greedy action selection strategy:
    • with probability \(\epsilon\), choose an action \(a \in \mathcal{A}\) uniformly at random
    • with probability \(1-\epsilon\), choose \(\arg \max _{\mathrm{a}} \mathrm{Q}_{\text{old}}(s, \mathrm{a})\)
  • \(\epsilon\) controls the trade-off between exploration vs. exploitation.

the current estimate of \(\mathrm{Q}\) values

"learning"

Q-Learning \(\left(\mathcal{S}, \mathcal{A}, \gamma, \alpha, s_0\right. \text{max-iter})\)

1. \(i=0\)
2. for \(s \in \mathcal{S}, a \in \mathcal{A}:\)
3.       \({\mathrm{Q}_\text{old}}(s, a) = 0\)
4. \(s \leftarrow s_0\)
5. while \(i < \text{max-iter}:\)
6.       \(a \gets \text{select}\_\text{action}(s, {\mathrm{Q}_\text{old}}(s, a))\)
7.       \(r,s' \gets \text{execute}(a)\)
8.      \({\mathrm{Q}}_{\text{new}}(s, a)  \leftarrow (1-\alpha){\mathrm{Q}}_{\text{old}}(s, a) + \alpha(r + \gamma \max_{a'}{\mathrm{Q}}_{\text{old}}(s', a'))\)
9.      \(s  \leftarrow s'\)
10.    \(i  \leftarrow (i+1)\)
11.      \(\mathrm{Q}_{\text{old}}  \leftarrow \mathrm{Q}_{\text{new}}\)
12. return \(\mathrm{Q}_{\text{new}}\)

Outline

  • Recap: Markov decision processes
  • Reinforcement learning setup
  • Model-based methods
  • Model-free methods
    • (tabular) Q-learning
      • \(\epsilon\)-greedy action selection
      • exploration vs. exploitation
    • (neural network) Q-learning
  • Reinforcement learning setup again
  • So far, Q-learning is only kinda sensible for (small) tabular setting. 
  • What do we do if \(\mathcal{S}\) and/or \(\mathcal{A}\) are large, or even continuous?
  • Notice that the key update line in Q-learning algorithm:

is equivalently:

\(\mathrm{Q}_{\text {new}}(s, a) \leftarrow\mathrm{Q}_{\text {old }}(s, a)+\alpha\left([r+\gamma \max _{a^{\prime}} \mathrm{Q}_{\text {old}}(s', a')] - \mathrm{Q}_{\text {old }}(s, a)\right)\)

new belief

\(\leftarrow\)

old belief

learning rate

+
(

target

-

old belief

)
\mathrm{Q}_{\text {new }}(s, a) \leftarrow(1-\alpha) \mathrm{Q}_{\text {old }}(s, a)+\alpha\left(r+\gamma \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)\right)
  • Reminds us of: when minimizing \((\text{target} - \text{guess}_{\theta})^2\)

\(\mathrm{Q}_{\text {new}}(s, a) \leftarrow\mathrm{Q}_{\text {old }}(s, a)+\alpha\left([r+\gamma \max _{a^{\prime}} \mathrm{Q}_{\text {old}}(s', a')] - \mathrm{Q}_{\text {old }}(s, a)\right)\)

new belief

\(\leftarrow\)

old belief

learning rate

+
(

target

-

old belief

)
  • Generalize tabular Q-learning for continuous state/action space:

\(\left(\text{target} -\mathrm{Q}_{\theta}(s, a)\right)^2\)

 

Gradient descent does: \(\theta_{\text{new}} \leftarrow \theta_{\text{old}} + \eta (\text{target} - \text{guess}_{\theta})\frac{d (\text{guess})}{d \theta}\) 

  1. parameterize \(\mathrm{Q}_{\theta}(s,a)\) 
  2. execute \((s,a),\) observe\((r, s'),\) construct the target
  3. regress \(\mathrm{Q}_{\theta}(s,a)\) against the target, i.e. update \(\theta\) via gradient-descent methods to minimize                    

\(r+\gamma \max _{a^{\prime}} \mathrm{Q}_{\theta}\left(s^{\prime}, a^{\prime}\right)\)

Outline

  • Recap: Markov decision processes
  • Reinforcement learning setup
  • Model-based methods
  • Model-free methods
    • (tabular) Q-learning
      • \(\epsilon\)-greedy action selection
      • exploration vs. exploitation
    • (neural network) Q-learning
  • Reinforcement learning setup again
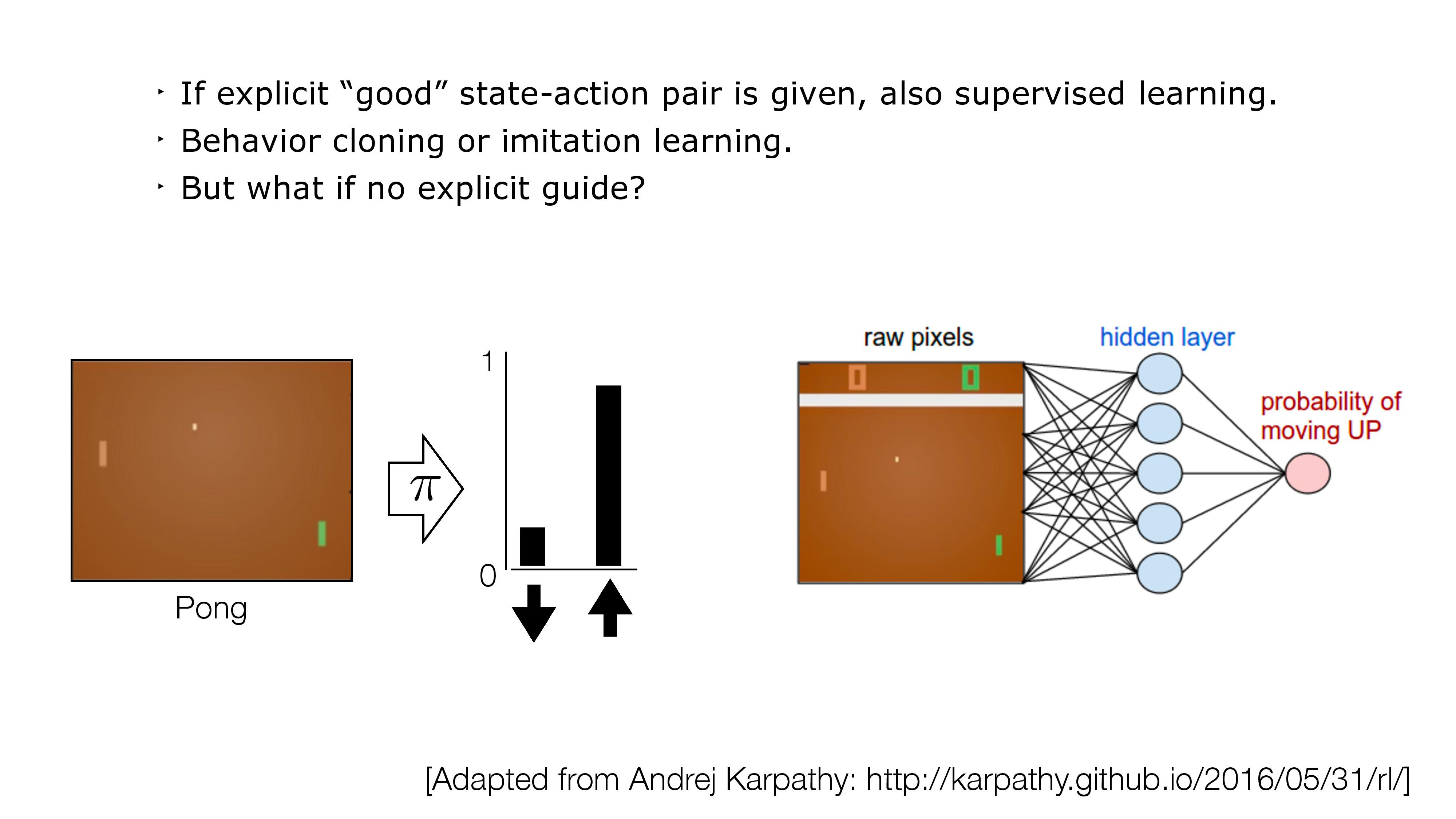
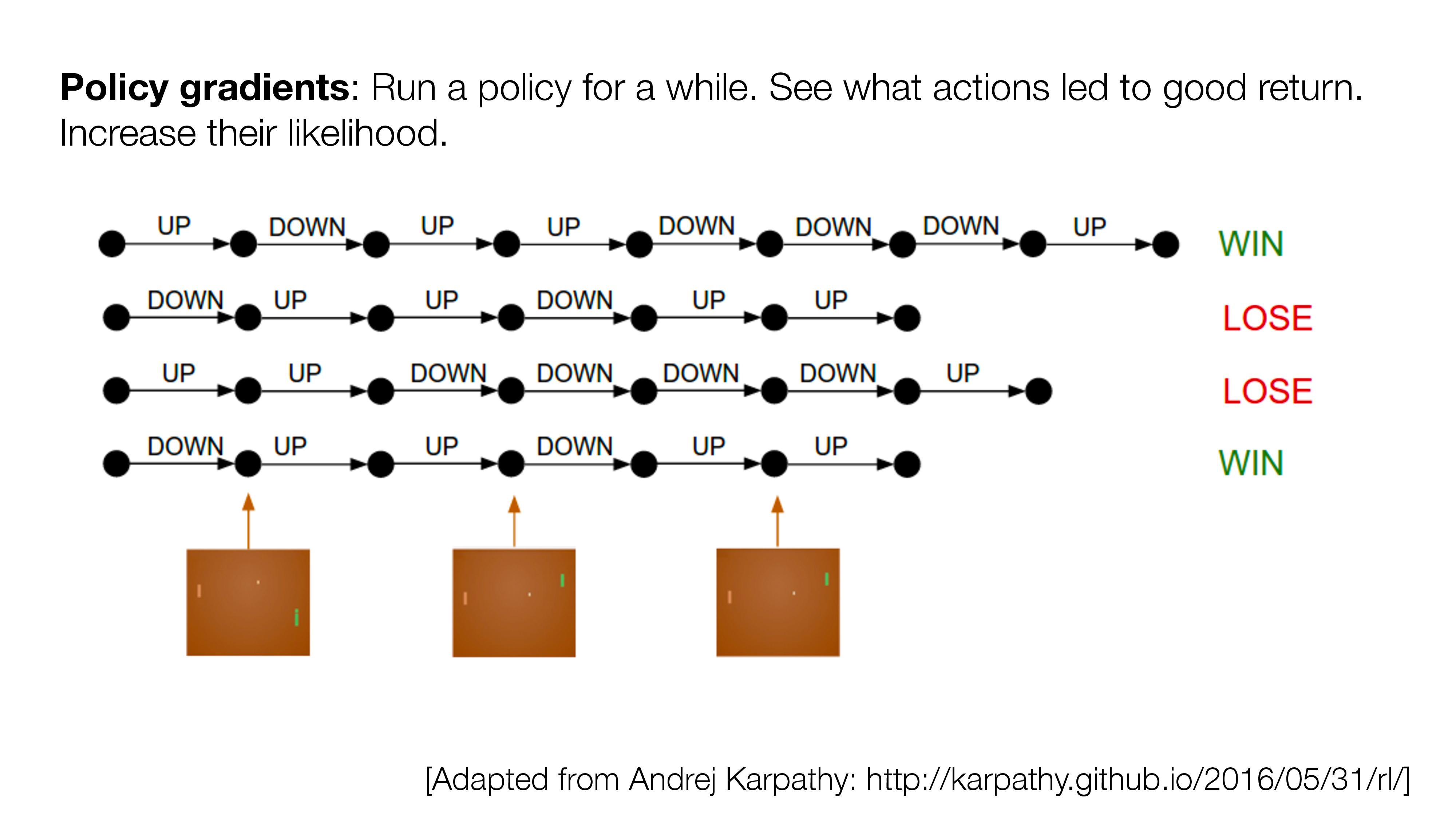
  • If no direct supervision is available?
  • Strictly RL setting. Interact, observe, get data, use rewards as "coy" supervision signal.

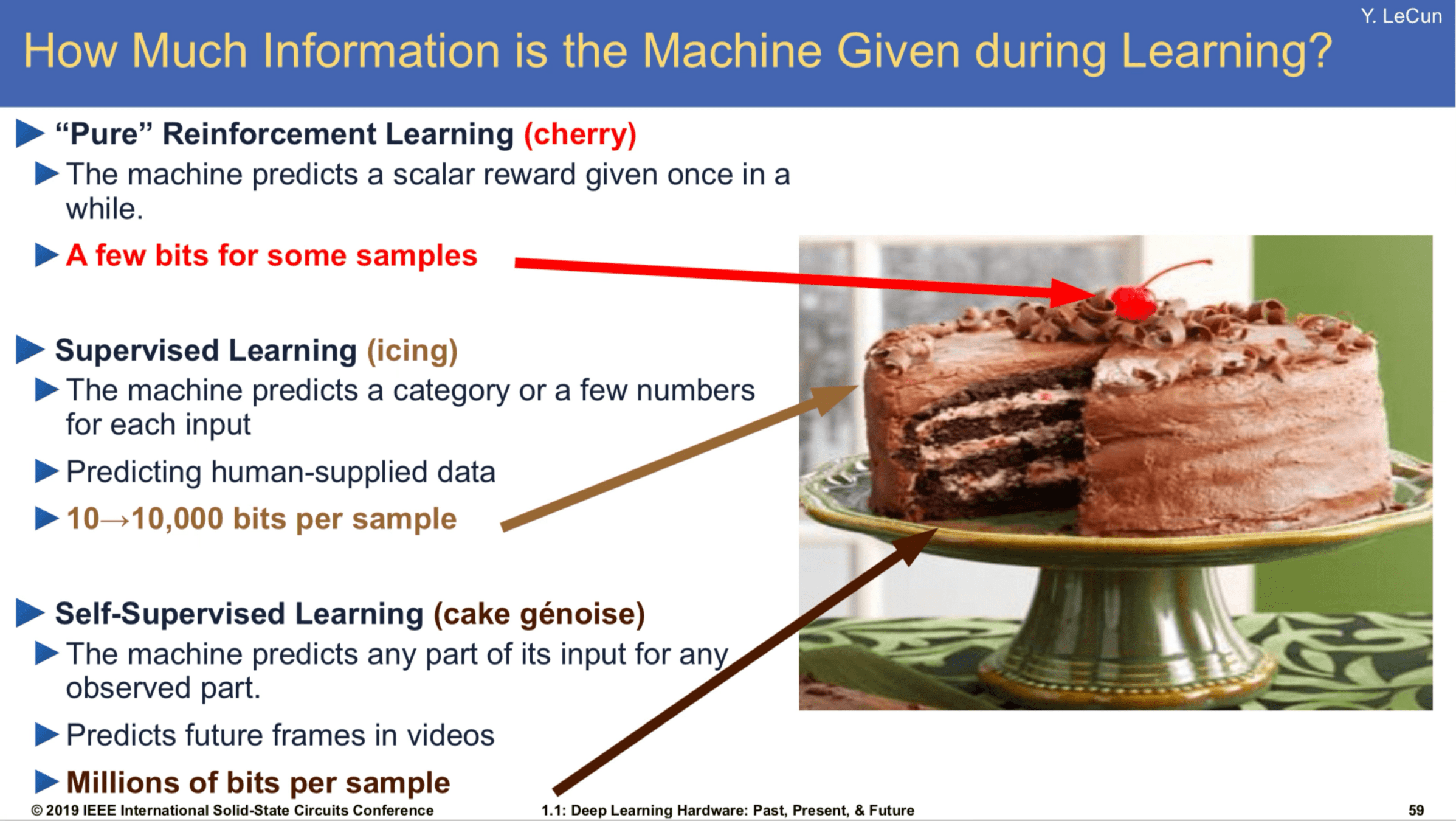
[Slide Credit: Yann LeCun]

Reinforcement learning has a lot of challenges:

  • Data can be very expensive/tricky to get
    • sim-to-real gap
    • sparse rewards
    • exploration-exploitation trade-off
    • catastrophic forgetting
  • Learning can be very inefficient
    • temporal process, compound error
    • super high variance
    • learning process hard to stabilize

... 

Summary

  • We saw, last week, how to find good  in a known MDP:  these are policies with high cumulative expected reward.
  • In reinforcement learning, we assume we are interacting with an unknown MDP, but we still want to find a good policy.  We will do so via estimating the Q value function.
  • One problem is how to select actions to gain good reward while learning.  This “exploration vs exploitation” problem is important.
  • Q-learning, for discrete-state problems, will converge to the optimal value function (with enough exploration).
  • “Deep Q learning” can be applied to continuous-state or large discrete-state problems by using a parameterized function to represent the Q-values. 

Thanks!

We'd love to hear your thoughts.