Lecture 4: Linear Classification

Shen Shen

Feb 21, 2025

11am, Room 10-250

Intro to Machine Learning

\boxed{h}

Supervised Learning

Algorithm

\rightarrow

\(\mathcal{D}_\text{train}\)

\rightarrow

🧠⚙️

Hypothesis class

Hyperparameters

Objective (loss) function

Regularization

Recap:

regressor

\in \mathbb{R}^d

\in \mathbb{R}

\downarrow

"Use" a model

"Learn" a model

\rightarrow

\downarrow

Recap:

"Use" a model

"Learn" a model

\rightarrow

\downarrow

train, optimize, learn, tune,

adjusting/updating model parameters

gradient based

\boxed{h}

Supervised Learning

Algorithm

\rightarrow

\(\mathcal{D}_\text{train}\)

\rightarrow

🧠⚙️

Hypothesis class

Hyperparameters

Objective (loss) function

Regularization

regressor

\in \mathbb{R}^d

\in \mathbb{R}

\downarrow

predict, test, evaluate, infer

applying the learned model

no gradients involved

Supervised Learning

Algorithm

🧠⚙️

Hypothesis class

Hyperparameters

Objective (loss) function

Regularization

Today:

classifier

\in \mathbb{R}^d

\in \text{a discrete set}

\downarrow

\rightarrow

\boxed{h}

\(\mathcal{D}_\text{train}\)

\rightarrow

{"Fish", "Grizzly", "Chameleon", ...}

\(\{+1,0\}\)

\(\{😍, 🥺\}\)

\rightarrow

Today:

\rightarrow

new feature

"Fish"

new prediction

{"Fish", "Grizzly", "Chameleon", ...}

\boxed{h}

\downarrow

y \in

\downarrow

Supervised Learning

Algorithm

🧠⚙️

Hypothesis class

Hyperparameters

Objective (loss) function

Regularization

image adapted from Phillip Isola

Outline

Linear (binary) classifiers
- to use: separator, normal vector
- to learn: difficult! won't do
Linear logistic (binary) classifiers
- to use: sigmoid
- to learn: negative log-likelihood loss
Multi-class classifiers
- to use: softmax
- to learn: one-hot encoding, cross-entropy loss

Outline

Linear (binary) classifiers
- to use: separator, normal vector
- to learn: difficult! won't do
Linear logistic (binary) classifiers
- to use: sigmoid
- to learn: negative log-likelihood loss
Multi-class classifiers
- to use: softmax
- to learn: one-hot encoding, cross-entropy loss

linear regressor

linear binary classifier

features

parameters

linear combination

predict

\(x \in \mathbb{R}^d\)

\(\theta \in \mathbb{R}^d, \theta_0 \in \mathbb{R}\)

\(\theta^T x +\theta_0\)

\(z\)

\(=z\)

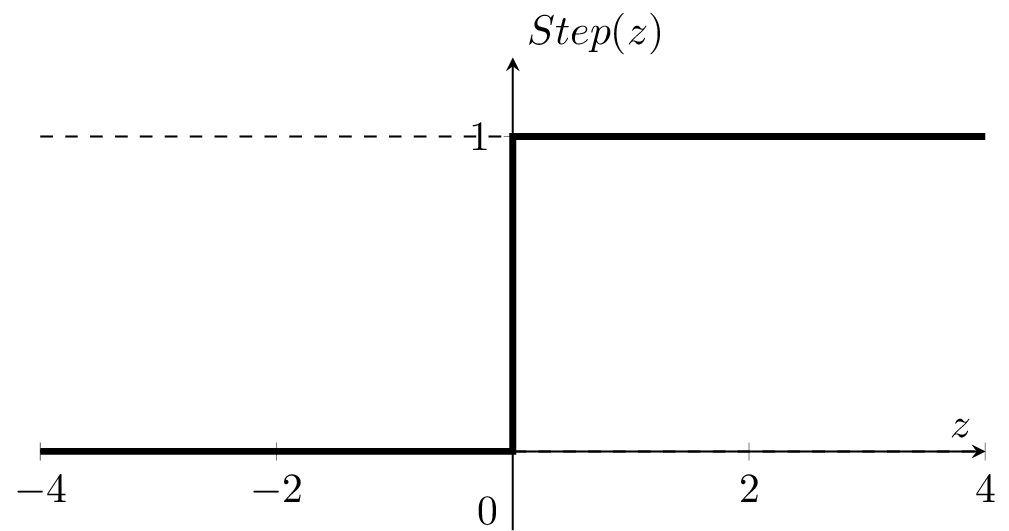
if \(z > 0\)

otherwise

\left\{ \begin{array}{l} \\ \\ \end{array} \right.

\(1\)

Outline

Linear (binary) classifiers
- to use: separator, normal vector
- to learn: difficult! won't do
Linear logistic (binary) classifiers
- to use: sigmoid
- to learn: negative log-likelihood loss
Multi-class classifiers
- to use: softmax
- to learn: one-hot encoding, cross-entropy loss

\mathcal{L}_{01}(g, a)=\left\{\begin{array}{ll} 0 & \text { if } \text{guess} = \text{actual} \\ 1 & \text { otherwise } \end{array}\right .

To learn a model, need a loss function.

=\left\{\begin{array}{ll} 0 & \text { if } \operatorname{step}\left(\theta^{\top} x^{(i)}+\theta_0\right) = y^{(i)} \\ 1 & \text { otherwise } \end{array}\right .

Very intuitive, and easy to evaluate 😍

One natural loss choice:

Very intuitive, and easy to evaluate 😍
Very hard to optimize (NP-hard) 🥺
- "Flat" almost everywhere (zero gradient)
- "Jumps" elsewhere (no gradient)

Outline

Linear (binary) classifiers
- to use: separator, normal vector
- to learn: difficult! won't do
Linear logistic (binary) classifiers
- to use: sigmoid
- to learn: negative log-likelihood loss
Multi-class classifiers
- to use: softmax
- to learn: one-hot encoding, cross-entropy loss

linear

binary classifier

features

parameters

linear

combination

predict

\(x \in \mathbb{R}^d\)

\(\theta \in \mathbb{R}^d, \theta_0 \in \mathbb{R}\)

\(\theta^T x +\theta_0\)

\(=z\)

linear logistic

binary classifier

if \(z > 0\)

otherwise

\left\{ \begin{array}{l} \\ \\ \end{array} \right.

\(1\)

if \(\sigma(z) > 0.5\)

otherwise

\left\{ \begin{array}{l} \\ \\ \end{array} \right.

\(1\)

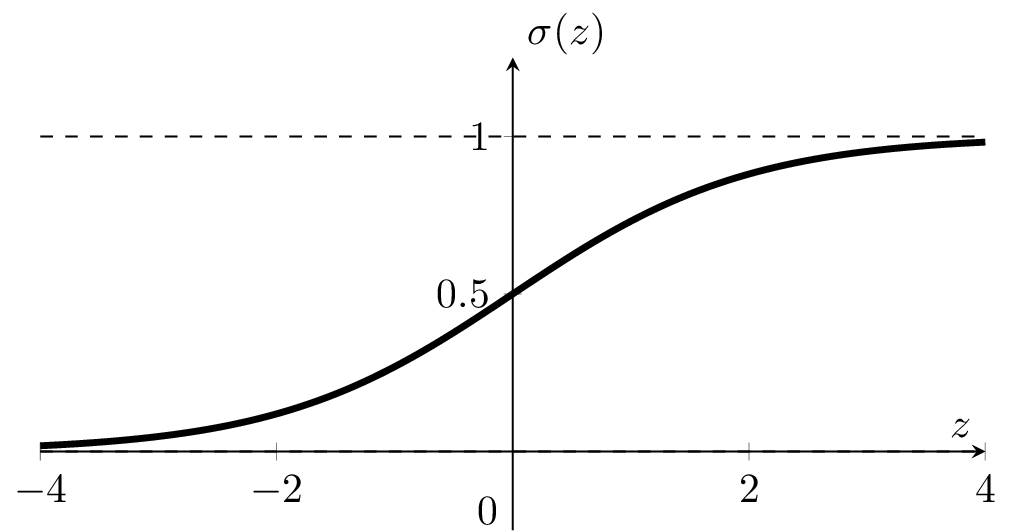
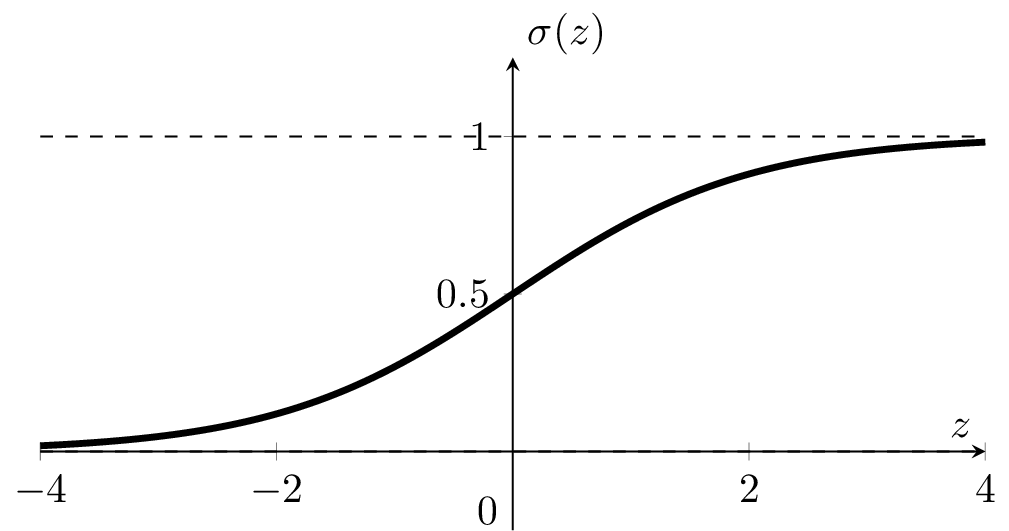
: a smooth step function

:= \frac{1}{1+e^{-z}}

Sigmoid

if \(\sigma(z) > 0.5\)

otherwise

\left\{ \begin{array}{l} \\ \\ \end{array} \right.

\(1\)

if \(z > 0\)

\left\{ \begin{array}{l} \\ \\ \end{array} \right.

\(1\)

otherwise

\(\sigma\left(\cdot\right)\) between \((0,1)\) vertically

(\(\sigma\left(\cdot\right)\) monotonic, very elegant gradient (see hw/rec)

\(\theta\), \(\theta_0\) can flip, squeeze, expand, or shift the \(\sigma\left(\cdot\right)\) curve horizontally

Sigmoid \(\sigma\left(\cdot\right)\) outputs the probability or confidence that feature \(x\) has positive label.

= \frac{1}{1+e^{-\left(\theta^{\top} x+\theta_0\right)}}

if \(\sigma(z) \)

> 0.5

Predict positive

= \frac{1}{1+e^{-z}}

e.g. to predict whether to bike to school using a given logistic classifier

1 feature:

\begin{aligned} g(x) & =\sigma\left(\theta x+\theta_0\right) \\ & =\frac{1}{1+\exp \left\{-\left(\theta x+\theta_0\right)\right\}} \end{aligned}

2 features:

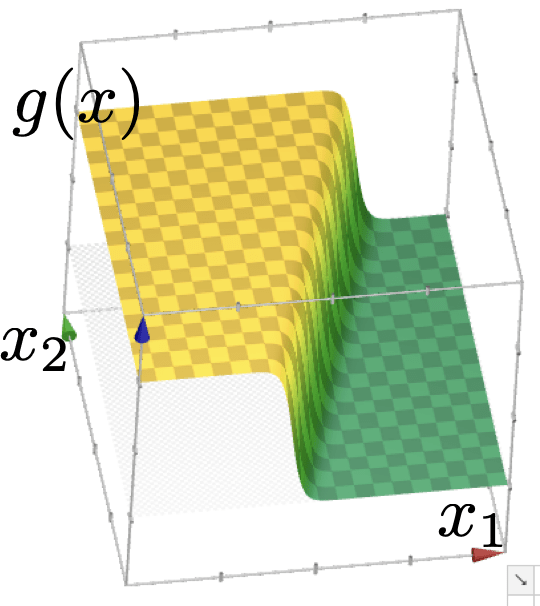
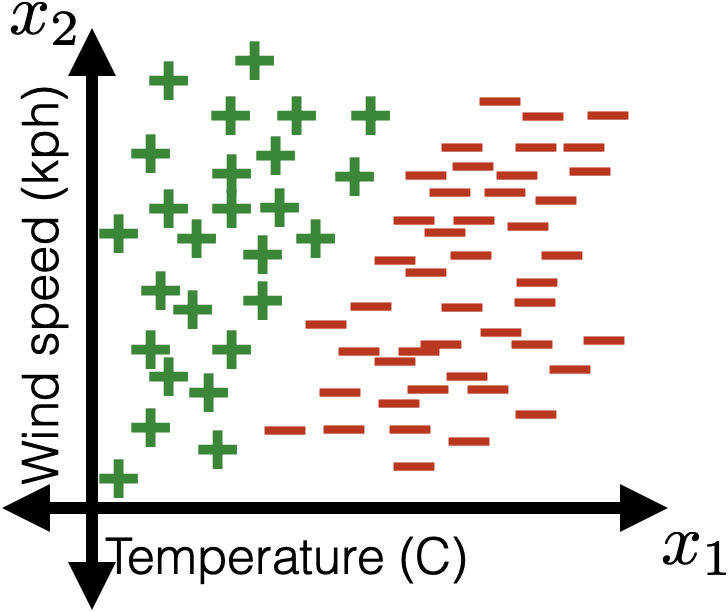
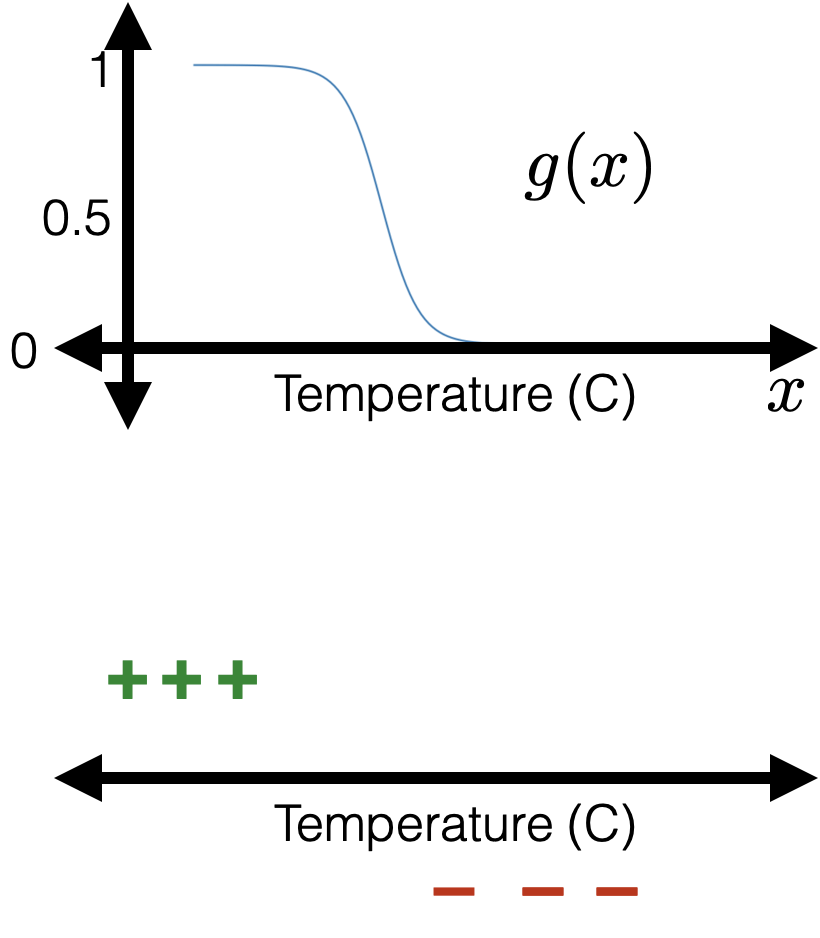
\begin{aligned} g(x) & =\sigma\left(\theta^{\top} x+\theta_0\right) \\ & =\frac{1}{1+\exp \left\{-\left(\theta^{\top} x+\theta_0\right)\right\}} \end{aligned}

image credit: Tamara Broderick

linear logistic classifier still results in the linear separator

\(\theta^T x+\theta_0=0\)

Outline

Linear (binary) classifiers
- to use: separator, normal vector
- to learn: difficult! won't do
Linear logistic (binary) classifiers
- to use: sigmoid
- to learn: negative log-likelihood loss
Multi-class classifiers
- to use: softmax
- to learn: one-hot encoding, cross-entropy loss

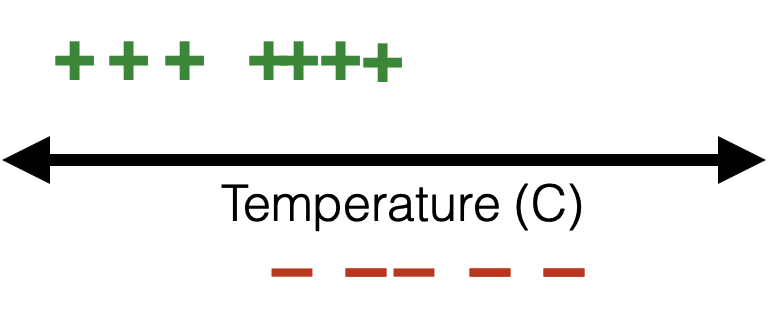
training data:

😍

🥺

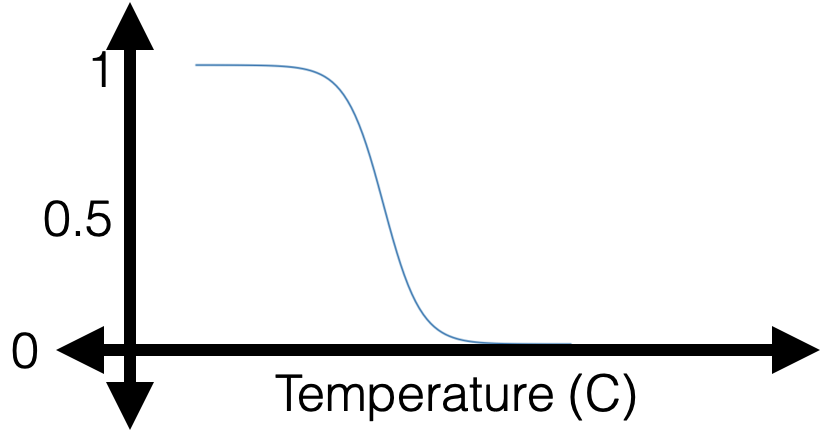
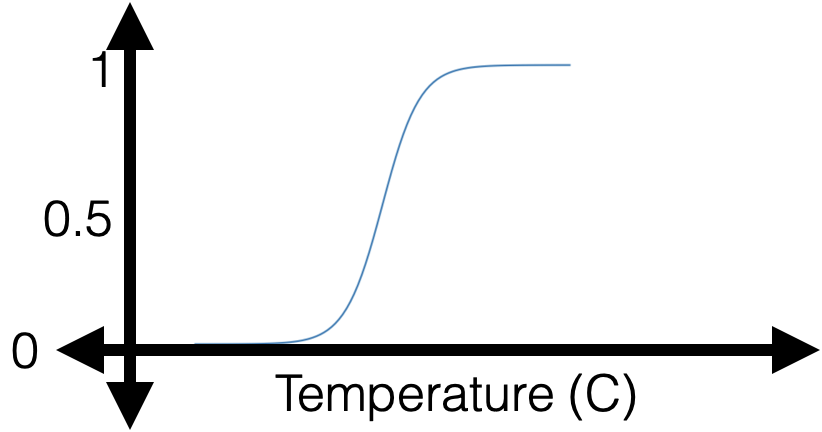
Recall, the labels \(y \in \{+1,0\}\)

g(x)=\sigma\left(\theta x+\theta_0\right)

= -[\text { actual } \cdot \log (\text { guess })+(1-\text { actual }) \cdot \log (1-\text { guess })]

= - \left[y \log g +\left(1-y \right) \log \left(1-g\right)\right]

\mathcal{L}_{\text {nll }}(\text { guess, actual })

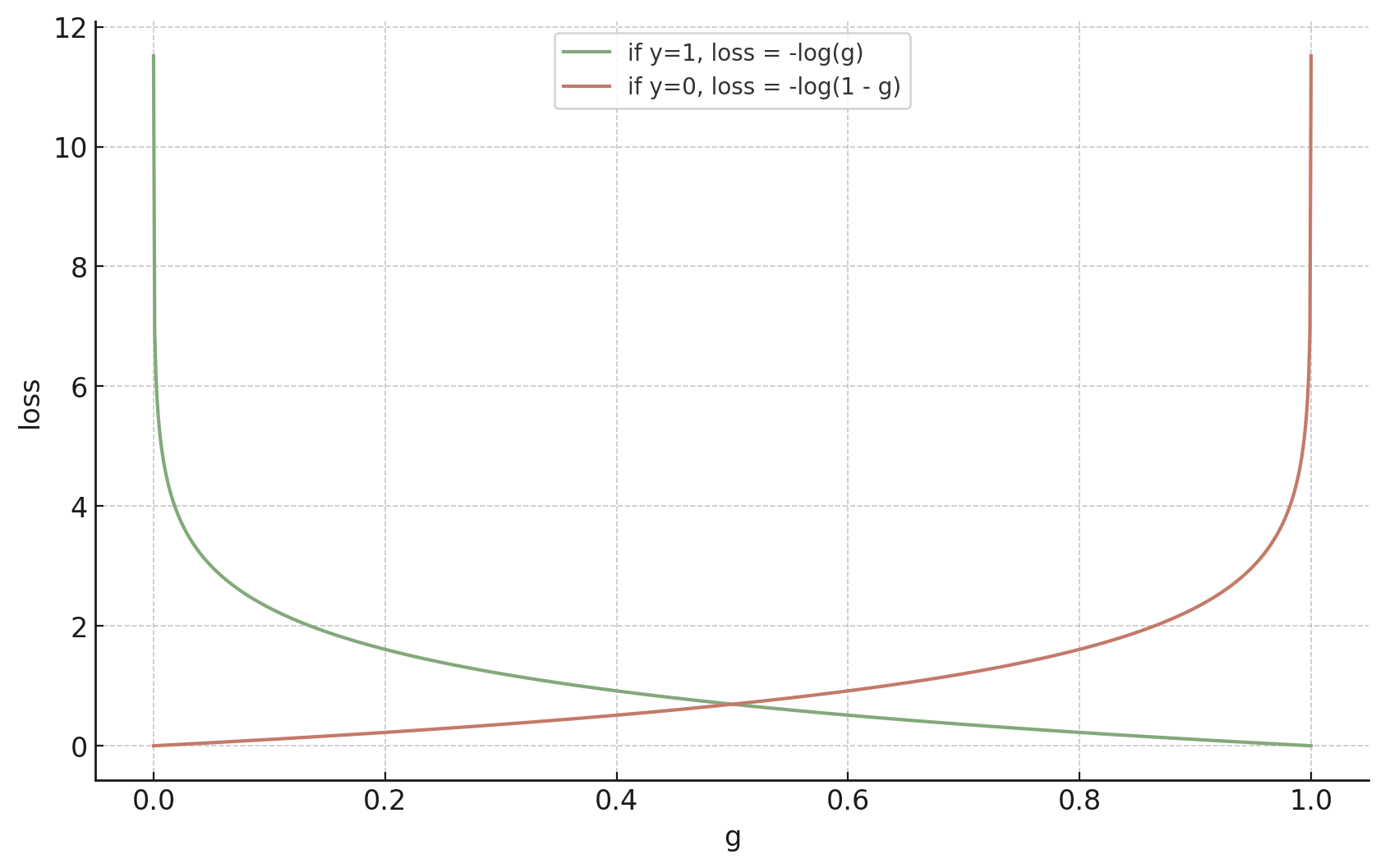
training data:

😍

🥺

= - \left[y \log g +\left(1-y \right) \log \left(1-g \right)\right]

\mathcal{L}_{\text {nll }}(\text { guess, actual })

If \(y = 1\)

😍

🥺

g(x)=\sigma\left(\theta x+\theta_0\right)

= - \log g

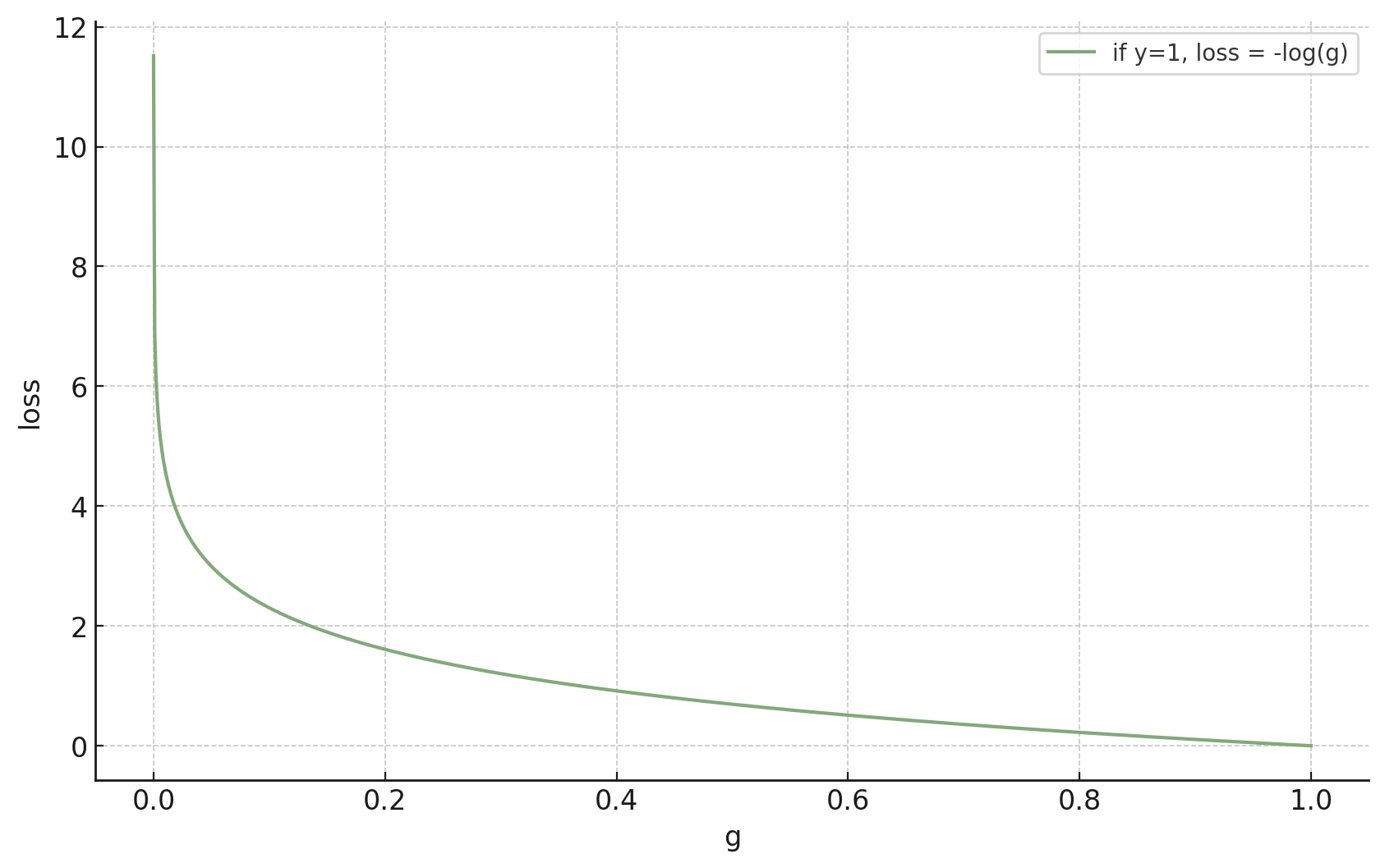
training data:

😍

🥺

If \(y = 0\)

😍

🥺

g(x)=\sigma\left(\theta x+\theta_0\right)

= - \left[y \log g +\left(1-y \right) \log \left(1-g \right)\right]

\mathcal{L}_{\text {nll }}(\text { guess, actual })

= - \left[\log \left(1-g \right)\right]

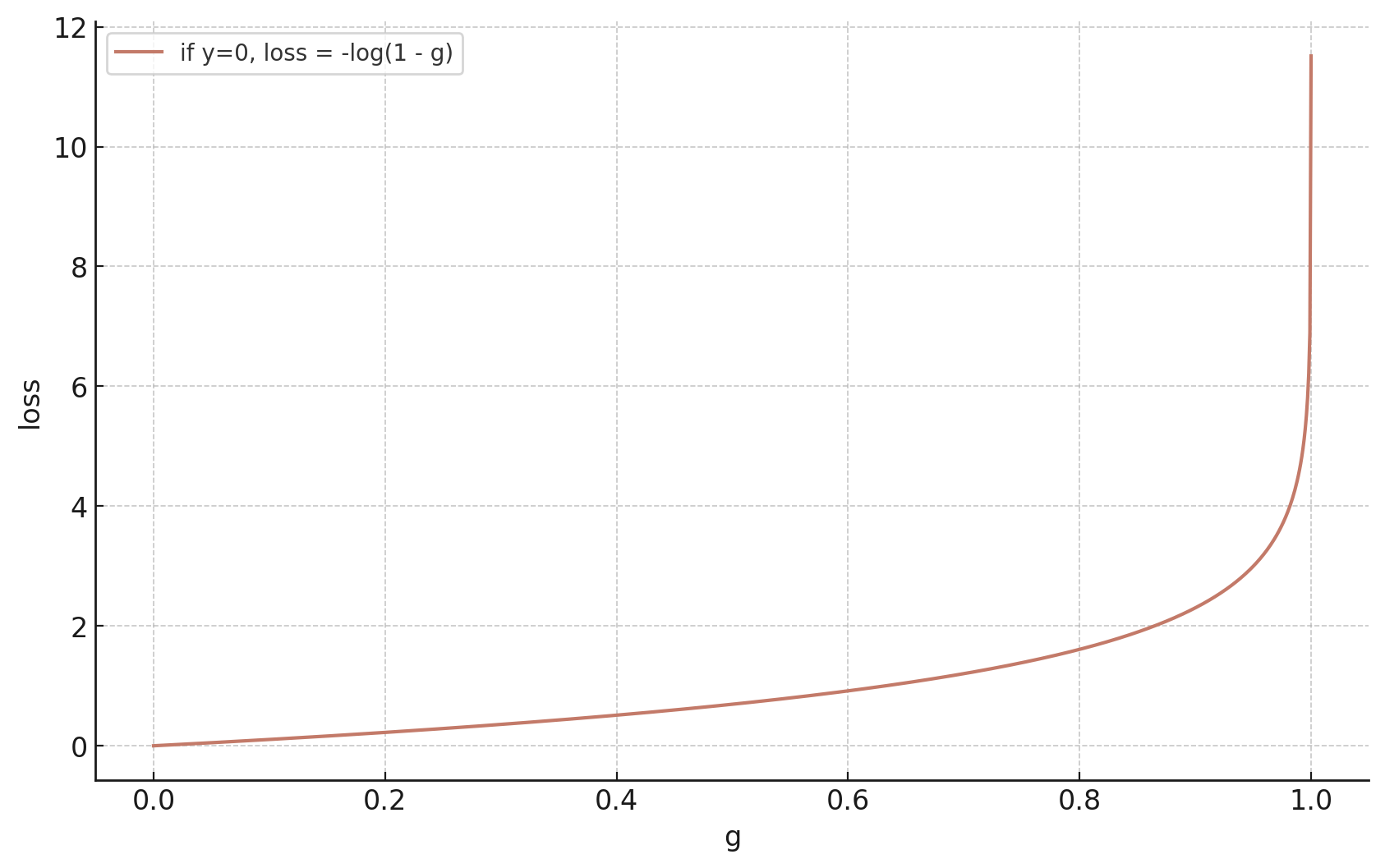
training data:

= - \left[y \log g +\left(1-y \right) \log \left(1-g \right)\right]

\mathcal{L}_{\text {nll }}(\text { guess, actual })

= - \log g

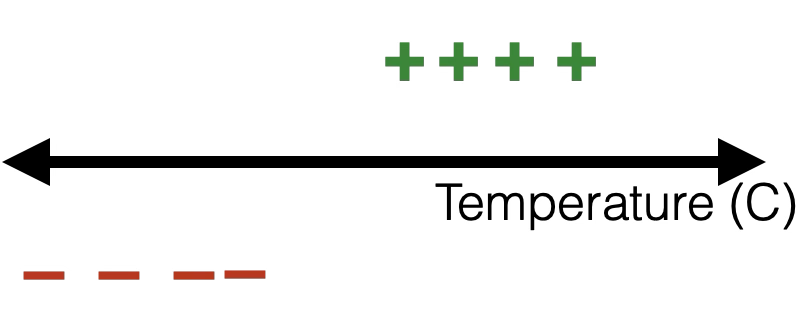
linear

binary classifier

features

parameters

linear combo

predict

\(x \in \mathbb{R}^d\)

\(\theta \in \mathbb{R}^d, \theta_0 \in \mathbb{R}\)

\(\theta^T x +\theta_0\)

\(=z\)

linear logistic

binary classifier

loss

\((g - y)^2 \)

- \left[y \log g +\left(1-y \right) \log \left(1-g\right)\right]

\left\{\begin{array}{ll} 0 & \text { if } g = a \\ 1 & \text { otherwise } \end{array}\right .

\left\{\begin{array}{ll} 1 & \text { if } z>0 \\ 0 & \text { otherwise } \end{array}\right .

\left\{\begin{array}{ll} 1 & \text { if } g = \sigma(z)>0.5 \\ 0 & \text { otherwise } \end{array}\right .

linear

regressor

closed-form or

gradient descent

NP-hard to learn

gradient descent only
need regularization to not overfit

optimize via

Outline

Linear (binary) classifiers
- to use: separator, normal vector
- to learn: difficult! won't do
Linear logistic (binary) classifiers
- to use: sigmoid
- to learn: negative log-likelihood loss
Multi-class classifiers
- to use: softmax
- to learn: one-hot encoding, cross-entropy loss

Video edited from: HBO, Sillicon Valley

🌭

\(x\)

\(\theta^T x +\theta_0\)

\(z \in \mathbb{R}\)

\(\sigma(z) :\) model's confidence the input \(x\) is a hot-dog

learned scalar "summary" of "hot-dog-ness"

\(1-\sigma(z) :\) model's confidence the input \(x\) is not a hot-dog

\sigma(z)=\frac{1}{1+\exp (-z)}

= \frac{\exp(z)}{1+\exp (z)}

fixed baseline of "non-hot-dog-ness"

= \frac{\exp(z)}{\exp(0) +\exp (z)}

🌭

\(x\)

\(\theta^T x +\theta_0\)

\(z \in \mathbb{R}\)

if we want to predict \(\{\)hot-dog, pizza, pasta, salad\(\}\)

❓

\(z \in \mathbb{R}^4\)

\left\{ \begin{array}{l} \\ \\ \end{array} \right.

distribution over these 4 categories

4 scalars, each one as a "summary" of a food category

Outline

Linear (binary) classifiers
- to use: separator, normal vector
- to learn: difficult! won't do
Linear logistic (binary) classifiers
- to use: sigmoid
- to learn: negative log-likelihood loss
Multi-class classifiers
- to use: softmax
- to learn: one-hot encoding, cross-entropy loss

🌭

\(x\)

\(\theta^T x +\theta_0\)

\(z \in \mathbb{R}^4\)

\left\{ \begin{array}{l} \\ \\ \end{array} \right.

distribution over these 4 categories

if we want to predict \(\{\)hot-dog, pizza, pasta, salad\(\}\)

❓

\( \begin{bmatrix} -0.23 \\ 3.67 \\ 1.47 \\ 0.44 \end{bmatrix} \)

\( \begin{bmatrix} 0.0173 \\ 0.8543 \\ 0.0947 \\ 0.0338 \end{bmatrix} \)

\operatorname{softmax}\left(z_j\right)\\=\frac{\exp \left(z_j\right)}{\sum_{i=1}^4 \exp \left(z_i\right)}

entries between (0,1), sums up to 1

training data

parameters

linear combo

predict

\(x \in \mathbb{R}^d,\)

\(\theta \in \mathbb{R}^d, \theta_0 \in \mathbb{R}\)

\(\theta^T x +\theta_0\)

\(=z \in \mathbb{R}\)

linear logistic

binary classifier

one-out-of-\(K\) classifier

\(\theta \in \mathbb{R}^{d \times K},\)

\(=z \in \mathbb{R}^{K}\)

\(\theta^T x +\theta_0\)

positive if \(\sigma(z)>0.5\)

category corresponding to the largest entry in softmax\((z)\)

\operatorname{softmax}(z)=\left[\begin{array}{c} \exp \left(z_1\right) / \sum_i \exp \left(z_i\right) \\ \vdots \\ \exp \left(z_K\right) / \sum_i \exp \left(z_i\right) \end{array}\right]

\sigma(z) = \frac{\exp(z)}{\exp(0) +\exp (z)}

\(\theta_0 \in \mathbb{R}^{K}\)

\(y \in \{0,1\}\)

\(x \in \mathbb{R}^d,\)

\(y: K\)-dimensional one-hot

Outline

Linear (binary) classifiers
- to use: separator, normal vector
- to learn: difficult! won't do
Linear logistic (binary) classifiers
- to use: sigmoid
- to learn: negative log-likelihood loss
Multi-class classifiers
- to use: softmax
- to learn: one-hot encoding, cross-entropy loss

image adapted from Phillip Isola

K =3

One-hot encoding:

Encode the \(K\) classes as an \(\mathbb{R}^K\) vector, with a single 1 (hot) and 0s elsewhere.
Generalizes from {0,1} binary labels

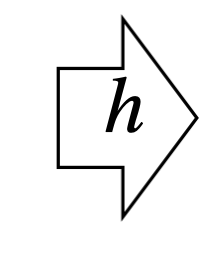
current prediction

\(g=\text{softmax}(\cdot)\)

feature \(x\)

true label \(y\)

\log(g)

[0,0,0,0,0,1,0,0, \ldots]

image adapted from Phillip Isola

loss \(\mathcal{L}_{\mathrm{nllm}}({g}, y)\\=-\sum_{\mathrm{k}=1}^{\mathrm{K}}y_{\mathrm{k}} \cdot \log \left({g}_{\mathrm{k}}\right)\)

feature \(x\)

true label \(y\)

\log(g)

[0,0,1,0,0,0,0,0, \ldots]

current prediction

\(g=\text{softmax}(\cdot)\)

image adapted from Phillip Isola

loss \(\mathcal{L}_{\mathrm{nllm}}({g}, y)\\=-\sum_{\mathrm{k}=1}^{\mathrm{K}}y_{\mathrm{k}} \cdot \log \left({g}_{\mathrm{k}}\right)\)

\mathcal{L}_{\mathrm{nllm}}({g}, y)=-\sum_{{k}=1}^{{K}}y_{{k}} \cdot \log \left({g}_{{k}}\right)

Generalizes negative log likelihood loss \(\mathcal{L}_{\mathrm{nll}}({g}, {y})= - \left[y \log g +\left(1-y \right) \log \left(1-g \right)\right]\)
Appears as summing \(K\) terms, but
for a given data point, only the term corresponding to its true class label matters.

Negative log-likelihood \(K-\) classes loss (aka, cross-entropy)

\(y:\)one-hot encoding label

\(y_{{k}}:\) either 0 or 1

\(g:\) softmax output

\(g_{{k}}:\) probability or confidence in class \(k\)

Classification

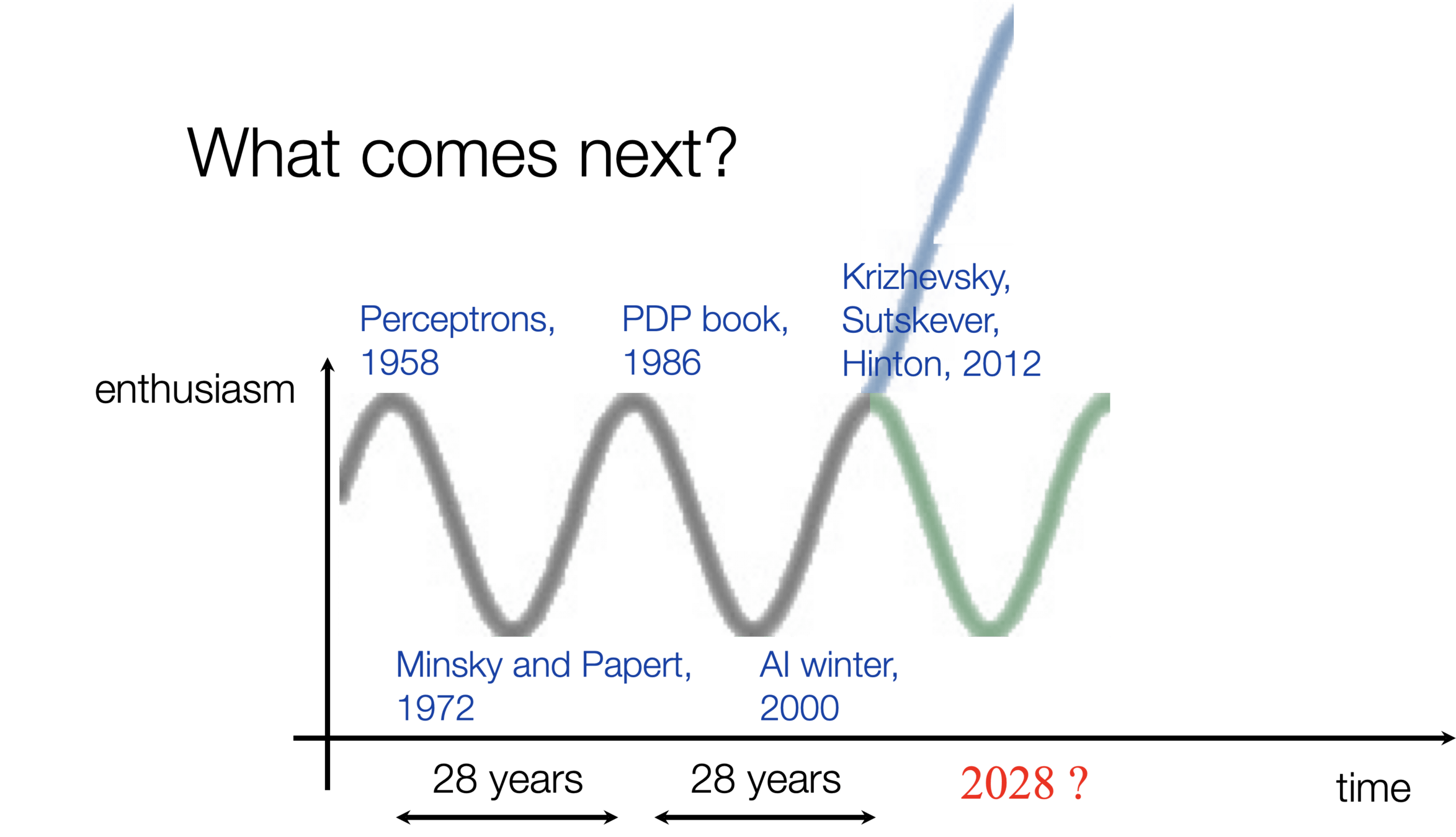
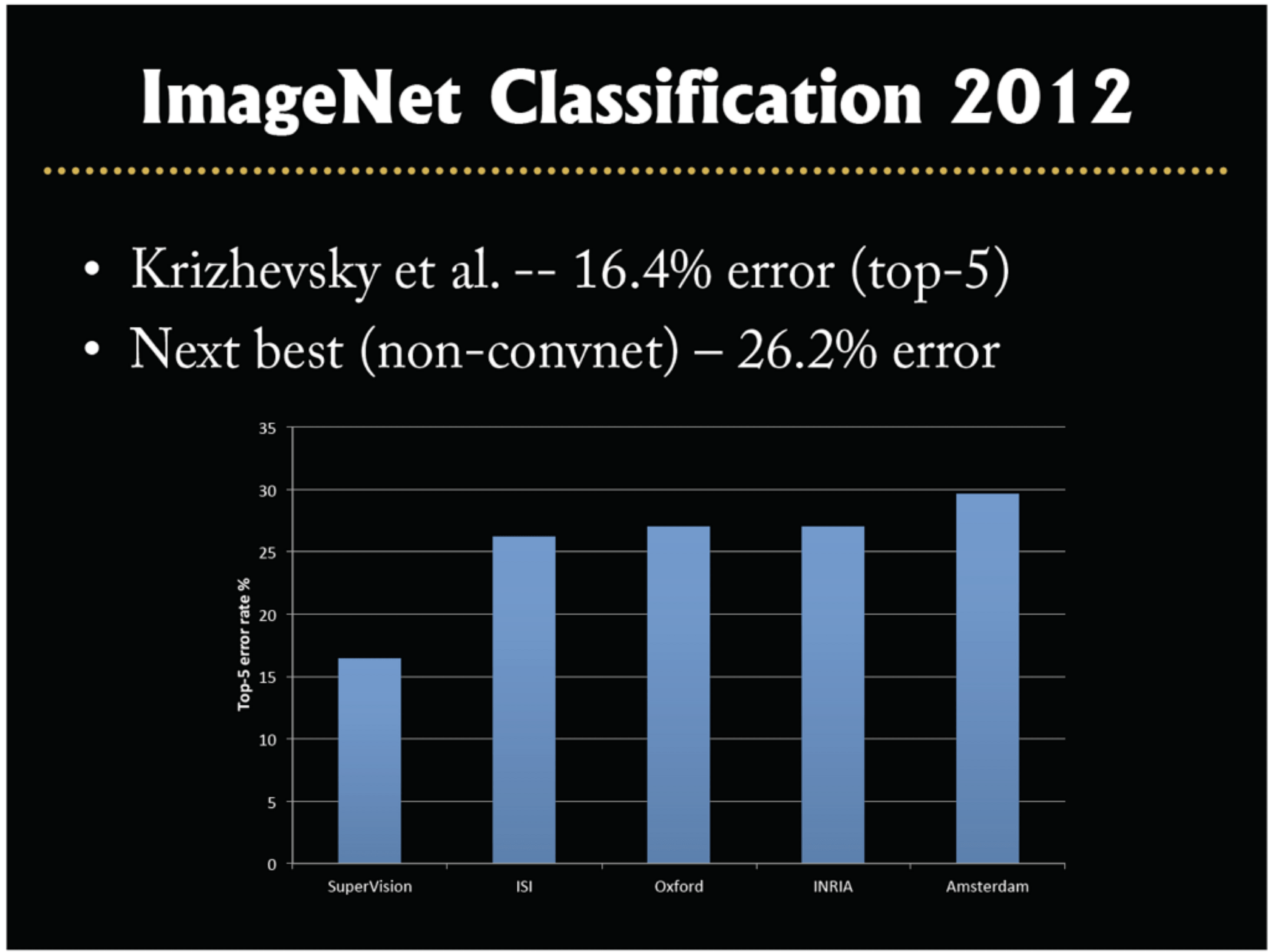
Image classification played a pivotal role in kicking off the current wave of AI enthusiasm.

Summary

Classification: a supervised learning problem, similar to regression, but where the output/label is in a discrete set.
Binary classification: only two possible label values.
Linear binary classification: think of \(\theta\) and \(\theta_0\) as defining a d-1 dimensional hyperplane that cuts the d-dimensional feature space into two half-spaces.
0-1 loss: a natural loss function for classification, BUT, hard to optimize.
Sigmoid function: motivation and properties.
Negative-log-likelihood loss: smoother and has nice probabilistic motivations. We can optimize via (S)GD.
Regularization is still important.
The generalization to multi-class via (one-hot encoding, and softmax mechanism)
Other ways to generalize to multi-class (see hw/lab)

Thanks!

We'd love to hear your thoughts.

Linear Logistic Classifier

Mainly motivated to address the gradient issue in learning a "vanilla" linear classifier
- The gradient issue is caused by both the 0/1 loss, and the sign functions nested in.

\mathcal{L}_{01}(x^{(i)}, y^{(i)}; \theta, \theta_0)=\left\{\begin{array}{ll} 0 & \text { if } \operatorname{sign}\left(\theta^{\top} x^{(i)}+\theta_0\right) = y^{(i)} \\ 1 & \text { otherwise } \end{array}\right .

But has nice probabilistic interpretation too.
As before, let's first look at how to make prediction with a given linear logistic classifier

(Binary) Linear Logistic Classifier

Each data point:
- features \([x_1, x_2, \dots x_d]\)
- label \(y \in\){positive, negative}
A (binary) linear logistic classifier is parameterized by \([\theta_1, \theta_2, \dots, \theta_d, \theta_0]\)
To use a given classifier make prediction:
- do linear combination: \(z =({\theta_1}x_1 + \theta_2x_2 + \dots + \theta_dx_d) + \theta_0\)
- predict positive label if

otherwise, negative label.

\sigma(z) = \sigma\left(\theta^{\top} x+\theta_0\right)

= \frac{1}{1+e^{-z}}

= \frac{1}{1+e^{-\left(\theta^{\top} x+\theta_0\right)}}

> 0.5

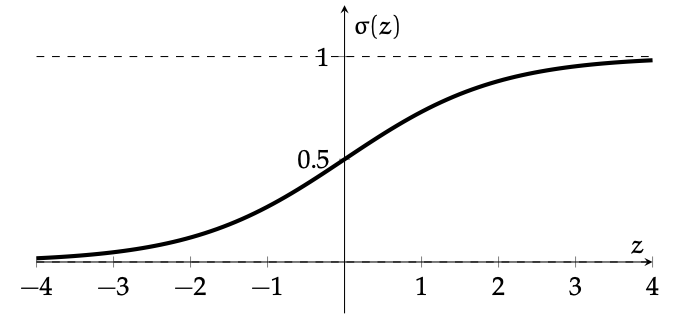
: a smooth step function

= \frac{1}{1+e^{-z}}

Sigmoid

if \(\sigma(z) > 0.5\)

otherwise

\left\{ \begin{array}{l} \\ \\ \end{array} \right.

\(1\)

linear

binary classifier

features

parameters

linear

combination

predict

\(x \in \mathbb{R}^d\)

\(A \in \mathbb{R}^{n \times n}, \theta_0 \in \mathbb{R}\)

\(\theta^T x +\theta_0\)

\(=z\)

linear logistic

binary classifier

if \(z > 0\)

otherwise

\left\{ \begin{array}{l} \\ \\ \end{array} \right.

\(1\)

if \(\sigma(z) > 0.5\)

otherwise

\left\{ \begin{array}{l} \\ \\ \end{array} \right.

\(1\)

\(X \in \mathbb{R}^{n \times d}\)