

Lecture 4: Linear Classification
(DRAFT)
Shen Shen
Feb 21, 2025
Intro to Machine Learning

Outline
- Recap, classification setup
- Linear classifiers
- Separator, normal vector, and separability
- Linear logistic classifiers
- Motivation, sigmoid, and negative log-likelihood loss
- Multi-class classifiers
- One-hot encoding, softmax, and cross-entropy
Outline
- Recap, classification setup
- Linear classifiers
- Separator, normal vector, and separability
- Linear logistic classifiers
- Motivation, sigmoid, and negative log-likelihood loss
- Multi-class classifiers
- One-hot encoding, softmax, and cross-entropy

💻 Compute/optimize/ train

Recap:
Learning algorithm
🧠 ⚙️
Hypothesis class
Hyperparameters
Objective (loss) functions
Regularization
(image adapted from Phillip Isola)
new feature \(x\)
new prediction \(y\)
\(\in \mathbb{R}\)
Training
Testing
(aka inferencing, or predicting)

Recap:
(image adapted from Phillip Isola)
- closed-form formula
- gradient descent






Classification Setup
(image adapted from Phillip Isola)




"Fish"
{"Fish", "Grizzly", "Chameleon", ...}
\(\in \)
A discrete set.
(image adapted from Phillip Isola)
new feature \(x\)
new prediction
Outline
- Recap, classification setup
-
Linear classifiers
- Separator, normal vector, and separability
- Linear logistic classifiers
- Motivation, sigmoid, and negative log-likelihood loss
- Multi-class classifiers
- One-hot encoding, softmax, and cross-entropy
Linear Classifier
- Each data point:
- features \([x_1, x_2, \dots x_d]\)
- label \(y \in\) {positive, negative} (or {dog, cat}, {pizza, not pizza}, {+1, 0})
- A (vanilla, sign-based, binary) linear classifier is parameterized by \([\theta_1, \theta_2, \dots, \theta_d, \theta_0]\)
- To use a given classifier make prediction:
- do linear combination: \(z =({\theta_1}x_1 + \theta_2x_2 + \dots + \theta_dx_d) + \theta_0\)
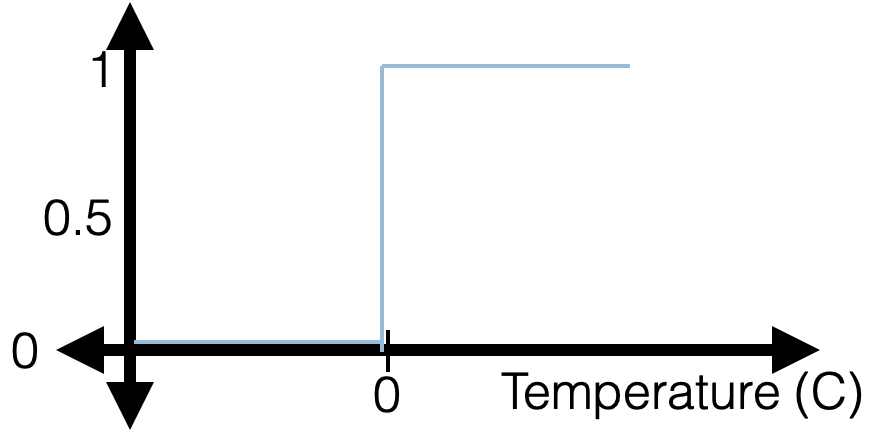
- predict positive label if \(z>0\), otherwise, negative label.
(vanilla, sign-based, binary) Linear Classifier
- Now let's try to learn a linear classifier
- One natural loss:
- Combined with the linear classifier hypothesis:
- Very intuitive, and easy to evaluate 😍
- Induced concept: separability
- Very hard to optimize (NP-hard) 🥺
- "Flat" almost everywhere (zero gradient)
- "Jumps" elsewhere (no gradient)

Outline
- Recap, classification setup
- Linear classifiers
- Separator, normal vector, and separability
-
Linear logistic classifiers
- Motivation, sigmoid, and negative log-likelihood loss
- Multi-class classifiers
- One-hot encoding, softmax, and cross-entropy
Linear Logistic Classifier
- Mainly motivated to address the gradient issue in learning a "vanilla" linear classifier
-
The gradient issue is caused by both the 0/1 loss, and the sign functions nested in.
-
- But has nice probabilistic interpretation too.
-
As before, let's first look at how to make prediction with a given linear logistic classifier
(Binary) Linear Logistic Classifier
- Each data point:
- features \([x_1, x_2, \dots x_d]\)
- label \(y \in\){positive, negative}
- A (binary) linear logistic classifier is parameterized by \([\theta_1, \theta_2, \dots, \theta_d, \theta_0]\)
- To use a given classifier make prediction:
- do linear combination: \(z =({\theta_1}x_1 + \theta_2x_2 + \dots + \theta_dx_d) + \theta_0\)
- predict positive label if
otherwise, negative label.
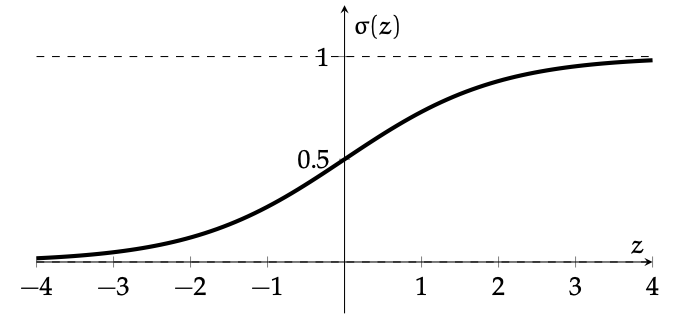
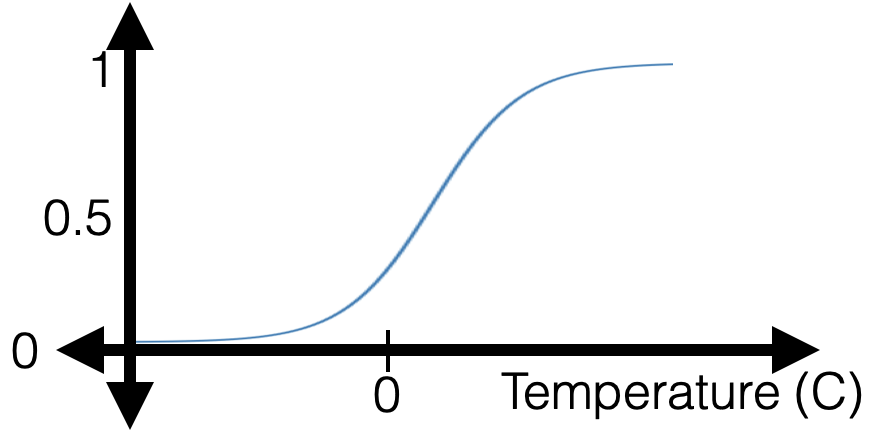
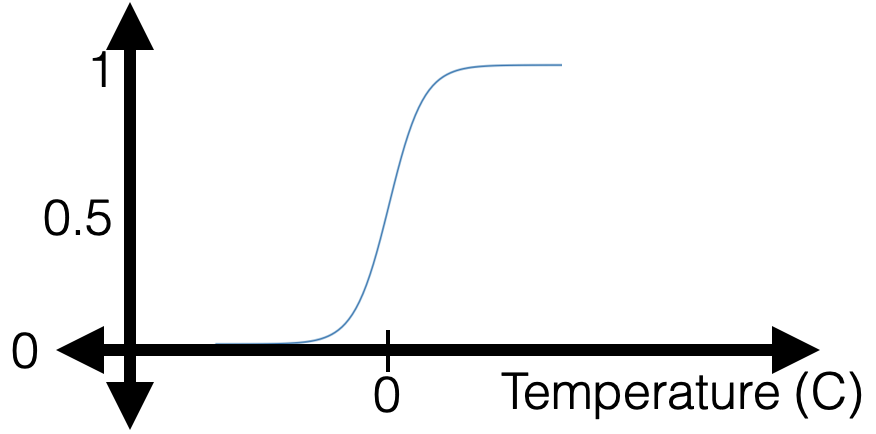
Sigmoid
: a smooth step function
-
"sandwiched" between 0 and 1 vertically (never 0 or 1 mathematically)
-
monotonic, very nice/elegant gradient (see recitation/hw)
- \(\theta\), \(\theta_0\) can flip, squeeze, expand, shift horizontally
-
\(\sigma\left(\cdot\right)\) interpreted as the probability/confidence that feature \(x\) has positive label. Predict positive if
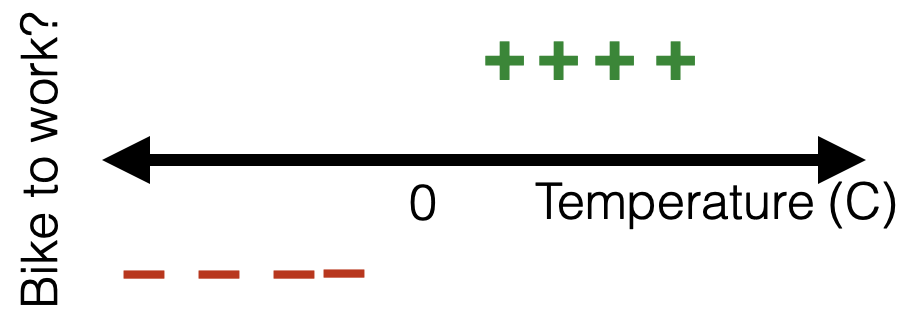
e.g. suppose, wanna predict whether to bike to school.
with given parameters, how do I make prediction?
1 feature:
2 features:
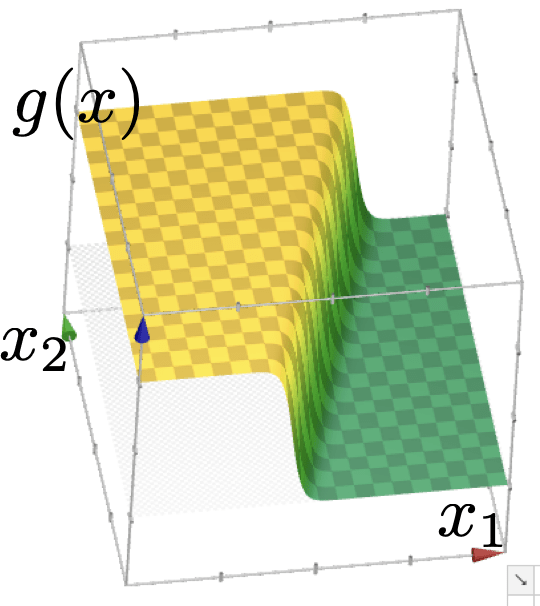

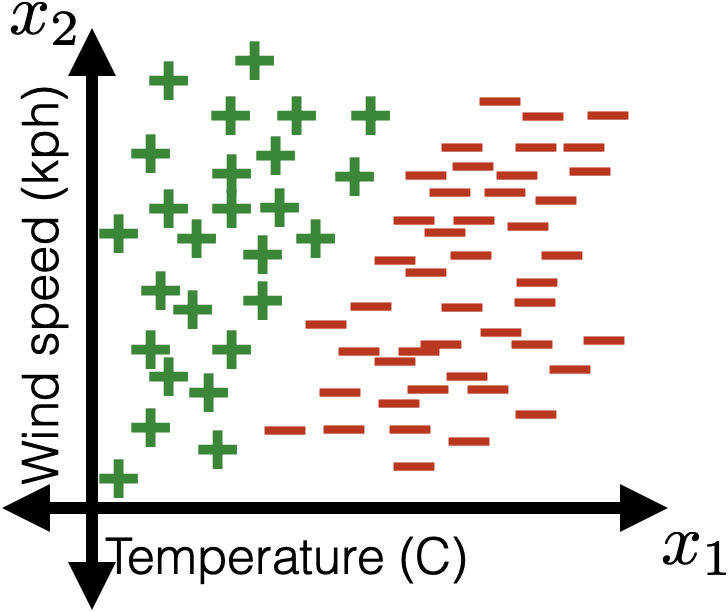
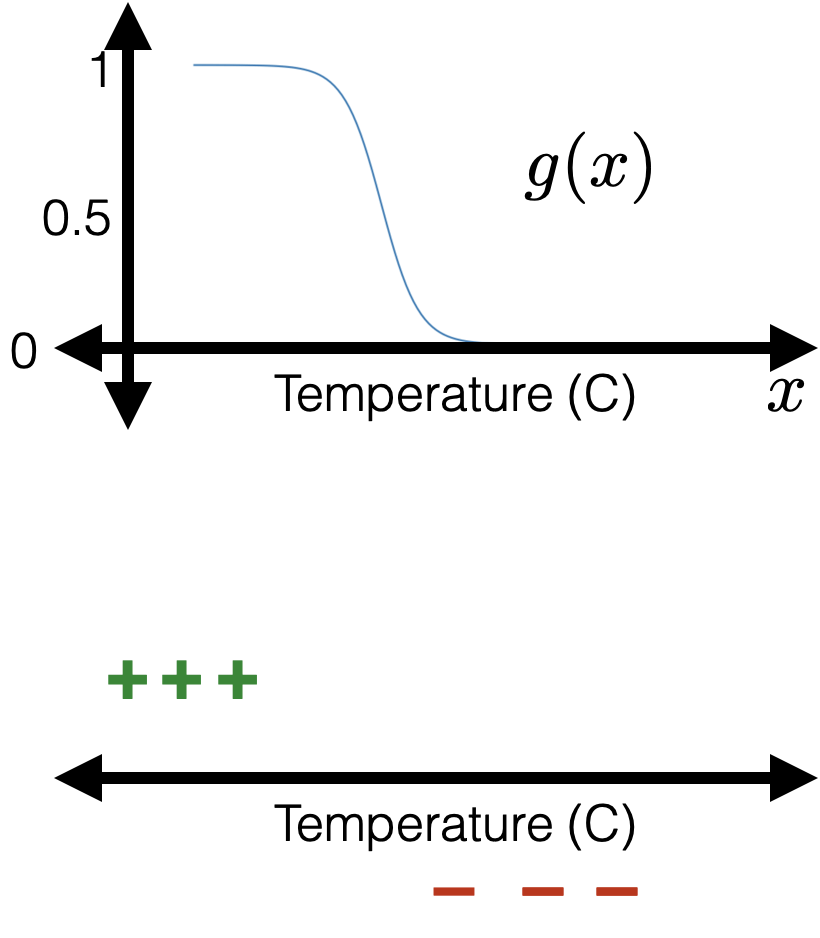
(image credit: Tamara Broderick)

Learning a logistic regression classifier
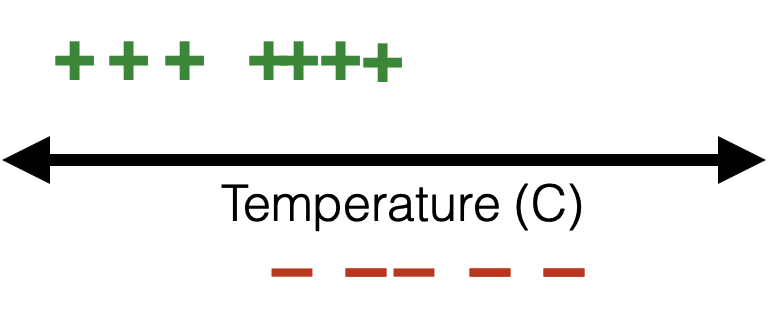
training data:
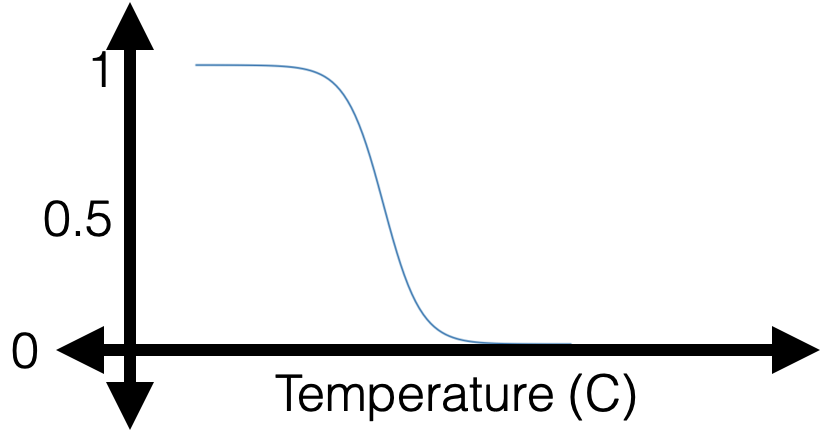
😍
🥺
- Let the labels \(y \in \{+1,0\}\)

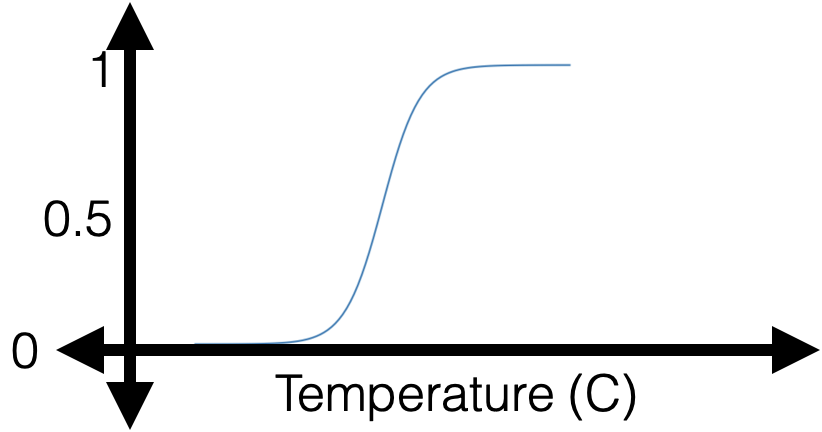
training data:


😍
🥺
If \(y^{(i)} = 1\)
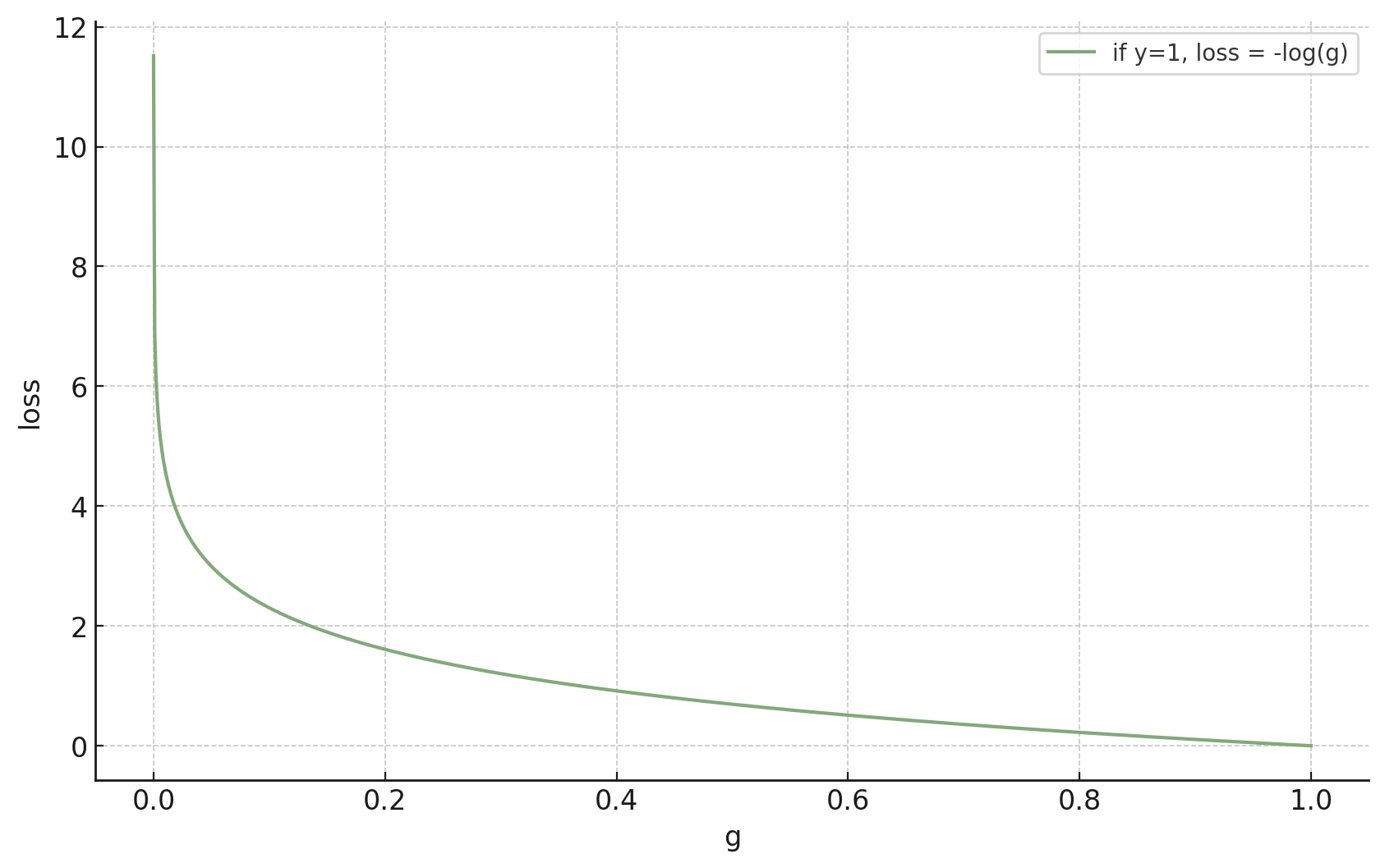
😍
🥺

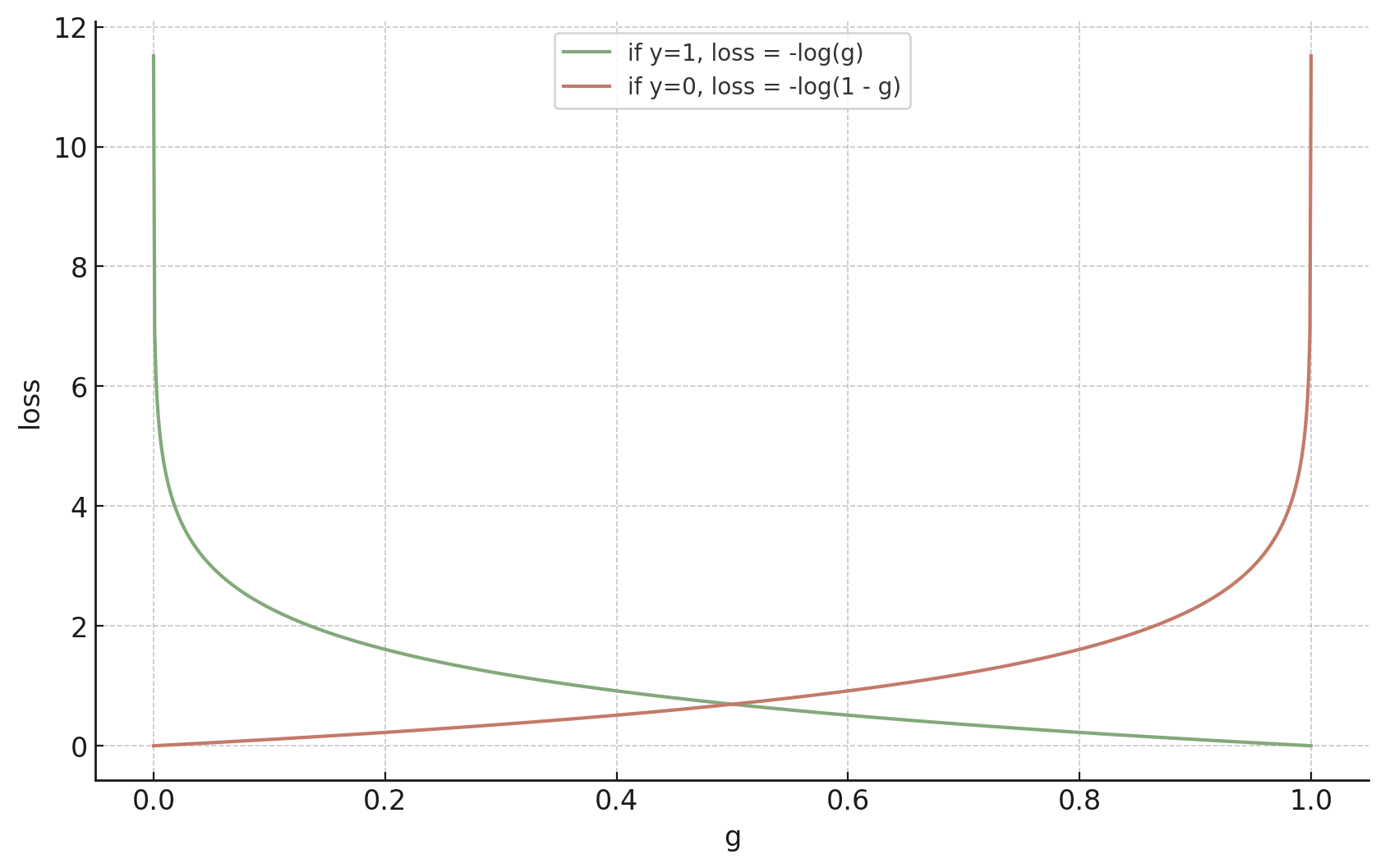
training data:


😍
🥺
If \(y^{(i)} = 0\)
😍
🥺
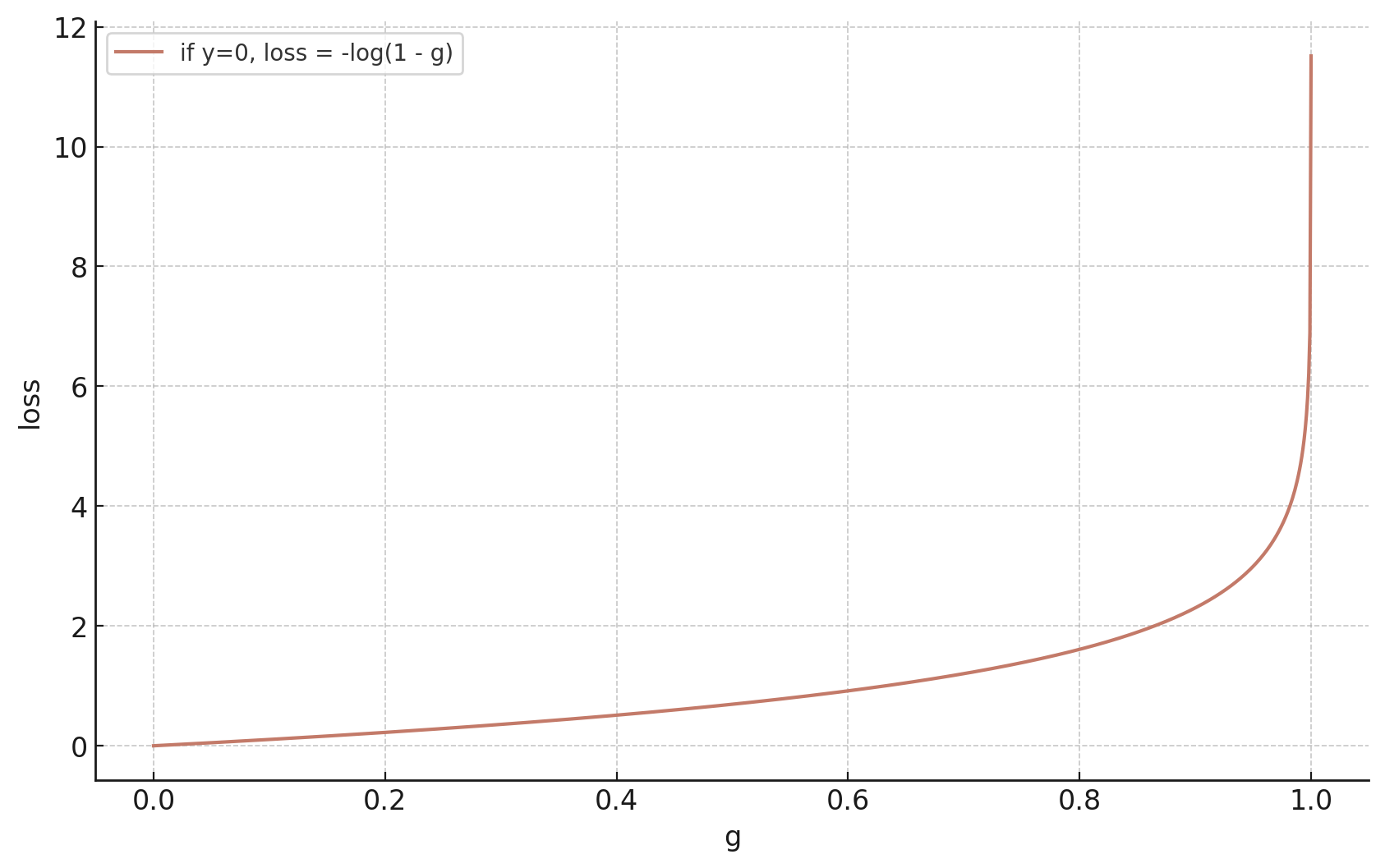
Logistic Regression
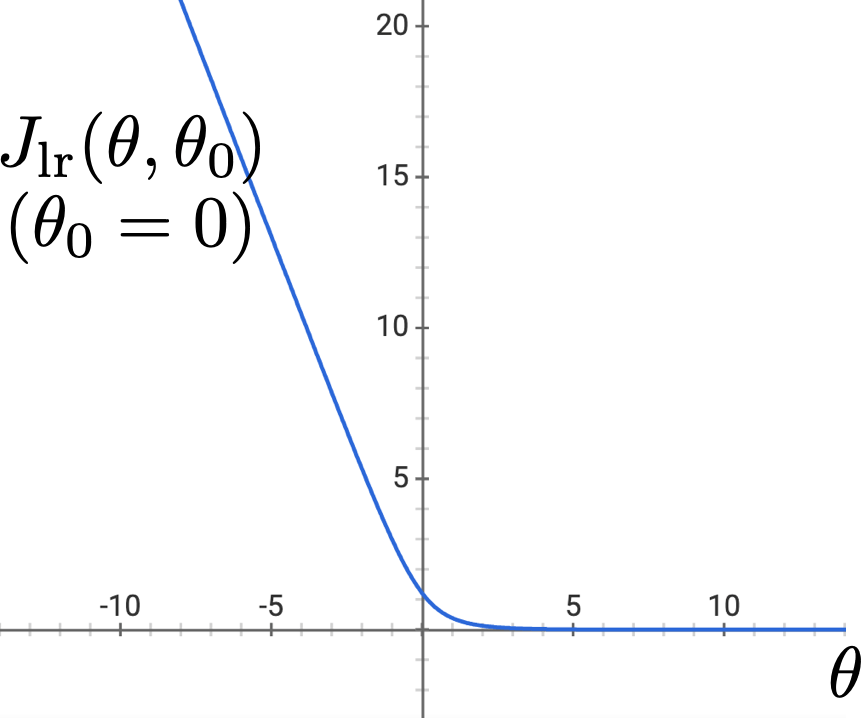
- Minimize using negative-log-likelihood loss: \(J_{lr} = \frac{1}{n} \sum_{i=1}^n \mathcal{L}_{\text {nll }}\left(\sigma\left(\theta^{\top} x^{(i)}+\theta_0\right), y^{(i)}\right)\)
- Convex, differentiable with nice (elegant) gradients
- Doesn't have a closed-form solution
- Can still run gradient descent
- But, a gotcha: when training data is linearly separable

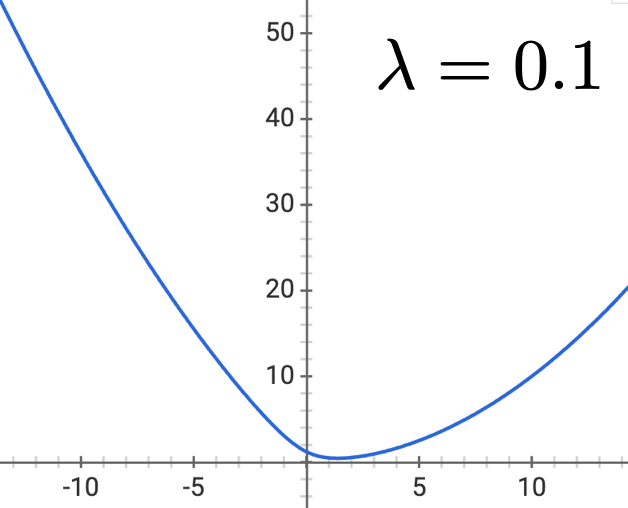
Regularized Logistic Regression

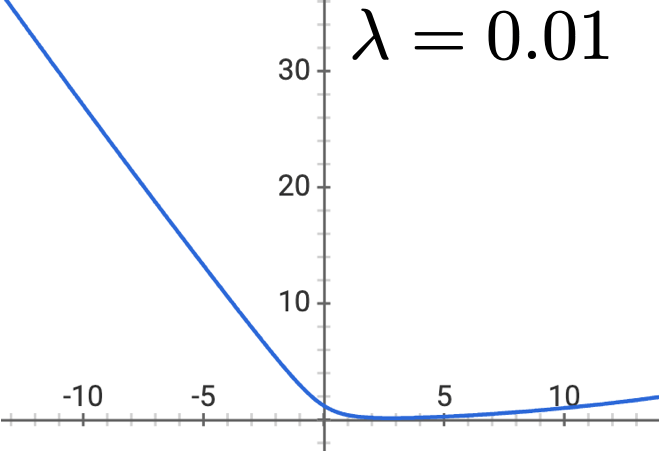
- \(\lambda \geq 0\)
- No regularizing \(\theta_0\) (think: why?)
- Penalizes being overly certain
- Objective is still differentiable and convex (gradient descent)


Outline
- Recap, classification setup
- Linear classifiers
- Separator, normal vector, and separability
- Linear logistic classifiers
- Motivation, sigmoid, and negative log-likelihood loss
-
Multi-class classifiers
- One-hot encoding, softmax, and cross-entropy
(image adapted from Phillip Isola)




\(\in \mathbb{R}^{K}\)
One-hot labels
- Generalizes from binary labels
- Suppose \(K\) classes
Softmax
Two classes
\(K\) classes
scalar
scalar
\(K\)-by-1
\(K\)-by-1
- Generalizes sigmoid
- Applies normalization on \(z\) element-wise
Negative log-likelihood multi-class loss
- Appears as sum of two terms
- Only one term "activates" for a single data point
- Appears as sum of \(K\) terms
- Only one term "activates" for a single data point
- Generalizes negative log likelihood loss
- Also known as cross-entropy
Two classes
\(K\) classes
(image adapted from Phillip Isola)



current prediction
\(g=\text{softmax}(\cdot)\)
feature \(x\)

true label \(y\)

loss \(\mathcal{L}_{\mathrm{nllm}}(\mathrm{g}, \mathrm{y})=-\sum_{\mathrm{k}=1}^{\mathrm{K}} \mathrm{y}_{\mathrm{k}} \cdot \log \left(\mathrm{g}_{\mathrm{k}}\right)\)

(image adapted from Phillip Isola)
feature \(x\)

true label \(y\)





current prediction
\(g=\text{softmax}(\cdot)\)
loss \(\mathcal{L}_{\mathrm{nllm}}(\mathrm{g}, \mathrm{y})=-\sum_{\mathrm{k}=1}^{\mathrm{K}} \mathrm{y}_{\mathrm{k}} \cdot \log \left(\mathrm{g}_{\mathrm{k}}\right)\)
Classification
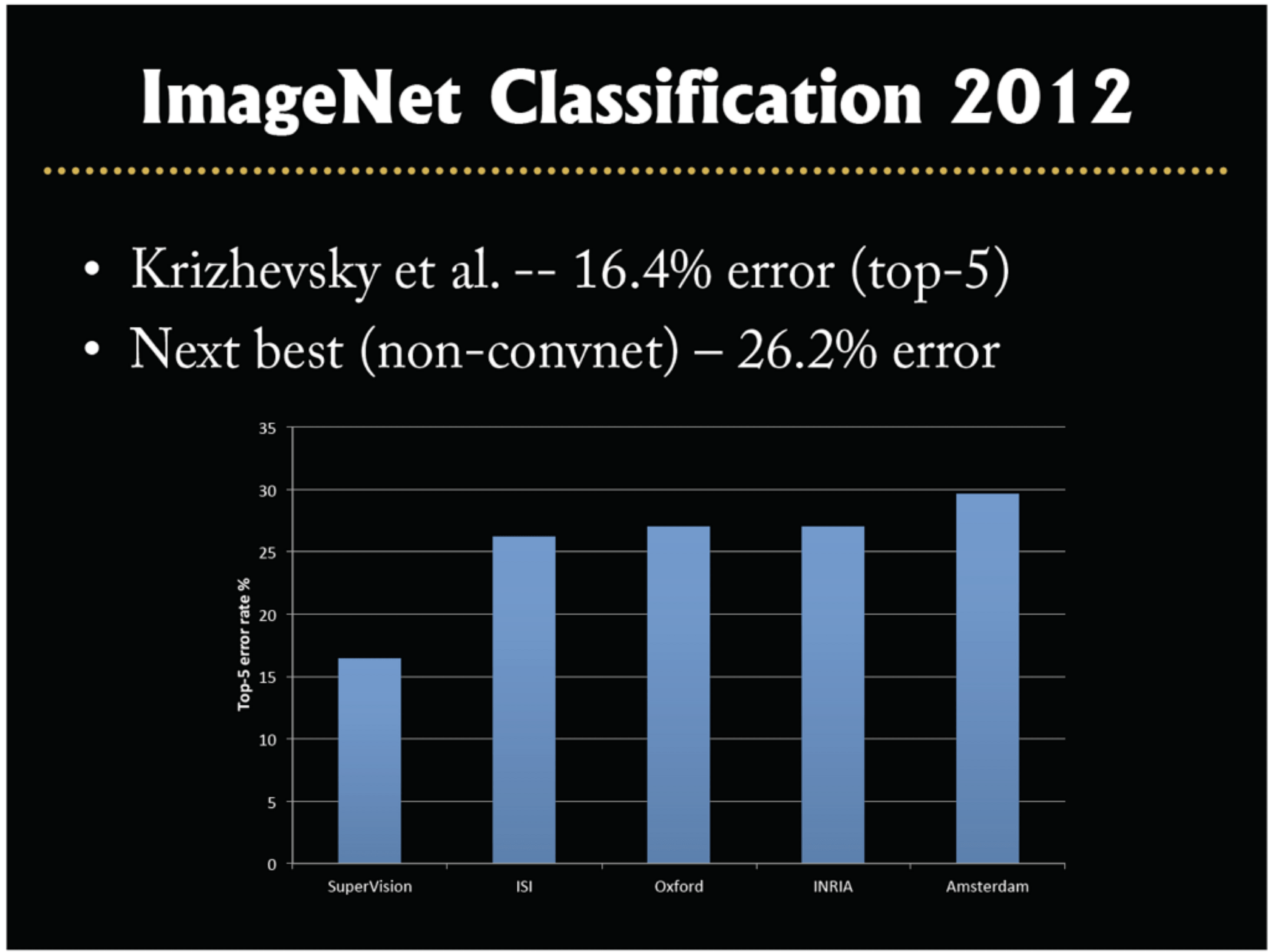
Image classification played a pivotal role in kicking off the current wave of AI enthusiasm
Summary
- Classification: a supervised learning problem, similar to regression, but where the output/label is in a discrete set.
- Binary classification: only two possible label values.
- Linear binary classification: think of \(\theta\) and \(\theta_0\) as defining a d-1 dimensional hyperplane that cuts the d-dimensional feature space into two half-spaces.
- 0-1 loss: a natural loss function for classification, BUT, hard to optimize.
- Sigmoid function: motivation and properties.
- Negative-log-likelihood loss: smoother and has nice probabilistic motivations. We can optimize via (S)GD.
- Regularization is still important.
- The generalization to multi-class via (one-hot encoding, and softmax mechanism)
- Other ways to generalize to multi-class (see hw/lab)
Thanks!
We'd love to hear your thoughts.