
Lecture 3: Generative Models: Diffusion
Modeling with Machine Learning for Computer Science
Outline
- Applications
- Diffusion high-level idea:
- forward process/reverse process
- connections to VAE etc.
- various objective functions
- Guidance (classifier guidance and classifier-free guidance)
- Beyond images
[Image credit: SDXL: Improving Latent Diffusion Models for High-Resolution Image Synthesis https://arxiv.org/pdf/2307.01952]
Text-to-image generation

Image credit: https://github.com/CompVis/stable-diffusion
Sketch-to-Image: coarse-grained control

Image credit: DreamBooth: Fine Tuning Text-to-Image Diffusion Models for Subject-Driven Generation https://arxiv.org/pdf/2208.12242
Image editing and composition

Diffusion “prior” for image restoration

Image credit: Zero-Shot Image Restoration Using Denoising Diffusion Null-Space Model https://arxiv.org/pdf/2212.00490
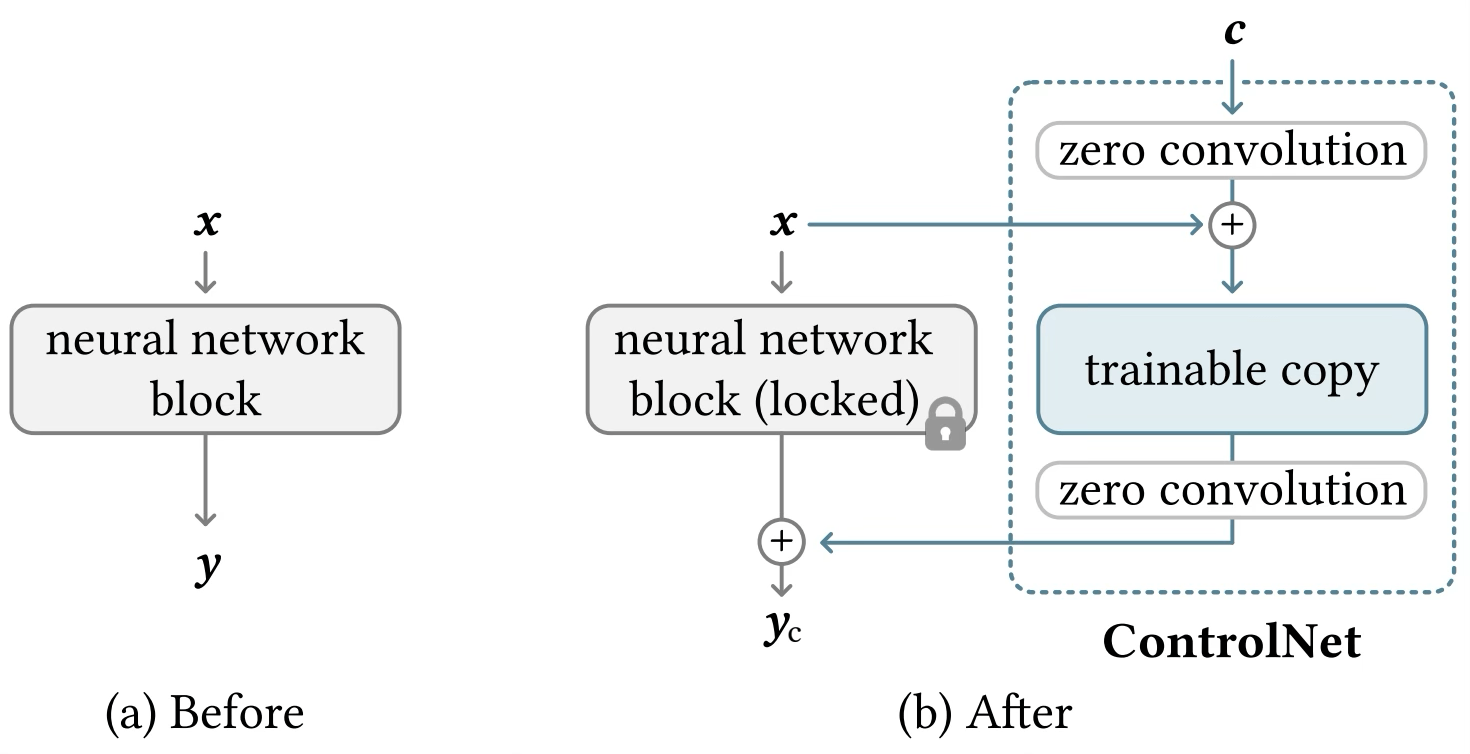
Image credit: Adding Conditional Control to Text-to-Image Diffusion Models https://arxiv.org/pdf/2302.05543
ControlNet: refined control

Text-to-audio generation
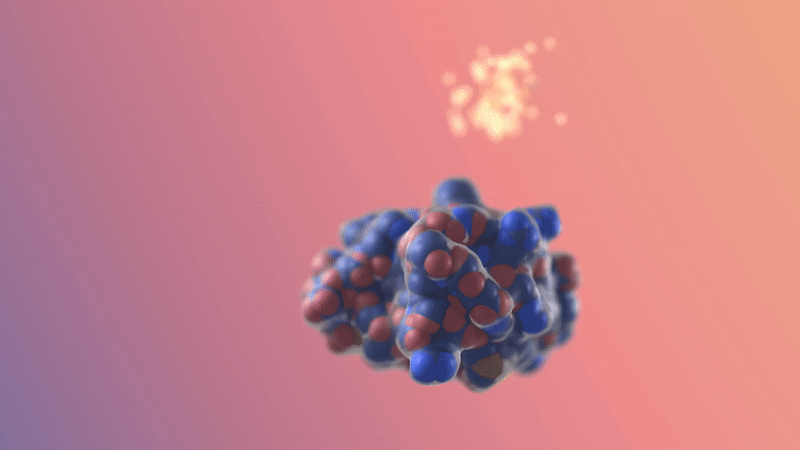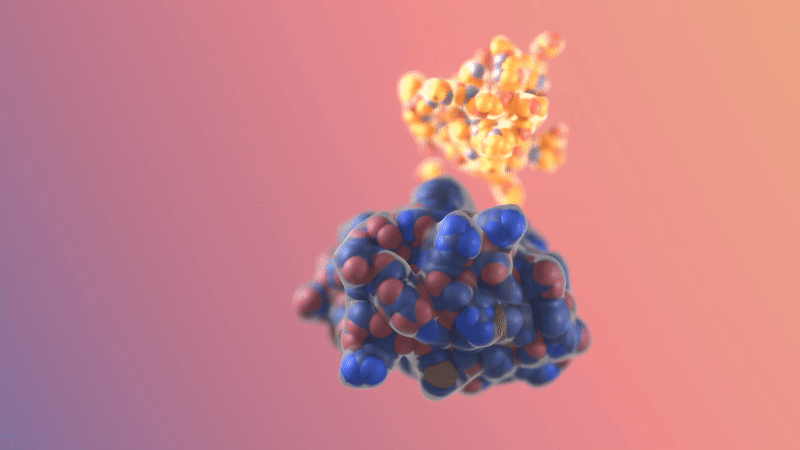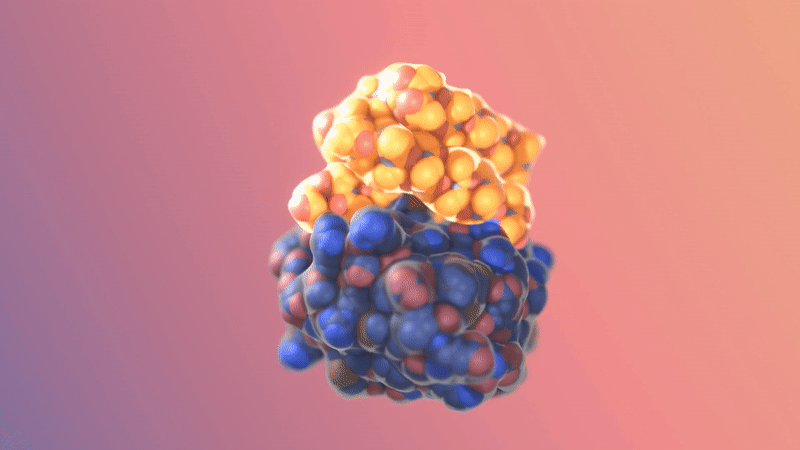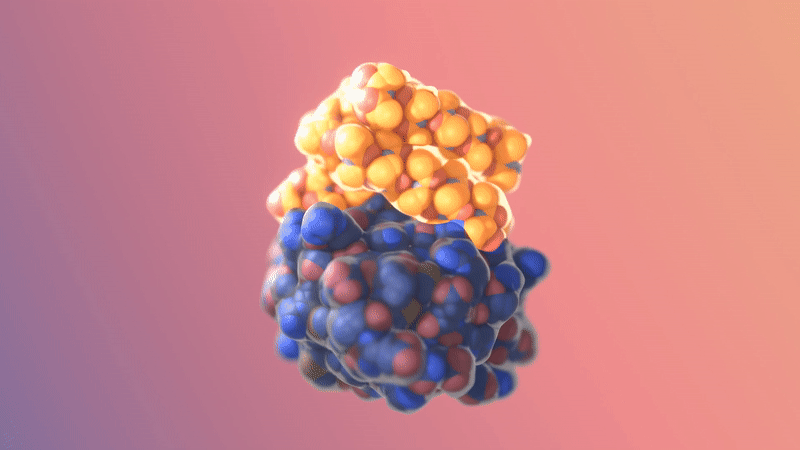
Image/video credit: RFDiffusion https://www.bakerlab.org
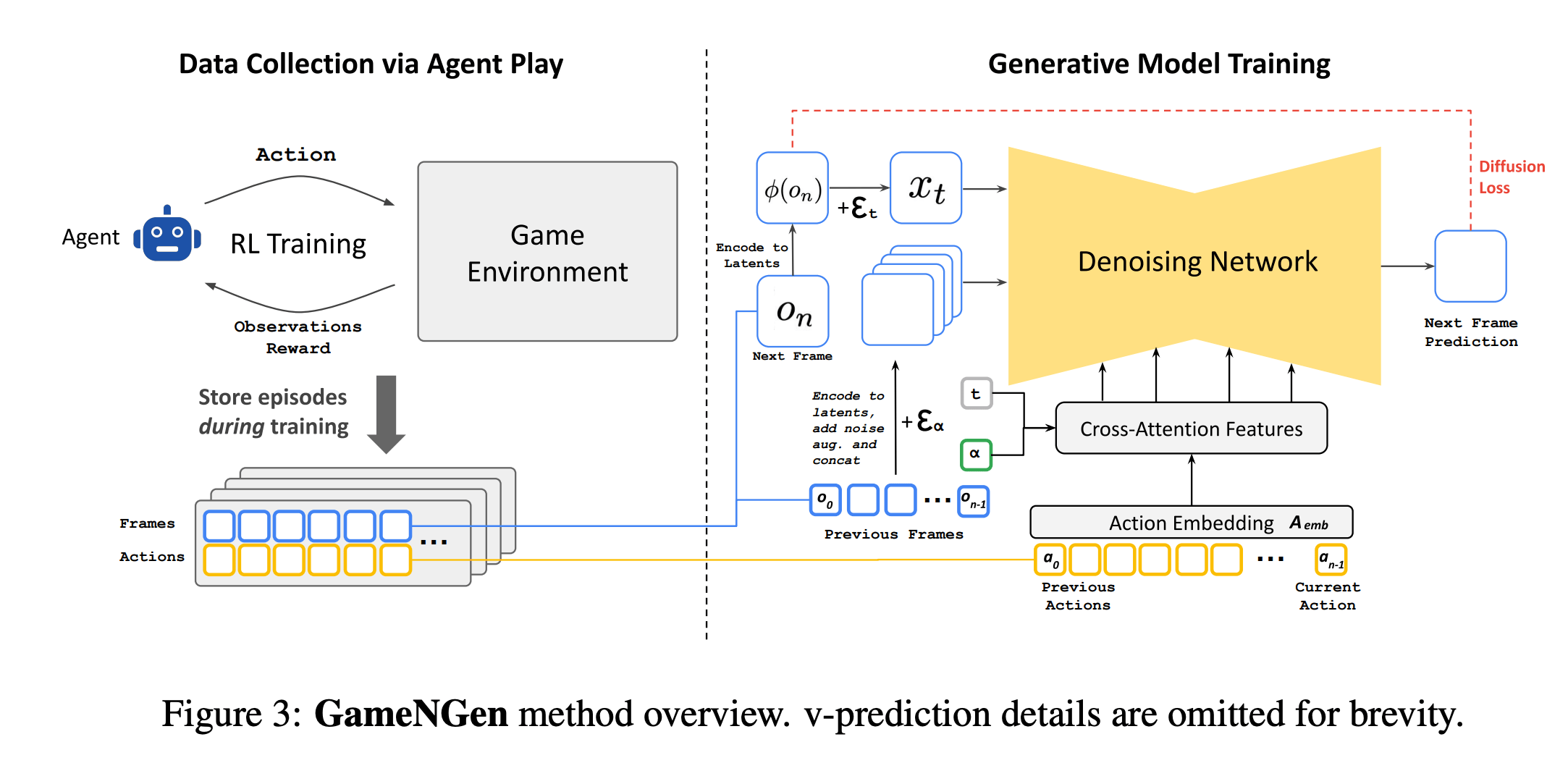
Key Idea: denoising in many small steps is easier than attempting to remove all noise in a single step
1. Forward Process
- Encoder is a fixed noising procedure \( q(x_t \mid x_{t-1}) \) which gradually adds noise to the clean data \( x_0 \), producing gradually noisy latent variables \( x_1, \dots, x_T \).
2. Backward Process
- A learned decoder \( p_\theta(x_{t-1} \mid x_t) \) aims to reverse the forward process, and reconstruct step by step moving from \( x_T \) back to \( x_0 \).
- During training, we optimize \( \theta \) so each reverse step approximates the true posterior \( q(x_{t-1} \mid x_t) \).
- At inference time, we start from pure noise \( x_T \sim \mathcal{N}(0, I) \) and apply this backward chain to generate samples.

For fixed \( \{\beta_t\}_{t \in [T]} \in (0, 1) \), let \[ q(x_t \mid x_{t-1}) := \mathcal{N}(x_t \mid \sqrt{1 - \beta_t} \, x_{t-1}, \beta_t I) \]
Equivalently, \[ x_t = \sqrt{1 - \beta_t} \, x_{t-1} + \sqrt{\beta_t} \, \epsilon, \quad \epsilon \sim \mathcal{N}(0, I) \]
\[ \Rightarrow \quad x_t = \sqrt{\bar{\alpha}_t} \, x_0 + \sqrt{1 - \bar{\alpha}_t} \, \epsilon, \quad \epsilon \sim \mathcal{N}(0, I) \]

\(\alpha_t=1-\beta_t, \quad \bar{\alpha}_t=\prod_{s=1}^t \alpha_s\)
can think of \(\sqrt{\beta_t} \approx \sigma_t-\sigma_{t-1}\) noise schedule difference
Fact:
- for small \(\beta, \exists \mu\left(x_0, x_t\right)\), s.t. \(q\left(x_{t-1} \mid x_t\right) \approx \mathcal{N}\left(x_{t-1} ; \mu\left(x_0, x_t\right), \beta_t I\right)\)
- for large \(T, q\left(x_T\right) \approx \mathcal{N}(0,1)\)

\(\alpha_t=1-\beta_t, \quad \bar{\alpha}_t=\prod_{s=1}^t \alpha_s\)
can think of \(\sqrt{\beta_t} \approx \sigma_t-\sigma_{t-1}\) noise schedule difference
Fact:
- for small \(\beta, \exists \mu\left(x_0, x_t\right)\), s.t. \(q\left(x_{t-1} \mid x_t\right) \approx \mathcal{N}\left(x_{t-1} ; \mu\left(x_0, x_t\right), \beta_t I\right)\)
- for large \(T, q\left(x_T\right) \approx \mathcal{N}(0,1)\)
\(q\left(x_{0: T}\right)=q\left(x_0\right) q\left(x_{1: T} \mid x_0\right)\)
\(=q\left(x_T\right) \prod_{t=1}^T q\left(x_{t-1} \mid x_t\right)\)
\(\approx \mathcal{N}(0, I) \prod_{t=1}^T \mathcal{N}\left(x_{t-1} ; \mu\left(x_0, x_t\right), \beta_t I\right)\)
by Markov
by the two facts
Choose to parameterize \(p_\theta\left(x_{t-1} \mid x_t\right)=\mathcal{N}\left(x_{t-1} ; \mu\left(x_0, x_t\right), \beta_t I\right)\), learn \(\hat{x}_0\left(x_t, t\right)\)
Exactly like a VAE.

There are two important variations to this training procedure:
- How noise is added (variance preserving/exploding)
- What quantity to predict (noise, data, …)
Re-parameterize:
\(x_t=x_0+\sigma_t \epsilon, \epsilon \sim \mathcal{N}(0, I)\)
\(x_0=z_0, \quad x_t=z_t / \sqrt{\bar{\alpha}_t}, \quad \sigma_t=\sqrt{\frac{1-\bar{\alpha}_t}{\bar{\alpha}_t}}\)
Re-parameterize variation tends to perform better in practice, keeps model input constant norm
Denoising diffusion models estimate a noise vector \(\epsilon\) \(\in \mathbb{R}^n\) from a given noise level \(\sigma > 0\) and noisy input \(x_\sigma \in \mathbb{R}^n\) such that for some \(x_0\) in the data manifold \(\mathcal{K}\),
\[ {x_\sigma} \;\approx\; \textcolor{green}{x_0} \;+\; \textcolor{orange}{\sigma}\, \textcolor{red}{\epsilon}. \]
- \(x_0\) is sampled from training data
- \(\sigma\) is sampled from training noise schedule (known)
- \(\epsilon\) is sampled from \(\mathcal{N}(0, I_n)\) (i.i.d. Gaussian)
A denoiser \(\textcolor{red}{\epsilon_\theta} : \mathbb{R}^n \times \mathbb{R}_+ \to \mathbb{R}^n\) is learned by minimizing
\[ L(\theta) := \mathbb{E}_{\textcolor{green}{x_0},\textcolor{orange}{\sigma},\textcolor{red}{\epsilon}} \Biggl[\Biggl\|\textcolor{red}{\epsilon_\theta}\Biggl(\textcolor{green}{x_0} + \textcolor{orange}{\sigma}\,\textcolor{red}{\epsilon}, \textcolor{orange}{\sigma}\Biggr) - \textcolor{red}{\epsilon}\Biggr\|^2\Biggr]. \]
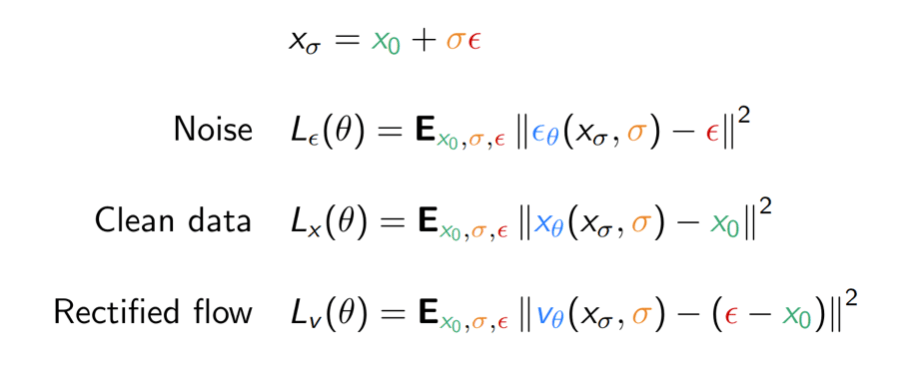
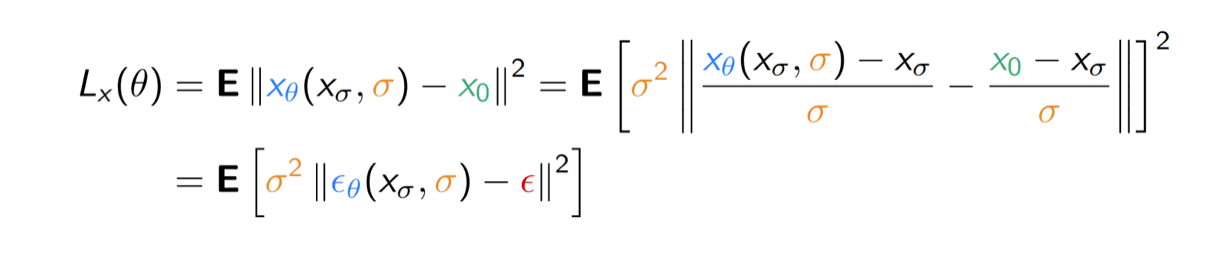
Mathematically equivalent for fixed \(\sigma\), but reweighs loss by a function of \(\sigma\) !
Score matching
Then the following holds \(\epsilon_\theta\left(x_t, t\right) \propto-\nabla_{x_t} \log q_t\left(x_t\right)\). (tweedies formula)
\(\hat{x}_0=\frac{1}{\sqrt{\bar{\alpha}_t}}\left(x_t-\sqrt{1-\bar{\alpha}_t} \hat{\epsilon}\right)\)
Can learn score instead (see hyvarinen score matching)
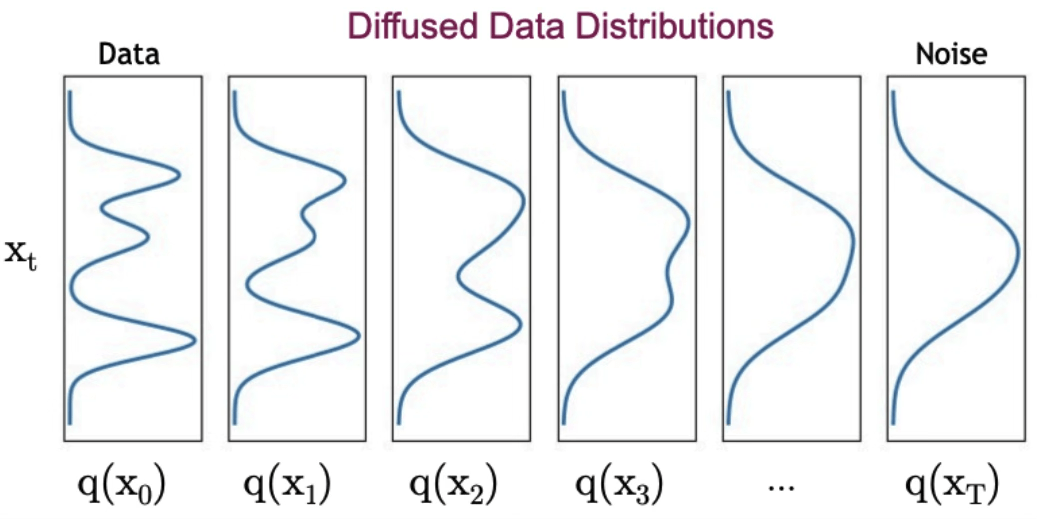
Let \(q_t\left(x_t\right)\) denote the marginal of \(x_t\)
\(x_{t-1}=\underbrace{\frac{1}{\alpha_t}\left(x_t-\frac{\beta_t}{1-\alpha_t} \epsilon_\theta\left(x_t, t\right)\right)}_{\mu_t}+\underbrace{\beta_t}_{\text {noise scale }} z\).
\(x_{t-1}=\sqrt{\bar{\alpha}_{t-1}} \hat{x}_0+\sqrt{1-\bar{\alpha}_{t-1}} \epsilon_\theta\left(x_t, t\right)\)
\(\hat{x}_0=\frac{x_t-\sqrt{1-\bar{\alpha}_t} \epsilon_\theta\left(x_t, t\right)}{\sqrt{\bar{\alpha}_t}}\)
DDPM sampling:
DDIM sampling (deterministic):
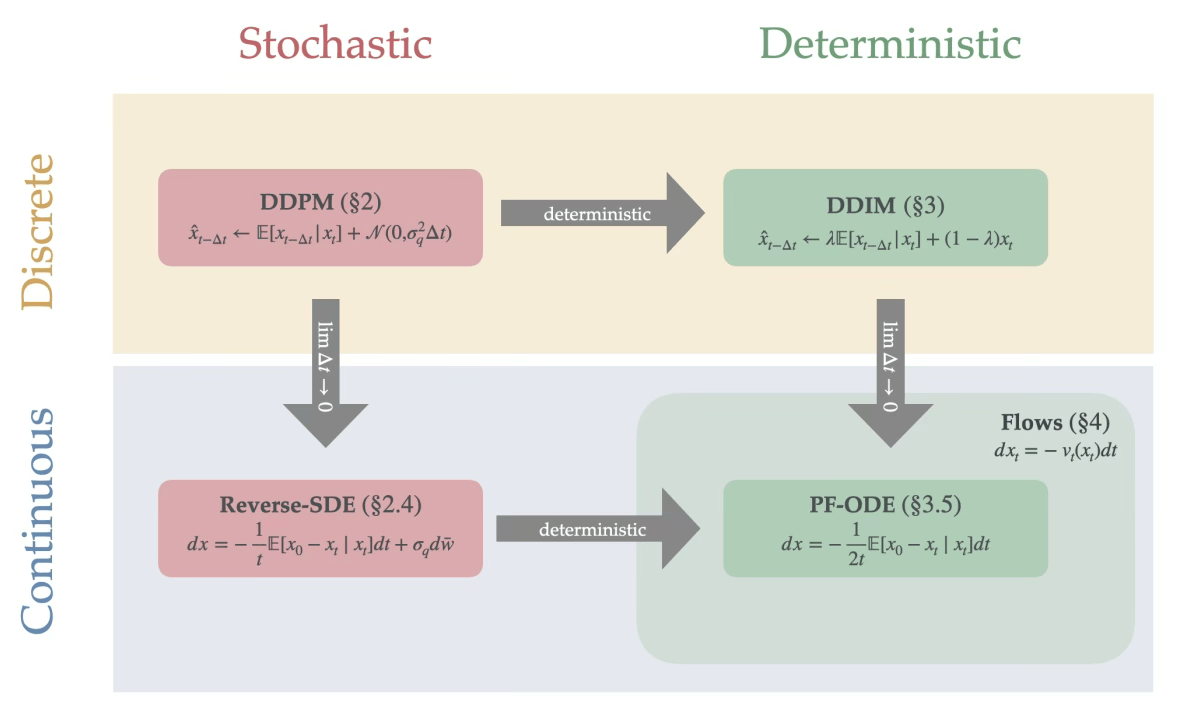
Image credit: Preetum Nakkiran, “step by step diffusion” https://arxiv.org/pdf/2406.08929

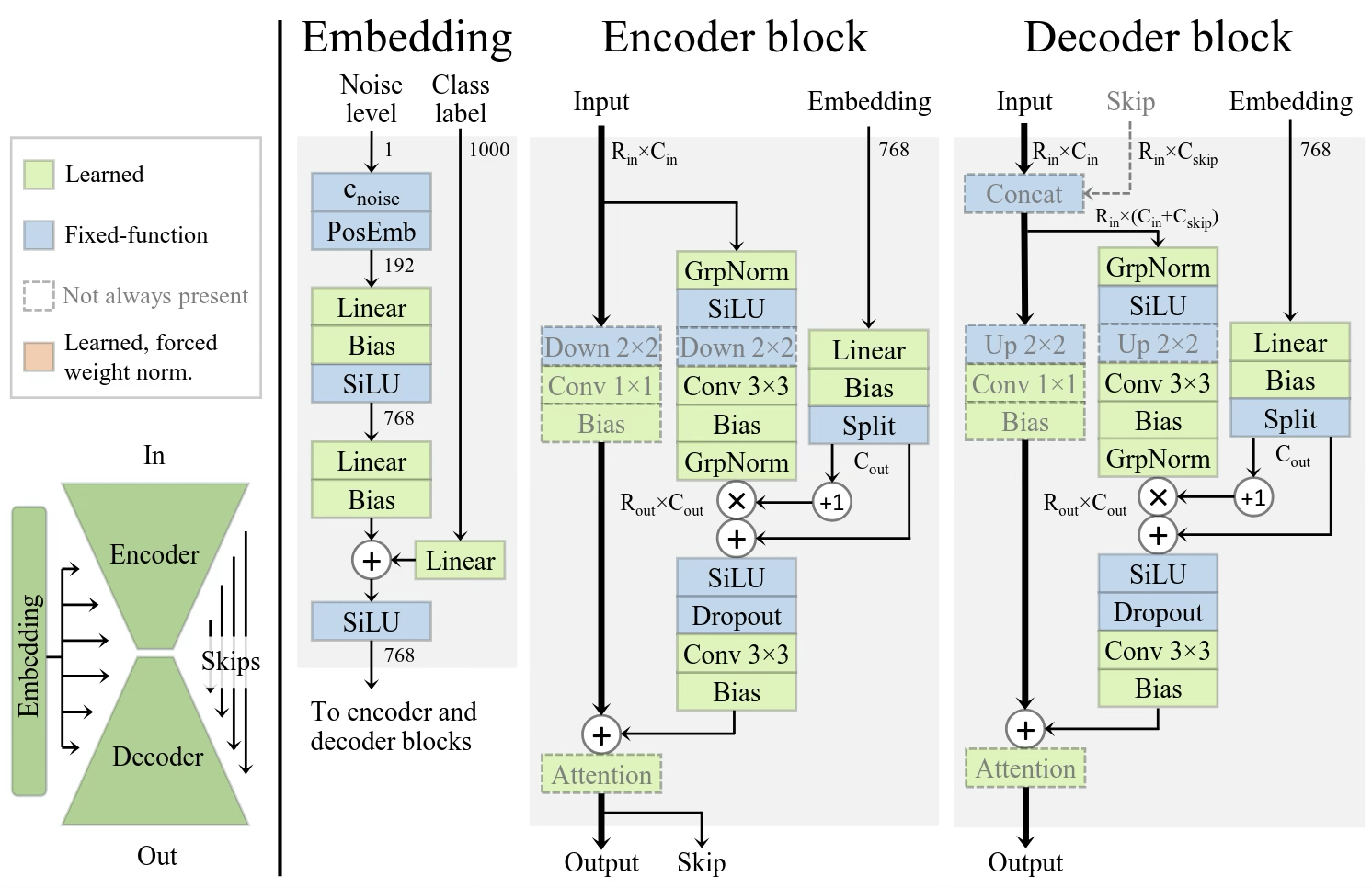
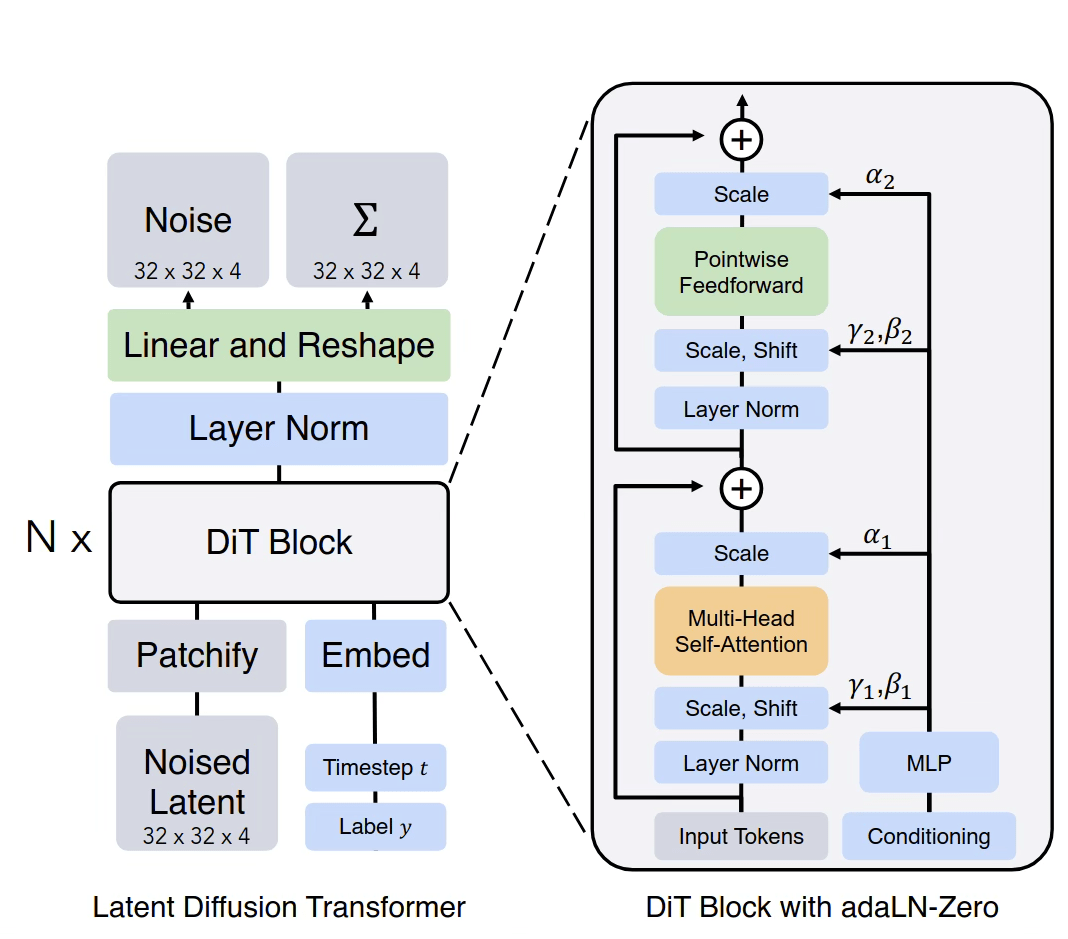
Commonly used architectures
Image credit: (left)Analyzing and Improving the Training Dynamics of Diffusion Models https://arxiv.org/pdf/2312.02696
Right: Scalable Diffusion Models with Transformers https://arxiv.org/pdf/2212.09748
conv U-Net
patch-wise transformers

Just add your conditioning variable \(y\) during training
Works in some cases, usually when the actual \(x\) is low dimensional
Unbiased distribution (in theory)
Doesn’t work in practice when scaled up
Generating \(p(x \mid y)\)
\(p(x \mid y)=\frac{p(y \mid x) \cdot p(x)}{p(y)}\)
Generating \(p(x \mid y)\): Classifier guidance
\(\Longrightarrow \log p(x \mid y)=\log p(y \mid x)+\log p(x)-\log p(y)\)
\(\Longrightarrow \nabla_x \log p(x \mid y)=\nabla_x \log p(y \mid x)+\nabla_x \log p(x)\)
train a classifier on noisy images
\(\Longrightarrow \nabla_x \log p(x \mid y) \approx s\nabla_x \log p(y \mid x)+\nabla_x \log p(x)\)

\(s\)
Image from classifier-free Diffusion Guidance, Ho et.al. 2022

Algorithm from Dhariwal & Nichol, 2021
\( \nabla_x \log p(x \mid y) \approx s\nabla_x \log p(y \mid x)+\nabla_x \log p(x)\)
- Train a classifier on noisy \(x\) (usually undesirable)
- At sampling time, compose its gradient with diffusion score
- Conditional sampling without training a conditional model
- Biased distribution if using a higher guidance strength
- Need discrete classes
Can we generate \(x\) better without training a classifier on noisy \(x\), and also generalize beyond class conditioning like language?
Generating \(p(x \mid y):\) Classifier guidance
Generating \(p(x \mid y):\) Classifier-free guidance
\(\nabla_x \log p(x \mid y) \approx s \nabla_x \log p(y \mid x)+\nabla_x \log p(x)\)
\(p(y \mid x)=\frac{p(x \mid y) \cdot p(y)}{p(x)}\)
\(\Longrightarrow \log p(y \mid x)=\log p(x \mid y)+\log p(y)-\log p(x)\)
\(\Longrightarrow \nabla_x \log p(y \mid x)=\nabla_x \log p(x \mid y)-\nabla_x \log p(x)\).
\( \approx s [\nabla_x \log p(x \mid y)-\nabla_x \log p(x)]+\nabla_x \log p(x)\)
- seemingly requires training a conditional diffusion, and an unconditional one
- can share parameter, and train the two together
Control Net
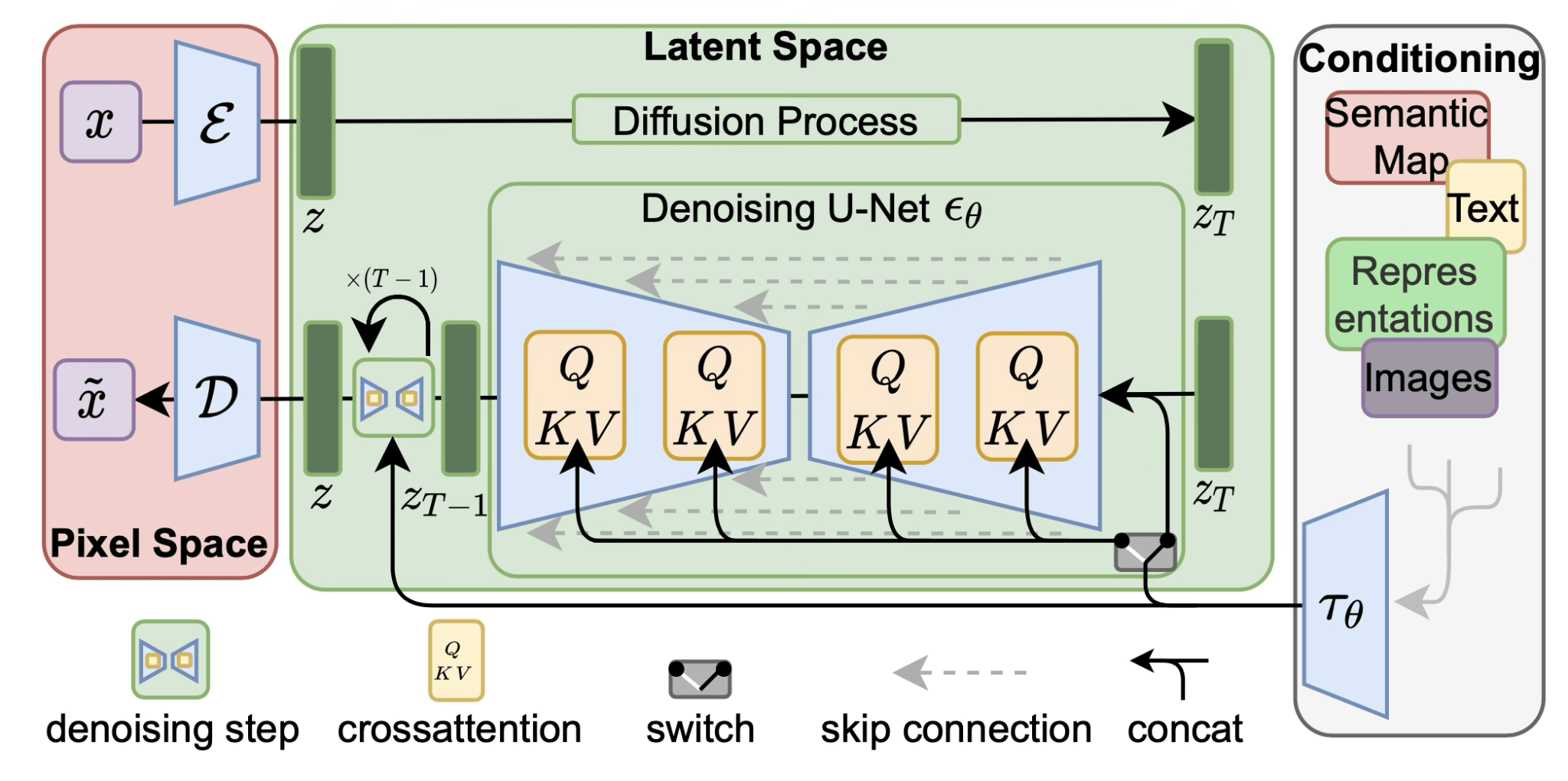
LDM,
Rombach & Blattmann, et al. 2022
U-Net with Conditioning Branch
https://arxiv.org/pdf/2502.09992
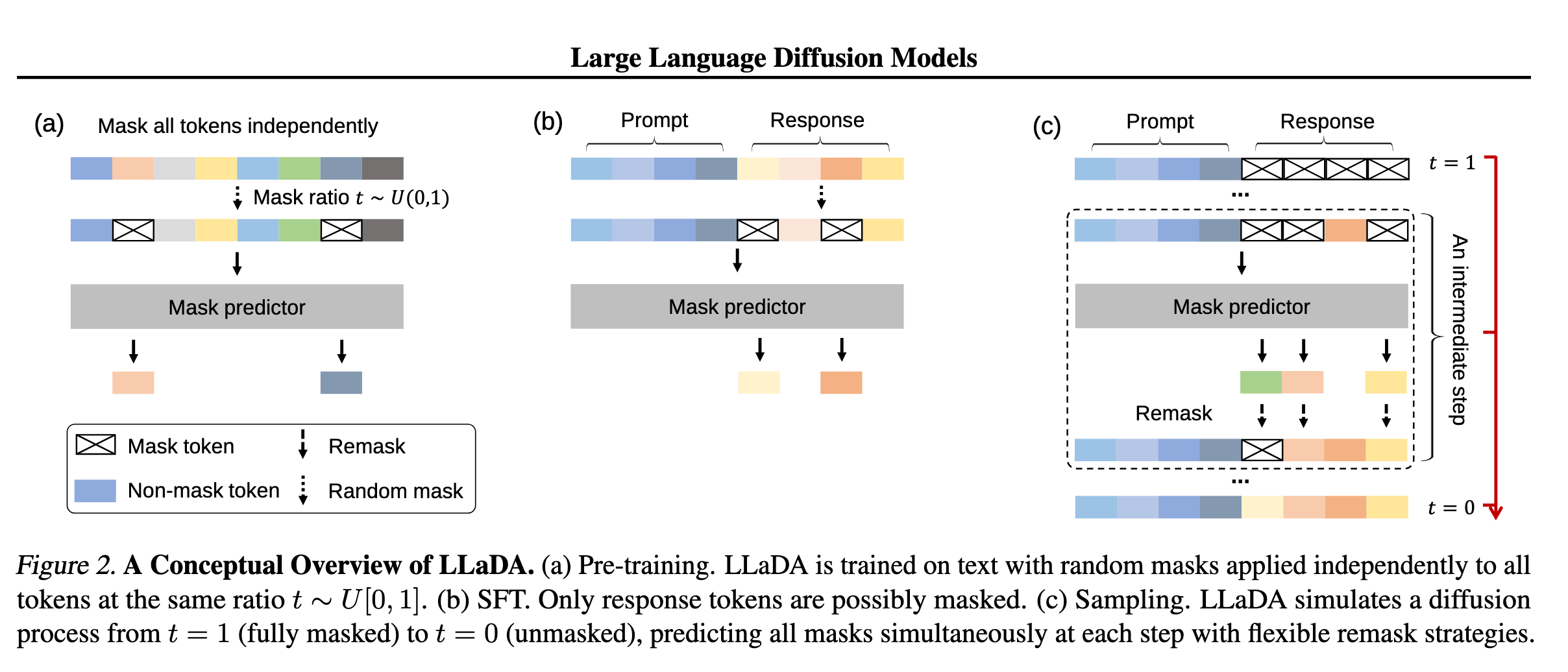
Beyond images?
https://arxiv.org/pdf/2502.09992
Beyond images?
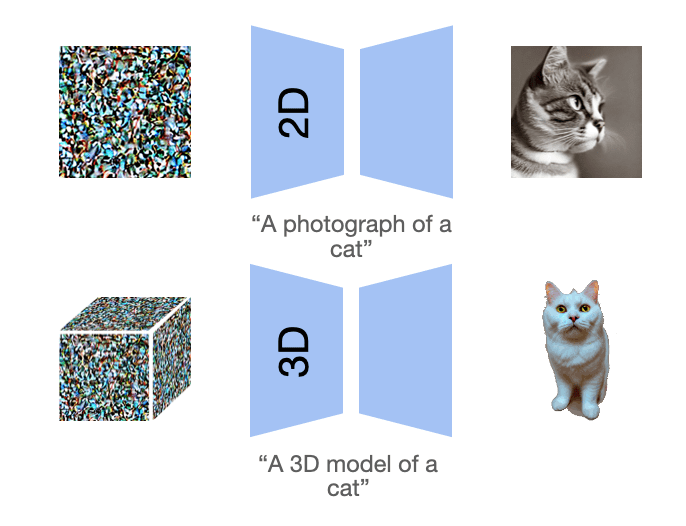

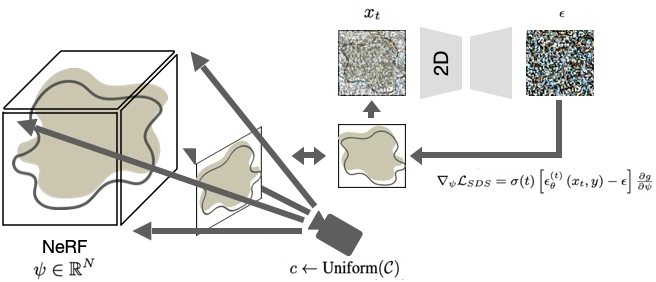
Poole, Ben, et al. "Dreamfusion: Text-to-3d using 2d diffusion." arXiv preprint arXiv:2209.14988 (2022).
Wang, Haochen, et al. "Score jacobian chaining: Lifting pretrained 2d diffusion models for 3d generation." Proceedings of the IEEE/CVF CVPR. 2023.

Beyond images?
Poole, Ben, et al. "Dreamfusion: Text-to-3d using 2d diffusion." arXiv preprint arXiv:2209.14988 (2022).
Wang, Haochen, et al. "Score jacobian chaining: Lifting pretrained 2d diffusion models for 3d generation." Proceedings of the IEEE/CVF CVPR. 2023.
Beyond images?

Power law of natural images
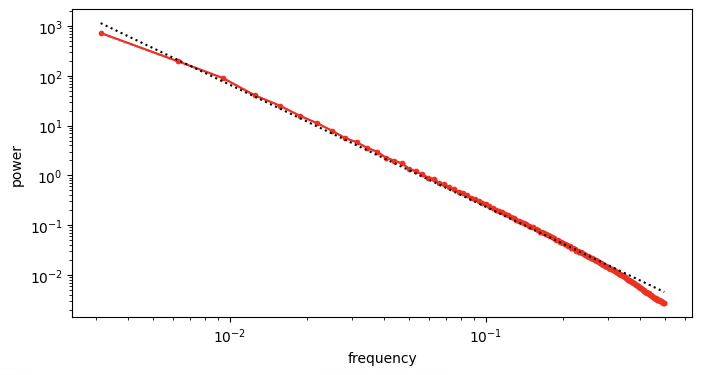
Gaussian noise has uniform power spectral density
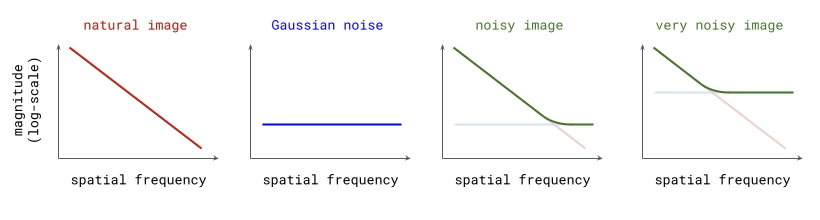
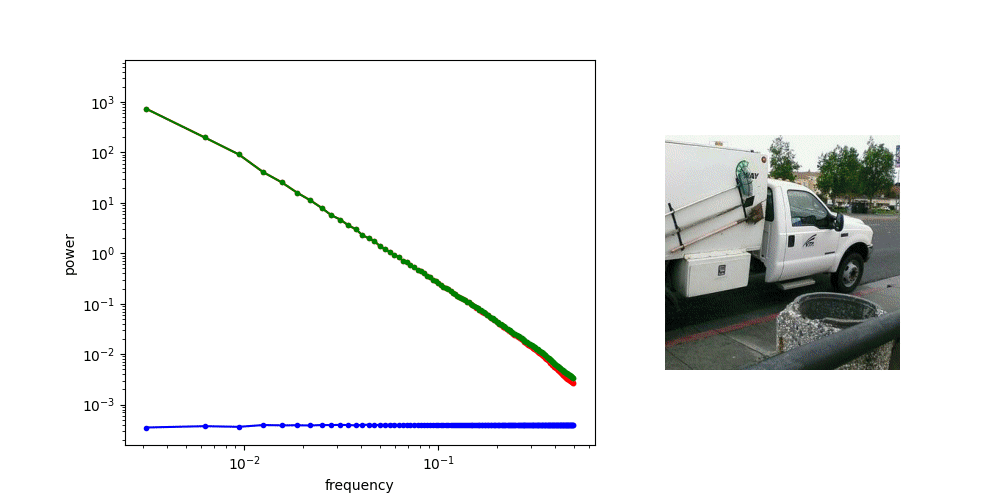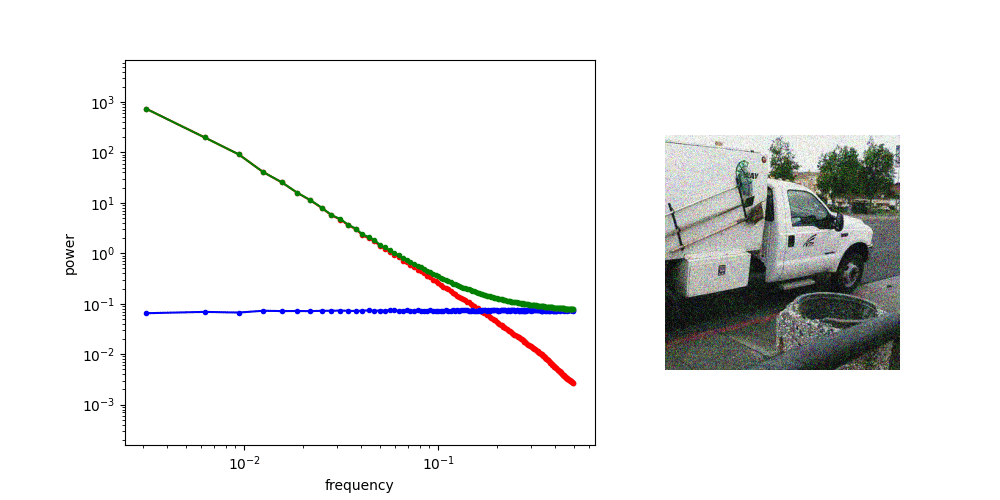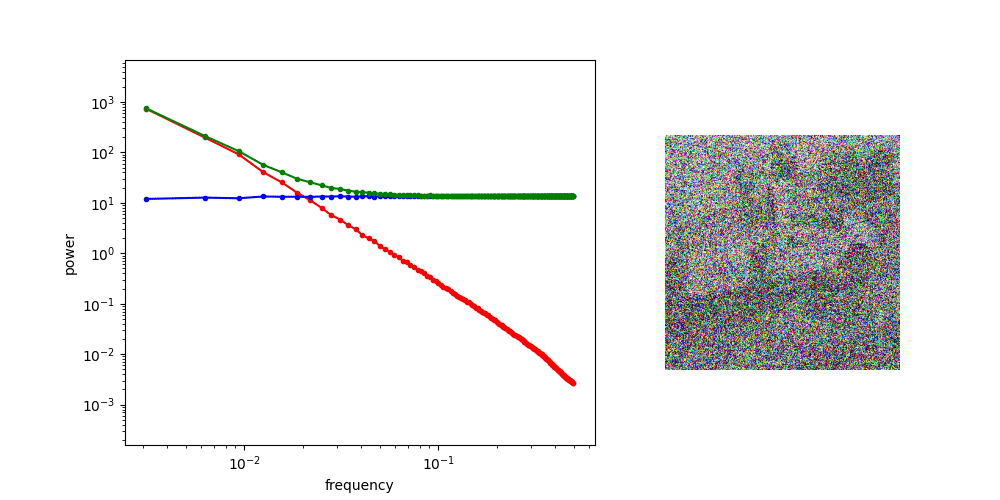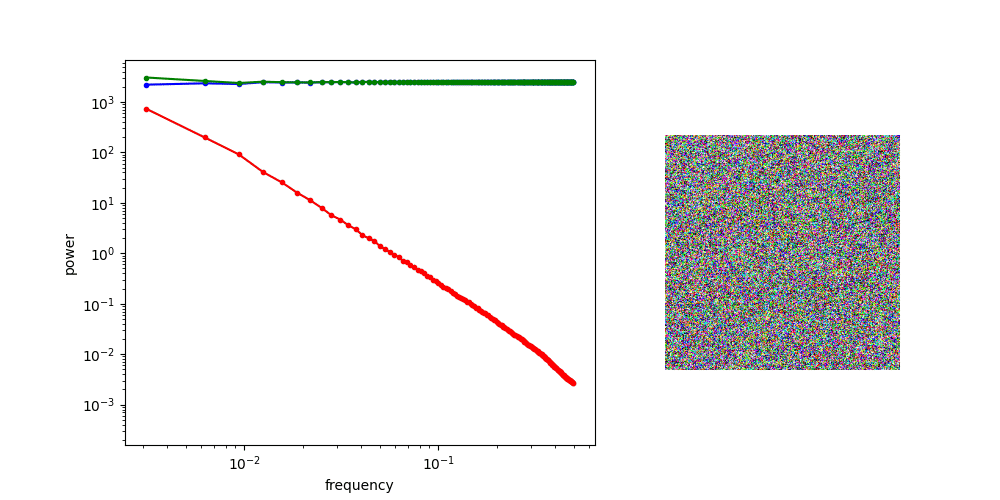
Adding Gaussian noise “drowns out” high frequency features first
for other applications, might worth investigating noise schedule
Thanks!
We'd love to hear your thoughts.