Characterising the Variability of the Black Hole at the Centre of our Galaxy using Multi-Output Gaussian Processes
Shih Ching Fu
shihching.fu@postgrad.curtin.edu.au
Supervisors:
Dr Arash Bahramian, Dr Aloke Phatak,
Dr James Miller-Jones, Dr Suman Rakshit
Sagittarius A* (Sgr A*)
- Supermassive Black Hole (SMBH) at the centre of the Milky Way.
- 4 million solar masses.
- ~27,000 ly from Earth
- Image created from observations taken in 2017 by the Event Horizon Telesope (EHT) Collaboration.
Anatomy of a Black Hole
Time domain astronomy
- Estimate the characteristic timescales of the variability in the black hole emissions.
- Characterise the relationship between emissions of different wavelengths, e.g, time delay between bands.
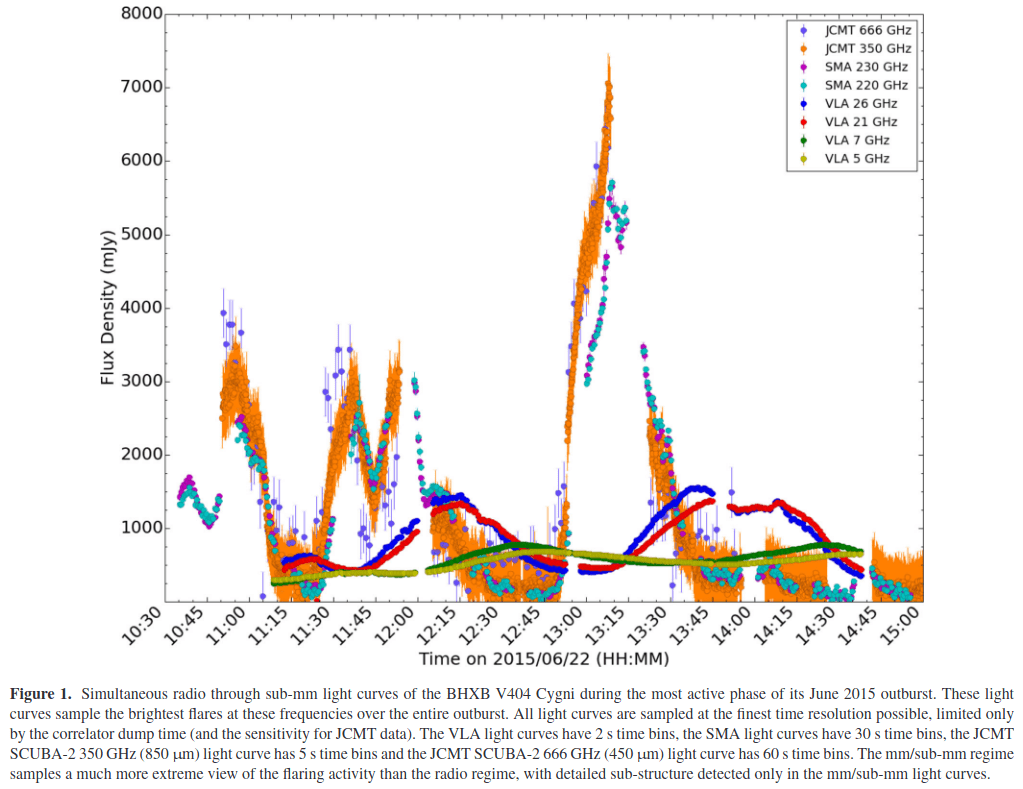
Credit: Tetarenko et al. (2017)
Black hole X-ray binary
V404 Cygni
Atacama Large Millimeter Array (ALMA)
- Chilean Atacama Desert at 5000m elevation.
- 66 high-precision dish antennas: 54 x 12m and 12 x 7m across.
- Radio and infrared.
- Member site of EHT Collaboration.
Credit: NRAO/AUI/NSF
Credit: ALMA (ESO/NAOH/NRAO)
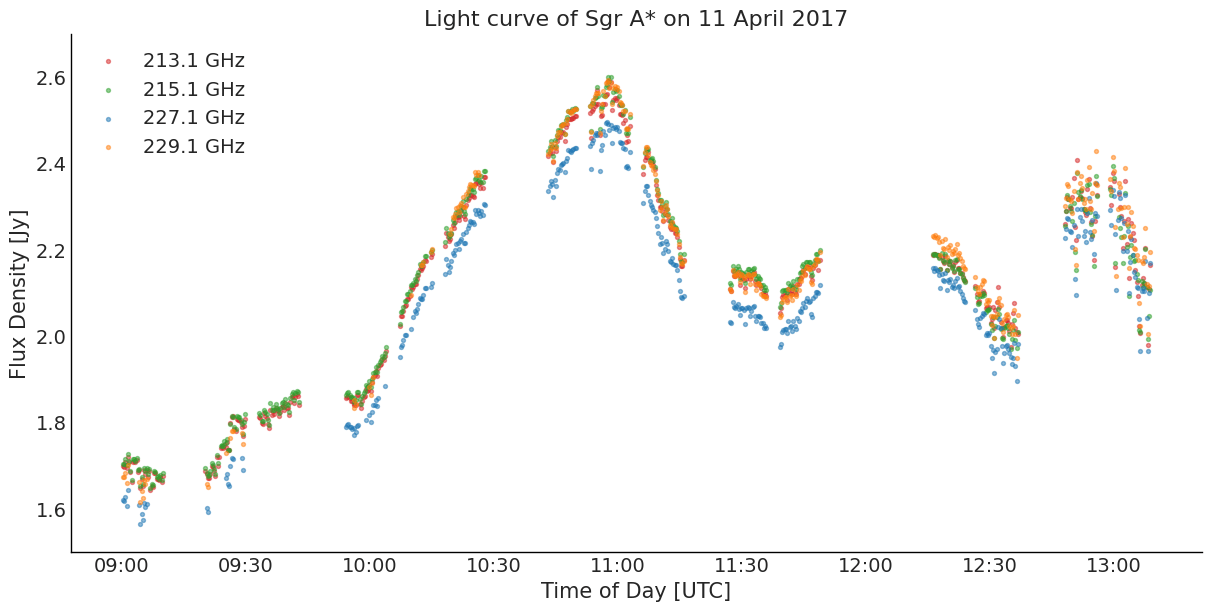
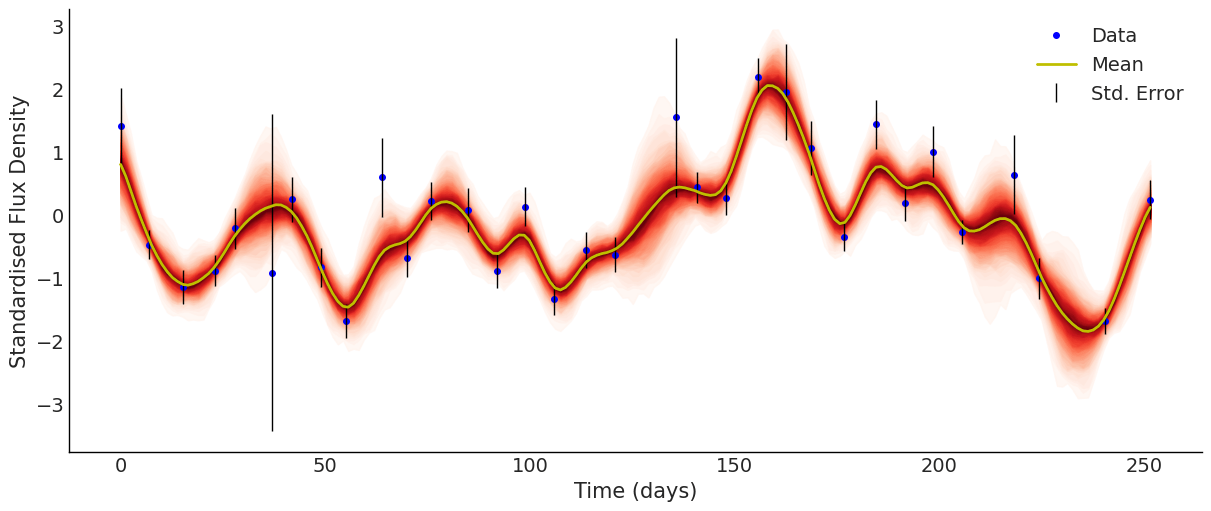
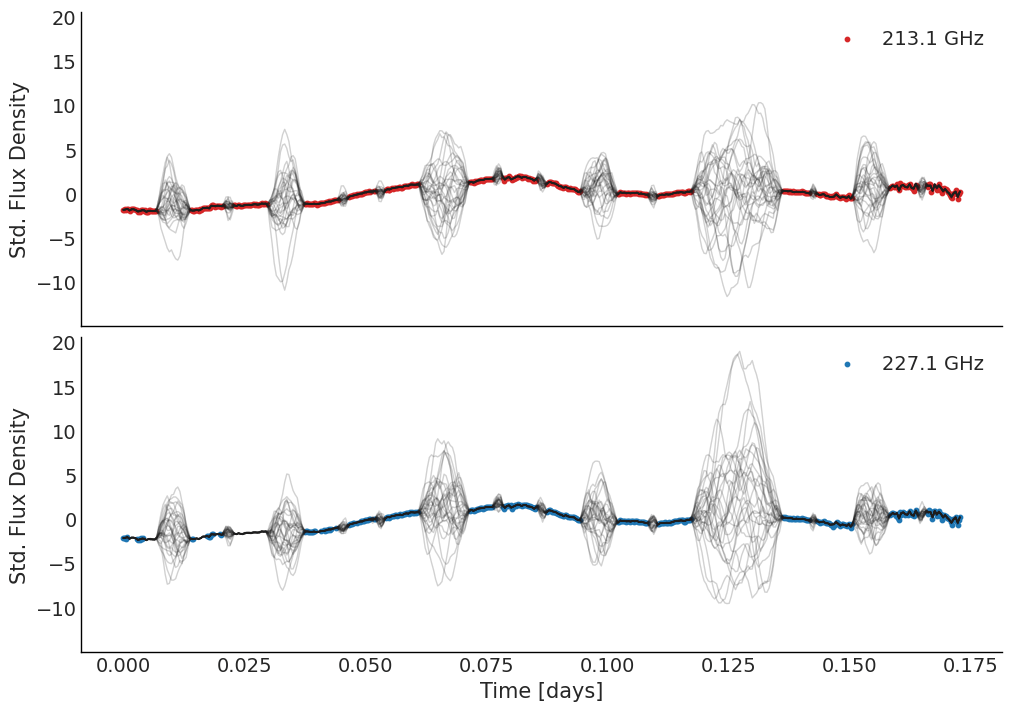
Multi-band Light Curve
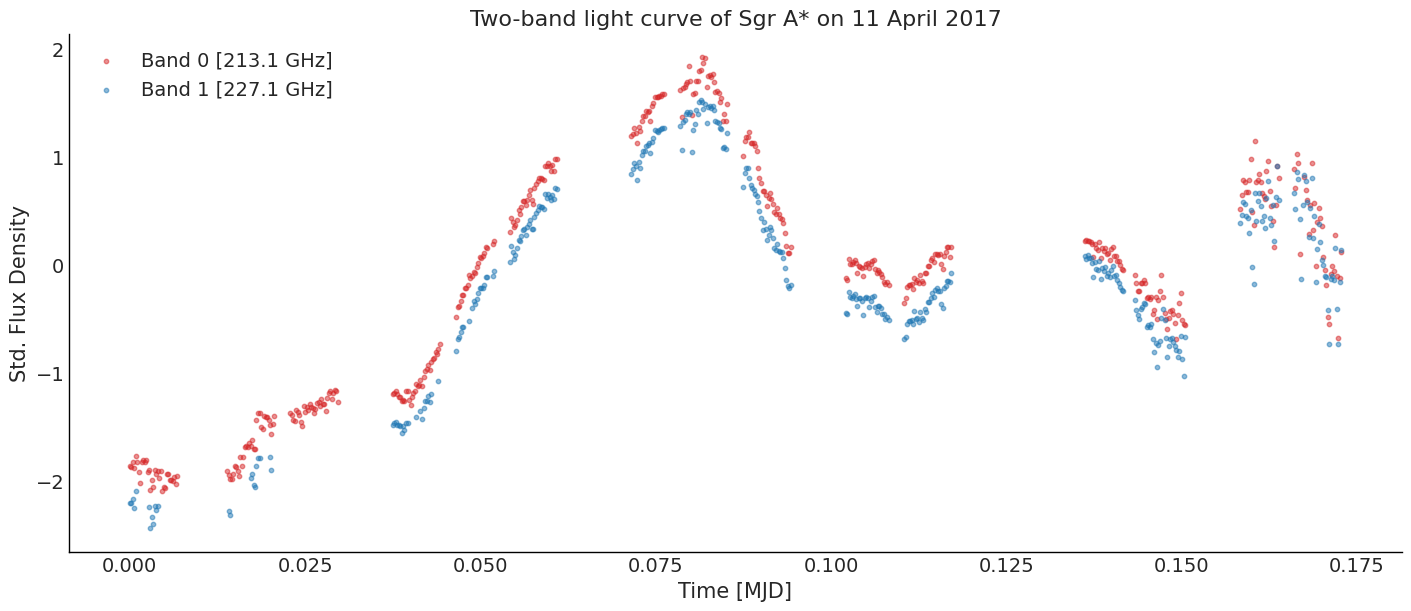
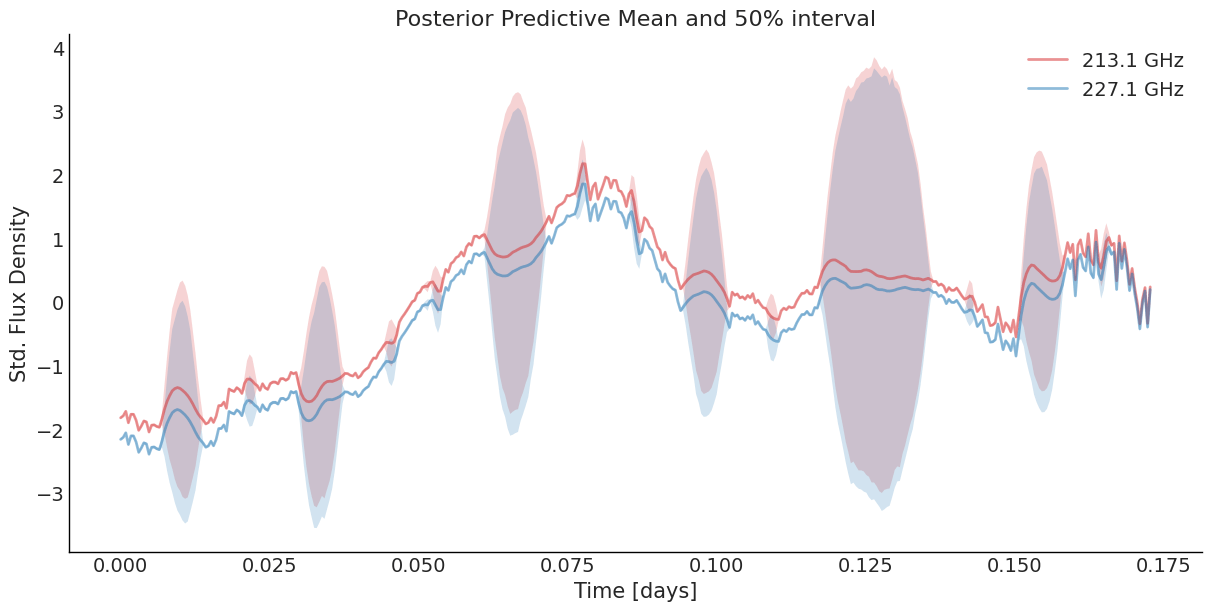
Two-band Light Curve
Gaussian Processes (GPs)
Extend multivariate Gaussian to 'infinite' dimensions.
- Mean function, \(\mu(t)\)
- Covariance or kernel function, \( \kappa(t,t'; \boldsymbol{\theta}) \)
\begin{bmatrix}
Y_1 \\
Y_2 \\
\vdots \\
\end{bmatrix} \sim \mathcal{GP} (\mu(t), \boldsymbol{K})
where \(\mu = \mu(t)\) and \( K_{ij} = \kappa(t_i, t_j; \boldsymbol{\theta}) \), for \( i,j = 1, 2, \dots \)
Rather than specify a fixed covariance matrix with fixed dimensions, compute covariances using the kernel function.
\boldsymbol{K} =
\begin{bmatrix}
K_{11} & \dots & K_{1.} \\
\vdots & \ddots & \vdots \\
K_{.1} & \dots & K_{..}
\end{bmatrix}
Multivariate Normal
Y is a vector of n Gaussian distributed random variables.
\begin{bmatrix}
Y_1 \\
\vdots \\
Y_n
\end{bmatrix} \sim \mathcal{N}_n (\boldsymbol{\mu}, \boldsymbol{\Sigma}_{n \times n})
\boldsymbol{\Sigma}_{n \times n} =
\begin{bmatrix}
\Sigma_{11} & \dots & \Sigma_{1n} \\
\vdots & \ddots & \vdots \\
\Sigma_{n1} & \dots & \Sigma_{nn}
\end{bmatrix}
where \(\boldsymbol\mu = (\mu_1, \dots, \mu_n)\) and \(\boldsymbol{\Sigma}\) is a \(n \times n \) covariance matrix.
\mathbf{\Sigma} =
\begin{bmatrix}
1 & 0 \\
0 & 1
\end{bmatrix}
\mathbf{\Sigma} =
\begin{bmatrix}
1 & 0.8 \\
0.8 & 1
\end{bmatrix}
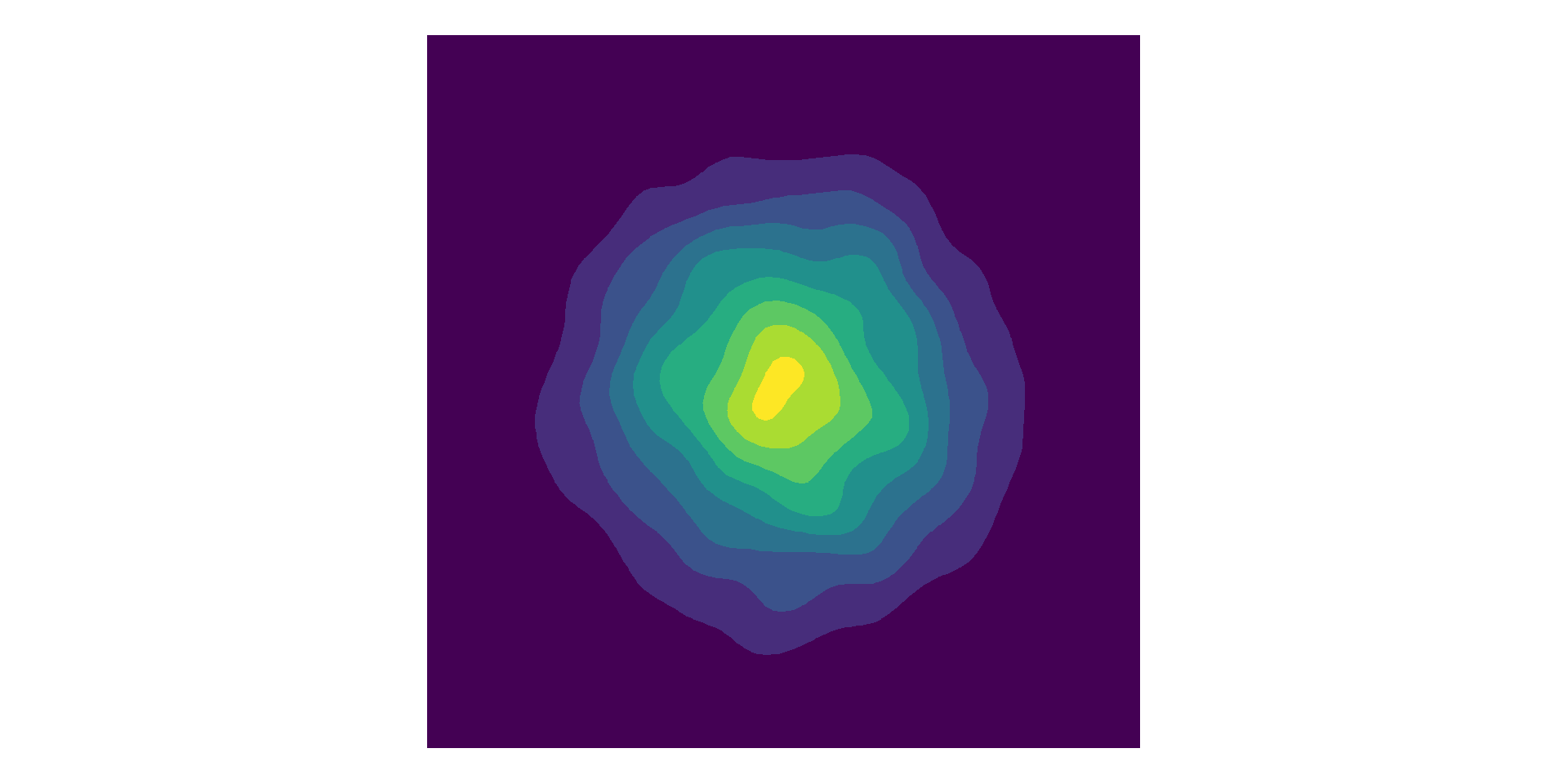
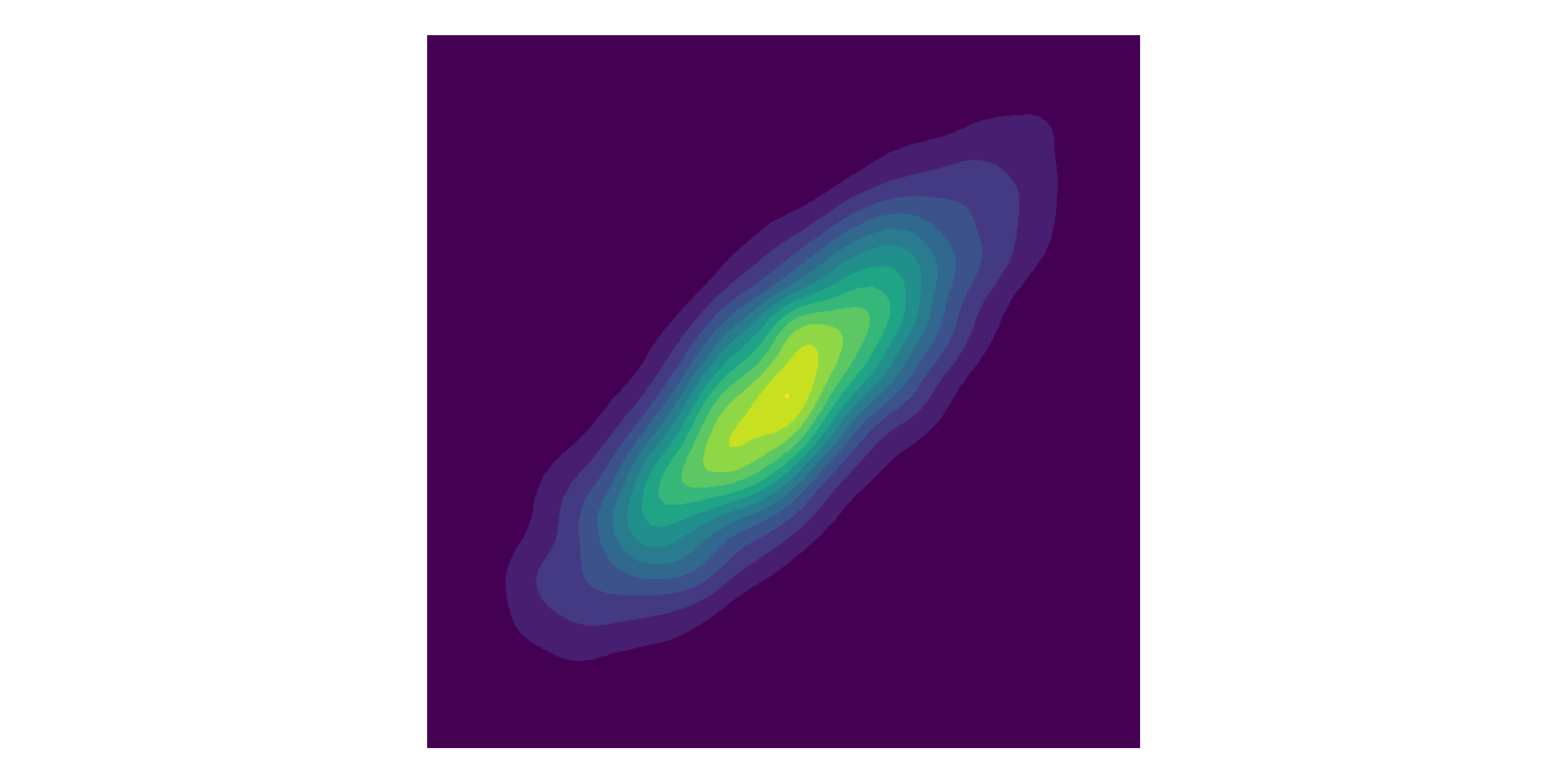
- Symmetric, positive semi-definite matrix.
- Linear combinations are also valid covariance matrices.
"Single-output" GP
f(\boldsymbol{x}) \sim \mathcal{GP}(\boldsymbol{0}, \kappa(\boldsymbol{x}, \boldsymbol{x}'; \boldsymbol{\theta}))
y(\boldsymbol{x}_i) = f(\boldsymbol{x}_i) + \varepsilon_i
\varepsilon_i \sim \mathcal{N}(0, \sigma^2)
\begin{bmatrix}
y(\boldsymbol{x}_1)\\
\vdots \\
y(\boldsymbol{x}_n)
\end{bmatrix} \sim \mathcal{N}\left(\begin{bmatrix}0\\ \vdots \\ 0 \end{bmatrix},
\begin{bmatrix}
\kappa(\boldsymbol{x}_1, \boldsymbol{x}_1) & \dots & \kappa(\boldsymbol{x}_1, \boldsymbol{x}_n) \\
\vdots & \ddots & \vdots \\
\kappa(\boldsymbol{x}_n, \boldsymbol{x}_1) & \dots & \kappa(\boldsymbol{x}_n, \boldsymbol{x}_n)
\end{bmatrix} + \sigma^2
\begin{bmatrix}
1 & \dots & 0 \\
\vdots & \ddots & \vdots \\
0 & \dots & 1
\end{bmatrix}\right)
\boldsymbol{y} \sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{K} + \sigma^2 \boldsymbol{I})
Multiple Output GP (MOGP)
\begin{bmatrix}
\boldsymbol{y}_1\\
\boldsymbol{y}_2
\end{bmatrix} \sim \mathcal{N}\left(\begin{bmatrix}\boldsymbol{0}\\ \boldsymbol{0} \end{bmatrix},
\begin{bmatrix}
\boldsymbol{K}_1 & \boldsymbol{0} \\
\boldsymbol{0} & \boldsymbol{K}_2
\end{bmatrix} +
\begin{bmatrix}
\sigma^2_1 \boldsymbol{I} & \boldsymbol{0} \\
\boldsymbol{0} & \sigma^2_2 \boldsymbol{I}
\end{bmatrix}\right)
\boldsymbol{y} \sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{K}_{\boldsymbol{f},\boldsymbol{f}} + \boldsymbol{\Sigma})
\(1 \times (n_1 + n_2)\)
\((n_1 + n_2) \times (n_1 + n_2)\)
Cross-covariance
\(\boldsymbol{K}_{\boldsymbol{f},\boldsymbol{f}}\)
f_1(\boldsymbol{x}) \sim \mathcal{GP}(\boldsymbol{0}, \kappa_1(\boldsymbol{x}, \boldsymbol{x}'))
\boldsymbol{y}_1 \sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{K}_1 + \sigma^2_1 \boldsymbol{I})
\mathcal{D}_1 = \{ ( \boldsymbol{x}_{i,1}, y_1(\boldsymbol{x}_{i,1}) ) ; i = 1, \dots, n_1\}
f_2(\boldsymbol{x}) \sim \mathcal{GP}(\boldsymbol{0}, \kappa_2(\boldsymbol{x}, \boldsymbol{x}'))
\boldsymbol{y}_2 \sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{K}_2 + \sigma^2_2 \boldsymbol{I})
\mathcal{D}_2 = \{ ( \boldsymbol{x}_{i,2}, y_2(\boldsymbol{x}_{i,2}) ) ; i = 1, \dots, n_2\}
MOGP Kernels
- Choose a cross-covariance function \( \operatorname{cov}[f_1(\boldsymbol{x}),f_2(\boldsymbol{x}')]\) such that \( \boldsymbol{K}_{\boldsymbol{f},\boldsymbol{f}}\) is a valid covariance matrix, i.e., positive semi-definite.
- Start with "separable" kernels where \(\boldsymbol{K}_{\boldsymbol{f},\boldsymbol{f}}\) is decomposed into submatrices.
\begin{bmatrix}
\boldsymbol{f}_1\\
\boldsymbol{f}_2
\end{bmatrix} \sim \mathcal{N}\left(\begin{bmatrix}\boldsymbol{0}\\ \boldsymbol{0} \end{bmatrix},
\begin{bmatrix}
\boldsymbol{K}_1 & \\
& \boldsymbol{K}_2
\end{bmatrix} +
\begin{bmatrix}
\sigma^2_1 \boldsymbol{I} & \boldsymbol{0} \\
\boldsymbol{0} & \sigma^2_2 \boldsymbol{I}
\end{bmatrix}\right)
\(\boldsymbol{K}_{\boldsymbol{f},\boldsymbol{f}}\)
?
?
Semiparametric Latent Factor Model (SLFM)
Fit each band as a linear combination of two latent GPs,
where \(d = 1,2,3,4\) output bands and \(q = 1,2\) latent processes
\begin{align*}
\begin{bmatrix}
\boldsymbol{f}_1\\
\boldsymbol{f}_2\\
\boldsymbol{f}_3\\
\boldsymbol{f}_4\\
\end{bmatrix} &=
\begin{bmatrix}
a_{1,1} & a_{1,2} \\
a_{2,1} & a_{2,2} \\
a_{3,1} & a_{3,2} \\
a_{4,1} & a_{4,2}
\end{bmatrix} \times
\begin{bmatrix}
u_1(\boldsymbol{x}) \\
u_2(\boldsymbol{x})
\end{bmatrix} =
\begin{bmatrix}
\boldsymbol{a}_1 & \boldsymbol{a}_2
\end{bmatrix} \times
\begin{bmatrix}
u_1(\boldsymbol{x}) \\
u_2(\boldsymbol{x})
\end{bmatrix}
\end{align*}
\boldsymbol{f}(\boldsymbol{x}) = \boldsymbol{a}_1 u_1 (\boldsymbol{x}) + \boldsymbol{a}_1 u_2 (\boldsymbol{x})
\begin{align*}
u_1(\boldsymbol{x}) &\sim \mathcal{GP}(\boldsymbol{0}, \kappa_1(x, x'))\\
u_2(\boldsymbol{x}) &\sim \mathcal{GP}(\boldsymbol{0}, \kappa_2(x, x'))
\end{align*}
f_d(\boldsymbol{x}) = \sum^4_q a_{d,q} u_q(\boldsymbol{x})
Alternatively,
Semiparametric Latent Factor Model (SLFM)
\begin{align*}
\boldsymbol{K}_{\boldsymbol{f},\boldsymbol{f}} &=
\begin{bmatrix}
\mathrm{cov}[f_1(\boldsymbol{x}), f_1(\boldsymbol{x'})] & \dots & \mathrm{cov}[f_1(\boldsymbol{x}), f_4(\boldsymbol{x'})]\\
\vdots & \ddots & \vdots \\
\mathrm{cov}[f_1(\boldsymbol{x'}), f_4(\boldsymbol{x})] & \dots & \mathrm{cov}[f_4(\boldsymbol{x}), f_4(\boldsymbol{x'})]
\end{bmatrix} \\
&= \sum^2_q \boldsymbol{a}_q \boldsymbol{a}_q^\top \otimes \kappa_q(\boldsymbol{x}, \boldsymbol{x}') \\
&= \sum^2_q \boldsymbol{B}_q \otimes \boldsymbol{K}_{f_q, f_q}
\end{align*}
Co-regionalisation Matrices
Kronecker product
Latent Process Model
\begin{align*}
[\boldsymbol{K}_{f_1, f_1}]_{i, j} &= \kappa_1(x, x'; \sigma_{\textrm{M32}}, \ell_{\textrm{M32}})\\
&= \sigma_\textrm{M32}^2 \left(1 + \sqrt{3}\frac{(x - x')^2}{\ell_\textrm{M32}}\right)\exp\left[-\sqrt{3}\frac{(x - x')^2}{\ell_\textrm{M32}}\right]
\end{align*}
\begin{gather*}
\sigma_\textrm{SE}, \sigma_\textrm{M32} \sim \mathcal{N}^+(0,1) \\
\ell_\textrm{SE}, \ell_\textrm{M32} \sim \mathrm{InvGamma}\left(\alpha = 3, \beta = \frac{1}{2} \times \lceil\textrm{range}(t)\rceil\right) \\
\ell_\textrm{SE}, \ell_\textrm{M32} > \textrm{min}(\Delta t) \\
\ell_\textrm{SE} > \ell_\textrm{M32} \\
\end{gather*}
Parameter model
u_1(\boldsymbol{x}) \sim \mathcal{GP}(\boldsymbol{0}, \kappa_1(x, x')) \qquad
u_2(\boldsymbol{x}) \sim \mathcal{GP}(\boldsymbol{0}, \kappa_2(x, x'))
\begin{gather*}
\sigma_{\textrm{M32}}, \sigma_{\textrm{SE}} \sim \mathcal{N}^+(0,1) \\
\ell_{\textrm{M32}}, \ell_{\textrm{SE}} \sim \mathrm{InvGamma}\left(\alpha = 3, \beta = \frac{1}{2} \times \lceil\textrm{range}(t)\rceil\right) \\
\ell_{\textrm{M32}}, \ell_{\textrm{SE}} > \textrm{min}(\Delta t) \\
\ell_{\textrm{SE}} > \ell_{\textrm{M32}} \\
\end{gather*}
[\boldsymbol{K}_{f_2, f_2}]_{i, j} = \kappa_2(x, x'; \sigma_{\textrm{SE}}, \ell_{\textrm{SE}}) = \sigma_{\textrm{SE}}^2 \exp\left\{ -\frac{(x - x')^2}{2\ell_{\textrm{SE}}^2}\right\}
Matern 3/2
Squared Exponential
Interested in the length scale hyperparameters \(\ell_{\textrm{M32}}\) and \(\ell_{\textrm{SE}}\)
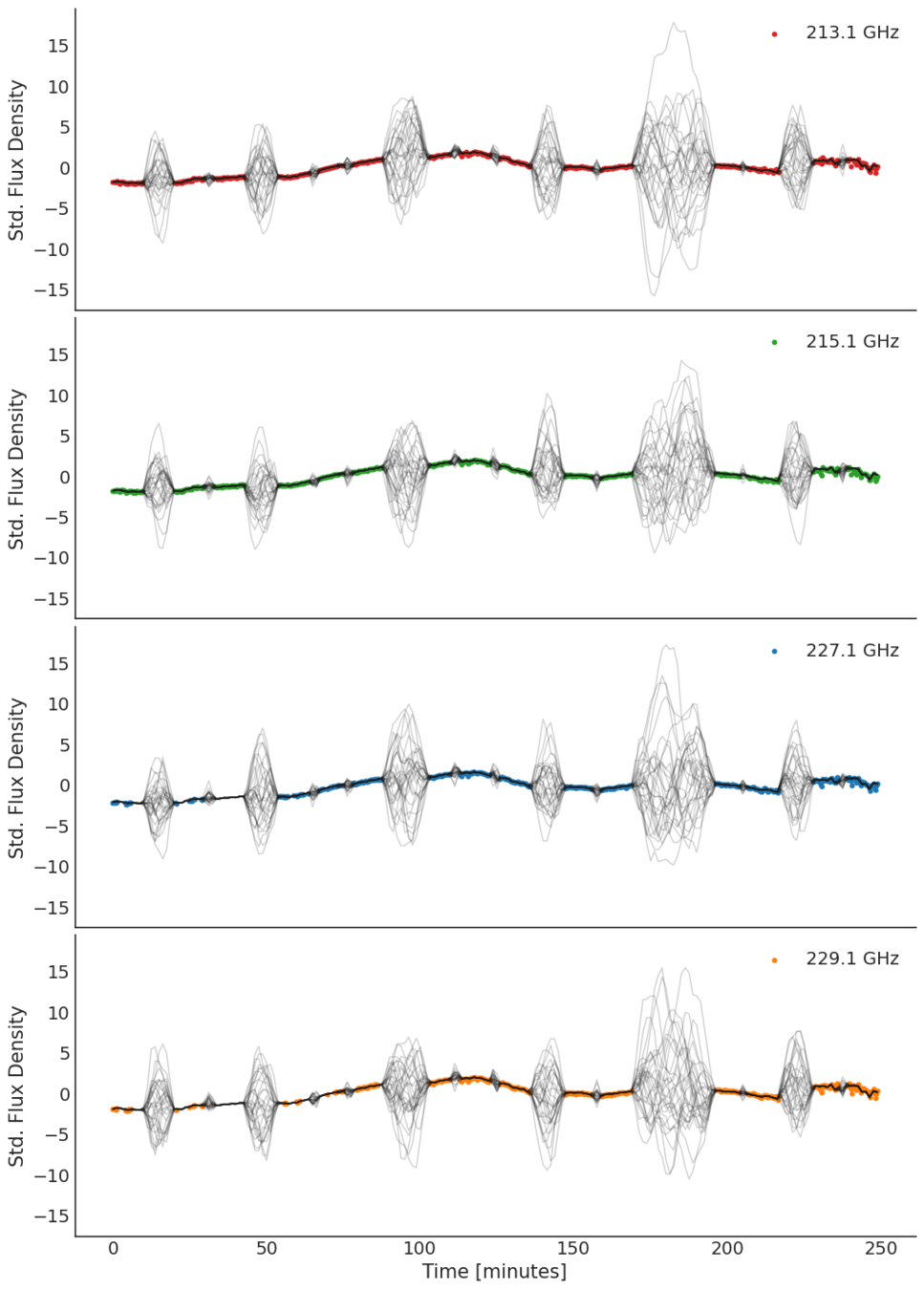
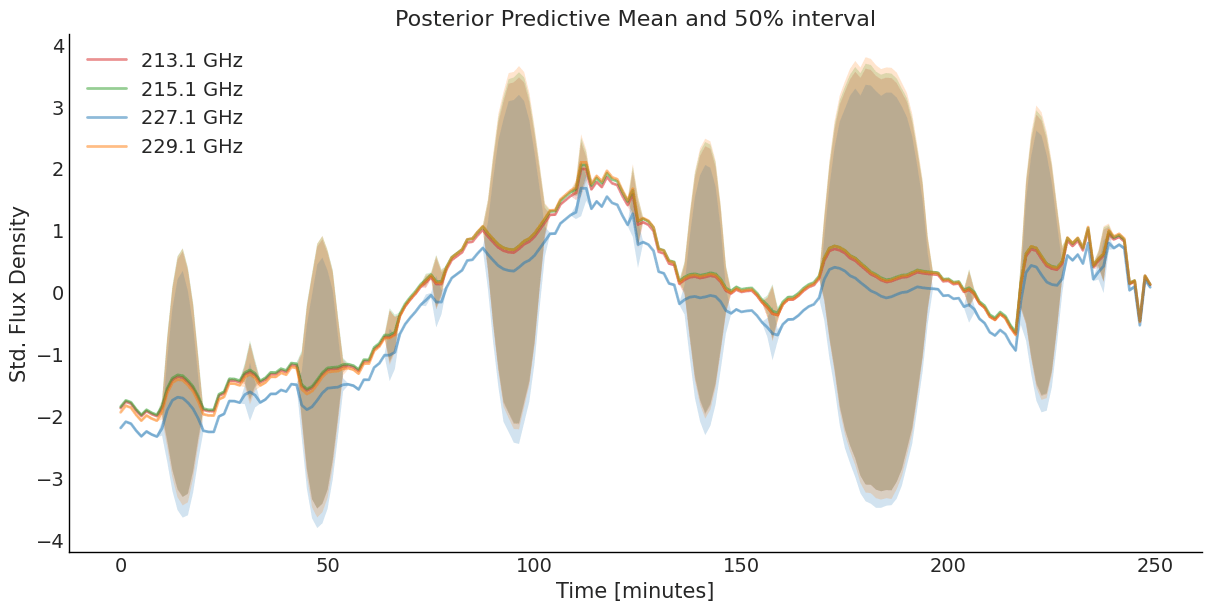
Four-band Light Curve
SLFM Fitting Result
\(\ell_{M32}\) = 7.20 minutes (94% HDI 4.32, 8.64)
\(\ell_{SE}\) = 33.1 minutes (94% HDI 27.4, 38.9)
NB: Fitted curves are perfectly aligned.
SLFM Result
\(\ell_{M32}\) = 7.23 minutes (94% HDI 5.04, 9.65)
\(\ell_{SE}\) = 25.6 minutes (94% HDI 18.9, 30.2)
NB: Fitted curves are perfectly aligned.
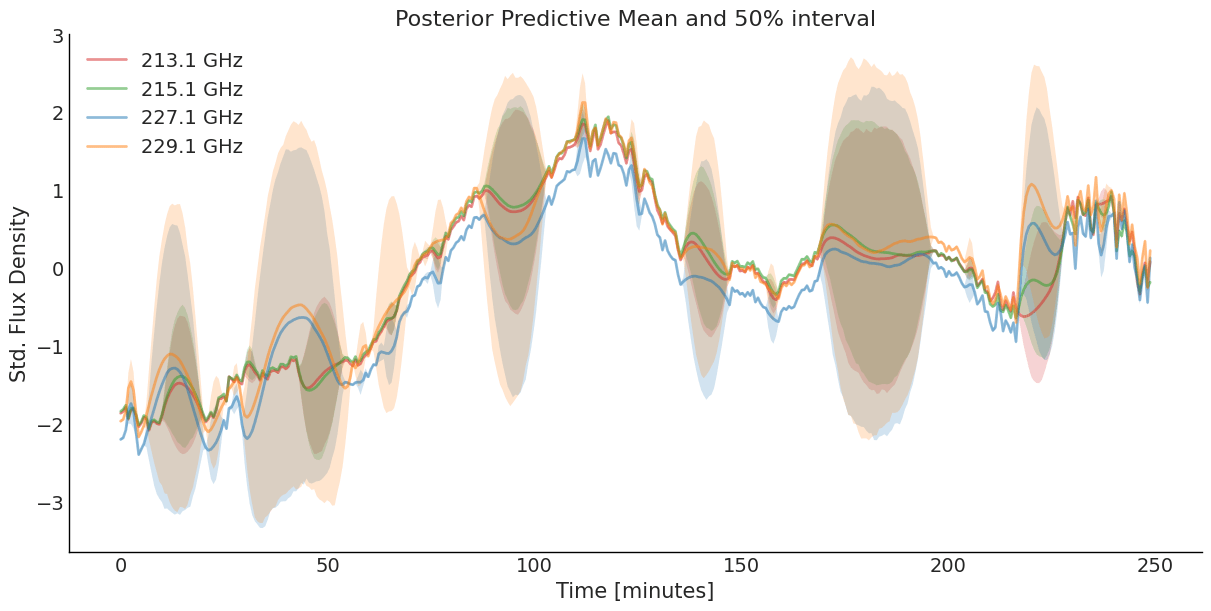
SLFM Fitting Result
\(\ell_{M32}\) = 7.20 minutes (94% HDI 4.32, 8.64)
\(\ell_{SE}\) = 33.1 minutes (94% HDI 27.4, 38.9)
NB: Fitted curves are perfectly aligned.
Naive Estimation of Band Delay
- Cross-correlation is a commonly used method to identify the lag between time series.
- But unevenly sampled data complicates this.
- Try resampling the data with a GP model and then compute cross-correlation between posterior predictive samples.
- Separable MOGPs obliterate time-delay information.
4-band
Light Curve
Fit 4 univariate GPs
Cross-correlation on posterior samples
Identify most likely time delay
Four Single-output GPs
\boldsymbol{K}_{\boldsymbol{f},\boldsymbol{f}} = \begin{bmatrix}
\boldsymbol{K}_1 & \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0} \\
\boldsymbol{0} & \boldsymbol{K}_2 & \boldsymbol{0} & \boldsymbol{0} \\
\boldsymbol{0} & \boldsymbol{0} & \boldsymbol{K}_3 & \boldsymbol{0} \\
\boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{K}_4
\end{bmatrix}
[\boldsymbol{K}_q]_{i, j} = \kappa_{q_\textrm{M32}}(x_i, x_j; \sigma_{q_\textrm{M32}}, \ell_{q_\textrm{M32}}) + \kappa_{q_\textrm{SE}}(x_i, x_j; \sigma_{q_\textrm{SE}}, \ell_{q_\textrm{SE}})
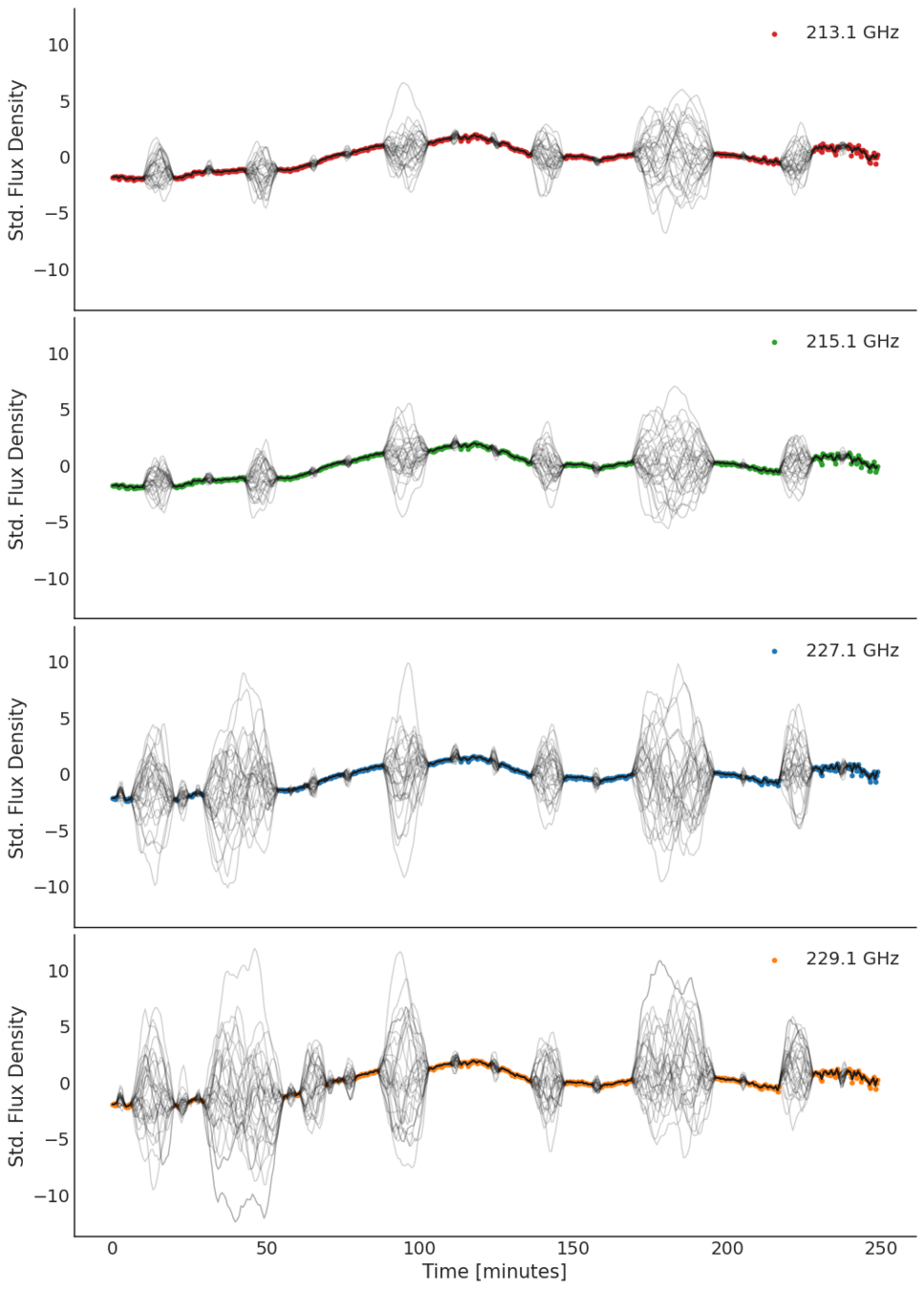
Four Single-output GPs
\boldsymbol{K}_{\boldsymbol{f},\boldsymbol{f}} = \begin{bmatrix}
\boldsymbol{K}_1 & \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0} \\
\boldsymbol{0} & \boldsymbol{K}_2 & \boldsymbol{0} & \boldsymbol{0} \\
\boldsymbol{0} & \boldsymbol{0} & \boldsymbol{K}_3 & \boldsymbol{0} \\
\boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{K}_4
\end{bmatrix}
[\boldsymbol{K}_q]_{i, j} = \kappa_{q_\textrm{M32}}(x_i, x_j; \sigma_{q_\textrm{M32}}, \ell_{q_\textrm{M32}}) + \kappa_{q_\textrm{SE}}(x_i, x_j; \sigma_{q_\textrm{SE}}, \ell_{q_\textrm{SE}})
Cross Correlation
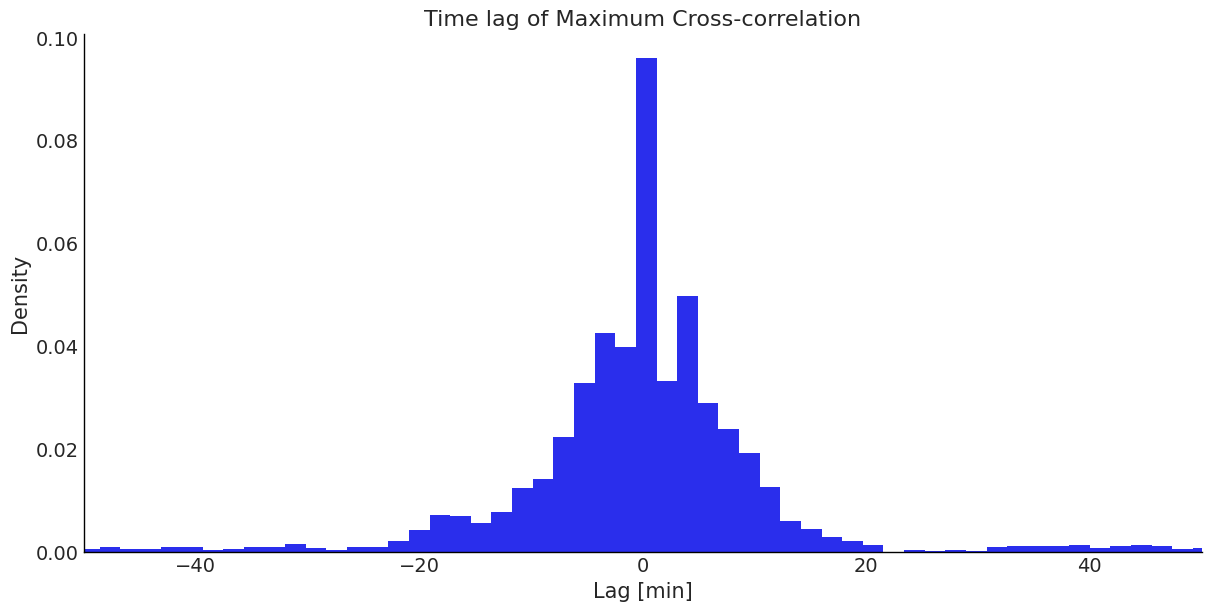
- Results are poor, most lags at zero.
- Model the time-delay term explicitly!
- Considering Spectral Mixture Kernel MOGPs
"Stop using computer simulations as a substitute for thinking"
Quantitude Podcast, Season 4, Episode 7
Summary
- Multi-band light curves of Sgr A* with different sampling rates.
- Tried using MOGP regression to characterise the:
- time scale of variation, and
- time delays between bands.
- Found two characteristic time scales: 7.2 and 33.1 minutes.
- Separable kernels cannot be used to model the cross-band time delays; need to parameterise these explicitly.
- Navigating the literature between astronomy, astrophysics, statistics, and machine learning, has been tricky.