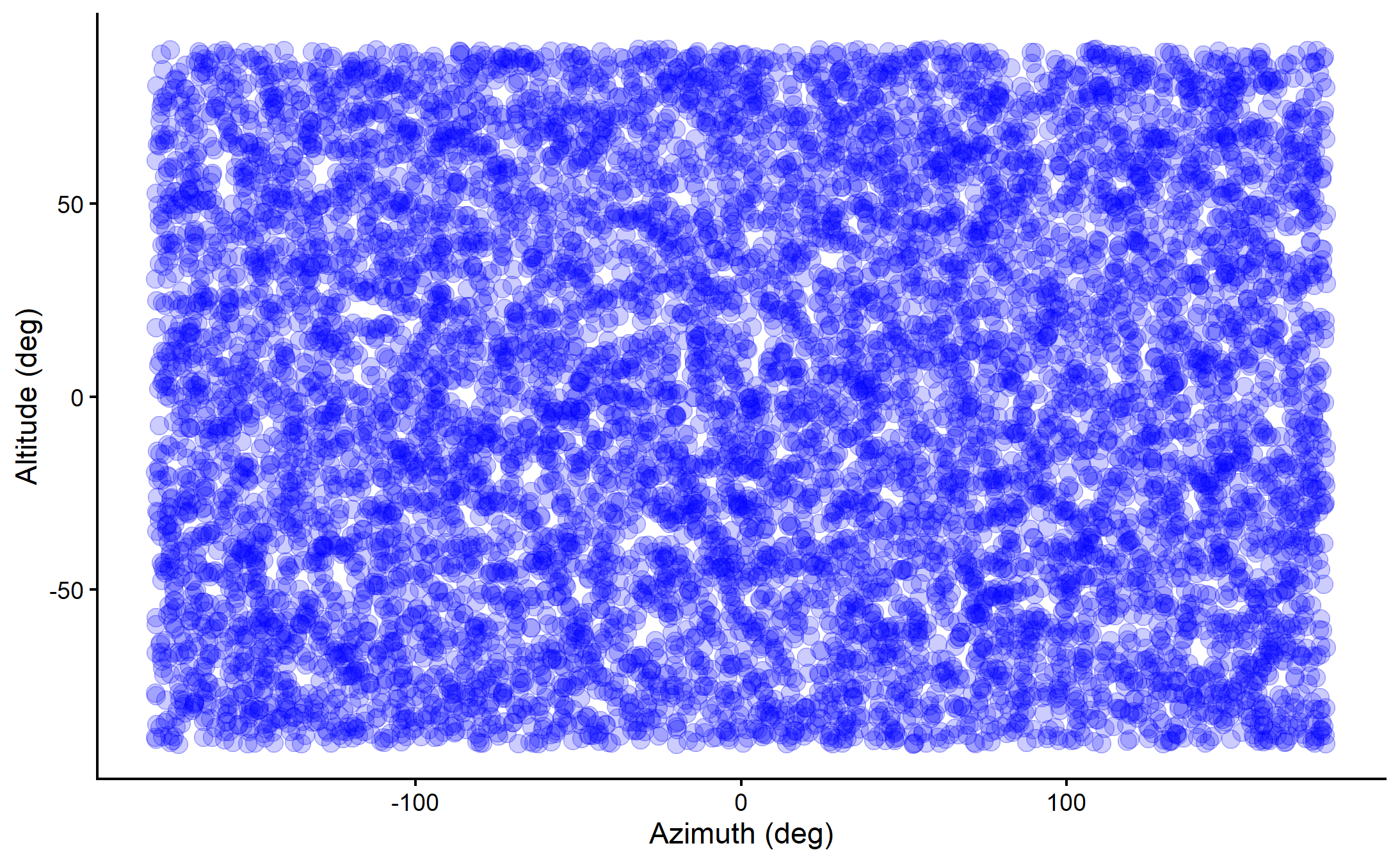
Uniform priors are not as uninformative as you might think

\(x\)

\(f_X(x)\)

shihching.fu@postgrad.curtin.edu.au

Conditional Probability

\mathrm{P}(B \mid A) = \frac{\mathrm{P}(A \cap B)}{\mathrm{P}(A)}

Probability of observing \(B\) given \(A\) has been observed.

\(A\)

\(\bar{A}\)

\(\mathrm{P}(A)\)

\(\mathrm{P}(\bar{A})\)

\(\mathrm{P}(B\mid A)\)

\(\mathrm{P}(\bar{B}\mid A)\)

\(\mathrm{P}(B\mid \bar{A})\)

\(A \cap \bar{B}\)

\(A \cap B\)

\(\bar{A} \cap \bar{B}\)

\(\bar{A} \cap B\)

\(\mathrm{P}(\bar{B}\mid A)\)

\mathrm{P}(A \cap B) = \mathrm{P}(A) \cdot \mathrm{P}(B \mid A)

Bayes' Theorem

\mathrm{P}(B \mid A) = \frac{\mathrm{P}(A \cap B)}{\mathrm{P}(A)}

\mathrm{P}(A \mid B) = \frac{\mathrm{P}(A \cap B)}{\mathrm{P}(B)}

\mathrm{P}(B \mid A) = \frac{\mathrm{P}(B) \cdot \mathrm{P}(A \mid B)}{\mathrm{P}(A)}

Probability of observing \(B\) given \(A\) has been observed, in terms of the probability of observing \(A\) if \(B\) is observed.

Bayesian Inference

Probability as a measure of "degree of belief".

\mathrm{P}(\mathrm{Hypothesis}\mid\mathrm{Data}) = \frac{\mathrm{P}(\mathrm{Hypothesis}) \cdot \mathrm{P}(\mathrm{Data} \mid \mathrm{Hypothesis})}{\mathrm{P}(\mathrm{Data})}

\mathrm{posterior} = \frac{\mathrm{prior} \times \mathrm{likelihood}}{\mathrm{normalising\; constant}} \propto \mathrm{prior} \times \mathrm{likelihood}

p(\theta \mid y) \propto p(\theta) \times p(y\mid \theta)

Example 1

Y \sim \mathcal{N}(\mu,.)

\mu \sim \mathcal{N}(0, 2^2)

\begin{align*} \bar{y} &= 3 \\ s &= 4 \\ n &= 10 \end{align*}

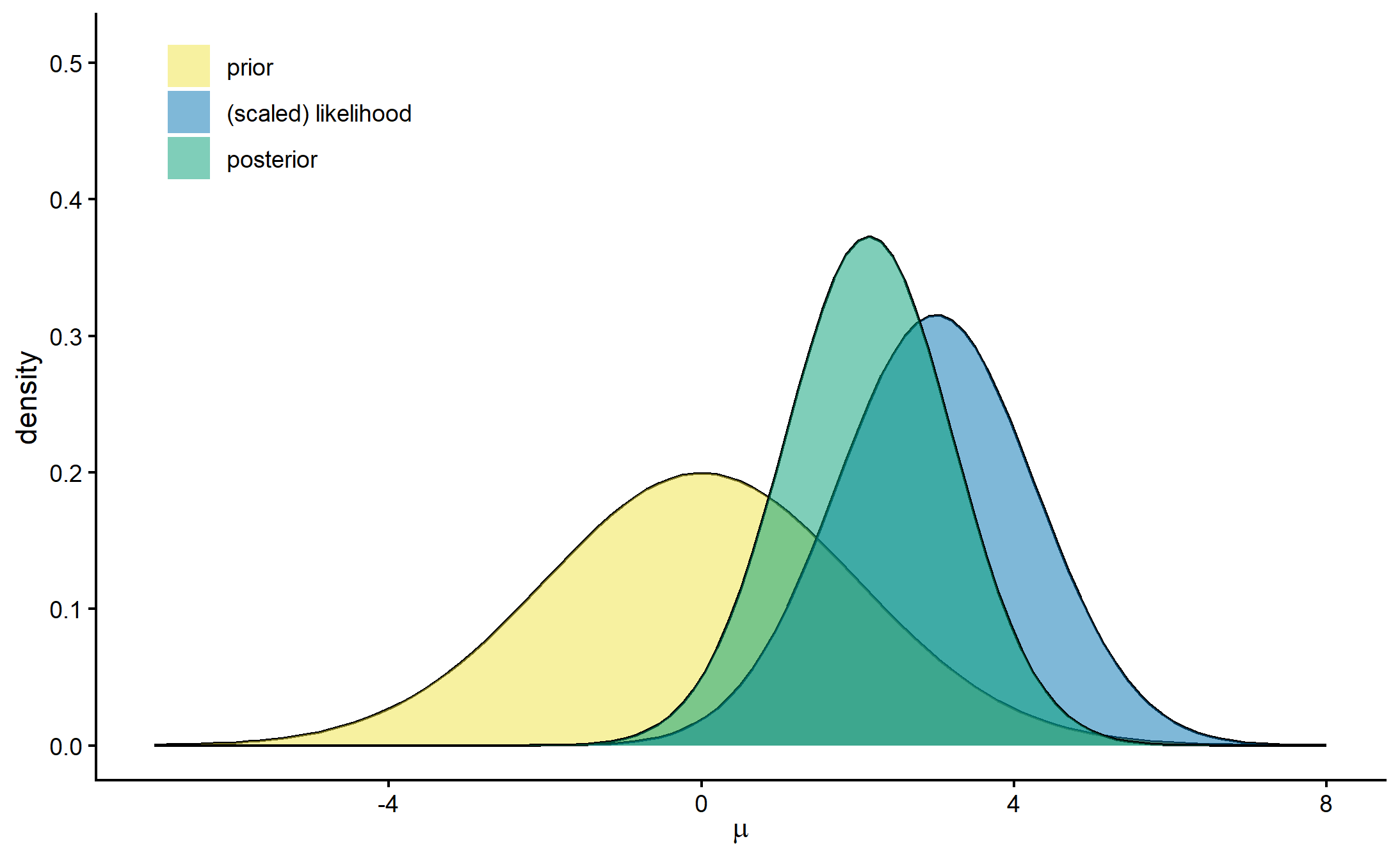
Likelihood

Prior

Observed data

Example 2

Y \sim \mathcal{N}(\mu,.)

\mu \sim \mathcal{N}(0, 1^2)

\begin{align*} \bar{y} &= 3 \\ s &= 4 \\ n &= 10 \end{align*}

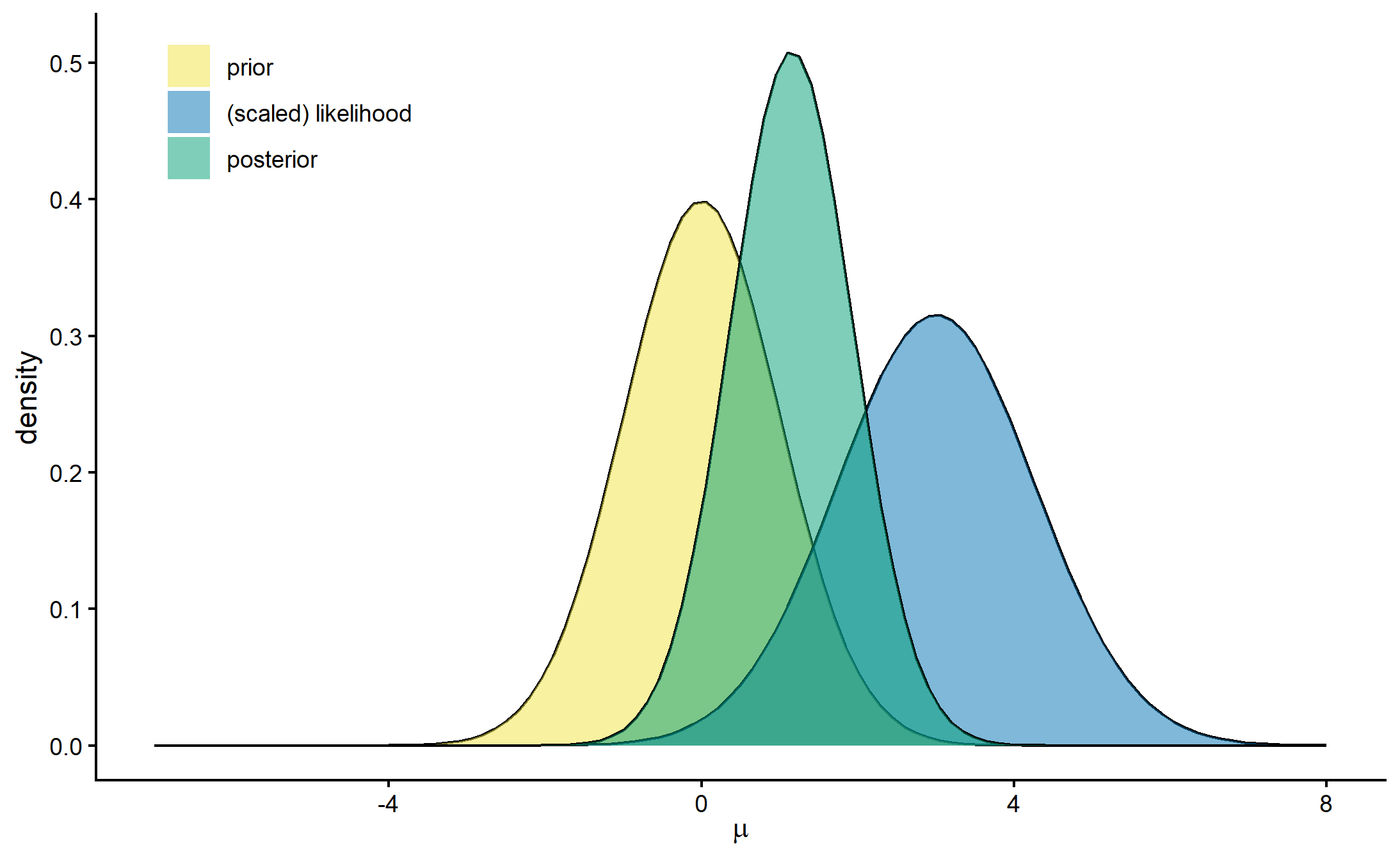
Likelihood

Prior

Observed data

The Prior Distribution

The distribution of the parameter of interest before any data is observed.
Can have a strong impact on the posterior estimate.
- Informative prior reflects having particular knowledge or information about the unknown parameter, e.g., typical range.
- Vague or diffuse prior reflects having little or uncertain information about the unknown parameter.

"Flat" Priors

A flat prior encodes the belief that all possible values of a parameter (perhaps within a range) are equally plausible.

\(x\)

\(f_X(x)\)

X \sim \mathrm{Uniform}[a,b]

Change of Coordinates

Altitude\(\quad\theta \sim \mathrm{Uniform}[-90^\circ, +90^\circ]\)

Azimuth\(\quad\phi \sim \mathrm{Uniform}[-180^\circ,+180^\circ]\)

Source: Wikipedia

Source: Wikimedia

Change of Coordinates

Altitude\(\quad\theta \sim \arccos(u),\quad u \sim \mathrm{Uniform}[-1, +1]\)

Azimuth\(\quad\phi \sim \mathrm{Uniform}[-180^\circ,+180^\circ]\)

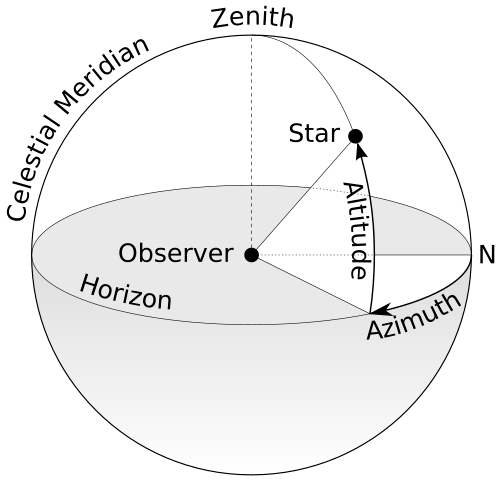
Source: Wikipedia

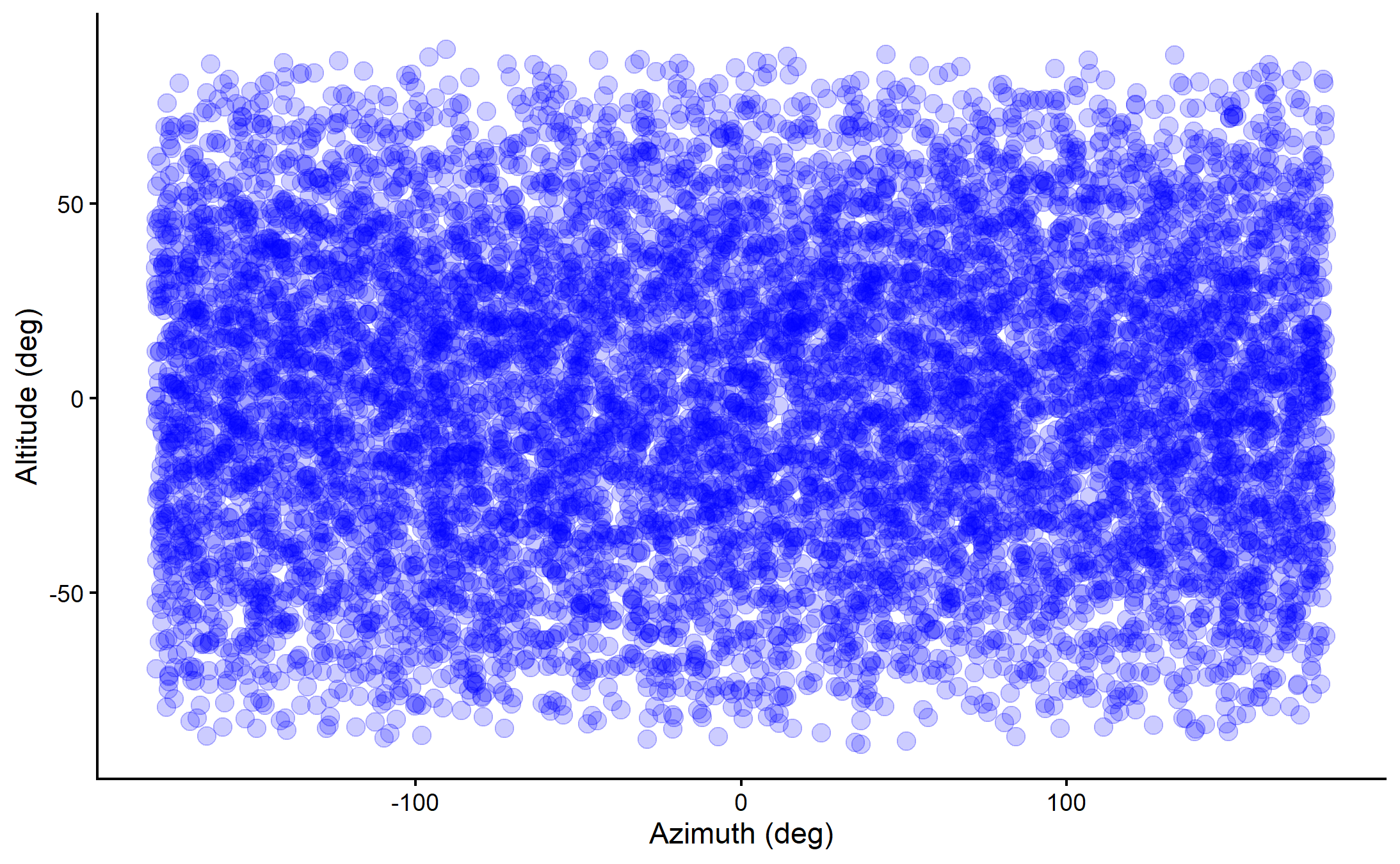
Source: Wikimedia

Hard Bounds

Hard bounds will completely exclude portions of the parameter space!
The support of the posterior distribution is inherited from the support of the prior distribution.

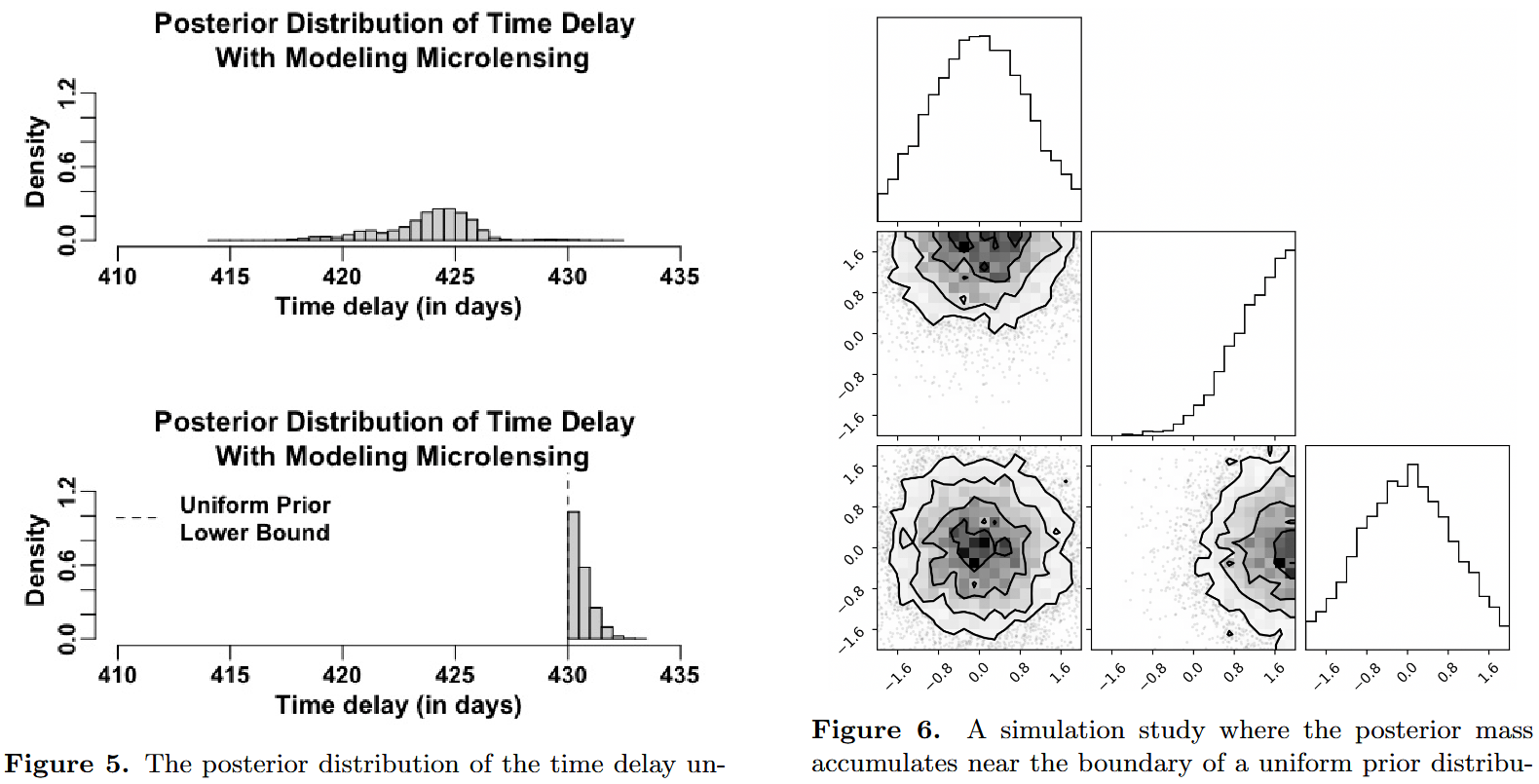
Source: Tak et al. (2024)

Change of Scale

\theta \sim \mathrm{Uniform}[10^{-3}, 10^1]

\log_{10}(\theta) \sim \mathrm{Uniform}[-3, 1]

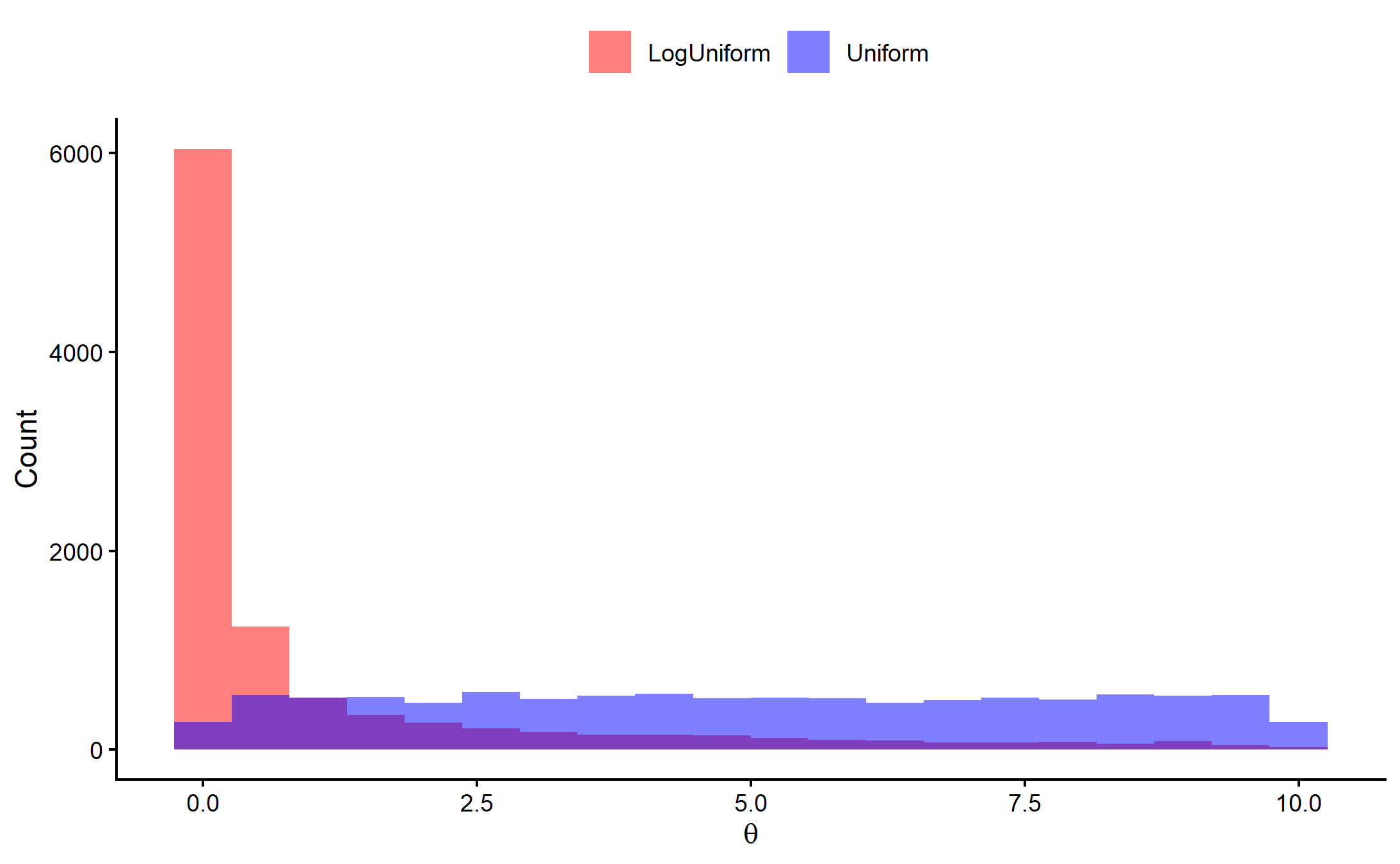
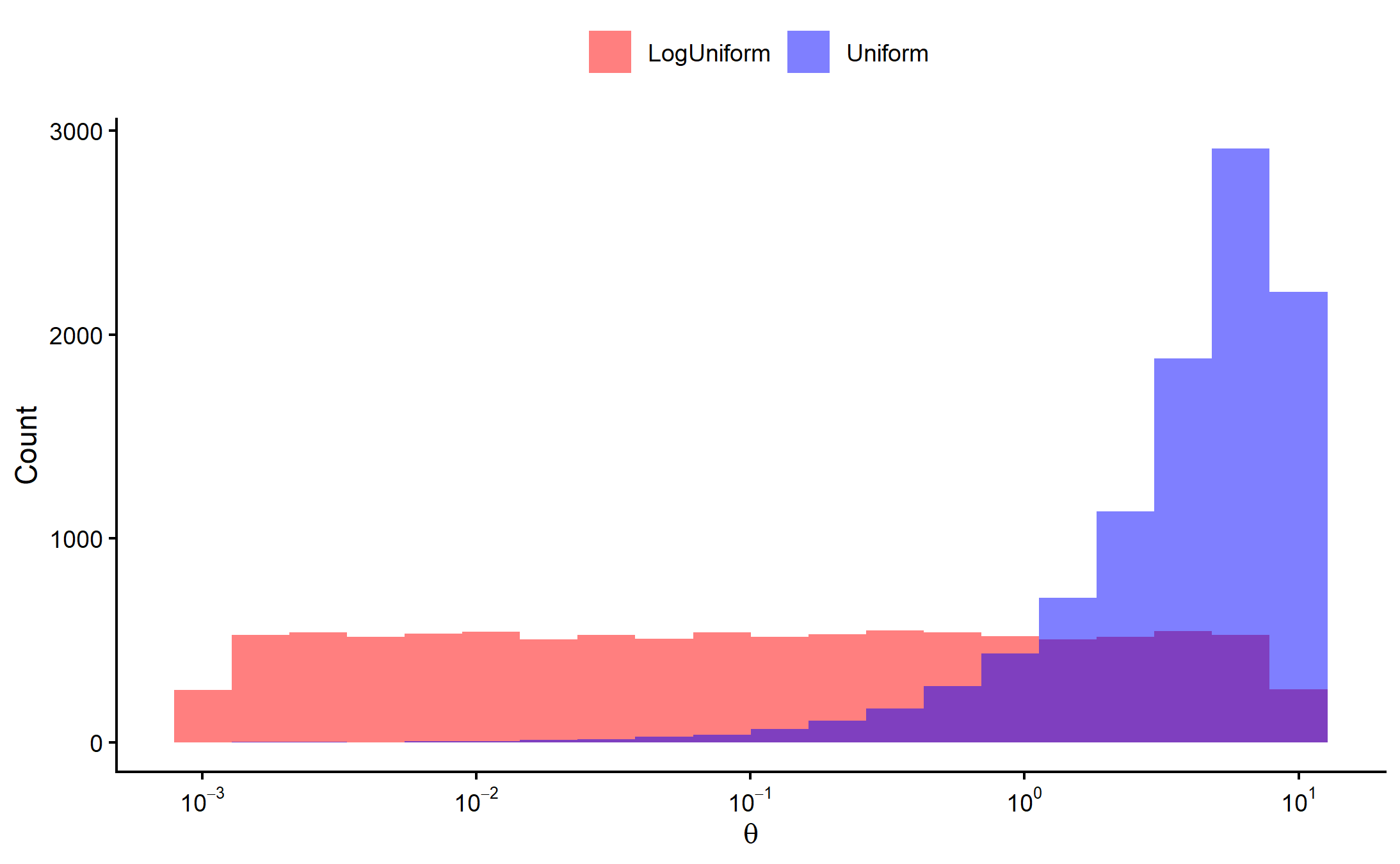
Text

Not the same!

General Advice

Diagnostics
- Prior predictive checks can reveal if parts of the parameter space are being overlooked.
- Scatter plot matrix of posteriors.
Remedies
- Apply an appropriate transformation to Uniform variates.
- Avoid hard boundaries, i.e., unbounded distributions with thin tails.
- Try Jeffreys Priors. These are non-informative prior distributions that are invariant under changes of coordinates for the parameter.

References

Tak, Hyungsuk, Yang Chen, Vinay L. Kashyap, et al. (2024) “Six Maxims of Statistical Acumen for Astronomical Data Analysis.” The Astrophysical Journal Supplement Series 275, no. 2 (2024): 30. https://doi.org/10.3847/1538-4365/ad8440.
Dogucu, Mine, Alicia A. Johnson, Miles Q. Ott (2021). Bayes Rules! An Introduction to Applied Bayesian Modeling. https://www.bayesrulesbook.com/.
Harold Jeffreys; An invariant form for the prior probability in estimation problems. Proc. A 1 September 1946; 186 (1007): 453–461. https://doi.org/10.1098/rspa.1946.0056