Applications of Grassmannians and Flag Manifolds
/ag23
this talk!
Aspects of Flag Manifolds with a View Towards Applications, July 11, 2023
Collaborators
Funding
National Science Foundation (DMS–2107700)
Simons Foundation (#709150 & #354225)
Florida State University
(The) Ohio State University
Johns Hopkins University
University of Georgia
Ochanomizu University
Kyoto University
Colorado State University
Université Paris-Saclay
Colorado State University
Flag Manifolds
Definition.
If \(V\) is an \(n\)-dimensional vector space and \(1 \leq d_1 < \dots < d_k = n\) is an increasing list of integers, then \(F\ell(d_1, \dots , d_k)\) is the flag manifold of nested linear subspaces \(\mathcal{S}_1 \subset \dots \subset \mathcal{S}_k = V\) with \(\dim(\mathcal{S}_i) = d_i\).
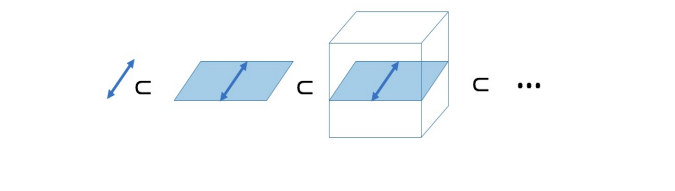
\(F\ell(d,n) = \operatorname{Gr}(d,V)\) is usually called the Grassmannian or Grassmann manifold of
\(d\)-dimensional subspaces of \(V\).
When \(d=1\), this is the projective space \(\mathbb{P}(V)\) of lines in \(V\).
Sometimes \(F\ell(n_1, \dots , n_k)\) where \(\sum_{j=1}^i n_j = d_i\).
Some Buzzwords Keywords
Flag manifolds are:
- Homogeneous Spaces (differential/Riemannian geometry)
- Projective Varieties (algebraic geometry)
- Coadjoint/Isotropy Orbits (Lie theory)
Applications of flag manifolds include:
Ye–Wong–Lim: flag manifolds are implicit in many tasks in numerical and statistical analysis, including mesh refinement, multiresolution analysis, and canonical correlation analysis.
Spectral Decomposition
\(A\) Hermitian, \(n \times n\).
with \(U\) unitary (i.e., \(U U^\ast = I_{n \times n}\)), and \(\Lambda = \text{diag}(\lambda_1, \dots , \lambda_n)\).
e.g., if \(\lambda_1 = \lambda_2 = 1\) and \(\lambda_3 = 0\), then \(\{u_1,u_2\}\) is an ONB for \(E_1\), \(\{u_3\}\) is an ONB for \(E_0\), but any other choice of ONBs would give a different valid \(U\).
What is unique is the flag \(E_1 \subset E_1 \oplus E_0\), which is a point in \(F\ell(2,3) = \operatorname{Gr}(2,\mathbb{C}^3)\).
Proposition.
For fixed \(\Lambda\), \(\{U \Lambda U^\ast : U \in U(n)\}\) is a flag manifold with signature determined by the multiplicities of the \(\lambda_i\).
Not unique!
Polymers and Polygons
A polymer in solution takes on an ensemble of random shapes, with topology as the unique conserved quantity.
Modern polymer physics is based on the analogy between a polymer chain and a random walk.
– Alexander Grosberg
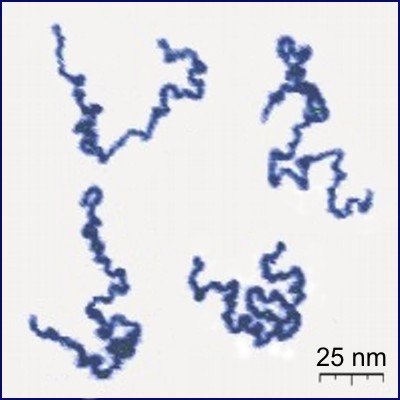
Protonated P2VP
Roiter/Minko
Clarkson University
Plasmid DNA
Alonso–Sarduy, Dietler Lab
EPF Lausanne
Polymers and Polygons
A polymer in solution takes on an ensemble of random shapes, with topology as the unique conserved quantity.
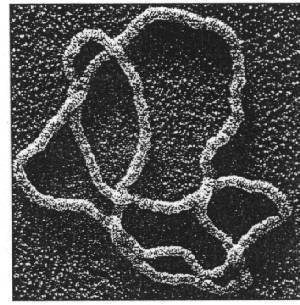
Knotted DNA
Wassermann et al.
Science 229, 171–174
Ansatz
Random polygon \(\Leftrightarrow\) Point in some (nice!) configuration space
Framework [with Deguchi and Cantarella]
By associating points in \(\operatorname{Gr}(2,\mathbb{C}^N)\) with piecewise-linear loops in \(\mathbb{R}^3\), get an \(E(3)\)-invariant representation. This was the first exactly-solvable model for loop random walks in \(\mathbb{R}^3\) with fixed scale.


Freely-Jointed Rings
Freely-jointed chain
\(\Longleftrightarrow\) point in \(\prod_{i=1}^N S^2 = \prod_{i=1}^N \mathbb{P}(\mathbb{C}^2)\)


Theorem [Kapovich–Millson, Hausmann–Knutson, with Cantarella]
Freely-jointed ring \(\Longleftrightarrow\) point in \(\prod_{i=1}^N \mathbb{P}(\mathbb{C}^2) /\!/SU(2) \simeq \operatorname{Gr}(2,\mathbb{C}^N)/\!/S(U(1)^N)\)
Algorithm [with Cantarella, Duplantier, and Uehara]
Sampling random freely-jointed rings in expected \(\Theta(N^{5/2})\) time.
Finite Frames
\(\mathbb{K} = \mathbb{R}\), \(\mathbb{C}\), or \(\mathbb{H}\). A (finite) frame in \(\mathbb{K}^d\) is a spanning set \(f_1, \dots, f_N \in (\mathbb{K}^d)^N\).

\(F = [f_1 \, f_2 \, \ldots \, f_N ] \in \mathbb{K}^{d \times N}\)
Data representation: \(\mathbb{K}^d \ni v \mapsto F^\ast v \in \mathbb{K}^N\) (the analysis operator).
Frames and Projectors
If \(\|f_i\|^2 = 1\) for all \(i\), the \(P_i := f_if_i^*\) are orthogonal projectors.
Unit-norm frames \(\Longleftrightarrow\) (certain) points in \(\prod_{i=1}^N \mathbb{P}(\mathbb{K}^d)\)
A frame is Parseval if \(v = \sum_i \langle f_i, v \rangle f_i = FF^\ast v\) for all \(v \in \mathbb{K}^d\).
i.e., \(FF^\ast = I_{d \times d}\), or equivalently \(F^\ast F\) is a rank-\(d\) orthogonal projector.
Parseval frames \(\Longleftrightarrow\) points in \(\operatorname{Gr}(d,\mathbb{K}^N)\).
In general, specifying the \(\|f_i\|^2\) determines a product of scaled projective spaces.
In general, specifying the spectrum of \(FF^\ast\) (or \(F^\ast F\)) determines a flag manifold.
Consequences
Generalized Frame Homotopy Theorem [with Needham]
The space of frames in \(\mathbb{C}^d\) (or \(\mathbb{H}^d\)) with any specified \(\|f_i\|^2\) and any specified spectrum of \(FF^\ast\) is always path-connected.
Theorem [with Needham]
In the above spaces, either there are no frames with full spark (i.e., full Kruskal rank), or the full spark frames have full measure.
Theorem [with Mixon, Needham, and Villar]
In the space of unit-norm frames, every full spark frame flows by gradient descent to a unit-norm\(^\ast\) Parseval frame. (And similarly for fusion frames.)
\(^\ast\) For technical reasons, actually equal-norm, not unit-norm.
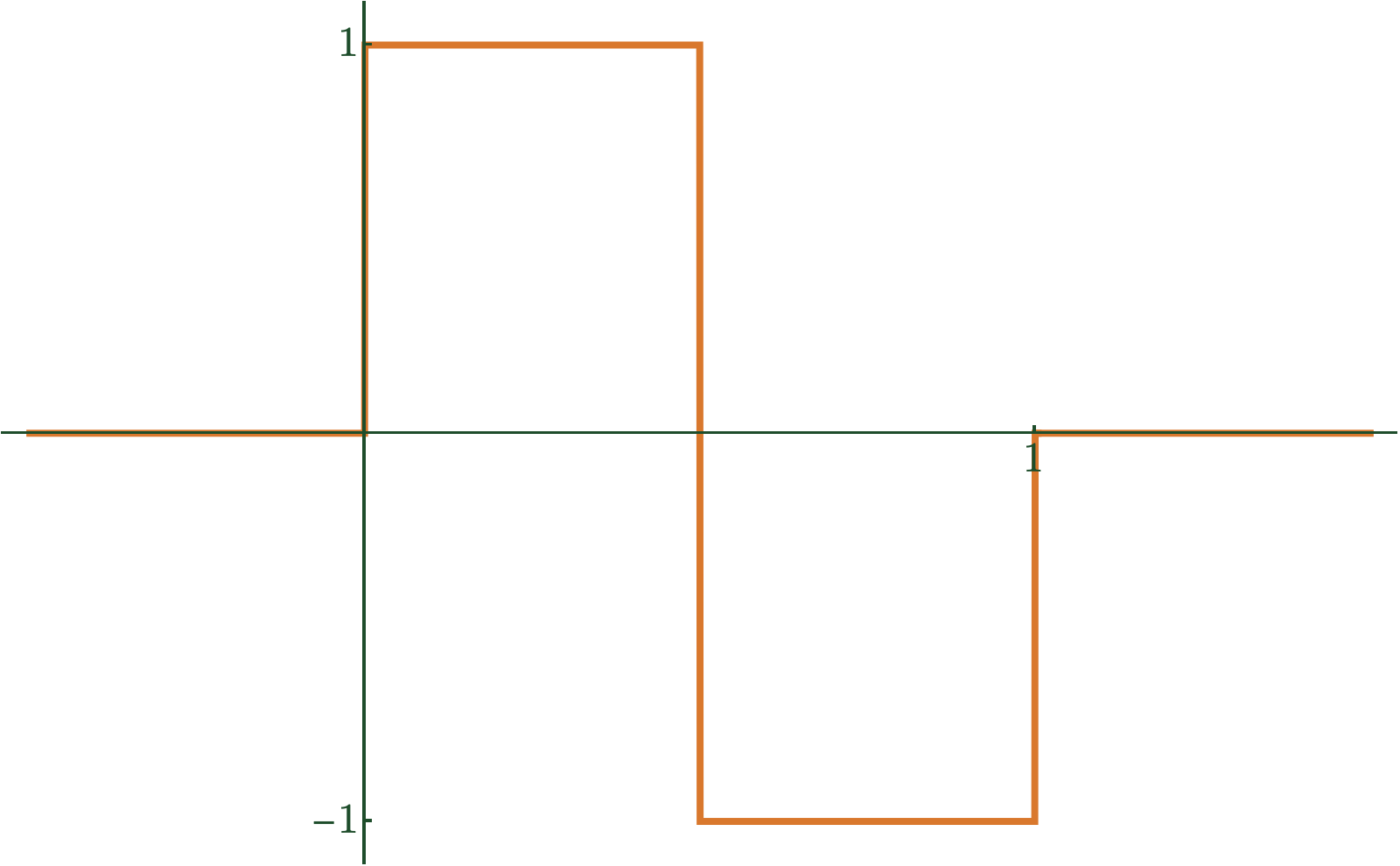
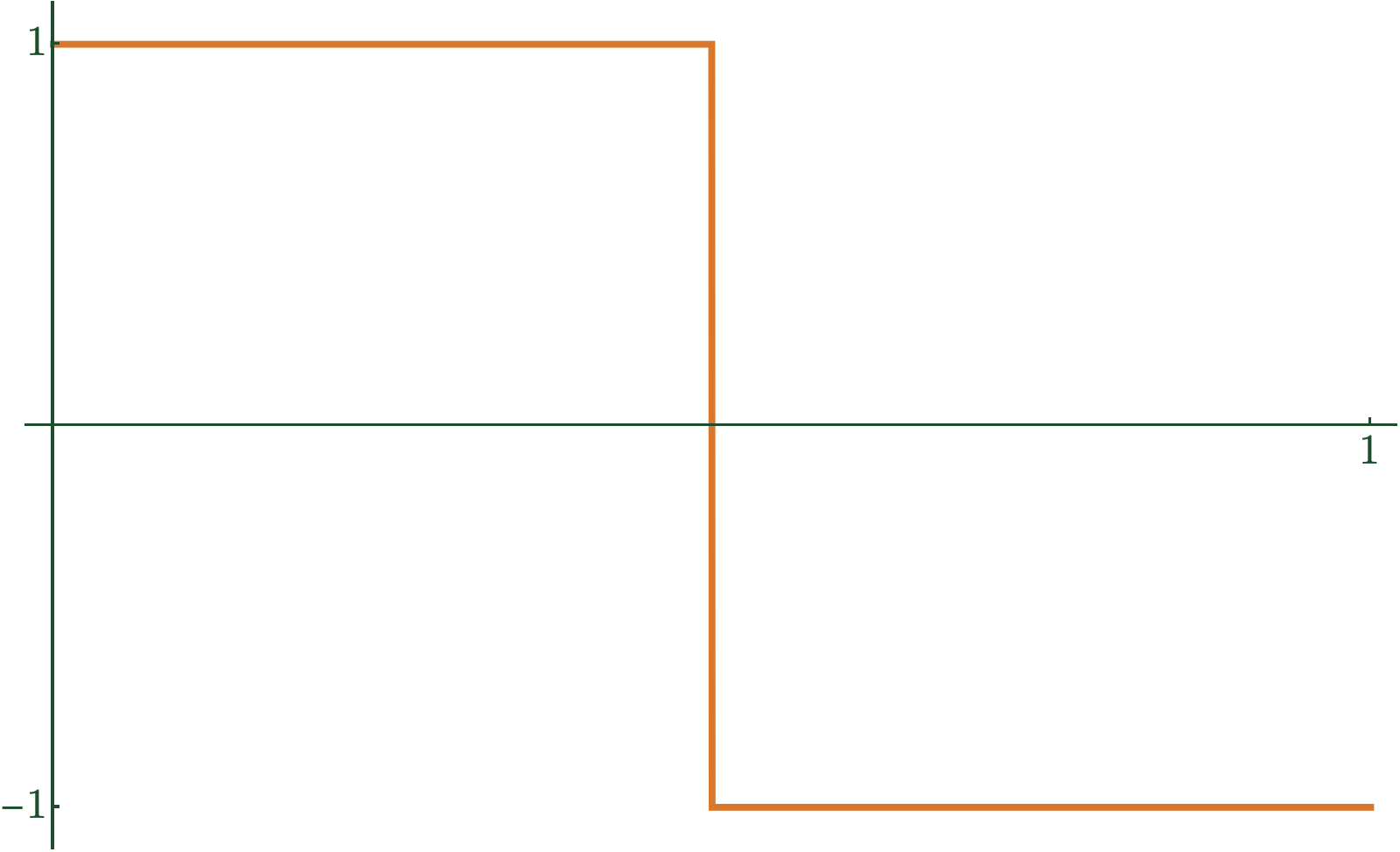
\(\psi(t)\)
Haar Wavelet
\(\psi_{n,k}(t) := 2^{n/2}\psi(2^n t - k)\)
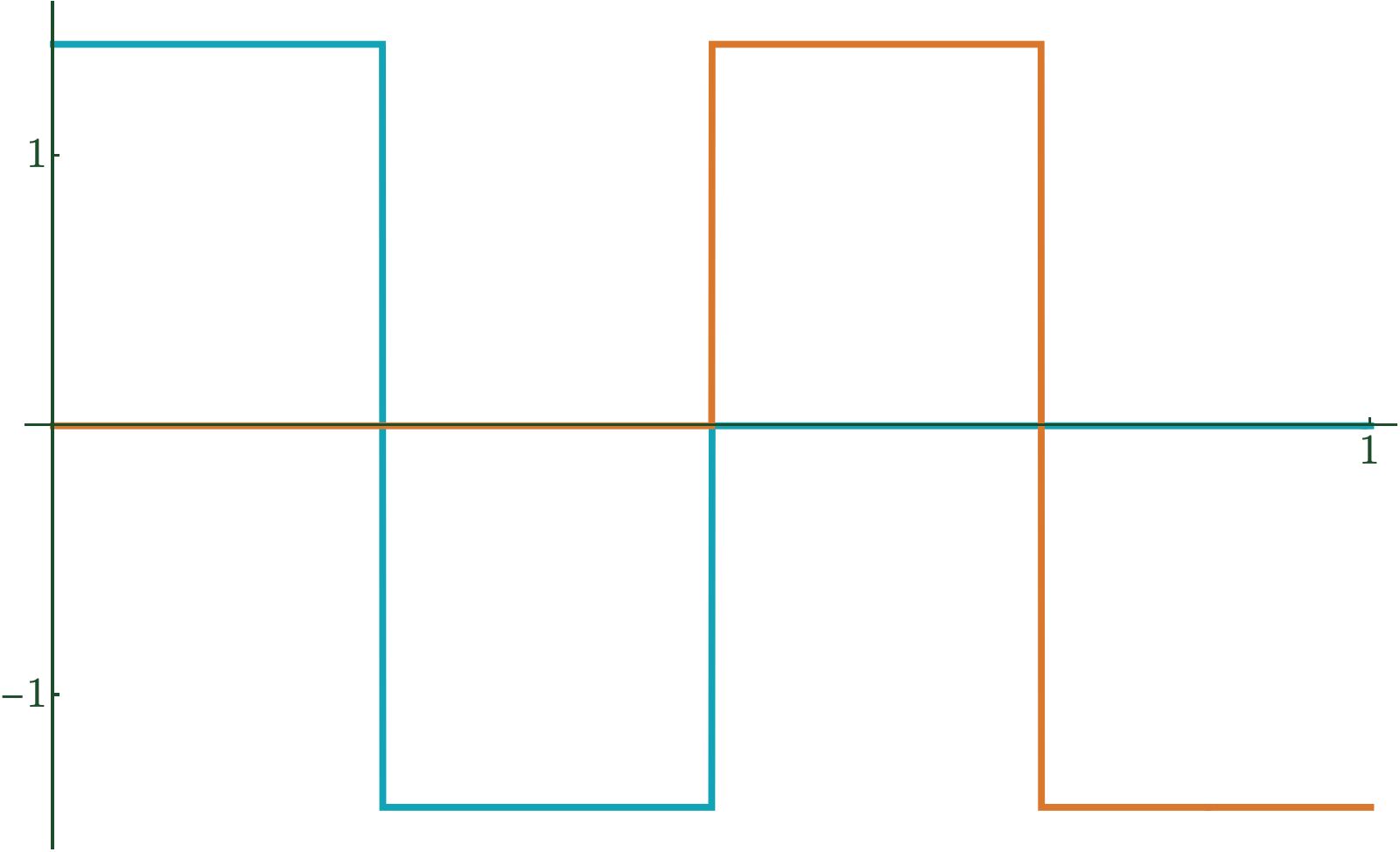
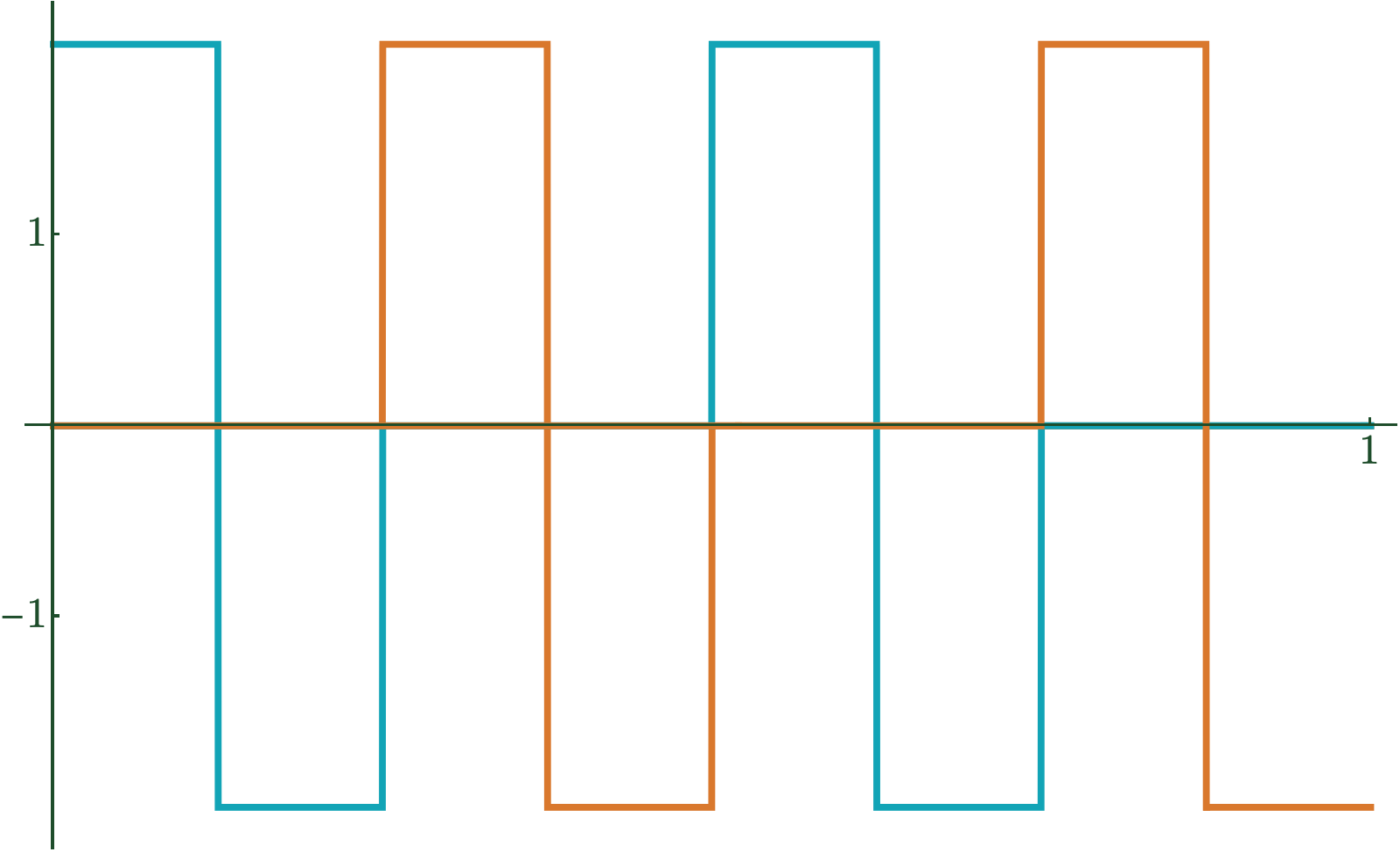
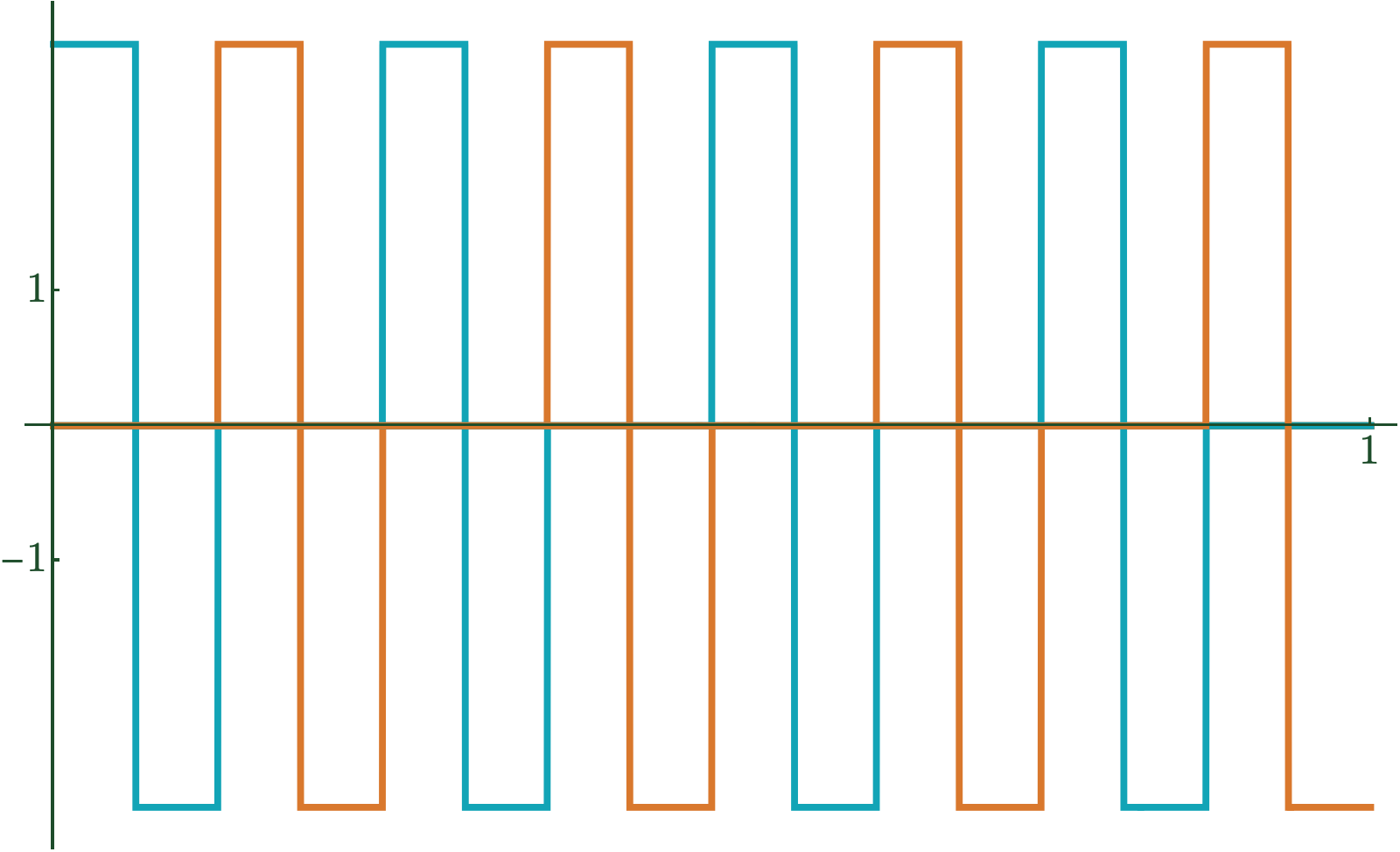

Wavelets and Projections
\(P_i(2n) = D_i(2n) D_i^T(2n)\)
\(2m \times 2n\) matrix \(A \mapsto P_i(2m) A P_j(2n)\)
\(\updownarrow\)
\(\mathcal{S} \in \operatorname{Gr}(n,\mathbb{R}^{2n})\)

\(D_2\)
\(D_4\)
Random
Daubechies Wavelet Projection


\(D_2\)

\(D_{24}\)
Daubechies Wavelet Projection
Theorem [with Collery and Peterson]
The Daubechies wavelets all live in a totally geodesic Schubert cycle in the Grassmannian.
Thank you!
Key References
Probability theory of random polygons from the quaternionic viewpoint
Jason Cantarella, Tetsuo Deguchi, and Clayton Shonkwiler
Communications on Pure and Applied Mathematics 67 (2014), no. 10, 1658–1699
Toric symplectic geometry and full spark frames
Tom Needham and Clayton Shonkwiler
Applied and Computational Harmonic Analysis 61 (2022), 254–287