Random Walks are Almost Closed
or
Loop Closure is Surprisingly Non-Destructive
/cta18
This talk!
Modern polymer physics is based on the analogy between a polymer chain and a random walk.
– Alexander Grosberg
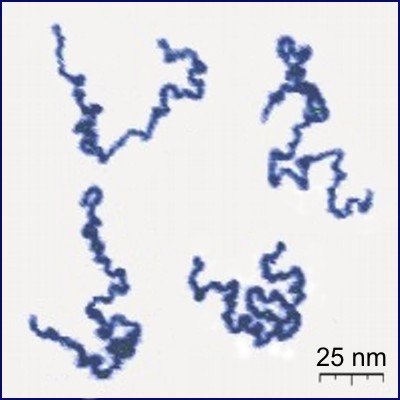
Protonated P2VP
Roiter/Minko
Clarkson University
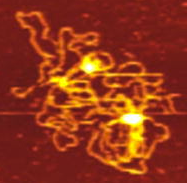
Plasmid DNA
Alonso–Sarduy, Dietler Lab
EPF Lausanne
Random walks
Is it almost closed?

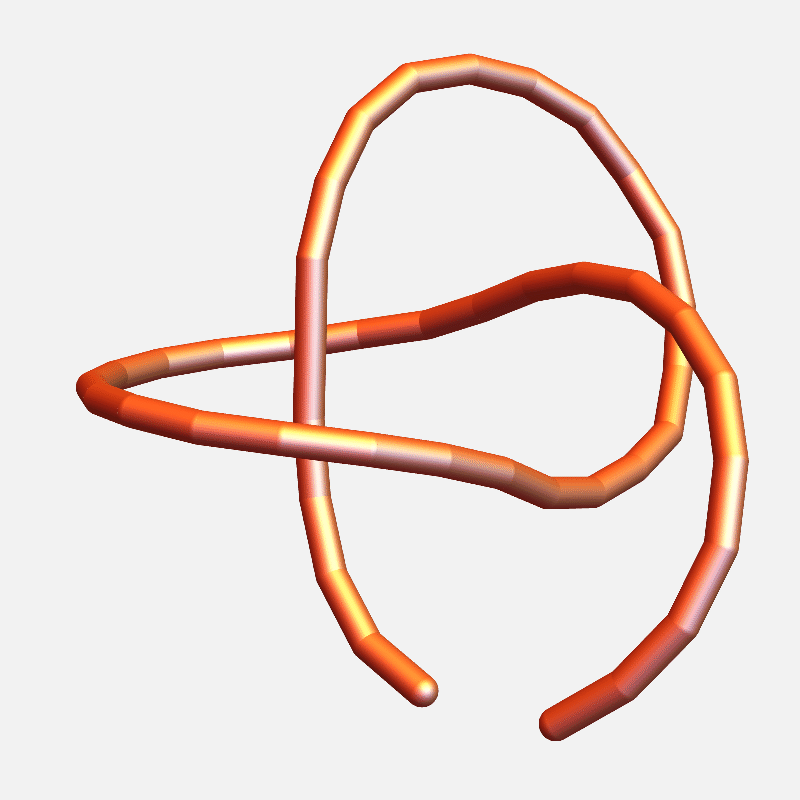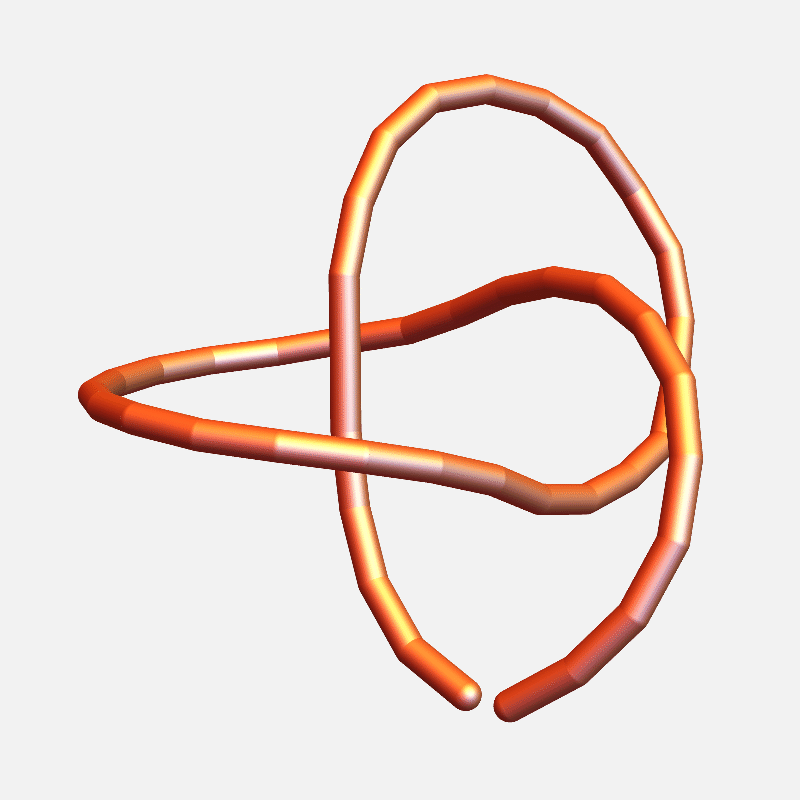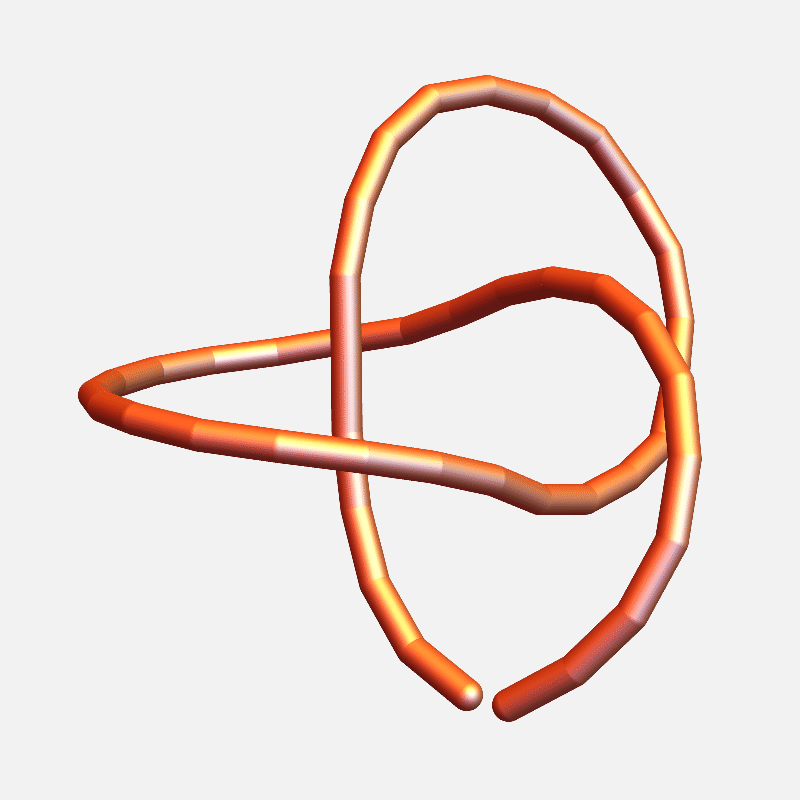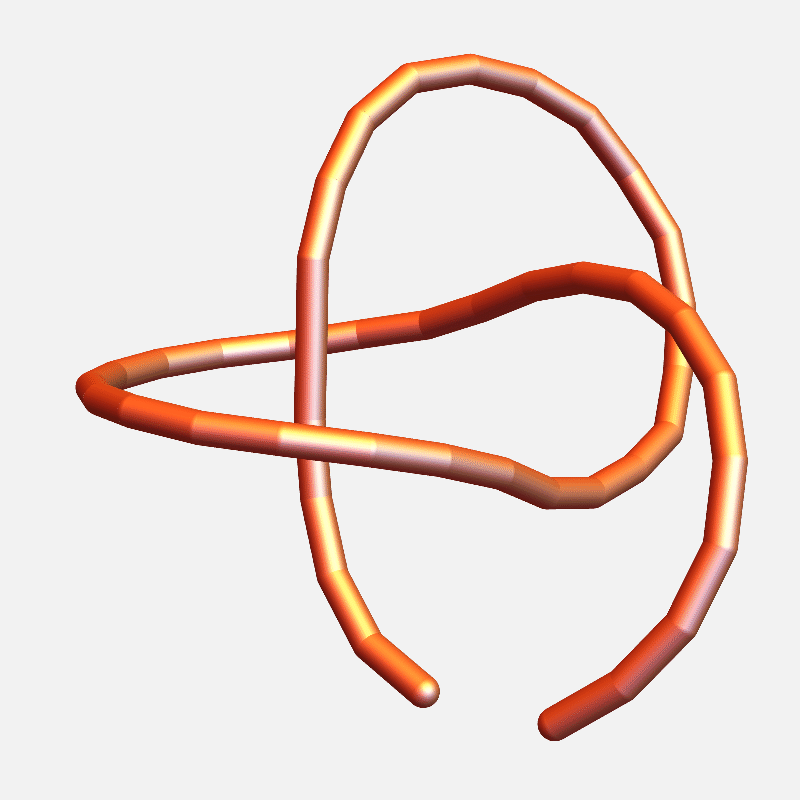



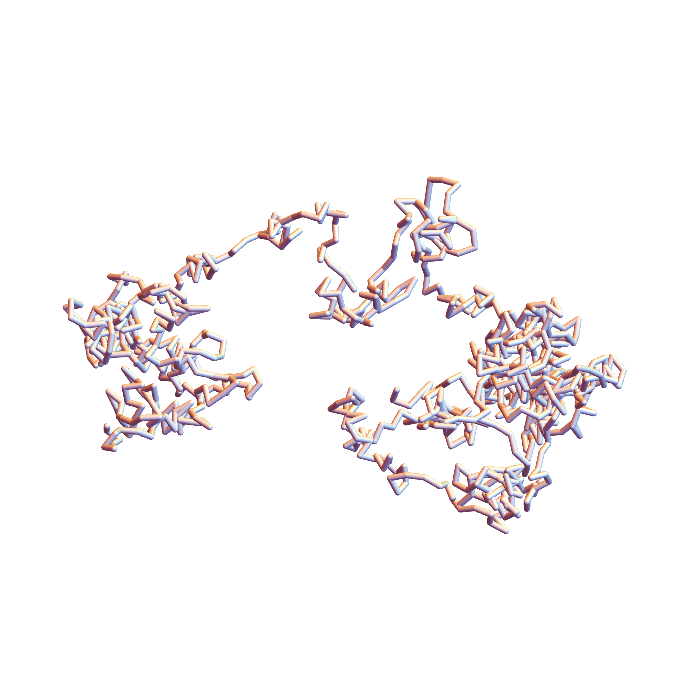
1QMG – Acetohydroxyacid isomeroreductase
Most random walks are almost closed(?)
Suppose \(e_1,\ldots , e_n\) are the edges of a random walk in \(\mathbb{R}^d\).
By Chernoff’s inequality,
Fixing edgelengths is trickier

end-to-end distance: 16.99
distance to closed: 5.64
end-to-end distance: 17.76
distance to closed: 0.68
Distance to a closed equilateral polygon
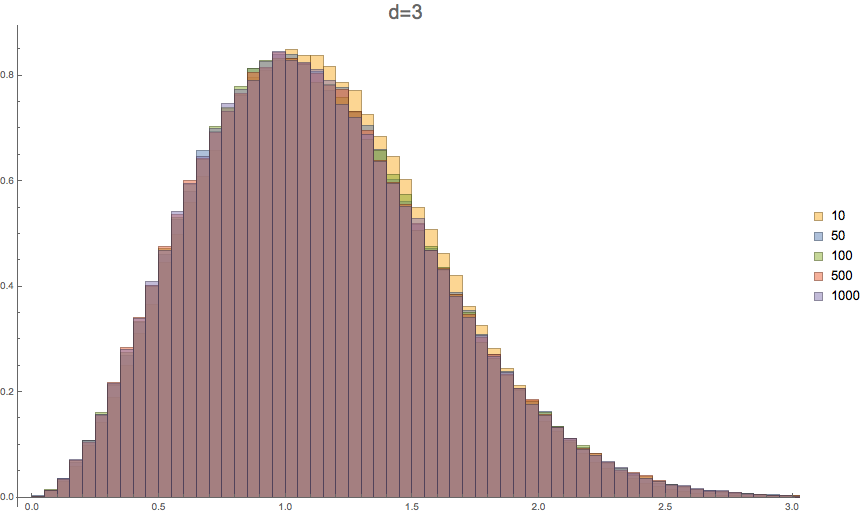
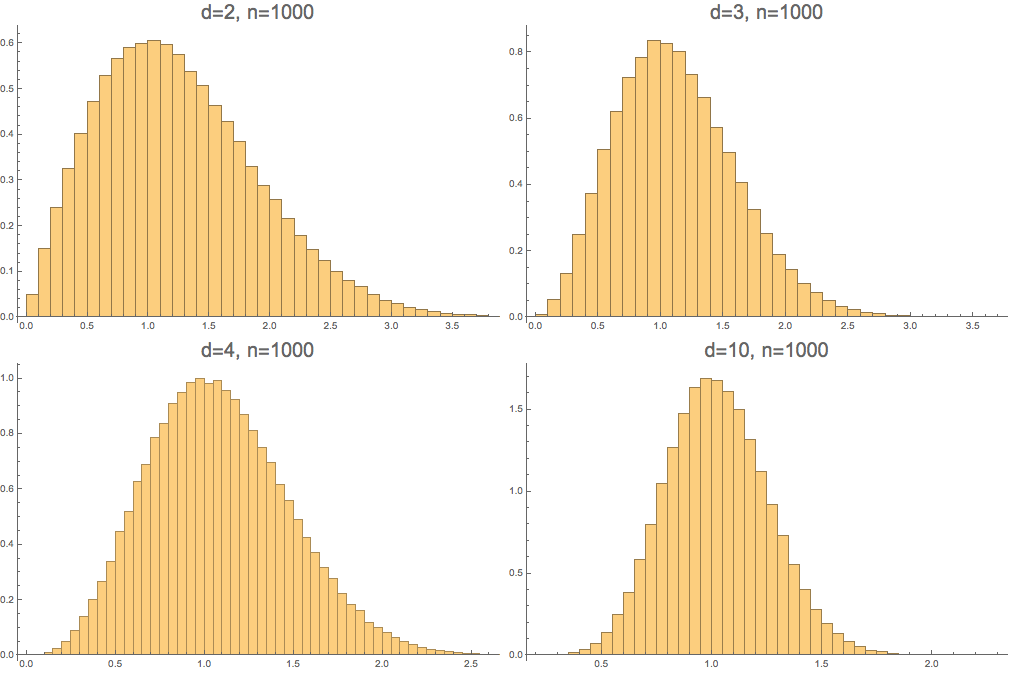
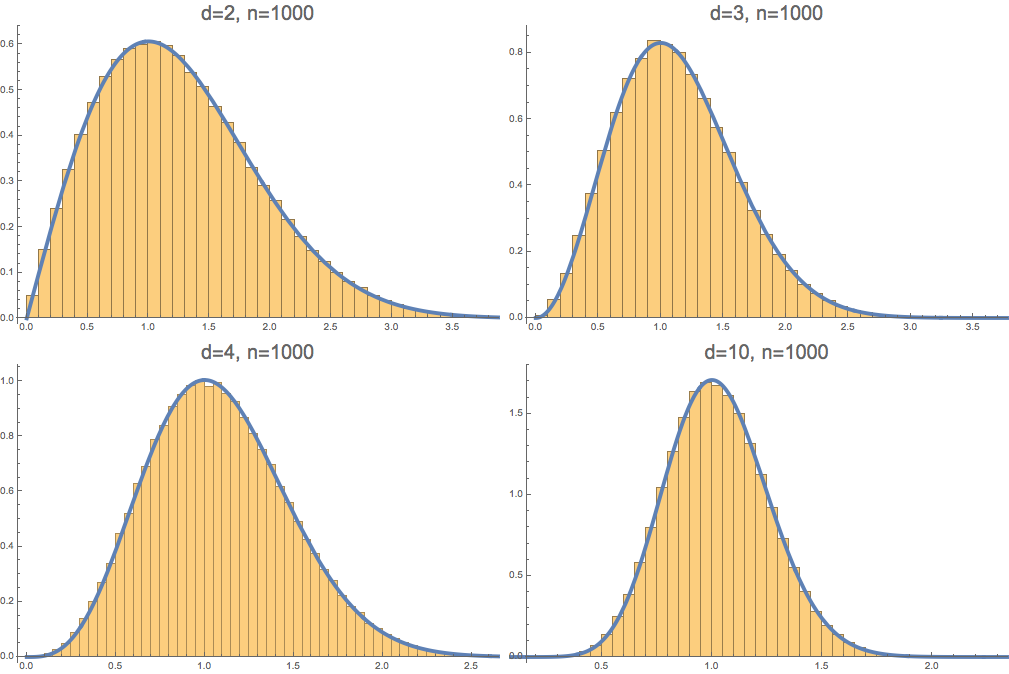
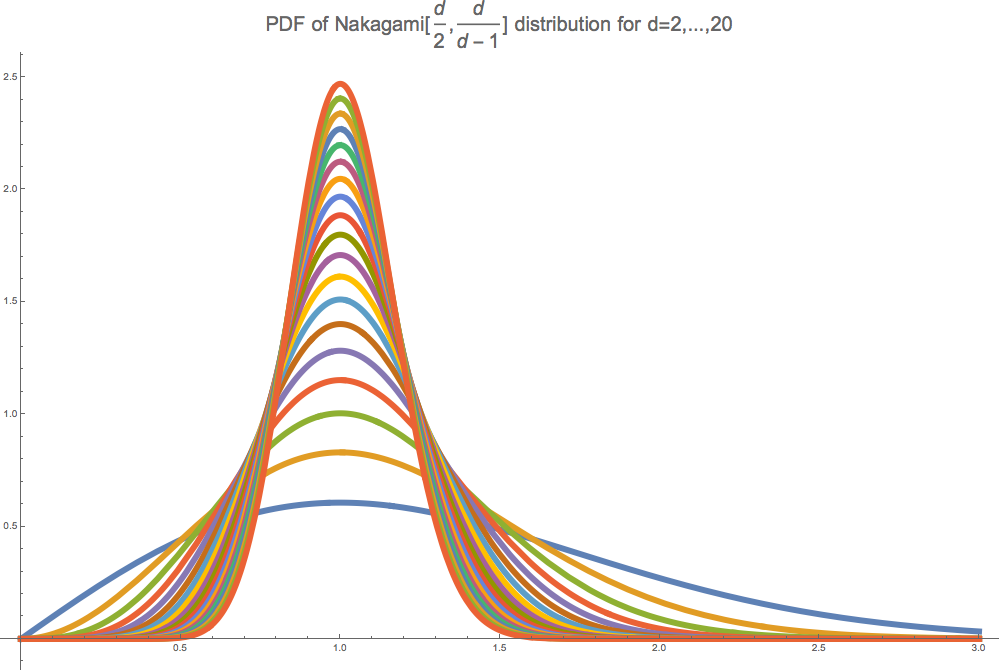
Proposition. As \(n \to \infty\), distance to the closest polygon to a random walk in \(\mathbb{R}^d\) converges in distribution to a Nakagami\(\left(\frac{d}{2},\frac{d}{d-1}\right)\) distribution.
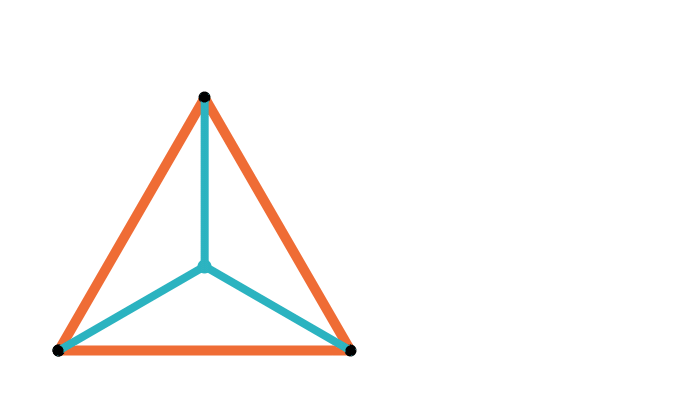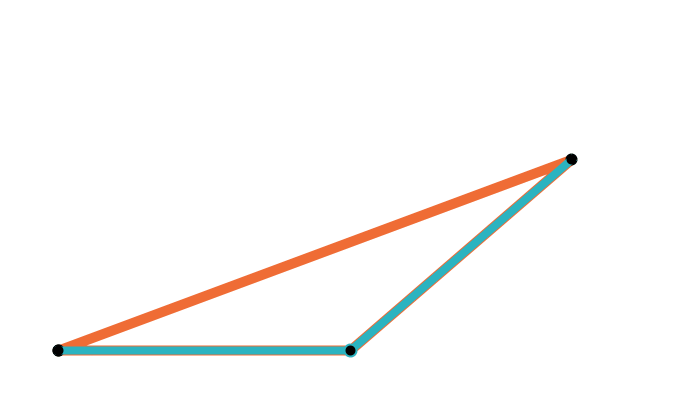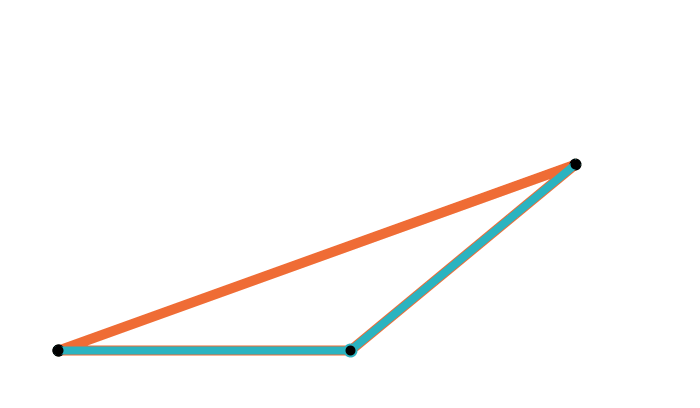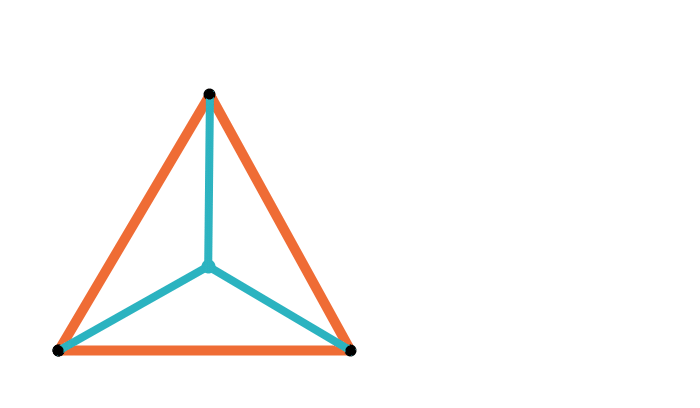
The geometric median
Definition
A geometric median (or Fermat-Weber point) of a collection \(X=\{x_1,\ldots , x_n\}\) of points in \(\mathbb{R}^d\) is any point closest to the \(x_i\):
\(\text{gm}(X)=\text{argmin}_y \sum \|x_i-y\|\)
Definition
A point cloud has a nice geometric median if:
- \(\text{gm}(X)\) is unique (\(\Leftarrow X\) is not linear)
- \(\text{gm}(X)\) is not one of the \(x_i\)
Geometric median of a triangle
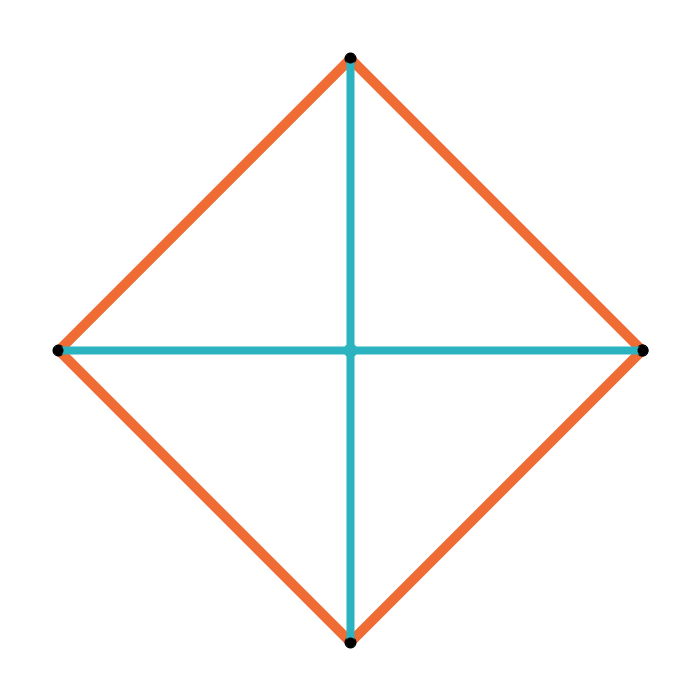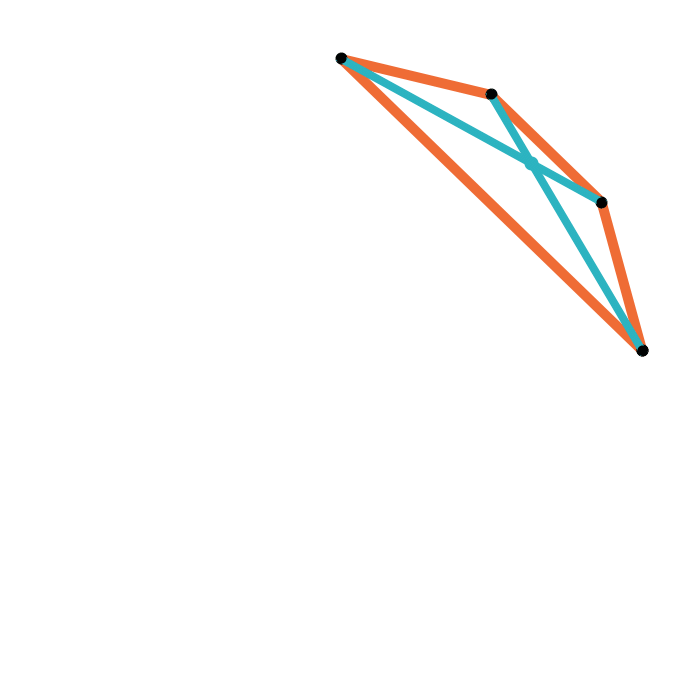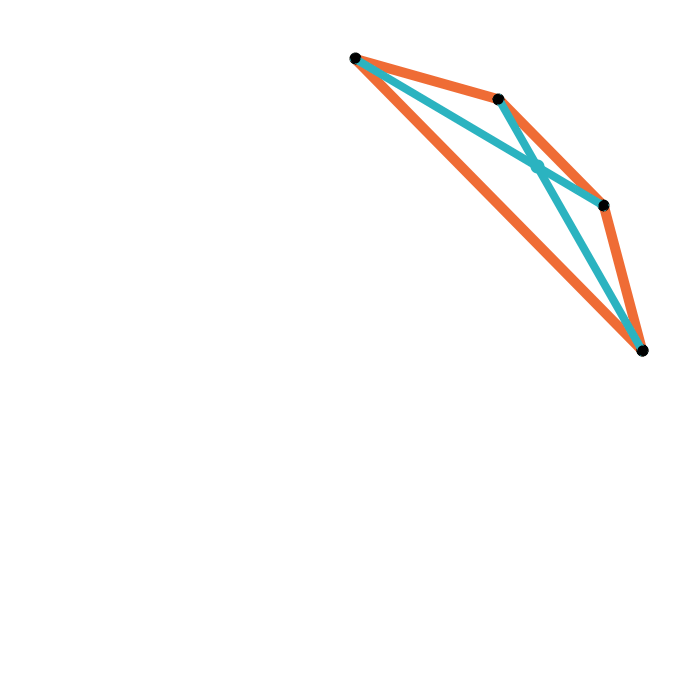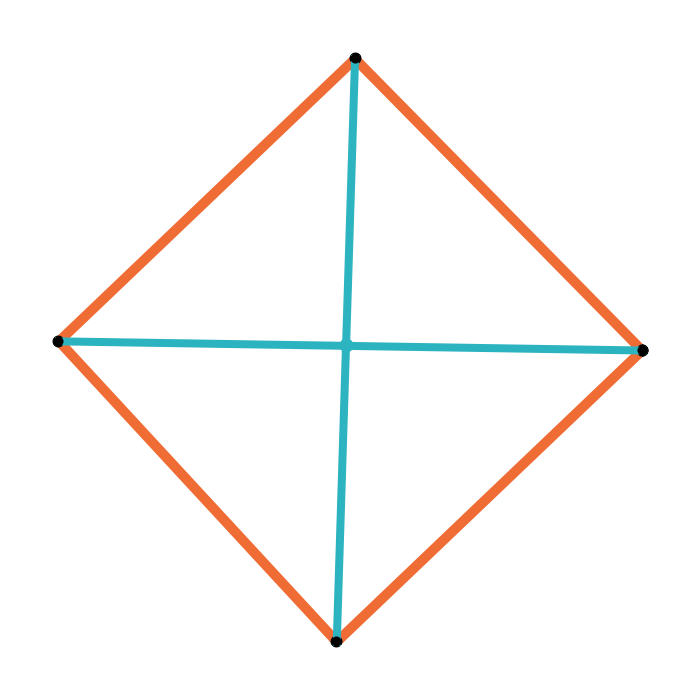
Geometric median of a quadrilateral
Geometric median closure
Definition
If the edge cloud \(X\) of an equilateral arm has a nice geometric median, the geometric median closure \(\text{gmc}(X)\) recenters the edge cloud at the geometric median.
\(\text{gmc}(X)_i = \frac{x_i-\text{gm}(X)}{\|x_i - \text{gm}(X)\|}\)
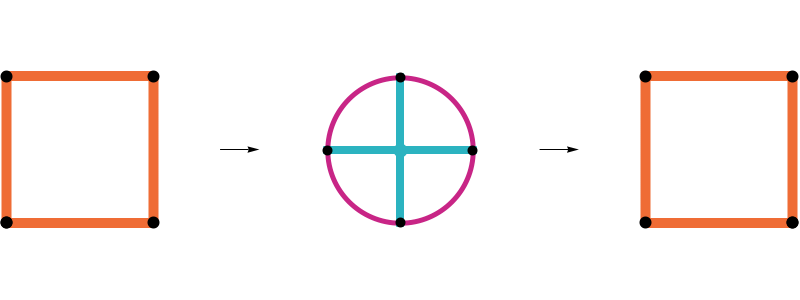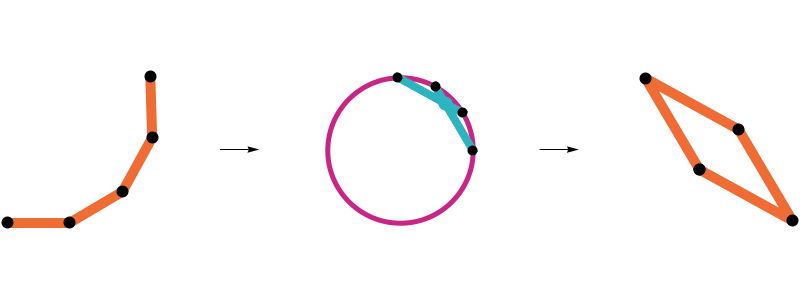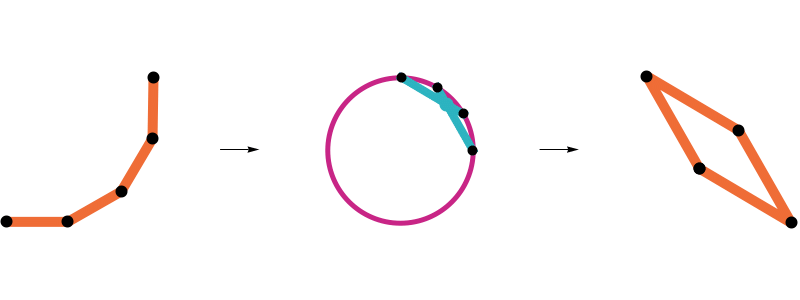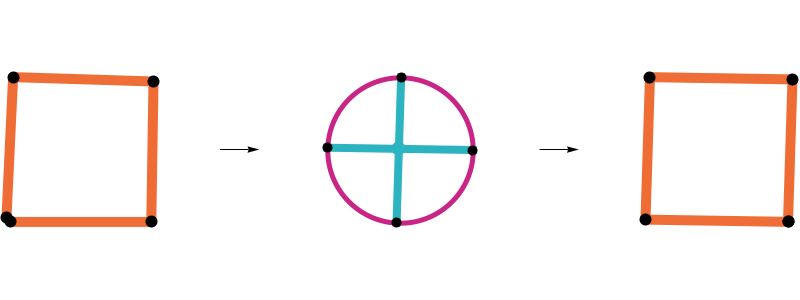
Closing a 17-edge arm
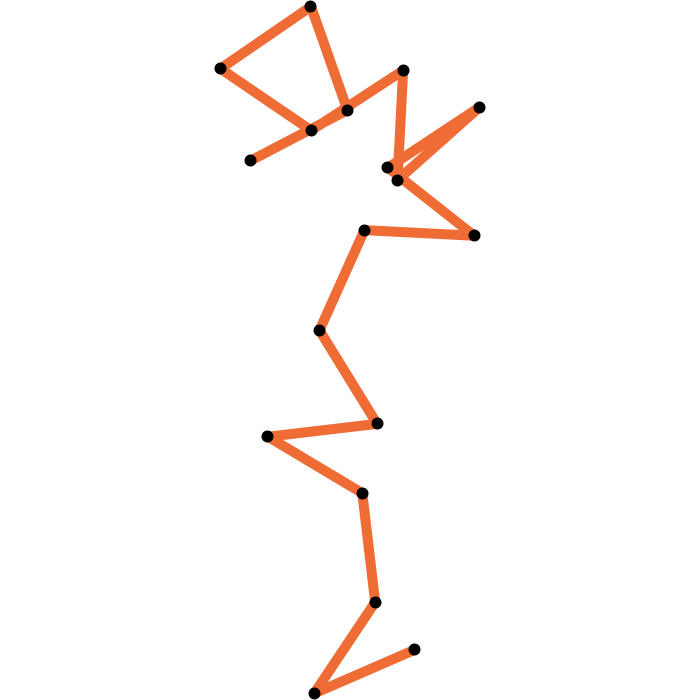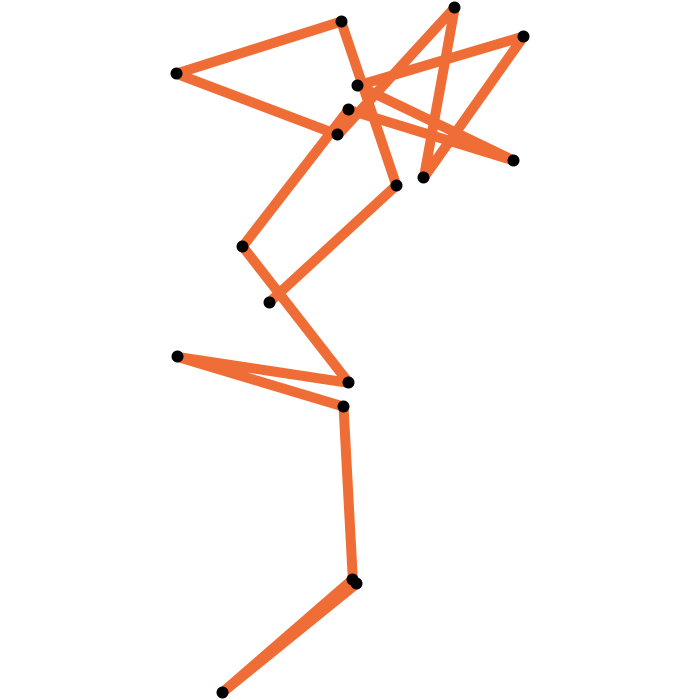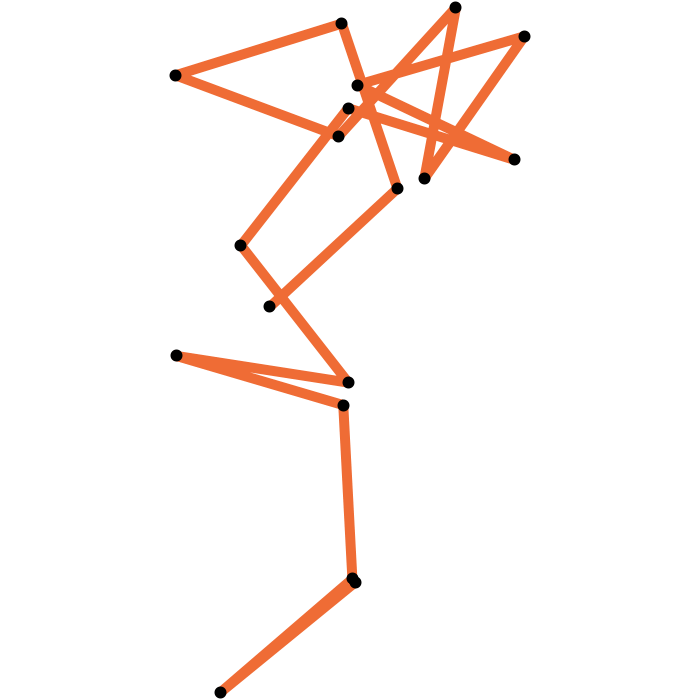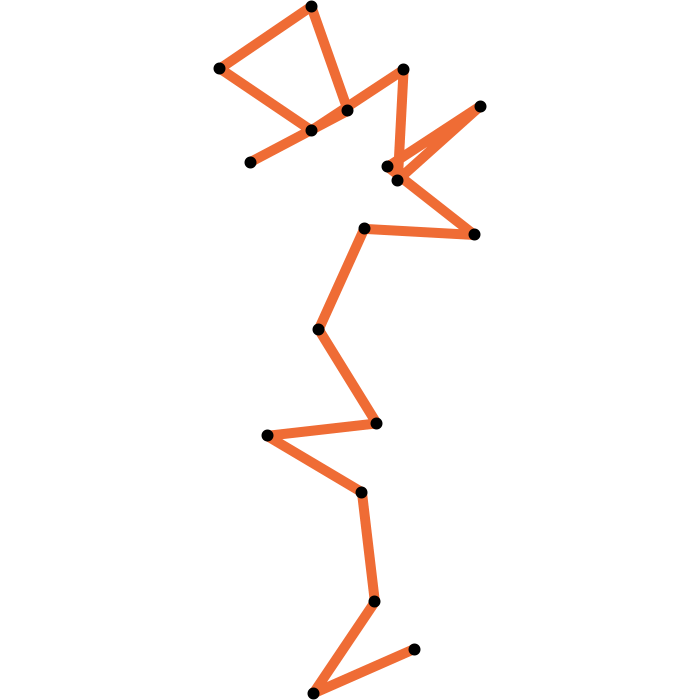
The geometric median closure is closed
Proposition (with Cantarella, Chapman, and Reiter)
If it exists, the geometric median closure of an arm is a closed polygon.
Proof
\(\text{gm}(X)\) minimizes the average distance function
\(\mathrm{Ad}_X(y) = \frac{1}{n}\sum_i \|x_i - y\|\),
which is convex everywhere and smooth away from the \(x_i\), and
\(\nabla \mathrm{Ad}_X(y) = \frac{1}{n}\sum_i \frac{x_i-y}{\|x_i-y\|}\).
The geometric median closure is optimal
Definition
An arm or polygon \(X\) is given by \(n\) edge vectors \(x_i \in \mathbb{R}^d\), or a single point in \(\mathbb{R}^{dn}\). The distance between \(X\) and \(Y\) is the Euclidean distance between these points in \(\mathbb{R}^{dn}\).
Theorem (with Cantarella, Chapman, and Reiter)
If \(X\) is an equilateral arm in \(\mathbb{R}^d\) with a geometric median closure, then \(\text{gmc}(X)\) is the closest equilateral polygon to \(X\).
Some neat bounds
Suppose \(X=(x_1,\ldots , x_n)\) consists of the edges of an \(n\)-step random walk in \(\mathbb{R}^d\). Let \(\mu=\|\mathrm{gm}(X)\|\).
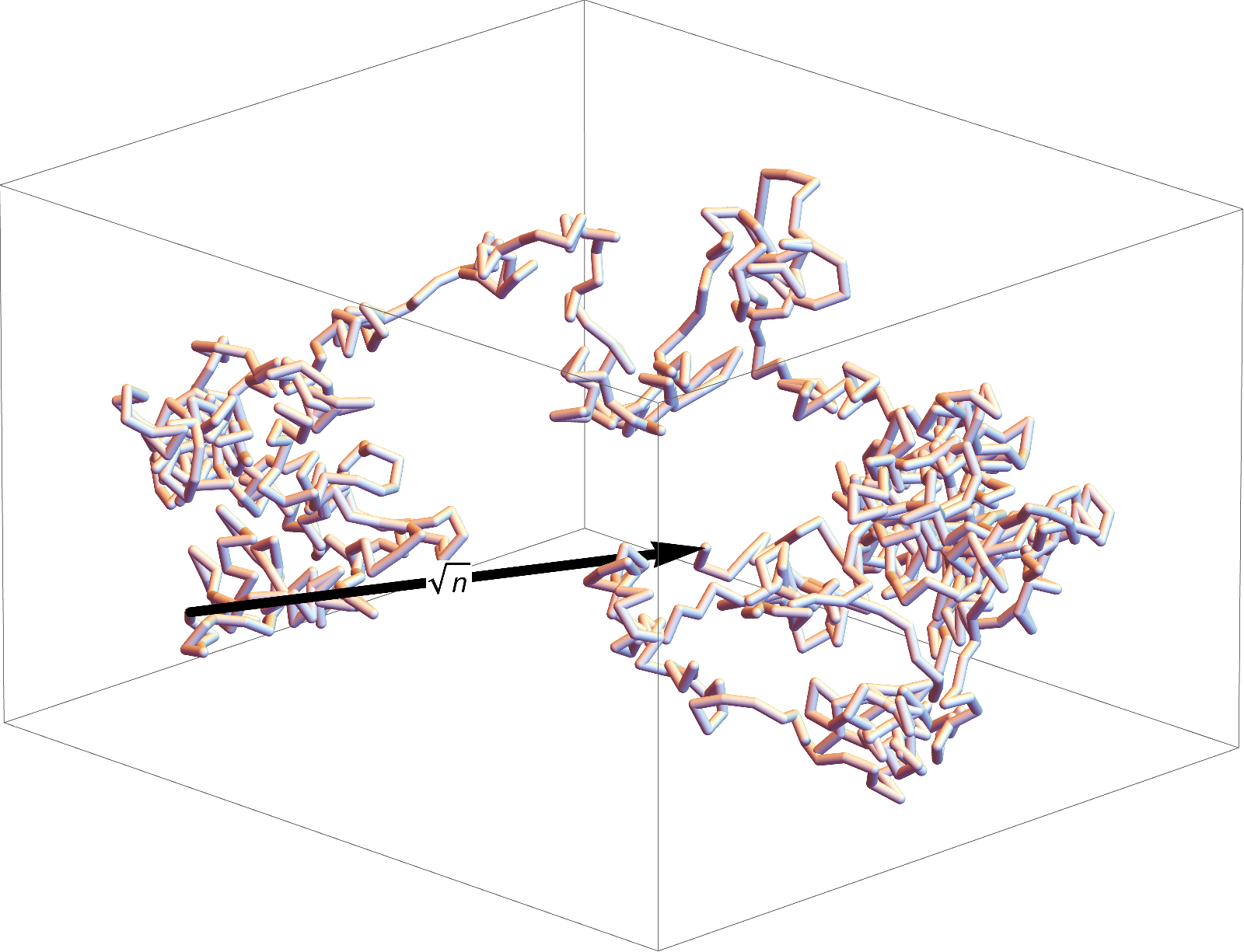
Lemma. \(d(X,\mathrm{Pol}(n,d))<\mu\sqrt{2}\sqrt{n}\)
In fact, \(d(X,\mathrm{Pol}(n,d)) \sim \mu\sqrt{\frac{d-1}{d}}\sqrt{n}\).
Lemma. If \(d_\mathrm{max-angular}(X,Y):=\max_i \angle(x_i,y_i)\), then
Loop closure doesn’t change much!

Small knots in proteins persist
3L05A
...whereas large knots often don’t
2HOCA
Closure mostly preserves small knots
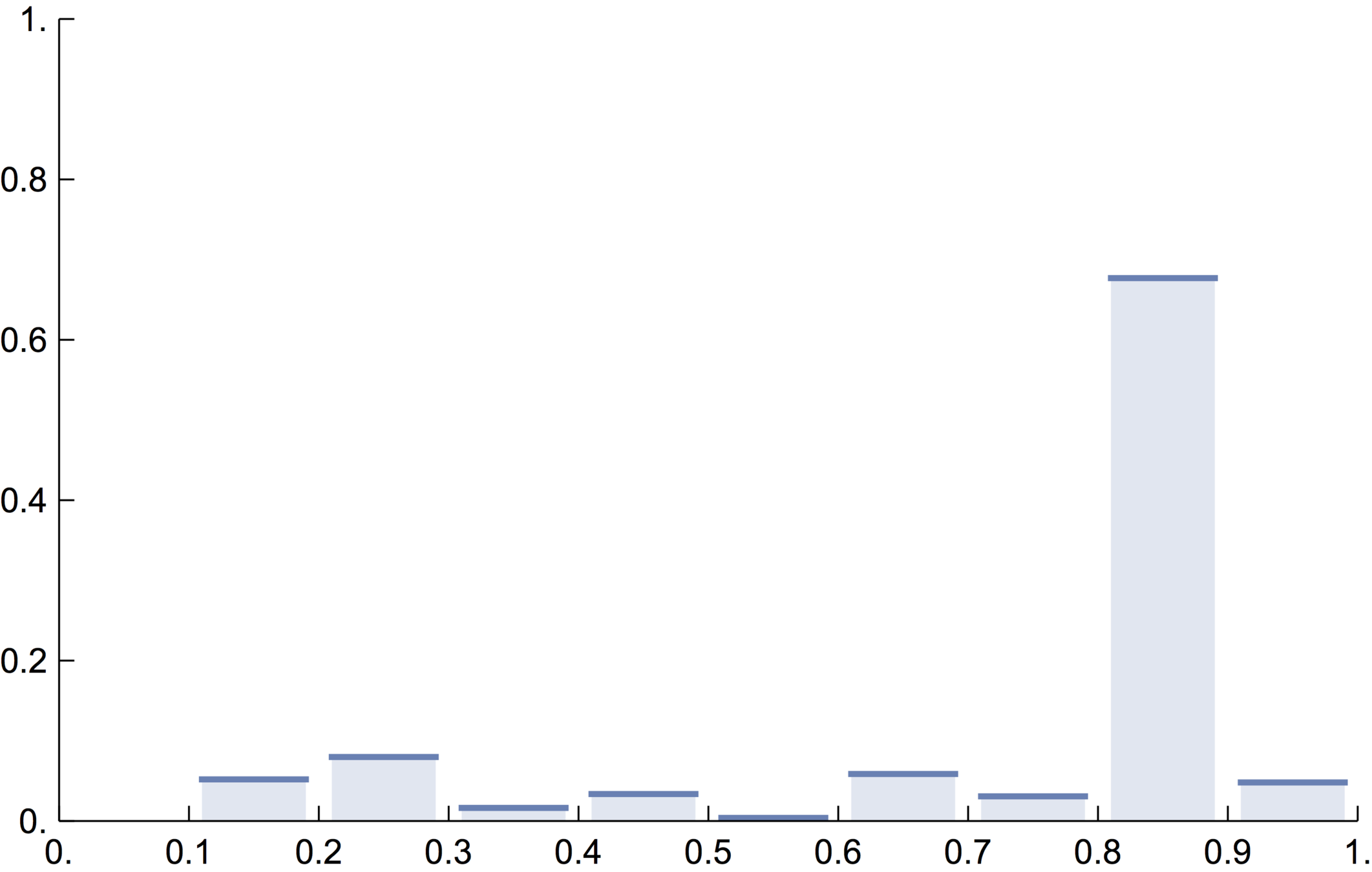
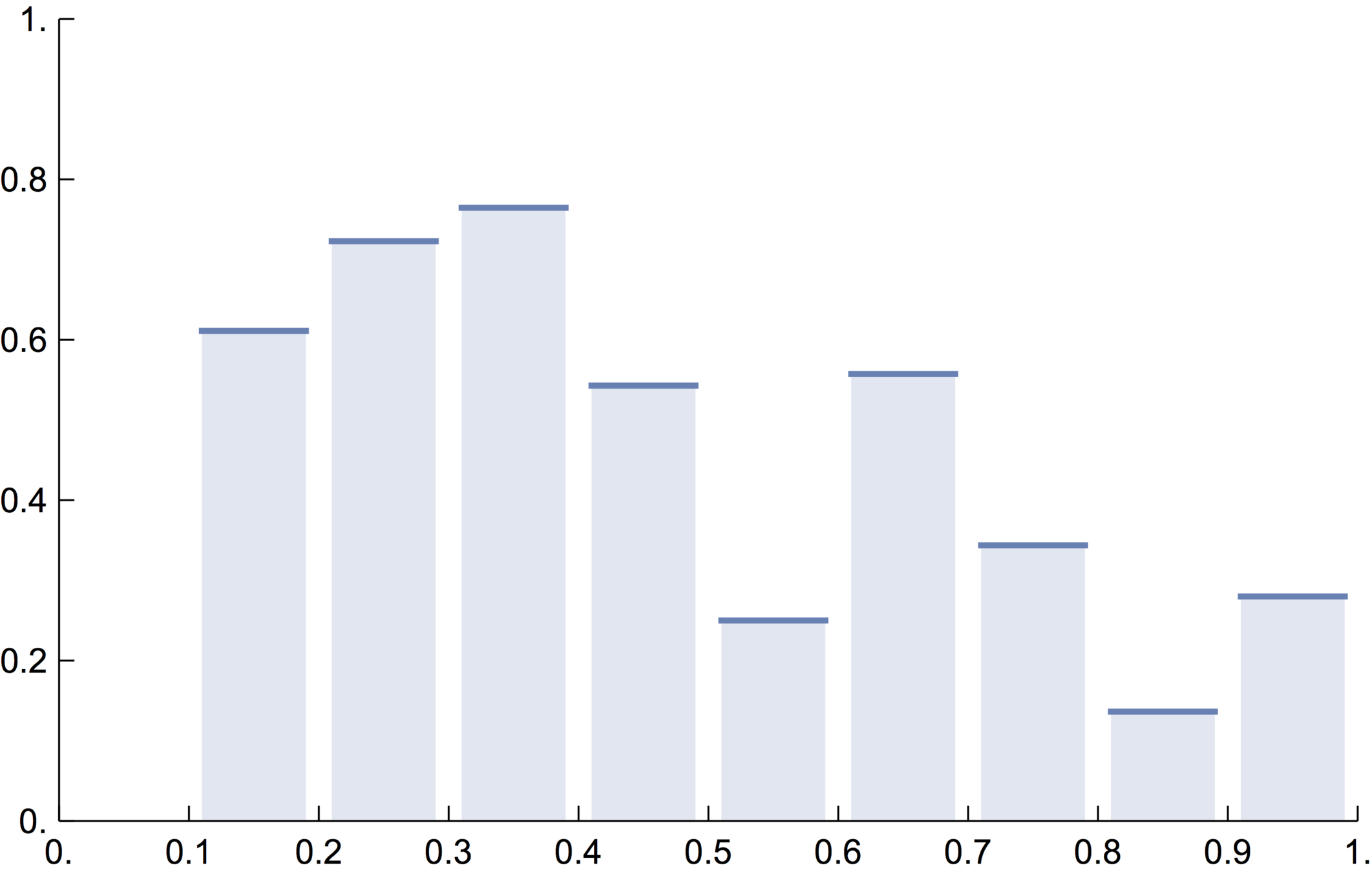
Knotted core size vs. Knotted closure probability
Knotted core size likelihood
~70% of closures knotted
~15% of closures knotted
~15% of proteins
~70% of proteins
For all proteins in KnotProt as of July 2, 2018
Main Theorem
Theorem (with Cantarella, Chapman, and Reiter)
If \(X\) consists of the edges of a random walk in \(\mathbb{R}^3\) and \(\mu=\|\mathrm{gm}(X)\|\), then for any \(r<\frac{5}{1000}\),
Corollary
For any \(\alpha < \frac{5}{1000} \sqrt{\frac{n}{2}}\),
Similar results hold in any dimension.
Provable vs. actual distance to closure
Provable: For \(n>\)1,280,000, \(\mathbb{P}(d(X,\mathrm{Pol}(n,3))<4)\geq 0.999\).
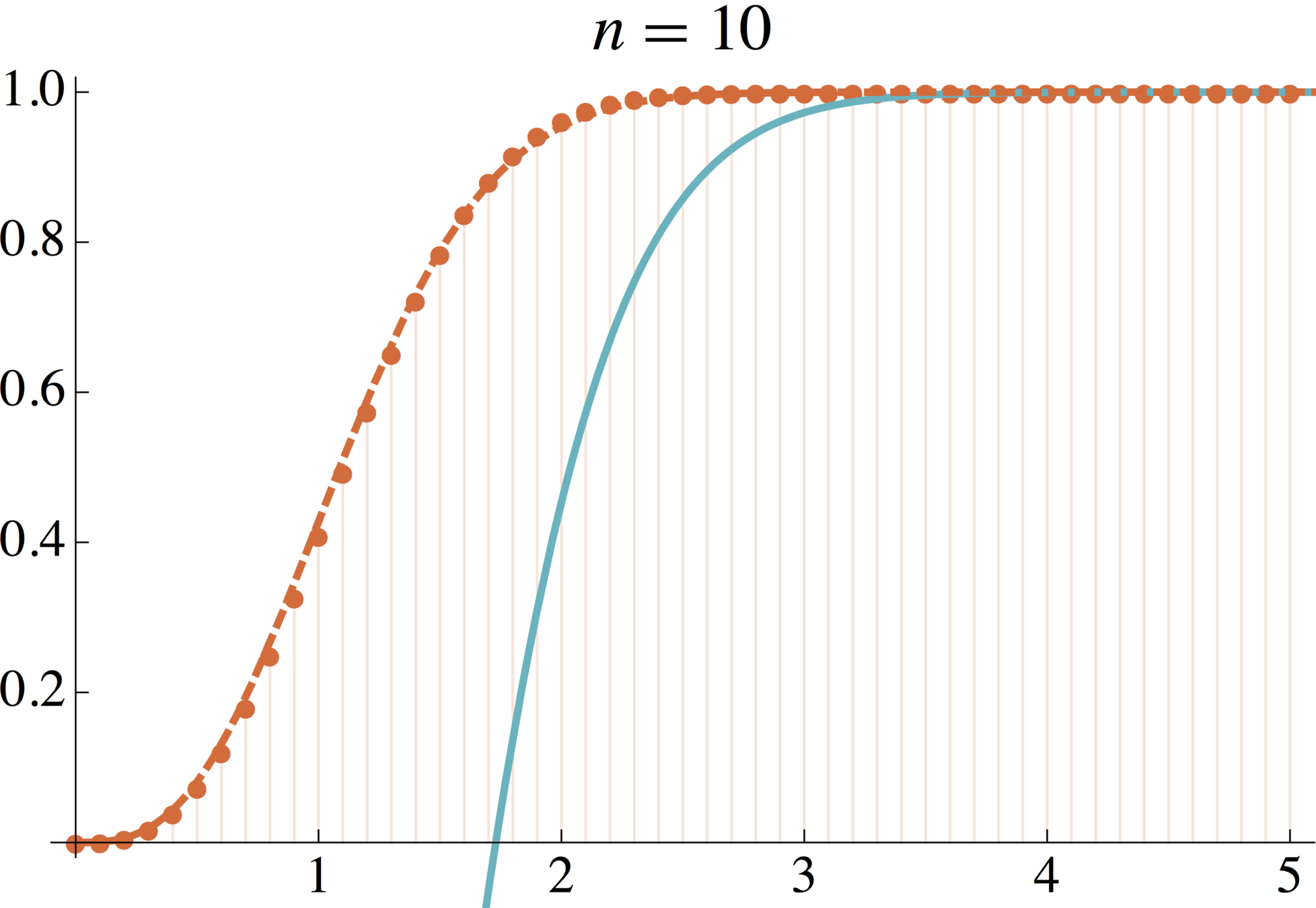
Actual: For \(n\geq10\), \(\mathbb{P}(d(X,\mathrm{Pol}(n,3))<3)\geq 0.999\).
Flow of the proof
Recall that \(\mathrm{gm}(X)\) is the unique minimizer of the convex function \(\mathrm{Ad}_X(y)\).
- The minimum eigenvalue of the Hessian of \(\mathrm{Ad}_X\) is very likely to be bounded below near the origin.
- \(\|\nabla \mathrm{Ad}_X(0)\|\) is very likely to be small.
- By Taylor’s theorem, the radial directional derivative must be positive outside some small ball, so the point where \(\nabla \mathrm{Ad}(y) = 0\)—namely, \(\mathrm{gm}(X)\)—must be inside this ball, and hence close to the origin.
Moral of the story
Closing a random walk is very unlikely to mess up the local structure of the walk.
Random walks are surprisingly close to closed polygons, for any \(n\), in any dimension, and for any fixed choice of edgelengths (not just equilateral!).
Thank you!
Reference
Open and closed random walks with fixed edgelengths in \(\mathbb{R}^d\)
Jason Cantarella, Kyle Chapman, Philipp Reiter, & Clayton Shonkwiler
Funding: Simons Foundation