Random Walks are Almost Closed
or
Loop Closure is Surprisingly Non-Destructive
/ne18
This talk!
Modern polymer physics is based on the analogy between a polymer chain and a random walk.
– Alexander Grosberg
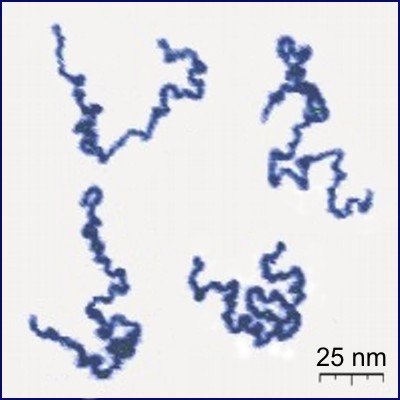
Protonated P2VP
Roiter/Minko
Clarkson University
Plasmid DNA
Alonso–Sarduy, Dietler Lab
EPF Lausanne
Random walks
Is it almost closed?

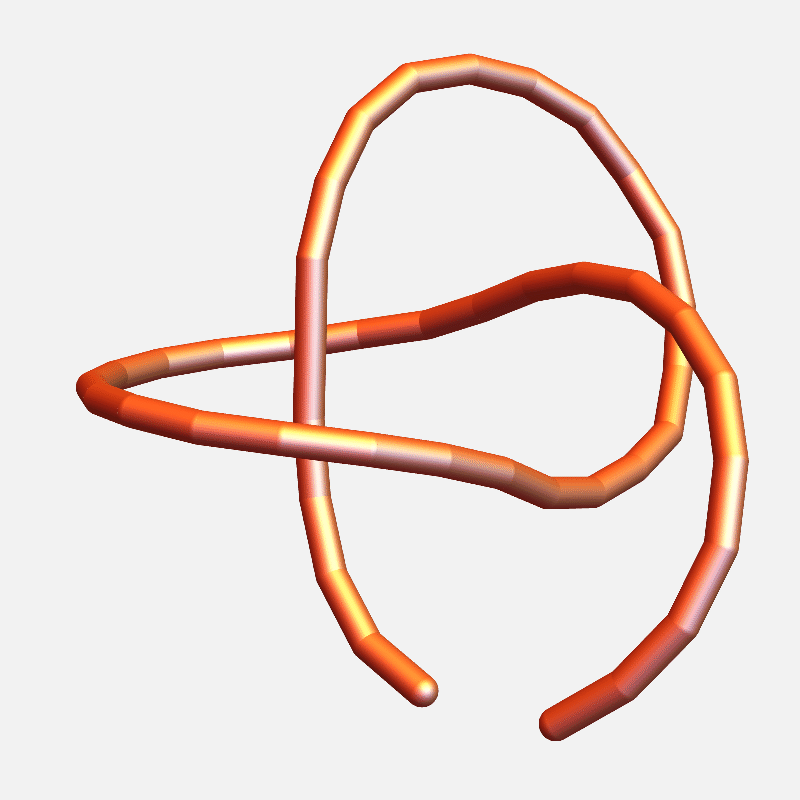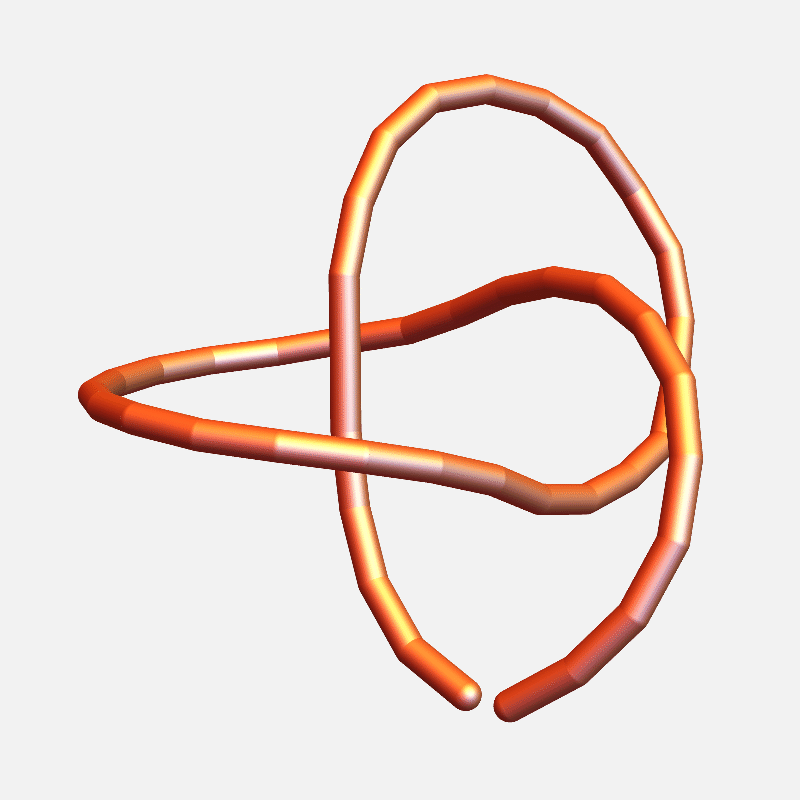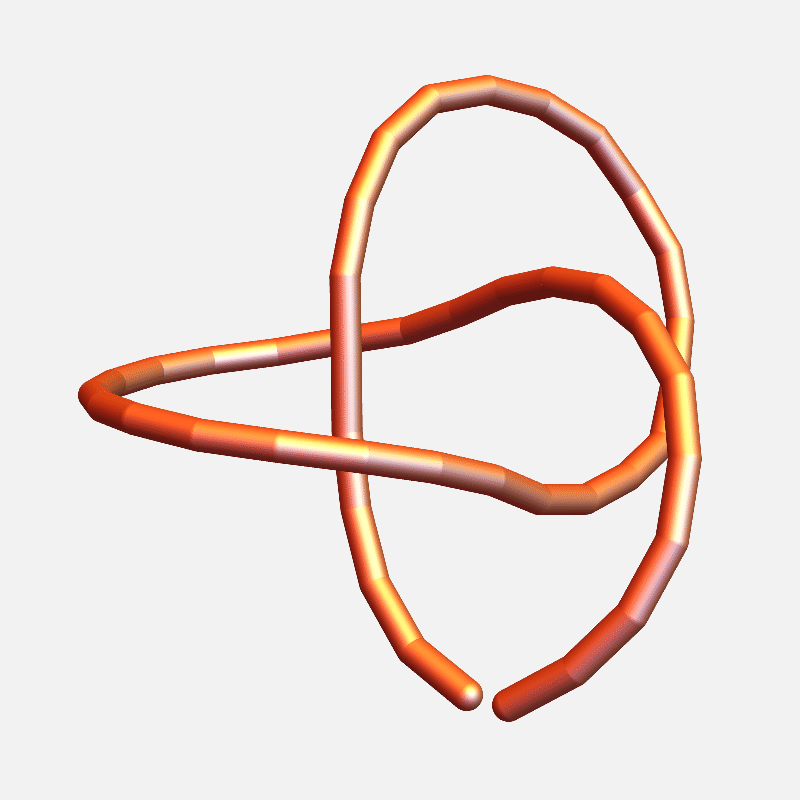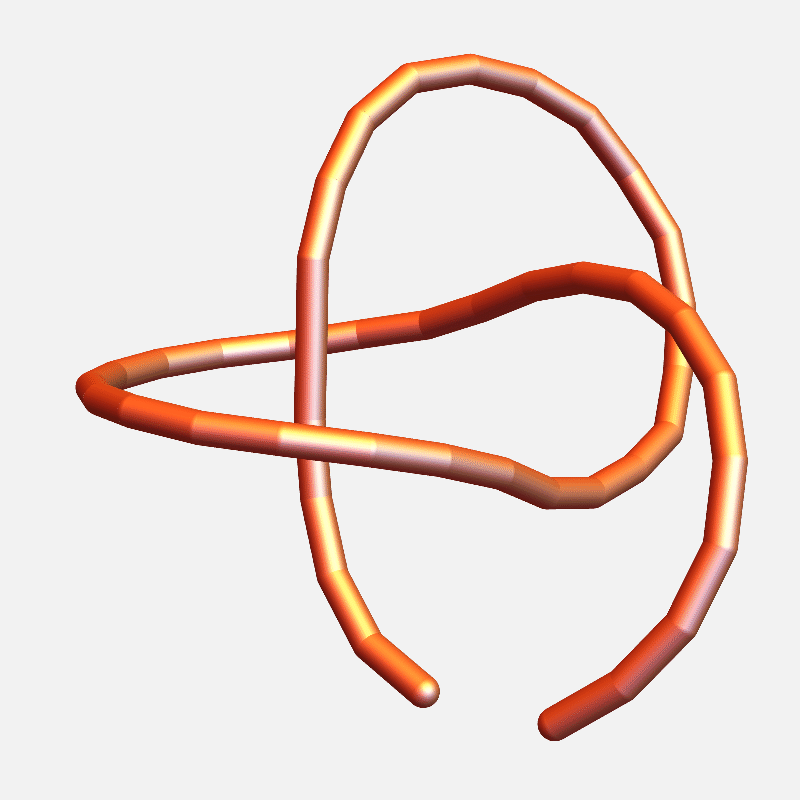



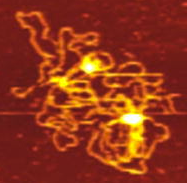
1QMG – Acetohydroxyacid isomeroreductase
Most random walks are almost closed(?)
Suppose \(e_1,\ldots , e_n\) are the edges of a random walk in \(\mathbb{R}^d\).
By Chernoff’s inequality,
Distance to polygons is tricky

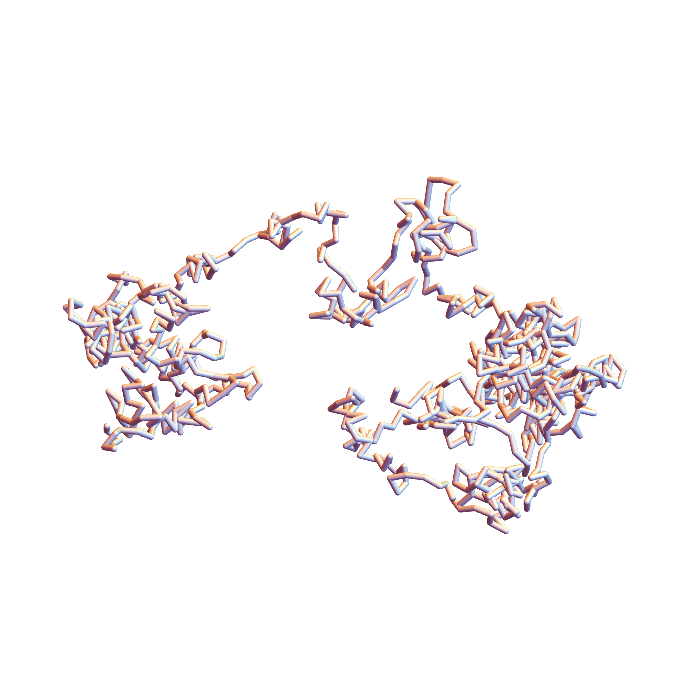
end-to-end distance: 16.99
distance to closed: 5.64
end-to-end distance: 17.76
distance to closed: 0.68
Distance to a closed polygon
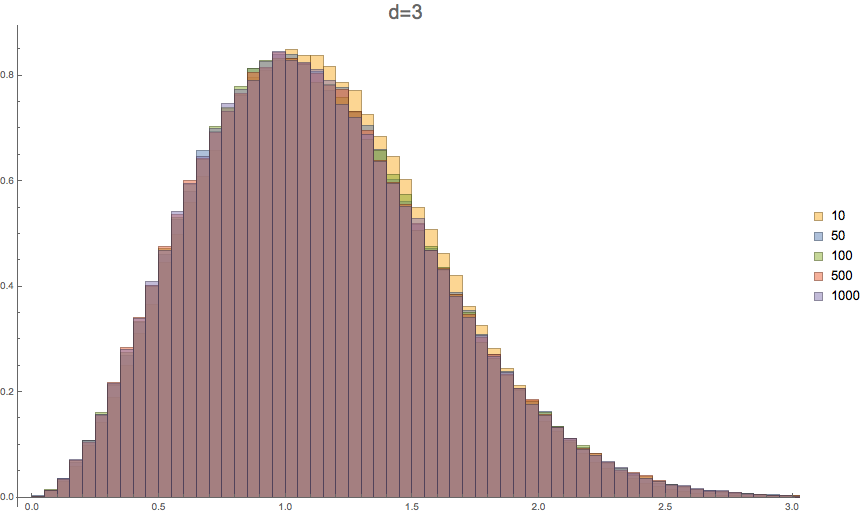
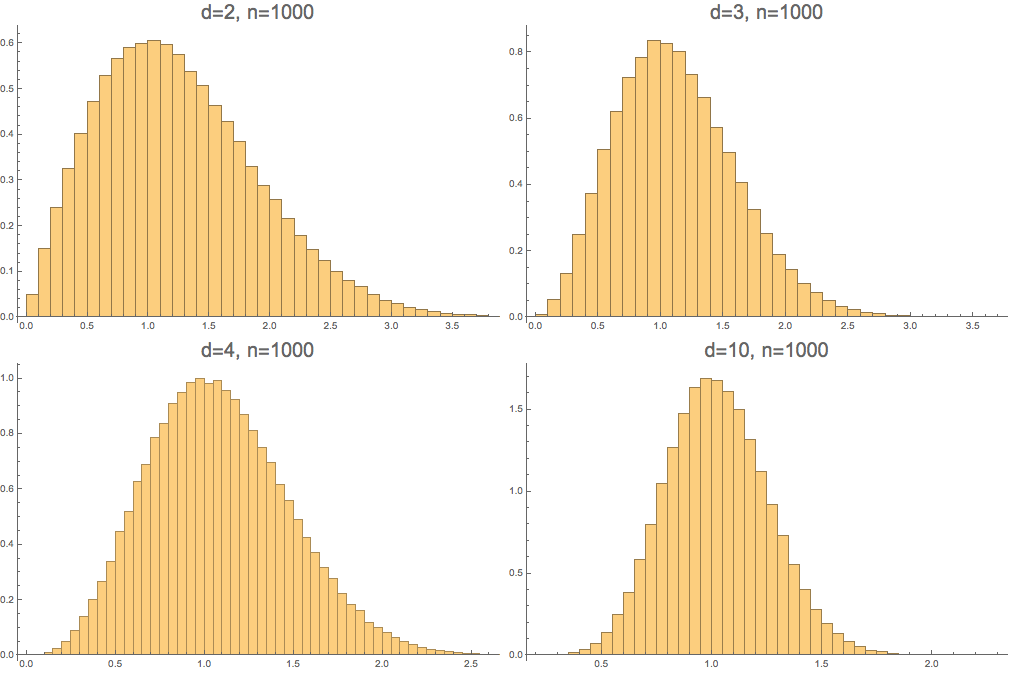
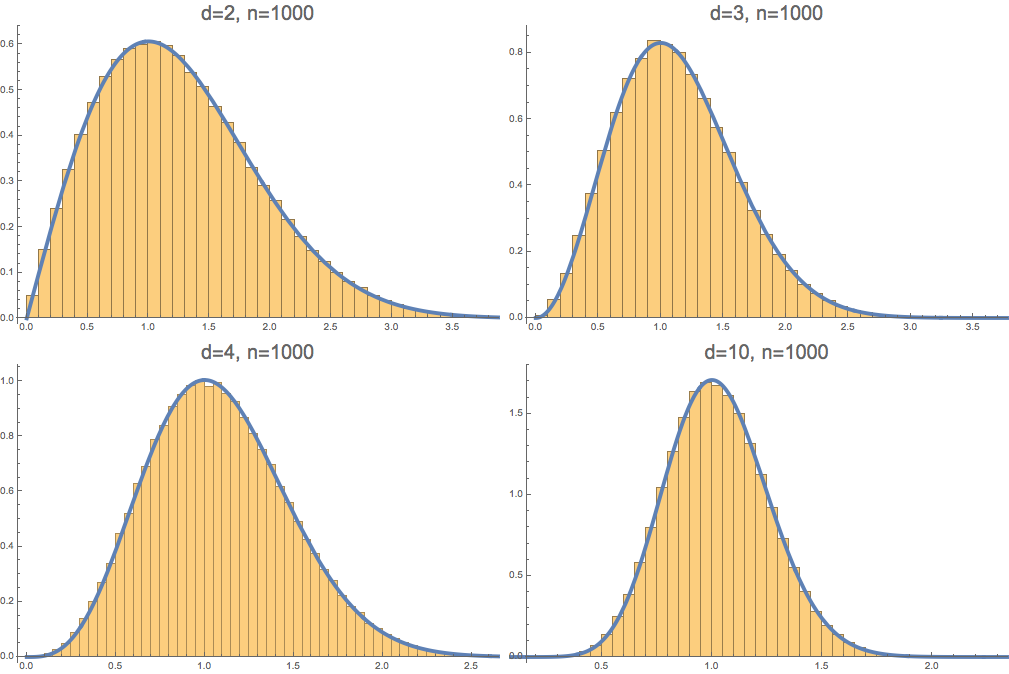
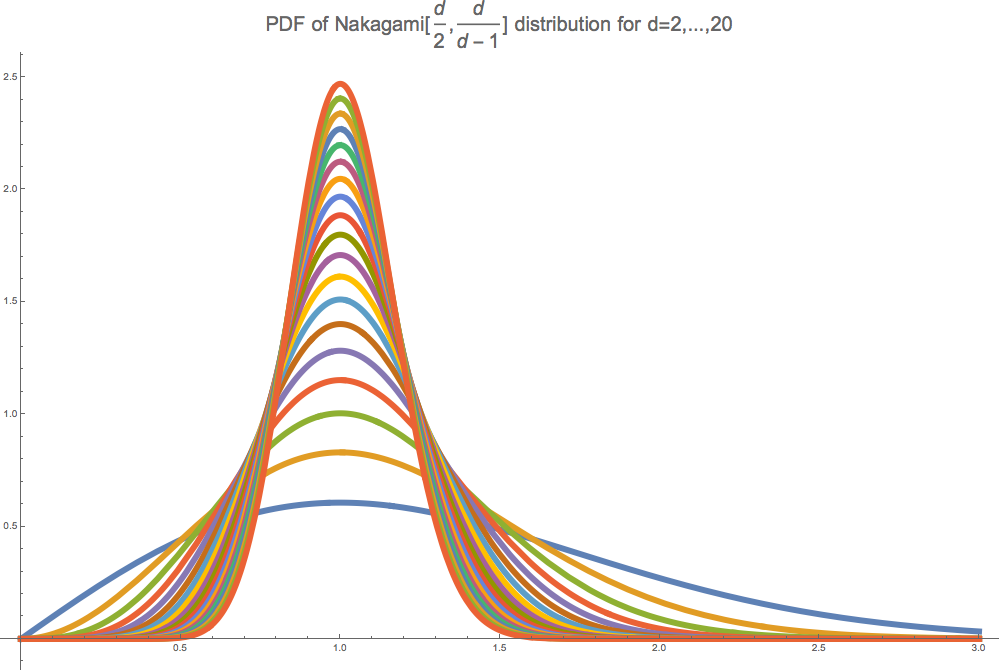
Conjecture. For \(n \to \infty\), distance to the closest polygon to a random walk in \(\mathbb{R}^d\) follows a Nakagami\(\left(\frac{d}{2},\frac{d}{d-1}\right)\) distribution.
The geometric median
Definition
A geometric median (or Fermat-Weber point) of a collection \(X=\{x_1,\ldots , x_n\}\) of points in \(\mathbb{R}^d\) is any point closest to the \(x_i\):
\(\text{gm}(X)=\text{argmin}_y \sum \|x_i-y\|\)
Definition
A point cloud has a nice geometric median if:
- \(\text{gm}(X)\) is unique (\(\Leftarrow X\) is not linear)
- \(\text{gm}(X)\) is not one of the \(x_i\)
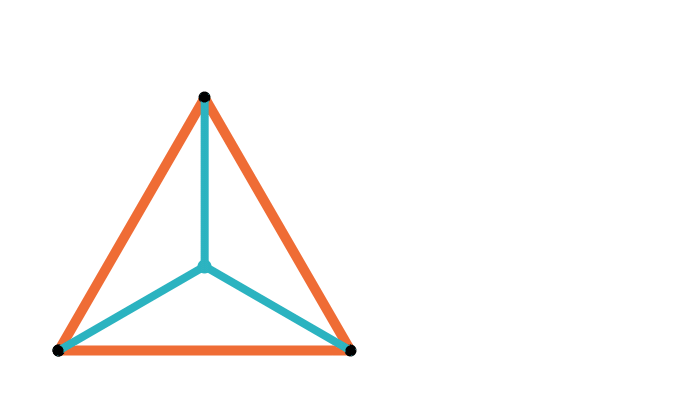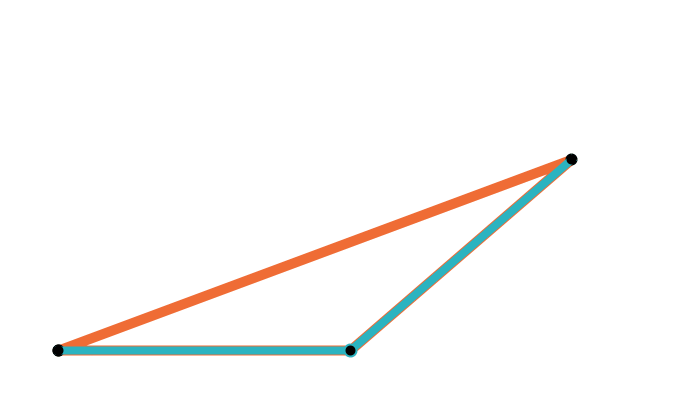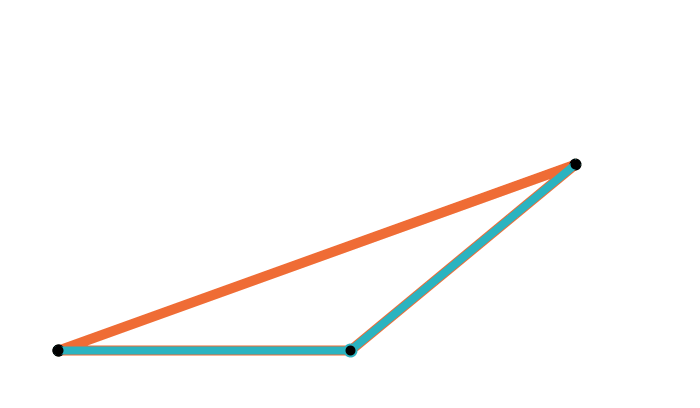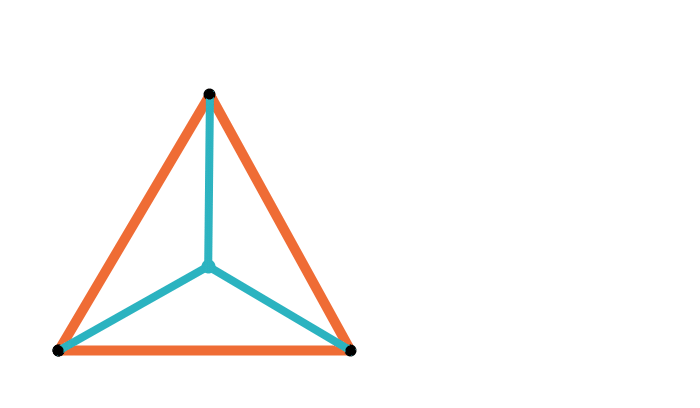
Geometric median of a triangle
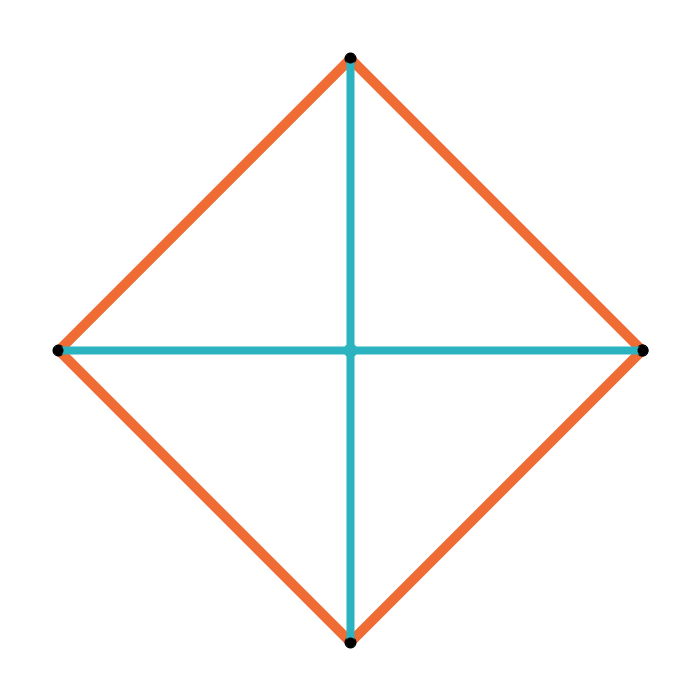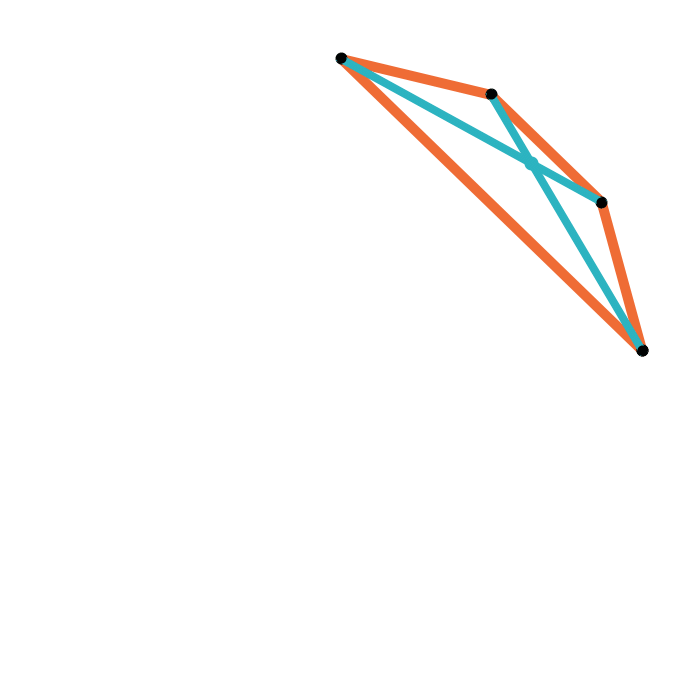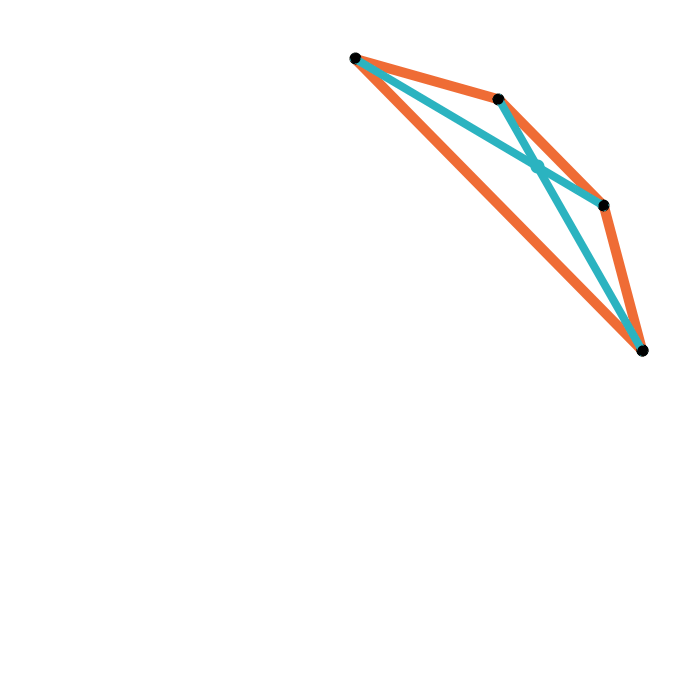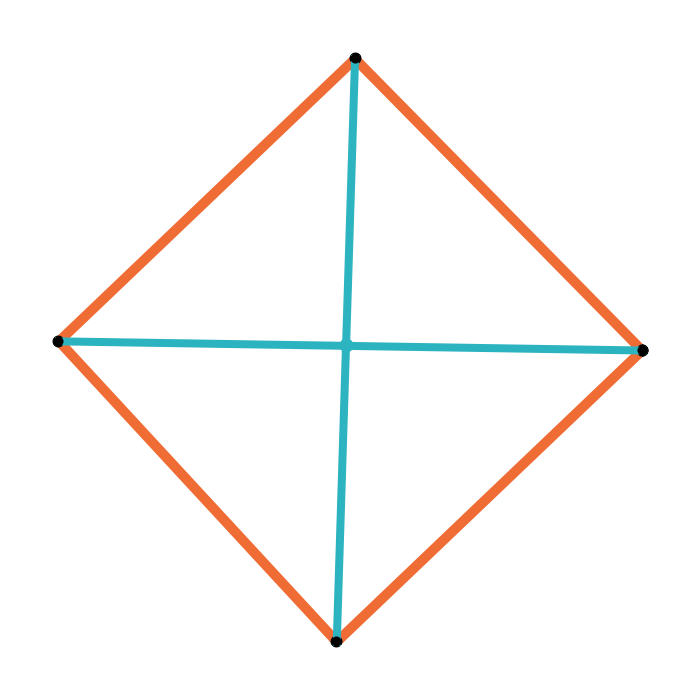
Geometric median of a quadrilateral
Geometric median closure
Definition
If the edge cloud \(X\) of an equilateral arm has a nice geometric median, the geometric median closure \(\text{gmc}(X)\) recenters the edge cloud at the geometric median.
\(\text{gmc}(X)_i = \frac{x_i-\text{gm}(X)}{\|x_i - \text{gm}(X)\|}\)
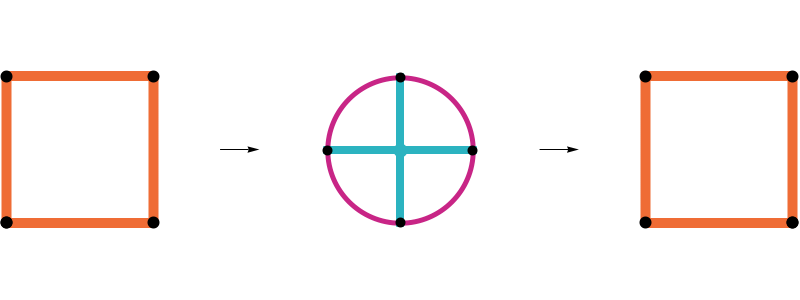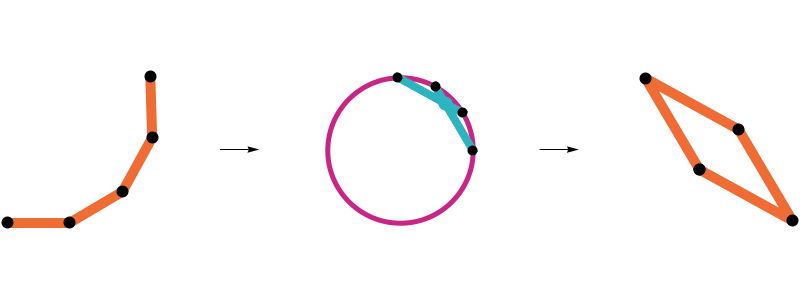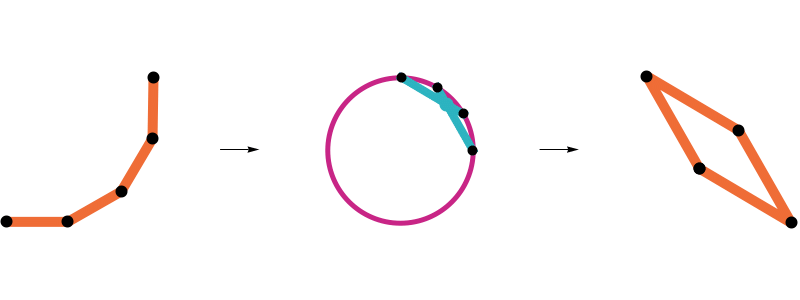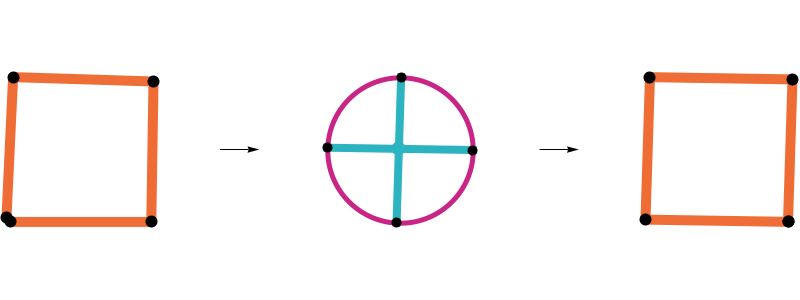
Closing a 17-edge arm
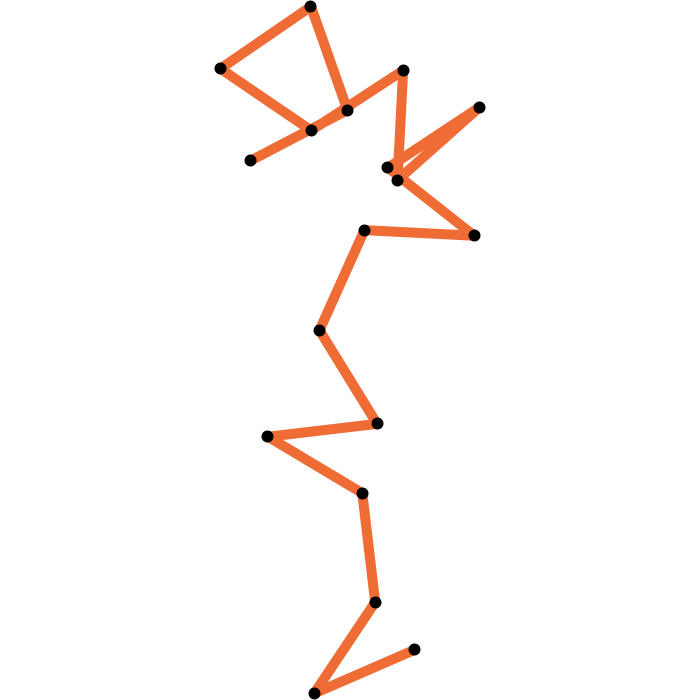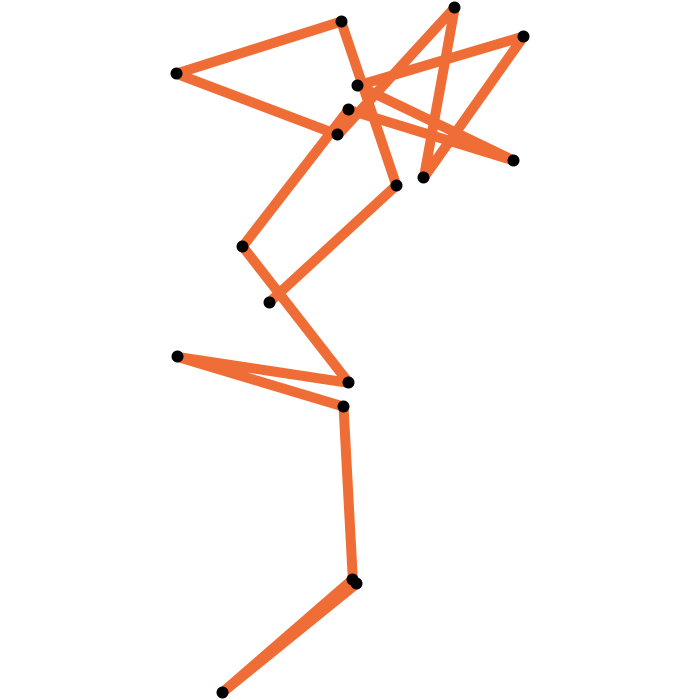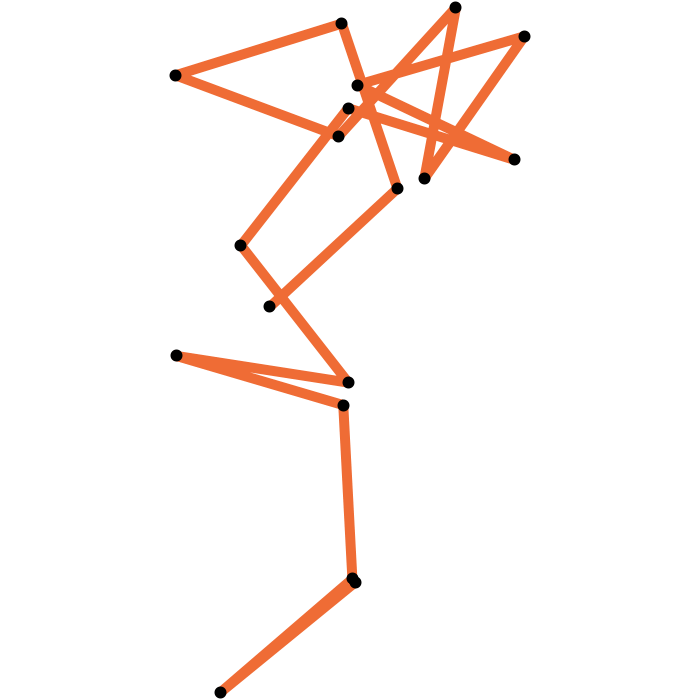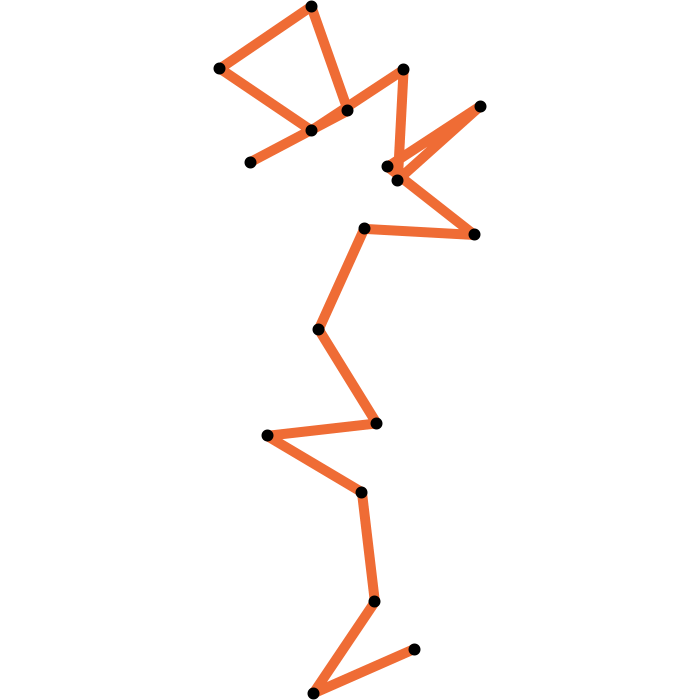
The geometric median closure is closed
Proposition (with Cantarella and Reiter)
If it exists, the geometric median closure of an arm is a closed polygon.
Proof
\(\text{gm}(X)\) minimizes the average distance function
\(\mathrm{Ad}_X(y) = \frac{1}{n}\sum_i \|x_i - y\|\),
which is convex everywhere and smooth away from the \(x_i\), and
\(\nabla \mathrm{Ad}_X(y) = \frac{1}{n}\sum_i \frac{x_i-y}{\|x_i-y\|}\).
The geometric median closure is optimal
Definition
An arm or polygon \(X\) is given by \(n\) edge vectors \(x_i \in \mathbb{R}^d\), or a single point in \(\mathbb{R}^{dn}\). The distance between \(X\) and \(Y\) is the Euclidean distance between these points in \(\mathbb{R}^{dn}\).
Theorem (with Cantarella and Reiter)
If \(X\) is an equilateral arm in \(\mathbb{R}^d\) with a geometric median closure, then \(\text{gmc}(X)\) is the closest equilateral polygon to \(X\).
Proof
Depends on the neat fact that if \(\|x_i\|=\|y_i\|\), then
\(\langle X, Y -X \rangle \leq 0\).
Some neat bounds
Suppose \(X=(x_1,\ldots , x_n)\) consists of the edges of an \(n\)-step random walk in \(\mathbb{R}^d\). Let \(\mu=\|\mathrm{gm}(X)\|\).
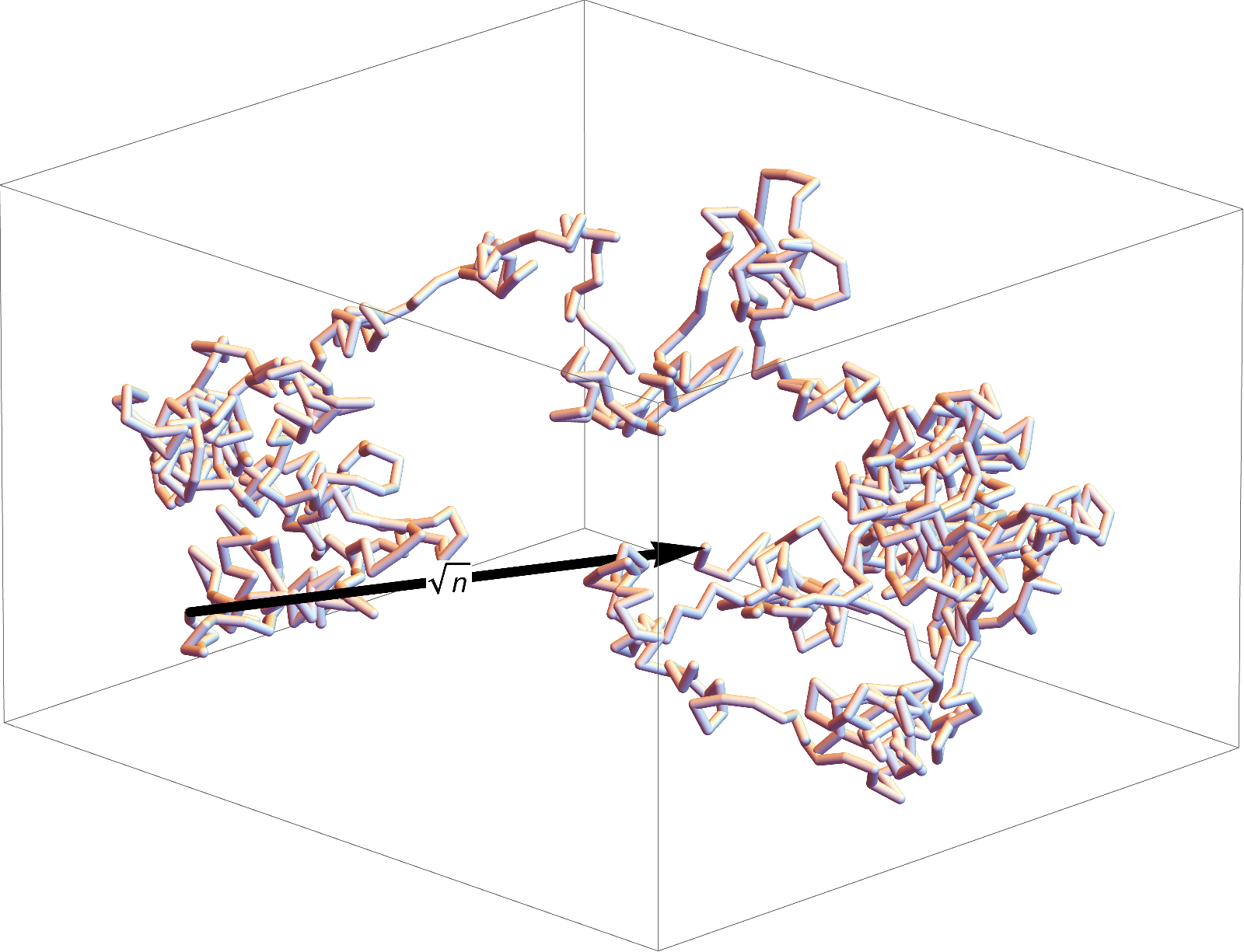
Lemma. \(d(X,\mathrm{Pol}(n,d))<\mu\sqrt{2}\sqrt{n}\)
In fact, \(d(X,\mathrm{Pol}(n,d)) \sim \mu\sqrt{\frac{d-1}{d}}\sqrt{n}\).
Lemma. If \(d_\mathrm{max-angular}(X,Y):=\max_i \angle(x_i,y_i)\), then
Loop closure doesn’t change much!

Main Theorem
Theorem* (with Cantarella & Reiter)
If \(X\) consists of the edges of a random walk in \(\mathbb{R}^d\) and \(\mu=\|\mathrm{gm}(X)\|\), then for any \(r<\frac{3}{7}\),
Corollary
For any \(\alpha < \frac{3}{7} \sqrt{\frac{n(d-1)}{d}}\),
\(d=3\)
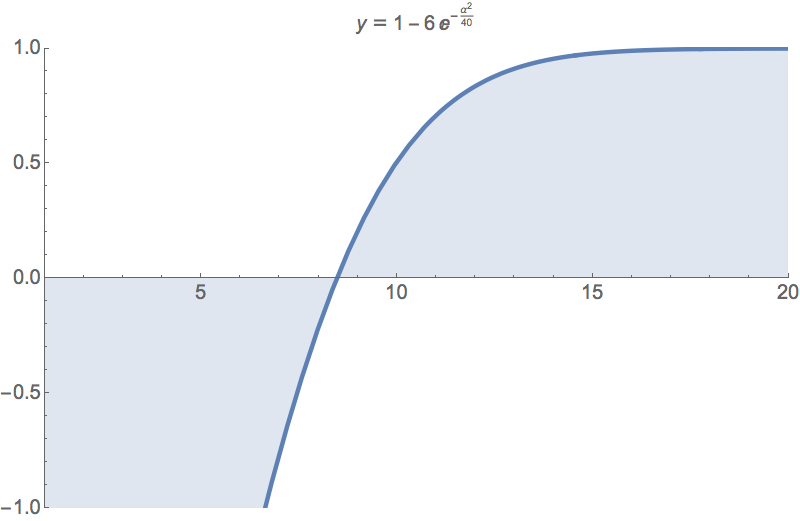
For \(n\) large enough
Flow of the proof
Recall that \(\mathrm{gm}(X)\) is the unique minimizer of the convex function \(\mathrm{Ad}_X(y)\).
- The minimum eigenvalue of the Hessian of \(\mathrm{Ad}_X\) is very likely to be bounded below near the origin.
- \(\|\nabla \mathrm{Ad}_X(0)\|\) is very likely to be small.
- Since \(\mathrm{Ad}_X\) is strictly convex, \(\nabla \mathrm{Ad}_X(y)=0\) for some \(y\) near the origin...but this \(y\) is exactly the point \(\mathrm{gm}(X)\).
Moral of the story
Closing a random walk is very unlikely to mess up the local structure of the walk.
Random walks are surprisingly close to closed polygons, for any \(n\) and in any dimension.
Thank you!
References
The symplectic geometry of closed equilateral random walks in 3-space
J. Cantarella & C. Shonkwiler
Annals of Applied Probability 26 (2016), no. 1, 549–596
A fast direct sampling algorithm for equilateral closed polygons
J. Cantarella, B. Duplantier, C. Shonkwiler, & E. Uehara
Journal of Physics A 49 (2016), no. 27, 275202
Concentration of measure for equilateral polygons in \(\mathbb{R}^d\)
J. Cantarella, P. Reiter, & C. Shonkwiler
In preparation
Funding: Simons Foundation