A Natural Map from Random Walks to Equilateral Polygons in Any Dimension
/cmo17
This talk!
Statistical physics viewpoint
A polymer in solution takes on an ensemble of random shapes, with topology as the unique conserved quantity.
Modern polymer physics is based on the analogy between a polymer chain and a random walk.
– Alexander Grosberg
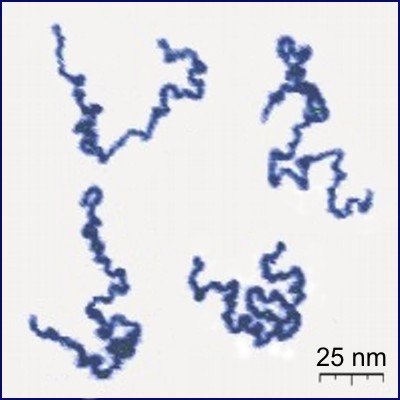
Protonated P2VP
Roiter/Minko
Clarkson University
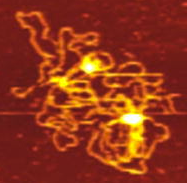
Plasmid DNA
Alonso–Sarduy, Dietler Lab
EPF Lausanne
Sampling random walks in \(\mathbb{R}^d\) is easy
Generate \(n\) independent uniform random points on \(S^{d-1}\) and treat them as an ordered list of edge vectors.

...but sampling random polygons was hard

Alvarado, Calvo, Millett, J. Stat. Phys. 143 (2011), 102–138
Key idea: commuting symmetries
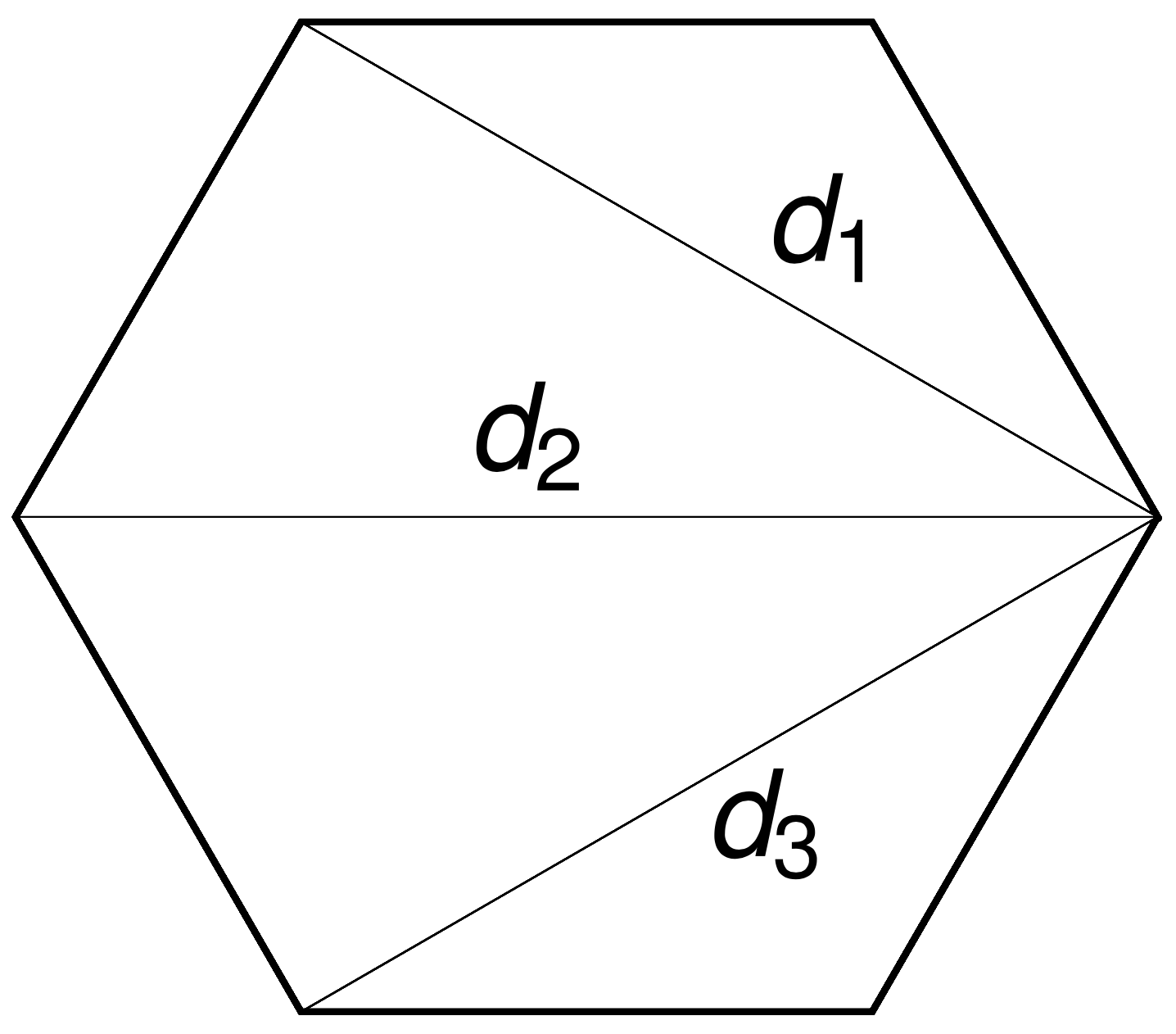
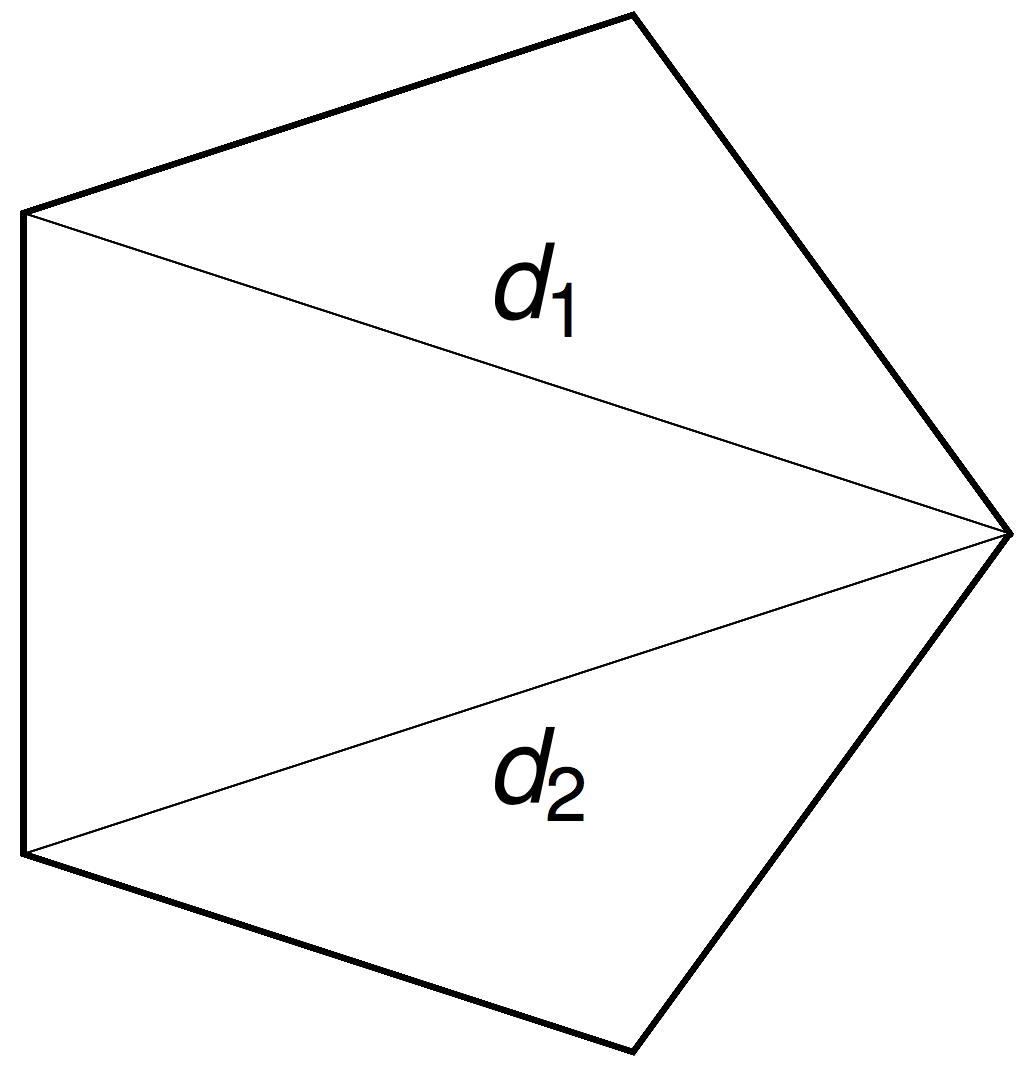
Rotations around \(n-3\) chords \(d_i\) by \(n-3\) angles \(\theta_i\) commute.


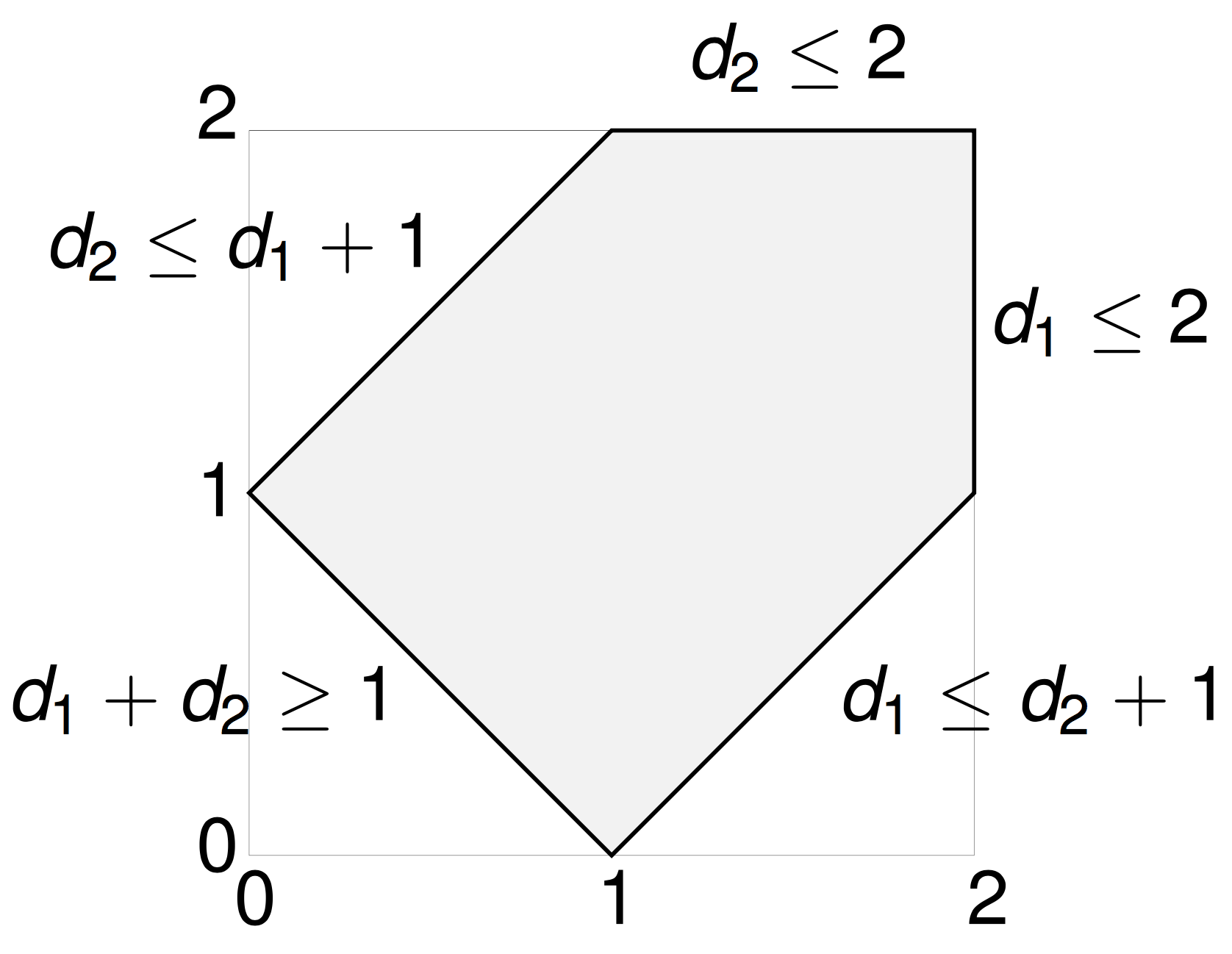
A polytope
The \((n-3)\)-dimensional moment polytope \(\mathcal{P}_n \subset \mathbb{R}^{n-3}\) is defined by the triangle inequalities
From action-angle coordinates to polygons
There exists an almost-everywhere defined map \(\alpha: \mathcal{P}_n \times (S^1)^{n-3} \to \text{Pol}_3(n)/SO(3)\).
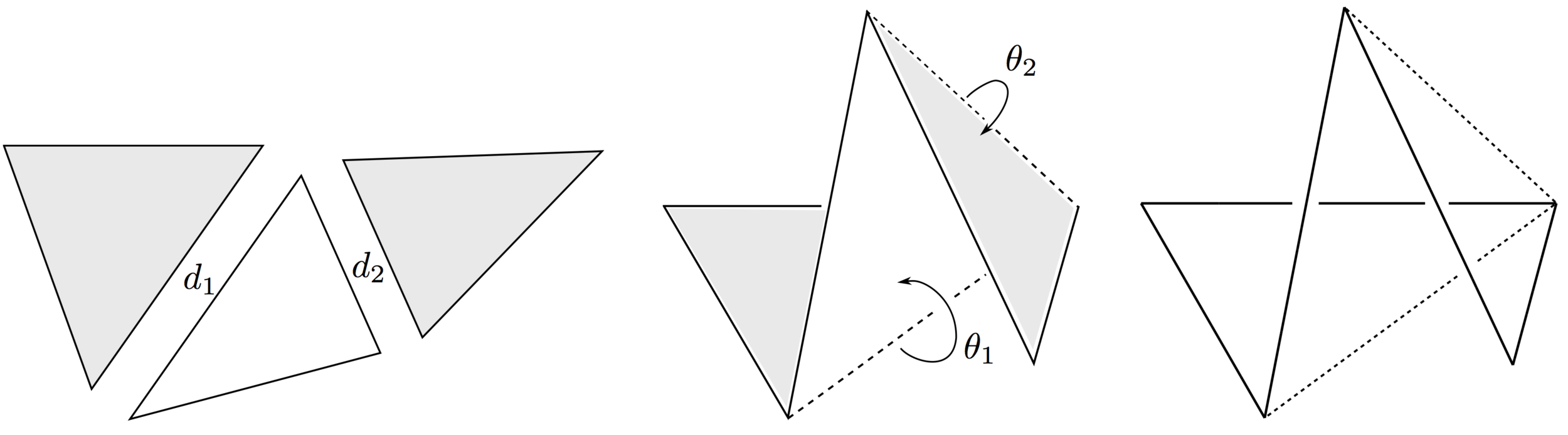
This is only sensible as a map to polygons modulo translation and rotation.
Sampling polygons in \(\mathbb{R}^3\)
Theorem (with Cantarella, 2016)
The map \(\alpha\) pushes forward the standard probability measure on \(\mathcal{P}_n \times (S^1)^{n-3}\) to the correct probability measure on \(\text{Pol}_3(n)/SO(3)\).
Corollary
Independently sampling \(\mathcal{P}_n\) and \((S^1)^{n-3}\) is a perfect sampling algorithm for equilateral \(n\)-gons in \(\mathbb{R}^3\).
Theorem (with Cantarella, Duplantier, Uehara, 2016)
A direct sampler with expected runtime \(\Theta(n^{5/2})\).
Kyle Chapman has an even faster sampler he will talk about on Thursday.
Unfortunately, this is all very special to 3 dimensions...
Strategy
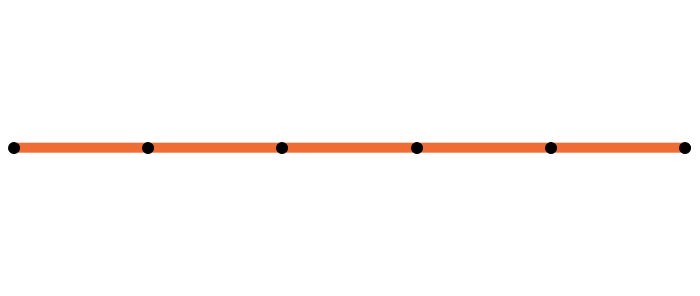
- Find a natural map \(g:\text{Arm}_d(n) \to \text{Pol}_d(n)\).
- Sample points in \(\text{Arm}_d(n)\) and apply \(g\).
- Hope the pushforward measure is almost uniform.
Efficient closure
Idea: \(g\) should map each arm to the closed polygon which is closest to it.
Problem: This is not well-defined on all of \(\text{Arm}_d(n)\).
What is the closest closed polygon?
Relatedly: \(\text{Arm}_d(n) \simeq (S^{d-1})^n\) and \(\text{Pol}_d(n)\) have different topologies, so there's no retraction defined on all of \(\text{Arm}_d(n)\).
The geometric median
Definition
A geometric median (or Fermat-Weber point) of a collection \(X=\{x_1,\ldots , x_n\}\) of points in \(\mathbb{R}^d\) is any point closest to the \(x_i\):
\(\text{gm}(X)=\text{argmin}_y \sum \|x_i-y\|\)
Definition
A point cloud has a nice geometric median if:
- \(\text{gm}(X)\) is unique (\(\Leftarrow X\) is not linear)
- \(\text{gm}(X)\) is not one of the \(x_i\)
Geometric median of a triangle
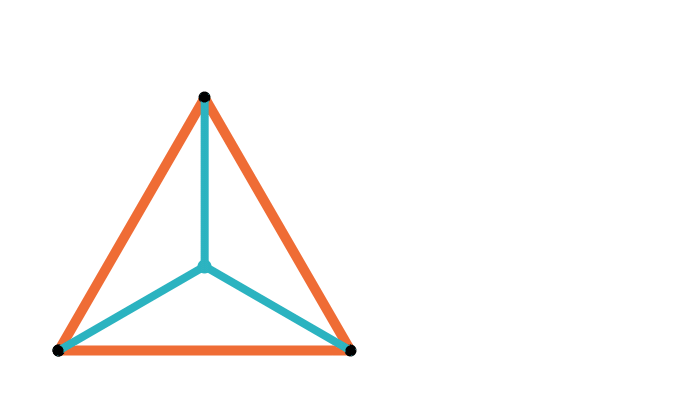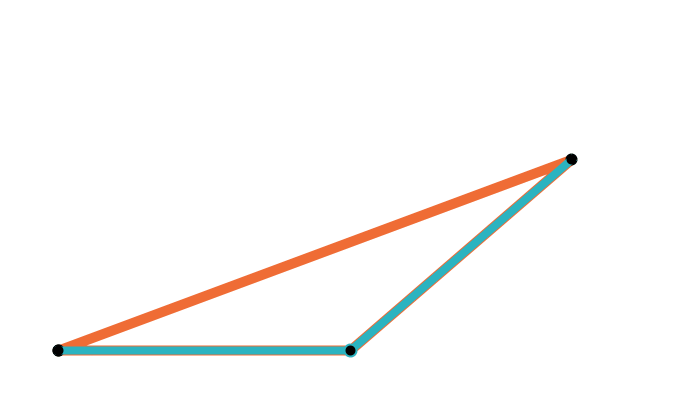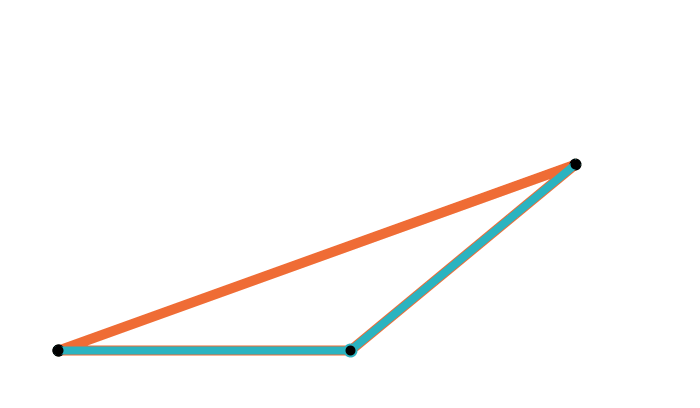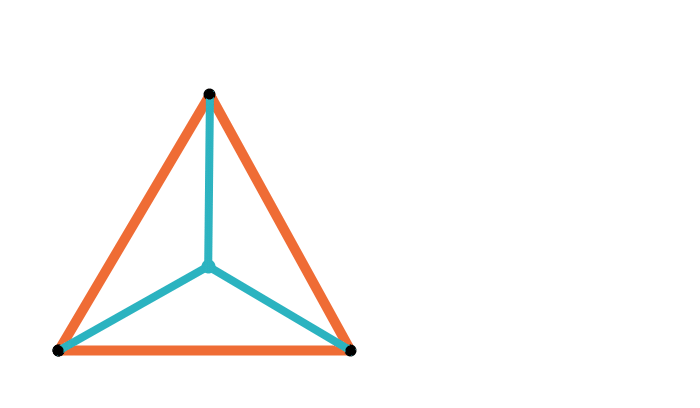
Geometric median of a quadrilateral
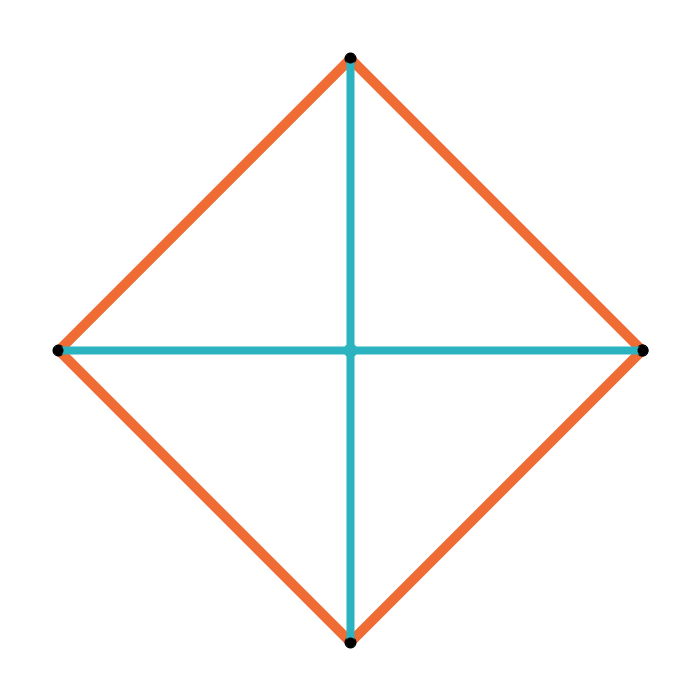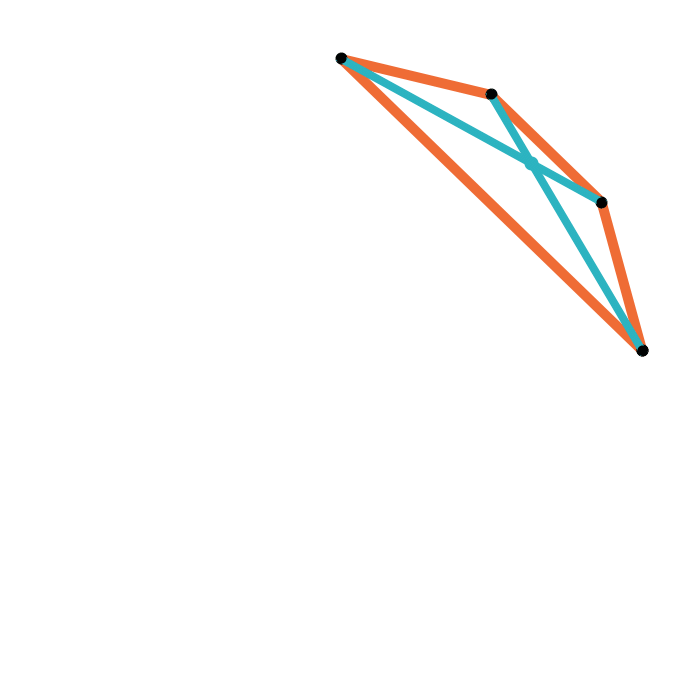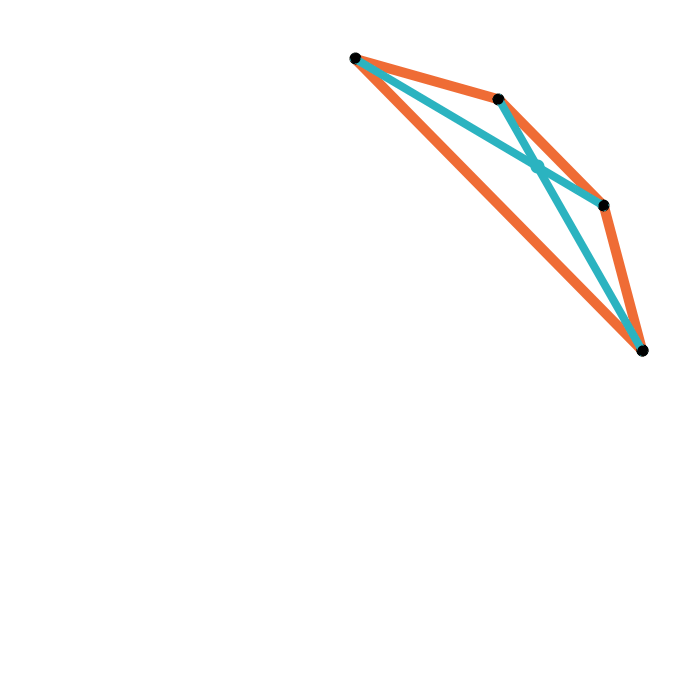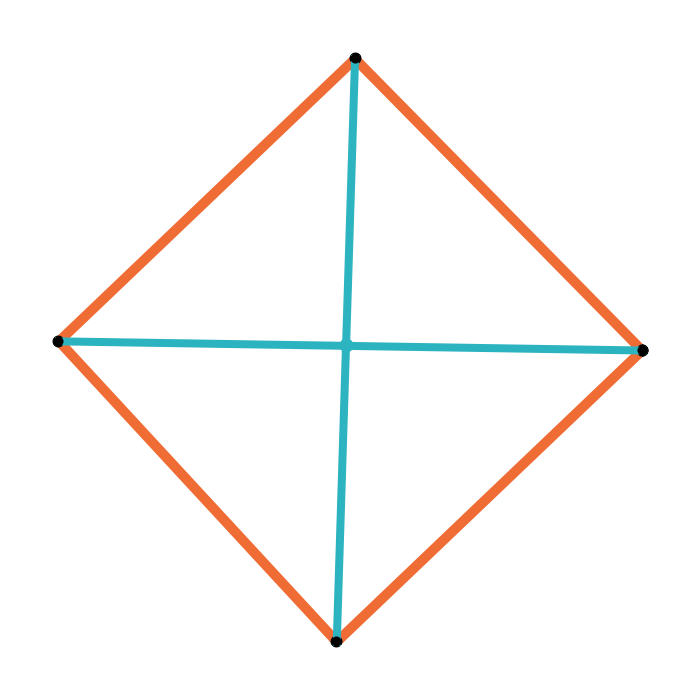
Geometric median closure
Definition
If the edge cloud \(X\) of an equilateral arm has a nice geometric median, the geometric median closure \(\text{gmc}(X)\) recenters the edge cloud at the geometric median.
\(\text{gmc}(X)_i = \frac{x_i-\text{gm}(X)}{\|x_i - \text{gm}(X)\|}\)
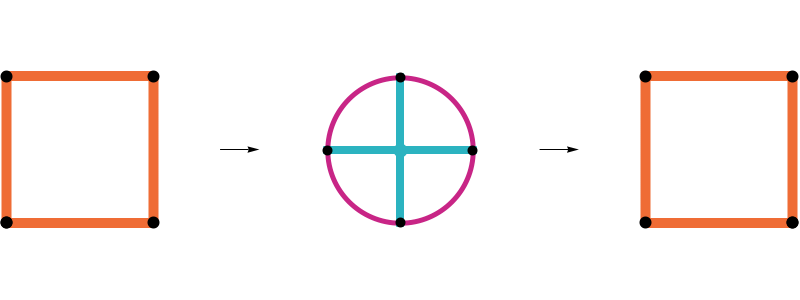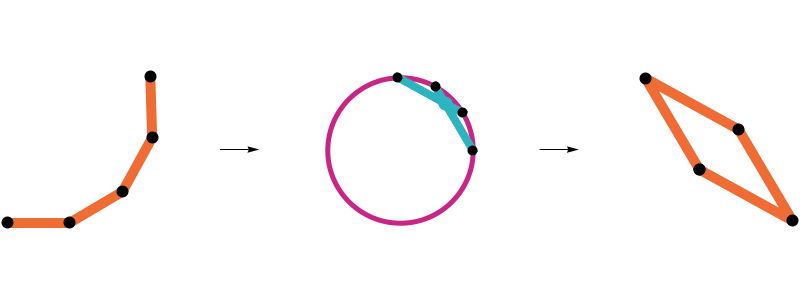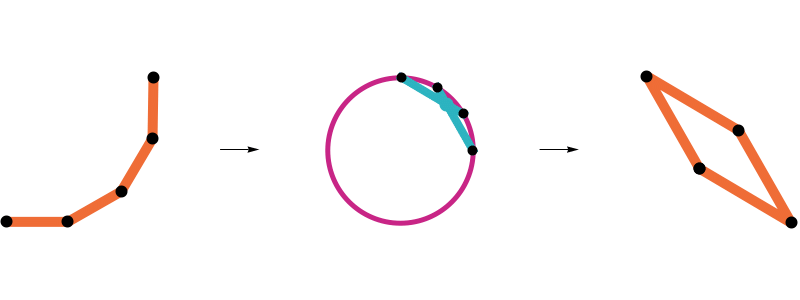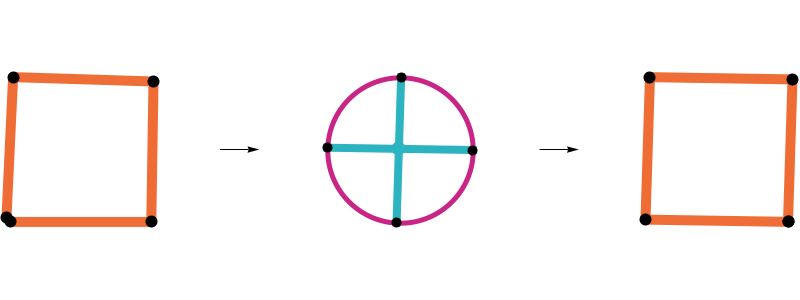
Closing a 17-edge arm
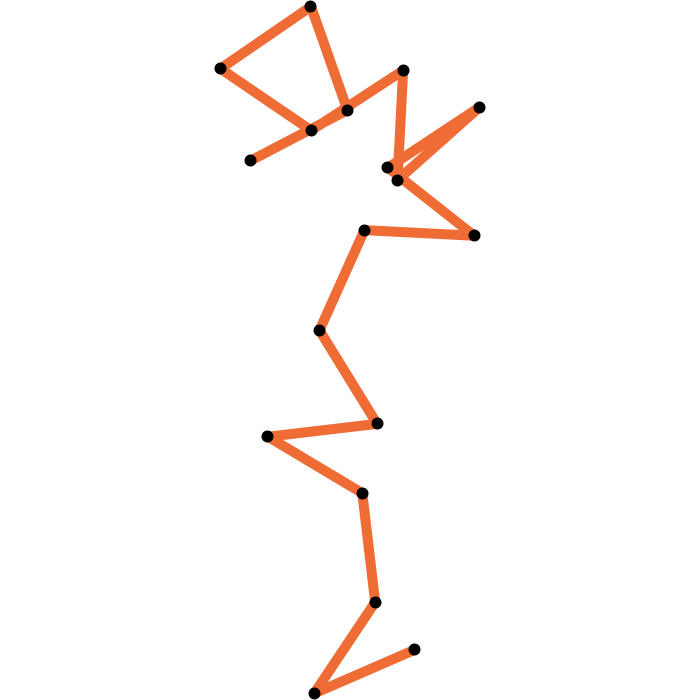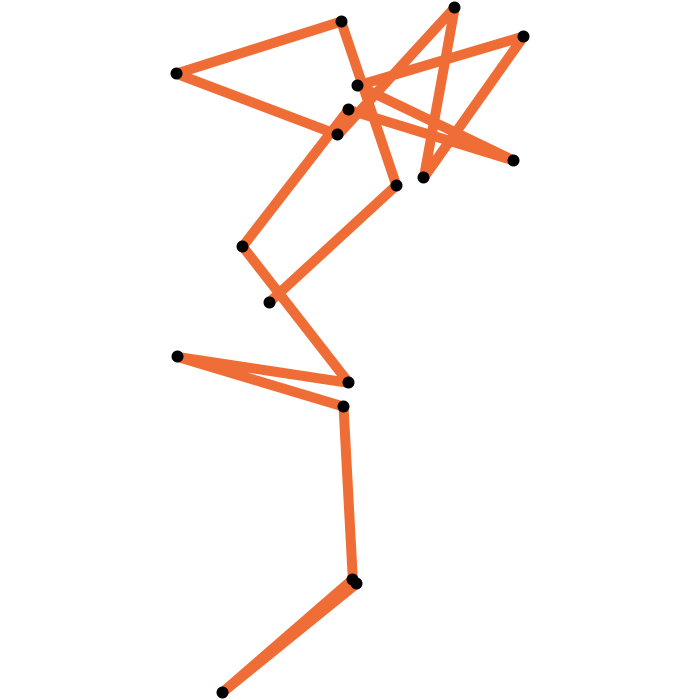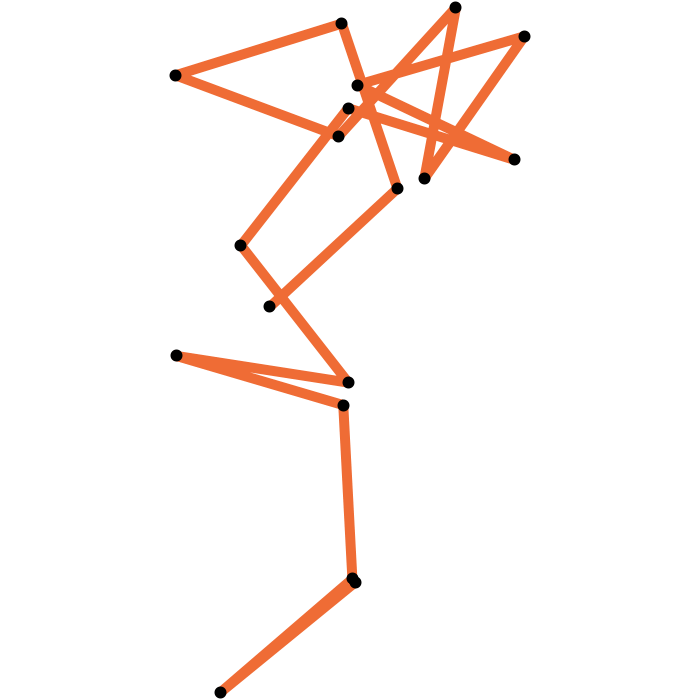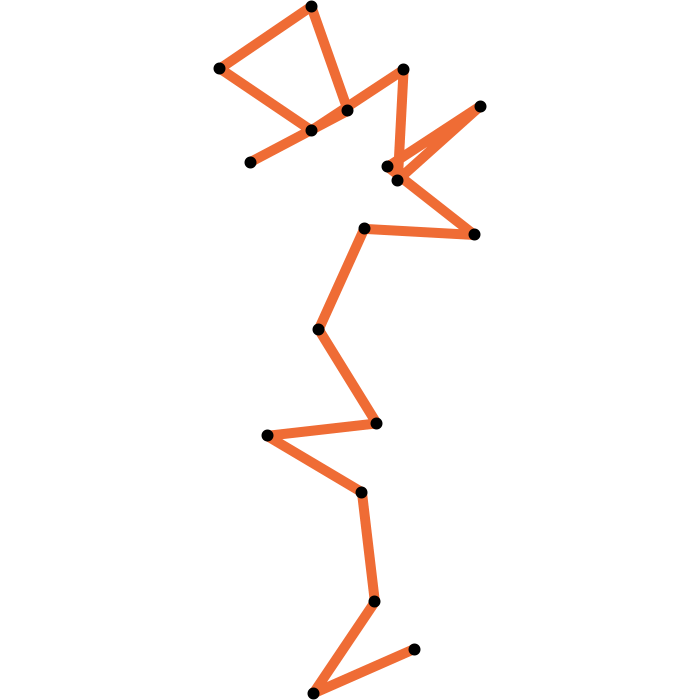
Loop closure

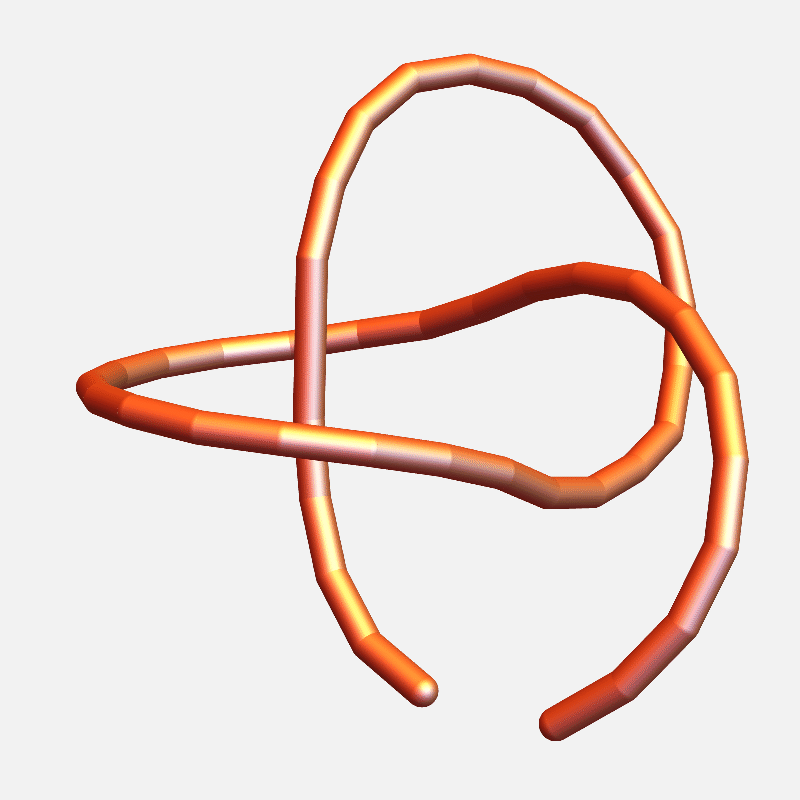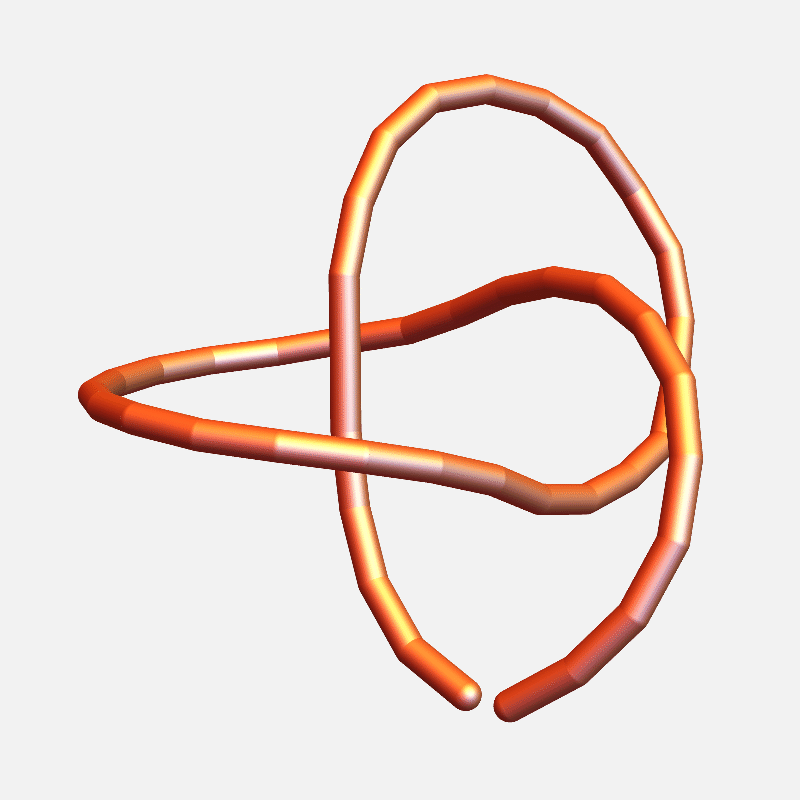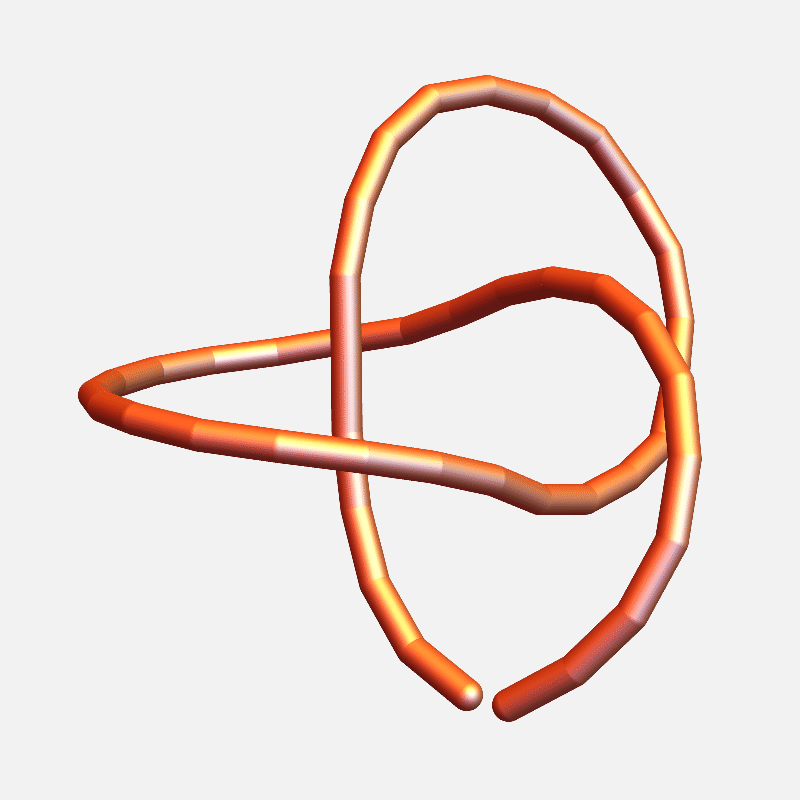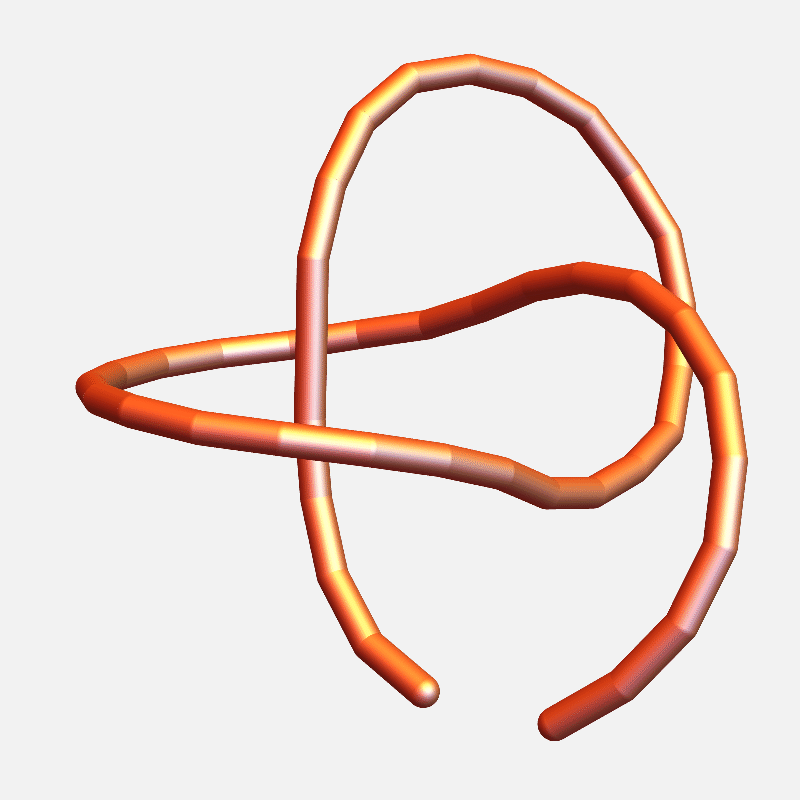


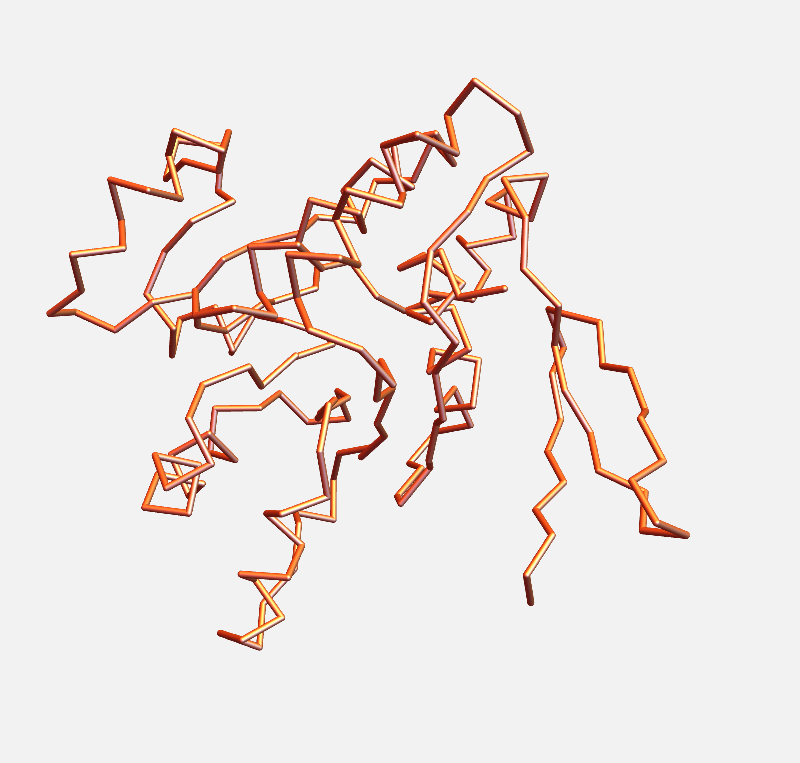

1QMG – Acetohydroxyacid isomeroreductase
The geometric median closure is closed
Proposition (with Cantarella)
If it exists, the geometric median closure of an arm is a closed polygon.
Proof
\(\text{gm}(X)\) minimizes the total distance function
\(d_X(y) = \sum_i \|x_i - y\|\),
which is convex everywhere and smooth away from the \(x_i\), and
\(\nabla d_X(y) = \sum_i \frac{x_i-y}{\|x_i-y\|}\).
The geometric median closure is optimal
Definition
An arm or polygon \(X\) is given by \(n\) edge vectors \(x_i \in \mathbb{R}^d\), or a single point in \(\mathbb{R}^{dn}\). The distance between \(X\) and \(Y\) is the Euclidean distance between these points in \(\mathbb{R}^{dn}\).
Theorem (with Cantarella)
If \(X\) is an equilateral arm in \(\mathbb{R}^d\) with a geometric median closure, then \(\text{gmc}(X)\) is the closest equilateral polygon to \(X\).
Proof
Depends on the neat fact that if \(\|x_i\|=\|y_i\|\), then
\(\langle X, Y -X \rangle \leq 0\).
gmc can fail, but not often
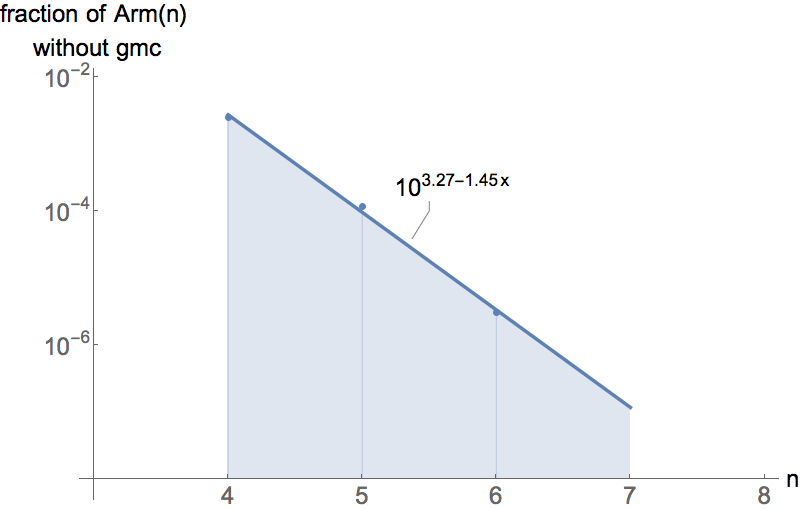
Theorem* (with Cantarella)
The fraction of \(\text{Arm}_d(n)\) without a geometric median closure \(\to 0\) exponentially fast in \(n\).
Proof strategy
\(\text{Ad}(p) = \sqrt{1+\|p\|^2}\ \Gamma\!\left(\frac{d}{2}\right) {}_2F_1\!\!\left(-\frac{1}{4},\frac{1}{4},\frac{d}{2},\frac{4\|p\|^2}{(1+\|p\|^2)^2}\right)\)
For a random point cloud \(X = (x_1, \ldots , x_n)\) on \(S^{d-1}\), want to show \(\text{gm}(X)\) is close to the origin (and therefore \(\text{gmc}(X)\) exists) with high probability.
Claim: This follows if we can show that \(d_X\) is \(L^\infty\) close to \(d \text{Ad}: B^d \to \mathbb{R}\), where \(\text{Ad}(p)\) is the average distance from \(S^{d-1}\) to \(p \in B^d\).
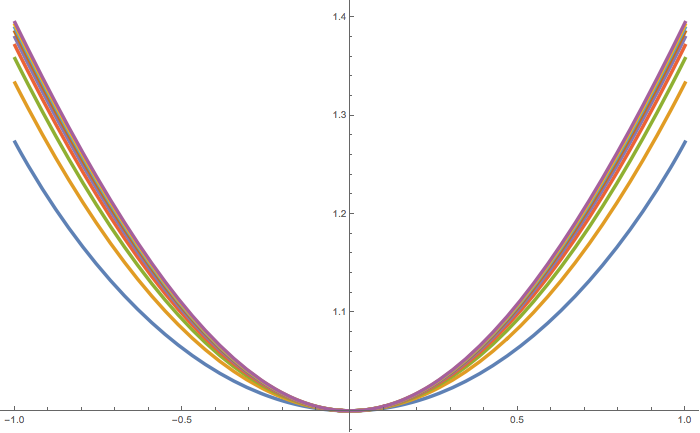
Lemma (Hjort & Pollard, 1993)
Let \(f\) be convex and \(g\) any function with unique argmin at 0. Let \(B_\delta\) be the ball of radius \(\delta\), \(M = \sup_{s \in B_\delta}|f(s) -g(s)|\), \(m = \inf_{s \in \partial B_\delta}|g(s) - g(0)|\). If \(M < m/2\), then argmin \(f \in B_\delta\).
Concentration of measure
Theorem (Bernstein inequality for Hilbert spaces)
Let \((\Omega,\mathcal{A},P\) be a probability space, \(H\) a separable Hilbert space, \(B > 0, \sigma > 0\). If \(\xi_1,\ldots , \xi_n:\Omega \to H\) are independent r.v.'s satisfying \(\mathbb{E}(\xi_i)=0, \|\xi_i\|_\infty \leq B, \mathbb{E}(\|\xi_i\|_H^2)\leq \sigma^2\), then
\(P\left(\left\|\frac{1}{n}\sum \xi_i\right\|_H \geq \sqrt{\frac{2\sigma^2 \tau}{n}} + \sqrt{\frac{\sigma^2}{n}} + \frac{2B\tau}{3n}\right) \leq e^{-\tau}\)
In our case, let \(\xi_i(p) = \|x_i-p\| - \text{Ad}(p)\) and \(H = L^2(B^d)\). Then, e.g.,
\(P\left(\left\|\frac{1}{n}d_X-\text{ad}\right\|_2 > \frac{30}{n^{1/3}}\right) \leq e^{-n^{1/3}} \)
In other words, \(d_X\) and \(d \text{Ad}\) are close in \(L^2\) with high probability
A reverse bound
Proposition (with Cantarella)
If \(f\) is differentiable on \(B^d\) with \(\|\nabla f\|_\infty \leq K\), then
Since \(\|f\|_1 \leq \text{Vol}(B^d) \|f\|_2\), we can combine this with the concentration result to see that \(d_X\) is \(L^\infty\) close to the average distance function with high probability, and hence the Hjort & Pollard lemma applies.
Is this a good sampler?
If \(X \in (S^{d-1})^n\) is chosen uniformly, then we've seen that \(\text{gmc}(X)\) exists with very high probability.
This produces some distribution on closed polygons.
Question
What is this distribution? Is it uniform?
We can test when \(d=3\)…
Chordlengths are (supposed to be) uniform
A more subtle test
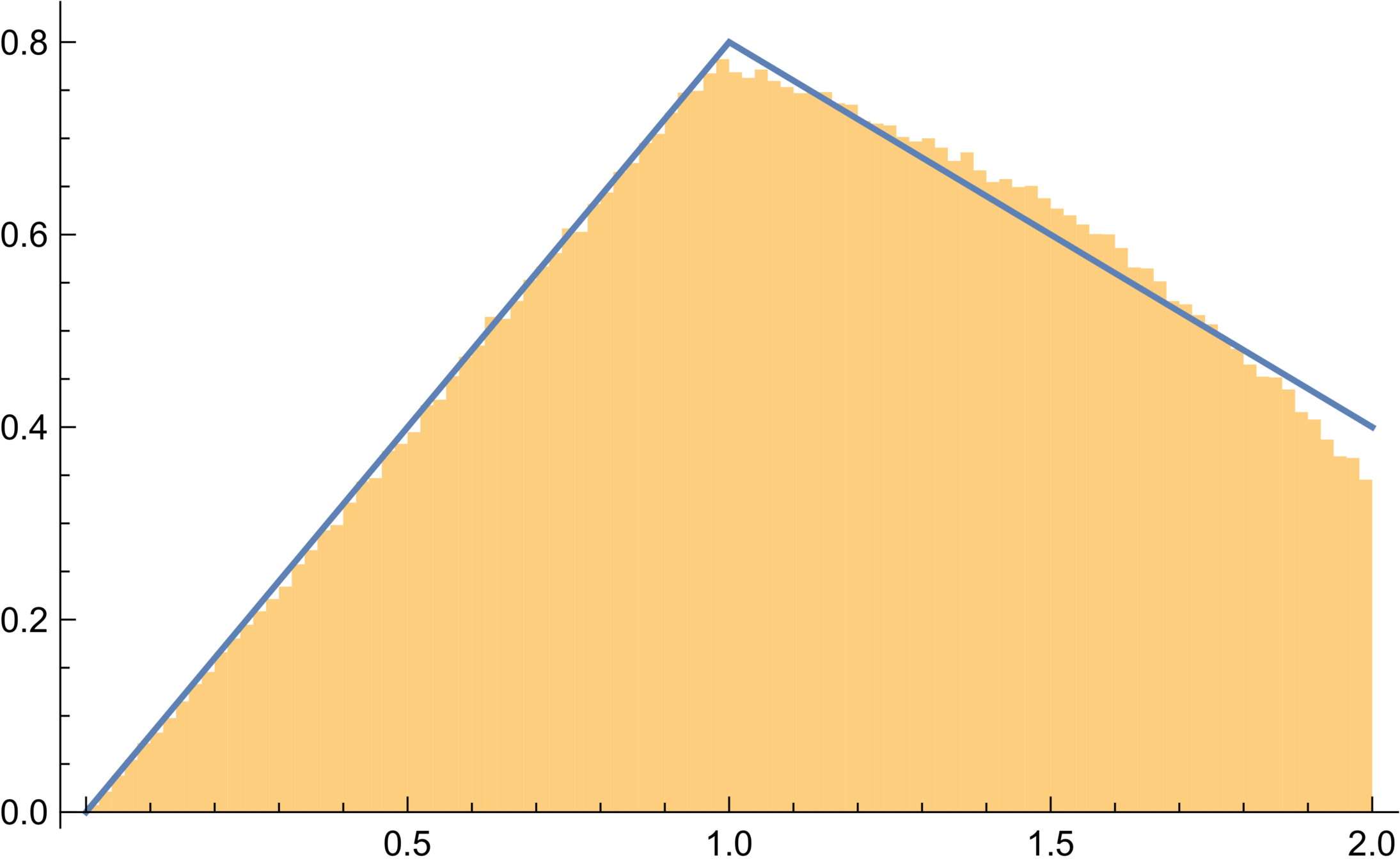
Histogram of chord lengths from ~ 1 million pentagons created by sampling arms and applying gmc, compared to exact pdf of random pentagons
Exact chord pdfs
Let \(\phi_n(\ell)\) be the density of the end-to-end distance in an \(n\)-step random flight. From Lord Rayleigh,
This is piecewise-polynomial of degree \(n-3\).
Proposition
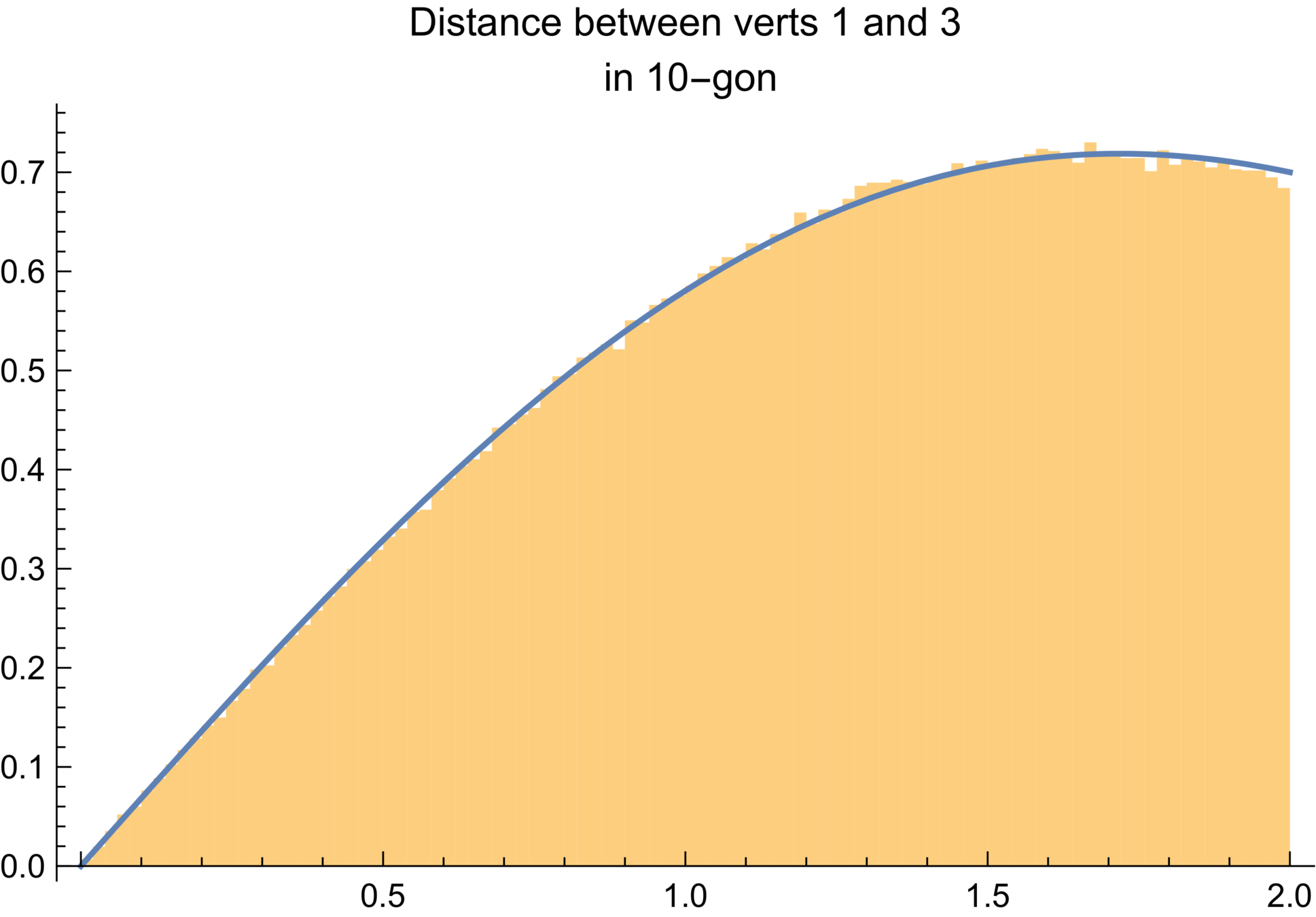
The pdf of the length of the chord connecting \(v_1\) to \(v_{k+1}\) in an \(n\)-gon is a constant multiple of
A more subtle test
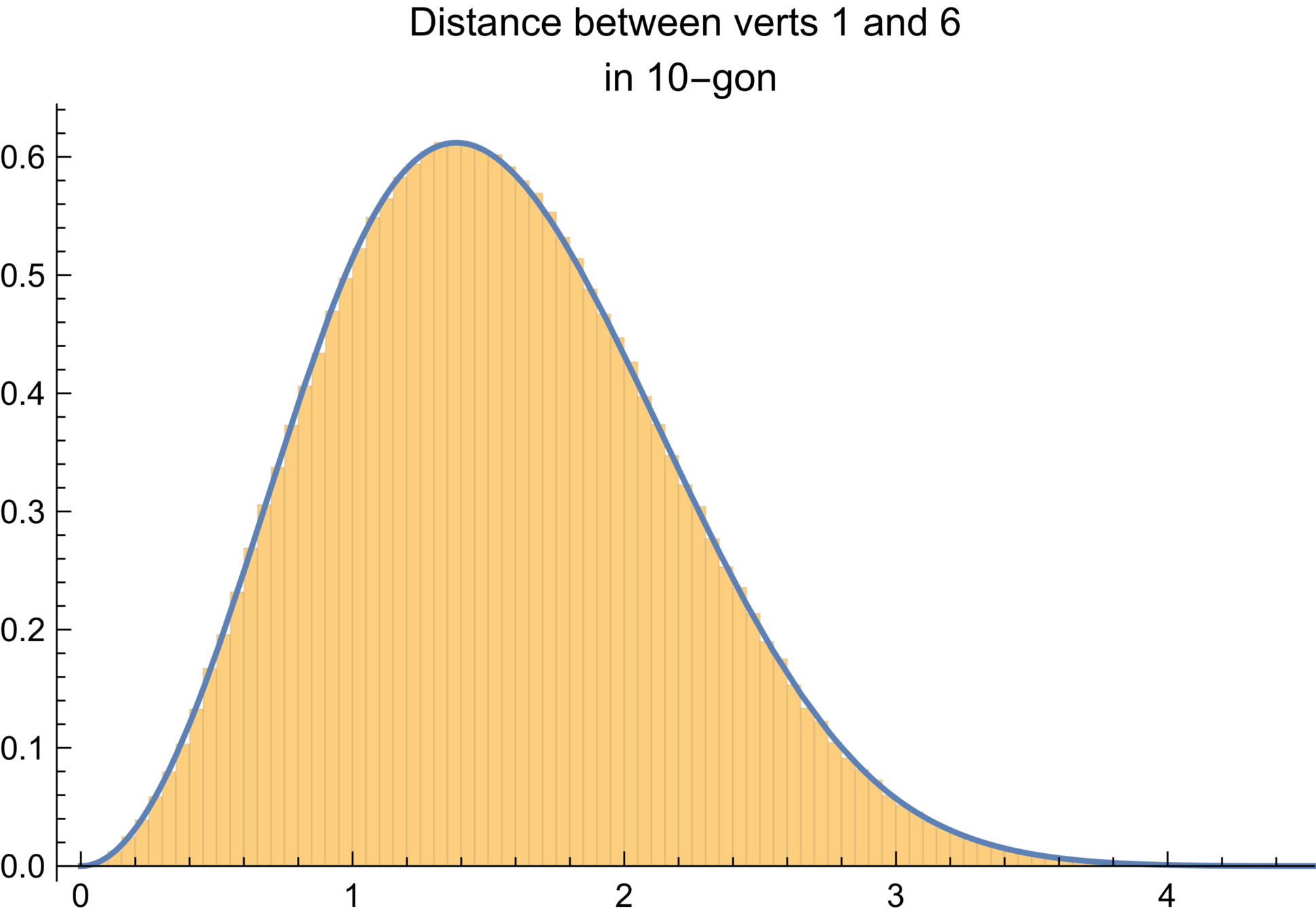
Histogram of chord lengths from ~ 1 million 10-gons created by sampling arms and applying gmc, compared to exact pdf of random 10-gons
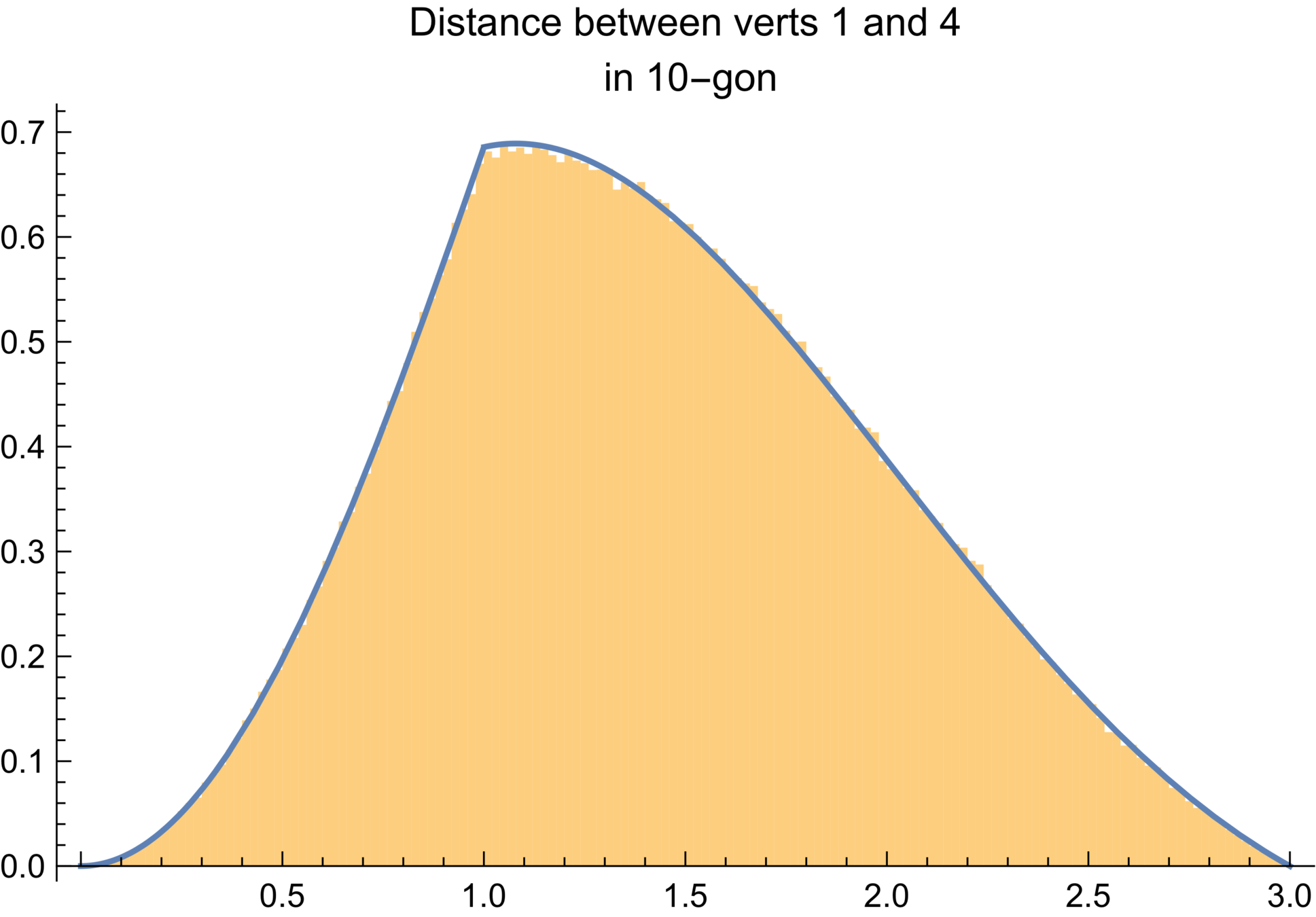
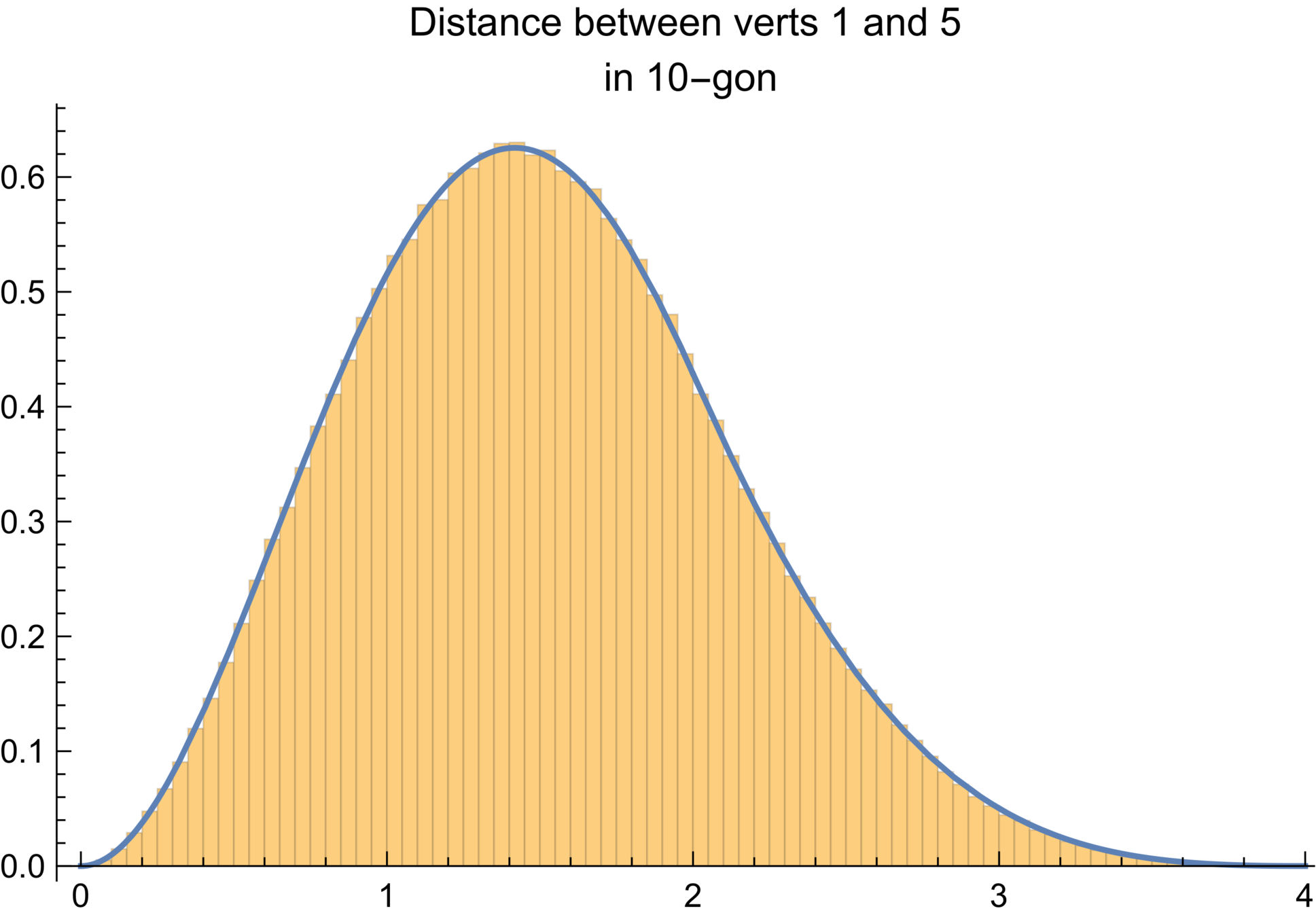
In the limit...
Conjecture
The probability measure generated by geometric median sampling converges (exponentially fast?) to the uniform distribution on equilateral \(n\)-gons as \(n \to \infty\).
Conjecture
The integral of any function which varies slowly enough with respect to any permutation-invariant probability measure on equilateral \(n\)-gons converges to the integral of the function with respect to the uniform distribution on equilateral \(n\)-gons as \(n \to \infty\).
Application: Polygon evolutions
Algorithm
To follow a flow in polygon space:
- Compute the infinitesimal variation \(V\) in \(\mathbb{R}^{dn}\) at \(X^{(n)}\) tangent to \(\text{Pol}_d(n)\) (or at least \(\text{Arm}_d(n)\)).
- Follow the exponential map in \(\text{Arm}_d(n)\) in direction \(V\) (to preserve edgelengths exactly).
- Use geometric median closure to get \(X^{(n+1)} \in \text{Pol}_d(n)\).
How far can you step?
A safe step distance
Definition
If \(P\) is a closed \(n\)-gon in \(\mathbb{R}^d\) with edge cloud \(X\) and \(\lambda_1\) is the first eigenvalue of \(X^TX\), define
Theorem (with Cantarella)
If \(P\) is a closed equilateral \(n\)-gon, every arm within \(d_{\text{safe}}\) of \(P\) has a geometric median closure. This distance bound is positive if \(P\) is not contained in a line.
The algorithm, redux
Algorithm
To follow a flow in polygon space:
- Compute the infinitesimal variation \(V\) in \(\mathbb{R}^{dn}\) at \(X^{(n)}\) tangent to \(\text{Pol}_d(n)\) (or at least \(\text{Arm}_d(n)\)).
- Find \(\lambda_1\) and use it to compute \(d_{\text{safe}}(X^{(n)})\).
- Follow the exponential map in \(\text{Arm}_d(n)\) in direction \(V\) (to preserve edgelengths exactly), but don't go further than \(d_{\text{safe}}\).
- Use geometric median closure to get \(X^{(n+1)} \in \text{Pol}_d(n)\).
Example: Energy-based carpenter’s rule

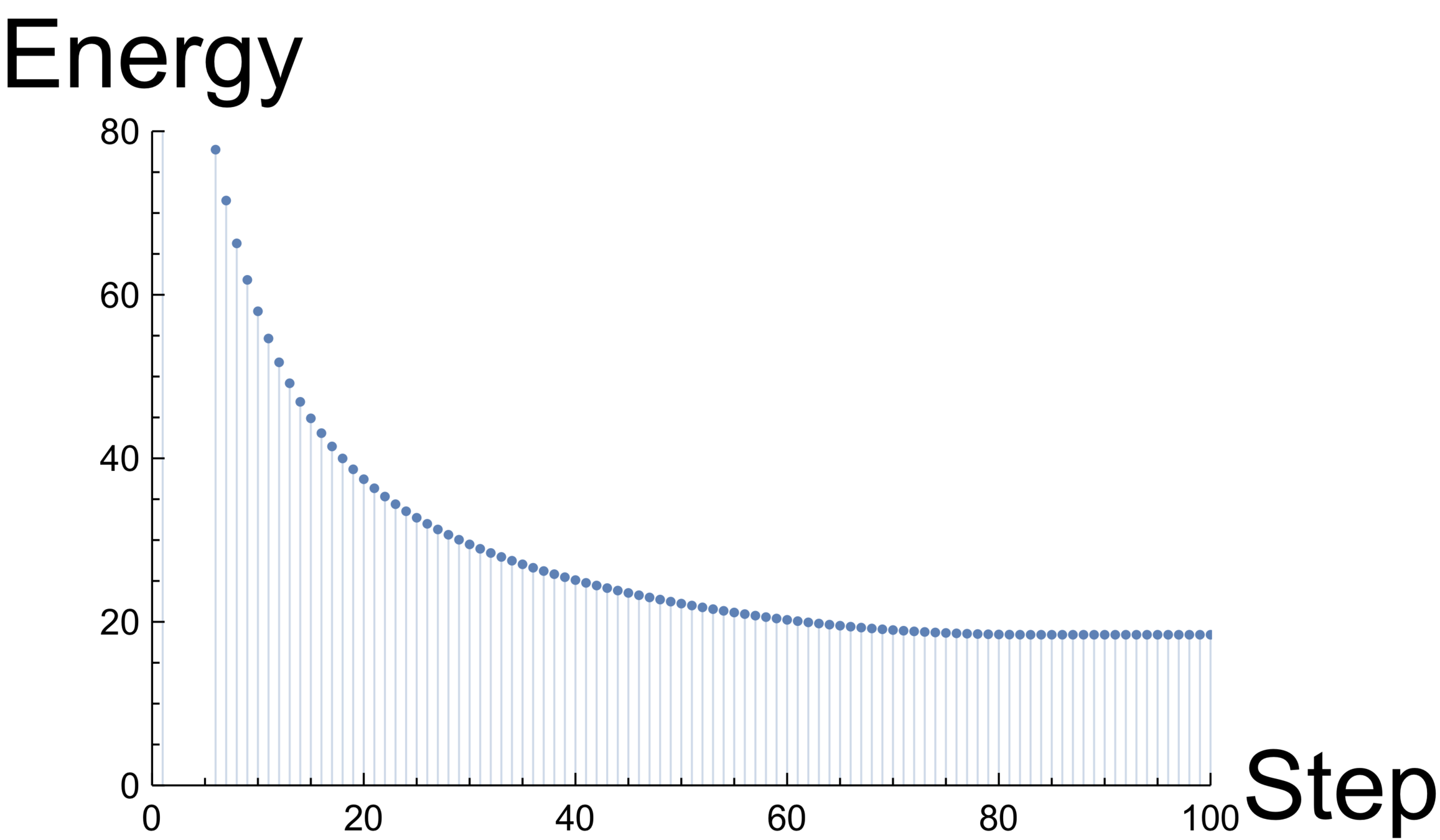
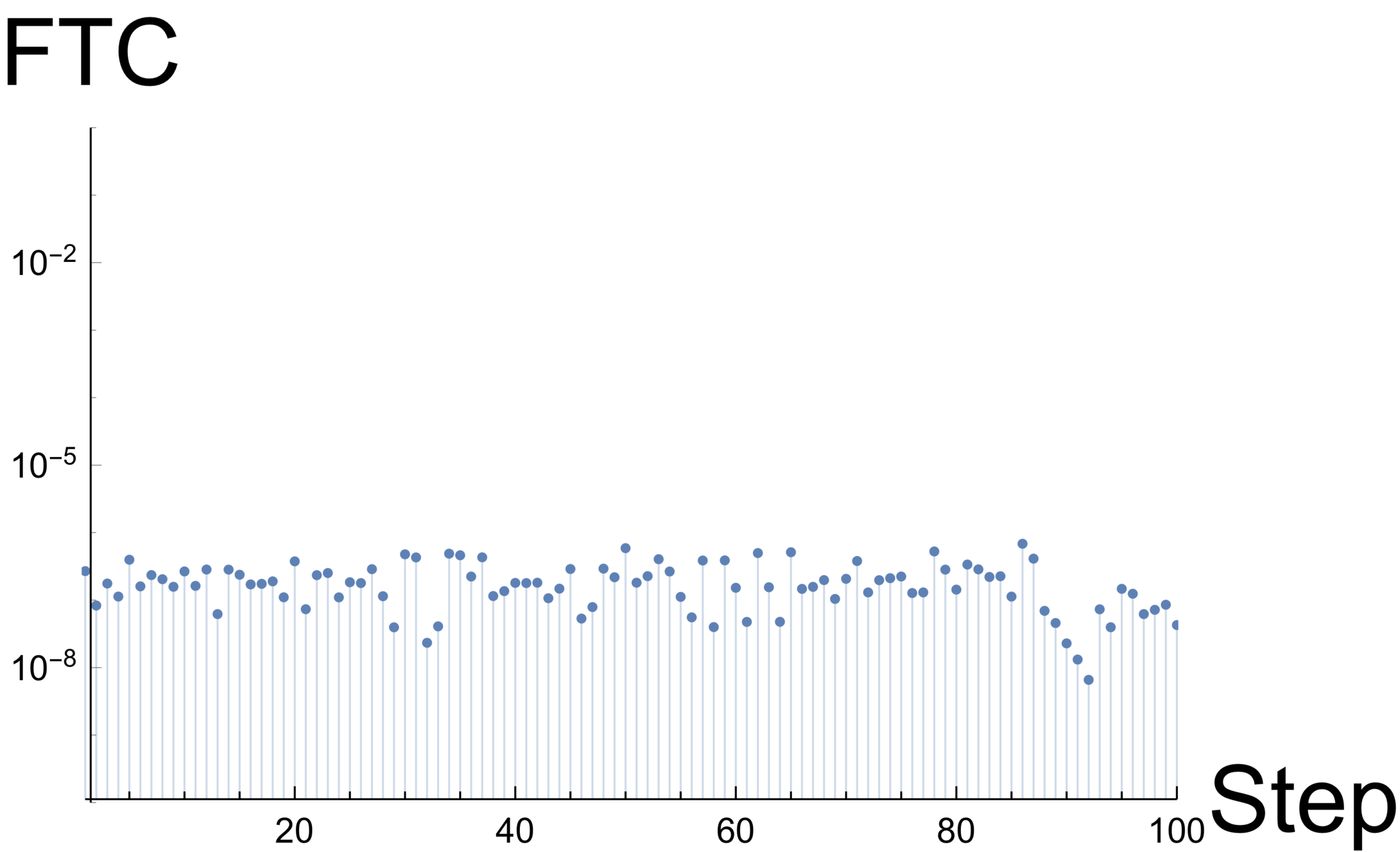
Recap
In any dimension
- The geometric median provides an optimal loop closure.
- It works on nearly all arms. The failure set is small, but somewhat hard to describe.
- The pushforward measure is almost uniform.
- These tools provide clean computational methods for polygon reconfigurations.
Thank you!
References
The symplectic geometry of closed equilateral random walks in 3-space
J. Cantarella & C. Shonkwiler
Annals of Applied Probability 26 (2016), no. 1, 549–596
A fast direct sampling algorithm for equilateral closed polygons
J. Cantarella, B. Duplantier, C. Shonkwiler, & E. Uehara
Journal of Physics A 49 (2016), no. 27, 275202
A natural map from random walks to closed polygons in any dimension
J. Cantarella & C. Shonkwiler
In preparation
Funding: Simons Foundation