Generating (and Computing with) Very Large Ensembles of Random Polygonal Knots

Clayton Shonkwiler

Colorado State University

shonkwiler.org

/birs24

this talk!

Knot Theory Informed by Random Models and Experimental Data

April 4, 2024

Key Points

Symplectic tools lead to efficient algorithms for sampling random polygonal knots in confinement.
Confinement boosts the likelihood of complicated knots: enriched sampling.

Elementary Knot Invariants

Definition.

The stick number of a knot \(K\), denoted \(\operatorname{stick}[K]\), is the minimum number of segments needed to create a polygonal version of \(K\).

\(\operatorname{stick}[3_1]=6\)

Elementary Knot Invariants

If \(v \in S^2\) and \(\gamma\) a closed curve, let \(\operatorname{b}_v(\gamma)\) be the number of local maxima of the projection of \(\gamma\) to the line through \(v\).

\(\operatorname{b}_{v_1}(\gamma)=2\)

\(v_1\)

\(v_2\)

\(\operatorname{b}_{v_2}(\gamma)=3\)

Elementary Knot Invariants

Definition.

If \(\gamma\) is a closed curve, its bridge number is

and its superbridge number is

\operatorname{b}(\gamma) := \min_v \operatorname{b}_v(\gamma)

\operatorname{sb}(\gamma) := \max_v \operatorname{b}_v(\gamma).

The bridge index of a knot \(K\) is

and the superbridge index is

\operatorname{b}[K] := \min_{\gamma \sim K} \operatorname{b}(\gamma)

\operatorname{sb}[K] := \min_{\gamma \sim K} \operatorname{sb}(\gamma).

\(\operatorname{b}[4_1]=2\) and \(\operatorname{sb}[4_1]=3\).

(Most of) What is Known

Theorem [Kuiper, Jin]

For any nontrivial knot \(K\),

\(\operatorname{b}[K] < \operatorname{sb}[K] \leq \frac{1}{2} \operatorname{stick}[K].\)

Theorem [Jeon–Jin]

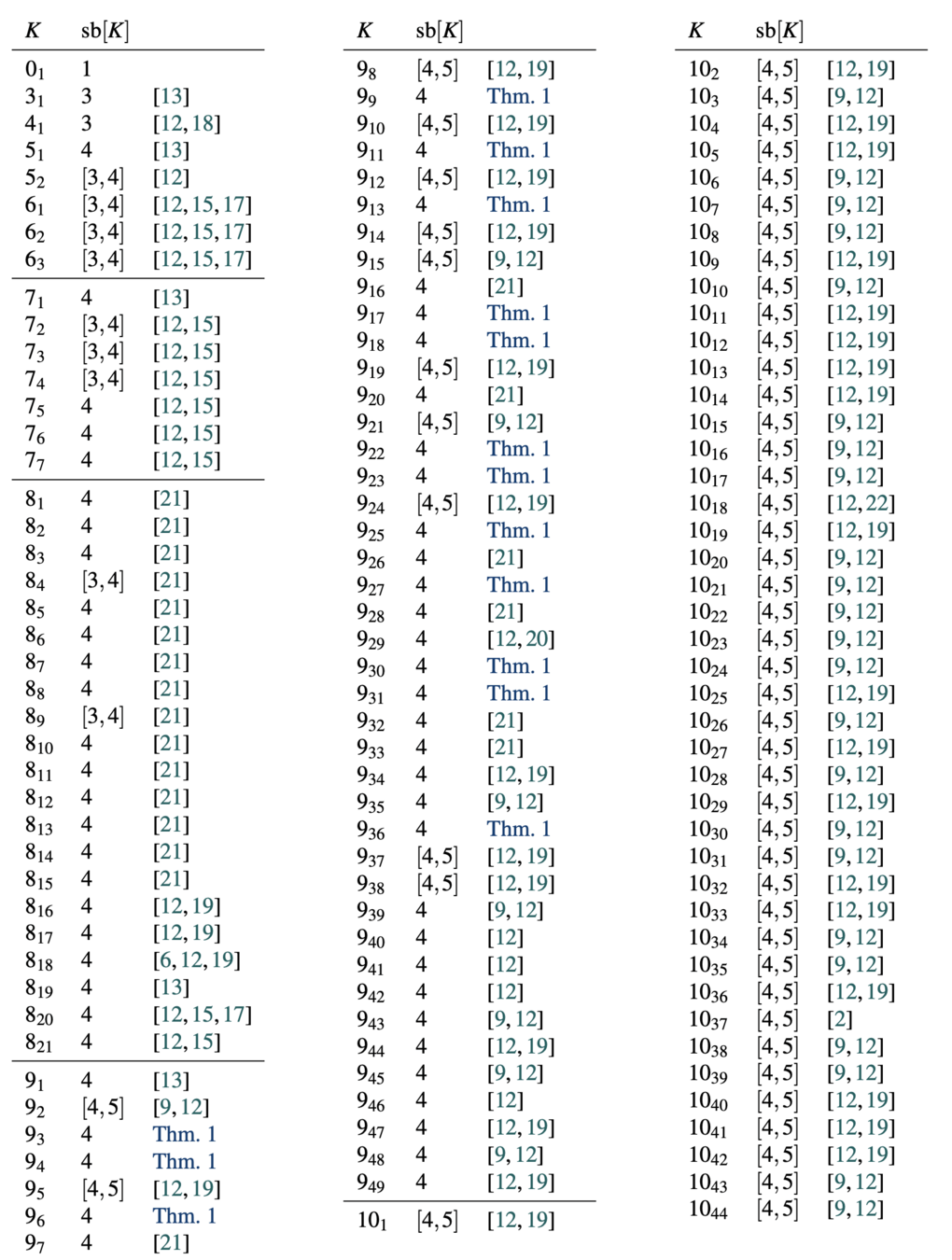
Every knot except \(3_1\) and \(4_1\) and possibly \(5_2\), \(6_1\), \(6_2\), \(6_3\), \(7_2\), \(7_3\), \(7_4\), \(8_4\), and \(8_9\) has superbridge index \(\geq 4\).

Theorem [Calvo]

Every knot except \(3_1\), \(4_1\), \(5_1\), \(5_2\), \(6_1\), \(6_2\), \(6_3\), \(8_{19}\), \(8_{20}\), \(3_1 \# 3_1\), and \(3_1\# -3_1\) has stick number \(\geq 9\).

Theorem [Kuiper, Jin, Adams et al., others]

The superbridge index is known for all torus knots, and the stick number is known for an infinite family of torus knots.

Mantra

Examples provide upper bounds!

Equilateral Polygons

The space of equilateral \(n\)-gons can be constructed as a symplectic reduction (see Kapovich–Millson and Hausmann–Knutson):

\operatorname{ePol}(n)=(S^2)^n/\!/_{\vec{0}}SO(3)

Continuous symmetry \(\Rightarrow\) conserved quantity

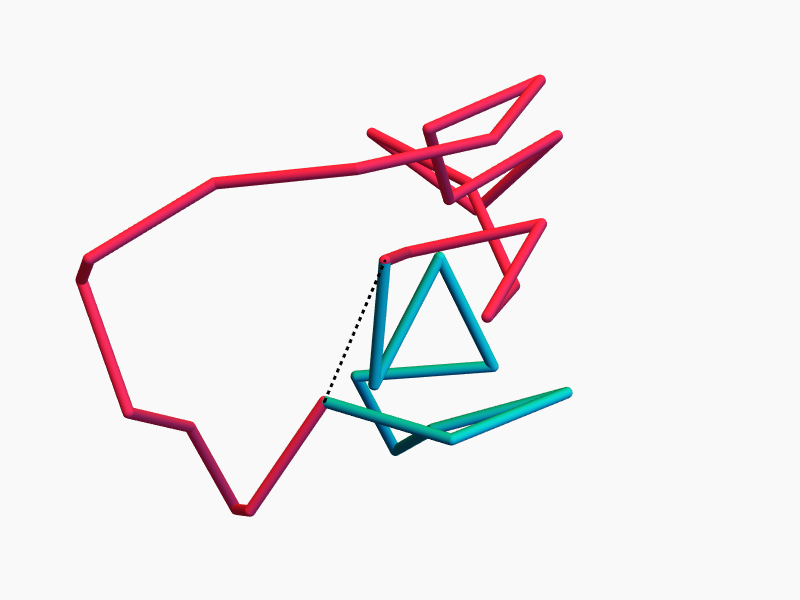
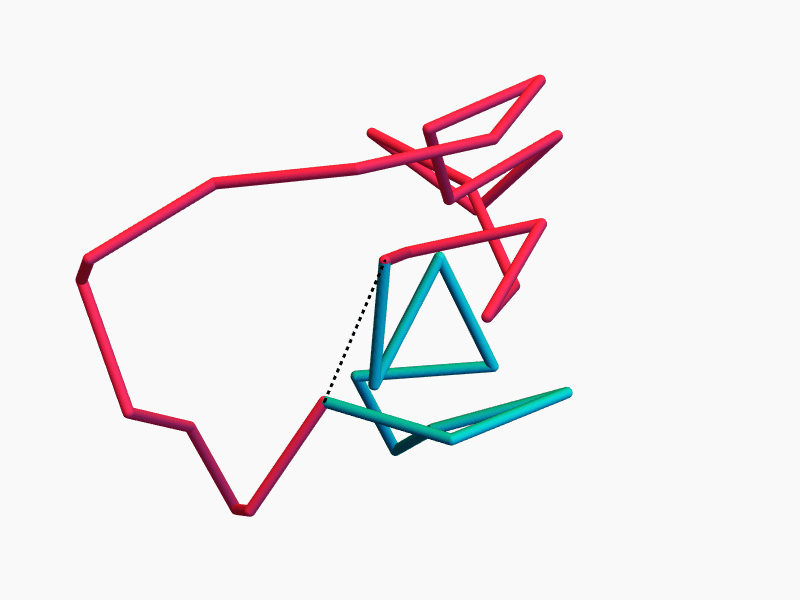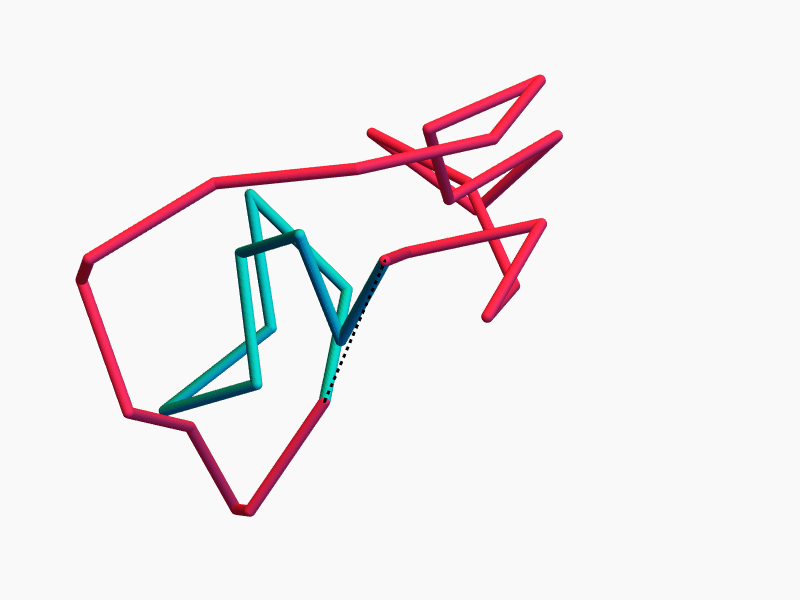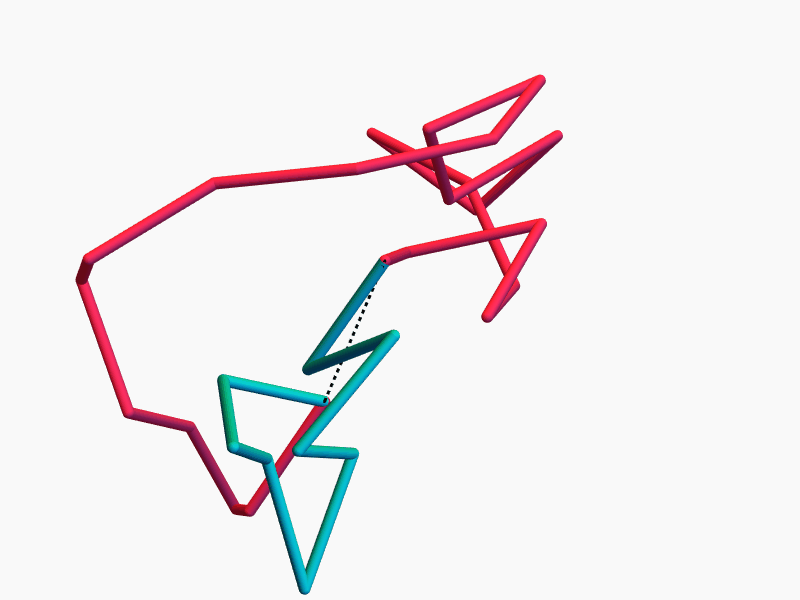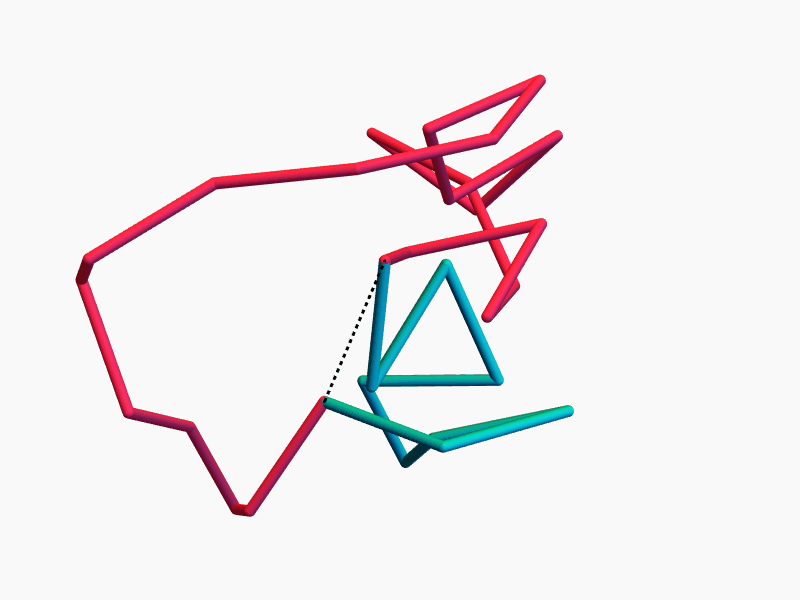
\(n-3\) commuting symmetries

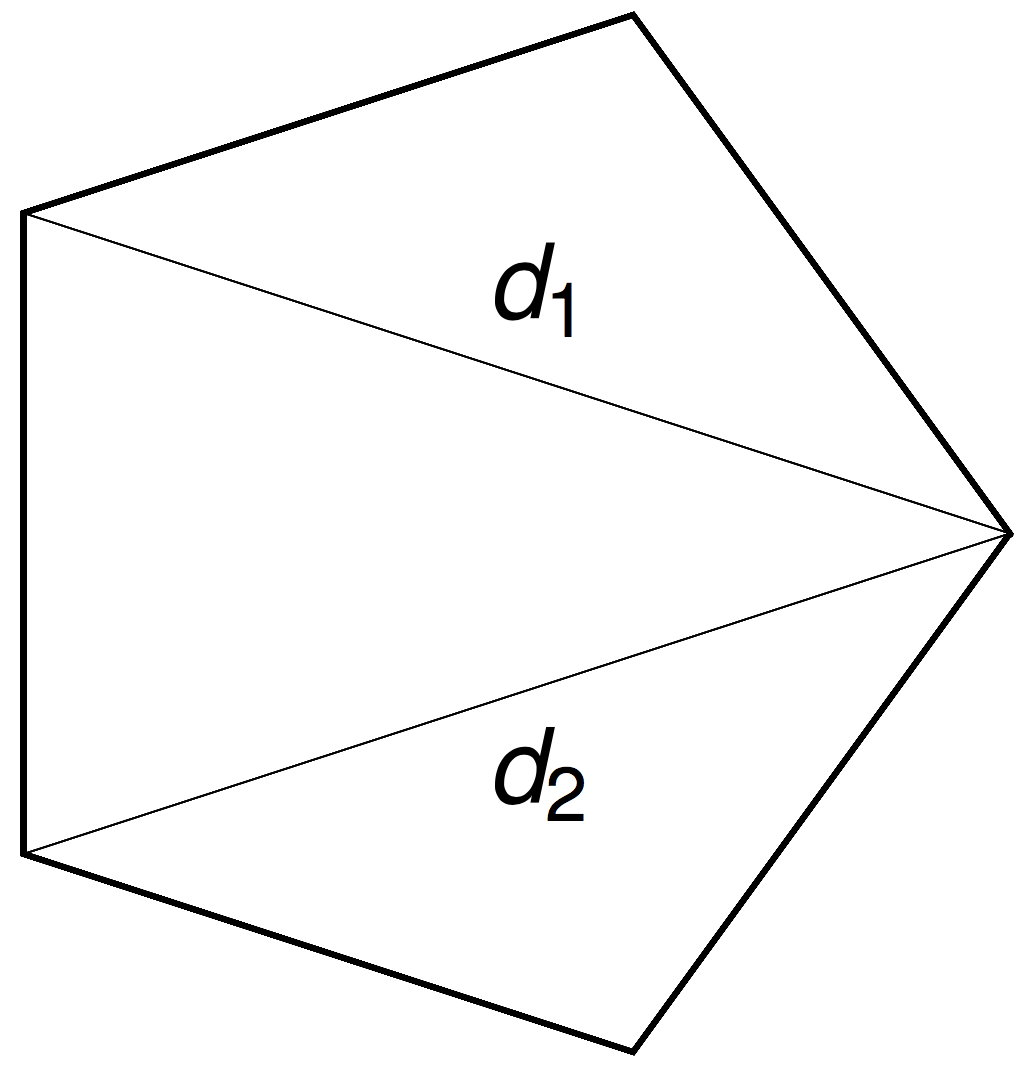
Rotations around \(n-3\) chords \(d_i\) by \(n-3\) angles \(\theta_i\) commute.

More precisely, \(\operatorname{ePol}(n)\) is (almost) toric, and the \(d_i\) and \(\theta_i\) are action-angle coordinates.

Chord distributions

Theorem [with Cantarella]

The joint distribution of \(d_1,\ldots , d_{n-3}\) and \(\theta_1, \ldots , \theta_{n-3}\) are all uniform on their domains.

Therefore, sampling equilateral \(n\)-gons is equivalent to sampling random points in the convex polytope of \(d_i\)’s and random angles \(\theta_i\).

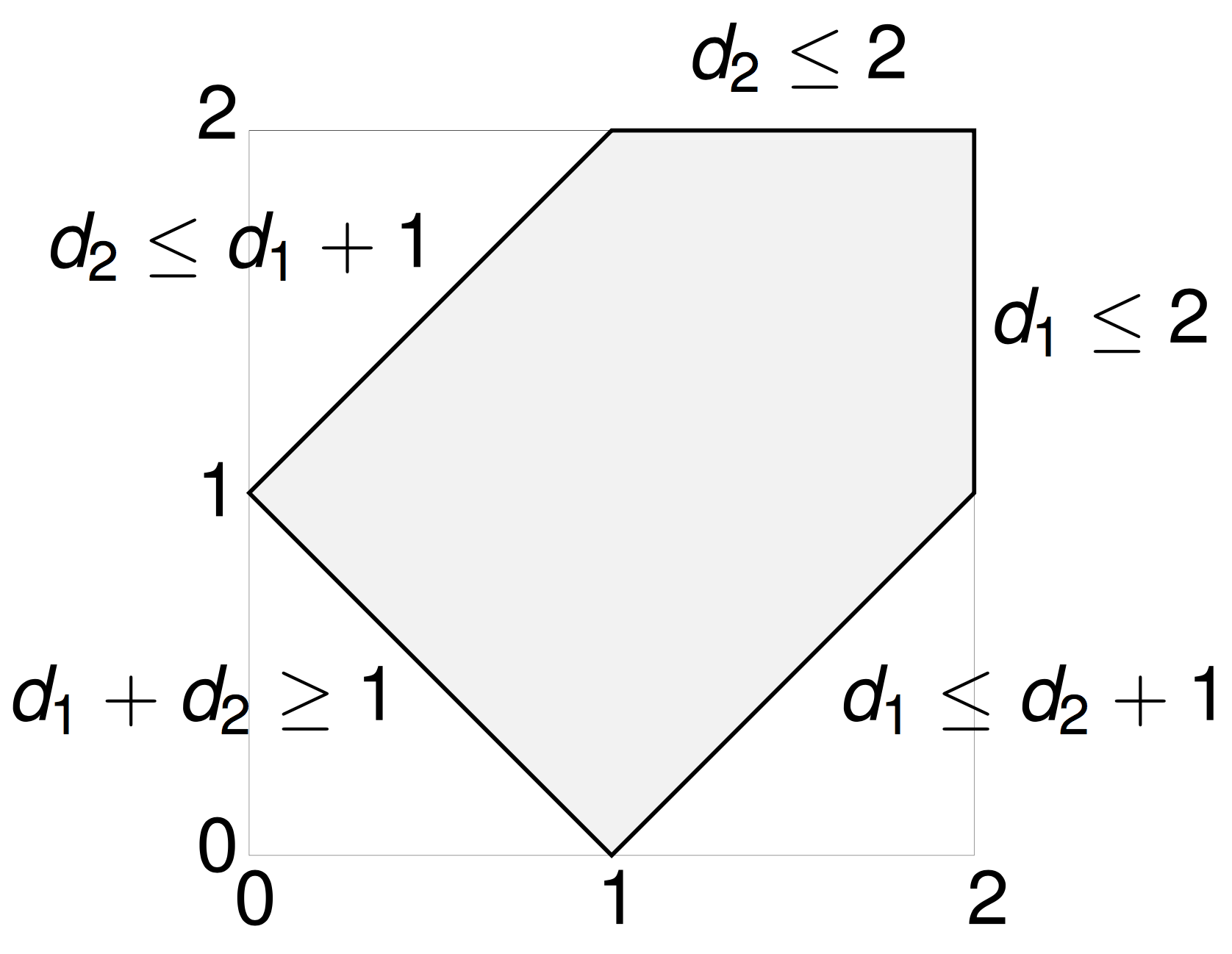
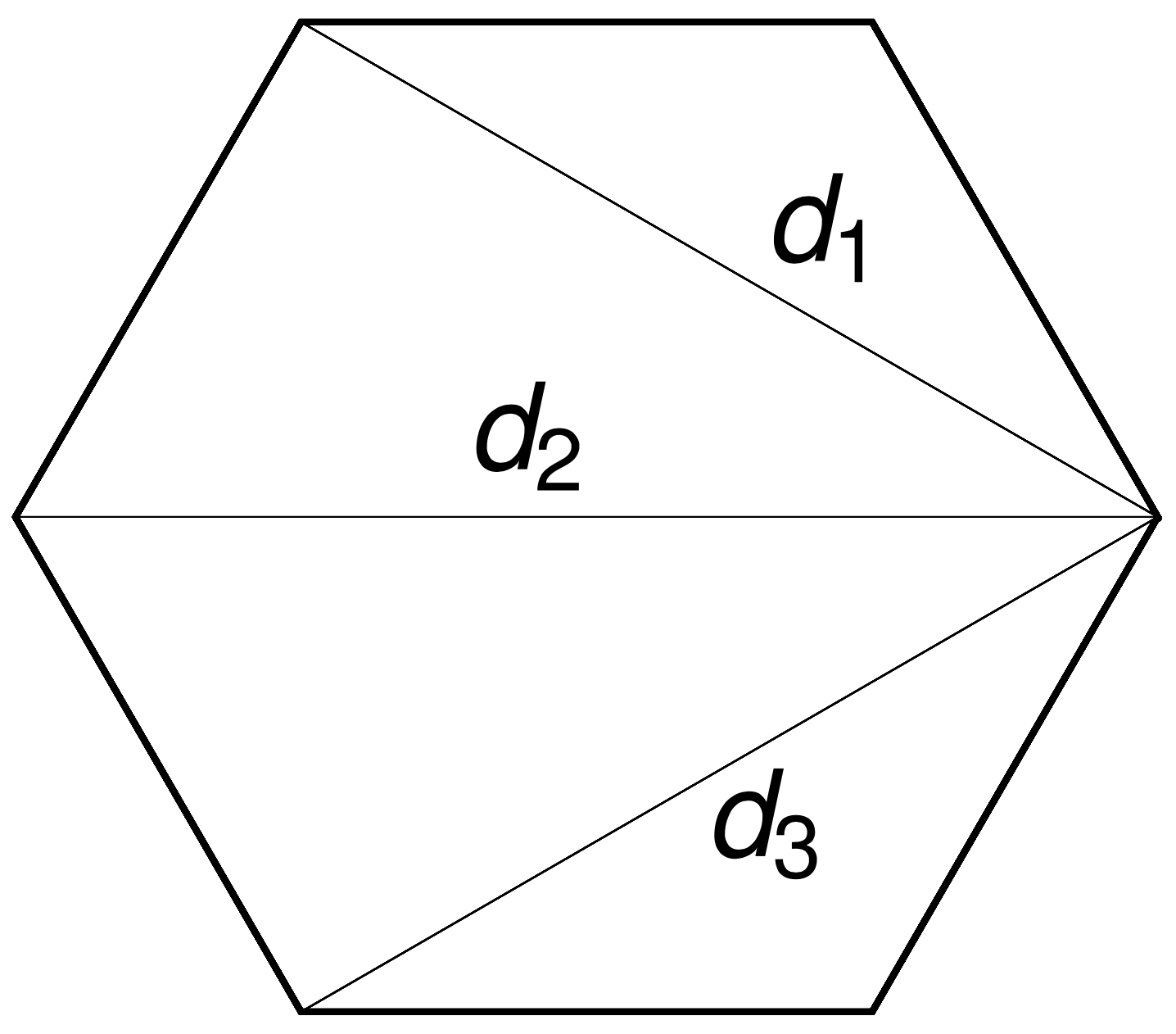
A polytope

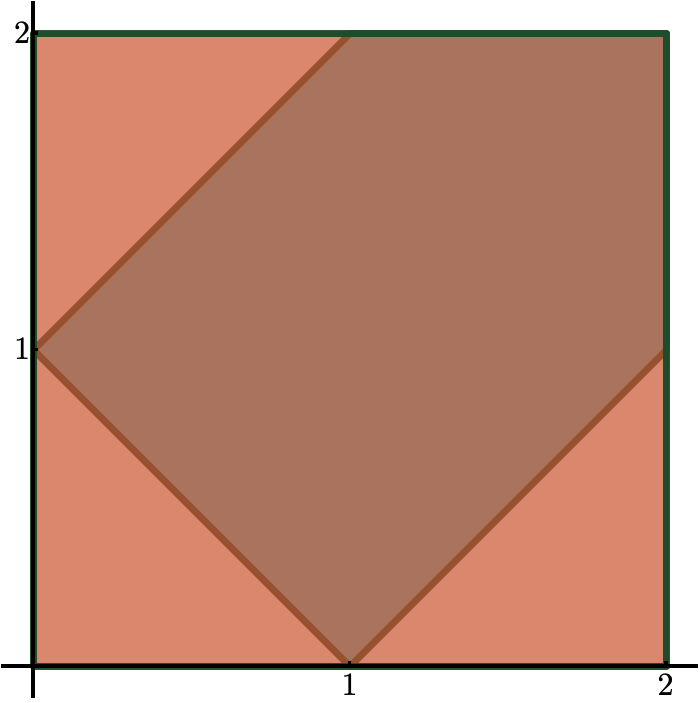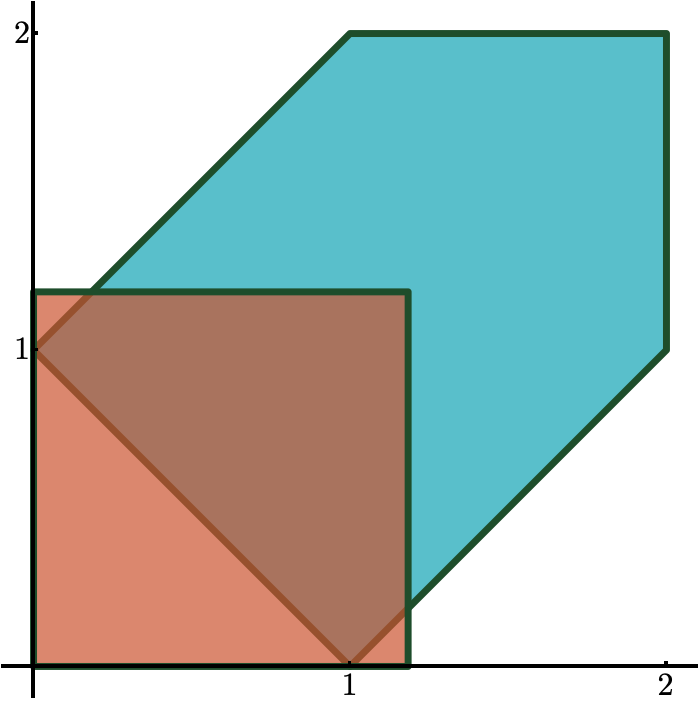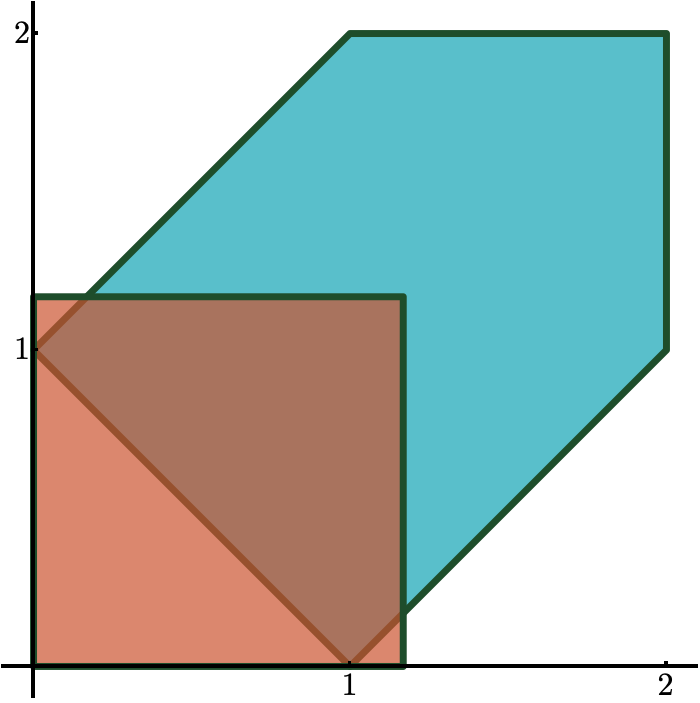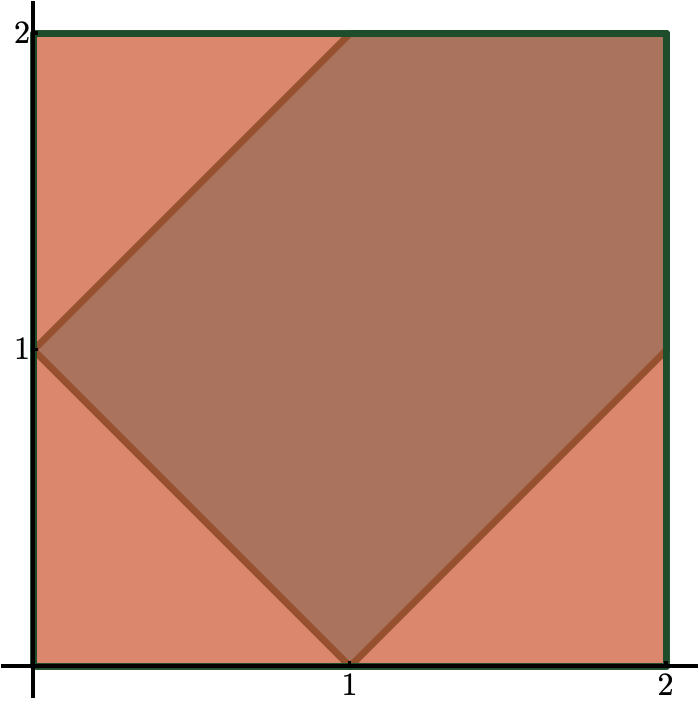
The \((n-3)\)-dimensional moment polytope \(\mathcal{P}_n \subset \mathbb{R}^{n-3}\) is defined by the triangle inequalities

0 \leq d_i \leq 2

1 \leq d_i + d_{i-1}

|d_i - d_{i-1}| \leq 1

0 \leq d_{n-3} \leq 2

Confined Polygons

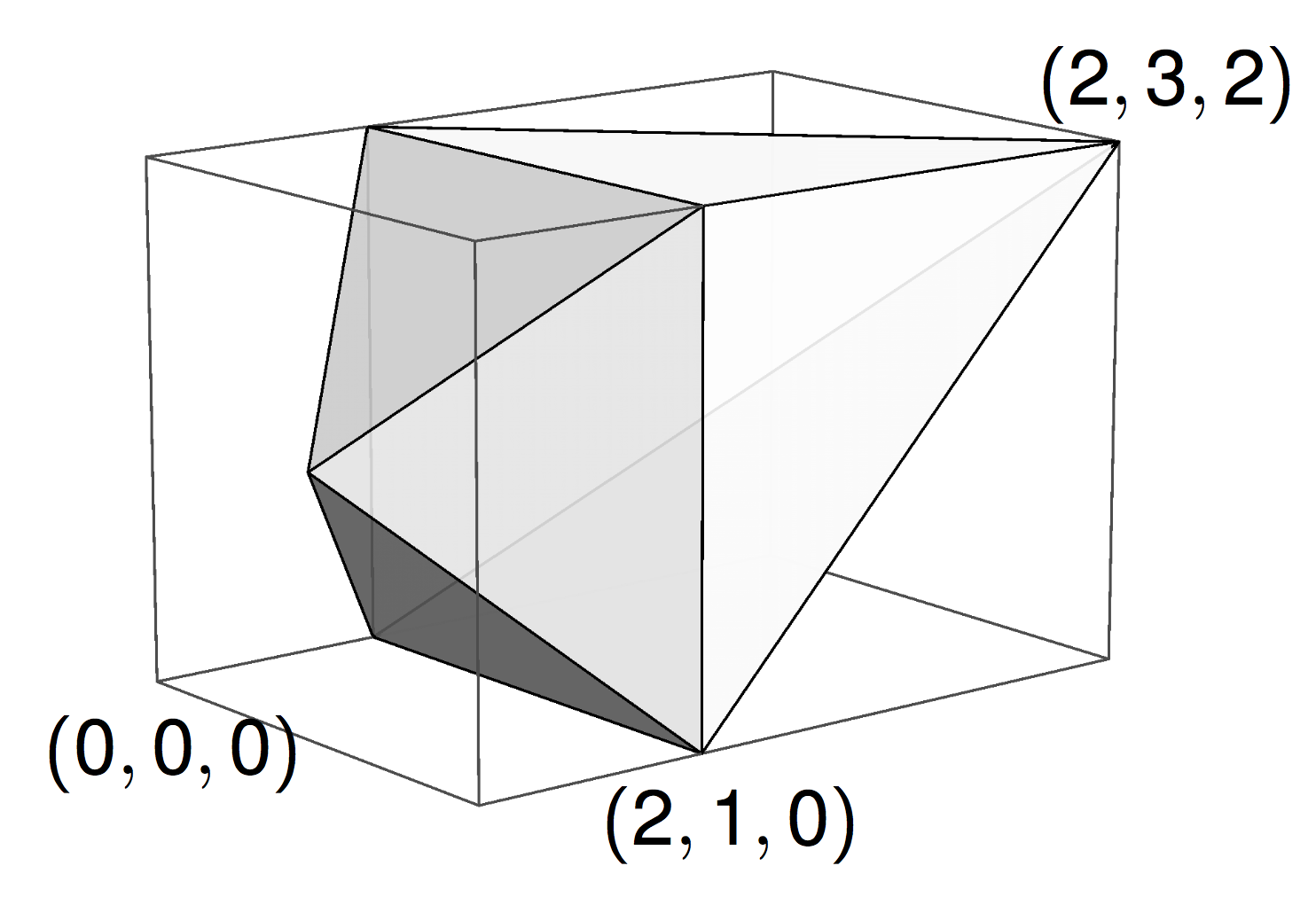
Gelbart & Knobler Science 323 (2009) 1682–1683

If we want to sample polygons in rooted, spherical confinement of radius \(R\), then we simply add the constraints \(d_i \leq R\) for all \(i\).

Sampling

Theorem [Smith, 1984]

For any convex polytope \(\mathcal{P}\), the hit-and-run Markov chain is uniformly ergodic with respect to Lebesgue measure on \(\mathcal{P}\).

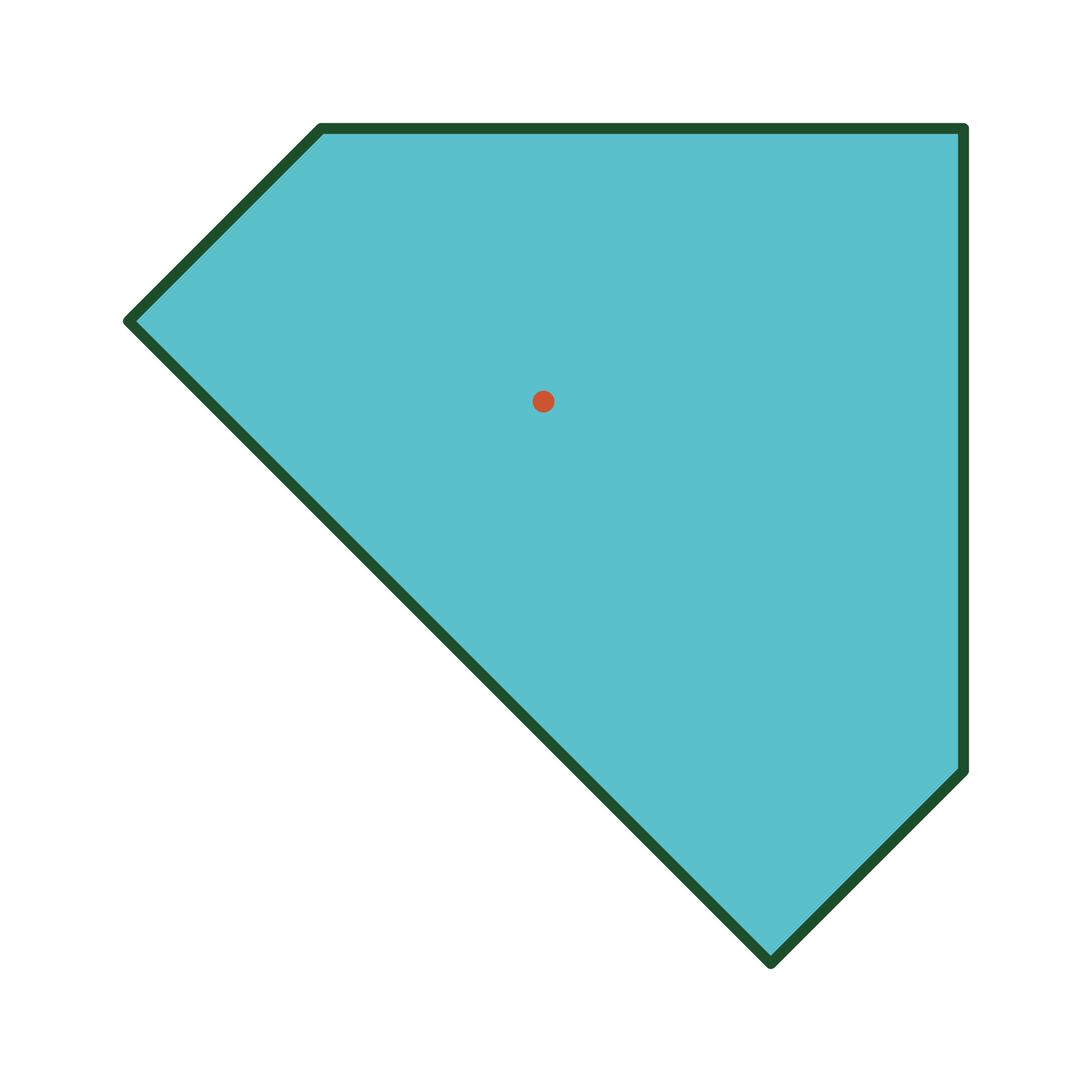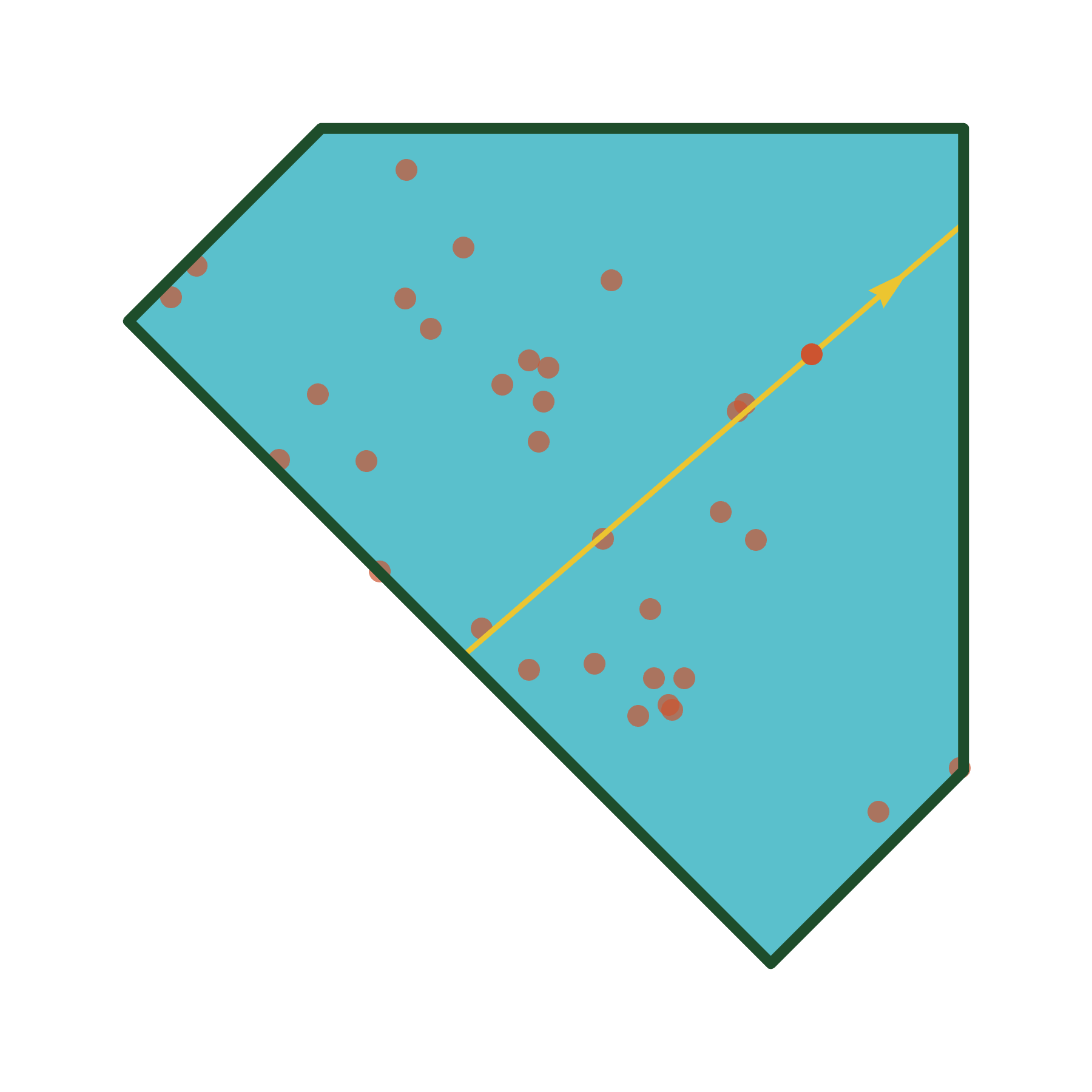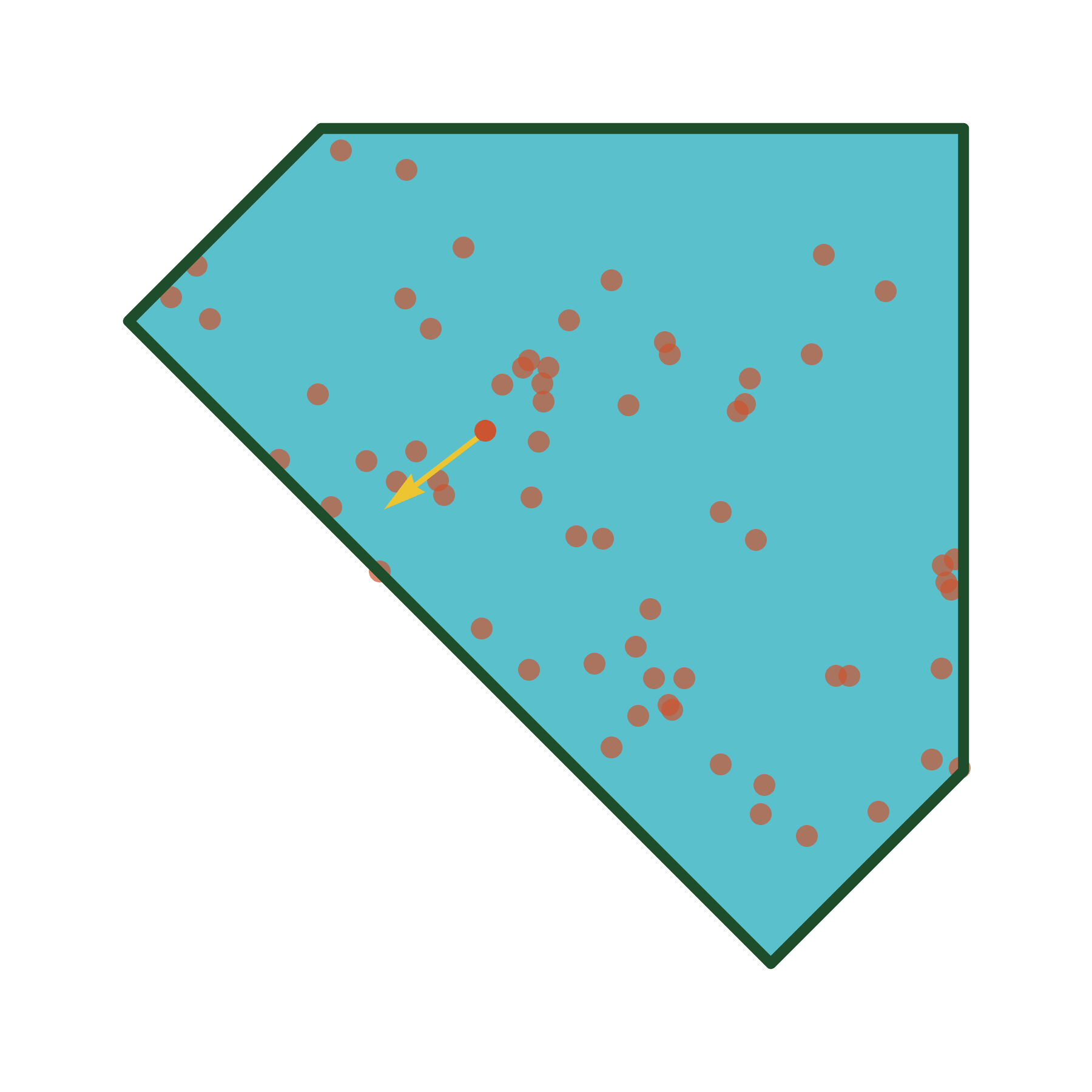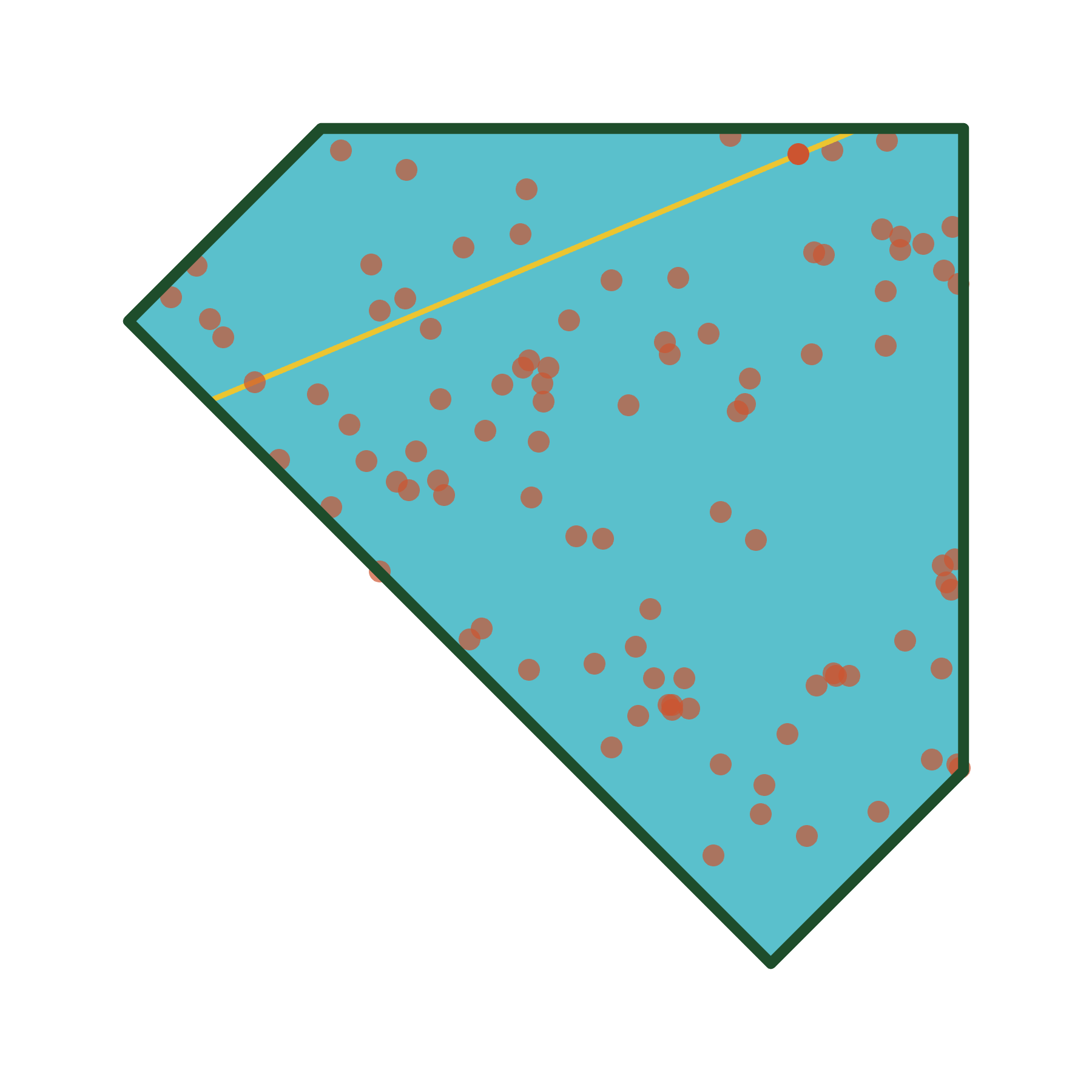
Simulations

Algorithm (w/ Cantarella)

A uniformly ergodic Markov chain for simulating random equilateral \(n\)-gons in rooted spherical confinement (implemented in plCurve).

More generally, a uniformly ergodic Markov chain for simulating random points from any toric symplectic manifold.

Strategy

Generate trillions of random polygons in tight confinement and look for new examples.

Pipeline

plCurve

vertices

PD code

HOMFLY

SnapPy

Hyperbolic volume

pyknotid

check for uniqueness

(Knot ID, vertices)

Verification for New Bounds

KnotPlot

DT code

KnotInfo’s

KnotFinder

Knot ID

vertices

Exact stick numbers

Theorem [with Eddy]

The stick number of each of the knots \(9_{35}\), \(9_{39}\), \(9_{43}\), \(9_{45}\), and \(9_{48}\) is exactly 9.

Corollary

Each of the knots \(9_{35}\), \(9_{39}\), \(9_{43}\), \(9_{45}\), and \(9_{48}\) has superbridge index equal to 4.

\(9_{35}\)

\(9_{39}\)

\(9_{43}\)

\(9_{45}\)

\(9_{48}\)

Proof.

\(\operatorname{b}(K) < \operatorname{sb}(K) \leq \frac{1}{2} \operatorname{stick}(K)\) and each of these knots has bridge index 3.

Proof.

The stick number is bounded below by 9, and we found 9-stick examples.

Theorem [with Eddy]

The equilateral stick number of each of the knots \(9_2\), \(9_3\), \(9_{11}\), \(9_{15}\), \(9_{21}\), \(9_{25}\), \(9_{27}\), \(10_8\), \(10_{16}\), \(10_{17}\), \(10_{56}\), \(10_{83}\), \(10_{85}\), \(10_{90}\), \(10_{91}\), \(10_{94}\), \(10_{103}\), \(10_{105}\), \(10_{106}\), \(10_{107}\), \(10_{110}\), \(10_{111}\), \(10_{112}\), \(10_{115}\), \(10_{117}\), \(10_{118}\), \(10_{119}\), \(10_{126}\), \(10_{131}\), \(10_{133}\), \(10_{137}\), \(10_{138}\), \(10_{142}\), \(10_{143}\), \(10_{147}\), \(10_{148}\), \(10_{149}\), \(10_{153}\), and \(10_{164}\) is less than or equal to 10.

The equilateral stick number of each of the knots \(10_3\), \(10_6\), \(10_7\), \(10_{10}\), \(10_{15}\), \(10_{18}\), \(10_{20}\), \(10_{21}\), \(10_{22}\), \(10_{23}\), \(10_{24}\), \(10_{26}\), \(10_{28}\), \(10_{30}\), \(10_{31}\), \(10_{34}\), \(10_{35}\), \(10_{38}\), \(10_{39}\), \(10_{43}\), \(10_{44}\), \(10_{46}\), \(10_{47}\), \(10_{50}\), \(10_{51}\), \(10_{53}\), \(10_{54}\), \(10_{55}\), \(10_{57}\), \(10_{62}\), \(10_{64}\), \(10_{65}\), \(10_{68}\), \(10_{70}\), \(10_{71}\), \(10_{72}\), \(10_{73}\), \(10_{74}\), \(10_{75}\), \(10_{77}\), \(10_{78}\), \(10_{82}\), \(10_{84}\), \(10_{95}\), \(10_{97}\), \(10_{100}\), and \(10_{101}\) is less than or equal to 11.

The equilateral stick number of each of the knots \(10_{76}\) and \(10_{80}\) is less than or equal to 12.

In particular, all knots up to 10 crossings have equilateral stick number \(\leq 12\).

Stick number bounds

Theorem [with Eddy, —]

The equilateral stick number of each of the knots \(9_2\), \(9_3\), \(9_{11}\), \(9_{15}\), \(9_{18}\), \(9_{21}\), \(9_{25}\), \(9_{27}\), \(10_8\), \(10_{16}\), \(10_{17}\), \(10_{18}\), \(10_{56}\), \(10_{68}\), \(10_{82}\), \(10_{83}\), \(10_{84}\), \(10_{85}\), \(10_{90}\), \(10_{91}\), \(10_{93}\), \(10_{94}\), \(10_{100}\), \(10_{103}\), \(10_{105}\), \(10_{106}\), \(10_{107}\), \(10_{110}\), \(10_{111}\), \(10_{112}\), \(10_{115}\), \(10_{117}\), \(10_{118}\), \(10_{119}\), \(10_{126}\), \(10_{131}\), \(10_{133}\), \(10_{137}\), \(10_{138}\), \(10_{142}\), \(10_{143}\), \(10_{147}\), \(10_{148}\), \(10_{149}\), \(10_{152}\), \(10_{153}\), and \(10_{164}\) is less than or equal to 10.

The equilateral stick number of each of the knots \(10_3\), \(10_6\), \(10_7\), \(10_{10}\), \(10_{15}\), \(\sout{10_{18}}\), \(10_{20}\), \(10_{21}\), \(10_{22}\), \(10_{23}\), \(10_{24}\), \(10_{26}\), \(10_{28}\), \(10_{30}\), \(10_{31}\), \(10_{34}\), \(10_{35}\), \(10_{38}\), \(10_{39}\), \(10_{43}\), \(10_{44}\), \(10_{46}\), \(10_{47}\), \(10_{50}\), \(10_{51}\), \(10_{53}\), \(10_{54}\), \(10_{55}\), \(10_{57}\), \(10_{58}\), \(10_{62}\), \(10_{64}\), \(10_{65}\), \(10_{66}\), \(\sout{10_{68}}\), \(10_{70}\), \(10_{71}\), \(10_{72}\), \(10_{73}\), \(10_{74}\), \(10_{75}\), \(10_{77}\), \(10_{78}\), \(10_{79}\), \(10_{80}\), \(\sout{10_{82}}\), \(\sout{10_{84}}\), \(10_{95}\), \(10_{97}\), \(\sout{10_{100}}\), and \(10_{101}\) is less than or equal to 11.

The equilateral stick number of each of the knots \(10_{76}\) and \(\sout{10_{80}}\) is less than or equal to 12.

In particular, all knots up to 10 crossings have equilateral stick number \(\leq 12\).

Stick number bounds

\(10_{16}\)

\(10_{84}\)

Higher-crossing knots

Theorem [with Blair, Eddy, and Morrison]

The knots \(13n_{592}\) and \(15n_{41,127}\) have bridge index 4, superbridge index 5, and stick number 10.

\(13n_{592}\)

\(15n_{41,127}\)

Proof.

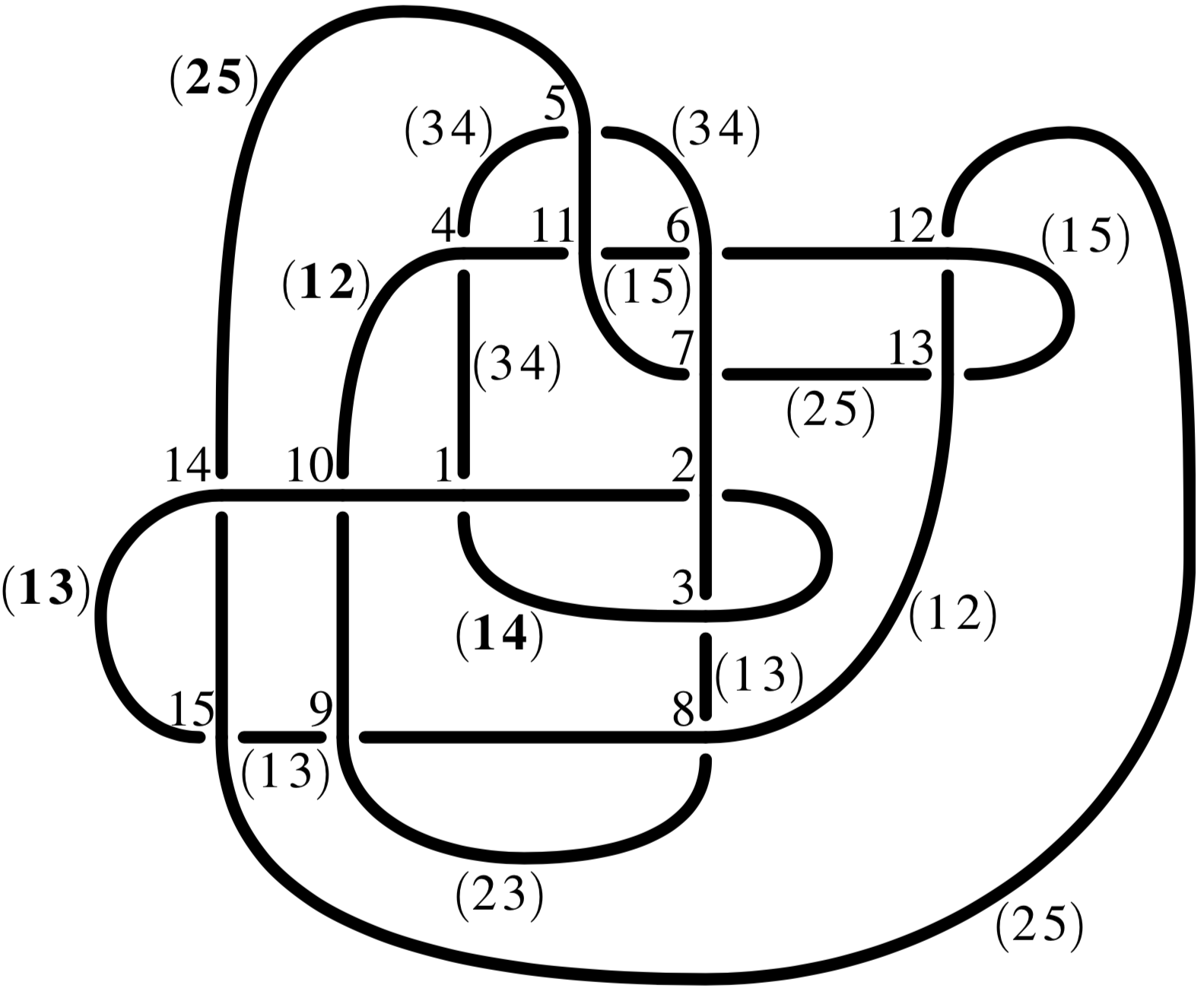
Surjective homomorphism \(\pi_1(S^3 \backslash 15n_{41,127}) \to S_5\), so

\(4 \leq \operatorname{b} < \operatorname{sb} \leq \frac{1}{2}\operatorname{stick} \leq 5\).

\(15n_{41,127}\)

\(\overline{13n_{592}}\)

Superbridge indices

Theorem [—]

The knots \(8_1\), \(8_2\), \(8_3\), \(8_5\), \(8_6\), \(8_7\), \(8_8\), \(8_{10}\), \(8_{11}\), \(8_{12}\), \(8_{13}\), \(8_{14}\), \(8_{15}\), \(9_7\), \(9_{16}\), \(9_{20}\), \(9_{26}\), \(9_{28}\), \(9_{32}\), and \(9_{33}\) all have superbridge index equal to 4.

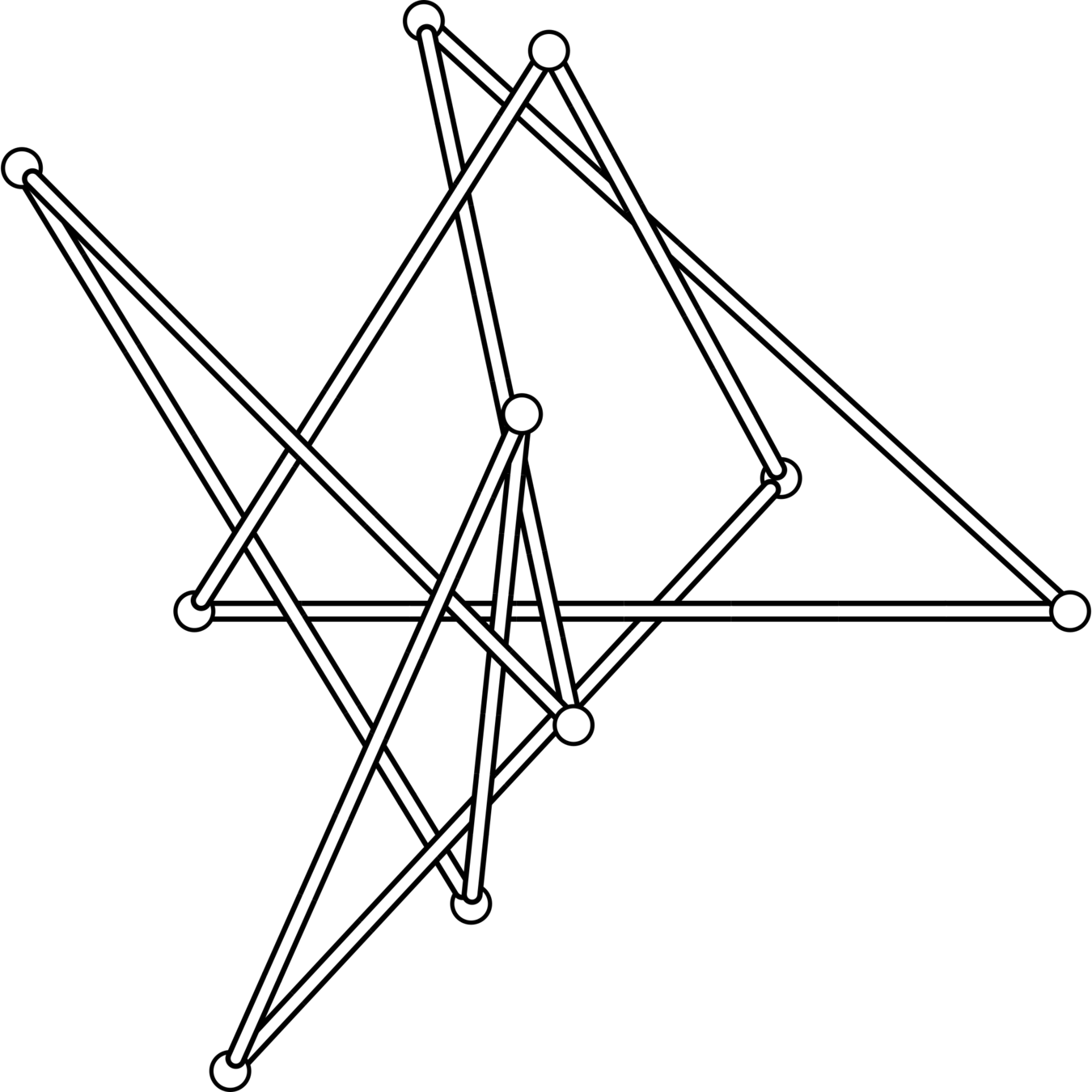
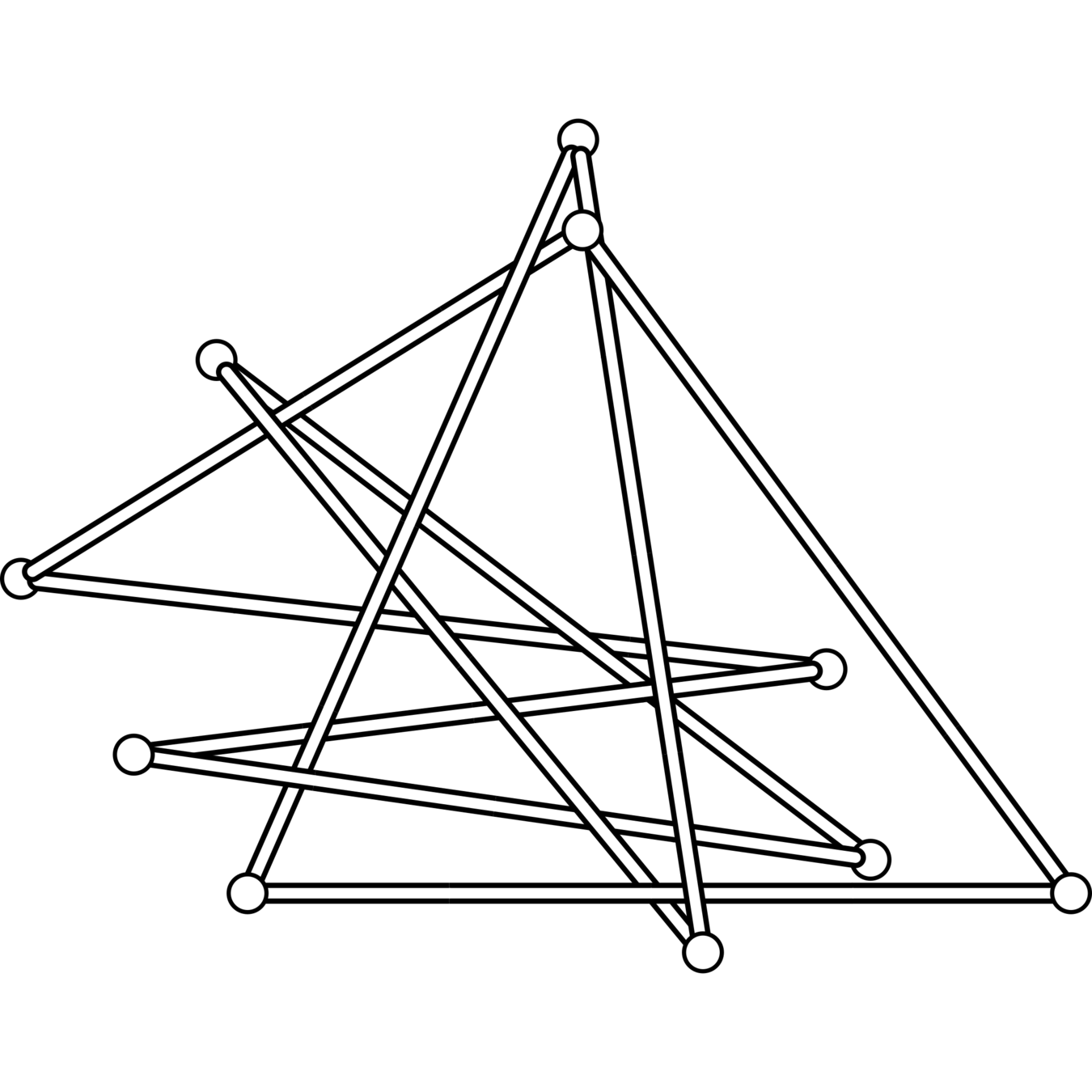
\(8_{10}\)

\(9_7\)

Proof.

For each knot, \(4 \leq \mathrm{sb}[K]\leq \frac{1}{2}\mathrm{stick}[K] \leq 5\).

If \(\mathrm{sb} = 5\) for a 10-stick realization, then there exists \(v\in S^2\) so that

\(v^T [e_1 | -e_2 | \cdots | -e_{10} ] \)

has all positive entries. By Gordan’s theorem, this system of linear inequalities is feasible if and only if

\([e_1 | -e_2 | \cdots | -e_{10}] u = 0\)

cannot be solved for a nonzero vector u with nonnegative entries.

Theorem [—]

The knots \(9_3\), \(9_4\), \(9_6\), \(9_9\), \(9_{11}\), \(9_{13}\), \(9_{17}\), \(9_{18}\), \(9_{22}\), \(9_{23}\), \(9_{25}\), \(9_{27}\), \(9_{30}\), \(9_{31}\), and \(9_{36}\) all have superbridge index equal to 4.

Stick numbers for 11-crossing knots

Theorem [in progress]

All prime knots through 11 crossings have stick number \(\leq 13\).

Proof.

I found explicit equilateral examples of all but four 11-crossing knots.

The four missing were \(11a_{175}, 11a_{176}, 11a_{220}, 11a_{306}\), which are all 2-bridge knots, and hence have stick number \(\leq 13\) by a result of Hu–No–Oh.

There are 85 11-crossing knots for which the best bound on stick number is 13: all of these are alternating.

Superbridge index through 11 crossings

Corollary.

All prime 11-crossing knots have \(\operatorname{sb}[K] \leq 6\).

Theorem [—]

All prime knots through 10 crossings have \(\operatorname{sb}[K]\leq 5\).

Proof.

The only 10-crossing knots which could potentially have stick number 12 are \(10_{37}\) and \(10_{76}\).

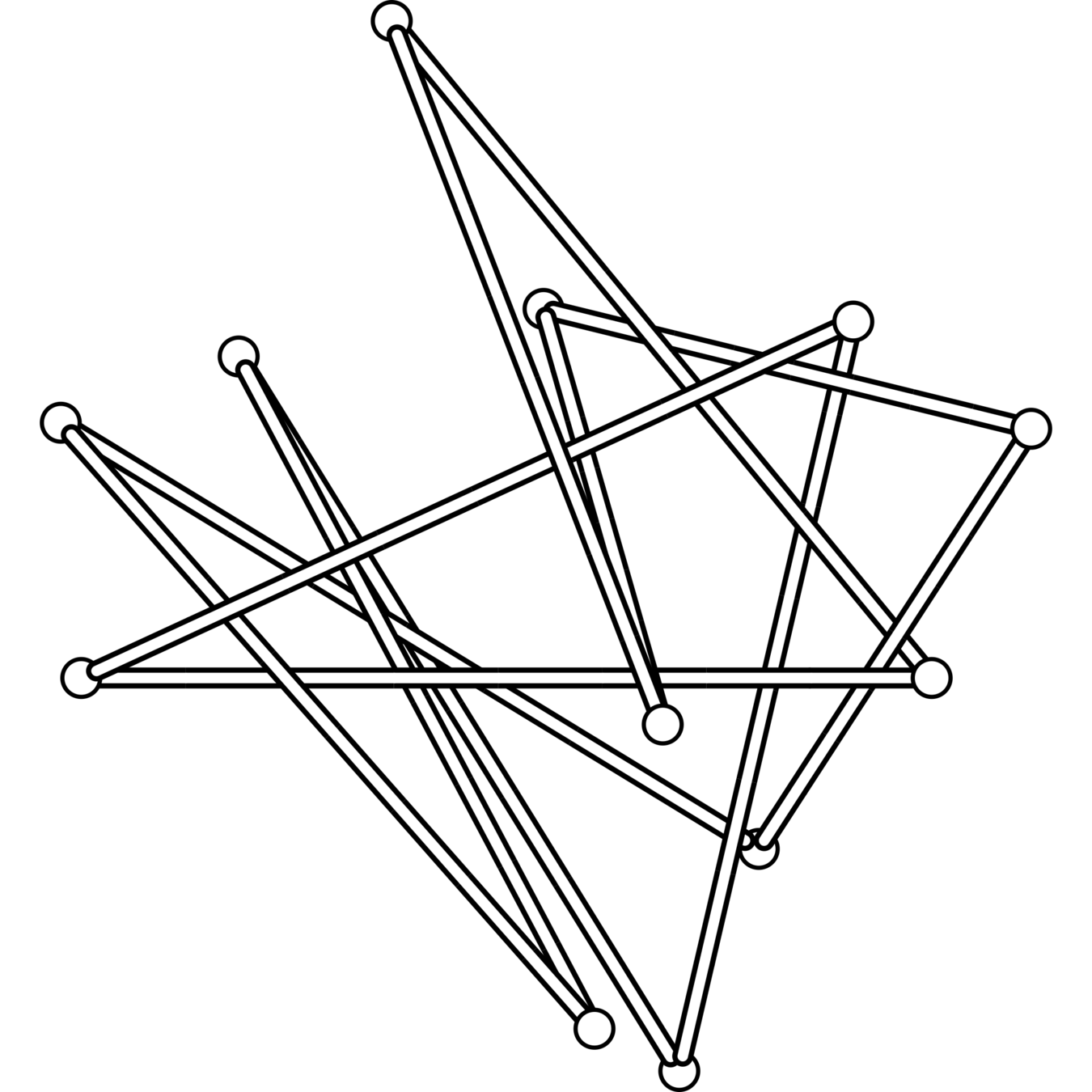
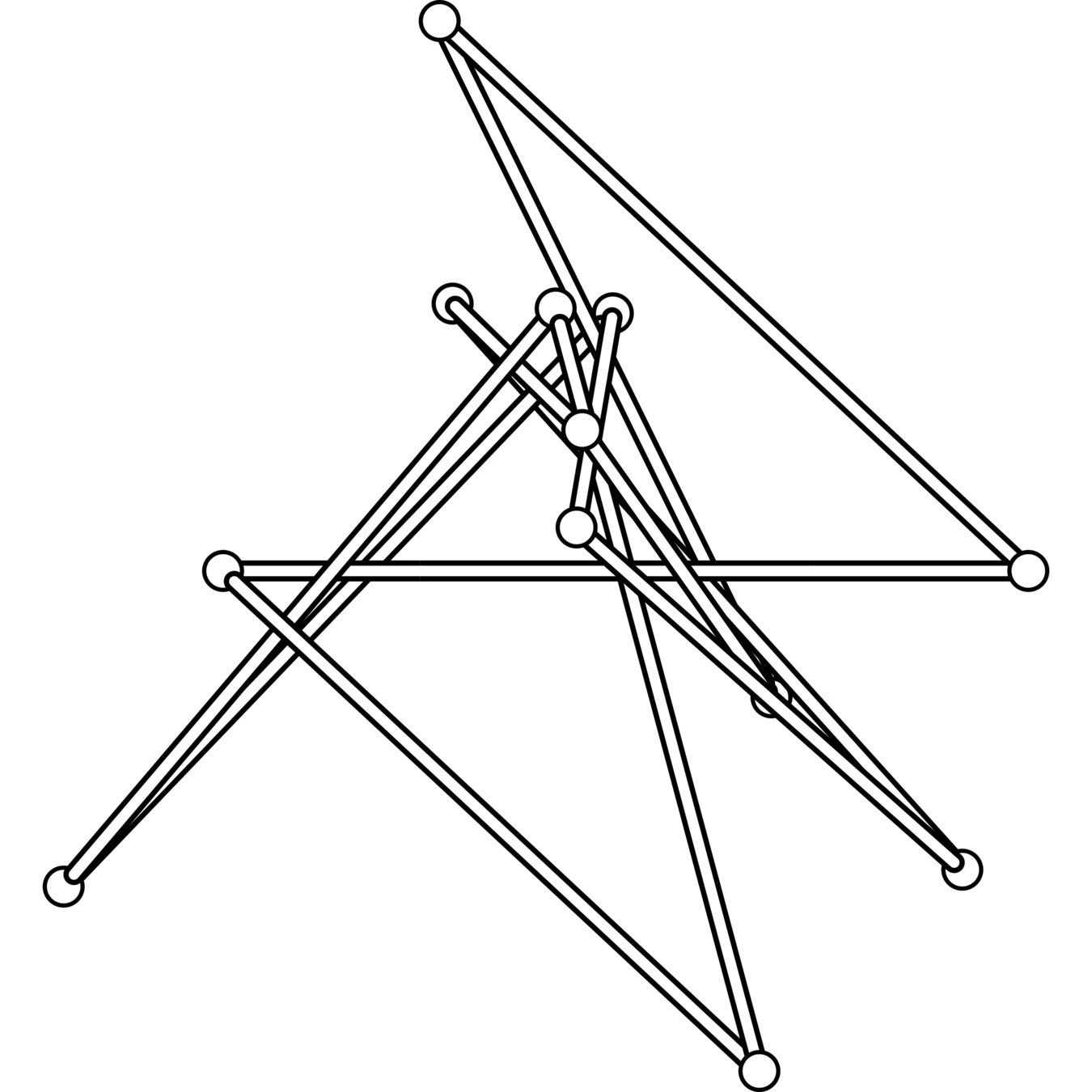
\(10_{37}\) (cf. Adams et al.)

\(10_{76}\)

Tables and code

Tables of best current stick number and superbridge index bounds in our papers…

…or on Github, along with source code!

Results have also been added to KnotInfo

Conjectures

Conjecture.

For all knots \(K\) with \(c[K]\geq 6\), \(\operatorname{stick}[K] \leq c[K]+2\).

True for 2-bridge knots [Hu–No–Oh], and for \((p,q)\) torus knots with \(2\leq p < q < 3p\) [Adams et al., Jin, Bennett, Adams and Shayler, Johnson et al]. Best general bound is due to Hu–Oh: \(\operatorname{stick}[K] \leq \frac{3}{2}(c[K]+1)\).

Conjecture.

For all knots \(K\) with \(c[K] \geq 7\), \(\operatorname{sb}[K] \leq \lceil\frac{c[K]}{2}\rceil\).

True for torus knots [Kuiper]. Best general bound follows from Huh & Oh’s stick number bound: \(\operatorname{sb}[K] \leq \frac{3}{4}(c[K]+1)\).

Conjecture.

Stick number and equilateral stick number are distinct invariants.

\(\operatorname{stick}[9_{29}]=9\), \(\operatorname{eqstick}[9_{29}]\leq 10\); this is the only example I know where the bounds don’t agree.

Tiny but suggestive data on satellites

Satellite	DT name	stick no. bound
Trefoil[–1/2]	K14n22180	12
Trefoil[1/2]	K14n26039	12
Trefoil[–3/2]	K15n59184	12
Trefoil[3/2]	K15n115646	12
Trefoil[–1]	K13n4587	13
Trefoil[1]	K13n4639	13
Trefoil[–3]	K15n40211	13
Trefoil[3]	K15n124802	13
Trefoil[–5]	K17ns12	13
Trefoil[5]	K17ns1	13