Stiefel Manifolds and Polygons
/linz2019
This talk!
Questions
- How to generate random triangles?
- What are optimal paths between triangles?
- How does this generalize to \(n\)-gons?

Wallpaper, joint with Anne Ligon Harding

Isometries

Frame from Nucleation
Lewis Carroll’s Pillow Problem #58
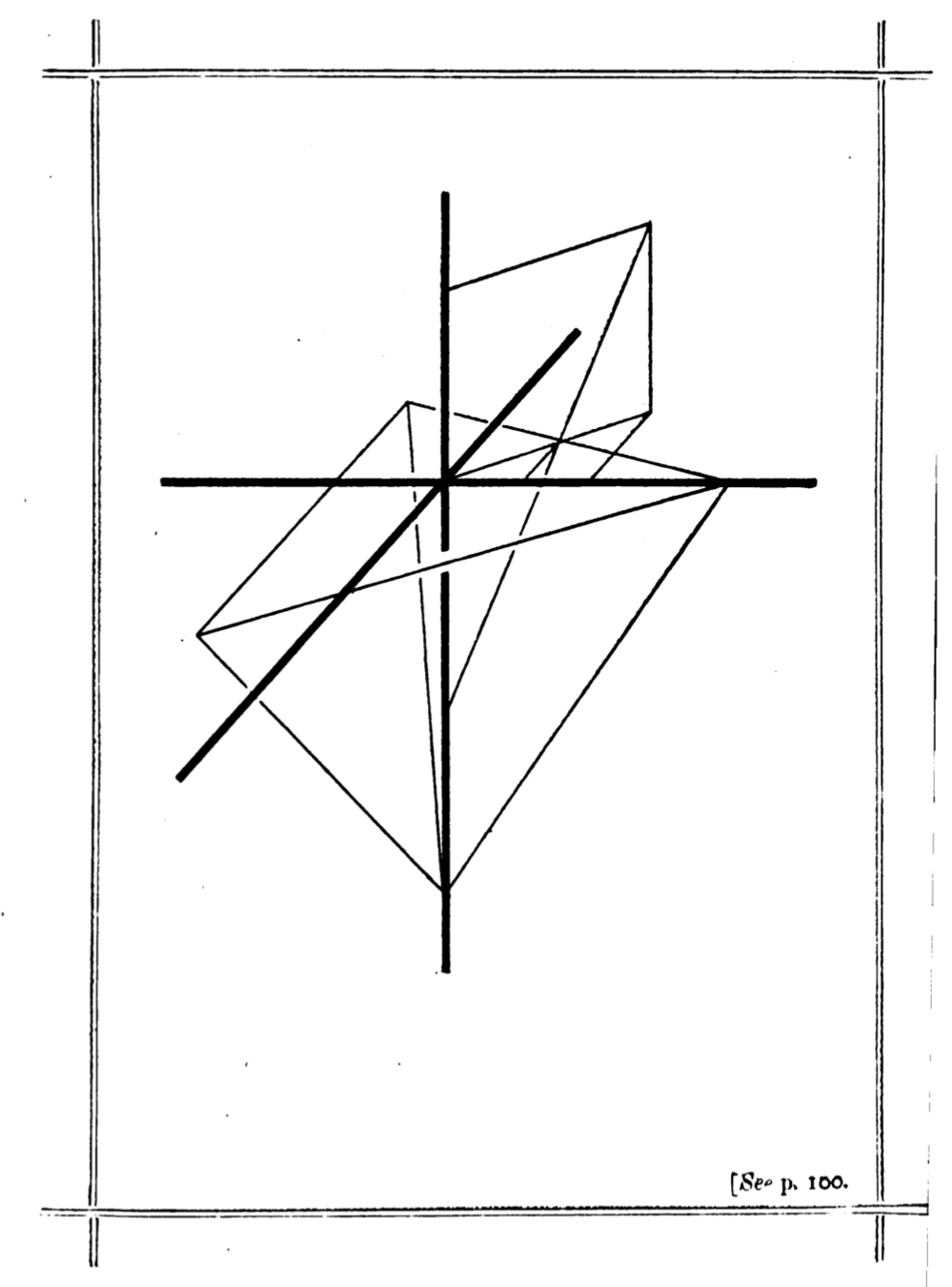


Earlier versions
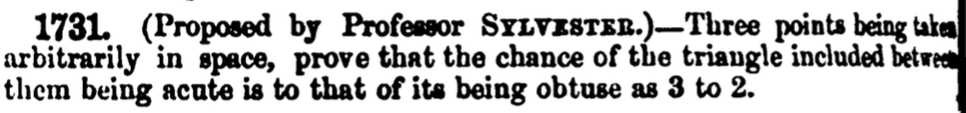

W. S. B. Woolhouse, Educational Times 18 (1865), p. 189
J. J. Sylvester, Educational Times 18 (1865), p. 68

W. S. B. Woolhouse, The Lady's and Gentleman's Diary 158 (1861), p. 76
J.J. Sylvester, Educational Times, April 1864
Sylvester’s four point problem

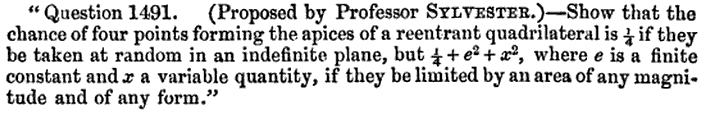
Stiefel manifolds and polygons
Let \(e_1, \ldots , e_n\) be the edges of a planar \(n\)-gon with total perimeter 2. Choose \(z_1, \ldots , z_n\) so that \(z_k^2 = e_k\). Let \(z_k = u_k + i v_k\).
The polygon is closed \(\Leftrightarrow e_1 + \ldots + e_n = 0\)
\(\sum e_k =\sum z_k^2 = \left(\sum u_k^2 - \sum v_k^2\right) + 2i \sum u_k v_k\)
The polygon is closed \(\Leftrightarrow \|\vec{u}\|=\|\vec{v}\|\) and \(\vec{u} \bot \vec{v}\)
Since \(\sum |e_k| = \sum u_k^2 + \sum v_k^2 = \|\vec{u}\|^2 + \|\vec{v}\|^2\), we see that \((\vec{u},\vec{v})\) is an orthonormal pair of vectors in \(n\)-dimensional space; the collection of such things is called the Stiefel manifold \(\mathrm{St}_2(\mathbb{R}^n)\).

Sampling the Stiefel manifold is super-easy!
StiefelSample[n_]:=Orthogonalize[RandomVariate[NormalDistribution[],{2,n}]]
560 random quadrilaterals
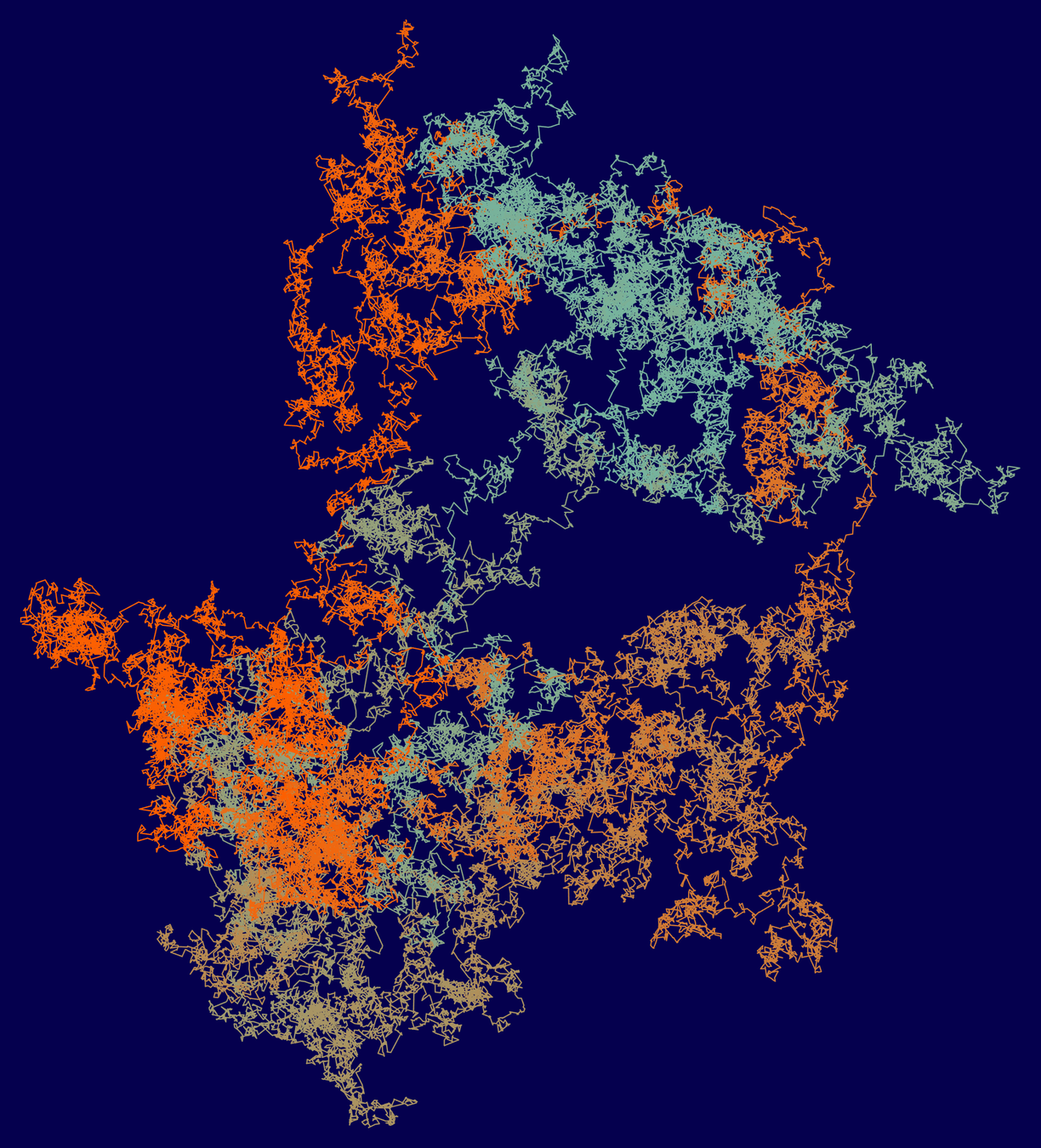
A random 100,000-gon
If you prefer your polygons convex…
Convexify[edges_] := SortBy[edges, PositiveArg[Complex @@ #] &];Permuting edges is an isometry of the Stiefel manifold, so this produces a uniform random sample of convex \(n\)-gons.
Random convex 20-gons

Polygon morphs are paths in the Stiefel manifold



A to Z, in the art exhibition

Polygons in 3D
\(n\)-gons in \(\mathbb{R}^3\) are parametrized by points in \(\mathrm{St}_2(\mathbb{C}^n)\), and we can do exactly the same sorts of things…

36 random 16-gons
Re-Tie



Framed Polygons
More precisely, points in \(\operatorname{St}_2(\mathbb{C}^n)\) map to framed polygons.




Framing
Thank you!
Funding: Simons Foundation
This talk: math.graphics/linz2019
References
Random triangles and polygons in the plane
Jason Cantarella, Tom Needham, Clayton Shonkwiler, and Gavin Stewart
The American Mathematical Monthly 126 (2019), 113–134
Probability theory of random polygons from the quaternionic viewpoint
Jason Cantarella, Tetsuo Deguchi, and Clayton Shonkwiler
Communications on Pure and Applied Mathematics 67 (2014), 1658–1699